2. 南京工业大学 计算机与信息工程学院, 南京 211816;
3. 南京信息工程大学 江苏省大气环境与装备技术协同创新中心, 南京 210044;
4. 南京信息工程大学 电子与信息工程学院, 南京 210044
2. College of Computer and Information Engineering, Nanjing Tech University, Nanjing 211816, China;
3. Jiangsu Collaborative Innovation Center on Atmospheric Environment and Equipment Technology, Nanjing University of Information Science and Technology, Nanjing 210044, China;
4. School of Electronics and Information Engineering, Nanjing University of Information Science and Technology, Nanjing 210044, China
随着自动驾驶技术的发展, 同时定位与地图构建技术(simultaneous localization and mapping, SLAM)已成为近些年的研究热点. SLAM的主要目标是在运动中利用携带传感器的移动平台, 实现自主定位, 并逐步对周围环境进行建图[1,2]. 目前, 无人车通常搭载多种传感器[3], 包括激光雷达、惯性测量单元、视觉相机和全球定位系统. 与其他传感器相比, 激光雷达在障碍物检测、高精度的距离测量和对光照纹理不敏感等方面具有突出优势, 因此, 以激光雷达为传感器的激光SLAM算法在自动驾驶领域具有非常广阔的应用前景[4].
基于特征的点云匹配方法主要涉及提取点云中的线、面特征, 随后对这些特征点云进行匹配. Zhang等[5]提出的LOAM (LiDAR odometry and mapping)为目前广泛使用的激光SLAM算法框架, 该算法使用了基于特征的匹配方法最近点迭代法(iterative closest point, ICP). ICP算法的核心是最小化点与点之间的距离, 然而在激光SLAM中雷达是处于运动状态的, 并非每一处点云都有匹配点, 且计算所有点云会带来过高的计算复杂度. 因此LOAM算法中对其进行了改进, 将原点云中的点与待配准点云中提取出的直线与平面特征点进行匹配, 极大地减少了计算量, 在结构化场景下有很好的效果, 但在非结构化场景下会因特征难以提取而表现不佳. 后来, Shan等[6]对LOAM进行轻量化的优化并增加后端优化模块, 引入地面特征, 通过提取地面点的平面特征以及非地面点的线条特征, 过滤掉无关的噪点, 有效减少了特征点的数量, 从而提高了点云匹配的精度和效率[7]. 文献[5,6]提出的基于特征的激光SLAM算法可以减少点云规模并利用同类点之间配准来提高定位精度, 但由于对特征的强依赖性, 使得系统在处理社区、街道等开放的非结构化环境中会因为难以提取可靠稳定的特征而出现退化问题, 并且没有能够根据场景结构的不同切换对应的点云匹配算法.
因此, 为了减少对特征的强依赖性, 一系列的基于概率分布与数学优化的激光SLAM方法被提出. 文献[8]提出的HDL_GRAPH_SLAM用基于数学优化的正态分布变换(normal distribution transform, NDT)进行点云匹配, 使用高斯分布模型来重新构建点云, 但其需要对点云数据进行事先的网格化处理[9], 导致计算复杂度高, 影响了点云匹配的效率. 文献[10]提出的相干点漂移算法CPD将一个点集看作是由一个概率密度函数生成的样本, 然后利用高斯混合模型来描述这个概率密度函数, 通过期望最大化算法来求解最优变换矩阵, 从而实现点云对齐. 能够处理非刚性变形、遮挡、噪声等问题, 并且在配准精度上也有一定的优势, 可以有效地运用于非结构化场景中. 但其需要通过期望最大化算法来求解最优变换矩阵, 计算复杂度高. 因此将CPD与ICP结合形成优势互补, 可以提高点云配准的精度和效率. 文献[11]提出了一种自适应的匹配方法, 当所提取的特征数量充足时, 该方法采用基于特征的匹配方法; 而当提取到的特征数量不足时, 则切换至基于概率分布的算法进行匹配. 然而, 仅凭特征数量无法准确区分场景结构, 因为特征的数量除了和场景的结构有关外, 还受到雷达的扫描线束以及点云重叠程度、场景几何特征等因素的影响. 此外, 基于数学优化的算法计算量大, 影响系统的实时性. 为了平衡系统的精度和实时性, 文献[12]提出了一种将NDT与ICP结合的算法, 该算法在使用ICP进行精细配准之前, 先添加NDT进行预配准, 有效地满足了系统的实时性, 但由于缺少对场景结构进行识别, 并根据不同的场景使用合适的高效算法, 难以适应开放复杂的实际应用场景.
综上所述, 为了能够在复杂场景下保证SLAM系统的精度和效率, 本文提出了一种联合CPD面向复杂场景的自适应激光SLAM算法CPD-LOAM. 首先根据场景结构的不同, 提出了场景特征变量(scene feature variable, SFV)的概念对场景结构进行初步判断, 并从几何特征的角度利用表面曲率进行验证, 来增强对场景结构辨识的准确性. 此外, 在非结构化场景下添加CPD算法进行点云预配准来解决该场景下难以提取可靠稳定的特征而出现退化的问题, 然后使用ICP算法进行点云再配准来提高SLAM系统的精度. 通过这种智能化的自适应机制, 可以避免将CPD算法应用于结构化场景, 有效减少配准过程中的误差和计算量, 提高点云配准的精度和效率, 有效地适应了场景的复杂多变.
1 CPD-LOAM算法原理为了解决传统激光SLAM算法无法正确区分场景结构并且在面对非结构化场景时会因为特征难以提取而失效的问题, 本文提出了场景特征变量与表面曲率用于判断和验证场景结构, 进而自适应地选择是否添加CPD进行点云预配准来解决非结构化场景下特征提取不佳的问题, 以适应场景的复杂多变. 算法框架如图1所示, 主要分为点云的特征提取、帧间匹配scan-to-scan配准和后端优化scan-to-map配准3个阶段.
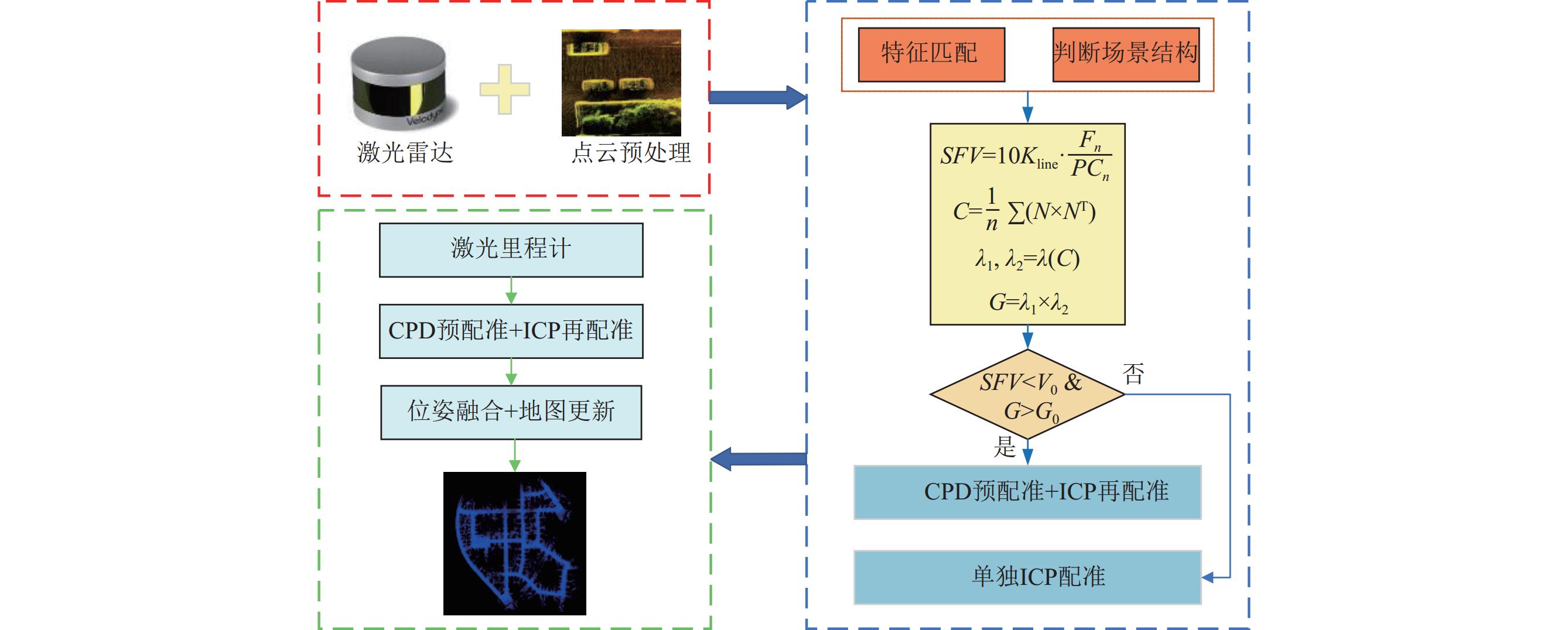
|
图 1 CPD-LOAM算法框架 |
在点云的特征提取阶段, 通过对原始激光数据进行运动去畸变和离群点移除操作, 将处理后的数据作为特征点云输出, 用于后续的点云配准算法中. 在帧间匹配scan-to-scan配准阶段, 通过提取出来的特征点云进行帧间匹配, 首次迭代时需要对场景结构进行判断, 计算场景特征变量SFV, 并通过验证表面曲率G来区分场景结构, 若为非结构化场景则需使用CPD算法来进行点云的预配准来解决特征的退化问题并为ICP算法提供良好初值以增加点云匹配的准确性. 第2次迭代则使用LOAM中的ICP算法, 因为ICP算法在精细配准方面表现良好, 它通过迭代寻找最近的点对来优化匹配结果, 但容易受到初始位置、噪声和离群点的影响, 在非结构化场景下表现不佳. 而CPD算法则在处理高噪声和离群点的情况时更加稳定和鲁棒, 通过最大化点云间的概率一致性来找到匹配, 对初始位置不太敏感. 所以在第1次迭代之后ICP算法有了良好初值, 第2次迭代则直接使用ICP算法即可. 然后更新参考帧的点云信息, 并通过当前帧与上一帧的匹配得到激光里程计数据. 在后端优化scan-to-map配准阶段, 先通过CPD算法进行点云预配准, 然后使用ICP算法进行点云再配准, 以便于更好地纠正里程计的漂移, 从而输出全局地图, 保证了地图的全局完整性.
1.1 特征提取由于点云数据会包含噪音与离群点[13–15], 对后续的算法处理产生干扰和误差, 并且点云数据非常庞大, 大规模点云数据在进行复杂算法处理时会消耗大量的计算资源, 因此需要去除离群点和减少数据量来提高计算准确性和效率. 本文通过对原始激光数据进行离群点移除以及体素滤波下采样操作, 将处理后的数据作为特征点云输出, 用于后续的点云配准算法当中.
1.1.1 离群点去除为了消除离群点对点云匹配算法产生的误差与干扰, 从激光雷达接收点云数据之后, 估计出每个点采集的时刻雷达所处的位置, 然后将一帧内所有点变换到统一坐标系下[16,17]. 当帧间运动估计完成后, 用该估计进行时间插值, 获得每个点所在采集时刻的雷达位姿, 从而将点云都转换到统一坐标系下. 每个点采集时刻的估计位姿采用线性插值实现, 设
| Tk−1,i=tk−1,i−tk−1tk−tk−1 ⋅ Tk−1 | (1) |
其中,
本文采用体素滤波的方法来减少计算资源的损耗, 将原始点云数据划分为小的边长为0.6 m的立方体单元, 每个立方体单元即为一个体素, 对于每个体素, 选择离体素中心最近的点作为采样点[18]. 将选择出的采样点组合起来, 形成新的点云数据.
1.2 帧间匹配scan-to-scan为了能够在复杂场景下正确区分场景结构, 本文提出一种基于预判和验证相结合的场景结构辨识方法, 首先引入场景特征变量, 对场景结构进行初步判断, 然后从几何特征角度通过表面曲率对其进行验证. 并且在非结构化场景下引入CPD算法进行点云预配准来解决特征提取不佳而退化的问题, 从而有效地适应场景结构的复杂多变. 帧间匹配阶段首次迭代时计算场景特征变量SFV, 并通过验证表面曲率G决定是否使用CPD算法来进行点云的预配准. 第2次迭代则使用LOAM中的ICP算法, 然后更新参考帧的点云信息, 并通过当前帧与上一帧的匹配得到激光里程计数据.
1.2.1 CPD算法在面对非结构化场景时, 由于特征难以提取会出现退化, 因此需要添加CPD算法进行点云的预配准. CPD算法的基本思想是通过最大化概率密度函数来估计点云之间的配准变换. 给定两个点集
| P(xn)=(1−ω)M∑m=11Mp(xn∣yn)+ω1N | (2) |
当点集Y中
| p(xn∣ym)=1(2πσ2)D/2e−‖xn−ym‖22σ2 | (3) |
其中, x是参考点云, y是待配准点云, n、m分别为点集X、Y的规模,
混合高斯模型的中心在配准过程中与变换参数
| E(θ,σ2)=−N∑n=1logM+1∑m=1P(ym)p(xn∣ym) | (4) |
由于变换参数
ICP算法的核心思想是通过最小化点云之间的距离来实现配准, 计算简便且精度较高, 然而在初始值不精确时会收敛到局部极值[19]. 因此在CPD算法进行点云预配准得到最佳变换矩阵后, 将其作为ICP算法的位姿初始值进行再配准, 从而避免ICP算法陷入局部极值. 本文采用传统LOAM算法中ICP的配准方式, 利用点云中的线特征或面特征进行匹配. 在进行匹配时, 我们通过迭代的方式来优化残差, 其中残差是由点到线或点到面的距离构造而成的[20].
原点云中的边缘点到目标点云中的边缘线、原点云中的平面点到目标点云中的平面的距离计算公式如下:
| dedge=|(ˆXL(k+1,i)−XL(k,j))×(ˆXL(k+1,i)−XL(k,l))||XL(k,j)−XL(k,l)| | (5) |
| dplane=|(ˆXL(k+1,i)−XL(k,j)) ⋅ [(XL(k,j)−XL(k,l))×(XL(k,j)−XL(k,m))]||(XL(k,j)−XL(k,l))×(XL(k,j)−XL(k,m))| | (6) |
其中, j, k, l, m为其在相应边缘点与平面点的集合中的特征标识,
将式(5)、式(6)构建的两个距离函数约束统一为:
| lossR,t[∑ˆXL(k+1,i)dedge,∑ˆXL(k+1,i)dplane] | (7) |
其中, R, t为当前帧与上一帧的相对位姿变换. 这样, 就可以把问题转换为求距离函数统一后的最小化的问题:
| R,t=argminR,t12Fn∑i=1‖lossR,t[∑ˆXL(k+1,i)dedge,∑ˆXL(k+1,i)dplane]‖2 | (8) |
其中,
CPD算法可以很好地应对非结构化场景, 但其需要通过期望最大化算法来求解最优变换矩阵, 计算代价高. 而在结构化场景下使用ICP算法进行配准可以提高系统运行的效率与精度, 二者结合可以形成优势互补. 因此, 为了将对应的算法应用到合适的场景中, 对于场景结构的判断尤其重要. 场景结构判断的流程图如图2所示.
由于特征的数量不仅与场景的结构相关, 同时还与激光雷达的扫描线束以及点云重叠程度、场景几何特征相关, 而原始的点云特征提取仅仅依靠特征的数量多少来区分场景结构, 这样是不准确的. 所以为了增加对场景结构判断的准确性, 本文使用了基于预判和验证相结合的场景结构辨识方法, 把每一帧点云配准算法之前的特征匹配的总数与其对应帧点云的数量的比值, 再将这个比值乘以十倍的激光雷达的线束构成场景特征变量SFV. 在进行首次迭代计算场景特征变量SFV之后, 需要计算当前帧的表面曲率G并通过判断场景几何特征对场景进行验证. SFV的计算公式为:
| SFV=10Kline⋅FnPCn | (9) |
其中,

|
图 2 场景结构判断流程 |
除了用SFV对场景结构进行初步判断外, 本文还结合表面曲率对其进行验证来提高对场景结构判断的准确性. 在每帧激光扫描下采样程度相同以及机器人的运动速度恒定的情况下, 理论上存在一个阈值
| C=1n∑(N×NT),λ1,λ2=λ(C) | (10) |
| G=λ1×λ2 | (11) |
其中, N为所计算点云P的法线方向向量, n表示最近邻点的数量,
当SFV小于
由于里程计累积误差的存在, 当前扫描帧的估计位姿与实际位姿之间存在较大偏差[21], 这会导致ICP算法匹配的初始值过大, 从而无法成功达到收敛状态. 而CPD算法收敛域较广, 因此在后端优化阶段首先使用CPD算法进行初步的非刚性形变配准, 然后再使用ICP算法进行精细的刚性变换优化. 通过组合这两种算法, 可以充分利用它们各自的优势, 有利于更好地纠正里程计的漂移, 提高点云配准的效率和精度. 最后将输出的位姿进行融合并更新, 最后输出轨迹和全局地图, 为后续的路径规划以及导航任务提供支持.
2 实验与分析为了评估算法的精度和效率, 本文进行了大量公共数据集实验和真实环境下的实车测试[22]. 实验平台为具有16 GB运行内存, 硬件环境为Intel i7处理器, 操作系统环境为Ubuntu 20.04, ROS (机器人操作系统)版本为noetic的个人笔记本电脑, 激光雷达为velodyne的16线雷达. 通过与LOAM, LeGO-LOAM, LIO-SAM算法对比, 来验证CPD-LOAM算法的精度和效率.
2.1 算法耗时分析正常情况下雷达扫描频率为5–20 Hz, 为了满足算法的实时性要求, 前端scan-to-scan帧间匹配算法的执行时间是不能超过100 ms的. 图3为无人车搭载velodyne 16线激光雷达在4种不同的点云配准算法下的匹配时间随着雷达扫描帧的变化数据, 录制的场景为室内结构化场景. 其中ICP和CPD是单独的点云配准算法, LOAM为原始算法, CPD-LOAM为本文提出的算法.

|
图 3 4种算法点云配准时间 |
图3很明显看出, 单独的点云配准算法ICP和CPD平均耗时均达到100 ms以上, 超时严重, 无法满足算法的实时性. ICP算法在点云精细配准方面表现良好, 但容易受到初始位置和噪声的影响, 且在寻找对应点时可能会产生较大的计算量, 特别是在非结构化场景的点云数据以及大规模点云数据中. 而CPD算法通过最大化点云间的概率一致性来找到匹配, 对初始位置不太敏感, 可以减少在寻找最近点时的计算复杂度. 两种算法均需要经历多次迭代, 所以耗时高. 结合使用ICP和CPD时, 先通过CPD进行预配准, 为ICP提供一个较好的初始位置, 然后利用ICP进行再配准, 两者形成优势互补, 从而减少整体的迭代次数和计算时间. 图3中可以看出, CPD-LOAM算法由于结合了ICP和CPD, 耗时最短, 可以满足实时性要求.
2.2 场景特征变量以及表面曲率效果验证本文选用室内图书馆结构化场景和室外社区非结构化场景来验证场景特征变量和表面曲率对于区分场景结构的可行性, 各场景的SFV以及表面曲率G随雷达扫描帧的变化如图4所示. 其中Library为图书馆室内结构化场景, 路径中大多都是规则形的桌椅、图书柜等; 而Community为社区室外非结构化场景, 包含了大量的建筑物以及树木草地等. 图4(a)显示, 结构化场景的SFV是明显超过非结构化场景的, 进而表明了SFV在初步区分场景的效果, 并且阈值在3.5–4.0之间. 图4(b)说明了表面曲率在验证结构化与非结构化场景时效果尤其明显, 图书馆室内结构化场景的表面曲率G接近于0, 而社区室外非结构化场景的表面曲率G在4.4左右, 表面曲率在结构化与非结构化场景中区分尤其明显, 证明了表面曲率验证场景结构的有效性.
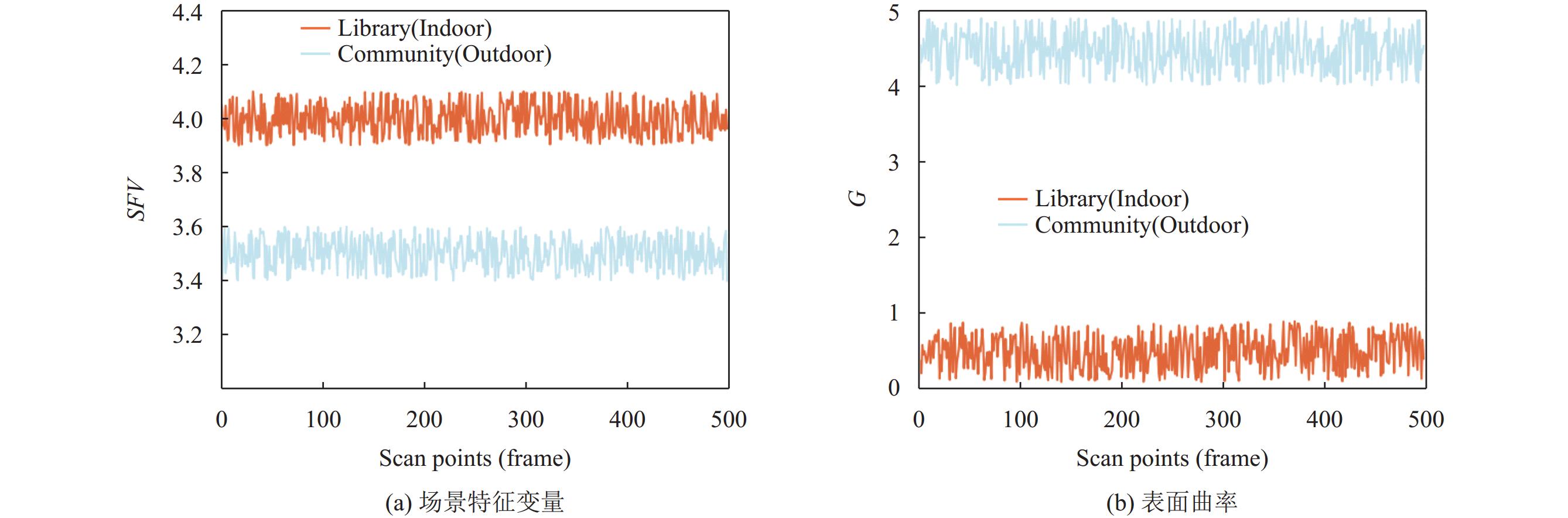
|
图 4 场景特征变量以及表面曲率效果验证 |
为了找到合适的阈值作为判断条件来区分场景结构, 本文通过线性插值的方法, 不断地调整
|
表 1 绝对位姿误差随阈值 |
2.3 定位与建图实验分析
为了验证CPD-LOAM算法定位与建图的精度以及鲁棒性, 本文首先将CPD-LOAM与LOAM进行对比, 再与经典的激光SLAM算法LeGO-LOAM, LIO-SAM对比, 采用了KITTI数据集的00序列进行实验, KITTI数据集包含了采集自乡村、城市和高速公路等多个场景的真实数据, 而00序列为大范围的城市环境, 包含大量的建筑物、树木与汽车, 同时也存在较多分岔路口、颠簸道路与直道, 结构化与非结构化场景交替混合, 对于算法稳定性的验证具有极高的可靠性. CPD-LOAM算法与LOAM算法的轨迹相对于KITTI地面真值轨迹的对比如图5所示.
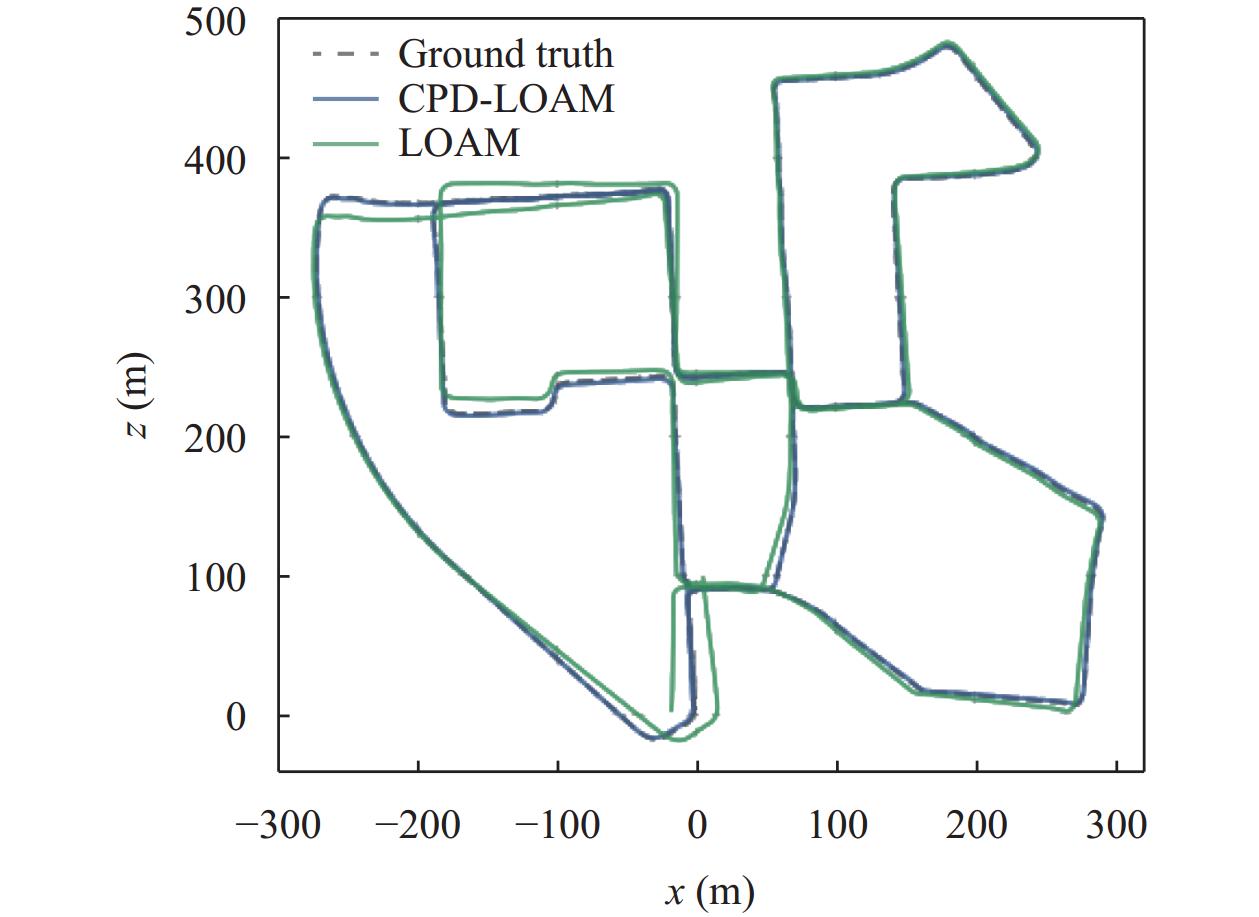
|
图 5 CPD-LOAM与LOAM算法的轨迹对比 |
从图5中可以很直观地看出, CPD-LOAM算法的轨迹与地面真值更加贴近. 通过表2进行分析, LOAM算法的轨迹均方根误差为8.472 m, CPD-LOAM算法的轨迹均方根误差为1.316 m, 定位精度提升了84.47%, 说明CPD-LOAM算法的精度远高于LOAM算法.
| 表 2 各算法绝对轨迹误差对比 (m) |
图6为CPD-LOAM与LeGO-LOAM、LIO-SAM在KITTI00序列数据集下的轨迹对比, 根据局部细节放大可以看出, CPD-LOAM算法轨迹最贴合地面真值, 表现最好, 其次是LeGO-LOAM, LIO-SAM效果相对较差, 因为该场景下道路较为颠簸, 车辆会产生震动以及多传感器的时间戳不同步, 因此00序列下的IMU数据表现不稳定, 易发生缺失与跳变, 而CPD-LOAM在这种情况下仍能够很好地完成定位与建图, 具有更高的鲁棒性. 结合表2和图7中可以看出, CPD-LOAM算法的轨迹均方根误差相较于传统LOAM算法以及LeGO-LOAM、LIO-SAM算法, 有明显降低, 相较LeGO-LOAM算法降低了55.88%, 相较LIO-SAM算法降低了30.52%.

|
图 6 CPD-LOAM、LeGO-LOAM、LIO-SAM算法轨迹对比 |
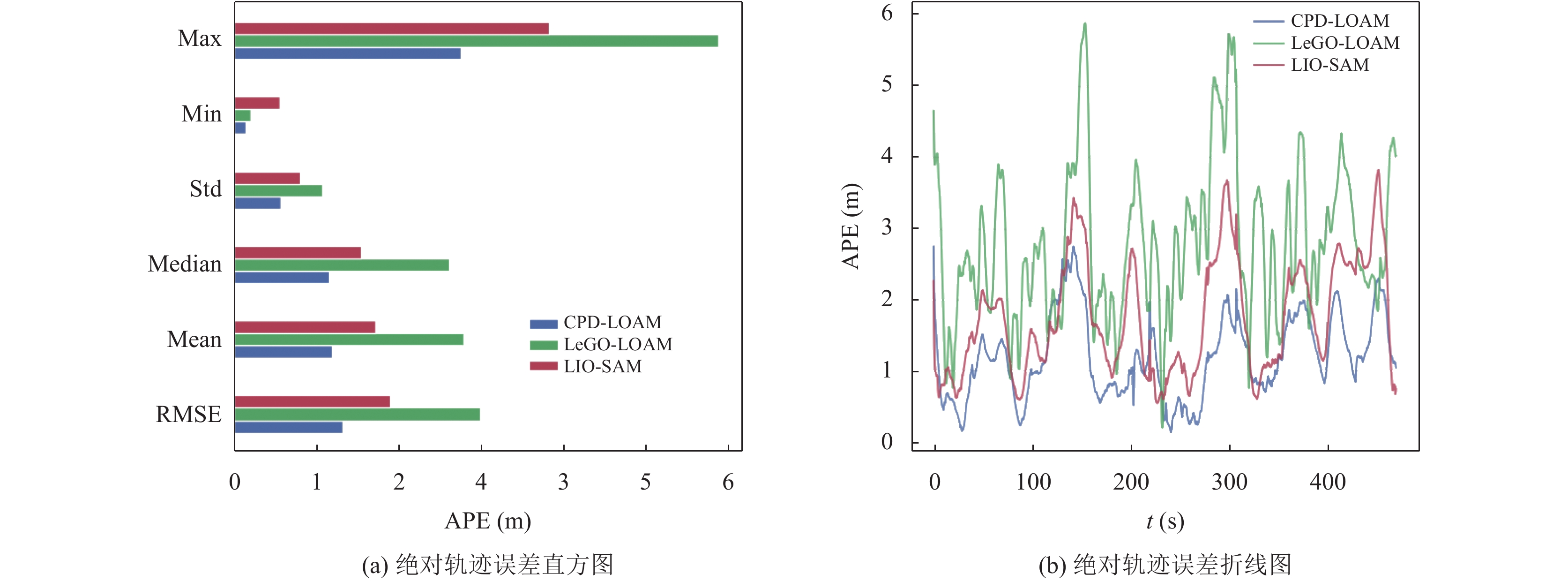
|
图 7 CPD-LOAM、LeGO-LOAM、LIO-SAM算法绝对位姿误差对比图 |
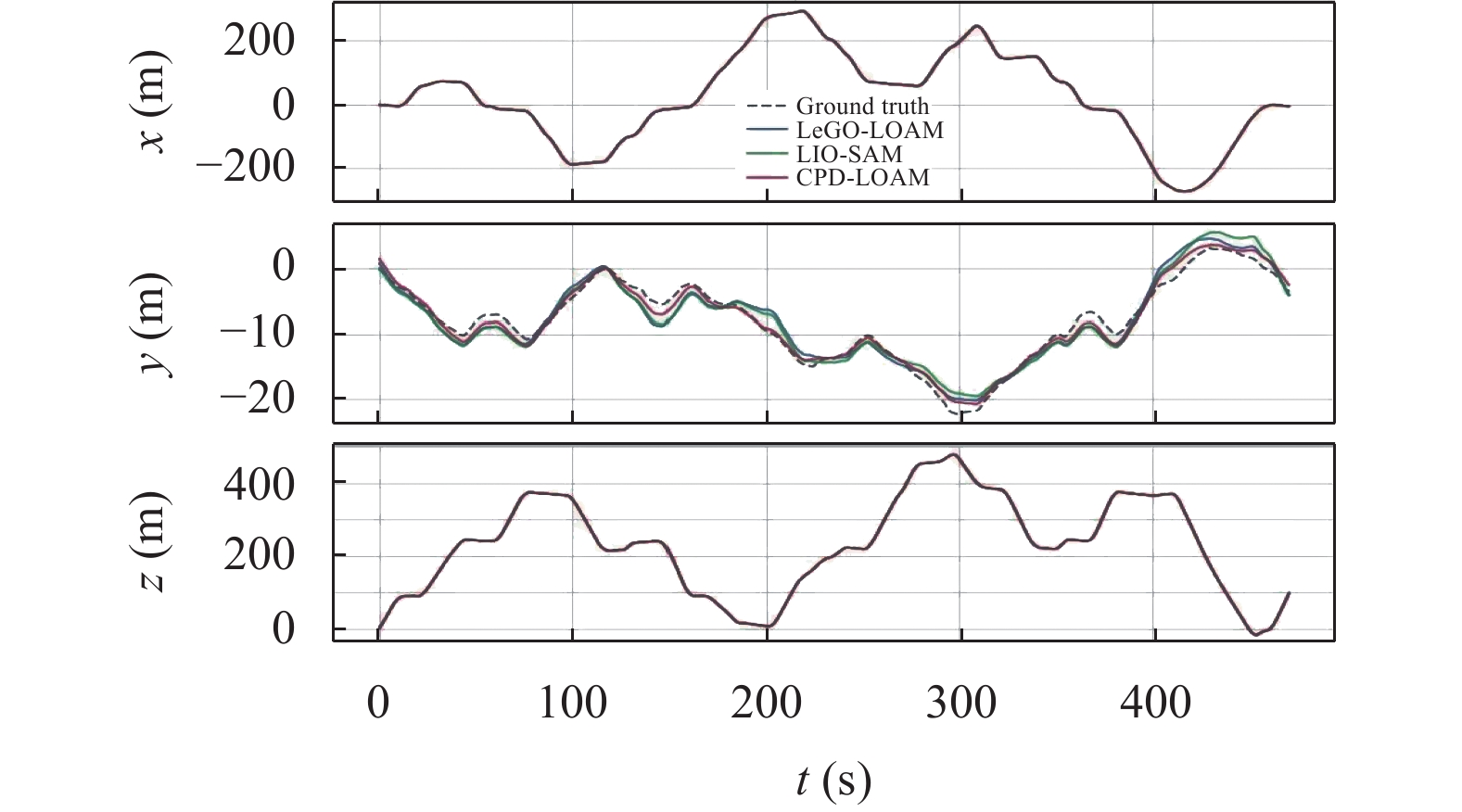
LeGO-LOAM、LIO-SAM和CPD-LOAM的三轴轨迹对比图如图8所示, 可以看出, 3种算法的轨迹在x和z轴上与真值最为接近, 而在y轴上有一定差异, 这与00序列的道路颠簸以及遮挡物较多有关. LeGO-LOAM由于采取了地面约束以及点云分割, 因此在平坦的道路上表现良好, 在颠簸的道路上会产生偏差. LIO-SAM由于在00序列下车辆的颠簸、震动以及多传感器的时间戳不同步, IMU的数据会产生丢失和跳变, 无法获得足够准确的惯性信息来获取车辆在低频运动下的状态和姿态, 从而导致误差累积. 而CPD-LOAM由于在非结构化场景下会引入CPD配准算法, 可以很好地适应非刚性的形变与遮挡问题, 通过建立概率模型和最大似然估计进行优化, 从而实现点云的对齐, 具有更高的精度和鲁棒性.
图9为CPD-LOAM与LOAM、LeGO-LOAM以及LIO-SAM算法在KITTI00序列下的建图结果, 可以看出CPD-LOAM算法的地图全局完整性明显优于其他两个算法, 未发生严重漂移. 在局部的分岔路口也可以看出, CPD-LOAM算法的树木、车辆等点云更为真实, 不会出现模糊不清与重影的情况.
|
图 8 CPD-LOAM、LeGO-LOAM、LIO-SAM三轴轨迹图 |

|
图 9 4种算法在KITTI数据集中的点云地图 |
3 结论
针对传统激光SLAM算法在面对复杂场景时无法区分场景结构, 并且在非结构化场景下会因为难以提取可靠稳定的特征而出现退化的问题, 本文提出一种联合CPD面向复杂场景的自适应激光SLAM算法. 首先引入场景特征变量的概念对场景结构进行初步判断, 然后从几何特征的角度利用表面曲率对其进行验证, 来提高对场景结构辨识的准确性. 此外, 根据辨识出的场景结构自适应地添加CPD点云配准算法来解决非结构化场景下特征退化的问题. 通过这种智能化的自适应机制, 可以有效减少配准过程中的误差和计算量, 提高点云配准的精度和效率, 从而有效地适应场景结构的复杂多变. 最后在KITTI数据集进行实验的验证, 实验结果表明: CPD-LOAM算法相较于传统LOAM算法, 定位精度提升了84.47%, 和LeGO-LOAM、LIO-SAM相比, 精度、效率以及鲁棒性也得到了更好地提升, 能够很好地适应复杂场景.
| [1] |
Fan YC, Zhang QC, Tang YL, et al. Blitz-SLAM: A semantic SLAM in dynamic environments. Pattern Recognition, 2022, 121: 108225. DOI:10.1016/j.patcog.2021.108225 |
| [2] |
傅强, 蒋雪薇, 成鹏. 低光照下的无人机异物检测与定位. 计算机系统应用, 2024, 33(2): 151-158. DOI:10.15888/j.cnki.csa.009400 |
| [3] |
王彬, 章浙涛, 何秀凤. 结合正态分布变换与线面ICP的弹性激光SLAM算法. 武汉大学学报(信息科学版), 2024, 49(4): 672-680. |
| [4] |
Li HS, Tian BL, Shen HM, et al. An intensity-augmented LiDAR-inertial SLAM for solid-state LiDARs in degenerated environments. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 8503610. |
| [5] |
Zhang J, Singh S. LOAM: LiDAR odometry and mapping in real-time. Proceedings of the 2014 Robotics Science & Systems Conference. Berkeley, 2014. 2–9.
|
| [6] |
Shan TX, Englot B. LeGO-LOAM: Lightweight and ground-optimized LiDAR odometry and mapping on variable terrain. Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Madrid: IEEE, 2018. 4758–4765.
|
| [7] |
Shan TX, Englot B, Meyers D, et al. LIO-SAM: Tightly-coupled LiDAR inertial odometry via smoothing and mapping. Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Las Vegas: IEEE, 2020. 5135–5142.
|
| [8] |
Koide K, Miura J, Menegatti E. A portable three-dimensional LiDAR-based system for long-term and wide-area people behavior measurement. International Journal of Advanced Robotic Systems, 2019, 16(2): 1729881419841532. [doi: 10.1177/1729881419841532]
|
| [9] |
Xu W, Cai YX, He DJ, et al. FAST-LIO2: Fast direct LiDAR inertial odometry. IEEE Transactions on Robotics, 2022, 38(4): 2053-2073. DOI:10.1109/TRO.2022.3141876 |
| [10] |
Myronenko A, Song XB. Point set registration: Coherent point drift. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(12): 2262-2275. DOI:10.1109/TPAMI.2010.46 |
| [11] |
Mohamed H, Moussa A, Elhabiby M, et al. A novel real-time reference key frame scan matching method. Sensors, 2017, 17(5): 1060. DOI:10.3390/s17051060 |
| [12] |
王庆闪, 张军, 刘元盛, 等. 基于NDT与ICP结合的点云配准算法. 计算机工程与应用, 2020, 56(7): 88-95. DOI:10.3778/j.issn.1002-8331.1904-0174 |
| [13] |
徐晓苏, 高佳誉, 周帅, 等. 基于改进GICP配准的激光-惯性SLAM算法. 中国惯性技术学报, 2023, 31(8): 814-822. |
| [14] |
Wei X, Lv JX, Sun J, et al. GCLO: Ground constrained LiDAR odometry with low-drifts for GPS-denied indoor environments. Proceedings of the 2022 International Conference on Robotics and Automation (ICRA). Philadelphia: IEEE, 2022. 2229–2235.
|
| [15] |
朱朔凌, 毛建旭, 王耀南, 等. 基于惯性导航角度补偿的室内激光SLAM方法. 电子测量与仪器学报, 2019, 33(3): 1-7. |
| [16] |
李荣华, 祁宇峰, 谢辉, 等. 面向未知环境的紧耦合激光SLAM方法. 红外与激光工程, 2023, 52(9): 20220839. |
| [17] |
尹胜楠, 崔学荣, 李娟, 等. 基于快速ACE算法的视觉里程计图像增强方法. 电子测量与仪器学报, 2021, 35(6): 27-33. |
| [18] |
郑川川, 柯福阳, 汤琴琴. 基于图优化的激光惯导紧耦合SLAM研究. 电子测量技术, 2023, 46(1): 35-42. |
| [19] |
许宇伟, 颜文旭, 吴炜. 相似场景下基于局部地图的激光SLAM前端算法改进. 机器人, 2022, 44(2): 176-185. |
| [20] |
付林, 郑佳楠, 何洪磊, 等. 面向大型室内场景的无人机三维激光雷达解耦SLAM方法. 电子测量技术, 2022, 45(13): 96-103. |
| [21] |
孙晓明, 宋滢. 紧耦合的移动端实时位姿优化方法. 计算机系统应用, 2022, 31(2): 207-212. DOI:10.15888/j.cnki.csa.008328 |
| [22] |
李志强, 朱明. 基于SuperPoint的轻量级特征点及描述子提取网络. 计算机系统应用, 2021, 30(11): 310-316. DOI:10.15888/j.cnki.csa.008191 |
 2024, Vol. 33
2024, Vol. 33



