作为生命体的基本结构和功能单位, 细胞储存着大量的生物信息. 在细胞的生长发育过程中, 诸多因素使得细胞转录信息趋向多样化, 激发了生物组织内细胞异质性的发生[1]. 近年来, 高通量测序技术[2]不断发展, 通过细胞的分子生物学特征识别细胞类型成为可能. 与传统批量测序(bulk-seq)技术[3]相比, 单细胞测序技术[4]允许在单一细胞层面下对基因组、转录组及表观组进行分析, 能准确呈现单细胞的基因构建及其表达状况, 从而揭示细胞间的异质性. 单细胞RNA测序技术(scRNA-seq)是单细胞测序技术的重要发展方向[5], 对单个细胞的转录组进行测序, 能够掌握每个细胞的变化, 探索基因调控机制, 发现新的细胞类型, 揭示复杂的生物学关联与过程.
scRNA-seq技术的核心应用在于鉴定和表征细胞群体, 这通常需要通过细胞聚类来完成. 然而由于技术的不完善以及生物体本身的复杂多变性[6] (如测序深度浅, 捕获率低, 批次效应, 细胞状态变化等), 导致 scRNA-seq 数据整体呈现出高维度、高噪声、高变异性、高稀疏性和高度不平衡的特征, 这给传统的聚类方法带来了极大的挑战, 迫切需要研究新的方法.
针对scRNA-seq数据的聚类方法得到了广泛的研究, 目前已经有大量的相关工作. 早期的聚类方法主要使用传统的机器学习技术. pcaReduce[7]使用 K-means聚类, 并结合 PCA 来进行降维, 识别簇相应的主成分并构建簇之间层次关系. Kiselev 等人提出了算法 SC3[8], 该算法对多种不同度量方法下的细胞距离矩阵数据应用 PCA 和拉普拉斯变换进行降维, 之后对所有主成分进行K-means聚类, 最后对所有的结果进行聚类集成. SIMLR[9]提出使用多个内核来学习样本相似性并在相似性矩阵上执行谱聚类. 为了发现和利用数据中的结构关系, 一些方法尝试用图来描述 scRNA-seq数据, 细胞作为节点, 而边则代表细胞之间的关联性, 之后采用图聚类算法进行聚类. 2015 年, Xu等人提出了一种基于准团(clique)的聚类方法 SNN-Cliq[10], 能够发现稀疏数据中的紧凑簇. SNN-Cliq 首先在细胞上构建共享最近邻居图, 之后在图上采用准团检测来识别细胞群体. Seurat[11]也使用共享最近邻居图来描述细胞之间的相似度, 并利用基于图的社区检测算法Louvain[12]对共享最近邻网络进行分割并生成不相交的聚类.
尽管这些方法采用各种手段实现了对scRNA-seq数据的聚类, 但是其所使用模型的固有表达能力往往有限, 导致模型在各种不同组织, 不同平台和不同规模的数据[13]上的泛化能力不足.
近年来, 深度学习技术发展迅速, 其灵活强大的计算模型使其展现出相比于传统机器学习技术更优异的性能, 在包括计算生物学在内的各个学科领域中得到了广泛的应用[14,15]. 目前, 在scRNA-seq数据分析领域已经有了许多的基于深度学习的方法实践[16].
为了处理 scRNA-seq 数据中普遍存在的丢失事件(dropout events), Eraslan 等人提出了一个深度计数自编码器模型 DCA[17]. 该模型把零膨胀的负二项分布模型(ZINB)[18]与自编码器结构结合起来, 使用 ZINB分布的负对数似然作为训练损失, 而不是传统的均方误差(mean square error)重构损失, 有效地实现了 scRNA-seq 数据的去噪和特征表示, 并在此基础上进行聚类. 深度嵌入聚类(DEC)[19]是一个基于自编码器的聚类模型, 它使用学生 t分布(student’s t-distribution)对聚类分布进行建模, 将原分布和目标分布之间的KL散度(Kullback-Leibler divergence)作为聚类损失, 该损失能直接地为聚类任务优化特征表示, 并且由此实现了特征表示和聚类分配的同步优化. Tian等人提出的模型 scDeepCluster[20]是对方法DCA和DEC的结合与优化, 一方面使用去噪的 ZINB自编码器, 获得鲁棒的数据表示; 另一方面, 采用和DEC类似的聚类损失, 直接为聚类任务优化特征表示. scziDesk[21]在scDeepCluster的基础上做了进一步的优化, scziDesk采用加权的软K-means 算法进行聚类, 并在聚类过程中添加了成对的亲和力约束. 以上这些方法采用自编码器学习细胞的编码表示, 相比传统方法, 能得到更有意义的特征, 但是它们往往只针对基因表达信息(细胞与基因的关系)进行建模, 并未考虑细胞与细胞之间的结构关系信息, 这可能会影响类簇识别的准确性.
图神经网络(graph neural network, GNN)[22]是深度学习领域目前热门的研究方向, 这主要得益于其在处理非结构化非欧氏空间的数据上的巨大优势. 此外, 传统的深度学习的一个核心假设是数据样本之间彼此独立, 然而实际的数据当中往往可能之间存在各种联系, 图神经网络能够充分利用图结构中所描述的节点与节点的关系信息, 这些结构关系信息将有助于模型学习到更深层次的数据特征. 就 scRNA-seq 数据而言, 由于测序的细胞往往来自同一个组织或器官, 细胞之间保持独立的可能性不大, 细胞间的关系是值得关注的重要信息. 为了利用细胞与细胞之间的关系信息, 一些研究开始在scRNA-seq数据上构建相应的图结构, 并使用图神经网络进行建模. scGNN[23]首先使用一个特征自编码器获取细胞的特征表示, 并由此构建细胞-细胞图, 经过一个图自编码器以捕捉细胞之间的关系信息, 并使用特定于细胞类型的聚类自编码器帮助模型发现细胞类别相关的信息. GraphSCC[24]通过使用图卷积神经网络把细胞之间的结构关系整合到 scRNA-seq 聚类中, 它还利用双重自监督模块对细胞进行聚类并指导训练过程. Li等人提出的ScGSLC[25]是一个基于图相似性学习的单细胞聚类框架, 它将scRNA-seq数据和蛋白质-蛋白质相互作用网络有效整合成一个图, 使用图卷积网络对图进行嵌入, 并计算图之间的相似性来聚类细胞. scDSC[26]通过K近邻(KNN)算法构建细胞-细胞图, 利用图神经网络以更好地捕捉细胞之间的关系信息, 结合基于ZINB模型的自编码器模块学习基因的表达模式. scGAC[27]应用网络去噪改善构建的细胞图, 然后通过图注意力自编码器学习细胞表示, 该编码器以不同的权重传递细胞间信息, 捕捉细胞间潜在的关系, 最后以自优化方法确定细胞簇. Yu等人提出了一个针对scRNA-seq 数据的深度图嵌入聚类方法 scTAG[28], 该方法使用多核卷积拓扑图神经网络(TAGCN)利用图重构学习细胞的低维特征表示, 并在此基础上执行深度聚类. 这些方法的实践展现出引入细胞之间的关系信息对于聚类任务的重要性, 但是scRNA-seq数据具有高维稀疏, 高噪声的特点, 在此基础上计算得到的细胞之间的图结构可能质量较低, 存在较多噪声, 从而影响最终的聚类结果.
在自监督学习中, 对比学习是一种简明且有效的学习范式, 近年来发展迅速, 在自然语言处理, 计算机视觉等领域已经得到了广泛的研究与应用[29–32], 成为学习词句或图像表示的有效方法. 对比学习要义在于识别同类实例的共同属性和鉴别异类实例的差异性, 其核心目标是训练一个编码器, 该编码器能够为同类数据生成相似的编码, 而为不同类数据生成差异较大的编码. 在大量的实验中, 对比学习展现出优异的性能, 有时甚至优于有监督的方法[33]. 对比学习在处理scRNA-seq数据方面同样有着独特优势, 一方面其特性与聚类任务相适应, 另一方面, 与基于重构的特征学习方法相比, 对比学习只需在特征空间中对样本进行比较, 这在一定程度上部分规避了原始数据中的稀疏性和噪声的影响. Contrastive-sc[34]是一种新颖的针对scRNA-seq 数据的对比学习聚类方法, 通过掩蔽一定比例的数据特征来获得增广数据. 与大多数对比学习的实践做法类似, 该方法将来自同一个原始样本的两个增广样本视为正样本, 而将所有其他样本对视为负样本. Wan 等人提出的scNAME[35]方法改进了传统的对比损失, 提出了一种新的邻域对比损失, 将正样本的范围扩大到邻域, 同时结合一个辅助的掩码估计任务, 更好地描述了特征之间的相关性和细胞的成对相似性. 借鉴经典对比学习框架MoCo[30]的做法, CLEAR[36]采用多种数据增强方法来模拟不同的噪声类型, 使用InfoNCE[37] 损失作为对比损失, 并结合编码器的动量更新策略为 scRNA-seq 数据生成良好的特征表示. scDCCA[38]是一种新型的深度对比聚类算法, 通过基于零膨胀负二项分布模型的去噪自编码器提取低维特征, 同时引入双重对比学习模块来捕捉细胞间的成对相似性. Xiong等人提出了一个基于图对比学习的scRNA-seq数据插补方法scGCL[39], 它通过对比学习总结全局和局部的语义信息, 并选取正样本来增强目标节点的表示.
由于scRNA-seq数据高维度、高稀疏、高噪声、高变异等特性, 细胞聚类一直充满挑战. 近年来, 深度学习技术特别是图神经网络和对比学习的广泛应用, 为聚类方法研究开辟了新的思路. 图神经网络能够有效利用细胞之间的关系信息, 这是很多模型所忽略的. 对比学习则能够在嘈杂的数据分布中学习到更加稳健的特征表示. 本文提出了一种联合对比学习和图神经网络的自优化单细胞聚类方法scCLG. 该方法一方面利用图神经网络对构建的细胞-基因图进行建模, 不仅考虑了基因的表达模式, 也能够有效地挖掘细胞之间的潜在特征关系; 另一方面使用对比学习加强模型训练, 减轻了原始数据中噪声的干扰, 从而学习到对聚类更加友好的特征表示. 具体而言, scCLG的主要工作如下.
(1)对scRNA-seq数据构建细胞-基因图, 尽可能保留原始数据中的信息, 通过图神经网络对图结构进行编码, 综合得到细胞的特征表示, 并在解码器中引入ZINB模型提供对数据分布结构的约束.
(2)通过子图采样和特征掩码的方式获取图的视图及其增广视图. 两个视图经过图编码器得到细胞的特征, 基于两个视图特征的差异在潜空间中进行对比学习, 这将指导编码器学习到更加清晰的特征表示.
(3)使用一种自优化的策略, 将聚类中心作为参数, 同步优化特征表示和聚类中心, 进一步提升聚类效果.
scCLG的创新主要在于图的构建方式和对比学习的策略. 首先, 选择构建细胞-基因图而非传统的细胞-细胞图, 能更准确地刻画原始数据. 其次, 采用了一种改进的对比学习策略, 使模型能学习到与聚类直接相关的特征. 为了验证该方法的有效性, 本文在多个真实的 scRNA-seq 数据集上进行了实验, 并与其他先进方法进行了比较, 实验结果表明, scCLG能学习到良好的细胞特征表示, 在聚类任务上展现出超越其他方法的表现.
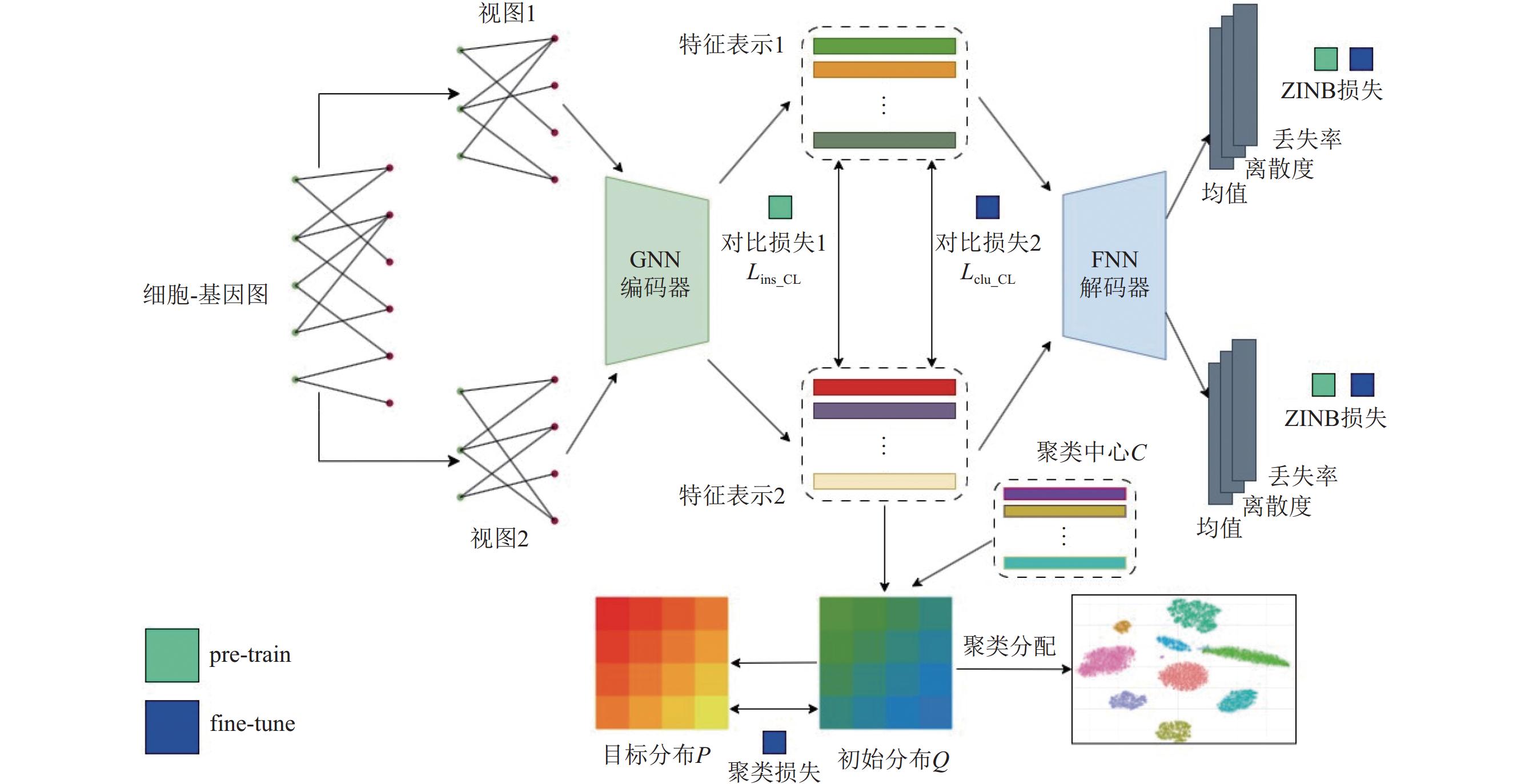
1 方法 1.1 概述scCLG整体将对比学习和图神经网络结合起来, 通过图神经网络学习细胞之间的结构关系信息, 对图结构进行数据增强, 使用对比学习进一步优化细胞特征表示. 模型的总体结构如图1所示.
|
图 1 scCLG整体结构 |
从图1可以看到, scCLG采用基于ZINB模型的自编码器来学习细胞特征, 网络结构主要是由一个 GNN 编码器和一个FNN (feedforward neural network, 前馈神经网络)解码器构成, FNN解码器后有3个独立的网络层用来计算ZINB分布的参数. 对图1所展现的模型工作流程, 进行简要介绍, 后续章节会详细说明. scCLG的运行分为两个阶段, 第1阶段称为预训练(pre-train)阶段, 第2阶段称为微调(fine-tune)阶段. 在预训练阶段, 首先基于预处理后的表达矩阵构建细胞-基因二部图. 网络训练时, 通过子图采样和特征掩码的方式获取原始图结构的两个增广视图, 接着两个视图均通过GNN编码器编码得到细胞的特征表示. 最后, 将细胞的特征输入到FNN解码器中, 获得用于重建数据的ZINB分布参数. 在预训练阶段, scCLG采用两种损失来优化模型. 第1种损失是基于重构的ZINB损失. 第2种损失是对比损失(图1中的对比损失1), 对于视图1中的细胞
|
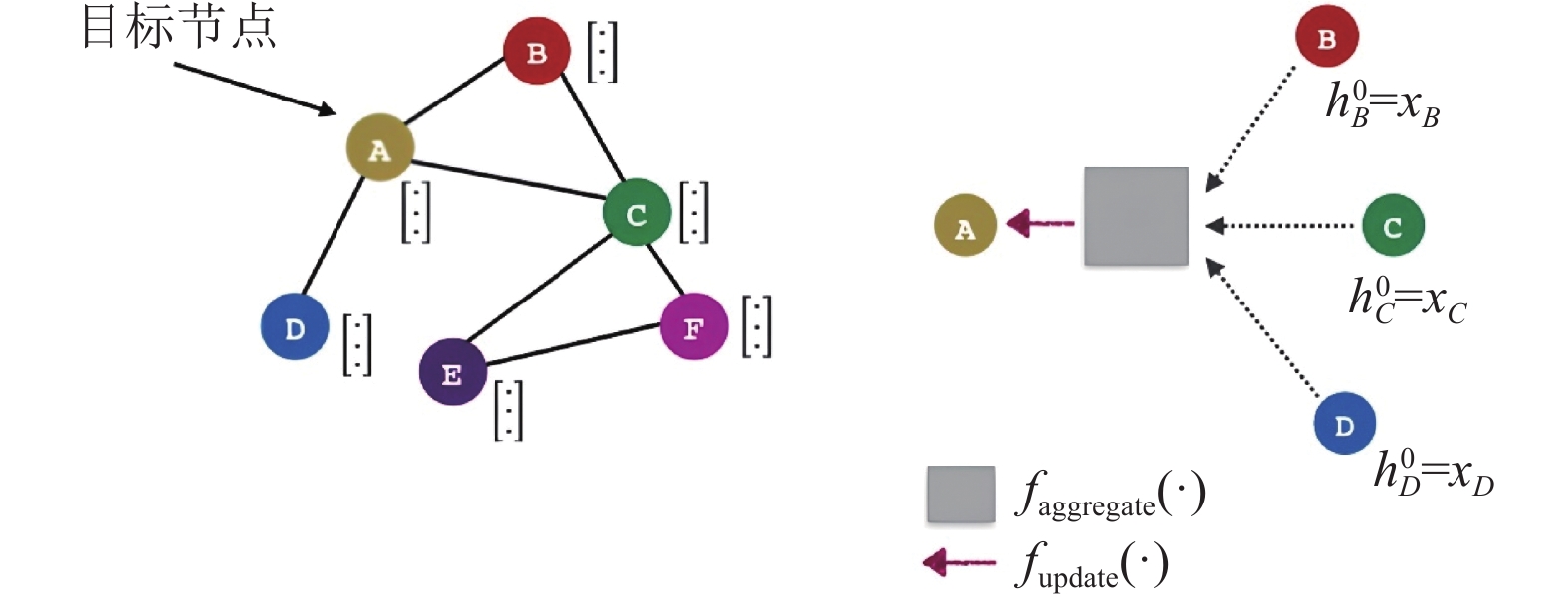
图 2 GraphSAGE的节点聚合方式 |
1.2 数据预处理
对于原始表达数据矩阵(
模型中建立的是细胞和基因之间的二部图, 所谓二部图, 简单地说就是图的节点可以分成不相交的两部分, 而图的每一条边对应的两个节点分别属于这两部分. 对应地, 模型中图的这两部分节点就是细胞节点和基因节点. 若用
对于得到的细胞-基因图, 增广视图采用子图采样结合掩盖掉一部分特征的方式进行. 具体而言, 子图采样应用Hu等人在 2020 年提出的异构图采样技术 HGSampling[41], 该技术在PyTorch Geometric[42]软件包中有相应的实现. 对于特征掩盖, 则是随机生成一定长度比例的mask向量, 将特征向量中对应位置上的值置为0即可, 细胞特征和基因特征都进行掩盖.
1.4 GNN编码器受文献[43]启发, scCLG 采用 GraphSAGE[44]这一图神经网络作为 GNN 编码器的选择. GraphSAGE是一种归纳式(inductive)的网络, 其目的在于学习一种节点表示的方法, 也就是说如何通过一个节点的局部邻居采样并聚合以获取该节点的特征, 而非为每个节点单独训练其特征表示, 其节点聚合方式如图2所示. 相比于直推式(transductive)的学习, GraphSAGE的优点在于训练时无需所有节点参与, 并且具有较强的泛化能力. 若用
| {h(k+1)ci=W′(k)ch(k)ci+W(k)gmeangj∈N(ci)(h(k)gj)h(k+1)gi=W′(k)gh(k)gi+W(k)cmeancj∈N(gi)(h(k)cj) | (1) |
其中,
相关方法中采用ZINB (zero inflated negative binomial, 零膨胀的负二项分布) 模型来对scRNA-seq数据的分布进行建模[17,20,28,39,45], 本文同样假设scRNA-seq 数据符合ZINB分布, 并进行相应建模. 具体而言, 负二项分布NB分布可以表示为:
| NB(x∣μ,θ)=Γ(x+θ)x!Γ(θ)(θθ+μ)θ(μθ+μ)x | (2) |
而 ZINB分布则是在NB分布的基础上加了一个零膨胀因子, 具体表示如下:
| ZINB(x∣π,μ,θ)=πδ0(x)+(1−π)NB(x∣μ,θ) | (3) |
其中,
| {M=S×exp(DWμ)Θ=exp(DWθ)Π=Sigmoid(DWπ) | (4) |
其中, S是一个对角矩阵, 其对角线上的值为对应位置细胞的大小因子(size factor).
| LZINB=−log(ZINB(Xcount∣π,μ,θ)) | (5) |
其中,
首先按前文所述方法构建细胞-基因图. 在训练时, 通过子图采样和特征掩码的方式构建两个增广视图
| l(zi)=−loge(sim(zi,z′i)/τ)∑j≠ie(sim(zi,zj)/τ)+∑je(sim(zi,z′j)/τ) | (6) |
其中,
| sim(a,b)=a⋅b‖a‖‖b‖ | (7) |
整体的对比损失为:
| Lins_CL=12NbNb∑i=1[l(zi)+l(z′i)] | (8) |
其中,
| L1=λ1Lins_CL+LZINB | (9) |
其中,
| LZINB=12(LZINB_1+LZINB_2) | (10) |
在这一阶段, 模型将基于预训练得到的编码器进行聚类并继续优化细胞的特征表示. 为了使聚类分配和特征学习能作为一个整体进行并相互受益, 受到文献[19]的启发, scCLG采用一种自优化的策略来达成这一目标. 假设给定一个软聚类分配分布矩阵Q, 其中Q的每一行代表一个细胞软聚类分配概率, 可以由矩阵Q计算得到目标分布矩阵P, 通过最小化分布P和Q之间的KL散度, 来实现聚类分配的优化. 这个KL散度, 称为聚类损失.
| Lcluster=KL(P||Q)=∑i∑jpijlogpijqij | (11) |
其中,
| qij=(1+‖zi−cj‖2/α)−α+12K∑j′=1(1+‖zi−cj′‖2/α)−α+12 | (12) |
其中, K是类别数目,
| pij=q2ij/fjK∑j′=1q2ij′/fj′ | (13) |
其中,
| fj=Nb∑i=1qij | (14) |
其中, fj代表软聚类频率,
首先通过前一个阶段训练的GNN编码器获取细胞的特征表示, 使用K-means算法进行初步聚类, 初始化聚类中心. 之后开始训练, 与前一阶段一样, 获取增广视图通过编码器和解码器计算ZINB损失. 不失一般性, 对视图2得到的中间特征进行上述的聚类分配, 得到相应的聚类损失. 前一个阶段的对比学习只将同一个细胞在不同视图中的特征视为正样本, 这可能会造成采样偏差[46], 产生不正确的负样本对(将同一个类别的细胞视为负样本). 模型尝试改进对比学习的策略, 利用可能的类别信息来缓解这种情况. 具体地, 不再进行样本本身之间的对比, 而是考虑样本和类别(聚类中心)进行对比. 对于细胞i有如下的对比损失:
| l′(zi)=−loge(sim(zi,cs)/τ)K∑j=1e(sim(zi,cj)/τ) | (15) |
其中,
| s=argmaxk(qik) | (16) |
式(15)代表的对比损失将鼓励细胞与其所在的聚类中心靠拢, 而远离其他的聚类中心, 这是有利于聚类任务的. 进一步地, 整体的对比损失可以表示为:
| Lclu_CL=1NbNb∑i=1l′(zi) | (17) |
其中,
经过以上分析, 微调阶段最终的损失函数如下:
| L2=λ2Lclu_CL+λ3Lcluster+LZINB | (18) |
其中,
为了全面地评估本文提出的方法 scCLG, 从已发表的研究中收集了10个真实的 scRNA-seq 数据集. 这些数据集都带有专家注释的类别标签, 本文将这些数据集中自带的标签作为其中细胞的真实标签. 标签信息只在模型进行聚类性能评估的时候才会用到. 这些数据集涵盖了各种规模, 来自多个测序平台和多个不同组织器官的 scRNA-seq数据. 数据集的详细信息在表1中列出, 包括数据集的名称和来源, 测序平台, 细胞数目, 基因数目以及真实的细胞类别数.
| 表 1 实验中用到的数据集(共10个) |
本文采用两个广泛使用的聚类效果评价指标来对模型的聚类性能进行评估, 分别是标准化互信息(normalized mutual information, NMI)和调整兰德系数(adjusted Rand index, ARI). NMI和ARI都可以用来衡量聚类结果和真实类别分布之间的相似程度. 给定两个聚类分配(标签向量) U和V, 它们之间的NMI的计算方式如下:
| NMI=2I(U,V)H(U)+H(V) | (19) |
其中,
| ARI=∑ij(nij2)−[∑i(ai2)∑j(bj2)]/(n2)[∑i(ai2)∑j(bj2)]/2−[∑i(ai2)∑j(bj2)]/(n2) | (20) |
其中,
scCLG是基于深度学习框架PyTorch[55]实现的, Python版本3.10.9, PyTorch版本1.13.1, CUDA版本11.7. 硬件环境, CPU为Intel(R) Xeon(R) CPU E5-2678 v3 @ 2.50 GHz, 显卡为NVIDIA GeForce RTX 3090, 操作系统为Ubuntu 18.04.6 LTS. GNN编码器是一个两层的GraphSAGE, 其隐藏层的维度分别为256, 64. 解码器是一个两层的全连接层网络, 其隐藏层的维度分别为64, 256. 细胞-基因图中基因节点的特征维度为64, 特征掩盖的比例为0.2. 批量大小(batch size)为
scCLG的聚类表现将和9个现有的先进scRNA-seq数据聚类方法进行比较, 分别是Seurat[11]、CLEAR[36]、Contrastive-sc[34]、GraphSCC[24]、scTAG[28]、scDeepCluster[20]、scDHA[56]、scVI[57]、SIMLR[9]. Seurat是一个广泛使用的scRNA-seq数据分析工具. 其聚类方法首先进行降维, 然后在共享的最近邻居图上使用 Louvain方法. CLEAR 是一个基于自监督对比学习的综合性scRNA-seq 数据分析工具. 它引入了一种新的数据增强方法, 并通过 InfoNCE 损失进行对比学习. Contrastive-sc是一个自监督的对比学习聚类方法, 它通过随机掩盖细胞的基因表达来获取增广样本. GraphSCC利用图卷积神经网络描述和利用细胞之间的结构关系, 通过双自监督模块优化模型学习到的表示. scTAG是一个基于图神经网络的scRNA-seq 数据聚类算法, 通过多核卷积拓扑图神经网络 (TAGCN)对图结构数据进行编码. scDeepCluster在去噪自编码器中引入了一个用来模拟scRNA-seq数据分布的 ZINB模型. scDHA 首先利用非负核自编码器进行特征选择, 并使用基于变分自编码器(VAE)的自学习网络将数据进一步投影到低维空间. scVI 是一个用于分析 scRNA-seq 数据的综合工具. 它使用 ZINB 模型和变分自编码器以深度生成方式建模 scRNA-seq 数据. SIMLR使用多核来学习样本之间的相似性并执行谱聚类.
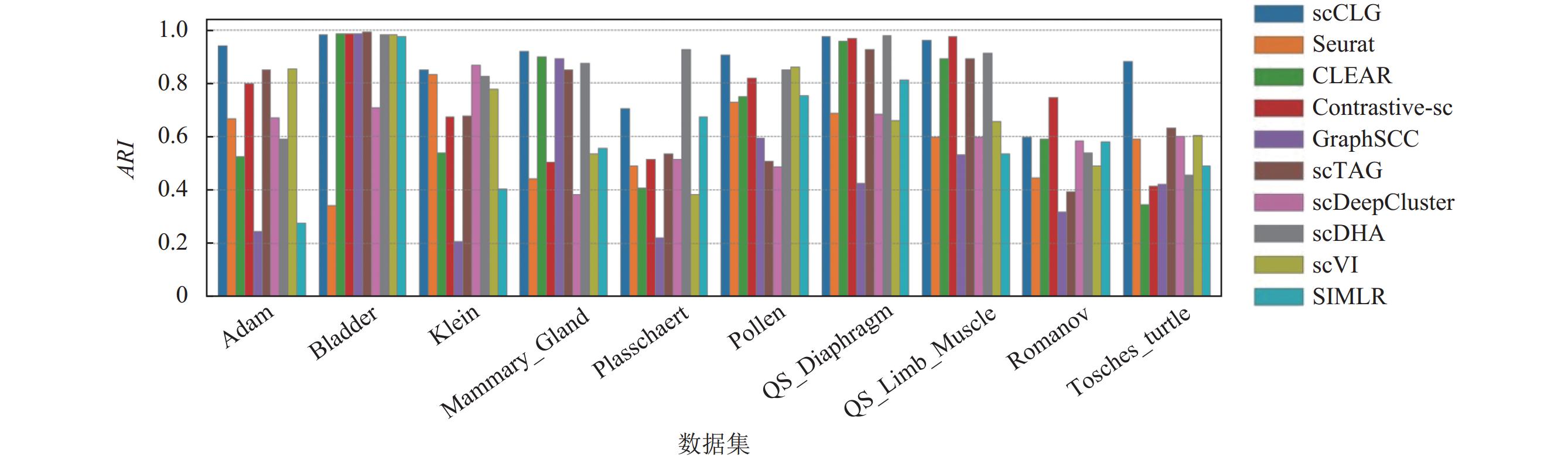
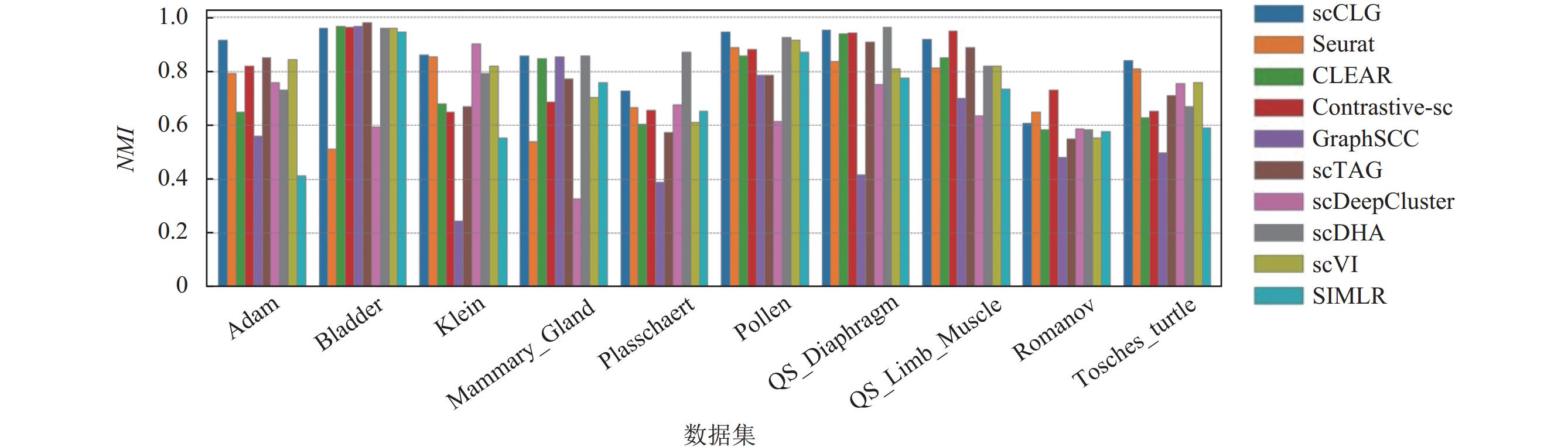
2.4 聚类性能比较为了对模型的聚类表现有更深的认识, 本文在10个真实的scRNA-seq数据集上将scCLG和上述9个聚类算法进行了比较. 图3 (ARI)和图4 (NMI)中展示了这些方法在不同数据集上的聚类结果, 其中每个数据集结果的第1列代表本文提出的方法.
|
图 3 各个算法在不同数据集上的ARI柱状图 |
|
图 4 各个算法在不同数据集上的NMI柱状图 |
从图3和图4中的结果可以看到, scCLG在10个数据集中的4个数据集(Adam, Mammary_Gland, Pollen, Tosches_turtle)上无论是ARI值还是NMI值都取得了最优的结果, 其他的最优结果分散在各个其他算法当中, 但其整体表现都不如本文提出的scCLG. 即使是在scCLG没有达到最优的数据集上, scCLG的性能也和最优的结果相当, 差距很小, 在每个数据集的结果当中, scCLG的表现都处于领先水平. 从整体上看, scCLG的聚类表现在每个数据集上都排在所有方法中的前列, 并且在不同数据集上的鲁棒性较好, 聚类性能没有发生较大的波动, 这表明scCLG泛化性较好, 对数据集不敏感, 并且可以有效处理不同规模的数据. 在细胞数最少的数据集Pollen (301个)和细胞数最多的数据集Tosches_turtle (
图5中展示了不同的方法在10个数据集上的ARI/NMI指标平均值, 无论是ARI还是NMI, scCLG都取得了最高的数值, 这证明了其相对于其他方法的优越性.

|
图 5 不同方法在10个数据集上的ARI、NMI均值 |
2.5 可视化分析
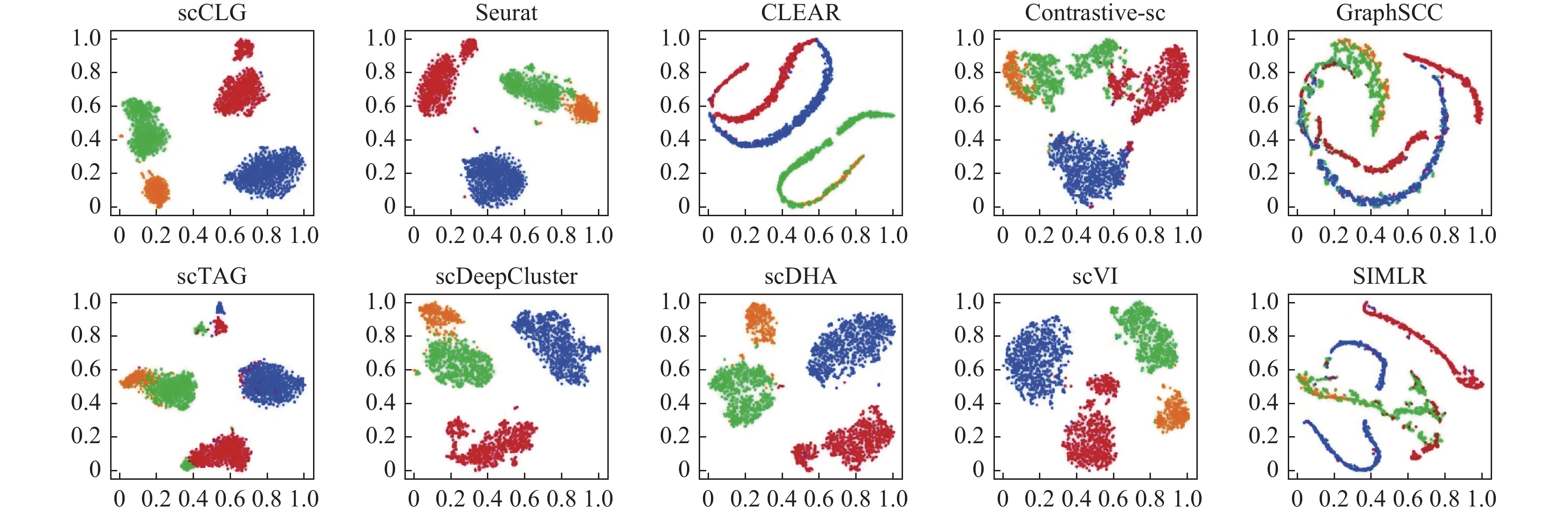
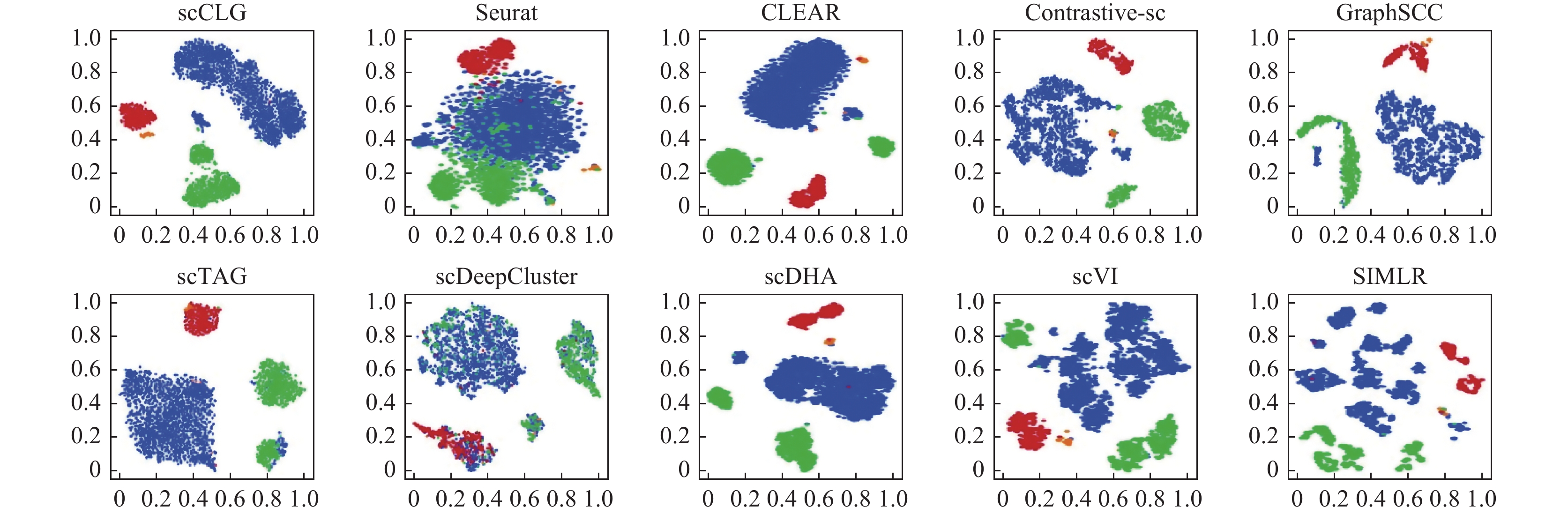
在scRNA-seq聚类的相关分析当中, 可视化是一种直观有效地展示不同类别的细胞的分布的手段. 本文采用 t-SNE[58]作为降维方法, 将各个方法得到的细胞的特征表示降到2维空间, 以便能在平面图形上把细胞的相对位置分布以散点图的形式绘制出来. 图6、图7中分别展示了上述10个方法在Klein和Mammary_Gland这两个数据集上的t-SNE可视化结果. 图6和图7上的一个点代表一个细胞, 点的颜色代表其真实的类别标签.
在Klein数据集中, scCLG将所有细胞分成了较为干净的 4 个部分, 不同类别之间区分明显, 同类别之间联系紧密, 这表明模型学习到了较为良好的特征表示. 其他方法中, scDHA 和 scVI 也有相对清楚的展示, 而 CLEAR 以及 GraphSCC 则表现较差, 整体呈线状分布并且难以区分各个类别. 在Mammary_Gland数据集上, scCLG 也相对清晰的显现出4个类别的存在(蓝、绿、红、橙, 其中橙色细胞较少, 位于红色细胞的下方一些的位置), 相对于其他方法, scCLG的可视化结果, 相同类簇聚集紧密, 不同类簇有区分, 没有大量的混杂, 并且较好地展现了橙色细胞(endothelial cell, 内皮细胞) 这一类簇, 而其他方法容易将这一小的类别和其他类别混在一起.
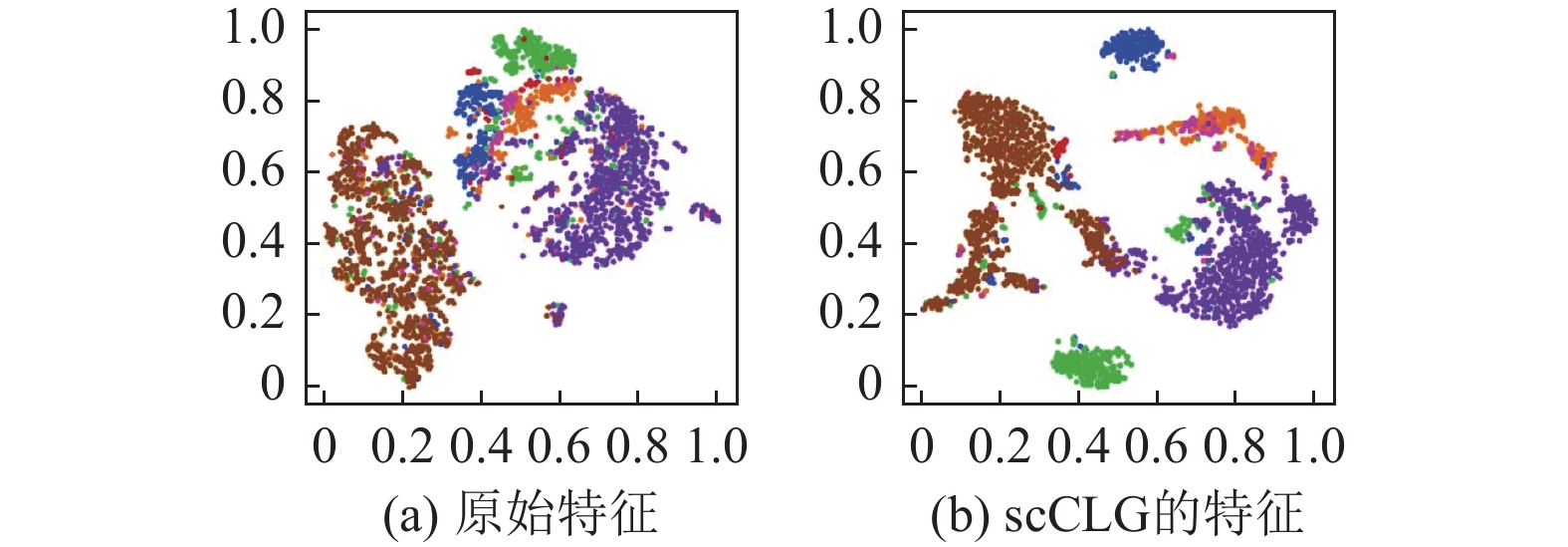
为了进一步地验证scCLG的特征表示水平, 了解 scCLG对于原始的数据特征的改善效果, 在Romanov数据集上进行了实验, 结果如图8所示.
|
图 6 Klein数据集上10个方法的t-SNE可视化结果 |
|
图 7 Mammary_Gland数据集上10个方法的t-SNE可视化结果 |
|
图 8 Romanov数据集上原始特征和scCLG得到的特征的可视化结果对比 |
可以看到, scCLG获得的特征表示与原始特征相比有较大的提升(聚类结果ARI=0.5965, NMI=0.6062), 这主要体现在对原始特征中混杂在一起的蓝色、绿色和橙色的细胞有了较为良好的区分, 同类型的细胞分布更紧密, 并且一定程度上减轻了棕色细胞和其他细胞的混杂.
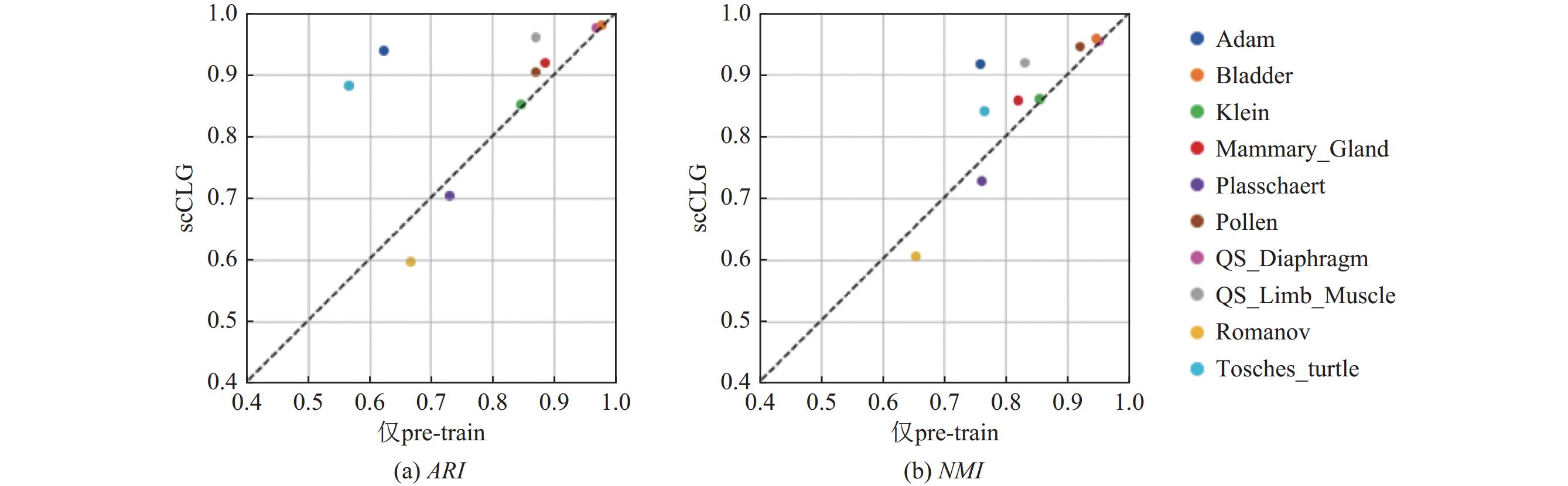
2.6 消融实验在微调阶段, scCLG采用了自优化的聚类损失以及基于类簇中心的对比损失来训练模型, 从原理上看, 这朝着聚类任务的目标优化了细胞的特征表示, 一般来说对模型的性能是会有所提升的. 为了进一步验证微调阶段的有效性, 本文设计了相关的消融实验. 具体的做法是去掉微调阶段, 只进行训练阶段1 (预训练阶段), 训练结束后对整个数据集的细胞进行编码得到其最终的特征表示, 并使用 K-means 算法来完成聚类. 在同样的10个数据集上进行了实验, 实验结果如图9所示. 图中的每一个点代表不同的数据集, 其横坐标代表消融实验(仅pre-train)的结果, 纵坐标代表原始模型 scCLG的结果, 图9(a)和图9(b)分别代表指标ARI和NMI的结果. 整体来看, 绝大部分数据点都落在了对角线y=x的上方, 也就是原始模型要优于消融模型, 这表明微调阶段确是对模型有帮助的, 并且在某些数据集(如: Adam)上有着比较明显的提升. 就Romanov数据集而言, 微调阶段反而让聚类精度下降, 这可能是因为聚类中心的初始化存在较多噪声, 经过训练引入了更大的偏差.
|
图 9 scCLG和其变体的聚类表现的消融实验结果比较 |
3 结语
细胞聚类是scRNA-seq数据分析中的关键任务, 但是由于技术局限以及生物体的复杂性, scRNA-seq数据整体呈现高维度、高稀疏、高噪声的特点, 这给聚类任务带来了挑战. 为此, 本文提出了一个联合对比学习和图神经网络的自优化单细胞数据聚类方法scCLG. 对比学习是一种强大的特征学习范式, 图神经网络则能有效地刻画细胞间的关系. 本方法通过构建细胞-基因二部图, 而非常规的细胞-细胞图, 尽可能保留原始表达矩阵中的信息, 使用图神经网络进行编码, 描述和利用了细胞之间的结构关系信息, 这有助于模型学习到更加丰富的深层次特征表示. 使用子图采样和特征掩盖的方式进行数据增强, 生成不同的视图用于对比学习. 在第1阶段(pre-train)的训练中, 采用常规的样本间的对比学习结合用来保持数据的局部结构的ZINB损失, 初步地训练了图编码器. 在第2阶段(fine-tune)的训练中, 进行自优化的聚类, 逐步优化聚类结果, 并结合聚类分配改进了对比学习的策略, 使得模型能从中感知到聚类的相关信息, 由此继续提升模型的特征表示能力. 不同的图构建方式以及聚类层面的对比学习策略是本方法的主要创新之处.
在10个真实的scRNA-seq数据集上进行了实验, 并与其他9个方法进行了比较. 结果表明, scCLG的聚类效果在近一半的数据集上能达到最优, 在所有的数据集上都处于领先水平, 并且就平均表现而言, scCLG显著优于比较的其他方法. scCLG展现出良好的鲁棒性, 可以有效处理来自不同组织、平台以及不同规模的各种scRNA-seq数据, 保持相对稳定的聚类性能, 这是其他方法所欠缺的. 同时, 可视化分析的结果表明, scCLG可以学习到良好的细胞特征表示.
scCLG的一个可能不足在于其运行成本, 模型的训练时间在细胞数量增多的时候有着相当的提升. 在对大规模的单细胞数据进行聚类的时候, 时间效率非常关键. 后续的研究应在保证聚类准确度的前提下, 加速模型学习的过程.
| [1] |
Buettner F, Natarajan KN, Casale FP, et al. Computational analysis of cell-to-cell heterogeneity in single-cell RNA-sequencing data reveals hidden subpopulations of cells. Nature Biotechnology, 2015, 33(2): 155-160. DOI:10.1038/nbt.3102 |
| [2] |
Reuter JA, Spacek DV, Snyder MP. High-throughput sequencing technologies. Molecular Cell, 2015, 58(4): 586-597. DOI:10.1016/j.molcel.2015.05.004 |
| [3] |
Malikic S, Jahn K, Kuipers J, et al. Integrative inference of subclonal tumour evolution from single-cell and bulk sequencing data. Nature Communications, 2019, 10(1): 2750. DOI:10.1038/s41467-019-10737-5 |
| [4] |
Eberwine J, Sul JY, Bartfai T, et al. The promise of single-cell sequencing. Nature Methods, 2014, 11(1): 25-27. DOI:10.1038/nmeth.2769 |
| [5] |
文路, 汤富酬. 单细胞转录组分析研究进展. 生命科学, 2014, 26(3): 228-233. |
| [6] |
Kiselev VY, Andrews TS, Hemberg M. Challenges in unsupervised clustering of single-cell RNA-seq data. Nature Reviews Genetics, 2019, 20(5): 273-282. DOI:10.1038/s41576-018-0088-9 |
| [7] |
Žurauskienė J, Yau C. pcaReduce: Hierarchical clustering of single cell transcriptional profiles. BMC Bioinformatics, 2016, 17: 140. DOI:10.1186/s12859-016-0984-y |
| [8] |
Kiselev VY, Kirschner K, Schaub MT, et al. SC3: Consensus clustering of single-cell RNA-seq data. Nature Methods, 2017, 14(5): 483-486. DOI:10.1038/nmeth.4236 |
| [9] |
Wang B, Ramazzotti D, de Sano L, et al. SIMLR: A tool for large-scale genomic analyses by multi-kernel learning. Proteomics, 2018, 18(2): 1700232. DOI:10.1002/pmic.201700232 |
| [10] |
Xu C, Su ZC. Identification of cell types from single-cell transcriptomes using a novel clustering method. Bioinformatics, 2015, 31(12): 1974-1980. DOI:10.1093/bioinformatics/btv088 |
| [11] |
Satija R, Farrell JA, Gennert D, et al. Spatial reconstruction of single-cell gene expression data. Nature Biotechnology, 2015, 33(5): 495-502. DOI:10.1038/nbt.3192 |
| [12] |
Blondel VD, Guillaume JL, Lambiotte R, et al. Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment, 2008, 2008(10): P10008. DOI:10.1088/1742-5468/2008/10/p10008 |
| [13] |
Svensson V, Vento-Tormo R, Teichmann SA. Exponential scaling of single-cell RNA-seq in the past decade. Nature Protocols, 2018, 13(4): 599-604. DOI:10.1038/nprot.2017.149 |
| [14] |
LeCun Y, Bengio Y, Hinton G. Deep learning. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [15] |
Eraslan G, Avsec Ž, Gagneur J, et al. Deep learning: New computational modelling techniques for genomics. Nature Reviews Genetics, 2019, 20(7): 389-403. DOI:10.1038/s41576-019-0122-6 |
| [16] |
Bao SQ, Li K, Yan CC, et al. Deep learning-based advances and applications for single-cell RNA-sequencing data analysis. Briefings in Bioinformatics, 2022, 23(1): bbab473. DOI:10.1093/bib/bbab473 |
| [17] |
Eraslan G, Simon LM, Mircea M, et al. Single-cell RNA-seq denoising using a deep count autoencoder. Nature Communications, 2019, 10(1): 390. DOI:10.1038/s41467-018-07931-2 |
| [18] |
Risso D, Perraudeau F, Gribkova S, et al. A general and flexible method for signal extraction from single-cell RNA-seq data. Nature Communications, 2018, 9(1): 284. DOI:10.1038/s41467-017-02554-5 |
| [19] |
Xie JY, Girshick R, Farhadi A. Unsupervised deep embedding for clustering analysis. Proceedings of the 33rd International Conference on Machine Learning. New York: PMLR, 2016. 478–487.
|
| [20] |
Tian T, Wan J, Song Q, et al. Clustering single-cell RNA-seq data with a model-based deep learning approach. Nature Machine Intelligence, 2019, 1(4): 191-198. DOI:10.1038/s42256-019-0037-0 |
| [21] |
Chen L, Wang WN, Zhai YY, et al. Deep soft K-means clustering with self-training for single-cell RNA sequence data. NAR Genomics and Bioinformatics, 2020, 2(2): lqaa039. DOI:10.1093/nargab/lqaa039 |
| [22] |
Wu ZH, Pan SR, Chen FW, et al. A comprehensive survey on graph neural networks. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(1): 4-24. DOI:10.1109/tnnls.2020.2978386 |
| [23] |
Wang JX, Ma AJ, Chang YZ, et al. scGNN is a novel graph neural network framework for single-cell RNA-seq analyses. Nature Communications, 2021, 12(1): 1882. DOI:10.1038/s41467-021-22197-x |
| [24] |
Zeng YS, Zhou X, Rao JH, et al. Accurately clustering single-cell RNA-seq data by capturing structural relations between cells through graph convolutional network. Proceedings of the 2020 IEEE International Conference on Bioinformatics and Biomedicine (BIBM). Seoul: IEEE, 2020. 519–522. [doi: 10.1109/BIBM49941.2020.9313569]
|
| [25] |
Li JY, Jiang W, Han H, et al. ScGSLC: An unsupervised graph similarity learning framework for single-cell RNA-seq data clustering. Computational Biology and Chemistry, 2021, 90: 107415. DOI:10.1016/j.compbiolchem.2020.107415 |
| [26] |
Gan YL, Huang XY, Zou GB, et al. Deep structural clustering for single-cell RNA-seq data jointly through autoencoder and graph neural network. Briefings in Bioinformatics, 2022, 23(2): bbac018. DOI:10.1093/bib/bbac018 |
| [27] |
Cheng Y, Ma XL. scGAC: A graph attentional architecture for clustering single-cell RNA-seq data. Bioinformatics, 2022, 38(8): 2187-2193. DOI:10.1093/bioinformatics/btac099 |
| [28] |
Yu ZH, Lu YF, Wang YH, et al. ZINB-based graph embedding autoencoder for single-cell RNA-seq interpretations. Proceedings of the 36th AAAI Conference on Artificial Intelligence. AAAI, 2022. 4671–4679. [doi: 10.1609/aaai.v36i4.20392]
|
| [29] |
Chen T, Kornblith S, Norouzi M, et al. A simple framework for contrastive learning of visual representations. Proceedings of the 37th International Conference on Machine Learning. PMLR, 2020. 1597–1607. Chen T, Kornblith S, Norouzi M, et al. A simple framework for contrastive learning of visual representations. Proceedings of the 37th International Conference on Machine Learning. PMLR, 2020. 1597–1607. |
| [30] |
He KM, Fan HQ, Wu YX, et al. Momentum contrast for unsupervised visual representation learning. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 9726–9735. [doi: 10.1109/cvpr42600.2020.00975]
|
| [31] |
Grill JB, Strub F, Altché F, et al. Bootstrap your own latent a new approach to self-supervised learning. Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2020. 1786.
|
| [32] |
Caron M, Misra I, Mairal J, et al. Unsupervised learning of visual features by contrasting cluster assignments. Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2020. 831.
|
| [33] |
Ericsson L, Gouk H, Hospedales TM. How well do self-supervised models transfer? Proceedings of 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 5410–5419. [doi: 10.1109/cvpr46437.2021.00537]
|
| [34] |
Ciortan M, Defrance M. Contrastive self-supervised clustering of scRNA-seq data. BMC Bioinformatics, 2021, 22(1): 280. DOI:10.1186/s12859-021-04210-8 |
| [35] |
Wan H, Chen L, Deng MH. scNAME: Neighborhood contrastive clustering with ancillary mask estimation for scRNA-seq data. Bioinformatics, 2022, 38(6): 1575-1583. DOI:10.1093/bioinformatics/btac011 |
| [36] |
Han WK, Cheng YQ, Chen JY, et al. Self-supervised contrastive learning for integrative single cell RNA-seq data analysis. Briefings in Bioinformatics, 2022, 23(5): bbac377. DOI:10.1093/bib/bbac377 |
| [37] |
van den Oord A, Li YZ, Vinyals O. Representation learning with contrastive predictive coding. arXiv:1807.03748, 2018.
|
| [38] |
Wang J, Xia JF, Wang HY, et al. scDCCA: Deep contrastive clustering for single-cell RNA-seq data based on auto-encoder network. Briefings in Bioinformatics, 2023, 24(1): bbac625. DOI:10.1093/bib/bbac625 |
| [39] |
Xiong ZH, Luo JW, Shi WW, et al. scGCL: An imputation method for scRNA-seq data based on graph contrastive learning. Bioinformatics, 2023, 39(3): btad098. DOI:10.1093/bioinformatics/btad098 |
| [40] |
Wolf FA, Angerer P, Theis FJ. SCANPY: Large-scale single-cell gene expression data analysis. Genome Biology, 2018, 19(1): 15. DOI:10.1186/s13059-017-1382-0 |
| [41] |
Hu ZN, Dong YX, Wang KS, et al. Heterogeneous graph Transformer. Proceedings of the 2020 Web Conference. Taipei: ACM, 2020. 2704–2710. [doi: 10.1145/3366423.3380027]
|
| [42] |
Fey M, Lenssen JE. Fast graph representation learning with PyTorch geometric. arXiv:1903.02428, 2019.
|
| [43] |
Lee J, Kim S, Hyun D, et al. Deep single-cell RNA-seq data clustering with graph prototypical contrastive learning. Bioinformatics, 2023, 39(6): btad342. DOI:10.1093/bioinformatics/btad342 |
| [44] |
Hamilton WL, Ying R, Leskovec J. Inductive representation learning on large graphs. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 1025–1035.
|
| [45] |
Wei MQ, Liu RJ, Wang YJ, et al. Deep zero-inflated negative binomial model and its application in scRNA-seq data integration. SoutheastCon 2023. Orlando: IEEE, 2023. 901–905. [doi: 10.1109/SoutheastCon51012.2023.10115099]
|
| [46] |
Chuang CY, Robinson J, Lin YC, et al. Debiased contrastive learning. Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2020. 735.
|
| [47] |
Adam M, Potter AS, Potter SS. Psychrophilic proteases dramatically reduce single-cell RNA-seq artifacts: A molecular atlas of kidney development. Development, 2017, 144(19): 3625-3632. DOI:10.1242/dev.151142 |
| [48] |
The Tabula Muris Consortium. A single-cell transcriptomic atlas characterizes ageing tissues in the mouse. Nature, 2020, 583(7817): 590-595. DOI:10.1038/s41586-020-2496-1 |
| [49] |
Klein AM, Mazutis L, Akartuna I, et al. Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells. Cell, 2015, 161(5): 1187-1201. DOI:10.1016/j.cell.2015.04.044 |
| [50] |
Plasschaert LW, Žilionis R, Choo-Wing R, et al. A single-cell atlas of the airway epithelium reveals the CFTR-rich pulmonary ionocyte. Nature, 2018, 560(7718): 377-381. DOI:10.1038/s41586-018-0394-6 |
| [51] |
Pollen AA, Nowakowski TJ, Shuga J, et al. Low-coverage single-cell mRNA sequencing reveals cellular heterogeneity and activated signaling pathways in developing cerebral cortex. Nature Biotechnology, 2014, 32(10): 1053-1058. DOI:10.1038/nbt.2967 |
| [52] |
The Tabula Muris Consortium, Overall Coordination, Logistical Coordination, et al. Single-cell transcriptomics of 20 mouse organs creates a Tabula Muris. Nature, 2018, 562(7727): 367-372. DOI:10.1038/s41586-018-0590-4 |
| [53] |
Romanov RA, Zeisel A, Bakker J, et al. Molecular interrogation of hypothalamic organization reveals distinct dopamine neuronal subtypes. Nature Neuroscience, 2017, 20(2): 176-188. DOI:10.1038/nn.4462 |
| [54] |
Tosches MA, Yamawaki TM, Naumann RK, et al. Evolution of pallium, hippocampus, and cortical cell types revealed by single-cell transcriptomics in reptiles. Science, 2018, 360(6391): 881-888. DOI:10.1126/science.aar4237 |
| [55] |
Paszke A, Gross S, Massa F, et al. PyTorch: An imperative style, high-performance deep learning library. Proceedings of the 33rd International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2019. 721.
|
| [56] |
Tran D, Nguyen H, Tran B, et al. Fast and precise single-cell data analysis using a hierarchical autoencoder. Nature Communications, 2021, 12(1): 1029. DOI:10.1038/s41467-021-21312-2 |
| [57] |
Lopez R, Regier J, Cole MB, et al. Deep generative modeling for single-cell transcriptomics. Nature Methods, 2018, 15(12): 1053-1058. DOI:10.1038/s41592-018-0229-2 |
| [58] |
van der Maaten L, Hinton G. Visualizing data using t-SNE. Journal of Machine Learning Research, 2008, 9(86): 2579-2605. |
 2024, Vol. 33
2024, Vol. 33



