城市交通估计是指对城市交通需求、流量、拥堵和交通规划方案等进行定量分析和预测的过程. 城市交通估计对于城市规划、交通管理、环境评估、未来预测和投资决策等方面都具有重要的意义. 它为城市交通系统的发展和优化提供了科学依据, 有助于实现城市的可持续发展和提升居民的生活质量.
本文的城市交通估计主要针对的是交通流量, 交通流量在城市交通估计中具有重要的作用, 它为交通需求预测、道路容量评估、交通模拟和仿真、拥堵缓解和交通管理等提供了基础数据, 帮助决策者制定合理的交通规划和管理策略, 以提高城市交通系统的效率和可持续性. 许多不同的方法已经被提出来估算城市交通流量, 这些方法从不同的角度进行研究. 经典的流量估计方法已经在文献[1–4]广泛研究, 这些方法使用历史交通数据来训练机器学习模型, 试图捕捉过去交通情况、环境特征和未来交通之间的相关性. 近年来, 许多城市交通估计工作已经采用深度神经网络[5,6]来建模时空自相关性. 例如, 文献[7]将卷积神经网络(CNN)[8]和门控循环单元(GRU)[9]结合起来预测城市中的交通流量; 文献[10]将图卷积神经网络(GCN)[11]和长短期记忆力网络(LSTM)结合起来, 利用GCN和LSTM捕捉交通数据的时空关联性, 来提高交通流量预测的准确性; 文献[12,13]利用GCN和GRU捕获交通数据的时空关联性, 来对交通流量进行准确预测; 文献[14,15]将GCN和自注意力机制(self-attention)[16]相结合, 大大提高了交通流量预测的精度. 上述模型要进行准确的交通流量估计, 需要大量的历史交通观测数据, 包括交通流量、速度、拥堵情况等. 然而, 在城市道路修建前无法获取这些数据, 在这种情况下, 由于缺乏数据, 数据驱动的方法可能无法有效地估计城市交通流量.
由于城市道路部署前无法获得交通观测数据, 上述方法无法解决在城市道路部署前估计路网的交通流量问题, 为了解决这个难题, 本文提出了一种新的条件城市交通生成对抗网络(Curb-GAN), 该网络可以根据不同的路网结构和外部特征信息在连续相关时间段提供有效的交通流量估计. 提出的Curb-GAN利用条件GAN[17]结构来控制生成的交通流量, 并使用训练好的生成器来估计未来的交通流量. Curb-GAN具有一些新颖的设计, 例如使用GCN来捕获道路网络的空间自相关性, 以及利用GRU和self-attention来捕获不同时隙的时间自相关性. 综上所述, 本文的主要贡献如下: (1)本文将条件城市交通流量估计问题建模为交通流量数据生成问题, 提出了一种新的深度学习生成模型Curb-GAN, 该模型可以生成连续时段的未来交通流量估计; (2)模型框架包含GCN模块和Attention-GRU模块, 旨在捕捉跨时空区域的共享模式, 即交通状态如何随着时间变化、潜在的道路网络结构而演变; (3)在两个真实世界的时空数据集上进行了广泛的实验, 以评估我们提出的Curb-GAN. 实验结果验证了Curb-GAN可以显著提高城市交通流量估计性能, 并且在这两个数据集上表现结果都优于基线方法.
1 相关网络模型 1.1 生成对抗网络生成对抗网络(generative adversarial network, GAN)是由Goodfellow等人[18]于2014年提出的, GAN的起源可以追溯到计算机科学领域的生成模型和对抗性学习的研究. Goodfellow在他的博士论文中提出了生成对抗网络的创意, 并与他的研究团队一起在2014年的一篇论文[18]中详细描述了GAN的原理和方法. GAN由生成器和判别器两个主要组件组成. 生成器试图生成与真实数据相似的合成数据, 而判别器则试图区分真实数据和生成器生成的数据. 两个网络相互博弈, 通过反复迭代训练来提高生成器和判别器的性能, 最终达到生成逼真数据的目的.
GAN常用于图像数据的生成, 但对于序列数据的生成, 如文本、音频或时间序列数据, 传统的生成对抗网络(GAN)架构可能不太适用, 因为它们通常以固定长度的向量作为输入, 无法直接处理序列数据. 然而, 有一些扩展和变体的GAN模型可以用于序列数据的生成, 比如条件生成对抗网络(conditional generative adversarial network, CGAN), 在传统的GAN模型中, 生成器的输入是随机噪声向量, 但在条件GAN中, 生成器的输入除了随机噪声, 还包括条件向量或条件序列. 这样, 生成器可以根据给定的条件生成相应的序列数据. Yu等人[19]在2017年提出了SeqGAN方法, 这是一种使用生成对抗网络(GAN)和策略梯度方法来生成逼真的文本序列的方法. 由此得到启发, 我们也可以利用CGAN结构来生成交通流量数据.
1.2 图神经网络图神经网络(graph neural network, GNN)是一种用于处理图数据的机器学习模型. 早期的神经网络模型, 如感知机和多层感知机(multilayer perceptron), 主要适用于处理向量或矩阵数据, 然而, 对于非结构化数据, 如图数据, 传统的神经网络模型往往无法直接应用. 图神经网络的发展源于对图数据建模和分析的需求, 它的发展可以追溯到20世纪80年代, 当时研究人员开始探索如何将神经网络扩展到非欧几里德结构的数据表示中. 2004年, Scarselli等人[20]提出了一种基于递归神经网络(recursive neural network)的图神经网络模型, 用于处理树形结构数据, 这是GNN发展的早期尝试之一.
2017年, Kipf等人[11]提出了一种基于图卷积操作的图神经网络模型, 用于处理图数据. 这些模型利用局部邻居节点的信息来更新每个节点的表示, 从而实现对图结构的学习和推理, 从此, 图神经网络的研究和应用迅速发展. 研究人员提出了各种改进和变体, 包括图卷积网络、图注意力网络(graph attention network)[21]、图生成模型(graph generative model)等, 这些模型在社交网络分析、分子化学、推荐系统等领域展现出了强大的建模能力.
GNN的变体图卷积网络(graph convolutional network, GCN)应用十分广泛, GCN是一种用于处理图数据的深度学习模型, 旨在学习节点的表示和图结构的特征. 它通过在节点之间传播和聚合信息来捕捉节点的上下文信息, 并将这些信息用于节点的表示学习和预测任务.
GCN的核心思想是将每个节点的特征表示更新为其与邻居节点的特征表示的加权平均, 这种加权平均的权重由图的邻接矩阵和节点特征共同确定, 通过多层的图卷积操作, GCN可以逐步聚合更广泛范围的邻居信息, 从而丰富节点的表示.
GCN在交通领域的应用有助于解决多种与交通相关的问题, 包括路网分析、交通流预测、交通信号优化等. GCN可以利用路网的拓扑结构和历史交通流量数据来预测未来的交通流量, 通过在路网上进行信息传播和邻居聚合, GCN可以捕捉交通流量中的时空依赖关系, 提高交通流预测的准确性和鲁棒性. 基于GCN的强大能力, 我们使用GCN来捕捉路网的空间相关性, 进行城市交通流量估计.
1.3 注意力机制注意力机制最早由Bahdanau等人[22]在2014年提出, 这篇论文引入了注意力机制来改善神经机器翻译模型的性能, 并在机器翻译任务中取得了显著成功, 自此以后, 注意力机制被广泛应用于深度学习模型中, 包括自然语言处理、计算机视觉和其他领域, 为模型提供了对输入数据的关注和处理能力的提升.
Vaswani等人[16]于2017年提出了一种名为Transformer的模型架构, 它完全基于注意力机制, 摒弃了传统的循环神经网络(RNN)和卷积神经网络(CNN). 在该论文中, 作者指出传统的序列模型在处理长距离依赖关系时存在一些问题, 并提出了自注意力机制可以作为一种可替代的建模方法. 自注意力机制能够根据输入序列中不同位置之间的相关性, 动态地计算每个位置的权重, 从而使模型能够灵活地关注输入序列中的不同部分.
1.4 门控循环单元门控循环单元(gated recurrent unit, GRU)是一种改进的循环神经网络(RNN)模型, 旨在解决传统RNN模型在序列建模任务中遇到的长期依赖问题和梯度消失或梯度爆炸的挑战. GRU通过引入门控机制, 有效地捕捉序列中的长期依赖关系, 并更好地控制信息的流动. 它由更新门和重置门组成, 通过使用Sigmoid函数来决定是否更新和重置隐藏状态, 从而灵活地决定是否保留过去的信息和如何整合当前的输入. GRU在自然语言处理、语音识别、机器翻译等序列建模任务中得到了广泛应用, 并在处理长文本序列时相比传统的RNN模型展现出更好的效果. 它具有简单的结构和较少的参数量, 使得训练和推理过程更高效. GRU的引入为序列建模领域带来了新的突破, 并为解决实际应用中的序列数据建模问题提供了一种有力的工具. 本文中我们结合GRU和注意力机制来处理交通数据的时间关系, 更好的估计城市交通流量数据.
2 条件城市交通生成对抗网络为了解决有条件的城市交通流量估计问题, 我们受到了条件GAN的启发, 交通流量估计问题类似于条件图像序列生成问题, 将路网节点间的距离关系矩阵和外部信息特征视为条件, 将某一节点在一个时隙内的交通流量分布视为一个“图像”, 将每个节点的交通状态视为一个“像素”值. 因此条件GAN结构很有可能用于解决条件城市交通流量估计问题, 但是简单的条件GAN模型不能很好地捕获交通流量数据的空间和时间自相关性. 因此我们提出了一种新的生成模型Curb-GAN, 该模型可以更准确地捕获交通流量数据的空间自相关性和时间依赖性, 将路网节点间的距离关系矩阵和外部信息特征作为条件, 在连续时间内生成真实的交通流量估计.
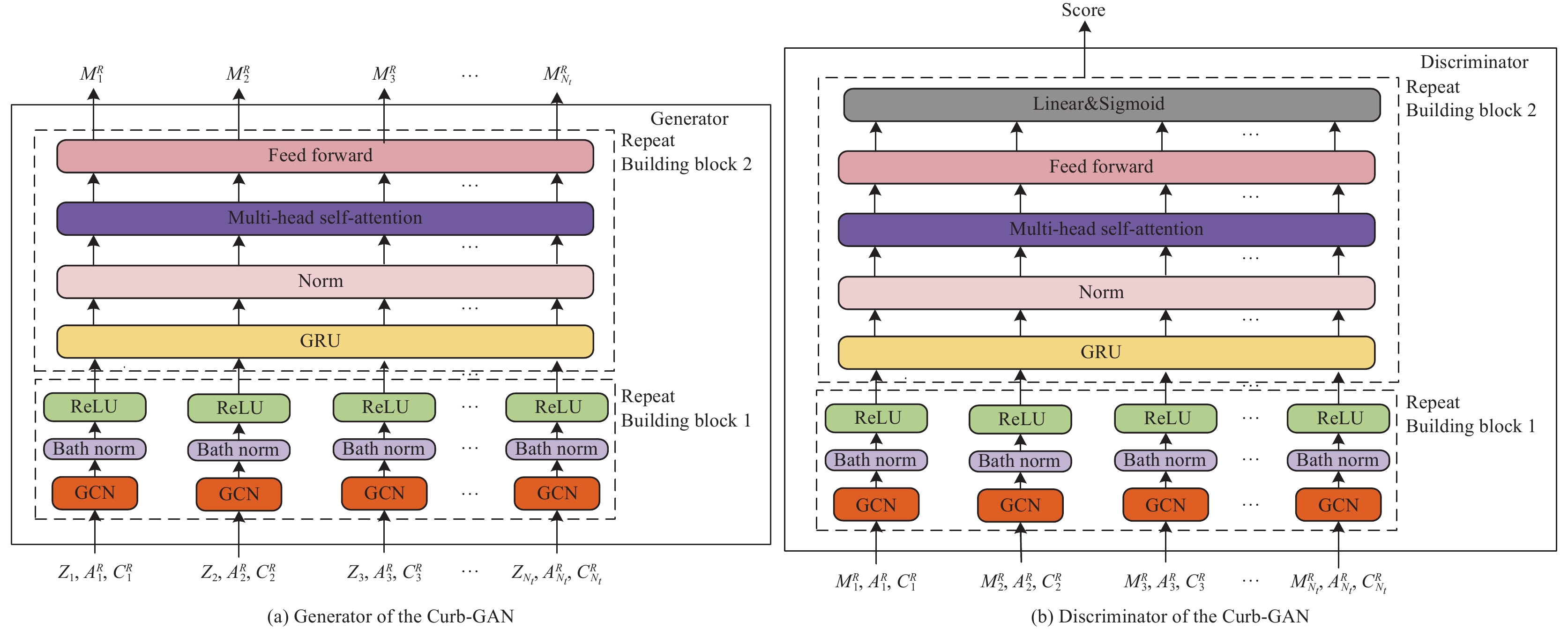
在本节中, 我们介绍了本文的条件交通流量生成模型Curb-GAN的体系结构, 该模型整体架构如图1所示, 本文采用条件GAN结构, Curb-GAN由生成器G和判别器D组成, 生成器和判别器结构相同, 由Building block 1和Building block 2两部分构成.
|
图 1 Curb-GAN框架图 |
Building block 1用GCN来处理交通流量数据的时间相关性, Building block 2采用自注意力机制和GRU来处理交通流量数据的时间相关性, 并且输出我们想要的交通流量数据或者是一个标量分数.
2.1 图卷积层(GCN层)GCN是一种用于处理图结构数据的神经网络模型, 在城市区域, 复杂的底层道路结构约束着城市交通流量的变化, 而且交通道路拓扑结构是图的形式, 所以我们在Curb-GAN的生成器和判别器中, 使用GCN来处理节点和边的特征, 以学习图的结构和模式. 这样可以在生成器中生成具有图结构的数据, 在判别器中对图数据进行分类或判别. 在生成器中和判别器中, 可以使用GCN来进行节点特征的聚合和传播, 以生成新的节点特征. 这样, 生成器可以逐步生成具有图结构的交通流量数据, 判别器可以对数据来进行判别是否为真实的流量数据. 鉴于GCN强大的图结构学习能力, 我们使用GCN来捕获路网的空间自相关性. GCN可以有多层, 层间传播规则如式(1)所示:
| f(H(l),A)=σ(ˆD−12ˆAˆD−12H(l)W(l)) | (1) |
其中, A为邻接矩阵, D为度矩阵, H(l)为输入特征, 即节点的特征表示, W(l)为网络参数,
交通流量数据是序列数据, 除了考虑城市交通流量的空间自相关性对交通流量的影响, 流量节点之间的时间依赖性也非常重要, 它是生成准确交通流量估计必须考虑的关键因素. 在Building block 2中我们使用GRU和自注意力层来捕捉交通流量数据的时间相关性.
GRU是一种门控循环神经网络, 常用于处理序列数据的建模和生成. 在生成器中, 我们使用GRU来处理交通流量的时间序列关系, 接受GCN层生成的序列片段作为输入, 并生成下一个序列元素. 这样, 生成器可以逐步生成连续的序列数据, 然后再作为注意力机制的输入; 在判别器中, 使用GRU作为序列数据的编码器, 以学习序列的表示. 这样, 判别器可以在对生成的序列数据进行评估时, 考虑序列中的时序关系和上下文信息. GRU的输入是时间步长为t的图卷积层的输出Ht, 其中Ht−1表示时间步长为t−1时的隐藏状态. 重置门rt决定之前的单元状态ht–1是否重要, 而更新门ut决定是否应该用候选状态ct替换单元状态ht. 单个cell的GRU计算过程如式(2)–式(5)所示:
| ut=σ(ωu[Ht,ht−1]+bu) | (2) |
| rt=σ(ωr[Ht,ht−1]+br) | (3) |
| ct=tanh(ωc[Ht,(rt⊙ht−1)]+br) | (4) |
| ht=ut⊙ht−1+(1−ut)⊙ct | (5) |
其中, ω和b分别是权重和偏置, σ和tanh表示Sigmoid和tanh激活函数.
自注意力机制经常处理包含文本、音频和视频在内的时间序列数据, 并从中学习时间依赖性. 因此我们在G和D中, 在GRU后都应用了自注意力机制(SA), 以增强模型捕获节点之间局部和全局时间相关性的能力. 自注意力的输入和输出是两个向量序列, 在自注意过程中, 输入序列中的每个向量被线性变换成查询、键和值3个向量. 每个输出向量被计算为所有值的加权和, 其中权重是Softmax层的输出, Softmax层的输入是对应查询与所有键的缩放点积. 由于一系列查询、键和值可以以矩阵Q、K和V的形式组合并并行计算, 因此自注意力函数的计算如式(6)所示:
| Attention(Q,K,V)=Softmax(QKT/√dk)V | (6) |
其中, dk是K的维度.
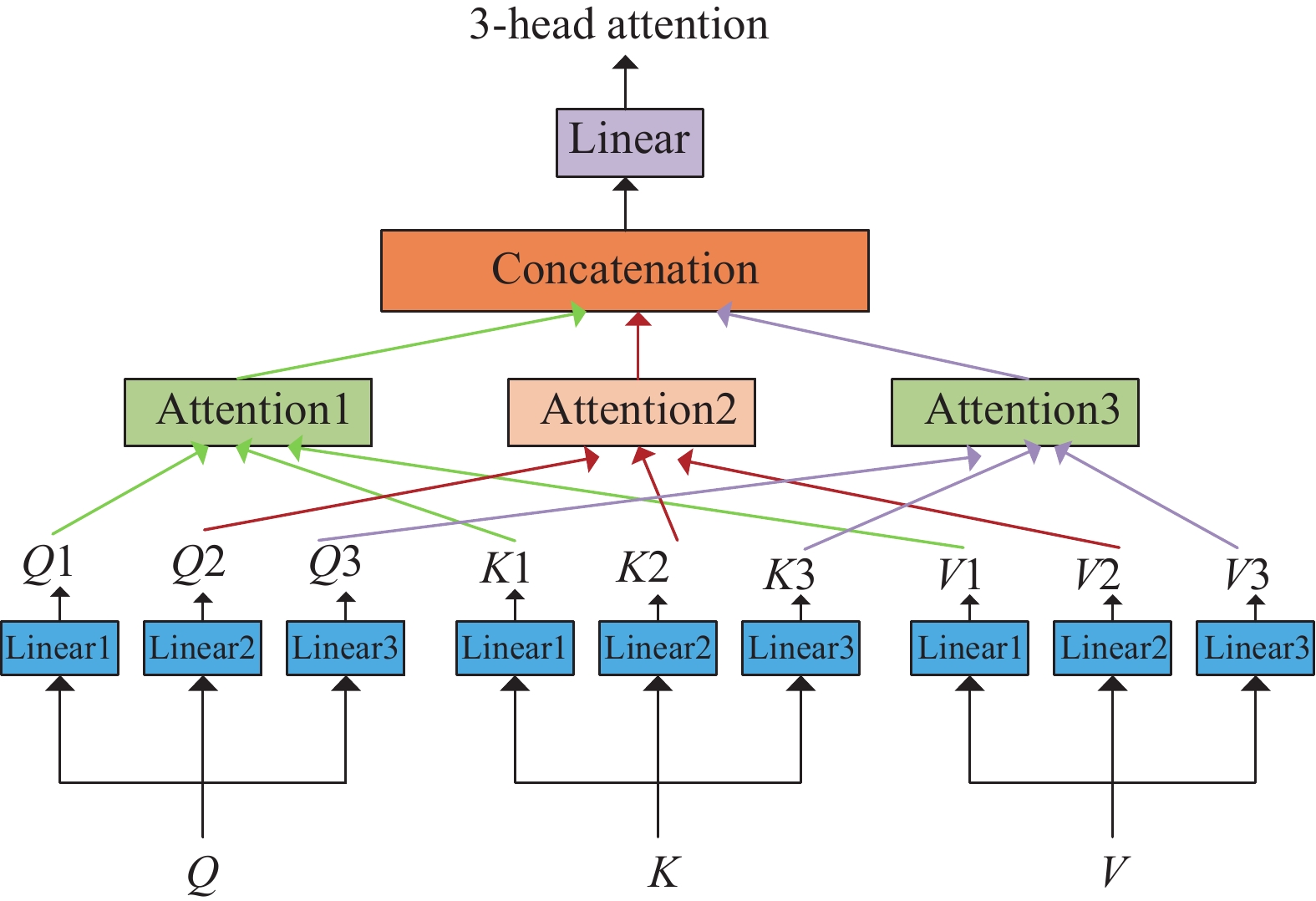
在本文中, 我们采用的是多头自注意力机制, 其中Q, K和V被线性转换h次, 从而我们得到h个不同的关注, 然后将它们连接在一起并经过线性转换得到最终的值, 多头注意力机制的计算过程如式(7)所示:
| MultiHead(Q,K,V)=Concat(h1,h2,⋯,hh)Wowherehi=Attention(QWQi,KWki,VWVi) | (7) |
图2展示了一个3头注意力机制的例子.
|
图 2 3头注意力例子 |
2.3 Curb-GAN模型
为了生成以城市路网节点距离关系矩阵和外部信息特征为条件的连续时间段的交通流量估计, 我们采用了条件生成对抗(CGAN)结构. 图1展示了Curb-GAN的整体结构, Curb-GAN包含一个生成器G和一个判别器D. 生成器G的目的是生成连续时隙中与真实时隙相似的流量分布序列, 使鉴别器D不能很好地将生成的流量分布序列与真实时隙序列区分开来.
生成器G的目的是根据路网节点距离关系矩阵和外部信息特征生成连续时隙顺序流量分布. 生成器G的输入包括4部分: (1)噪声张量Z={z1, z2,…,
鉴别器D对输入的流量分布给出一个分数, 如果输入的是真实的流量分布序列, 鉴别器试图提高输出分数, 如果输入的是生成器G生成的流量分布序列, 则试图降低输出分数. 鉴别器D的输入包括4部分: (1)连续时隙的流量分布张量MR; (2)根据路网拓扑结构构建的邻接矩阵张量A={A1, A2,…,
因此, Curb-GAN的损失函数建模为带有额外L2惩罚的最大最小博弈, 如式(8)所示:
| min | (8) |
在生成器G和鉴别器D内部, 我们应用了GCN层、GRU层和自注意力机制, 有助于捕获时空自相关性. 如图1所示, G和D内部有两个模块Building block 1和Building block 2, 它们都可以堆叠多次.
Building block 1由GCN层和批处理归一化和激活函数(如ReLU或LeakyReLU)组成. Building block 2由GRU层、多头自注意力层和由ReLU作为激活函数的两个全连接层组成的前馈网络组成, 每层网络层之后都要进行归一化操作.
2.4 Curb-GAN训练在训练过程中, 我们应用了时间反向传播算法(BPTT), Curb-GAN的训练过程是通过交替训练生成器和判别器来进行的, 即分步训练. 在每个训练步骤中, 首先训练判别器D, 然后训练生成器G. 这样的交替训练过程可以持续进行多个迭代, 直到模型达到收敛状态. Curb-GAN的损失函数建模为带有额外L2惩罚的最大最小博弈, 具体来说使用的是交叉熵损失函数(cross entropy loss), 具体收敛函数如式(9)–式(12)所示, 最终的目标是使生成器生成的交通流量数据样本在判别器中被正确分类(真实样本为真, 生成样本为假), 同时使判别器无法准确区分生成的样本和真实样本. 详细的训练过程如算法1所示.
算法1. Curb-GAN训练过程
输入: 训练迭代次数k, 一个训练集P, 初始化的G和D.
输出: 训练好的G和D.
1. 在每个训练迭代iter内:
2. repeat
3. 从训练集P中抽取样本P0
4. 从高斯分布中得到样本B
5. 用G生成 Õ
6. 从训练集Z中得到 Ô
7. 用式(10)更新D以最大化式(9)
8. 用式(12)更新G以最大化式(11)
9. until iter>k
算法1中鉴别器D和生成器G分别在第3–7行和第8行更新. 定义在训练集P中包含n个样本, 表示为P={(C1, A1, M1),…,(Cn, An, Mn)}, 定义P0={(C1, A1, M1),…,(Cm, Am, Mm)}(算法第3行), 作为包含m个样本的P的子集, 其中m<n. 定义B={Z1, Z2, Z3,…,Zm}作为从高斯分布中采样的m个噪声张量的集合(算法第4行), Õ ={1, 2,…,m}作为由G生成的m个流量分布张量的集合(算法第5行), i=G(Ci, Ai, Zi). 定义Ô={1, 2,…,m}作为从训练集P中采样的m个流量分布张量的集合(算法第6行). 在每次训练迭代中我们用式(9)和式(10)更新鉴别器D的参数和学习率. 然后我们用式(11)和式(12)更新生成器G的参数以及学习率. 训练好后, 我们使用训练良好的生成器G生成目标地区连续时隙的估计交通流量分布.
| \begin{split} \tilde{V}_D= & \frac{1}{m} \sum_{i=1}^m\left( \log \left(1-D\left(C^i, A^i, \tilde{M}^i\right)\right)+ \log D\left(C^i, A^i, M^i\right) \right. \\ &+\log \left(1-D\left(C^i, A^i, \hat{M}^i\right) \right) \end{split} | (9) |
| \mathop \theta \nolimits_D = \mathop \theta \nolimits_D + \mathop \eta \nolimits_D \nabla {\mathop V\limits^ \sim _{\mathop \theta \nolimits_D }}\left( {\mathop \theta \nolimits_D } \right) | (10) |
| \tilde{V}_G=\frac{1}{m} \sum_{i=1}^m \log D\left(G\left(C^i, A^i, Z^i\right)\right) | (11) |
| \mathop \theta \nolimits_G = \mathop \theta \nolimits_G + \mathop \eta \nolimits_G \nabla {\tilde V _{\mathop \theta \nolimits_G }}\left( {\mathop \theta \nolimits_G } \right) | (12) |
我们评估了Curb-GAN在PeMSD4、PeMSD8两个真实时空数据集上的性能. 数据集的详细信息如表1所示, 下面是详细的介绍.
| 表 1 实验中使用的数据集 |
PeMSD4: 它表示由Caltrans绩效测量系统(PeMS)收集的旧金山湾区的交通数据. 一个传感器的测量结果被汇总成5 min的窗口, 包括交通流量、平均速度和平均占用率. 该数据集由307个传感器在2018年1月1日–2018年2月28日期间的记录组成.
PeMSD8: 该数据集包括2016年7月1日–2016年8月31日圣贝纳迪诺地区的交通信息, 包括170个环路检测器. 与PeMSD4类似, 有3个维度的数据, 包括交通流量、平均速度和平均占用率.
对于PeMSD4和PeMSD8, 我们的目标是交通流量估计. 我们按照时间顺序将把前80%的数据用来训练模型, 剩下20%的数据用来进行测试.
3.2 对比网络模型为了评估Curb-GAN模型的性能, 将本文模型与8种基线模型对比, 基线模型详细介绍如下.
FC-SA[22,23]: 该方法采用条件GAN结构, 在生成器和鉴别器内部均采用堆叠的全连接层和自注意力层.
CNN-SA[24,25]: 该方法采用条件GAN结构, 在生成成器和鉴别器内部采用堆叠的标准卷积层和自注意力层.
FC-GRU[23,25]: 该方法采用条件GAN结构, 在生成器和鉴别器内部均采用堆叠的全连接层和GRU层.
CNN-GRU[23,26]: 该方法采用条件GAN结构, 在生成器和鉴别器内部均采用堆叠的标准卷积层和GRU层.
FC-SA+GRU[23,27]: 该方法采用条件GAN结构, 在生成器和鉴别器内部均采用堆叠的全连接层和自注意力、GRU层.
CNN-SA+GRU[23,28] :该方法采用条件GAN结构, 在生成器和鉴别器内部均采用标准卷积层和自注意力、GRU层.
GCN-GRU[23,29]: 该方法采用条件GAN结构, 在生成器和鉴别器内部采用堆叠图卷积层和多层GRU.
GCN-SA[21,23]: 该方法采用条件GAN结构, 在生成器和鉴别器内部采用堆叠图卷积层和自注意力层.
3.3 评价指标我们使用平均绝对百分比误差(MAPE)和均方根误差(RMSE)来评估Curb-GAN, 计算公式如式(13)、式(14)所示:
| MAPE = \frac{1}{{{N_s}{N_t}}}\sum\limits_{s = 1}^{{N_s}} {\sum\limits_{t = 1}^{{N_t}} | {y_{s, t}}} - {\hat y _{s, t}}|/{y_{s, t}} | (13) |
| {\textit{RMSE}} = \sqrt {\frac{1}{{{N_s}{N_t}}}\sum\limits_{s = 1}^{{N_s}} {\sum\limits_{t = 1}^{{N_t}} {{{({y_{s, t}} - {{\hat y}_{s, t}})}^2}} } } | (14) |
其中, ys,t为在第s个节点和第t个时隙观测到的真实交通状态, 为相应的预测值.
3.4 实验设置用于训练所有模型的数据是间隔5 min进行采集的, 我们一次生成的数据是一个小时的数据, 所以Nt=12, 因此MR、DR、AR、CR的序列长度为12.
Curb-GAN模型结构如下: 模块1堆叠4次, 模块2堆叠3次, 并且使用双头注意力机制. 生成器中构建块1的初始输入特征为312, 堆叠构建块1的隐藏特征为{64, 32, 16, 1}. 鉴别器中构建块1的初始输入特征为5, 堆叠构建块1的隐藏特征为{16, 32, 64, 1}. 使用Adam优化器训练Curb-GAN, β1 = 0.5, β2 = 0.999, 学习率为2×10−4, 训练150个epoch, batch size为64.
3.5 实验结果竞争基线和Curb-GAN的性能如表2和表3所示. 对于每个数据集, 使用测试集的数据来测试模型性能, 对于深度学习模型, 我们对每个模型进行了多次训练和测试, 使用测试的平均结果计算RMSE和MAPE.
| 表 2 在PeMSD8数据集上的交通流量估计的性能结果 |
| 表 3 在PeMSD4数据集上的交通流量估计的性能结果 |
3.6 实验结果分析
对于平均性能, 在两个数据集上的交通流量估计任务中, Curb-GAN在两个指标上都优于所有基线. 具体来说在PeMSD8数据集上, Curb-GAN在RMSE和MAPE上分别比所有基线都平均提高了47.33%和83.70%; 在PeMSD4据集上, Curb-GAN在RMSE和MAPE上分别比所有基线都平均提高了45.54%和71.93%. 与所有基线相比我们的Curb-GAN取得了显著的改进, 因为Curb-GAN使用了GCN、GRU和多头注意力机制很好地捕捉了路网的时空自相关性. GCN-SA和GCN-GRU的结果与其他基线相比, 明显效果更好, GCN-SA和GCN-GRU同时捕获空间和时间自相关性, GCN-GRU使用了GRU处理时间相关性, 但由于GRU的模型表达性和非并行计算的限制, 其估计效果不如Curb-GAN, 从而导致更多的训练时间和较低的生成质量. 目前最具竞争力的模型是GCN-SA和GCN-GRU, 但Curb-GAN可以更好地学习时空模式, 从而获得更低的误差.
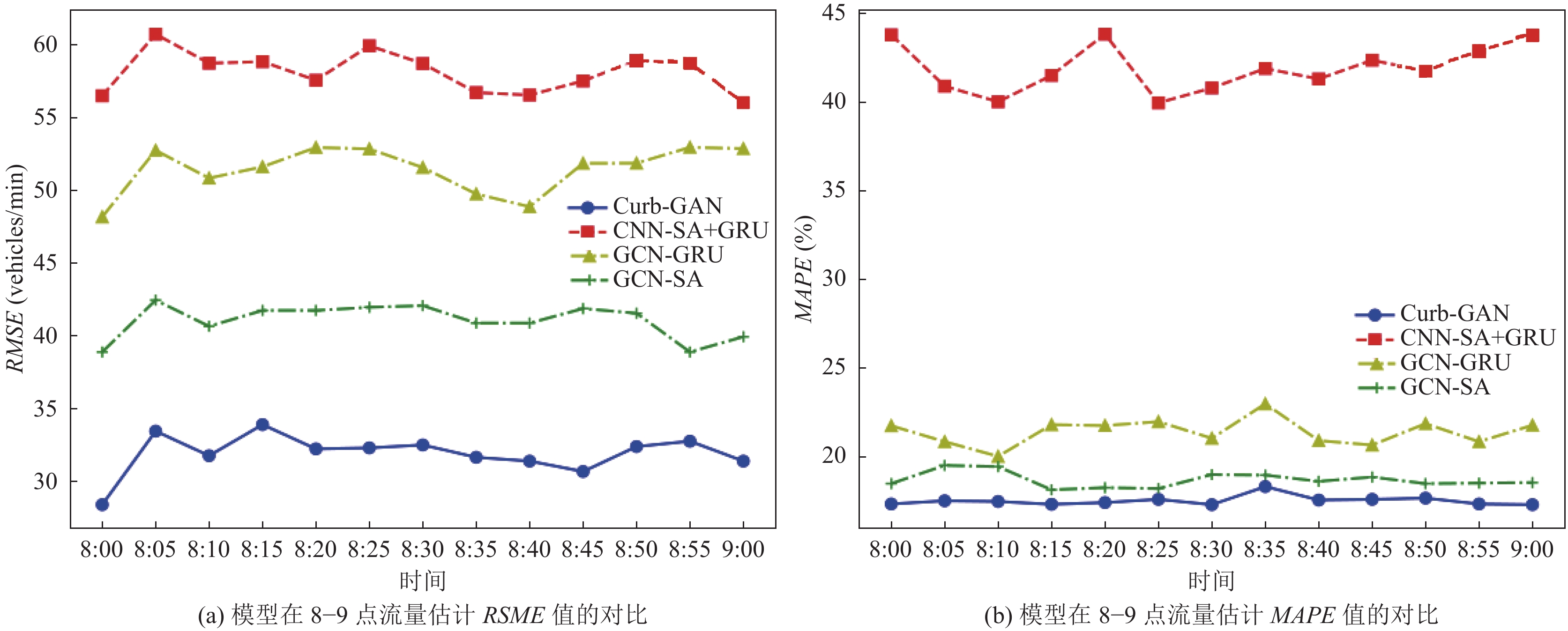
由于Curb-GAN能够提供连续时隙的交通流量估计, 为了说明Curb-GAN在每个时隙的交通流量估计中的有效性, 我们在Curb-GAN和3种最有竞争力的基线模型(包括CNN-SA+GRU、GCN-GRU和GCN-SA)上进行了实验. 以PeMSD8数据集为例, 使用特定时间段的平均生成结果计算统计量. 实验结果如图3(a)和图3(b)所示, 在特定时间段的每个时间点中, Curb-GAN的性能最好. 结果表明, Curb-GAN能较好地捕捉时空自相关性, 具有稳定、优异的连续时隙城市交通流量估计能力.
|
图 3 连续时隙交通流量估计所选模型的比较 |
4 结语
本文将条件城市交通流量估计问题建模为交通流量数据生成问题, 提出了一种新的深度生成模型Curb-GAN, 该模型可以生成连续时段的未来城市交通流量估计. Curb-GAN能够对空间和时间的自相关性进行建模, 并在连续的时隙中产生一系列的交通流量数据. 使用现实世界的时空交通数据集来评估了我们的Curb-GAN, 训练有素的生成器能够生成真实的交通流量数据序列, 并且我们提出的Curb-GAN显著优于所有基线模型.
| [1] |
Castro PS, Zhang DQ, Li SJ. Urban traffic modelling and prediction using large scale taxi GPS traces. Proceedings of the 10th International Conference on Pervasive Computing. Newcastle: Springer, 2012. 57–72.
|
| [2] |
Herring R, Hofleitner A, Abbeel P, et al. Estimating arterial traffic conditions using sparse probe data. Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems. Funchal: IEEE, 2010. 929–936.
|
| [3] |
Yuan J, Zheng Y, Zhang CY, et al. T-drive: Driving directions based on taxi trajectories. Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems. San Jose: ACM, 2010. 99–108.
|
| [4] |
谢宏, 刘敏, 陈淑荣. 基于ICA和SVM的道路网短时交通流量预测方法. 计算机应用, 2009, 29(9): 2550-2553. |
| [5] |
LeCun Y, Bengio Y, Hinton G. Deep learning. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [6] |
Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe: Curran Associates Inc., 2012. 1097–1105.
|
| [7] |
Zhang JB, Zheng Y, Qi DK. Deep spatio-temporal residual networks for citywide crowd flows prediction. Proceedings of the 31st AAAI Conference on Artificial Intelligence. San Francisco: AAAI, 2017. 1655–1661.
|
| [8] |
LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
| [9] |
Cho K, Van Merriënboer B, Gulcehre C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation. Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing. Doha: Association for Computational Linguistics, 2014. 1724–1734.
|
| [10] |
Yu B, Yin HT, Zhu ZX. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. Proceedings of the 27th International Joint Conference on Artificial Intelligence. Stockholm: AAAI Press, 2017. 3634–3640.
|
| [11] |
Kipf TN, Welling M. Semi-supervised classification with graph convolutional networks. Proceedings of the 5th International Conference on Learning Representations. Toulon: ICLR, 2017.
|
| [12] |
Zhao L, Song YJ, Zhang C, et al. T-GCN: A temporal graph convolutional network for traffic prediction. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(9): 3848-3858. DOI:10.1109/TITS.2019.2935152 |
| [13] |
Li YG, Yu R, Shahabi C, et al. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting. Proceedings of the 6th International Conference on Learning Representations. Vancouver: ICLR, 2018.
|
| [14] |
徐丽, 符祥远, 李浩然. 基于门控卷积的时空交通流预测模型. 计算机应用, 2023, 43(9): 2760-2765. DOI:10.11772/j.issn.1001-9081.2022081146 |
| [15] |
Zhang XY, Huang C, Xu Y, et al. Spatial-temporal convolutional graph attention networks for citywide traffic flow forecasting. Proceedings of the 29th ACM International Conference on Information & Knowledge Management. ACM, 2020. 1853–1862.
|
| [16] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. arXiv:1706.03762, 2017.
|
| [17] |
Mirza M, Osindero S. Conditional generative adversarial nets. arXiv:1411.1784, 2014.
|
| [18] |
Goodfellow I, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets. Proceedings of the 27th International Conference on Neural Information Processing Systems—Vol. 2. Montreal: MIT Press, 2014. 2672–2680.
|
| [19] |
Yu LT, Zhang WN, Wang J, et al. SeqGAN: Sequence generative adversarial nets with policy gradient. Proceedings of the 31st AAAI Conference on Artificial Intelligence. San Francisco: AAAI Press, 2017. 2852–2858.
|
| [20] |
Scarselli F, Gori M, Tsoi AC, et al. The graph neural network model. IEEE Transactions on Neural Networks, 2009, 20(1): 61-80. DOI:10.1109/TNN.2008.2005605 |
| [21] |
Velickovic P, Cucurull G, Casanova A, et al. Graph attention networks. Proceedings of the 6th International Conference on Learning Representations. Vancouver: ICLR, 2018.
|
| [22] |
Bahdanau D, Cho K, Bengio Y. Neural machine translation by jointly learning to align and translate. arXiv:1409.0473, 2014.
|
| [23] |
Mogren O. C-RNN-GAN: Continuous recurrent neural networks with adversarial training. arXiv:1611.09904, 2016.
|
| [24] |
Yu AW, Dohan D, Luong MT, et al. QANet: Combining local convolution with global self-attention for reading comprehension. Proceedings of the 6th International Conference on Learning Representations. Vancouver: ICLR, 2018.
|
| [25] |
Castán-Lascorz MA, Jiménez-Herrera P, Troncoso A, et al. A new hybrid method for predicting univariate and multivariate time series based on pattern forecasting. Information Sciences, 2022, 586: 611-627. DOI:10.1016/j.ins.2021.12.001 |
| [26] |
Tan CQ, Sun FC, Zhang WC, et al. Multimodal classification with deep convolutional-recurrent neural networks for electroencephalography. Proceedings of the 24th International Conference on Neural Information Processing. Guangzhou: Springer, 2017. 767–776.
|
| [27] |
Ott J, Lin ZH, Zhang Y, et al. Recurrent neural networks with limited numerical precision. arXiv:1608.06902, 2016.
|
| [28] |
Qin Y, Song DJ, Cheng HF, et al. A dual-stage attention-based recurrent neural network for time series prediction. Proceedings of the 26th International Joint Conference on Artificial Intelligence. Melbourne: AAAI Press, 2017. 2627–2633.
|
| [29] |
Hang R, Li MX. Spatial-temporal adaptive graph convolutional network for skeleton-based action recognition. Proceedings of the 16th Asian Conference on Computer Vision. Macao: Springer, 2022. 172–188.
|
 2024, Vol. 33
2024, Vol. 33



