2. 中国电子科技集团第十五研究所 西安研发中心, 西安 710005
2. Research and Development Center of Xi’an, the 15th Research Institute of China Electronics Technology Group, Xi’an 710005, China
在单目标跟踪[1]中, 目标模型的设计[2,3]、融合[4,5]和更新[6]是跟踪问题的关键. 在不同的跟踪场景下, 如何设计模型是首要考虑因素. 其次在进行模型融合和更新时, 需要重点关注置信度量化与融合策略以及模型更新策略, 这是目标跟踪研究的关键所在.
单模态建模容易降低算法的准确性和鲁棒性, 且过分依赖于特定数据. 多模态方法通过结合图像、激光雷达和深度图像等多种数据[7–10], 提高了处理跟踪问题的能力. 例如, Gong等人提出的DCFE算法[11]利用颜色特征和注意力机制来强化目标区域的特征, 提高检测性能. 虽可有效提高目标检测能力, 但算法的复杂性限制了其计算效率, 并且在非特定(如非水下)场景中可能不够有效, 导致信息丢失.
模型融合的成功关键在于选择合适的融合方法, 这直接决定了目标跟踪的性能. 一种方法是集成学习[12], 如Zhao等人提出的GADE-Net算法[13], 它通过结合不同模型的参数来提高目标检测的准确度, 并减少决策随机性和过拟合问题, 但这增加了计算复杂度和对高质量标注数据的需求. 另一种方法是使用多尺度神经网络, 比如孙备等人提出的MUC算法[14–16], 该算法引入了多尺度互交叉注意力模块以提升伪装目标检测的精度, 并融合了多种数据类型以更准确地定位目标. 尽管这些方法在提高检测准确性方面表现出色, 但在需要快速反应且计算资源有限的场景下, 它们的优势可能不会完全显现.
目标跟踪在实际应用中常受到光照、遮挡和图像质量变化的影响, 这些因素都可能导致目标外观的显著变化, 因此模型的及时更新变得至关重要. 为应对这一挑战, 一些研究提出了不同的模型更新策略. 例如, Zhang等人提出的SSIT算法[17]采用了一种增量学习方法, 它基于样本选择来优化训练过程, 避免了训练信息丢失问题, 但这也使得训练更加复杂. Li等人提出了一种基于DCF框架的动态学习率算法[18], 这种方法可以根据目标的运动变化动态调整学习率, 以适应目标外观的变化. 然而, 在遮挡情况下, 这种方法可能会导致过拟合, 从而影响跟踪性能.
本文着眼单目标跟踪步骤中所出现的问题, 在构建颜色模型的前提下, 为HOG特征引入双线性插值[19]以建立高维度形状模型; 针对上述多模态模型[20]设计深层次高置信度模型融合策略, 特别提出量纲层级及其归一化标准, 对模型内、模型间的多种置信度, 分别实施平均权衡机制和高置信度倾向的自适应权衡机制, 确保融合目标的高置信度; 最后根据不同模型的更新需求, 设计模型分级非线性学习率曲线及参数, 同时设定学习率的波动上下限, 以保持模型跟踪模板的稳定性和可靠性; 并采用粒子滤波的搜索方式, 提高在线跟踪目标的速度和鲁棒性.
1 目标多模态模型设计与搜索策略 1.1 目标多模态模型设计本文将颜色特征视为快速识别目标的关键因素, 首先将目标
| Cm=Xmmax | (1) |
其中,
|
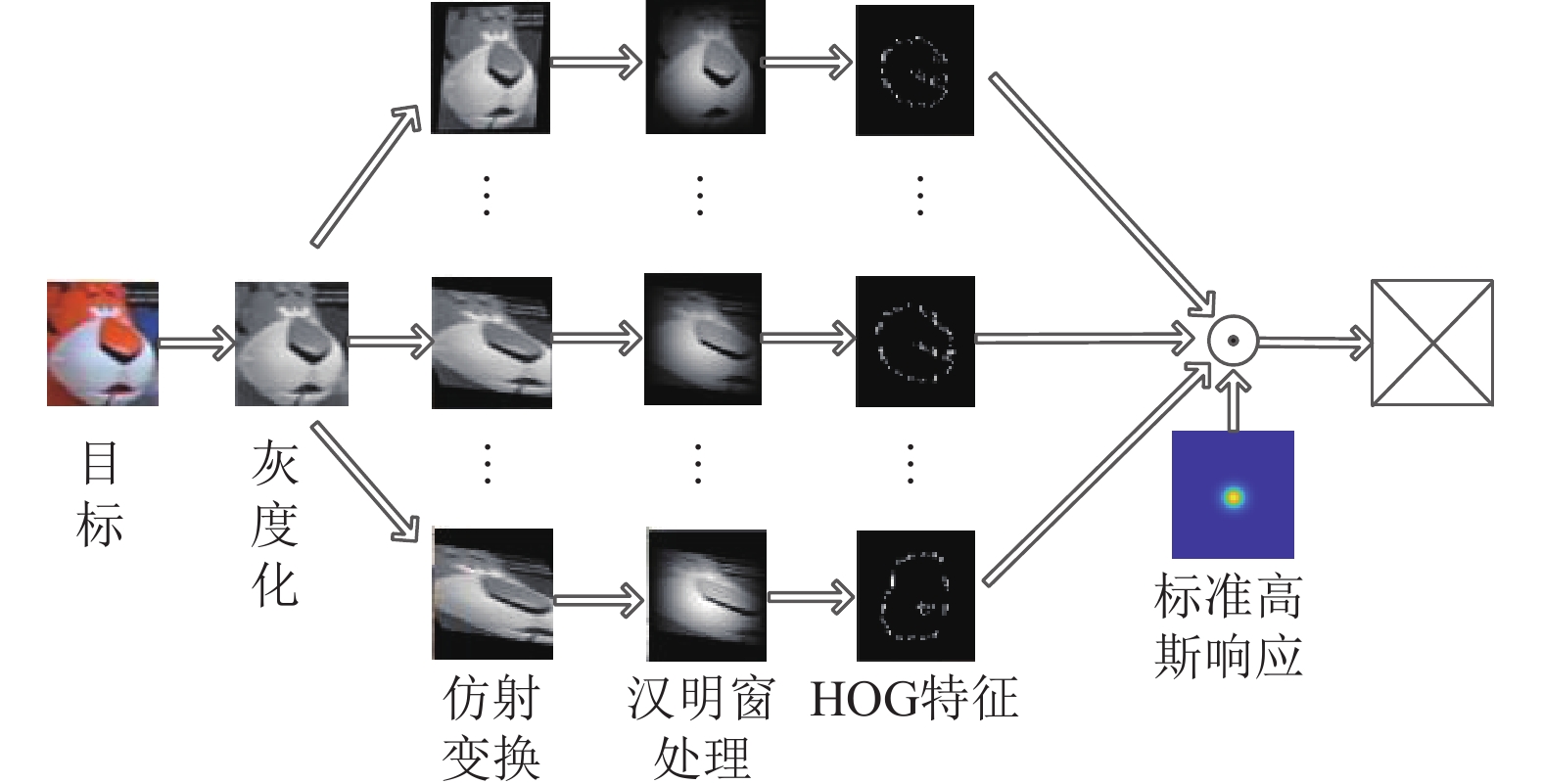
图 1 形状模型建模过程 |
形状模型训练过程如下: 依据卷积定理, 在频域中变量有如下关系:
| F(g) = F(f) \odot {F^*}(h) | (2) |
其中,
| {H^*} = \frac{{G_i}}{{F_i}}, \quad i = 1, {\text{ }}2, \cdot \cdot \cdot {\text{ }}, N | (3) |
| \mathop {\min }\limits_{{H^*}} {\sum\limits_{i = 1}^N {\left| {F_i \odot {H^*} - G_i} \right|} ^2} | (4) |
由此得到最优解
| {H^*} = \frac{{\displaystyle\sum\limits_{i = 1}^N {G_i \odot F_i^*} }}{{\displaystyle\sum\limits_{i = 1}^N {F_i \odot F_i^*} }} | (5) |
其中,
在目标跟踪中, 当前帧的目标大致位于前一帧附近, 为了降低运行开销, 增加算法速度, 使用粒子滤波方法[20]预测当前帧的目标位置特别合适. 这种方式可以限制目标在当前帧的搜索范围, 并且搜索过程中粒子只需移动一次, 提升了搜索效率. 粒子
如图2所示, 一旦获得第一帧的目标, 就会在目标的位置周围分配一组若干的粒子框, 作为初始运动模型. 考虑到跟踪速度和搜索范围, 本文设置了50个粒子框. 接着这些粒子框会根据式(6)进行转移, 从而预测目标可能出现在当前帧中的所在位置:
| \left\{ \begin{gathered} M_t^i(x) = 2\times M_{t - 1}^i(x) - M_{t - 2}^i(x) + {R_x} \\ M_t^i(y) = 2\times M_{t - 1}^i(y) - M_{t - 2}^i(y) + {R_y} \\ M_t^i(s) = 2\times M_{t - 1}^i(s) - M_{t - 2}^i(y) + {R_s} \\ \end{gathered} \right. | (6) |
其中,

|
图 2 运动粒子模型示意图 |
2 多模态模型信息的准确量化 2.1 形状模型信息量化表达的局限性
在第1.2节中描述的目标搜索过程中, 候选粒子框与目标的多模型需要进行相似度计算. 然而, 由于颜色模型和形状模型是两种不同类型的跟踪器, 候选粒子框在形状模型计算时存在一些容易被忽视的问题. 例如, 文献[20]中在使用计算形状模型相似度信息时, 会以跟踪响应中心位置的值作为两者之间相似度. 但这样可能会导致两个问题.
(1) 在目标经历形变、旋转或部分遮挡时, 单纯依赖中心响应值来衡量相似度往往不能准确反映实际情况, 这一限制可能会降低跟踪的准确度. 此外, 跟踪响应的中心值会受到局部噪声、背景变动或光照条件改变的干扰, 进而影响到相似度评估的准确性. 这种情况下, 算法可能会误判候选目标框的有效性, 尤其在目标与背景相近或背景较为复杂的环境中, 错配和跟踪偏差的风险会明显增加.
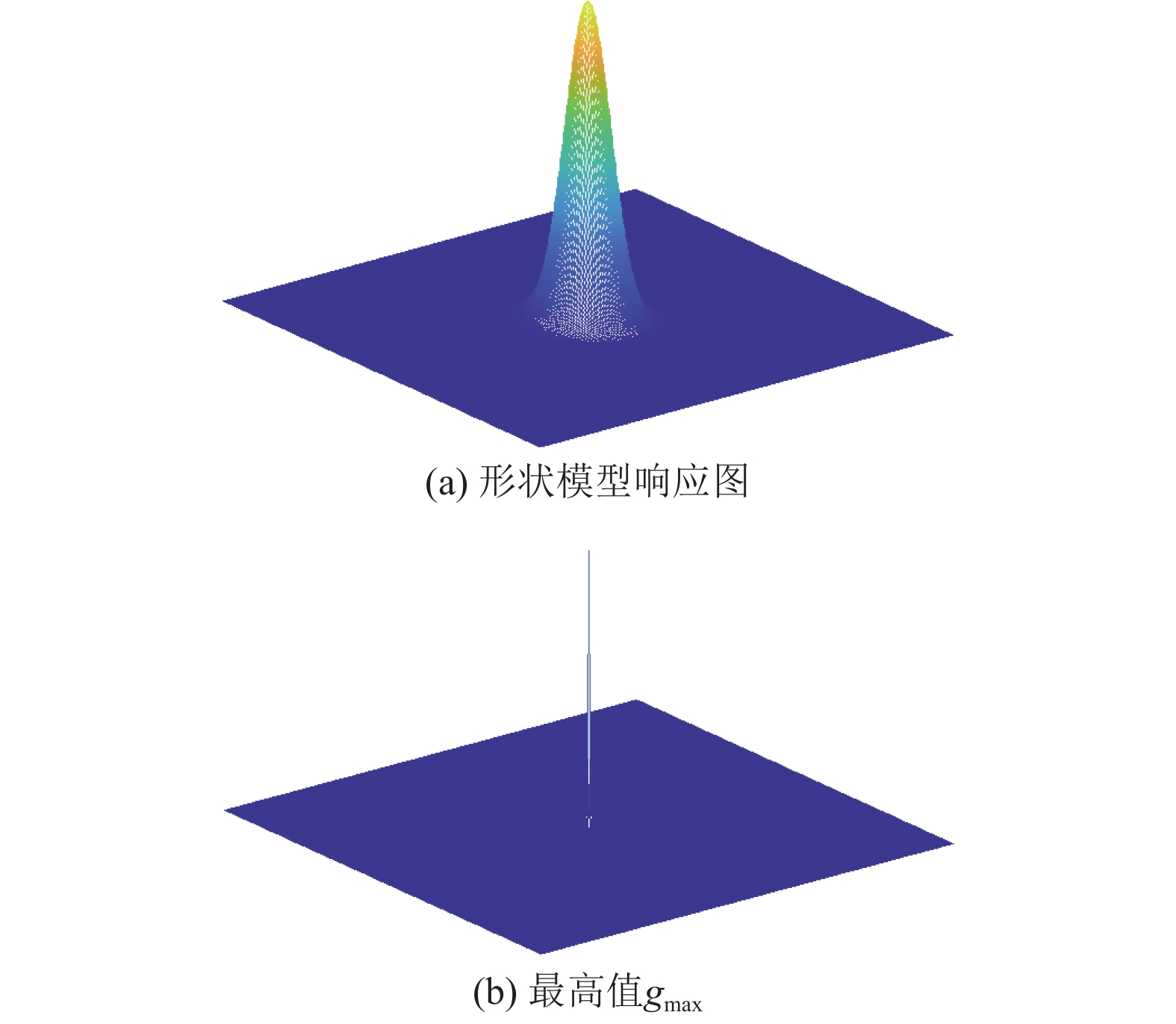
(2) 如图3(a)所示, 形状模型的响应图代表了候选区域在特定空间下的全面表达, 包含了丰富的全局信息分布. 最高响应值仅占整个响应图的小部分, 导致大量有效信息未被充分利用. 若仅依赖图3(b)所示的gmax作为评估标准, 会忽略关键的全局信息, 尤其在gmax未能全面代表整体信息的场合下更为显著, 进而造成目标模型与实际潜在目标框之间的错配.
2.2 模型的全局信息量化如第2.1节所述, 模型信息的表述会直接影响模型的正确融合. 因此, 本文首先将候选框颜色模型与目标颜色模型的巴氏距离
DSST算法[21]中使用单一模型时, 无法全面捕获目标的多维度信息, 导致算法在处理复杂背景或光照变化时的鲁棒性降低. 为解决第2.1节中形状信息缺失和DSST算法中的问题, 本文设计了一种利用响应图全局信息的多置信度表达, 通过结合PSR和APCE这两个指标, 分别记为
| gp_i = \frac{{g_{\max} - \mu _{s1}}}{{\sigma_{s1}}} | (7) |
| ga_i = \frac{{|g_{\max} - g_{\min}{|^2}}}{{mean\left( {\displaystyle\sum\limits_{w, h} {{{\left( {{g_{w, h}} - g_{\min}} \right)}^2}} } \right)}} | (8) |
式(7)中
|
图 3 形状模型两种信息的差异 |
3 多模态模型的融合与更新策略 3.1 模型深层次权衡融合策略设计
如第2.2节所述, 候选框具有多个可量化的置信度, 然而在特定场景中确定目标时, 需要对置信度进行评判, 从而权衡它们以获取最终的融合结果.
SAMF算法[21]在如何具体执行模型融合及其权重动态调整的详细描述不够明确, 包括模型选择的标准、权重的计算方法以及自适应策略等具体细节, 为了填补此空白, 本文提出了一种较为简易的深层次权衡融合策略, 能在个别置信度不佳时, 通过不同置信度的相互调整, 确保整体的准确性, 从而提高跟踪的精度与稳定性.
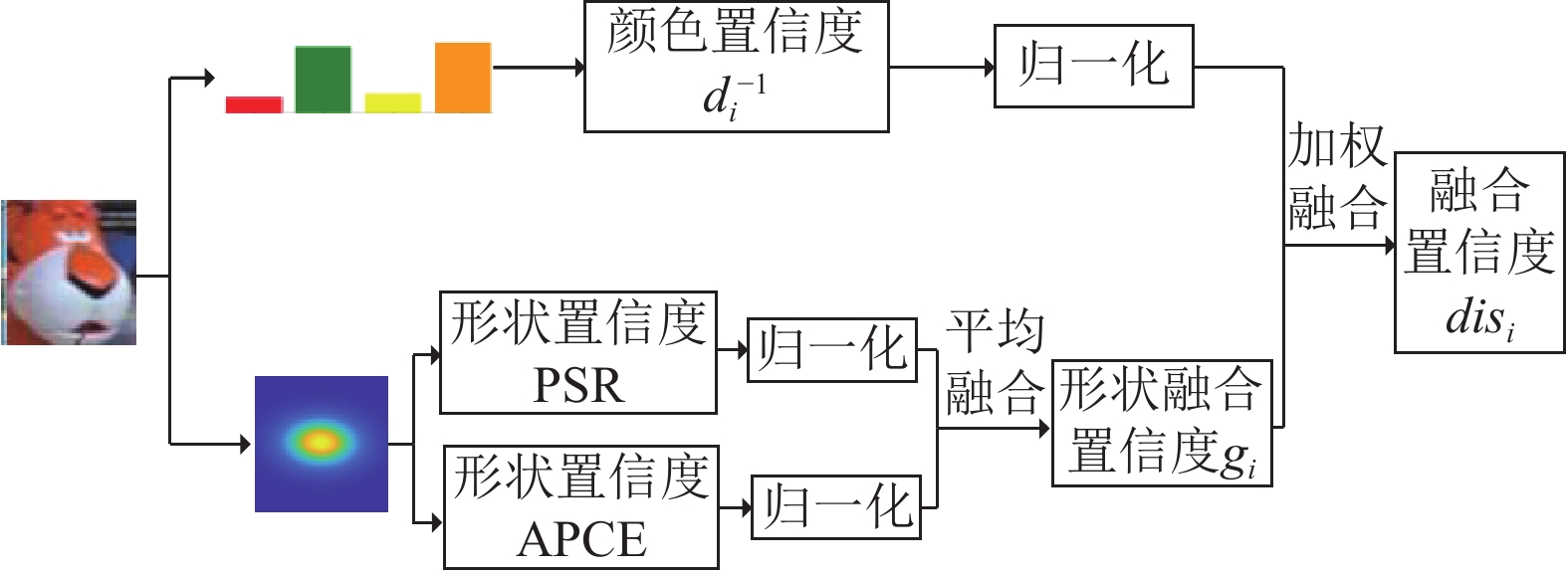
针对以上需求, 本文首先设定一个从0到1的指标范围作为融合框架, 然后进行形状模型两种置信度的浅层融合. 之后以高置信度为融合标准, 将形状置信度
|
图 4 模型深层次权衡融合策略 |
两种置信度的相似度极限分别记为
| g_{i}=\frac{1}{2}\left(\frac{g a_{i}}{g a_{\max }}+\frac{g p_{i}}{g p_{\max }}\right) | (9) |
在不同模型间的融合之前, 同样也需要计算归一化的颜色置信度:
| d_i^{ - 1} = \frac{{dt_i^{ - 1}}}{{d_{c\min}^{ - 1}}} | (10) |
式(10)中,
针对不同模型间的置信度融合, 本文设计了一种高置信度权衡机制, 根据颜色模型和形状模型的波动程度做动态调整, 力求获取高置信度的候选框. 融合后的值
| dis_i=(1-\tau )d_{i}^{-1}+\tau g_i\text{ }\text{, }i=\text{1}\text{, }\text{2}\text{, }\cdots\text{, }M | (11) |
其中,
由第3.1节中式(11)可知, 模型间融合的核心点在于融合权重参数
为解决SAMF算法[21]因参数调整繁琐而导致初始化设置复杂、调试难度增加的问题, 本文提出了一种偏向高置信度的融合参数选择策略. 该策略主要基于一个简化的准则: 注意力仅聚焦于高置信度, 在融合过程中为其分配更高的权重, 策略如下所示.
(1)
(2)
(3)
| \tau= \begin{cases}0.5+0.5\left(\dfrac{g_i-d_i^{-1}}{\min \left\{g_i, d_i^{-1}\right\}}\right), & d_i^{-1}>\varepsilon_1 且 g_i>\varepsilon_2 \\ 0, & d_i^{-1}>\varepsilon_1 且 g_i \leqslant \varepsilon_2 \\ 1, & d_i^{-1} \leqslant \varepsilon_1 且 g_i>\varepsilon_2\end{cases} | (12) |
(4)
| \left\{ \begin{gathered} 0,{\text{ }}{d_{{i}}}^{ - 1} > {g_i} \\ {\text{1, }}{d_{{i}}}^{ - 1} \leqslant {g_i} \\ \end{gathered} \right. | (13) |
经过实验, 本文将
在得到当前帧目标的位置后, 需要分别对颜色和形状模型进行更新, 这个过程当中, KCF算法[21]使用固定式的学习率更新模型, 固定学习率意味着模型更新的速度和强度在整个跟踪过程中保持不变, 这可能不适用于所有场景, 特别是在目标外观发生快速或显著变化的情况下. 并且如果目标在连续几帧内遭受遮挡或显著形变, 可能导致模型过度拟合于最近的错误样本, 从而导致跟踪偏差. 为解决此问题, 本文设计一种非线性分级平衡更新策略, 确定非线性分级学习率曲线函数, 作为模型在学习和优化过程中的“步长”控制器. 在设计曲线时, 在不同阶段考虑了模型更新的学习率强度, 并限制其波动范围以保持模型的稳定性和避免过拟合. 记:
| \left\{ \begin{gathered} d_{\min}^{ - 1} = \mathop {\max }\limits_i \{ d_i^{ - 1}\}, \\ {g_{\max}} = \mathop {\max }\limits_i \{ g_i\}, \\ \end{gathered} \right.{\text{ }}i = 1, 2, \cdots , M{\text{ }} | (14) |
式(14)中通过当前帧的最优颜色置信度
(1) 颜色模型更新策略: 当前帧的最优颜色模型记为
| C_u(t+1)=(1-\lambda) C_u(t)+\lambda C_u^*(t), \quad u=1, \cdots, m | (15) |
其中,
| \lambda = \left\{ \begin{gathered} 0.08{(d_i^{ - 1} - 0.16)^3} + 0.05,\begin{array}{*{20}{c}} {}&{d_{\min}^{ - 1} > {\varepsilon _1}} \end{array} \\ 9.76{(d_i^{ - 1} - 0.16)^3} + 0.05,\begin{array}{*{20}{c}} {}&{d_{\min}^{ - 1} \leqslant {\varepsilon _1}} \end{array} \\ \end{gathered} \right. | (16) |
式(15)中
当
(2) 形状模型更新策略: 当前帧的目标
| \left\{ \begin{gathered} {A_t} = (1 - \eta ) \times{A_{t - 1}} + \eta \times{g_t} \odot F_t^* \\ {B_t} = (1 - \eta )\times{B_{t - 1}} + \eta \times{F_t} \odot F_t^* \\ {H^*} = {A_t}/{B_t} \\ \end{gathered} \right. | (17) |
与上述颜色模型更新的分析类似, 形状模型更新系数
| \eta = \left\{ \begin{gathered} 0.07{(g_i - 0.12)^3} + 0.05,{\text{ }}\;\; g_{\max} > \varepsilon_ 2 \\ 23.15{(g_i - 0.12)^3} + 0.05,{\text{ }}g_{\max} \leqslant \varepsilon _2 \\ \end{gathered} \right. | (18) |
当
本文提出的多模态深层次高置信度融合跟踪算法, 通过结合颜色模态和形状模态的多置信度, 利用深层次高置信度融合策略, 实现了高精度的目标跟踪. 该算法具体如算法1所示.
算法1. 多模态深层次高置信度融合跟踪算法
输入: 图像序列
输出: 每一帧图像的目标位置
step 1. 在第1帧对给定目标分别建立颜色和形状模型.
根据式(1)建立目标的颜色模型
step 2. 随机初始化粒子群的状态:
| \scriptstyle S_i = \{ P, R, V{\text{,}}a\} , {\text{ }}i{\text{ = 1, }}\cdots{\text{, }}M |
在第1帧目标位置及其附近放置粒子群. 粒子的具体含义参见第1.2节.
step 3. 对候选目标进行粒子滤波搜索获得最优解.
a) 粒子根据式(6)进行转移, 根据式(7)和式(8)分别计算每个粒子
b) 根据式(9)融合形状响应置信度
c) 选择当前帧
step 4. 模型更新.
a) 根据式(15)和式(16)更新颜色模型
b) 根据式(17)和式(18)更新形状滤波器模型
step 5. 在下一帧循环step 3和step 4.
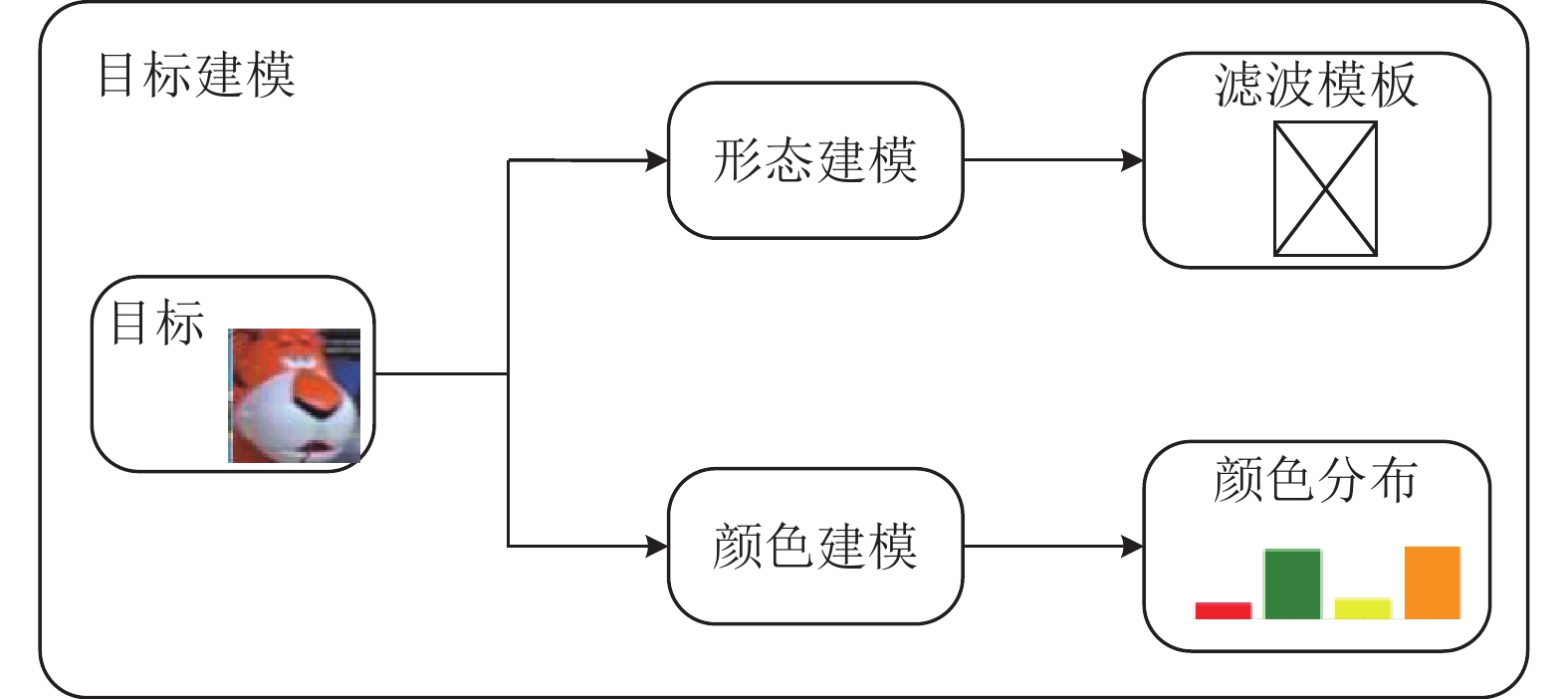
图5和图6分别展示了算法中目标建模流程和算法的具体步骤以及它们在整体跟踪流程中的协同作用.
在跟踪流程的起始阶段, 算法首先对输入视频序列的第1帧中的目标进行分析, 分别通过step 1和step 2建立多模态模型和粒子初始化.
随后算法进入到跟踪搜寻目标的过程, 在每一新帧图像中执行step 3, 通过这个步骤, 候选框和多模态模型进行置信度计算与融合, 之后经过排序筛选后得到该帧的目标并进行粒子重采样.
一旦确定了当前帧的目标, 算法即通过step 4进行模型更新, 对颜色模型和形状模型进行微调和迭代, 确保模型的持续适应性和跟踪的准确性.
最终, 通过step 5算法实现对整个视频序列的连贯跟踪. 在这个阶段, step 3和step 4步骤循环执行, 直至视频的最后一帧.
|
图 5 目标建模示意图 |
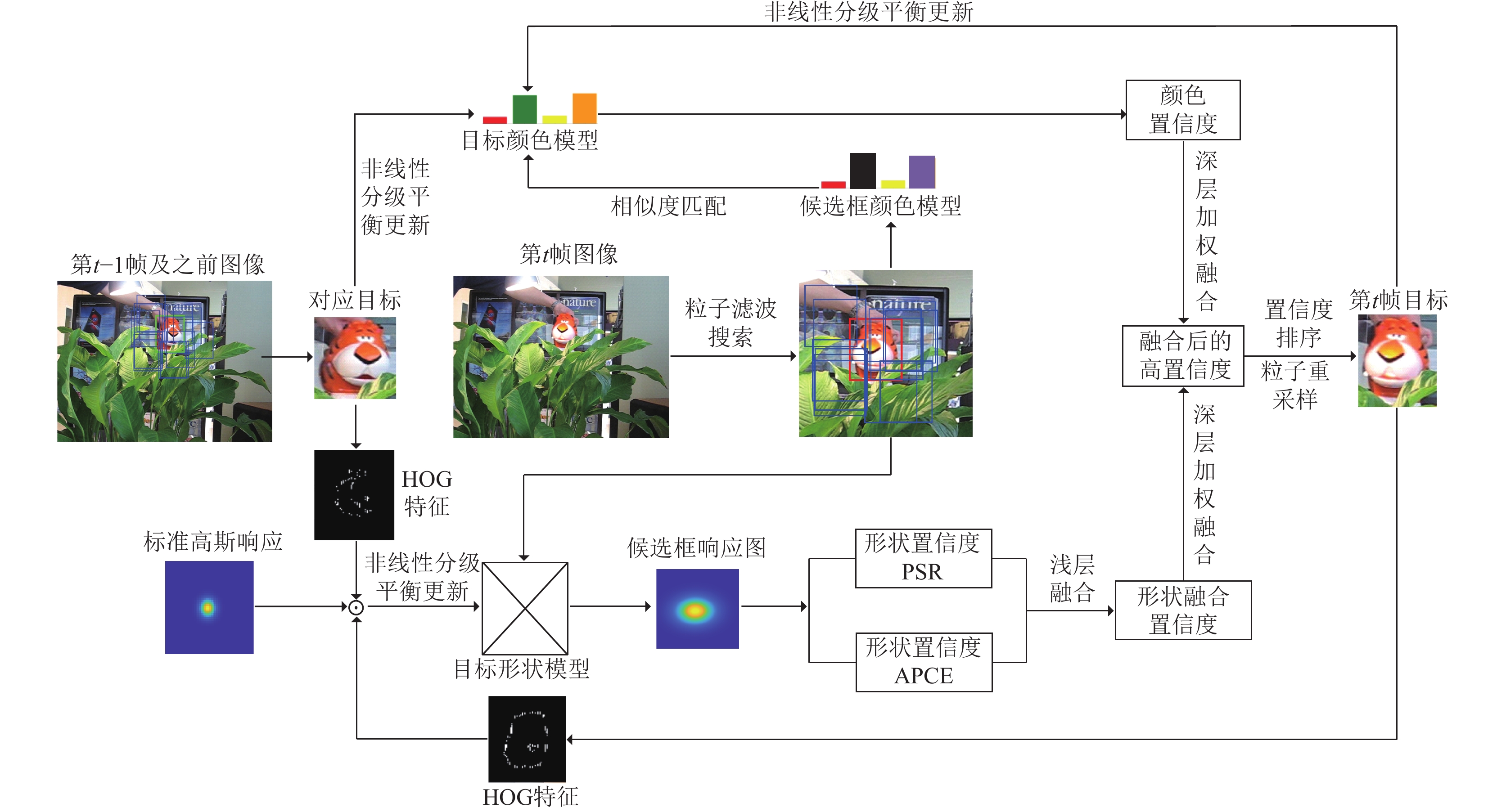
|
图 6 本文算法跟踪示意图(视频帧从t=2开始) |
5 实验与结果分析
本文所使用的测试数据集OTB-2015包含的视频序列有11个属性解释, 涉及各种挑战性因素, 是最权威的视觉目标跟踪数据集之一. 实验环境的技术参数为: Intel Core 1135G7的CPU, 主频2.40 GHz, 内存40 GB, 编程平台VS2022, 实验评估平台Matlab R2022a.
为了充分评估本文算法, 实验从中选取了一些与本文最相关的顶尖算法[21]作为对比, 分别为SAMF、fDSST、DSST、Staple、KCF、KCF-GaussHog和KCF-LinearHog.
本文算法改进了SAMF算法的模型融合方式, 以增强目标描述的准确性, 并创新性地引入了一个高置信度准则, 提供了一种比SAMF算法更加复杂和精细的策略. 本算法融合了KCF及其变种算法所依赖的HOG特征模型, 以及Staple算法使用的颜色直方图模型, 不同的是本算法通过多模态模型的多置信度融合, 超越了前者的单一模型依赖和后者简单模型的融合方法. 不同于DSST和fDSST算法通过尺度滤波器达成的尺度适应, 本算法通过模型融合策略提升了对目标尺寸变化的适应能力. 此外提出的模型更新机制与上述比较算法中的策略均不相同, 体现了明显的创新性.
本文使用5种指标评价上述算法的性能: 中心误差(CLE)、重叠率(OS)、精确率(accuracy rate)、成功率(success rate)和平均帧率(FPS). 中心误差和重叠率的计算式为:
| C L E=\sqrt{\left(x_T-x_G\right)^2+\left(y_T-y_G\right)^2} | (19) |
| OS = \frac{{s{\text{(}}{R_T} \cap {R_G}{\text{)}}}}{{s({R_T} \cup {R_G})}} | (20) |
式(19)和式(20)中,
图7展示了本文算法(以下简称该算法)与其他相关顶尖算法在OTB数据集测试的一次通过性(OPE)跟踪精确率和成功率. 图7(a)中方括号内的数值表示中心误差阈值为20时的精确率, 而图7(b)中方括号内的数值表示重叠率阈值为0.5时, 对应算法的跟踪成功率. 从图7中可以观察到, 算法在整体OPE评估指标中显示出了最好的跟踪精确率(0.798), 尤其是当中心误差阈值大于20时, 该算法在所有参照算法中的精确率最高; 从跟踪成功率角度分析, 在重叠率大于0.3时, 该算法的成功率均显著优于其他参照算法. 以上两方面的结果均证明本文方法使目标更容易被跟踪, 证明了该算法的优越性. 表1展示了图7中所有算法在数据集上的定量指标. 可看出该算法的平均CLE和OS指标在所有参照算法中表现最好, 平均CLE为30.57, 比次优的Staple算法减少1.48, 平均OS为0.609, 比次优的KCF算法提高2.3%, 且FPS为15.67, 满足一般实时性要求.

|
图 7 算法OPE跟踪精确率和成功率图 |
| 表 1 各个算法的性能对比 |
5.2 不同场景下算法评估
本文选取了光照、平面外旋转、尺度变化、变形以及离开视野等具体场景进行多方位定性定量评估, 图8给出所参照的所有算法在特定场景的跟踪结果, 可定量印证本文算法跟踪效果.
同时本文也列出了所参照算法在特定场景的直观对比, 可定性印证本文算法的跟踪效果, 如图9所示.

|
图 8 不同场景下OPE跟踪精确率和成功率图 |

|
图 8 不同场景下OPE跟踪精确率和成功率图(续) |
如图8和图9所示, 该算法在光照变化和平面外旋转场景中的精确率分别为0.758和0.790, 均为所有算法中最优, 当CLE阈值大于20、OS阈值大于0.4时, 该算法的精确率和成功率显著优于参照算法. shaking序列的第10–364帧和sylvester序列的第

|
图 9 算法在不同场景的直观对比结果(正红色实线框为本文算法) |

|
图 9 算法在不同场景的直观对比结果(正红色实线框为本文算法)(续) |
6 结论
本文提出了一种多模态深层次高置信度融合跟踪算法. 通过构建高维度多模态模型, 提出了量纲层级统一的归一化标准; 此外, 设计了平均权衡机制和高置信度倾向的自适应权衡机制, 实现多模态模型的置信度融合; 同时, 设计了模型分级非线性学习率曲线及参数, 设定了学习率的波动上下限, 完成模型的非线性分级平衡更新; 采用了粒子滤波搜索方式筛选潜在目标, 提高了跟踪速度. 实验结果表明, 在OTB-2015数据集上, 该算法取得了较好的效果, 验证了算法的有效性和泛化能力. 但是本文算法仍存在不足: 模型更新的超参数调整耗时且困难, 导致在某些跟踪场景下无法进行有效跟踪, 并且仅能对预选框等比例缩小或放大, 影响正确目标的选取. 后续将着重于解决这些问题, 向更多场景进行高指标泛化.
| [1] |
Ni JJ, Wang XT, Gong T, et al. An improved adaptive ORB-SLAM method for monocular vision robot under dynamic environments. International Journal of Machine Learning and Cybernetics, 2022, 13(12): 3821-3836. DOI:10.1007/s13042-022-01627-2 |
| [2] |
齐滨, 田金, 邹男, 等. 量测驱动的自适应似然无源弱目标跟踪. 声学学报, 2023, 48(5): 959-970. DOI:10.12395/0371-0025.2022029 |
| [3] |
徐文, 吴雨桑, 张婷. 多阵列水下多目标跟踪的分布式算法研究. 信号处理, 2023, 39(10): 1764-1774. |
| [4] |
Xiu CB, Ma YF. Kernel correlation filter tracking strategy based on adaptive fusion response map. IET Image Processing, 2022, 16(4): 937-947. DOI:10.1049/ipr2.12156 |
| [5] |
陈仁祥, 谢文举, 徐向阳, 等. 基于数据融合和改进MoCo的工业机器人抖动原因识别. 仪器仪表学报, 2023, 44(7): 112-120. |
| [6] |
张惊雷, 宫文浩, 贾鑫. 基于自引导注意力的双模态校准融合目标检测算法. 模式识别与人工智能, 2023, 36(9): 793-805. |
| [7] |
Yue YY, Yang Y, Yu YT, et al. Improving multi-object tracking by full occlusion handle and adaptive feature fusion. IET Image Processing, 2023, 17(12): 3423-3440. DOI:10.1049/ipr2.12874 |
| [8] |
段可欣, 闫文君, 刘凯, 等. 融合双谱特征的雷达辐射源个体识别方法. 海军航空大学学报, 2023, 38(5): 382-390. |
| [9] |
夏鸿斌, 黄凯, 刘渊. 多特征融合短会话推荐模型. 模式识别与人工智能, 2023, 36(4): 354-365. |
| [10] |
Anzid H, Le Goic G, Bekkari A, et al. A new SURF-based algorithm for robust registration of multimodal images data. The Visual Computer, 2023, 39(4): 1667-1681. |
| [11] |
Gong TY, Zhang MM, Zhou Y, et al. Underwater image enhancement based on color feature fusion. Electronics, 2023, 12(24): 4999. DOI:10.3390/electronics12244999 |
| [12] |
Nanni L, Faldani G, Brahnam S, et al. Improving foraminifera classification using convolutional neural networks with ensemble learning. Signals, 2023, 4(3): 524-538. DOI:10.3390/signals4030028 |
| [13] |
Zhao M, Yang R, Hu M, et al. Deep learning-based technique for remote sensing image enhancement using multiscale feature fusion. Sensors, 2024, 24(2): 673. DOI:10.3390/s24020673 |
| [14] |
孙备, 党昭洋, 吴鹏, 等. 多尺度互交叉注意力改进的单无人机对地伪装目标检测定位方法. 仪器仪表学报, 2023, 44(6): 54-65. |
| [15] |
Bhat G, Danelljan M, van Gool L, et al. Learning discriminative model prediction for tracking. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 6181−6190.
|
| [16] |
周天奕, 丁卫平, 黄嘉爽, 等. 模糊逻辑引导的多粒度深度神经网络. 模式识别与人工智能, 2023, 36(9): 778-792. |
| [17] |
Zhang YC, Liu YD, Yang GM, et al. SSIT: A sample selection-based incremental model training method for image recognition. Neural Computing and Applications, 2022, 34(4): 3117-3134. DOI:10.1007/s00521-021-06515-4 |
| [18] |
Li D, Li S, Wei Q, et al. Dynamic learning rate of template update for visual target tracking. Mathematics, 2023, 11(9): 1988. DOI:10.3390/math11091988 |
| [19] |
Zhou RG, Wan C. Quantum image scaling based on bilinear interpolation with decimals scaling ratio. International Journal of Theoretical Physics, 2021, 60(6): 2115-2144. DOI:10.1007/s10773-021-04829-6 |
| [20] |
陈昭炯, 叶东毅, 林德威. 基于背景抑制颜色分布新模型的合成式目标跟踪算法. 自动化学报, 2021, 47(3): 630-640. |
| [21] |
刘艺, 李蒙蒙, 郑奇斌, 等. 视频目标跟踪算法综述. 计算机科学与探索, 2022, 16(7): 1504-1515. DOI:10.3778/j.issn.1673-9418.2111105 |
 2024, Vol. 33
2024, Vol. 33



