无线传感网络(wireless sensor network, WSN)由大量静止或者移动的自组织传感器节点所构成, 其目的是对监测区域中目标的信息进行采集和处理^[1]并将数据传送给用户, 用户根据收到的数据做出决策^[2]. 无线传感网络在生活中的很多方面都有着广泛的应用, 如灾害报警、结构监测^[3,4]等. 线性无线传感网络(LWSN)是无线传感网络中具有线性拓扑结构的网络, 其在许多场景下都有着广泛的应用, 如铁路、天然气或石油管道等^[5–10]. 由于此类基础设施对LWSN具有很高的可靠性要求, 因此在设计LWSN之初需要一种能够准确评估LWSN可靠性的方法, 其中连通性与覆盖率是LWSN可靠性研究的重要指标.

目前已有一些学者在LWSN可靠性的方面进行研究. Çıbuk等^[11]提出了一种防止网络中节点之间通信中断的方法, 如果网络中的节点失效, 则激活其相邻节点、扩大相邻节点的通信范围. 但该文献仅研究单个节点与网络断开连接的情况并没有分析连续多个节点失效的情况. Mo等^[12]提出了MDD (multivalued decision diagram)算法来评估具有主干节点混合分层结构的LWSN连通可靠性, 其方法与传统的枚举方法相比更有效, 但该文献在研究LWSN可靠性的过程中没有考虑覆盖率. Mohamed等^[13]提出了一种同时研究LWSN的连通性与覆盖率的可靠性评估方法, 通过测试不同的MJF、NSR, 以评估LWSN的可靠性, 其思想对于LWSN的可靠性评估具有重要意义. 但该文献中节点的故障概率遵循二项分布, 无法准确反映节点随时间变化的寿命特征. Tripathi等^[14]介绍了无线传感网络中分析覆盖率的概率感知probabilistic sensor coverage模型. 如果节点对目标区域的感知概率低于期望阈值, 则节点对该区域的监测失效. Yang等^[15]针对平面结构和集群结构的LWSN提出了一种基于0/1圆盘感知模型的可靠性分析方法, 该模型中节点感知目标的概率恒定. 如果节点存活, 则节点对监测范围内目标的感知概率为100%; 如果节点失效, 则节点对监测范围内目标的感知概率为0. 因此, 节点对区域的监测仅有两种情况, 即全覆盖与未覆盖. 由于该模型忽略了使模型复杂化的细节, 导致对LWSN的可靠性评估结果高于实际值.

感知数据是传感网络正常运行过程中极其重要的任务. 传感器节点的感知覆盖通常被假定为在所有方向上均匀分布, 遵循0/1圆盘感知模型. 在节点的感知半径内发生的事件被假定以概率1被探测到, 而超出这个影响范围的事件被假定未被探测到. 这种理想化模型已经广泛应用于最近的研究工作中, 以预测目标区域的总体覆盖率. 然而, 这个模型是基于对所有传感器在圆盘形状的区域内实现完美覆盖的不现实假设. 实际上, 传感器的感知能力随着覆盖半径增加呈概率分布, 因此本文提出了一种基于概率感知模型的LWSN可靠性的分析方法, 并在上述研究的基础上进行了几点改进. 一是为克服系统状态空间过大的问题, 本文采用了非递归的二元决策树构造LWSN的系统状态集合. 二是针对传感器的覆盖可靠性随覆盖半径而变化的现象, 本文引入了概率感知模型. 该模型是一种持续性监测过程, 通过传感器与目标之间的距离反映感知概率, 概率值即表示传感器对目标点的置信度. 最后, 通过对不同连通性与覆盖率的LWSN进行仿真实验, 该方法对比文献[15]能够对LWSN的可靠性进行更精准地评估.

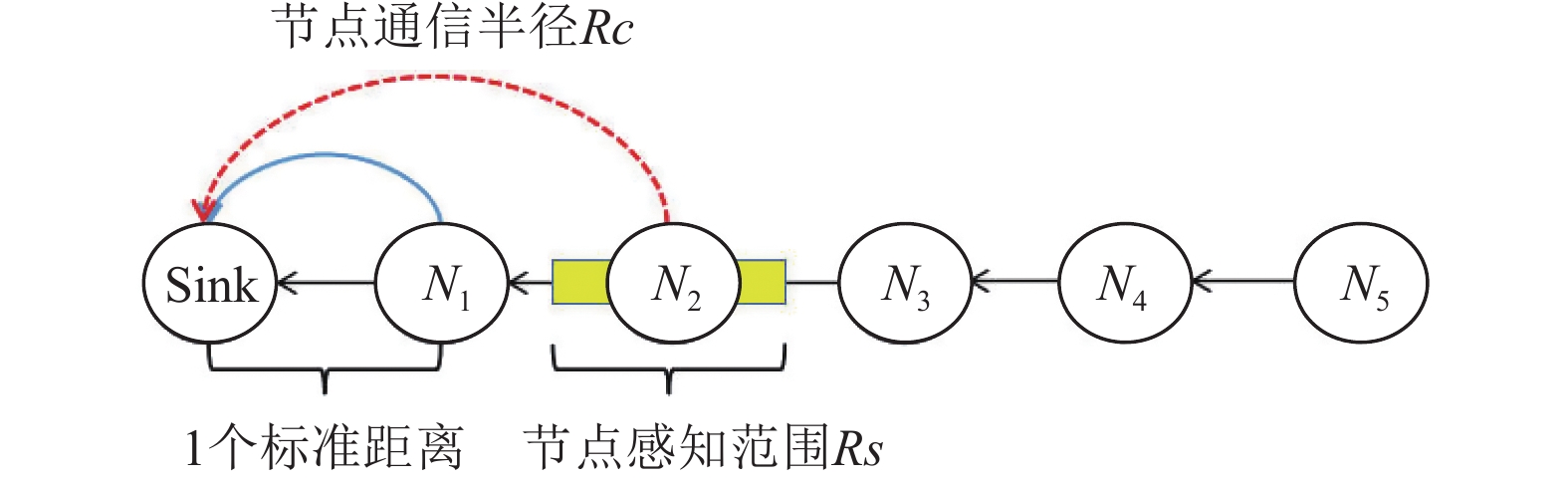
1 模型分析 1.1 相关理论知识

学者通常将LWSN定义为由大量同构、等距的传感器组成且拓扑结构为线性的无线传感网络, 其中相邻传感器之间的距离被定义为一个标准距离. 连通性与覆盖率是LWSN可靠性的重要指标. 传感器节点的最大跳跃因子MJF (maximum jump factor), 本文用Rc表示, 即传感器节点单侧与相邻节点通信的数量. 通信半径越大, Rc越大. 每个传感器都有固定的感知范围NSR (node sensing range), 本文用Rs表示, Rs越大, 节点的感知范围越大. 网络模型如图1所示.

例如, 在一个具有5个传感器的LWSN中, 节点的通信半径Rc=1且感知范围Rs=1. 假设LWSN中节点都正常工作, 图2为基于0/1圆盘感知模型下网络的覆盖情况, 工作节点对感知范围内目标的监测概率恒为100%. 由于传感器对目标的感知概率随距离的增加而降低, 因此传感器可能对覆盖边缘处目标的监测出现不确定性. 如果传感器对某处目标的感知概率低于规定阈值, 则节点对该区域的监测失效. 假设传感器对覆盖边缘目标的感知概率低于期望阈值, 图3为基于概率感知模型下网络的覆盖情况.

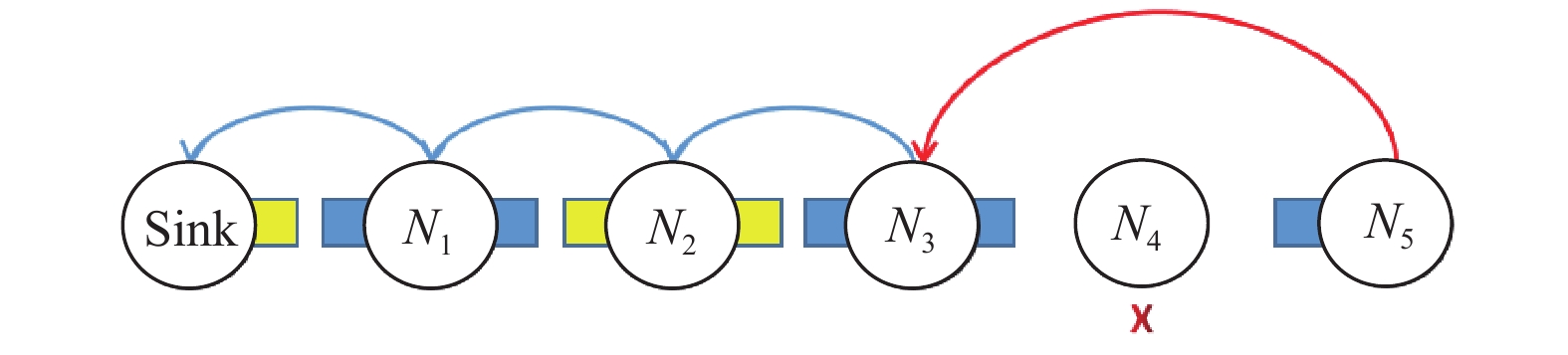
连通性与覆盖率密切相关, 如果某些位于LWSN前面的传感器节点连续失效, 即使后面的传感器节点是运行的, 数据仍可能无法顺利地被传送到Sink节点. 本文将处于工作状态并且能够顺利地将数据传送到Sink节点的传感器节点称为工作节点. 如图4所示, 如果N₄失效, 即使N₅正常运行, 其数据仍然无法传回Sink节点.

在提高网络可靠性的研究中, 学者可通过如图5扩大传感器的通信半径或如图6扩大传感器的感知范围, 以提高LWSN的可靠性. 因此, 本文需要针对不同Rc、Rs的LWSN进行可靠性评估.

1.2 利用决策树分析LWSN的连通性

在一个具有n个传感器节点的LWSN中, 本文使用$\overrightarrow {\mathbf{Z}} $=(X₁,X₂,X₃,…,X_i,…,X_n)来代表网络的系统状态(system state vector, SSV), 其中传感器节点的状态用X_i表示, 它是一个布尔类型的变量如式(1)所示:

$ {X}_{{i}}=\left\{\begin{array}{l} 0, \quad 节点{N}_{i}失效\\ 1, \quad 节点{N}_{i}工作\end{array} \right.$

(1)

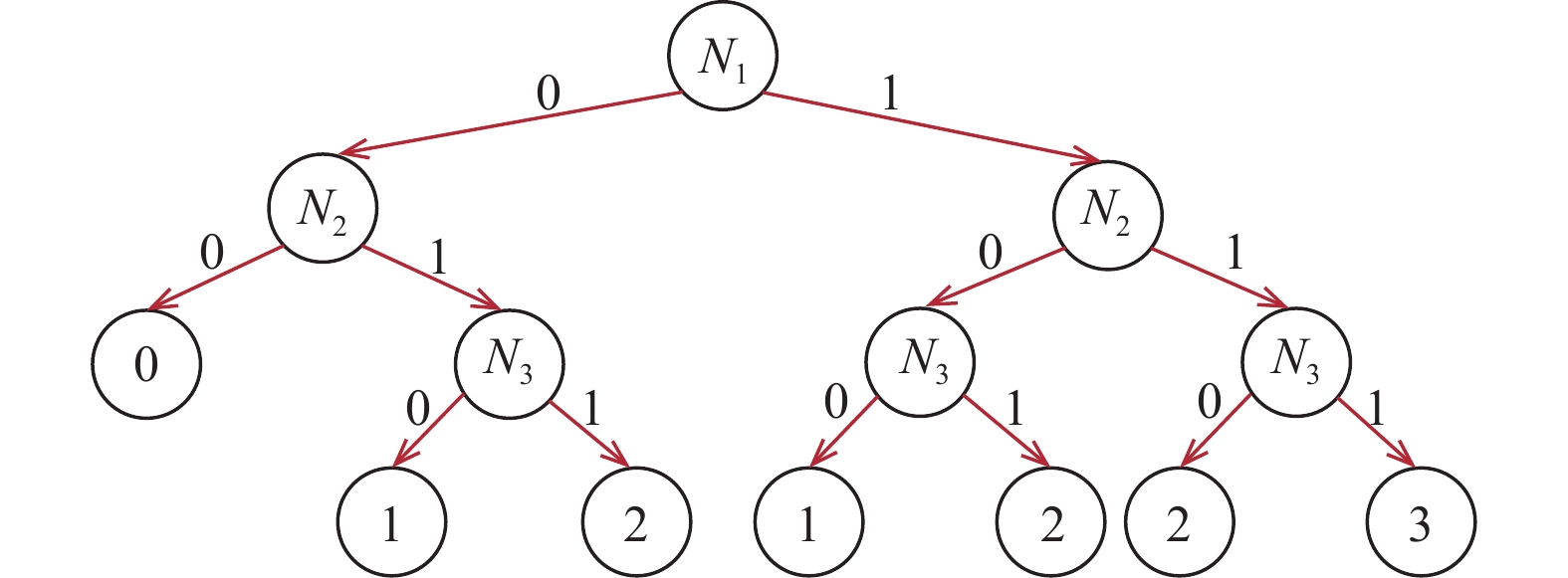
一个具有n个节点的LWSN存在2ⁿ种系统状态, 但研究表明有些系统状态向量是无效的. 例如, 一个具有3个传感器节点的LWSN其系统状态向量集合为(0, 0, 0)、(0, 0, 1)、(0, 1, 0)、(0, 1, 1)、(1, 0, 0)、(1, 0, 1)、(1, 1, 0)、(1, 1, 1). 假设传感器节点的通信半径Rc=2, 且工作节点的数量为1, 则存在两种有效情况: (0, 1, 0)、(1, 0, 0), 其中系统状态向量(0, 0, 1)无效, 因为网络已经从第1个节点处断开. 因此为减少冗余, 本文采用二元决策树构造系统状态集合. 图7是基于上述情形所绘制的决策树, 其叶子节点的值是网络中运行节点的数量, 路径上的权值为节点的状态, 每条路径代表着LWSN的一种系统状态. 通过对该决策树进行深度遍历, 可获取LWSN的系统状态集合.

1.3 引入概率感知模型分析覆盖率

根据不同的设计需要, 即使在线性无线传感网络中存在一些故障的节点也不会影响网络的整体功能. 本文定义网络覆盖参数, 假设LWSN的总范围为$l$、所有节点监测的感知范围为$c$, 则网络覆盖参数为$\gamma = \dfrac{c}{l}$ , 本文将覆盖率大于$\gamma $的系统状态向量集合称为符合要求的系统状态向量集合$f(\gamma )$.

假设N₁位于LWSN的头部, N_n位于尾端. 由于LWSN中节点按照线性排列, 其监测范围可看作一条直线. 在一个具有n个节点的LWSN中, 节点对目标的感知概率随距离呈指数变化如式(2)所示:

$ Cov\left( {p, {N_i}} \right) = \left\{ {\begin{array}{*{20}{l}} 0,&{d\left( {p, {N_i}} \right) \gt Rs} \\ {{{\mathrm{e}}^{ - \omega d{{\left( {p, {N_i}} \right)}^\alpha }}}},&{Rs - {r_e} \lt d\left( {p, {N_i}} \right) \leqslant Rs} \\ 1,&{d\left( {p, {N_i}} \right) \leqslant Rs - {r_e}} \end{array}} \right. $

(2)

其中, $Cov(p, {N_i})$为传感器对该处目标的感知概率, $d(p, {N_i})$为目标与节点N_i之间的欧氏距离, $ \alpha 、\omega $为传感器节点在不同功率等级下工作的物理参数, 该参数与传感器的类型和物理特性相关, ${r_e}$是理想条件下传感器感知范围的边界值.

在概率感知模型中, 目标与传感器的距离对于目标的感知概率影响较大. 其中有些目标距离传感器节点很远, 虽然这些目标位于传感器节点的感知范围内, 但传感器对其感知的影响程度却很小, 甚至可以忽略, 因此定义有效感知范围对于简化问题求解, 降低网络复杂度有非常重要的意义, 本文用$Ru$表示. 假设节点对目标的期望感知概率(desired detection probability, DDP)为80%, 当$d(p, {N_i}) \leqslant Ru$时, 则传感器对该位置的感知概率不低于80%, 该位置被覆盖; 如果$d(p, {N_i}) \geqslant Ru$时, 则传感器对该位置的感知概率低于80%, 该位置没有被覆盖.

基于概率感知模型LWSN中每个节点的感知范围如式(3)所示, 其中i为LWSN中传感器的序号.

$ R({N_i}) = \left\{ {\begin{array}{*{20}{l}} {[0, Ru]}, \\ {[i - {{1 - }}Ru, i{{ - 1}} + Ru]}, \\ {[i - 1 - Ru, i - 1]}, \end{array}\begin{array}{*{20}{l}} {\;\;\;\;\;i = 1} \\ {\;\;\;\;\;1 \lt i \lt n} \\ {\;\;\;\;\;i = n} \end{array}} \right. $

(3)

根据节点的状态X_i, N_i的感知范围如式(4)所示, 其中$\varnothing $代表该节点的监测范围为空.

$ C({N_i}) = \left\{ {\begin{array}{*{20}{l}} {R({N_i})}, \\ \varnothing, \end{array}} \right.\begin{array}{*{20}{c}} {\;\;\;\;\;\;{X_{{i}}} = {\text{1}}} \\ {\;\;\;\;\;\;{X_i} = {\text{0}}} \end{array} $

(4)

基于决策树提供的系统状态向量集合, 通过合并各节点的感知范围, 获得系统状态集合的覆盖率, 并筛选出满足$\gamma $的系统状态集合如式(5)所示:

$ \gamma (\overrightarrow {\mathbf{Z}} ) = \frac{{ \bigcup \mathop {_{i = 1}}\limits^{length(\overrightarrow {\mathbf{Z}} )} C(N{}_i)}}{l} $

(5)

1.4 可靠性评估

Weibull分布在可靠性分析中经常用于产品的寿命分布, 以便估计产品的可靠性和失效概率. 本文采用Weibull分布反映节点随时间变化的故障概率, 如式(6)所示:

$ F(t) = 1 - {{\mathrm{e}}^{ - {{(\lambda t)}^\beta }}} $

(6)

其中, $ F(t) $是传感器节点基于Weibull分布在不同时刻的故障概率, $\lambda $是比例系数, $\beta $是形状系数. 根据传感器节点的状态X_i, 节点在不同时刻下的状态概率${P_i}(t)$可通过式(7)获得:

$ {P_{\text{i}}}(t) = \left\{ {\begin{array}{*{20}{l}} {F(t)},&{{X_i} = 0} \\ {1 - F(t)},&{{X_i} = 1} \end{array}} \right. $

(7)

基于当前的系统状态向量集合, 当前系统状态向量集合在t时刻的可能性可通过对集合内节点状态的概率累乘获取, 如式(8)所示:

$ P(\overrightarrow {\mathbf{Z}} , t) = \prod\limits_{i = 1}^{length(\overrightarrow {\mathbf{Z}} )} {{P_i}(t)} $

(8)

通过统计符合要求的系统状态集合的概率, 得到LWSN在某一时刻满足网络覆盖参数的可能性, 以达到对LWSN的可靠性评估, 如式(9)所示:

$ {P_\gamma }(t) = \sum\limits_{\overrightarrow {\mathbf{Z}} \in {{f}}(\gamma )} {P(\overrightarrow {\mathbf{Z}} , t)} $

(9)

基于0/1圆盘感知模型分析LWSN的覆盖率会导致将监测失效区域纳入LWSN的有效感知范围, 评估结果往往比实际结果偏大. 为提高评估的准确性, 本文引入概率感知模型, 该模型通过节点与目标间的距离计算节点对范围内目标的感知概率, 进而评估覆盖率.

2 模型实现 2.1 基于决策树获取系统状态向量集合

本文使用元组(Value, CDamage)作为决策树中每个中间节点或叶子节点的参数, 其中Value是当前系统状态下工作的节点数, CDamage是连续失效的节点数. 决策树的构建依赖于Rc的取值, 如果CDamage等于Rc则表示网络断开. 本文定义了算法1, 该算法声明队列pNodes与cNodes以避免递归. 其中, 队列pnodes用于保存下一轮循环的可操作节点即节点X_i+1; 队列cnodes用于保存当前操作节点的孩子节点, 其作用在于合并参数相同的孩子节点降低系统资源开销. 构造决策树的算法如算法1.

算法1. 建立决策树

输入: LWSN总节点数N, Rc.

输出: 决策树.

1 pNodes, cNodes←$\varnothing $;

2 创建根节点X_i(0, 0), 并添加到pNodes中;

3 i=2;

4 while i≤N do

5　 for pNode in pNodes do

6　　　 gCDamage←pNode.CDamage, gValue←pNode.Value;

7　　　 if gValue≥Rc–1

8　　　　 create leaf X_i(gValue, gCDamage+1);

9　　　　 connect leaf to pNode’s 0-edge;

10　　　 create node X_i(gValue+1, 0);

11　　　 node=SearchOrAdd(X_i, cNodes, i);

12 　　　 connect node to pNode’s 1-edge;

13 　　　else

14　　　　 create node X_i(gValue, gCDamage+1);

15 　　　　node=SearchOrAdd(X_i, cNodes, i);

16　　　　 connect node to pNode’s 0-edge;

17　　　　 create node X_i(gValue+1, 0);

18 　　　　node=SearchOrAdd(X_i, cNodes, i);

19　　　　 connect node to pNode’s 1-edge;

20 　　　end

21 　end

22 　pNodes←cNodes, cNodes←$\varnothing $;

23　 i++;

24 end

25 Addleaf(pNodes);

算法1的具体步骤如下.

步骤1: 初始化队列pNodes、cNodes. 同时为传感器节点N₁创建一个根节点X₁, 将其元组设置为(0, 0), 即当前连接的运行节点数为0, 连续失效的节点数为0, 然后将根节点X₁添加到队列pNodes中. 其中, 在pNodes队列中的节点被定义为pNode.

步骤2: 遍历队列pNodes. 在循环流程中, 应为每个pNode构造其孩子节点. 其中, 变量gValue用于保存当前系统状态下工作节点数, 变量gCDamage用于保存当前系统状态下连续失效的节点数. 如果pNode中CDamage等于Rc–1, 则构造一个叶子节点并与pNode节点的0边相连接, 其中叶子节点的Value值不变, 表明网络从此处的断裂, 即第8, 9行. 另一边, 构造节点X_i并使其与pNode的1边相连接, X_i的Value的值为pNode的Value+1、CDamage值清零, 表明该节点运行, 即没有连续失效的节点.

步骤3: 如果某些元组的参数相同如图6所示, 通过将其合并以降低冗余如图8所示. 在第11行中, 本文设计了算法2, 其功能为合并参数相同的元组. 该算法分为两种情况: 如果当前节点是LWSN的最后一个节点且在cNodes队列中存在具有相同Value值的元组; 如果当前节点不是最后一个节点且在cNodes队列中存在具有相同Value和CDamage值的元组. 通过遍历队列cNodes, 寻找是否存在符合以上要求的节点, 如果存在则返回相对应的节点, 否则将新节点加入到队列cNodes中并返回自身.

算法2. SearchOrAdd

输入: cNodes, X_i, i.

输出: cNodes中的X_i.

1 for node in cNodes do

2　 if i==N

3　　 if node.Value==X_i.Value

4 　　　return node;

5　　 end

6　 else

7　　 if node.Value==X_i.Value and node.CDamage==X_i.CDamage

8　　　 return node;

9　　 end

10　 end

11 end

12 append X_i into cNodes;

13 return X_i;

步骤4: 如果pNode中的CDamage值小于Rc–1, 则意味着在网络未断开的情况下, 接下来的节点可能会失效, 因此根据pNode的两种情况分别创建节点X_i并将节点X_i连接到pNode上, 即第14–19行.

步骤5: 传感器节点N_i处理完毕后, 将队列cNodes复制到pNodes中为处理传感器节点N_i+1做准备, 并清空队列cNodes.

步骤6: 循环结束之后, 需要为网络的尾节点添加叶子节点, 具体实现如算法3所示.

算法3. Addleaf

输入: pNodes.

1 for pNode in pNodes do

2　　 gCDamage←pNode.CDamage, gValue←pNode.Value;

3　　 create leaf X_i(gValue, gCDamage+1);

4　　 connect leaf to pNode’s 0-edge;

5　　 create leaf X_i(gValue+1, 0);

6 　　connect node to pNode’s 1-edge;

7 end

通过对算法1生成的决策树进行深度优先遍历获得LWSN的系统状态集合, 为后续的覆盖率的分析提供样本. 该算法对比基于对系统所有状态的穷列枚举, 算法的时间复杂度为O(n³), 空间复杂度为O(n).

2.2 分析LWSN的覆盖率

概率感知模型依赖于传感器的相关参数, 通过调整节点的参数, 以计算节点的有效监测范围Ru. 为统计统计符合覆盖要求的系统状态集合$f(\gamma )$, 本文在算法4中声明一个队列coverageSSV, 其中变量totalLength为当前系统状态下的实际感知范围. 同时, 还需要统计当前系统状态下工作的节点数operationCount与失效的节点数dieCount, 为下一步的可靠性分析做准备. 算法4如下所示.

算法4. 计算LWSN的覆盖率

输入: 节点的相关参数α、ω, 期望感知概率DDP, 网络覆盖参数$ \gamma $, 感知范围Rs.

输出: 队列coverageSSV.

1 根据式(2)计算节点的有效覆盖范围Ru, 并初始化队列coverageSSV和变量totalLength;

2 for $\scriptstyle \overrightarrow {\boldsymbol{Z}} $ in SSVs do

3　 判断头节点是否工作, 如工作则添加其有效覆盖范围到totalLength中并且将operationCount加1, 否则将dieCount加1

4　 i=2

5　 for i≤SSVs.size do

6　　 判断当前节点是否工作, 如工作则operationCount+1, 否则dieCount+1并进行下轮循环

7 　　如果当前节点的右侧区域与前面Rs个节点的右侧区域存在重叠, 则删除重叠区域

8 　　计算当前节点的左侧感知区域, 共分两种情况: 1) 与左侧节点存在重叠, 则与左侧节点的感知区域进行合并. 2) 与左侧节点不存在重叠, 则直接添加其有效覆盖范围到totalLength

9 　　添加当前节点的右侧区域到totalLength, 如超出边界则截断

10 　end

11 　根据式(5)计算该组的覆盖率, 如果满足要求, 则将该组添加到coverageSSV

12 end

算法4的具体步骤如下.

步骤1: 首先根据传感器节点的相关参数与感知范围Rs计算节点的有效监测范围Ru, 并初始化队列coverageSSV与变量totalLength.

步骤2: 判断系统状态向量集合是否遍历完毕. 如果是, 跳出循环, 否则继续执行. 在随后的循环过程中, 将计算每一组状态向量$ \overrightarrow {{{\mathbf{Z}}}} $的覆盖率.

步骤3: 判断当前系统状态的头节点是否工作, 如果头节点工作则将其右侧区域添加到实际感知范围totalLength中. 需要注意的是, LWSN的头节点与尾节点与中间节点的覆盖范围存在差异, 头节点只覆盖其右侧区域, 尾节点只覆盖其左侧区域, 中间节点的覆盖范围分为左右两侧区域.

步骤4: 分析后面的节点, 如果节点失效则将变量dieCount加1, 并进行下轮循环.

步骤5: 如果节点工作且感知范围超过一个标准距离, 则可能会出现覆盖范围重叠的现象. 因此, 需要判断当前节点感知区域是否与前面Rs个节点的感知区域存在重叠的情况. 如果当前节点的右侧感知范围与前面节点的右侧感知范围存在重叠, 即前面节点的右侧感知区域超过了当前节点的左侧感知区域并额外覆盖了部分右侧区域, 则删除重叠区域长度; 如果当前节点的左侧感知范围与前面节点的右侧感知范围存在重叠, 则将当前节点的左侧覆盖区域与前面节点的右侧覆盖区域做并集处理; 如果不存在重叠区域, 则将当前节点覆盖区域添加到实际覆盖范围totalLength中即可.

步骤6: 如果当前节点的感知范围超出了网络的边界范围, 则需要对节点的覆盖区域与网络的边界区域做交集处理.

步骤7: 最后, 判断当前系统状态的覆盖率是否符合要求, 如果符合要求则将该集合添加到队列coverageSSV中.

2.3 基于Weibull分布评估网络可靠性

考虑一个由n个传感器节点组成的线性无线传感网络, 传感器节点的故障分布满足式(6). 给定任务时间t=T, 即可计算节点的不可靠性$F(t)$, 这与状态集合中的状态0相关联; 节点的可靠性${{1 - }}F(t)$, 这与状态集合中的状态1相关联. 对于每组符合要求的系统状态向量集合, 可根据每个节点状态的概率进行累乘处理获得当前系统状态的可靠性. 最后, 线性无线传感网络在时间T下的可靠性可以用集合$f(\gamma )$概率之和表示.

在分析集合$f(\gamma )$的可靠性过程中, 如果对$f(\gamma )$中节点的状态逐个分析, 则会增加算法的时间复杂度. 为了减少对$f(\gamma )$的遍历次数, 我们声明了变量operationCount与dieCount以统计当前系统状态下节点的状态, 因此当前系统状态的可靠性可通过式(10)获取:

$ P(\overrightarrow {{{\mathbf{Z}}}} , t) = {{{(1 - }}F(t))^{operationCount}}{\times}F{(t)^{dieCount}} $

(10)

2.4 算法流程

具体流程如下.

(1) 为评估具有不同连通性的LWSN, 基于算法1通过输入网络的总节点数N与节点的通信半径Rc获取具有不同连通性的决策树, 决策树的每条路径对应着一种LWSN的有效系统状态, 其中0边代表节点失效1边代表节点工作, 如果某节点连续失效的节点数CDamage等于Rc则表示网络从该处断开. 通过对该决策树深度优先遍历得到LWSN的系统状态集合. 其中, 算法2用于合并参数相同的元组以减小系统开销, 如果网络的总节点数越多则效果越明显, 算法3用于为网络的尾节点添加叶子节点.

(2) 由于本文提出的算法具有通用的特点, 其中传感器节点间的距离使用一个标准距离表示, 因此传感器节点的相关参数需要对应调整. 在算法4中, 通过调整传感器节点的相关参数, 计算节点的有效监测范围Ru. 根据每种LWSN的系统状态计算其实际覆盖范围totalLength, 最后基于式(5)判断当前系统状态是否符合要求, 如果符合要求则将该集合添加到队列cove-rageSSV中, 为下一步的可靠性分析做准备.

(3) 基于Weibull分布统计队列coverageSSV中符合要求的系统状态集合在不同时刻出现的可能性, 以达到对LWSN的可靠性评估.

3 案例研究

在本节中, 本文将根据案例分析LWSN的可靠性. 假设在LWSN中有18个同构、等间距的传感器节点, 每个节点符合Weibull分布, 经过大量的研究表明, 式(6)中参数取λ=3×10⁻⁵, β=1.2为宜. LWSN的可靠性要求为覆盖长度至少达到总覆盖长度的80%, 即LWSN覆盖参数$ \gamma = {\text{80\% }} $. 本文将基于概率感知模型分析LWSN的可靠性, 并与0/1圆盘概率模型进行对比, 得出一些结论.

本节将分别研究Rc和Rs值从1到3的各种情况. 首先, 使用算法1为传感器通信半径从1到3的线性无线传感网络生成决策树, 并对决策树进行遍历以获取系统状态向量集合. 然后, 基于算法4根据节点的相关参数计算节点的有效监测范围. 其中, 节点的相关参数与Rs相关, 本文将式(3)中节点的路径损耗指数$\alpha $恒置为1, 通过修改节点的参数$\omega $改变节点的感知范围. 最后根据式(9)计算线性无线传感网络的可靠性.

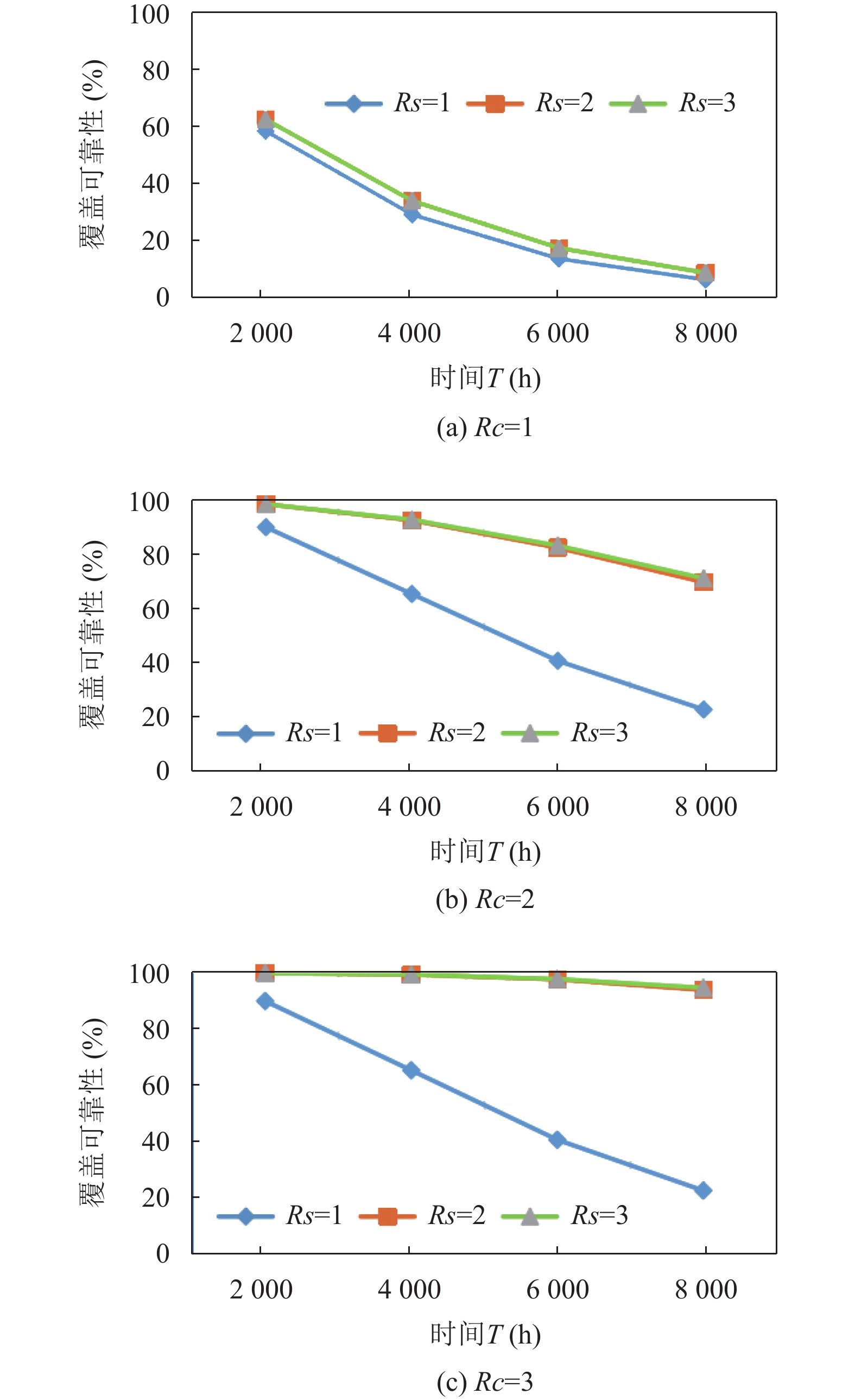
图9显示了采用概率感知模型对不同Rc、Rs取值的LWSN的可靠性概率曲线, 表1列出了分析后的样本结果.

我们可以发现Rc=1的曲线远低于Rc=2、3的曲线, 这说明连通性限制了可靠性. 当Rc=2时, 由于扩大了节点的通信半径导致传感器之间增加了可替代的路径, LWSN的连通性得到提升并导致覆盖可靠性得到提高.

此外, 当Rs=1时, 仅扩大Rc不会显著地增加LWSN的可靠性, 说明覆盖率同样限制了可靠性. 当Rc=3时, 对比Rc=2线性无线传感网络的覆盖可靠性明显提高. 当Rs=3时, 对比Rs=2其覆盖可靠性基本没有得到明显提高. 因此, 为了获得更多的覆盖可靠性, 我们应该使用Rs=2, 并尽可能地扩大Rc.

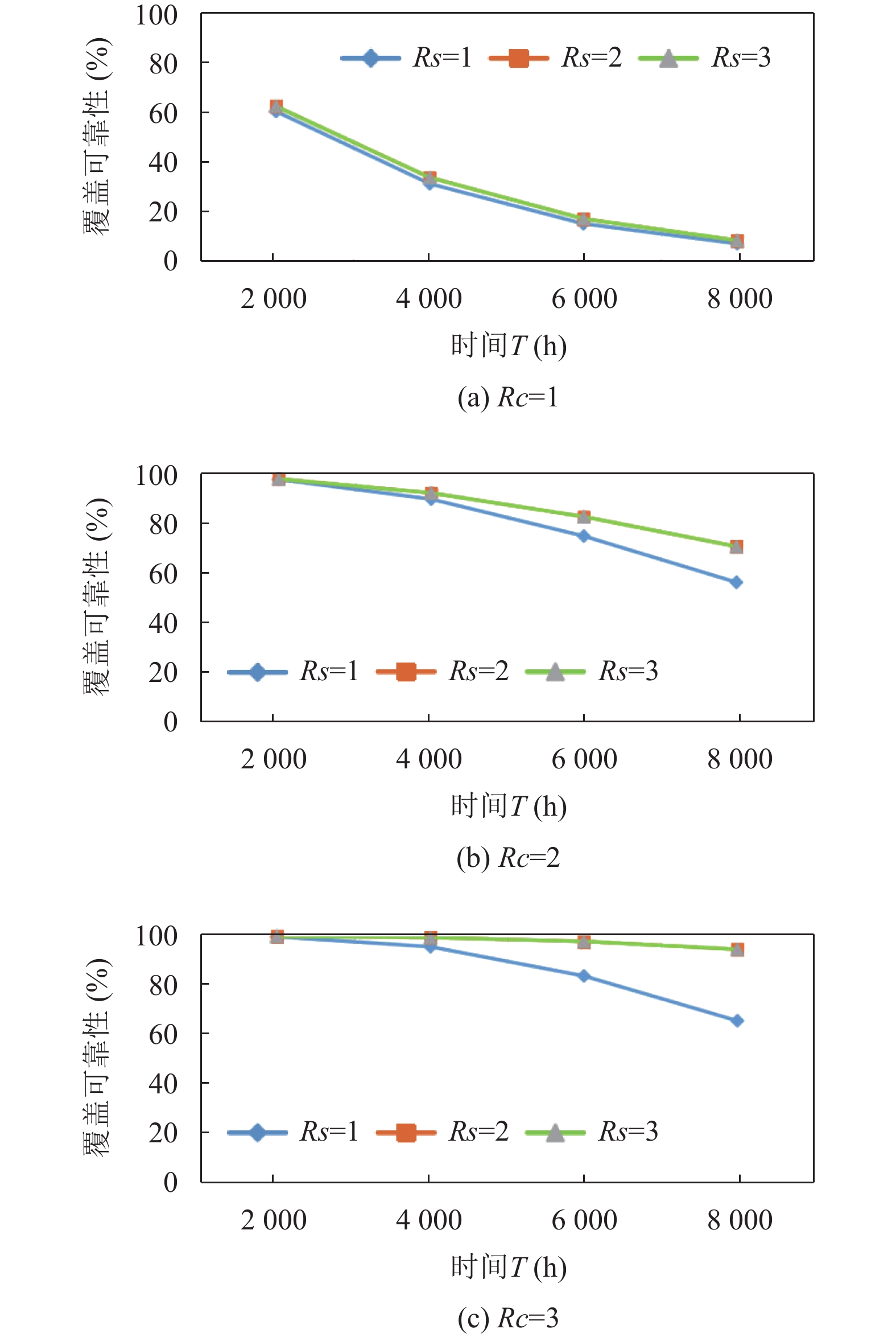
图10显示了采用0/1圆盘感知模型对不同Rc、Rs取值的LWSN的可靠性概率曲线, 表2列出了分析后的样本结果.

通过对比, 我们发现基于0/1圆盘感知模型的覆盖可靠性皆高于基于概率感知模型, 原因是0/1圆盘感知模型会将监测失效区域纳入LWSN的监测范围.

当Rs=1时, 由于节点之间的感知范围不存在重叠的情况, 该模型会将每个节点监测失效的区域重新添加到有效的监测区域, 因此其覆盖可靠性会明显高于概率感知模型. 当Rs=2时, 其覆盖可靠性与概率感知模型下Rs=3的覆盖可靠性近乎相同. 当Rs=3时, 其覆盖可靠性与Rs=2相同.

实验结果表明, 仅扩大网络的连通性或覆盖率无法显著地增加LWSN的可靠性, 需将两种指标结合一同考虑. 如果设计网络时需要保证网络的可靠性在80%以上且检测时间低于6 000 h, 则Rc=2、Rs=2是一个很好的选择; 如果监测时间超过6 000 h, 则Rc=3、Rs=2是一个很好的选择. 假设LWSN的可靠性≤80%表示监测系统需要立即维护, 可以看出在约6 000 h时, 需要维护Rc为2且Rs=2的LWSN. 因此, 该模型不仅可用于分析LWSN的可靠性, 还可用于计算何时需要对LWSN进行维护. 对比0/1圆盘感知模型, 我们可知当Rs=1时, 其可靠性相对于实际误差最大, 当Rs=2时, 其节点的感知范围几乎达到概率感知模型下Rs=3的程度, 因此在实际工程中采用0/1圆盘感知模型分析线性无线传感网络的可靠性可能导致设计出的网络在任务时间内其可靠性达不到规定要求.

4 结语

LWSN的可靠性评估至关重要, 用户采用合适的评估方法便可以准确地了解LWSN的运行状态, 以便在合适的时间对网络进行维护. 对比以往的研究, 为忽略使模型复杂化的细节, 学者们通常采用0/1圆盘感知模型分析LWSN的可靠性, 在同等条件下其结果往往高于实际值.

本文提出了一种采用概率感知模型的LWSN可靠性分析方法, 该模型对比0/1圆盘感知模型更加符合实际情况, 通过计算传感器节点的有效监测范围, 对不同Rc、Rs的LWSN进行可靠性评估. 经仿真实验表明, 该方法能够为LWSN的可靠性进行更精确的评估, 并且通过与0/1圆盘感知模型进行对比展现了其优越性, 评估结果可为LWSN的设计提供准则.