党的二十大报告将“城乡人居环境明显改善, 美丽中国建设成效显著”列入未来5年的主要目标任务, 《中共中央国务院关于做好2023年全面推进乡村振兴重点工作的意见》中也明确指出, 要“扎实推进农村人居环境整治提升, 推动农村生活垃圾源头分类减量, 及时清运处置”. 由此可见, 农村生活垃圾的及时清运和无害化治理已经成为党和国家关注的重点问题. 一方面, 随着生活垃圾源头分类减量措施的深入推行, 农村地区生活垃圾清运量增长趋势减缓, 但近5年来依旧维持在6800万吨左右的高位水平, 仍给垃圾及时清运带来了巨大的压力. 而另一方面, 乡村振兴战略中关于生态宜居建设也对垃圾及时清运提出了更高的要求.

然而, 农村地区生活垃圾清运问题与城市地区存在较大的差异, 传统的城市生活垃圾清运模式显然不适用于农村地区的生活垃圾清运问题. 不同于城市较为密集和均匀的人口分布特点, 农村地区人员密集程度不一, 差异化较大, 且随农忙、假日等因素影响存在显著的时变差异. 因此, 采用城市区域中传统的固定收运周期收运垃圾时, 常出现由于收运不及时造成二次污染的现象或者车辆收运能力利用不足、运力浪费的问题. 针对农村地区生活垃圾产生的特点, 制定可变收运周期的生活垃圾清运计划, 对提升农村地区生活垃圾清运效率及降低清运成本具有显著意义.

垃圾分类下的农村地区可变周期性收运路径优化问题是周期性车辆路径问题(periodic vehicle routing problem, PVRP)的特殊应用. PVRP于1974年被提出^[1], 是经典车辆路径问题的推广, 求解的时间范围以周期为单位. 以传统PVRP为基础, 垃圾收运问题衍生出3个重要变体: 带时间窗口的PVRP^[2–4]、多站点PVRP^[5–7]和带服务选择的PVRP^[1,3–5]. 目前, 从研究目标看, 现有文献对周期性垃圾收运问题的思考多从成本^[8–12]和环境因素^[9,13]两方面对该问题进行优化; 从算法方面看, 学者们主要选取整数规划^[8,9,13]、禁忌搜索^[10,14]、邻域搜索^[15,16]、模拟退火^[17]、蚁群算法^[11,18]等算法对问题进行求解. 如尚春剑等在垃圾分类基础上提出了带时间窗异构周期性混合车辆路径问题的模型, 并应用改进蚁群算法对问题进行求解, 得到良好效果^[11]. Zhao等设计了统一的建模策略规划多周期内每个时期废物处理设施的位置达到配送总成本和总风险最小化^[12]. Rahimi等提出了一种多周期多目标混合整数线性规划来设计和规划不确定条件下的逆向物流网络使环境影响最小化^[9].

现有成果从多角度对垃圾收运PVRP进行了研究, 但基于农村地区待收运点垃圾量的变化制定可变周期的文献相对较少. 由于各类垃圾日产量不同, 且不同地区的农村生活垃圾物理、化学属性差异较大, 对于各类垃圾各个地区, 采用传统的固定收运周期收运垃圾往往会产生收运不及时的问题. 因此, 可考虑根据垃圾点的特征, 制定不同的收运计划, 采用可变周期对农村地区生活垃圾进行收运. 如Gómez等在西班牙西北部农村地区调整周期间垃圾点的收集频次, 并在多目标自适应内存编程 (MOAMP) 框架内应用禁忌搜索, 从而最大限度地降低了运输成本、提高了服务水平^[10].

综上, 本文针对农村地区的生活垃圾产生特点, 考虑生活垃圾分类要求下的可变收运周期, 以运输费用、车辆延误到达惩罚成本和环境处罚为目标, 构建农村地区生活垃圾分类收运路径优化模型, 设计了变邻域模拟退火算法对模型展开求解. 接着通过Solomon系列算例, 深入剖析算法的实际效能; 最后, 为了更具体地展现模型和算法的实用性, 以重庆市某区县的垃圾收运系统为实际案例, 进行分析与验证, 进一步确认了本文提出的模型和算法的有效性.

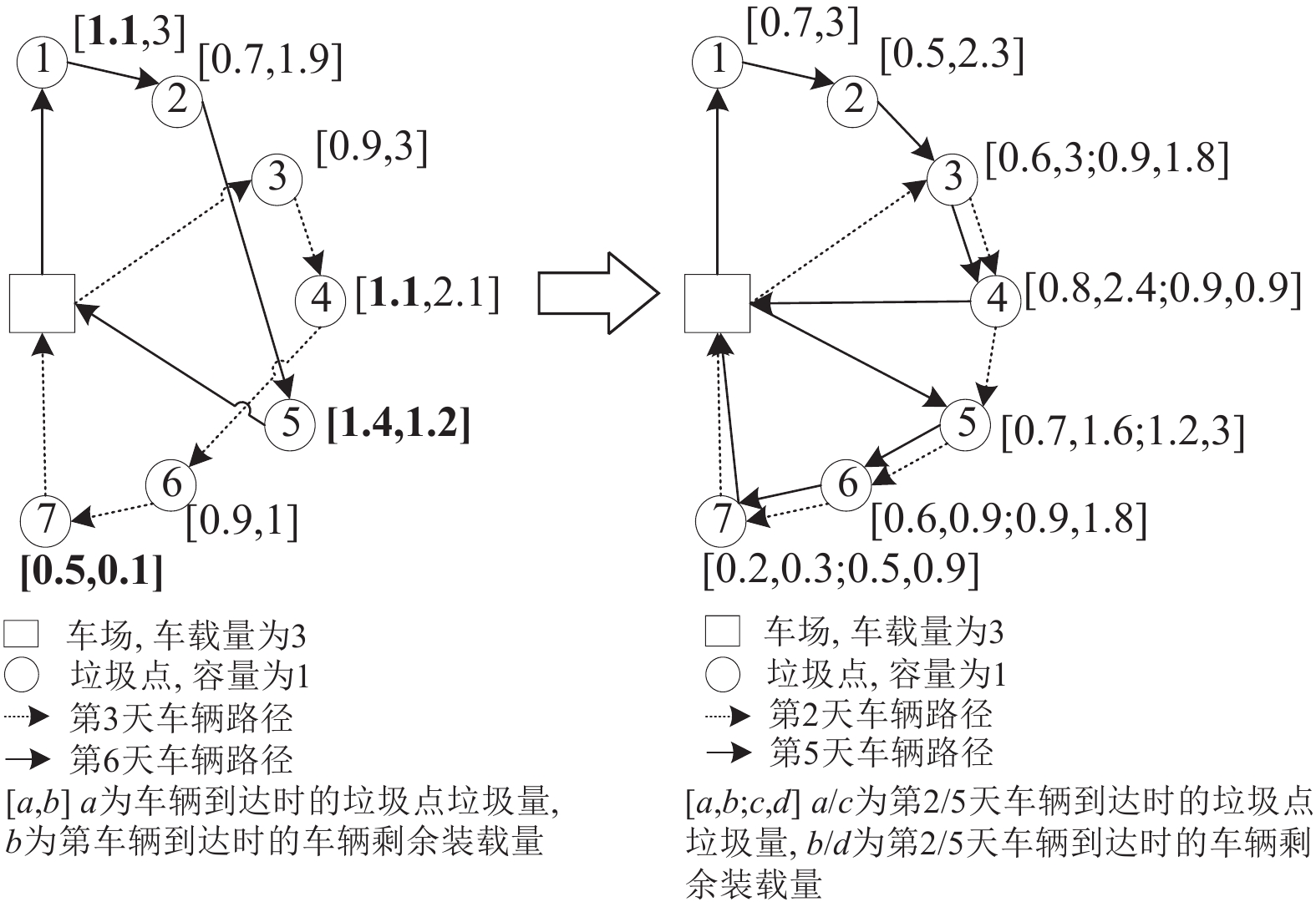
1 问题描述及数学模型 1.1 问题描述

在传统的农村地区垃圾收运过程中, 垃圾的收运周期和路线是固定的, 其收运体系相对简单, 但易出现垃圾溢出的现象. 如图1左所示: 假设垃圾点容量为1 t, 车辆载重量为3 t, 收运周期为每3天进行1次收运. 在收运前, 第1、4、5垃圾点已经溢出; 在收运第5、7垃圾点时, 车辆剩余装载量小于垃圾点的垃圾量. 基于农村地区实际情况和垃圾收运模式特征, 为较好解决此类问题, 本文采用可变收运周期对垃圾进行收运. 如图1右所示: 原定第3天收运的垃圾点更改为每3天内收运, 其他假设不变. 调整后的车辆路径安排能最大限度利用车载量且不造成环境污染. 清运车辆从车场出发, 依次经过指定垃圾点收集分类好的垃圾, 每辆清运车所收集垃圾的总容量不超过该清运车的容量. 给定周期内各垃圾点只被同一车辆服务1次且最多1次, 未满足垃圾点给定时间窗约束, 给予一定惩罚. 求解目标为最小化整个周期内的运输成本、惩罚成本与环境成本, 做如下假设:

① 车辆以恒定速度行驶, 并且具有相同的固定成本和可变成本;

② 垃圾运输成本与运输距离呈正相关关系;

③ 每个垃圾点清运量已知, 不同类别的垃圾清运量不同.

1.2 模型建立

建立模型之前, 先对符号定义进行介绍, 如表1所示.

1.2.1 目标函数

将车辆的固定成本、运输成本、违反时间窗约束的惩罚成本以及车辆延迟到达导致垃圾溢出, 进而形成环境负效应的惩罚成本作为总成本, 则目标函数为:

$ \min Q = \sum\limits_{i = 0}^V {\sum\limits_{j = 0}^V {\sum\limits_{t = 1}^T {\sum\limits_{k = 1}^K {p_{ij}^k{d_{ij}}X_{ijt}^k + \sum\limits_{i = 0}^V {{P_i}} } } } } + \alpha \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^V {{M_i}} } $

(1)

1.2.2 约束条件

$ \sum\limits_{j = 0}^V {X_{ijt}^k = } \sum\limits_{j = 0}^V {X_{jit}^k},\; \forall i \in V, \forall k \in K, \forall t \in T $

(2)

$ {f_i} \leqslant \sum\limits_{k = 1}^K {\sum\limits_{t = 1}^T {Y_{it}^k} } ,\; \forall i \in V $

(3)

$ \sum\limits_{j = 0}^V {X_{0jt}^k} \leqslant G,\; \forall k \in K, \forall t \in T $

(4)

$ s{e_j} \geqslant \sum\limits_{i = 0}^V {({t_{ij}} + s{l_i})X_{ijt}^k} ,\; \forall j \in V, \forall k \in K, \forall t \in T $

(5)

$ \sum\limits_{i \in S} {\sum\limits_{j \in S} {X_{ijt}^k \leqslant |S|} } - 1,\; \forall k \in K, \forall t \in T, S \subseteq V, |S| \geqslant 2 $

(6)

$ \sum\limits_{i = 0}^V {w_{it}^hY_{it}^k \leqslant {q^k}} ,\; \forall h \in H, \forall k \in K, \forall t \in T $

(7)

$ {P}_{i}=\left\{\begin{array}{ll}c{e}_{i}({e}_{i}-s{e}_{i}), & s{e}_{i}<{e}_{i}\\ 0, & {e}_{i}\leqslant s{e}_{i}<{l}_{i}\\ c{l}_{i}(s{e}_{i}-{l}_{i}), & s{e}_{i}\geqslant {l}_{i}\end{array}\right. $

(8)

$ {M_i} = \max \left\{ {{q_{it}} - {q_i}, \left. 0 \right\}} \right.,\; \forall i \in V, \forall t \in T $

(9)

式(2)表示单个周期里任意从车场出发的清运车均返回该车场; 式(3)确保各垃圾点在对应周期内的收运频率不得小于其规定要求; 式(4)确保使用某类型的车辆数量不超过可用的同类型车辆数量; 式(5)表示垃圾点j的服务开始时间约束; 式(6)表示消除子回路; 式(7)表示清运车k清运完该路线所有垃圾点的装载量不超过车辆的容量限制; 式(8)定义了偏离时间窗范围的惩罚函数, 针对清运垃圾点i的时刻, 在指定的清运时间内该处罚值为0; 式(9)记录溢出垃圾点i的溢出量.

2 算法设计

本文将上述垃圾收运路径优化模型的求解分为两个阶段, 分别为可变周期设定和路径优化阶段. 在可变周期设定阶段, 编写程序制定可变周期规则, 确定收运阈值, 并根据时间窗和车载量等约束求得初始垃圾点清运方案; 在路径优化阶段, 结合已规划路径中尚未清运的垃圾点, 采用变邻域模拟退火算法及时调整车辆路径.

2.1 收运阈值的设定

因垃圾点的收运阈值决定了垃圾点的清运量、周期更新情况及车辆访问频率. 如垃圾收运阈值设置的太低, 则会因为提前清理而降低系统的收运效率; 如将垃圾收阈值设置的太高, 在收运过程中垃圾会外溢, 将对环境产生二次污染^[19]. 为此, 垃圾点收运阈值的设定需要作为重点检查目标. Wu等通过算例计算表明, 垃圾收集阈值为0.65–0.75时为最佳^[20]. Hannan等分析发现将垃圾收运阈值设在0.7可以最大程度地节省成本并降低碳排放量^[21]. Akhtar等^[22]、Hannan等认为将垃圾收运阈值定在0.7–0.75之间, 能够达到减少收运距离、提高收运效率、减少燃料消耗和CO₂排放的目的^[22,23]. 因此本文选取垃圾点收运阈值进行灵敏度分析, 分析结果选取较优解.

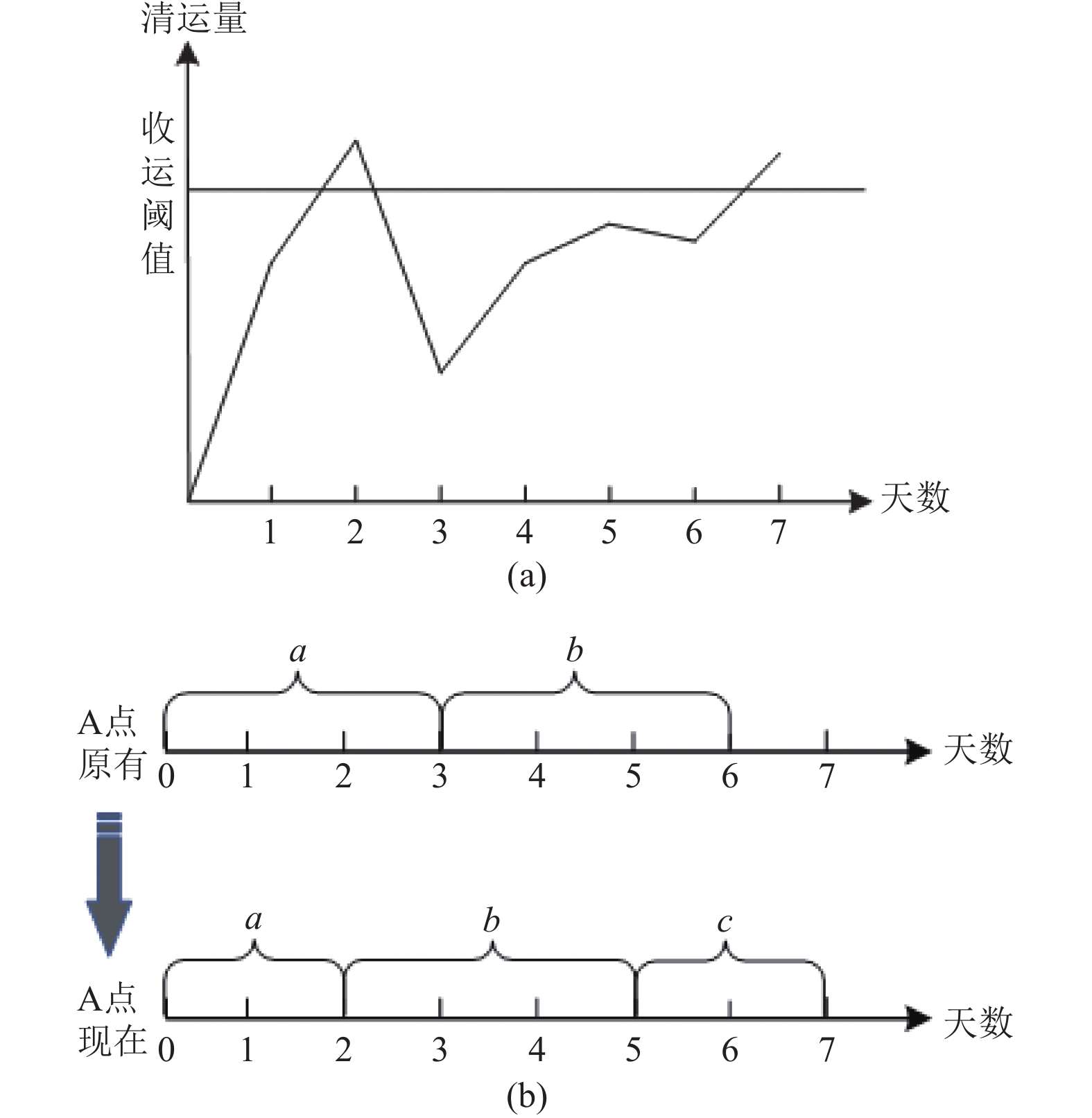
2.2 可变周期制定规则

可变周期制定规则如图2所示: 以垃圾点A为例, 图2(a)为A点的每日清运量. A点原有收运周期为每3天收运1次, 现周期的变化由收运阈值决定, 若在设定的收运阈值以下, 此点不强制性清运, 但到达或超过设定阈值时必须清运. 如A点在第2天和第7天均超过收运阈值, 需即刻清运. 观察第3–5天A点清运量一直未超过收运阈值, 因周期时长已达3天, 在第5天需对其清运. 另外, 任意垃圾点被清运后将其清运周期更新, 从被清运日开始重新计算周期, 如周期a在第2天清运结束后的新清运周期为第3–5天.

2.3 初始路径的构建

本文的初始路径采用随机选择法和最近邻法相结合的方法构建. 首先确定待收运垃圾点的位置、垃圾点的收运阈值和收运周期及需要的车辆数量等参数. 而后以车场为起点, 随机选择一个垃圾点插入, 再依据当前收运车剩余装载量和时间窗约束, 从剩余未被清运的垃圾点选择最近的垃圾点插入到当前路径, 直至当前路径不存在可行插入点时, 新增一条路径. 最后重复上述步骤, 直至所有垃圾点均在路径中, 形成选定周期的初始配送方案, 生成周期内每日的初始访问路线.

2.4 编码与解码

模拟退火算法在解决车辆路径问题时要经历编码和解码两个环节. 本文借鉴文献[24]的编码解码方式, 采用垃圾点编号的顺序编码方式为周期内的每日路径构建解序列, 如图3所示. 假定现有10个生活垃圾收集点, 其编号为1–10, 车场为0. 图3中的个体表示车辆1从车场0出发, 依次清运垃圾点5、7、6、10后返回0, 车辆2从车场0出发, 依次清运垃圾点9、3、4、8、1、2后返回车场0.

2.5 邻域搜索算子

为进一步改善模拟退火算法性能, 提高求解效率, 在模拟退火算法的退温过程中嵌套变邻域搜索算法, 从不同邻域中搜索不同的垃圾点更新路径. 首先使用轮盘赌选出所使用的邻域结构搜索算子, 并按所选搜索算子进行路径的更新. 本文根据文献[25]确定以下3种邻域搜索算子操作: Insertion、Reversion和Swap, 如图4所示. 图4左为原始路径, 随机选取到该路径中第2、5个垃圾点, 对其进行变换至图4右: 假设首先选择第5个垃圾点, 然后选择第2个垃圾点, Insertion为将第1个位置上的元素插入到第2个元素后面, 即将第5个垃圾点的编号插入到第2个垃圾点的编号之后; Reversion为将这两个位置之间的元素进行逆序排列; Swap为将这两个位置上的元素进行交换.

2.6 变邻域模拟退火算法整体流程

模拟退火(SA)是一种基于Metropolis采样稳定性的方法, 它从高温点出发, 在邻域结构内随机搜索, 对其进行局部优化, 并在给定的条件下对其进行迭代优化, 直至达到问题较优解. SA在理论上已被证明从某一较高初温度出发、伴随着快速的温度下降速率, 能以概率1收敛到全局最优解^[26]; 同时, 变邻域搜索算法(VNS)可改善SA可能陷入局部最优的情况. 因此, 本文引入VNS的思想, 提出改进的模拟退火算法.

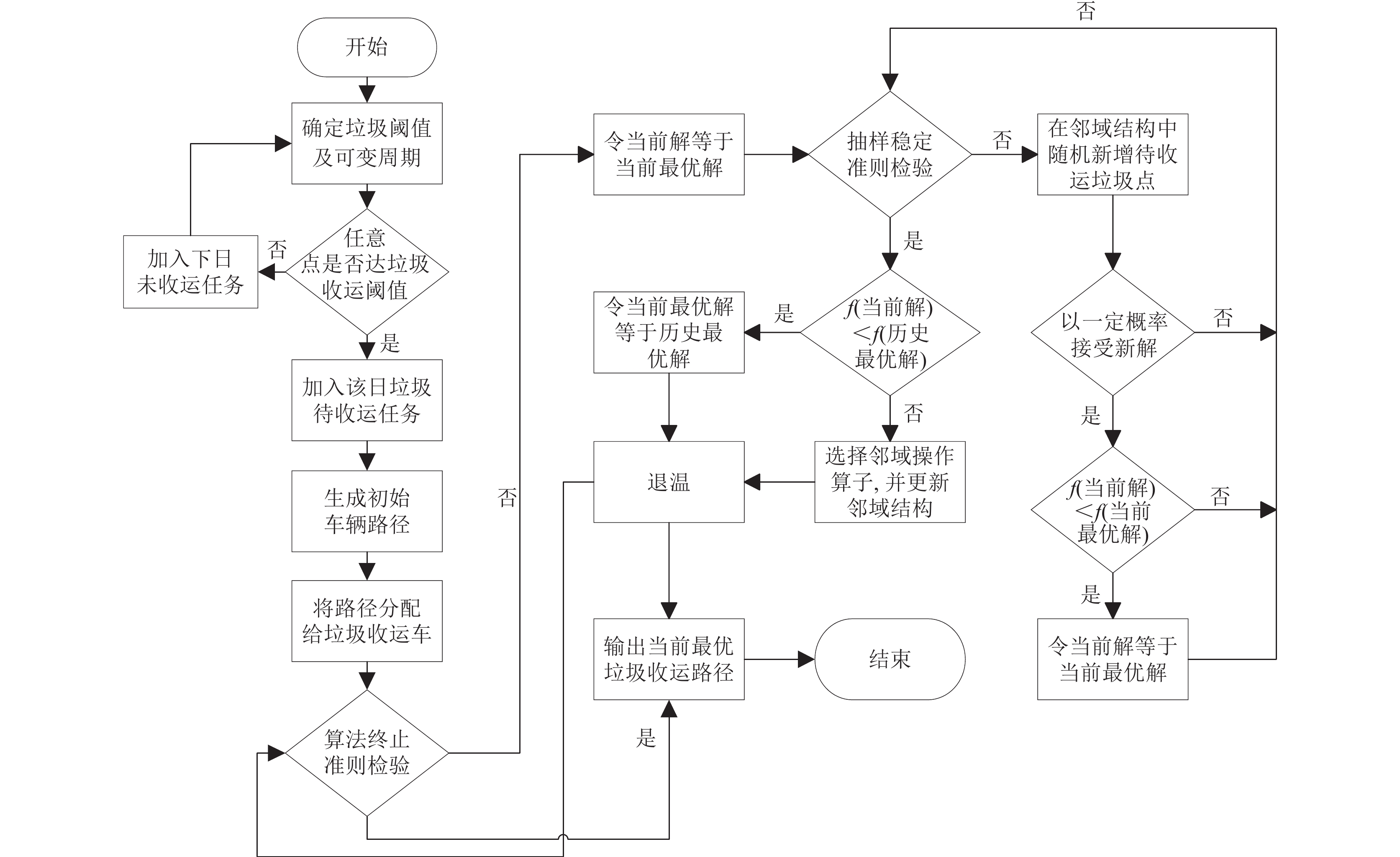
本文设计的变邻域模拟退火算法(SA-VNS)是将模拟退火算法和变邻域搜索算法相结合, 在模拟退火算法的退温过程中嵌套变邻域搜索算法, 从不同邻域中搜索不同的垃圾点更新初始路径, 同时也要满足SA的Metropolis抽样稳定准则, 以确保新解的可行性, 使得生成新路径的收敛速度加快, 更大概率跳出局部最优、取得更优解. 算法流程如图5所示.

3 算例分析

结合实际调研情况进行算例验证分析, 设定相关参数: 垃圾点的存储容量为0.2 t, 垃圾清运车辆装载量为2 t, 垃圾收运阈值为0.12 t, 垃圾桶产生的垃圾量服从离散均匀分布^[20]. 变邻域模拟退火算法中初始温度T0为1000, 冷却因子为0.99, 外层循环最大迭代次数为1500, 里层循环最大迭代次数为50; 车辆发车的固定成本为200 元/辆, 车辆行驶速度为60 km/h, 车辆行驶成本为1.5 元/km; 车辆延迟到达的惩罚系数α为分段函数$\alpha = \left\{ {\begin{array}{*{20}{l}} {20n, }&{n = 1}&{} \\ {30n, }&{n = 2}&{} \\ {40n, }&{n \geqslant 3}&{} \end{array}} \right.$ (n为延迟清运的天数). 本文算法采用Matlab R2022b编码实现, 计算机内存为16.00 GB, CPU为双核酷睿i5-10210U, 主频1.6 GHz.

3.1 基于标准算例的数值分析

本文基于国际公认的Solomon VRP基准算例集中部分标准测试算例, 结合实际问题差异对数据进行调整后对算法进行有效性验证.

首先通过Solomon VRP基准算例R102分析变邻域模拟退火算法在固定周期及可变周期的计算结果. 再选取算例集中同规模、不同类型的C类、R类和RC类部分算例与其他算法结果进行对比. 每个测试算例运行10次算法, 对计算结果进行对比分析.

3.1.1 垃圾收运阈值灵敏度分析

参数的设置影响着算法结果的优劣, 因此本文首先对垃圾点的收运阈值进行灵敏度分析. 考虑到农村地区的实际情况, 将生活垃圾分类分为两大类并分别设置收运周期, 易腐垃圾对应周期I、其他垃圾对应周期II. 本文选取R102为样本作灵敏度分析, 将周期I设定为3天内收运、将周期II设定为7天内收运. 垃圾收运阈值w设置从0.6开始, 以0.1为步长增至0.9, 在每个预设阈值下进行10次求解, 并将所得到的总成本、总距离和车辆使用数为比较指标, 得到了如表2、表3所示的解. 其中best、aver表示算法所求的最小值和平均值.

由表2可知, 在易腐垃圾的R102算例中, 当w=0.6时, 成本最大, 车辆数最多, 距离最长; 随着w值依次增加, 成本、车辆数、距离这3个指标随之降低; 在w=0.9的情况下, 成本、车辆数、距离的结果都较优. 由表3可知, 针对其他垃圾, 当w=0.6时, 成本、车辆数、距离的最小值和平均值都最大; 随着w值逐步增加, 成本、车辆数、距离这3个指标依次降低; 当w=0.9时, 成本、车辆数、距离的最小值和平均值都较优. 同样地, 对于C203、RC208, 从表4的计算结果可以看出, 当w=0.9时, 成本、车辆数、距离的最小值和平均值都较优. 因此, 综合考虑算法求解品质和稳定性, 本文在Solomon标准库的3类算例中, 选取w=0.9进行后续算例求解和分析.

3.1.2 计算结果分析

为进一步分析本文所提算法的表现, 本文在R类测试算例的基础之上, 选取同规模、不同类型的R101、C202和RC205算例进行算法表现分析, 并将本文提出的SA-VNS算法分别与经典的VNS算法与SA算法的运行结果进行对比, 当阈值w=0.9时, 反复求解10次算例, 分别求出总成本、总距离和车辆数的平均值, 对比分析结果如表5及表6所示. 其中, SA-VNS-FIX为在考虑固定周期的情况下使用SA-VNS算法所求结果, 环境成本为超过垃圾点阈值未收运造成的环境污染导致的惩罚成本.

从表5和表6可以看出, 对于各类型、不同周期的算例, 本文所提出的算法在总成本、距离上比 VNS、SA算法结果更出色, 具有更好的寻优性. 相较于可变周期而言, 固定周期的运输成本略小于可变周期, 但加上采用固定周期收运垃圾产生的环境惩罚成本, 固定周期总成本均大于可变周期的总成本, 即采用可变周期具有更大成本效益. 由表7可知, 总成本指标在不同算例上均有改进, 相较于FIX, 本文算法在RC205算例上的成本节约最为显著, 分别为42.7%和133.4%. 相较于VNS, 本文算法在C202和RC205算例上的成本节约最为显著, 分别为3.1%和2.2%. 与SA相比, 本文算法在C202算例上节省的费用最大, 分别达到10.0%和5.9%. 因此, 本文提出的算法具有很好的寻优能力, 可有效求解农村生活垃圾可变周期车辆路径问题.

3.2 仿真算例

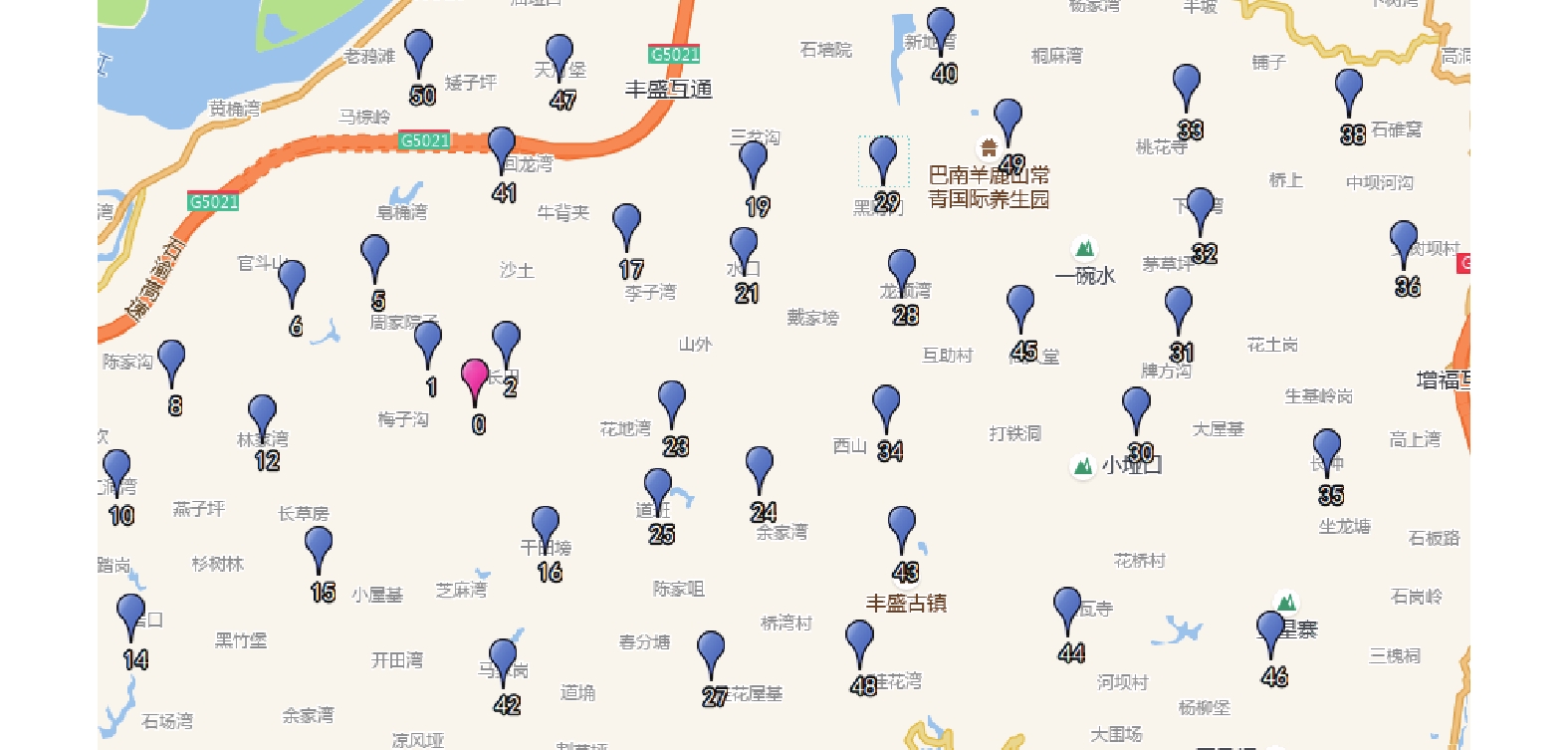
为了进一步检验该模型与算法的有效性, 选择重庆市巴南区的数个农村所涉及的50个垃圾点和1个垃圾中转站. 考虑到农村的实际情况, 有害垃圾和可回收垃圾都较少, 所以本文仿真易腐及其他垃圾的收运过程. 垃圾中转站标号为0, 垃圾点标号为1–50, 中转站及垃圾点的分布见图6, 经纬度分布如附录A所示.

3.2.1 仿真算例垃圾收运阈值灵敏度分析

由表8和表9可以看出, 对于仿真算例, 当收运阈值w从0.6增加到0.9时, 垃圾I的总成本、车辆数和总距离的均值和最小值基本都呈现逐步减小的变化趋势; 垃圾II的总成本和车辆数的均值和最小值呈倒U形变化规律, 总距离的均值和最小值呈现逐步减小的变化规律. 在w=0.6的情况下, 垃圾II的车辆数量的最小值和均值及总成本的最小值结果较优; 在w=0.9的情况下, 垃圾I、II的总成本、总距离的均值和最小值结果更优. 因此, 综合来看, 对于此仿真算例, 本文选取垃圾收运阈值w=0.9作为设定阈值.

3.2.2 仿真算例结果分析

为验证垃圾可变周期收运方案有效性, 分别用固定周期收运和可变周期收运方案对仿真算例反复进行10次模拟计算; 同时与经典算法SA、VNS进行比较, 将仿真算例以SA算法、VNS算法重复求解10次. 其中所有收运方案都将垃圾收运阈值考虑在内, 并采用对应算法规划所有垃圾点的收运路径, 以期最大限度地降低运输成本、固定成本和惩罚成本.

最后得到总成本、环境惩罚成本以及总距离的平均值如表10所示. 本文设计的可变周期模拟退火算法在仿真算例不同周期中的总成本、总距离均优于固定周期收运方案、SA收运方案以及VNS收运方案. 与传统的固定周期收运方案相比, 本文提出的垃圾可变周期收运方案减去了环境惩罚成本, 在收运垃圾I时总成本上优化了110% , 总距离上优化了1.2%, 在收运垃圾II时总成本上优化了289%. 综上, 本文所提出的垃圾可变周期收运策略不仅有助于在一定程度上减少车辆运输成本, 更能有效降低因清运不及时所引发的环境二次污染风险, 实现经济效益与环境效益的双赢.

4 结论与展望

本文基于农村地区垃圾分类的背景, 以标准测试算例与实例为对象, 以最小化运输成本、固定费用、车辆延迟到达惩罚成本和环境惩罚成本为目标, 构建可变周期收运路径优化模型. 采用变邻域模拟退火这一融合算法, 并设计两阶段算法进行求解. 研究结果显示, 与传统的固定周期收运方案相比, 本文所使用的可变周期收运策略其优点是既能在一定程度上能够降低车辆运输成本, 也能有效降低因为无法及时处理而造成的环境二次污染. 针对周期内的每日, 在后续研究中还将考虑垃圾点清运量实时更新的情况; 同时也可考虑连续性或非连续性的可变周期的制定规则, 以此提升收运系统的效能, 构建更加高效、精准的求解算法.