1 引言

图像超分辨率(super-resolution, SR)旨在从低分辨率图像(low resolution, LR)重建高分辨率图像(high resolution, HR). 它是一种基础的低层次视觉任务, 其目标是利用先进的图像处理和机器学习技术重建缺失的细节, 提高图像质量. 在遥感成像、视频处理、医学图像分析等方面具有广泛的应用.

SR方法可以概括为3种范式, 即基于插值的方法、基于优化的方法、基于学习的方法. 基于插值的方法主要依赖最近邻插值、双线性插值、双三次插值等操作来获得从LR图像到HR图像的映射. 尽管基于插值的方法简单易行, 但在高质量图像重建方面的性能较差. 为此, 部分研究者通过基于优化方法来恢复高质量的图像. 例如, 利用稀疏先验知识获得线性组合可有效预测HR图像. 迭代背投影(iterative back-projection, IBP)^[1]通过迭代计算模拟低分辨率图像与观测的低分辨率图像之间距离, 不断更新预测的HR图像. 虽然以上基于优化的方法在图像超分辨率方面取得了很好的效果, 然而, 这种方法往往具有巨大的参数, 计算成本高, 不能在一些计算资源有限的设备上实际使用. 在单图像超分辨率(single image super-resolution, SISR)领域, 探索实用和实时的SR解决方案已经成为一个日益增长的趋势. 为了解决这一问题, 基于深度学习技术的图像SR方法应运而生. 与传统方法相比, 基于深度学习的方法能够更好地捕捉图像中的细节和结构信息, 提高图像重建的质量和准确性. 此外, 在深度学习中卷积神经网络(convolutional neural network, CNN)具有良好的自学习能力, 能够针对图像获取过程中存在的模糊和噪声等退化因素提供有效预防. 因此, CNN在图像超分辨率领域得到了扩展.

Dong等^[2] 基于 CNN提出了一种图像超分辨率方法SRCNN (super-resolution CNN)对图像超分辨率做出了重大贡献, 该方法只使用了3个CNN层进行特征提取. 虽然与传统的图像超分辨率方法相比, 它获得了更好的性能, 但可扩展性差. Kim等^[3]以残差学习^[4]为基础, 提出了VDSR (very deep convolutional networks super-resolution)将网络深度增加到了20层, 并利用残差块加速模型收敛, 提高性能, 但增加了计算复杂度, 并且可能产生梯度消失的问题. Lim 等^[5]提出的突破性的EDSR (enhanced deep residual network for super-resolution)将网络层数叠加到60层以上, 其卓越的性能充分体现了网络深度对图像重建质量的深刻影响. 另外, Tai等^[6]利用门单元、跳跃连接和密集连接结构将获得的浅层特征继承到深层, 增强浅层对图像超分辨率的记忆能力. 虽然这些方法可以很好地实现图像的超分辨率, 但它们的输入较大, 可能会导致较大的计算成本.

随着注意力机制^[7–9]和Transformer^[10,11]模型在图像处理领域的引入, 极大地推动了SISR的发展. Zhang等^[8]设计的RCAN (residual channel attention network)通过残差结构来实现网络连接, 通过引入通道注意力来调整不同信道之间模型的权值, 增强网络对图像特征的建模能力. 肖子安等^[12]提出了一种多个级联的多尺度特征和坐标注意力模块, 实现对低分辨率遥感图像高频特征进行更充分的提取, 同时有效融合多尺度空间信息. Liang等^[13]在图像恢复领域引入了Swin Transformer, 并提出了swinIR (image restoration using Swin Transformer)方法. swinIR是一种基于Transformer的图像超分辨率方法, 它利用了Transformer的强大表达能力, 实现了超分辨率领域先进的性能. 无论使用的是注意力机制还是Transformer. 随着网络性能的提高, 模型参数的数量和计算工作量也显著增加, 使得超分辨率网络的实际应用变得不可行. 虽然这些方法是有效的, 并且极大地推动了图像超分辨率的发展, 但他们需要依赖更深的网络架构和强大的算力, 难以在资源受限设备实际应用. 此外, 以上方法获取的信息不能完全表达复杂场景下预测的高质量图像.

针对上述问题, 本文提出了一种宽结构图像动态超分辨率网络(wide-structure dynamic image super-resolution network, W-SDNet), 旨在不显著增加计算负担的前提下提升图像重建质量. W-SDNet采用了一种递进动态网络架构, 通过融合浅层特征提取块、残差增强块、宽增强块、特征细化块和构造块, 实现了对复杂场景中丰富特征的有效提取和细化. 本网络的核心在于动态调整网络结构以适应不同的图像内容, 从而更精确地重建高质量图像. 本文的主要贡献概括如下.

(1)引入了移位卷积残差块, 通过移位卷积层有效提取高频特征, 同时降低模型的参数数量和计算成本.

(2)提出了一个具有宽网络结构的动态宽增强块, 结合蓝图可分离卷积和边缘检测算法的增强空间注意力模块, 增强了模型对图像边缘特征表达能力.

(3)通过采用组卷积和信道分割操作, 进一步降低了计算复杂度, 并利用特征细化块精确地学习和细化获得的特征. 实验结果证明, 相比现有的主流方法, W-SDNet在提升重建效果和降低模型复杂度方面展现了显著的优势.

2 相关工作 2.1 用于图像超分辨率的轻量级模型

为了提高图像处理的效果而增加网络深度, 导致了巨大的计算成本, 不利于超分辨率方法在现实生活中的应用. 为了解决这个问题, 研究人员提出了越来越多的精确和高效的模型. Kim等^[14]和Tai等^[15]分别设计了DRCN (deeply-recursive convolutional network)和DRRN (deep recursive residual network)模型, 利用递归结构和参数共享机制, 大幅减少了模型参数的数量. 然而, 递归结构并没有减少计算工作量. Ahn等^[16]提出了一种具有群卷积的高效级联残差网络(cascade residual network, CARN), 提高了超分辨率的性能和效率. Hui等^[17]实现了一个轻量级信息多蒸馏网络(iterative mean distillation network, IMDN), 利用信息蒸馏机制(information distillation mechanism, IDM)逐级提取分层特征. RFDN (residual feature distillation network)^[18]改进了IMDN的体系结构, 提出了残差特征精馏网络, 用特征精馏连接代替IDM. 王一宁等^[19]利用密集块和反卷积提出一种拥有较少的层和参数的轻量密集神经网络模型, 在训练速度和内存消耗方面均取得了良好的效果. 周登文等^[20]设计了轻量化且高效的区域互补注意力和多维注意力模块, 在信道维度与空间维度对像素间的依赖关系建模, 实现了轻量SR. Gao等^[21]将多路注意力模块、轻量级卷积块组合在一起, 实现轻量级CNN, 以便获得更准确的信息, 提高图像超分辨率效果. 陈豪等^[22]针对网络复杂度较高的问题, 提出了基于Transformer-CNN的轻量SR方法, 使网络能够更好地捕获到图像中局部与全局的深度特征, 降低了推理时间.

根据上面提到的模型发现, 优化网络架构对于实现图像超分辨率的轻量级CNN是有效的. 虽然最近的轻量化SISR模型取得了良好的效果, 但在高频恢复图像细节方面仍存在一些问题. 所以考虑到获取的信息对复杂场景的鲁棒性, 利用动态门、多视图思想和深度网络的设计原则, 实现了一种基于CNN的轻量级的图像超分辨率.

2.2 图像超分辨率的动态神经网络

传统的神经网络结构一般是固定的, 不能根据不同的场景灵活变化, 这影响了他们在复杂场景中的表现. 针对这一问题, 研究人员开发了动态神经网络, 动态网络能够根据输入数据特征及上下文信息, 对网络结构和参数进行自适应调整, 增加网络的自适应性和灵活性, 并提高模型的鲁棒性和稳定性. 由于动态网络模型优越性, 已被应用于图像超分辨率领域. 例如, Shi等^[23]使用了一种内容自适应技术, 对齐现实世界中的图像以实现图像超分辨率. 内容自适应技术可以根据输入数据的特征和上下文信息, 动态地选择和调整网络的层次结构、连接方式和参数设置. 使网络更好地适应不同的输入数据, 并提高网络的性能和泛化能力. Wu等^[24]使用显著性感知模型来提取遥感图像中的显著性信息, 然后通过动态路由策略将低分辨率图像的特征映射动态地分配给高分辨率图像的不同区域, 以保留更多的细节信息进而实现超分辨率重建. Chen等^[25]通过边缘信息分配不同的网络来恢复图像超分辨率中的详细信息. 为了提高图像超分辨率的性能, 采用不同的注意机制分别提取局部和全局特征, 从而为图像超分辨率提供更有用的详细信息. 根据上述所提, 可以看到动态网络对于图像的超分辨率是有效的. 受此启发, 本文应用了一个动态网络实现图像超分辨率.

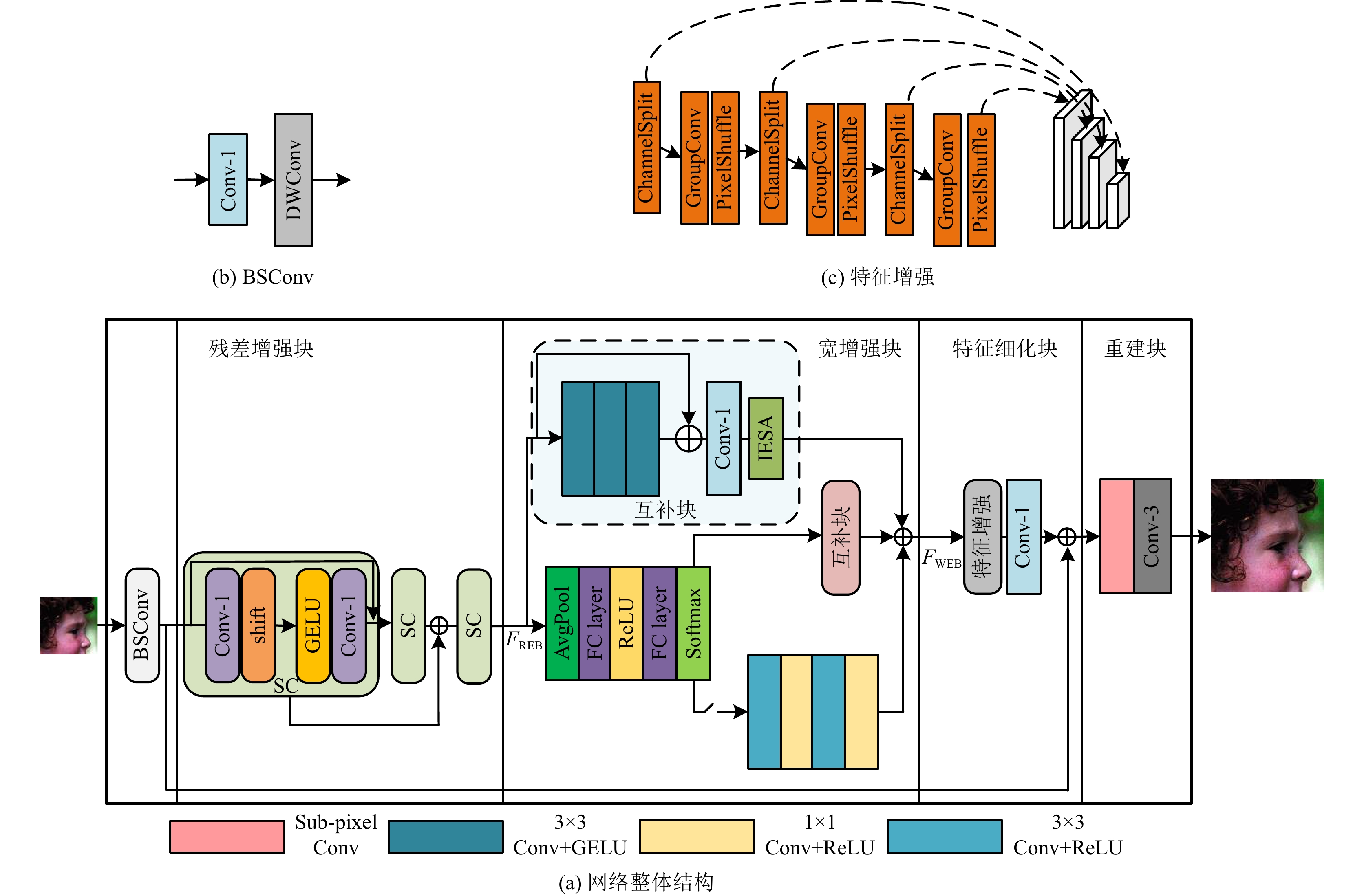
3 本文方法 3.1 网络架构

基于CNN的单图像超分辨率方法通常倾向于增加网络深度以提高图像处理性能. 然而, 这种方法容易导致计算成本增加, 并且不利于在低配置设备上实现. 此外, 单一的网络结构往往难以提取复杂场景中的丰富特征. 针对这些问题, 本文提出了一种新型的递进动态网络(W-SDNet). 整体结构如图1所示, 该网络由多个组件组成, 包括浅层特征提取块、残差增强块、宽增强块、特征细化块以及构造块. 首先, 低分辨率图像经过蓝图可分离卷积(blueprint separable convolution, BSConv)^[26]进行浅层特征的提取. 接下来, 通过由3个移位卷积残差块(shift-conv residual block, SC-ResBlock)组成的残差增强块, 对图像的层次信息进行提取和增强, 从而丰富特征的层次表达. 为了应对复杂场景的挑战, 引入了宽增强块. 这个模块采用结合改进增强空间注意力机制的互补块(complementary block, CBlock)和一个动态门机制, 以更有效地为复杂场景提取更丰富的信息. 通过这种设计, 网络能够更好地适应各种复杂场景, 并提取更具表达力的特征. 在宽增强块之后, 使用了特征细化块. 这个模块通过组卷积和信道分割的策略, 消除了宽增强块中可能产生的干扰, 进一步优化了从宽增强块中学习到的特征. 最后, 构造块负责通过上采样和卷积层, 将前述模块提取的特征和浅层特征进行整合, 以重建高质量的图像. 通过这种方式, W-SDNet不仅优化了特征提取的过程, 同时也提升了最终图像的重建质量. 实现过程如式(1)所示:

$ \begin{split} {I_{{\text{HR}}}} & = {\mathrm{W}} {\textit{-}}{\mathrm{SDNet}}({I_{{\text{LR}}}}) \\ & = {\mathrm{RB}}({\mathrm{FEB}}({\mathrm{WEB}}({\mathrm{REB}}({\mathrm{SF}}({I_{{\text{LR}}}}))))) \end{split} $

(1)

其中, ${I_{{\text{LR}}}}$表示低分辨率图像, W-SDNet表示W-SDNet的函数, SF、REB、WEB、FEB、RB分别表示浅层特征提取块、残差增强块、宽增强块、特征细化块、重建模块的函数. ${I_{{\text{HR}}}}$表示W-SDNet输出的高分辨率图像.

3.2 浅层特征提取块

浅层特征提取部分采用蓝图可分离卷积对输入图像进行浅层特征提取, BSConv具体架构如图1(b)所示. BSConv是深度可分离卷积(depthwise separable convolution, DSConv)^[27]的改进变体, 它由1×1卷积和深度卷积组成. 更好地利用了核内相关性, 相比于普通卷积减少了冗余运算, 文献[26]证明BSConv对于高效SR是有利的. $ {F_{{\text{SF}}}} $表示提取得到的浅层特征, 浅层特征提取过程可以表述为式(2):

$ {F_{{\text{SF}}}}{\text{ = }}{\mathrm{SF}}{\text{(}}{I_{{\text{LR}}}}{\text{)}} $

(2)

3.3 残差增强块

残差网络已经广泛应用在图像超分辨率领域, 大量研究表明, 通过增加网络层深度, 所提取的特征就越丰富, 但过深的网络层数会引起梯度爆炸或梯度消失的问题, 而多个残差连接的残差块可以很好地解决这个问题, 所以本文模型利用残差增强块对层次信息进行提取和增强. 残差增强块采用3个移位卷积残差块(shift-conv residual block, SC-ResBlock)提取深度信息, SC-ResBlock是由移位残差卷积层, GELU^[28]激活函数, 1×1卷积层组成. 最后使用残差学习操作收集浅层特征, 以增强模型的记忆能力.

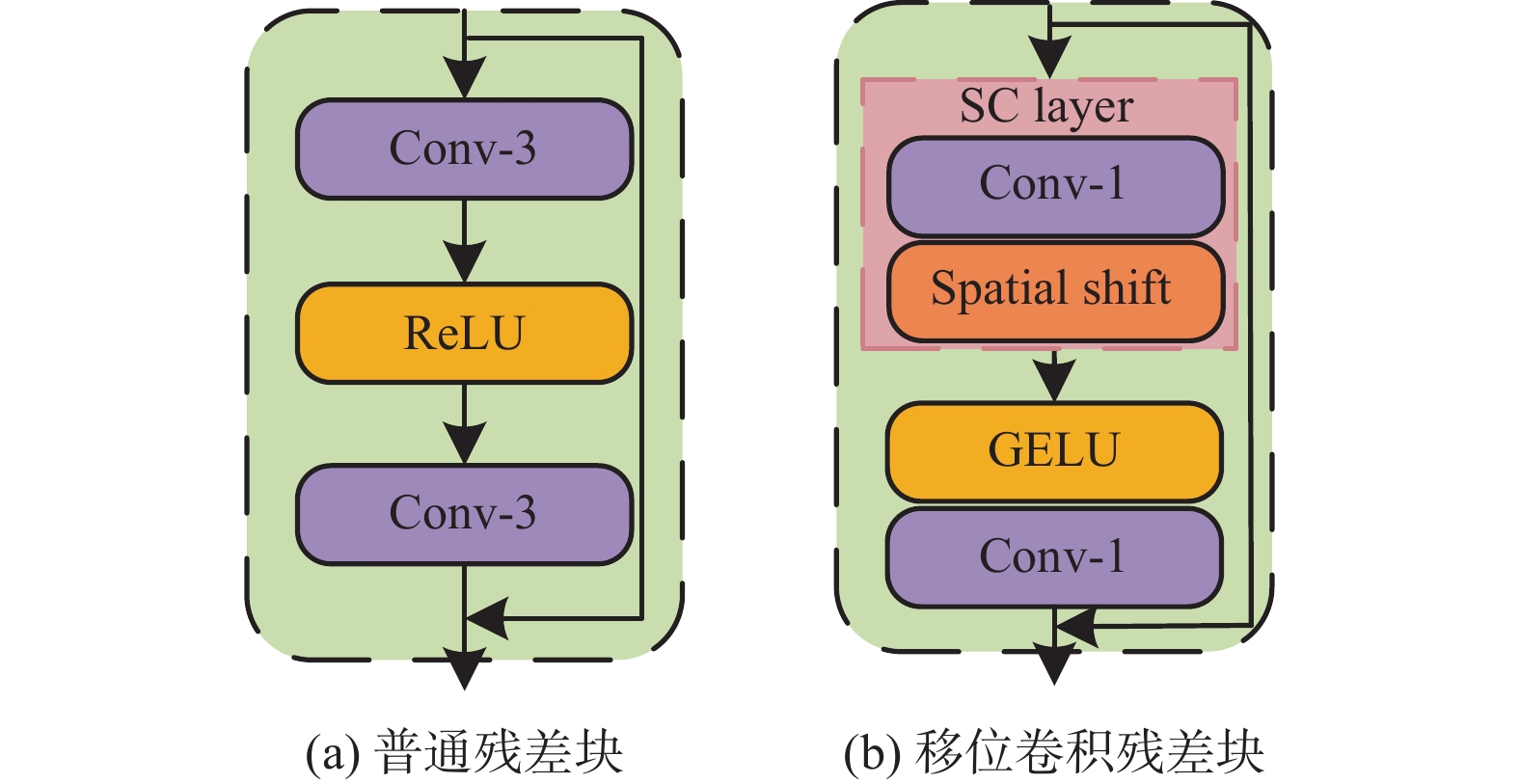
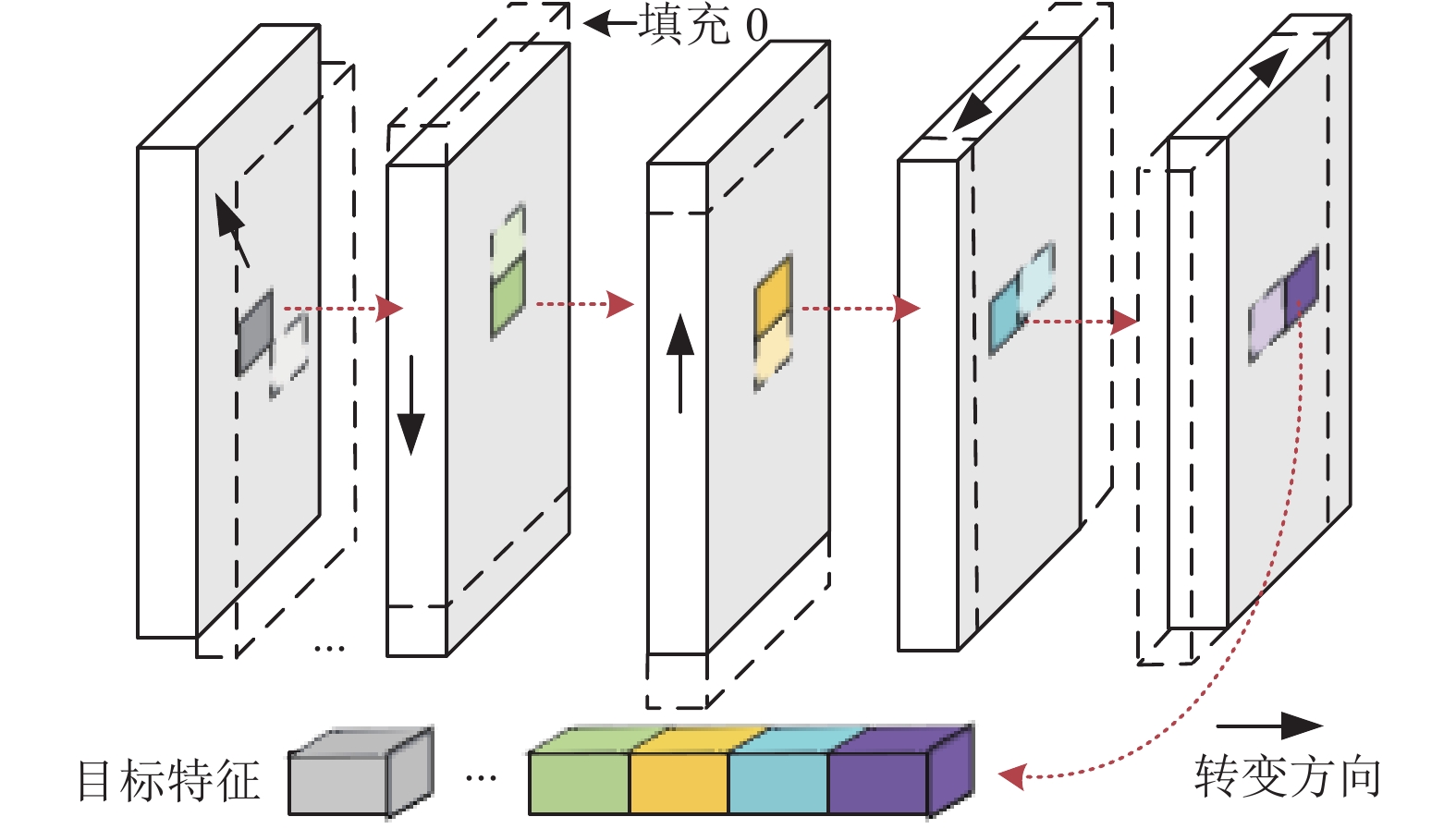
如图2(a)所示是文献[5]中提出的残差块, 广泛应用于SR网络中. 3×3卷积运算在平衡模型容量和计算成本方面具有一定优势, 但会增加参数和计算开销, 所以将3×3卷积层替换成计算成本更低的1×1卷积层, 虽然1×1卷积很大程度上减少了参数数量和计算成本, 但是由于1×1卷积操作只对单个像素的特征进行处理, 这会影响建模, 因此在这里通过空间移位操作^[29], 如图3所示. 通过重新排列特征图的空间位置, 在不增加计算成本的情况下, 增强了跨信道组的局部空间特征聚合. Shift-Conv层(简化为SC层)由1×1卷积层和空间移位操作堆叠, 因此SC层扩展了正常的1×1卷积, 具有局部特征聚合, 且参数更少. 与正常的3×3卷积相比, SC层在保持相当性能的同时显著减少了参数数量. 在激活单元方面, GELU具有良好非线性表达能力, 逐渐成为近期研究的首选. 残差增强块具体操作如式(3):

$ \begin{split} {F_{{\text{REB}}}} & = {\mathrm{REB}}({F_{{\mathrm{SF}}}}) \\ & = {\mathrm{SC}}({F_{{\text{SF}}}} + {\mathrm{SC}}({\mathrm{SC}}({F_{{\text{SF}}}}))) \end{split} $

(3)

其中, REB表示残差增强函数, SC表示移位卷积残差操作, $ {F_{{\text{REB}}}} $表示经过残差增强操作的输出.

3.4 宽增强块

现有图像超分辨率网络普遍通过增加网络深度来提升网络重建效果, 但忽视了网络宽度对于网络影响, 根据GoogLeNet^[30], 已知增大宽度可以提取更多的互补信息, 以提高图像应用的性能. 受此启发, 构建了宽增强块, 用以增加网络特征表达能力, 提高网络性能, 进一步证明增加网络宽度对图像重建具有积极影响. 宽增强块紧跟在残差增强块之后, 接收残差增强块的输出$ {F_{{\text{REB}}}} $作为其输入, 该模块由双分支的4层网络并行结构组成, 每个分支各自执行不同的任务以增强特征表达. 第1分支用于深度信息的提取, 设计了一个互补块来实现. 第2分支由一个动态网络组成, 它使用平均池(AvgPool)、全连接层、ReLU激活函数、全连接层和Softmax组成的门机制来选择一个门, 即选择的动态门. 具体而言, 动态网络通过门机制的Softmax层预测两个关于是否激活选定的动态门的概率值, 这两个值的和为1, 每个值代表概率, 分别对应于是否激活选定的动态门. 如果第2个值大于0.75, 则该分支的输出为固定动态门和选定动态门输入, 否则, 它的输出只有一个固定门的输入. 其中固定动态门结构与互补块结构相同, 用以更好提取深层特征, 选择动态门由核为3×3的Conv+ReLU和核为1×1的Conv+ReLU两种组合堆叠. 最后通过残差学习收集互补特征, 其中各输入输出通道均为64, 过程可表示为式(4):

$ \begin{split} & {F_{{\text{WEB}}}} = {\mathrm{WEB}}({F_{{\text{REB}}}}) \\ & = ({\mathrm{CB}}({F_{{\text{REB}}}}) + {\mathrm{FDG}}({\mathrm{GM}}({F_{{\text{REB}}}})))\Theta {\mathrm{SDG}}({\mathrm{GM}}({F_{{\text{REB}}}})) \end{split} $

(4)

其中, ${F_{{\text{WEB}}}}$表示宽增强块输出. ${\mathrm{CB}}$、${\mathrm{GM}}$、${\mathrm{FDG}}$、${\mathrm{SDG}}$分别表示互补块、门机构、固定动态门、选定动态门函数. $\Theta $表示选择的门, 如果第2个结果大于0.75, $\Theta $为残差学习操作. 否则, $\Theta $表示被删除的部分.

3.4.1 互补块

为了增强特征表达能力和模型的鲁棒性, 在宽增强块中增加了互补块. 受文献[31]启发, 互补块采用剩余局部特征块, 在保持模型容量的前提下, 显著减少推理时间, 互补块只用3个叠加的Conv+GELU进行特征提取, 过程如式(5):

$ \left\{ \begin{gathered} {F_{{\text{refined1}}}} = {\mathrm{R}}{{\mathrm{M}}_1}({F_{{\text{REB}}}}) \\ {F_{{\text{refined2}}}} = {\mathrm{R}}{{\mathrm{M}}_2}({F_{{\text{refined1}}}}) \\ {F_{{\text{refined3}}}} = {\mathrm{R}}{{\mathrm{M}}_3}({F_{{\text{refined2}}}}) \\ \end{gathered} \right. $

(5)

其中, ${\mathrm{R}}{{\mathrm{M}}_{{i}}}$为第i个细化模块, ${F_{{\text{refined}}}}_{{i}}$为第i个细化特征, 经过多个局部特征细化步骤后, 将最后细化的特征$ {F_{{\text{refined}}}} $与跳过的特征$ {F_{{\text{REB}}}} $相加, 得到$ {F_{{\text{refined}}}} $, 过程如式(6):

$ {F_{{\text{refined}}}} = {F_{{\text{REB}}}} + {F_{{\text{refined}}3}} $

(6)

最后通过一个1×1卷积进行特征融合和降维, 通过改进的增强空间注意力模块, 增强边缘信息和重要信息表达能力. 如式(7):

$ {F_{{\text{WEB}}}} = {\mathrm{DSA}}({C_1}({F_{{\text{refined}}}})) $

(7)

其中, $ C_1 $表示1×1卷积, DSA表示注意力机制.

3.4.2 改进的增强空间注意力

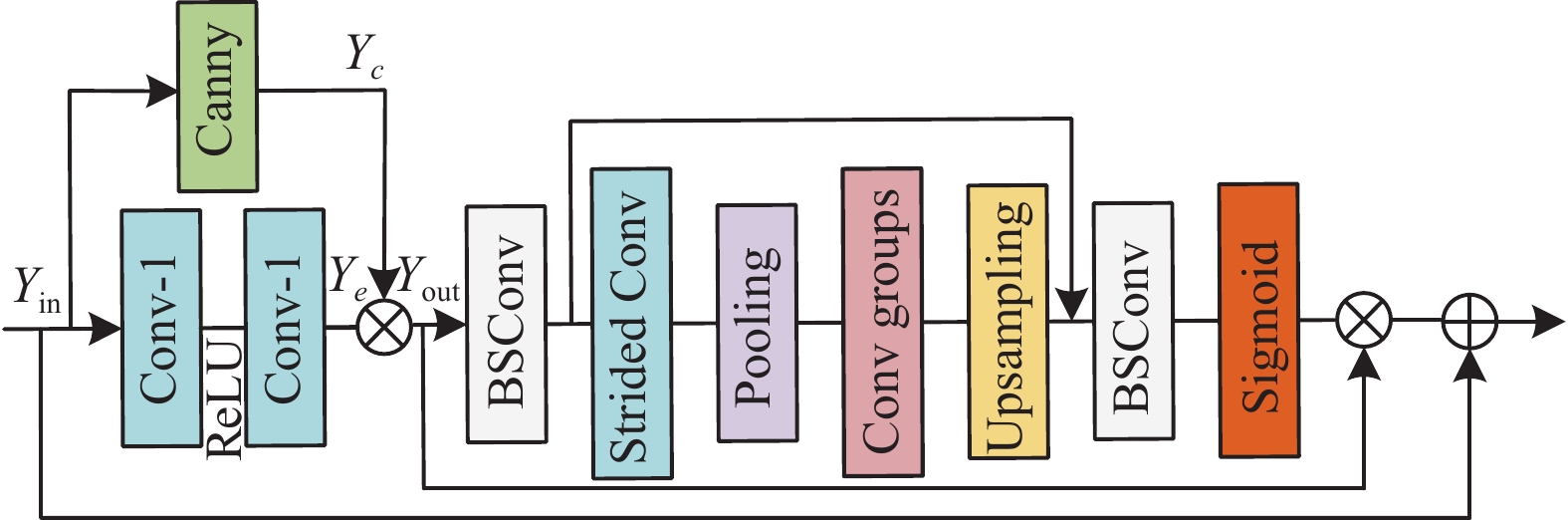
注意力机制提出以来被广泛应用到图像领域, 并取得了令人满意的效果, ESA (enhanced spatial attention)^[17]注意力是一种增强空间注意力的方法, 其在提升模型表达能力和改善长距离依赖方面具有有效性, 但随之而来的是参数量的增加和计算复杂度的增加, 另一方面, 在对图像的高低频信息进行区分和整合的过程中需要额外关注边缘信息, 因为图像每个通道都包含大量高低频信息分量, 而高频信息分量往往含有许多边缘信息, 但现有方法大都不注重边缘的高频信息^[32]. 为解决以上问题, 设计了如图4所示的IESA (improved enhanced spatial attention), 该注意力模块在ESA注意力机制的基础上, 融合了Canny边缘检测算子^[33], 对输入特征图进行边缘特征提取, 并与利用卷积操作得到的特征图进行融合运算. 得到边缘特征增强的特征图, 如式(8)所示:

$ \left\{ \begin{gathered} {Y_{{c}}} = {\text{Canny}}({Y_{{\text{in}}}}) \\ {Y_{{\text{out}}}} = {Y_{{e}}} \otimes {Y_{{c}}} \\ \end{gathered} \right. $

(8)

其中, $ {\text{Canny}}( \cdot ) $为Canny边缘检测算子.

针对参数量的增加和计算复杂度的增加的问题, 采用BSConv卷积代替原有的普通卷积, 因为与普通卷积相比, BSConv采用分离卷积方式, 降低了计算复杂度和参数量, 提升计算速度, 同时BSConv采用不同卷积核进行特征提取, 可以更好地捕捉到输入数据的局部和全局特征. 将经过边缘增强的特征图, 通过BSConv降低输入特征的通道维数. 然后使用大步卷积和大步最大池化层来减小空间大小. 通过一组卷积学习特征图空间维度之间的相关性, 采用基于插值的上采样来恢复空间大小. 为了提高效率结合跳跃连接, 通过BSConv对特征进行进一步处理, 恢复信道大小. 最后, 通过Sigmoid函数生成注意矩阵, 并乘以原始输入特征. 通过跳跃连接初始特征图与网络底层连接进行残差学习, 以降低网络训练难度.

3.5 特征细化块

为了防止宽增强块中某些成分的干扰, 对宽增强块中获得的特征进行特征细化. 通过组卷积逐渐添加高频细节, 并利用组卷积和信道分割操作来降低计算复杂度, 获得一组分辨率逐渐提高的特征图, 如图1(c)所示. 首先, 将输入的特征映射$ {M_{{\mathrm{in}}}} \in {\mathbb{R}^{C \times H \times W}} $沿着通道维度分成两部分, 其中一部分包含1/4的特征进行特征映射, 记为$ {\tilde M_1} \in {\mathbb{R}^{\frac{C}{4} \times H \times W}} $, 并保持为当前分辨率. 使用组卷积和像素变换向剩余的3/4特征映射$ \tilde M \in {\mathbb{R}^{\frac{{3C}}{4} \times H \times W}} $添加高频细节, 并将空间分辨率提高比例因子2. 然后, 将二级分辨率的特征图分成两部分, 保留1/3的特征图$ {M_2} \in {\mathbb{R}^{\frac{C}{4} \times 2H \times 2W}} $作为当前分辨率. 其余2/3特征映射$ {\tilde M_2} \in {\mathbb{R}^{\frac{{2C}}{4} \times 2H \times 2W}} $的分辨率通过使用群卷积和像素变换再次加倍. 最后, 将第3级分辨率的特征图沿通道维度分成两半. 一半的特征映射$ {M_3} \in {\mathbb{R}^{\frac{C}{4} \times 4H \times 4W}} $保持当前分辨率, 另一半$ {\tilde M_3} \in {\mathbb{R}^{\frac{C}{4} \times 4H \times 4W}} $使用卷积层和像素shuffle操作进行两次升级. 最后一级的分辨率是原始输入的8倍, 最后一级的特征映射记为$ {M_4} \in {\mathbb{R}^{\frac{C}{4} \times 8H \times 8W}} $. 因此, 得到了渐进分辨率的特征映射$ \left\{ {{{{M}}_{{t}}}} \right\}_{{{t}} = 1}^4 $. 该过程具体过程如式(9):

$ \left\{ \begin{gathered} {{M} _{\text{1}}}, {{\tilde M}_{\text{1}}}{\text{ = }}{{{\mathrm{Split}}}} {\text{(}}{{M} _{{\text{in}}}}{\text{) }} \\ {{M} _{\text{2}}}, {{\tilde M}_{\text{2}}}{\text{ = }}{{{{\mathrm{Split}}}}} {\text{(}}{{{{\mathrm{PixelShuffle}}}}} {\text{(}}{\mathrm{GroupConv}}_{3, 3C}^{{\text{(3)}}}{\text{(}}{{\tilde M}_{\text{1}}}{\text{)) }} \\ {{M} _{\text{3}}}, {{\tilde M}_{\text{3}}}{\text{ = }}{{{{\mathrm{Split}}}}} {\text{(}}{{{{\mathrm{PixelShuffle}}}}} {\text{(}}{\mathrm{GroupConv}}_{3, 2C}^{{\text{(2)}}}{\text{(}}{{\tilde M}_{\text{2}}}{\text{)) }} \\ {{M} _{\text{4}}}{\text{ = }}{{{{\mathrm{PixelShuffle}}}}} {\text{(}}{{{\mathrm{Conv}}} _{3, C}}{\text{(}}{{\tilde M}_{\text{3}}}{\text{))}} \\ \end{gathered} \right. $

(9)

其中, $ {\mathrm{GroupConv}}_{k, C}^{\left( n \right){\text{ }}}\left( \cdot \right) $表示一个卷积层, 其核大小为k×k, 信道数为C, 组数为n. $ {\mathrm{PixelShuffle}}( \cdot ) $为像素重洗操作. 通过组卷积运算得到的特征图经过一个1×1卷积进行通道融合, 得到特征细化块输出的特征图$ {F_{{\text{FRB}}}} $, 具体操作如式(10):

$ {F_{{\text{FRB}}}} = {C_1}({M_1}, {M_2}, {M_3}, {M_4}) $

(10)

3.6 重建块

重建块由亚像素卷积层和3×3卷积组成, 重建阶段首先由亚像素卷积对融合后特征图进行上采样, 再使用3×3卷积构建高质量图像. 得到最终高分辨率图像$ {F_{{\text{HR}}}} $具体过程可表示为式(11):

$ \begin{gathered} {F_{{\text{HR}}}} = {\mathrm{RB}}({F_{{\text{FRB}}}} + {F_{{\text{SF}}}}) = {C_3}({\textit{Sub}}{\text{(}}{F_{{\text{FRB}}}} + {F_{{\text{SF}}}}{\text{)}}) \end{gathered} $

(11)

其中, $ \left\{ {L_L^{{i}}, L_H^i} \right\}_{i = 1}^n $和Sub分别表示3×3卷积和亚像素卷积.

3.7 损失函数

在不增加计算成本的情况下, 增强了跨信道组的局部空间的均方误差(mean squared error, MSE)^[34]是SR任务的常用损失函数. 通过估计量与被估计量之间差异程度反应模型重建情况, 均方误差越小, 说明模型的预测能力越强. 通过实验对比MSE更适合模型, 所以为了更好地提升模型性能, 选择MSE作为损失函数来训练W-SDNet模型. 即将训练数据集的$ \left\{ {L_{{L}}^{{i}}, L_{{H}}^i} \right\}_{i = 1}^n $作用于MSE上训练W-SDNet模型, 其中$ L_{{L}}^{{i}} $和$ L_{{H}}^{{i}} $分别作为第i个低分辨率训练图像块和高分辨率训练图像块. 设n为训练图像patch的个数. 上面的描述可以表示为式(12):

$ L(p) = \frac{1}{{2n}}\mathop {\sum\limits_{i = 1}^n {\left\| {{\mathrm{W}} {\textit{-}}{\mathrm{SDNet}}(I_{{L}}^i) - I_{{H}}^i} \right\|^2} }\nolimits $

(12)

其中, L为MSE的损失函数, p表示学习到的参数.

4 实验结果分析 4.1 数据集

选取使用广泛的DIV2K^[35]公共数据集训练模型. DIV2K在NTIRE 2017挑战赛被提出, 并广泛应用于图像超分辨率领域. 该数据集由1000张高品质图像组成, 涵盖了包括人物、自然景观和生活场景在内的多种类型且分辨率均为2K图像. 选取其中800张用于训练, 100张用于验证, 100张用于测试. 测试时, 使用Set5^[36]、Set14^[37]、BSD100^[38]、Urban100^[39]、Manga109^[40]、AIM2019^[35]和RealSR^[41]测试数据集来评估不同算法的性能. 此外, 这些数据集中的每个图像都包含了3个版本×2、×3、×4的LR和HR图像.

所提方法采用了3个关键指标来全面评估超分辨率重建模型的性能: Y信道平均峰值信噪比(PSNR)、结构相似度(SSIM)、感知图像相似性(learned perceptual image patch similarity, LPIPS). PSNR和SSIM作为基础指标, 主要衡量图像质量的传统视觉特征, 其中高值代表更优的图像恢复质量. 为进一步评估图像的感知细节质量, 引入了LPIPS指标. LPIPS通过分析图像深层特征的差异, 专注于图像内容的感知属性, 低LPIPS值表示重建图像与原始图像在视觉上更为相似.

4.2 实验设置

本文实验在 NVIDIA RTX 3090 GPU 上进行; 选用Ubuntu 20.04版本, Python 3.8.13作为编程环境, 并选择深度学习框架PyTorch 1.13.1, CUDA 版本11.7, cuDNN 8.5.0; Batch和patch size分别设置为64, 步数是6E+5. 在实验中, 初始学习率为1E–4, 每走4E+5步, 学习速度就会减半. 采用Adam优化器进行优化, 其中参数β₁为0.9, β₂为0.999.

4.3 实验与结果分析

为了验证W-SDNet的先进性, 对 W-SDNet算法与已有先进算法进行了广泛的实验对比. 实验结果如表1–表3 所示, 分别展示了所提算法与其他先进算法在 2 倍、3 倍、4 倍超分辨率任务上的客观评价指标结果(其中加粗字体表示最优结果, 下划线字体表示次优结果, *表示重新复现的结果).

由表1–表3可以看出, 本文方法在不同放大倍数上大都取得了最优和次优的良好表现. 当放大倍数为4时, 相比于其他算法, 本文算法在5个测试数据集中均取得了最优的PSNR. 在Set5数据集放大倍数为3时, 相比于DSRNet^[42], 本文方法获得的PSNR和SSIM提高了0.06 dB和0.0009, 同时参数量相比于DSRNet降低了20.76%. 综上所述, 可以看出本文算法可以在减少参数量的同时获得更优秀的性能指标.

为了进一步评估图像的感知细节质量, 将提出的W-SDNet在质量更高的AIM2019和RealSR数据集上做了进一步的测试, 并与现有的主流方法ZSSR、DASR等方法进行了实验对比分析, 对比结果如表4所示. 实验结果表明, 相比于其他先进的超分辨率模型, 所提方法在两个数据集上均展现出了优异的感知图像重建性能. 特别是在RealSR数据集上, 低LPIPS值表明本文方法能够有效地减少图像间的感知差异, 重建出与原始图像在视觉上更为接近的高质量图像.

将提出的W-SDNet与经典模型LapSRN、VDSR, 先进轻量级模型IMDN、RFDN, 基准模型DSRNet进行了视觉质量比较, 在Urban100测试数据集上放大4倍SR结果如图5和图6所示. 对于img_078可以发现LapSRN和VDSR生成的图像相对模糊, 条纹存在伪影, 线条变形, 而本文提出W-SDNet虽然存在形变, 但相比于其他方法纹理更清晰, 更贴近高分辨率图像. 对于img_096发现LapSRN、VDSR、IMDN、DSRNet不仅产生的图像模糊, 而且线条变形严重, 不能准确恢复图像纹理细节, W-SDNet恢复了图像大多细节, 失真更小具有更好的视觉效果. 对于图片纹理细节恢复的优势, 得益于本文提出的融合边缘检测算子的注意力机制, 更加关注边缘纹理信息, 使生成的SR图像可以更好表达边缘特征.

4.4 模型复杂度分析

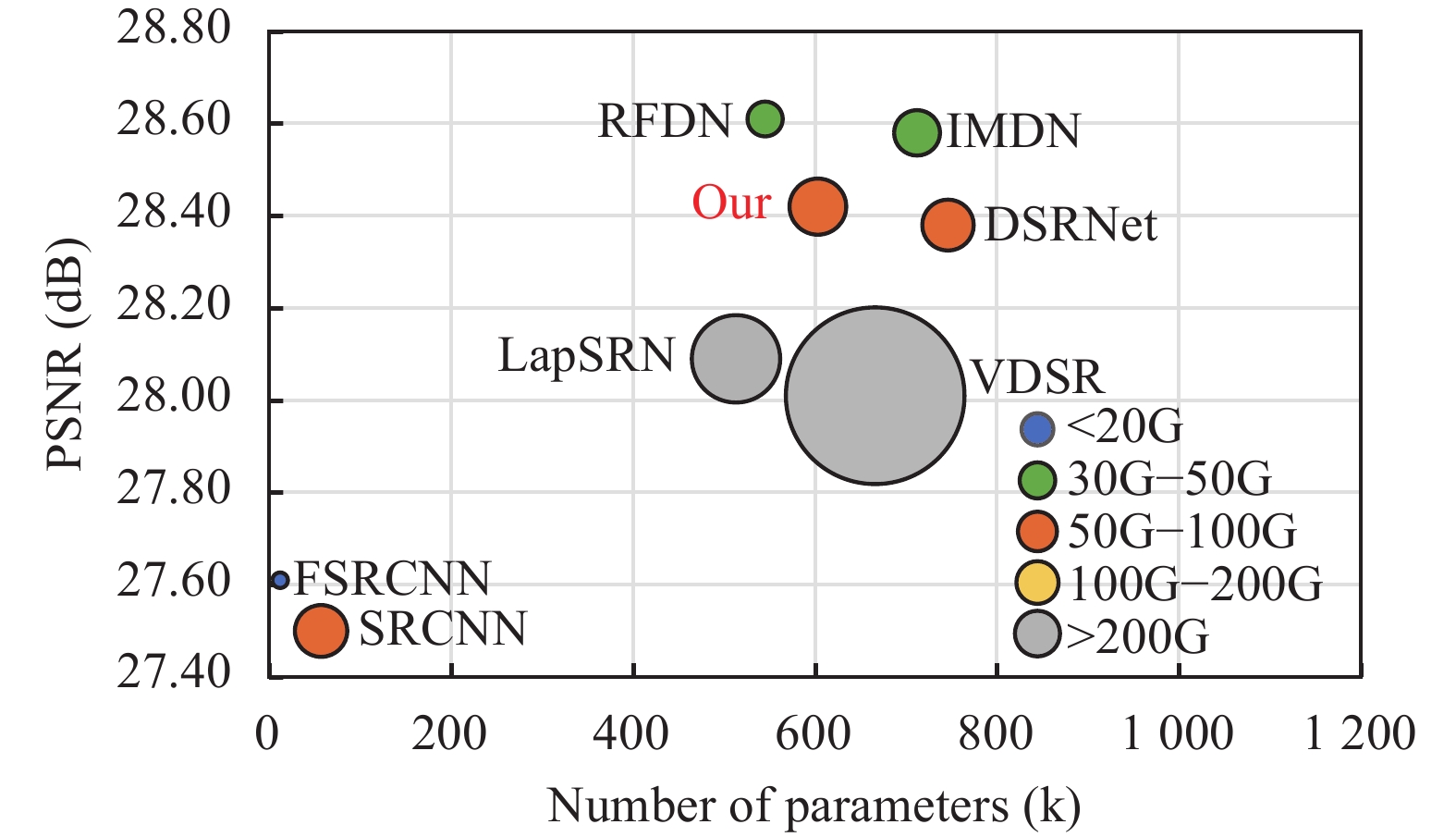
在本节中, 对算法的模型复杂度进行了研究, 包括大小、运行时间、Flops, 并与其他经典图像超分辨率算法进行了比较. 如表5和图7所示, 本文提出的方法平均运行时间在所提方法中排名第四, 虽然SRCNN、FSRCNN、VDSR运行时间相比于本文方法更短, 但本文算法的PSNR显著高于这3种模型, 且参数量和Flops少于VDSR. 表5中IMDN与RFDN的PSNR略高于本文方法, 但本文方法参数量更少的同时单幅图像平均运行时间仅为这两种方法的1/4. 通过以上实验对比分析, 本文方法很好地平衡了模型性能和运行时间之间的矛盾, 保持性能的同时降低了模型的参数量和运行时间.

4.5 消融实验

为了验证算法各模块的有效性进行了消融实验, 通过在Set14数据集上放大2倍的SSIM、PSNR的变化, 验证移位残差块、互补块、注意力机制、特征增强块的有效性, 以及门机制中阈值的选取和损失函数的选取.

(1)验证移位残差块, 互补块, 特征增强块有效性. 在验证各模块有效性之前, 将DSRNet作为基线网络, 对DSRNet中对应模块进行替换, 通过模型参数量和PSNR变化来验证各模块对模型性能. 通过表6所示, 可以发现移位残差块和特征细化块可以在损失很少的PSNR情况下, 极大地减少模型的参数. 而互补块虽然增加了一些参数和运算量, 但对模型的重建性能提高有帮助, 通过各模块的组合, 可以在不损失重建效果的情况下, 减少模型参数, 提升模型性能. 这表明各模块对于提升图像超分辨率性能指标是有效的.

(2)验证互补块IESA的有效性. 为了验证本文提出的IESA注意力模块的有效性, 在本文算法的基础上通过替换其他3种不同的注意力模型, 对比不同注意力机制对于网络参数量和PSNR、SSIM的变化情况, 验证增强注意力机制性能. 通过表7所示, 不同注意力对于网络参数量以及PSNR、SSIM具有不同的影响. 仅使用通道平均值的SA 和CCA的模型虽然参数较少, 但性能明显比使用ESA和本文注意力模型的差. 而使用本文的模型保持与ESA相当参数的同时, 取得了比使用 ESA 的模型更好的性能. 所以尽管本文提出的注意力增加了少量参数, 但是获得了最好的PSNR和SSIM. 证明该注意力模型具有有效性.

(3)门机制中阈值的选取. 宽增强块中动态门阈值的选取对于动态神经网络十分重要, 阈值选取的好坏直接影响动态网络的性能, 所以选择一种二分法来设置他的阈值. 选取了0.5、0.75、0.9这3个值来作为动态门的备选阈值. 通过实验, 如表8所示, 发现当阈值为0.75时, 网络的PSNR高于其他阈值的PSNR, 所以选择0.75作为动态门阈值.

(4)损失函数的选取. 为了探索不同损失函数对于模型的影响, 选取了在图像超分辨率领域使用最广泛的L1 Loss (mean absolute error, MAE)、L2 Loss (mean squared error, MSE)和平滑L1损失(smooth L1 Loss, SLL) 3种损失函数和文献[50]提出的FFT损失函数(fast Fourier transform loss function, FFT). 在Set14数据集放大倍数为4倍下, 比较模型使用这4种不同损失函数的PSNR.

通过表9所示, 发现本文方法使用MSE损失函数获得了最高的PSNR, 并且在实验中发现L1 Loss收敛速度较慢, SLL Loss的PSNR比较低, FFT Loss开始收敛速度很慢, 后续甚至出现梯度消失的问题, 所以通过综合考量, 决定使用MSE作为本文模型的损失函数.

5 结语

本文提出的一种具有宽网络结构的图像动态超分辨率网络(W-SDNet), 包含浅层特征提取块、残差增强块、宽增强块、特征细化块和构造块. 设计了引入移位卷积层的移位残差块(SC-ResBlock), 减少模型参数数量和计算成本. 构建了具有双分支4层并行网络结构的动态宽增强块, 并在其中嵌入了结合BSConv和边缘检测算法的增强空间注意力模块(IESA), 提取更丰富的信息, 增强所获得的超分辨率模型对不同应用场景的适用性. 最后选用组卷积和信道分割操作来降低计算复杂度, 提高模型重建速度. 通过大量实验结果表明, W-SDNet不仅可以方便地获取丰富的结构信息, 而且具有轻量化的特点, 很好地平衡了图像重建性能和运行时间之间的矛盾. 未来希望在此模型的基础上实现任意尺度图像超分辨率.