深度学习方法^[1–4]的巨大成功得益于丰富而高质量的有标签数据. 然而这种依赖也限制了其应用, 这是因为现实中获取大量高质量的数据需要不限于人力, 财力, 物力等昂贵的成本. 与机器相比, 人类具有强大的学习能力, 在只给定少量样本的情况下就能正确区分两个不同的图像. 例如, 通过几张图片的学习, 人类就能辨别一个新的鸟类, 并且能够从其他未见过的鸟类中进行区分.

小样本学习 (few-shot learning, FSL)^[5]作为机器学习方法之一, 模拟人类在数据稀缺条件下学习完成任务的能力. 然而, 现有方法^[6–9]主要关注闭集场景, 即机器学习分类的可见样本和需预测的未见样本都属于同一类别集. 这种闭集属性会导致在开放集识别中表现不佳, 容易将未知类别样本错误地识别为已知类别样本.

为解决这一问题, 开放集识别 (open-set recognition, OSR)^[10]任务被提出. 开放集识别不仅能够分类已知类别, 还能准确识别新出现的类别^[11]. 一般情况下, OSR方法利用大量数据重构已知类别的分布, 并通过设置阈值拒绝未知类别样本. 然而, 小样本学习任务无法保证足够的训练样本. 因此, 直接将OSR方法^[12–14]应用于小样本学习任务往往会导致过拟合, 从而产生次优的未知类别识别效果.

因此, 小样本开放集识别 (few-shot open-set recognition, FSOSR)^[15–20] 在机器学习中提出了一个重要的挑战, 因为它需要有效区分已知类别和准确检测未知类别样本. 由于每个类可用于训练的实例数量有限, 这使得任务变得更加复杂. 因此, 研究FSOSR对提高机器学习系统的泛化能力具有重要理论研究意义. 此外, 其应用潜力也涵盖了许多现实世界的场景, 包括但不限于: (1) 计算机视觉领域: 如图像识别^[15–21]、目标检测^[22–24]和图像分割^[25,26]等. 由于现实世界中的数据通常是不完整和不均衡的, FSOSR 可以帮助模型更好地适应数据分布, 提高泛化能力和鲁棒性. (2) 遥感图像分析^[27–30]领域. 由于地理环境的多样性和数据获取的困难性, 遥感图像分析通常只能获得少量标注样本, 同时需要有效识别未知地物. 因此, FSOSR可以通过帮助系统更好地适应不同环境和数据获取条件, 提高准确性和鲁棒性. (3) 网络流量分类^[31,32]领域. 由于需要分类的网络流量数据通常是不完整和不平衡的, 应用FSOSR 可以帮助网络安全系统更好地识别未知的网络流量, 并提高对潜在威胁的识别能力. 尽管FSOSR应用前景广阔, 但自提出以来仍未得到充分的研究, 相关工作较少, 这也加大了其研究难度. 因此, 进一步的研究和探索对于推动FSOSR领域的发展至关重要.

特定于图像识别任务的FSOSR的研究工作从2020年开始, Liu等人^[15]首次提出研究结合小样本学习和开放集识别的重要性, 并引入元学习的训练模式到开放集识别中, 提出了PEELER方法. PEELER方法综合了原型网络ProtoNet^[8]和元学习训练模式, 将原始的episode扩展为开放episode, 添加了伪未知类, 将开放集识别泛化到小样本学习设置中. 该方法利用开放集和交叉熵损失, 使未知类样本在每个已知类别上预测尽可能小的置信值, 以有效区分已知类别和未知类别. 然而, Jeong等人^[16]在2021年讨论了开放episode训练方法依赖伪未知类样本质量的局限性, 并提出了基于一致性变换思想的SnaTCHer方法, 无需使用伪未知类样本, 而是使用变换器如FEAT的预训练模型, 将已知和未知的查询以及一组原型重新映射到一个新的空间来计算距离, 强调一致性变换对放大已知和未知实体之间的差异的重要性. 另一方面, Deng等人^[17]在2022年提出了RFDNet方法, 强调了伪未知类的可用性, 并引入参照数据集以通过特定任务的相对特征偏移生成器学习特征的相对偏移量, 并结合特定于伪未知类的间距开放集损失, 以提高已知类别和未知类别之间边界不明确情况下的判别能力. 除此之外, 还有一些方法如TANE^[19]和ProCAM^[20], 它们利用伪未知类样本并尝试构建未知类样本分布. 这些方法将原来的N分类问题转换为N+m识别问题, 但通常依赖于伪未知样本特征或复杂的训练策略, 这两者都可能带来复杂性和不确定性. 最近, Che等人^[18]间接考虑了未知类分布, 提出了多关系间距损失方法MRM, 通过在具有可学习半径的超球上聚合相同类的样本的同时增加一个间距来分离不同类, 来提取成对样本的多重关系, 扩大不同类别之间的边界, 动态细化已知类别的决策边界, 在无依赖伪未知类样本情况下, 隐式描绘未知类别的分布. 尽管MRM致力于构造边界精细的已知类分布, 但其识别效果仍有限. 伪未知样本虽存在局限性, 但其潜力仍值得进一步探索.

尽管SnaTCHer简单有效, 但该方法仅利用已知类样本训练, 获取到的特征仍可能导致获取到的特征包含一些非必要的开放信息, 使得特征不够紧凑和类别性. 这可能会限制模型在进行一致性变换时的效果. 因此, 本文在SnaTCHer方法的基础上进行了改进, 提出基于特征解耦和开放性学习方法, 强制模型学习两部分的特征属性: 类别性和开放性, 通过利用伪未知类样本解耦更具表达力的类别性特征, 增强一致性变换效果, 进一步扩大开集未知类与闭集已知类之间的差异, 有效缓解模型构造出的已知类边界分布模糊问题. 具体而言, 解耦模块将与闭集类无关的特征分离出来, 结合开放性学习损失进行特征的开放性学习, 从而得到紧凑的类别性特征. 同时, 通过度量学习增强与闭集类紧密相关的类别性信息的提取. 为了进一步突显已知和未知样本之间的差异, 将类别性特征的相似度度量值与开放性特征的反开放性分值结合起来作为损失优化对象, 更好地引导模型学习到更具区分性的特征表示. 在公共基准数据集miniImageNet和tieredImageNet上大量实验结果表明, 本文方法在准确分类已知类样本的同时, 对未知类样本判定表现出优越的性能.

1 方法 1.1 小样本开放集识别问题定义

小样本的学习采取Vinyals等人^[33]提出的基于episode的模式进行. FSOSR与FSL任务之间的区别在于是否考虑了未知类样本的存在. 因此, 可以在FSL基础上定义FSOSR任务.

无论是训练还是测试阶段, 都是由多个episode构成, 每个episode有相应的识别任务. 首先, 每个episode分为两个集合, 一个是支持集, 定义为$ {D^s} = \{ (x_i^s, y_i^s)\} _{i = 1}^{Nk} $, 其中$x_i^s$的标签$y_i^s \in {C^s}$, ${C^s}$是识别任务已知类标签集, $N$为总类别数, $k$为每类样本数, 因此小样本任务通常也称为N-way k-shot任务. 另外一个是查询集, 定义为$ {D^q} = \{ (x_i^q, y_i^q)\} _{i = 1}^M $, $M$为查询样本总数量. 根据开放集识别设置, ${D^q}$可再分为查闭集$ {D^{{q_l}}} = \{ (x_i^{{q_l}}, y_i^{{q_l}})\} _{i = 1}^{{N_l}{k_l}} $和查开集$ {D^{{q_o}}} = \{ (x_i^{{q_o}}, y_i^{{q_o}})\} _{i = 1}^{{N_o}{k_o}} $. 值得注意的是, 其中$ y_i^{{q_l}} $属于已知类标签集${C^s}$, 而$ y_i^{{q_o}} $是未知类标签集 ${C^o}$的一部分并且确保${C^s} \cap {C^o} = \varnothing $. 符号${N_l}$、${N_o}$、${k_l}$和${k_o}$分别代表查闭集和查开集的类别总数和每类的样本数. FSOSR任务的目的就是保证属于${C^s}$样本分类准确度, 并将属于${C^o}$样本从已知类别集${C^s}$中区分.

1.2 模型结构

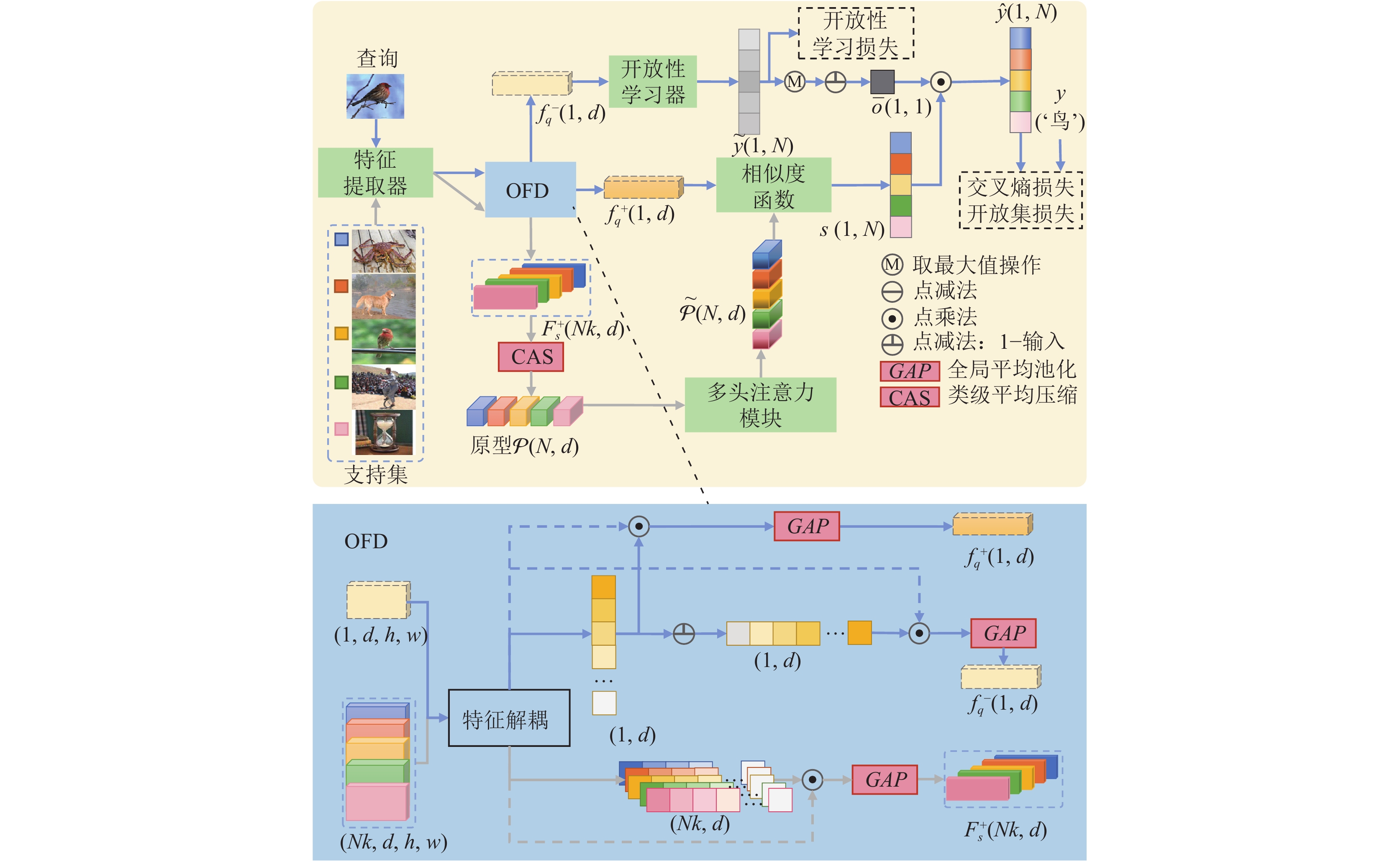
本文方法的模型结构如图1所示. 支持集和查询经过特征提取器后获得相应的特征图$ f \in {R^{d \times h \times w}} $、d、h和w分别表示通道数, 高度和宽度. 接着利用特征解耦模块OFD将与闭集类无关的特征初步分离出来, 然后将这些分离的特征输入到开放性学习器上, 并结合开放性学习损失进行特征的开放性学习, 间接强迫OFD解耦紧凑的类别性特征. 同时, 通过度量学习增强与闭集类紧密相关的特征的类别性信息提取. 模型在训练和梯度反馈过程中利用开放性学习和类别性学习, 使OFD能够获得更高的解耦能力. 为了进一步突显已知和未知样本之间的差异, 将类别性特征的相似度度量值$s$与开放性特征的反开放性分值$ \bar o $结合起来作为损失优化对象, 更好地引导模型学习到更具区分性的特征表示.

具体地, 支持集和查询经过OFD 模块解耦特征, 可以获得3条分支特征嵌入, 分别是包含闭集语义信息的支持集嵌入$ F_s^ + \in {R^{Nk \times d}} $, 查询嵌入$ f_q^ + \in {R^d} $, 以及富含开集语义信息的查询嵌入$ f_q^ - \in {R^d} $. 获取$ F_s^ + $的目的为了获得每个已知类的原型, 这样第1条分支利用$ F_s^ + $可以获得初始原型$ \mathcal{P} $并应用多头注意力模块增强原型. 随后, 第2条分支获得的$ f_q^ + $与增强原型$ \tilde {\mathcal{P}} $一起输入到相似度函数以获取类相似度度量值$s$. 第3条分支将$ f_q^ - $输入到开放性学习器学习特征开放性, 进而评估其反开放性分值$ \bar o $, 反开放性分值越高, 属于开放空间的可能性越低. 最后汇总$ \bar o $与$s$可得到类预测分值$ \hat y $, 用于损失计算.

1.3 特征解耦

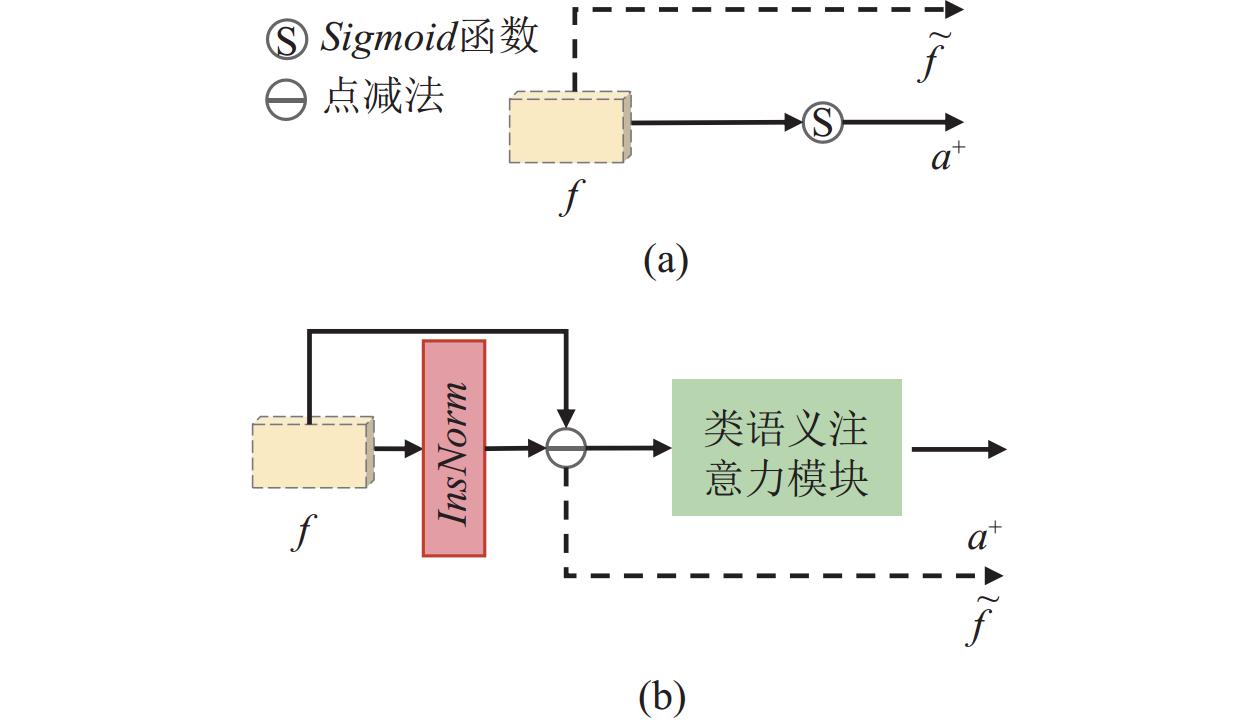
特征解耦思想已经在其他研究领域如领域自适应^[34–36], 分布外检测^[37–39]等证明其在提升模型性能方面非常有效, 但在FSOSR仍未应用, 本文应用其思想将特征解耦成两部分分别用于特征类别性学习和特征开放性学习. 如图1下半部分所示, 利用解耦算法FD获得差异特征$\tilde f$和特征的类语义信息注意力权重${a^ + }$, 并用1与${a^ + }$的差异值获得开放性信息权重, 以获得紧凑必要的类特征${f^ + }$与开放性特征${f^ - }$, 实现过程如下所示:

$ \tilde f, {a^ + } = \mathit{FD} (f)$

(1)

$ {f^ + } = {GAP} ({a^ + } \odot \tilde f) $

(2)

$ {f^ - } = {GAP} ((1 - {a^ + }) \odot \tilde f) $

(3)

其中, $ {FD} ( \cdot ) $表示特征解缠操作, $ \odot $表示点乘操作, $ {GAP} ( \cdot ) $为全局平均池化. 本文提出两种FD, 第1种如图2(a)所示, 把用Sigmoid函数归一化的结果作为${a^ + }$, 过程如式(5)所示:

$ \tilde f = f $

(4)

$ {a^ + } = \mathit{Sigmoid} (\tilde f) $

(5)

本文把这种解耦方式的方法记作FDOL. 另一种如图2(b)所示, 引入运用注意力机制解耦特征的类语义注意力模块CSA. 常用注意力机制方法包括通道注意力^[40], 空间注意力^[41], 通道与空间相结合的注意力^[42]等, 本文根据Woo等人^[42]提出的CBAM生成4种变体, 记为CA、SA、CBAM1和CBAM2, 以寻找更适用的注意力来解耦特征, 具体如式(7)–式(10)所示.

$ \tilde f = f - {InsNorm} (f) $

(6)

$ {a}^+=\mathrm{CA}(\tilde{f})=\mathit{Sigmoid}({Conv}({\tilde{f}}^{c}_{\rm avg})+{Conv}({\tilde{f}}^{c}_{\mathrm{max}}))$

(7)

$ {a}^+=\mathrm{SA}(\tilde{f})=\mathit{Sigmoid}({Conv}(\tilde{f})\odot {Concat}({\tilde{f}}^{s}_{\rm avg}, {\tilde{f}}^{s}_{\mathrm{max}}))$

(8)

$ \left\{\begin{array}{l}\tilde{f}={f}'=(\mathrm{CA}(\tilde{f})\odot \tilde{f})\\ {a}^+=\mathrm{CBAM}1({f}')=\mathrm{SA}({f'})\end{array} \right.$

(9)

$ {a}^+=\mathrm{CBAM}2(\tilde{f})=\mathrm{SA}(\mathrm{CA}(\tilde{f})\odot \tilde{f})$

(10)

其中, $ {InsNorm} ( \cdot ) $表示实例归一化操作, $ {Conv} ( \cdot ) $为卷积操作, $ {\tilde f^c}_{\rm avg} $、$ {\tilde f^c}_{\max } $分别是在通道维度取均值和最大值得到的特征, $ {\tilde f^s}_{\rm avg} $、$ {\tilde f^s}_{\max } $分别是在空间维度取均值和最大值得到的特征. 本文把结合注意力的特征解耦方法分别称FDOL-CA, FDOL-SA, FDOL-CBAM1, FDOL- CBAM2.

1.4 特征开放性学习

查询经过OFD模块可获得解耦特征$ f_q^ + $和$ f_q^ - $, $ f_q^ + $经过度量学习进行特征类别性学习, 以获得类预测分值. 度量学习过程需要计算特征与类原型之间的相似度来判定其归属的类别, 因此需要获取度量学习的另一比照对象, 即类原型, 而类原型利用经过解耦的紧凑的支持集特征$ F_s^ + $获得. 具体地, 首先通过类级平均压缩, 即对每个类所有的支持集特征进行均值化, 如式(11)所示:

$\left\{ \begin{gathered} {\mathcal{P}_c} = {CAS} (F_{{s_c}}^ + ) = \frac{1}{k}\sum\limits_{i = 1, f_{{s_c}, i}^ + \in F_{{s_c}}^ + }^k {f_{{s_c}, i}^ + } \\ \mathcal{P} = \{ {\mathcal{P}_1}{\text{, }} \cdots {\text{, }}{\mathcal{P}_c}{\text{, }} \cdots {\text{, }}{\mathcal{P}_N}\} \\ \end{gathered} \right.$

(11)

其中, $ \mathcal{P} $为初始原型集合, $ \mathit{CAS} ( \cdot ) $是类级平均压缩, $ F_{{s_c}}^ + $是支持集中属于类别c的类别性特征集, $ f_{{s_c}, i}^ + $是$ F_{{s_c}}^ + $中的每一个特征. 其次, 本文与SnaTCHer方法一致, 采用多头注意力模块增强原型, 不同的是, 增强之前的原型是经过解耦模块解耦的更具有类别性信息的支持集嵌入得来的, 因此原型特征也更具判别性, 更能促进多头注意力模块学习. 多头注意力出自Transformer^[43], 其思想是将输入特征应用可学习的变换矩阵映射成3个不同的空间特征(如查询, 键和值), 利用不同空间的特征相互作用实现注意力学习, 如式(12)所示:

$ \left\{\begin{split} & {R}(\mathcal{P})=\frac{1}{N}{\mathit{Softmax}}(({{W}_{Q}}\mathcal{P}){{({{W}_{K}}\mathcal{P})}^{\top}}/\sqrt{d})({{W}_{V}}\mathcal{P}) \\ & \tilde{\mathcal{P}} ={T}(\mathcal{P})={LN}(\mathcal{P}+R(\mathcal{P})) \end{split}\right. $

(12)

其中, $ \tilde {\mathcal{P}} $为增强原型集, N为原型总个数, ${W_Q}$, ${W_K}$和${W_V}$是可学习变换矩阵, d是特征大小, ${T} ( \cdot )$表示多头注意力模块, ${LN} ( \cdot )$表示层正则化.

度量学习中相似度计算基于欧氏距离函数, 如式(13)所示:

$ {s_c} = - {dist} (f_q^ + , {\tilde {\mathcal{P}}_c}) = - {\left\| {f_q^ + - {{\tilde {\mathcal{P}}}_c}} \right\|^2} $

(13)

其中, ${s_c}$表示查询与c类原型${\tilde {\mathcal{P}}_c}$的相似度值, ${dist} ( \cdot , \, \cdot )$表示欧氏距离函数的平方, 将$s$作为类预测初始分值.

查询解耦后的另一特征$ f_q^ - $经过开放性学习器来学习N个对应于N个已知类的开放性预测值$ \tilde y $, 取$ \tilde y $的最大值后用1取反来获得反开放性分值$ \bar o $, 最后将$s$与$ \bar o $作点乘运算可获得最终类预测值$ \hat y $, 其过程如式(16)所示:

$ \tilde y = {\rm OL} (f_q^ - ) $

(14)

$ \bar o = 1 - \max (\tilde y) $

(15)

$ \hat y = s \odot \bar o $

(16)

其中, 开放性学习器OL由多个MLP构成, $ \max ( \cdot ) $表示取最大值操作.

与SnaTCHer方法相似, 本文方法也利用一致性变换的思想获得查询的开放性判定分值. 然而, 本文方法与SnaTCHer方法的不同之处在于利用伪未知类样本进行特征解耦的开放性学习, 从而使查询特征更具表达力和类别性, 进一步增强了一致性变换效果, 扩大了开集未知类与闭集已知类之间的差异. 为了实现一致性变换, 首先将查询特征与初始原型集$ \mathcal{P} $计算获得所属类预测, 然后根据预测结果用查询特征替换预测的类原型以获得替换集$ {\mathcal{P}^q} $. 接着, 利用以多头注意力模块${T} ( \cdot )$为变换器修改替换集, 最后计算增强的原型集$ \tilde {\mathcal{P}} $和增强的替换集$ {\tilde {\mathcal{P}}^q} $之间的总差异和作为开放性判定分值$u$, 其过程如式(19)所示:

$ {\mathcal{P}^q} = \mathcal{P} - \{ {\mathcal{P}_c}\} + \{ f_q^ + \} $

(17)

$ {\tilde {\mathcal{P}}^q} = {T} ({\mathcal{P}^q}) $

(18)

$ u = \sum\nolimits_{i = 1}^N {{dist} (\tilde {\mathcal{P}}_i^q, {{\tilde {\mathcal{P}}}_i})} $

(19)

其中, ${\tilde {\mathcal{P}}_i}^q$, ${\tilde {\mathcal{P}}_i}$分别来自增强替换原型集和原型集的某个原型.

1.5 训练损失

经过特征开放性学习, 可获得类预测概率集$ p $和开放性预测概率集$ \tilde p $, 如式(20)、式(21)所示:

$ {p_c} = {\mathit{Softmax}} ({\hat y_c}), \;p = \{ {p_1}, \cdots , {p_c} \cdots , {p_N}\} $

(20)

$ {\tilde p_c} = {\mathit{Softmax}} ({\tilde y_c}), \;\tilde p = \{ {\tilde p_1}, \cdots , {\tilde p_c} \cdots , {\tilde p_N}\} $

(21)

其中, ${p_c}$, ${\hat y_c}$, $ {\tilde p_c} $和${\tilde y_c}$分别为查询对于c类原型的类预测概率, 类预测值, 类开放性预测概率和类开放性预测值.

在损失设计上, SnaTCHer方法仅在已知类样本利用交叉损失监督模型类别性特征学习, 在引入伪未知类样本情况下, 监督力度有限. 因此, 本文提出一种结合交叉熵损失$ {l_{\rm ce}} $、开放集损失$ {l_{\rm os}} $^[15]以及提出的开放性学习损失$ {l_{\rm ol}} $来促进类别性特征学习的损失. 具体而言, $ {l_{\rm ce}} $能促进已知类内部的紧凑性和不同类之间的可分离性. $ {l_{\rm os}} $则促进未知类尽可能远离每个已知类. 而$ {l_{\rm ol}} $的目的是监督已知类样本, 使其能够从特征解耦模块分离出更多的开放性特征, 保留更紧凑的类别性特征, 而对于未知类样本的监督作用则相反, 这样可以迫使模型提高特征解耦能力, 间接促进类别性特征学习. 总损失如式(22)所示:

$ {l_{\rm total}} = (1 - \eta - \mu ){l_{\rm ce}} + \eta {l_{\rm os}} + \mu {l_{\rm ol}} $

(22)

其中, 超参数$ \eta $和$\mu $ (均在0和1之间)分别用于控制开放集损失和开放性学习损失的影响程度. 接下来将对这些损失进行详细说明.

1) 交叉熵损失仅应用在已知类查询上, 监督模型正确识别已知类查询并作分类, 如式(23)所示:

$ {l_{\rm ce}} = - \frac{1}{{{M_l}}}\sum\nolimits_{i = 1}^{{M_l}} {\sum\nolimits_{c = 1}^N {{y_{i, c}}\log {p_{i, c}}} } $

(23)

其中, $ {M_l} $表示查询闭集的大小. $ {y_{i, c}} $和$ {p_{i, c}} $分别是属于类c查询样本的真值和类预测概率值.

2) 开放集损失实际是负熵损失, 仅应用在未知类查询, 在训练过程中, 当遇到来自未知类的查询样本时, 模型应避免将高概率分配给任何已知类, 如式(24)所示:

$ {l_{\rm os}} = \frac{1}{{{M_o}}}\sum\nolimits_{i = 1}^{{M_o}} {\sum\nolimits_{c = 1}^N {{p_{i, c}}\log {p_{i, c}}} } $

(24)

其中, $ {M_o} $表示查询开集的大小.

3) 开放性学习损失是负熵损失的拓展. 假设输入开放性学习器的特征是解耦效果较好的开放性特征, 则对于已知类查询的开放性特征包含的开放属性较高, 即不属于任何已知类, 因而对任何已知类别产生的开放性预测值都低, 而对于未知类查询, 则相反, 其开放性特征包含的开放属性较低, 因而对已知类别产生的开放性预测值都偏高. 因此, 开放性损失如式(25)所示:

$ \begin{split} {l_{\rm ol}} =& \frac{1}{{{M_l}}}\sum\nolimits_{i = 1}^{{M_l}} {\sum\nolimits_{c = 1}^N {{{\tilde p}_{i, c}}\log {{\tilde p}_{i, c}}} }\\ & - \frac{1}{{{M_o}}}\sum\nolimits_{i = 1}^{{M_o}} {\sum\nolimits_{c = 1}^N {{{\tilde p}_{i, c}}\log {{\tilde p}_{i, c}}} } \end{split}$

(25)

其中, $ {\tilde p_{i, c}} $分别是查询对类别c的类开放性预测概率值.

2 实验

为了验证所提出的方法的优势与有效性, 本节在miniImageNet^[33]数据集和tieredImageNet^[6]数据集上与其他先进方法进行了性能比较实验, 同时进行大量消融实验验证所提出模块的有效性.

2.1 数据集

miniImageNet 和tieredImageNet 是FSL和FSOSR研究中最常用的数据集之一. miniImageNet 和 tieredImageNet 源自扩展的 ImageNet 数据集. 在 miniImageNet 中, 有 100 个类, 每个类 600 个图像, 图像分辨率分别为 84×84 像素. 通常, 这 100 个类细分为 64 个用于训练, 16 个用于验证和 20 个用于测试. 相反, tieredImageNet 具有 608 个类, 总共779165个图像, 所有图像的分辨率均为 84×84 像素, 分为 351 个用于训练, 97 个用于验证和 160 个用于测试.

2.2 度量指标

FSOSR方法使用两个主要指标进行全面评估, 包括准确度(Acc)和受试者工作特征曲线下面积 (AUROC). Acc是一种通用指标, 用于衡量模型的闭集分类性能, 可以与其他方法进行清晰的比较, 实验结果报告了95%的置信区间. AUROC遵循既定规范^[10], 是开集检测能力的重要指标. 它衡量模型区分已知和未知样本的能力, 其中较高的AUROC表示在识别和分类 FSOSR 中未知样本方面具有更好的性能.

2.3 实现细节

本文所有实验基于PyTorch框架, Python 3.8语言实现, 在64位Ubuntu 18.04操作系统运行, CUDA为11.4版本, GPU为NVIDIA 1e04, 显存10 GB, 内存64 GB.

本方法将ResNet12^[2] 作为特征提取器, 图像经过特征提取可获得一个640通道的特征图. 在此之前, 本文使用FSL方法FEAT^[9]在ImageNet上对特征提取器进行预训练来获取初始参数, 再以此为基础进行微调. 模型训练包括10 000个episode, 测试经历 600个 episode, 采用SDG优化器来训练网络, 特征提取器的初始学习率为0.0002, 其他模块的初始学习率为0.002, 在2 000个episode学习率衰减一半. 每一个episode, 无论是用于训练还是测试, 都遵循 n-way k-shot 任务配置. n的值保持常量值 5, 而k选取1或5, 有助于验证每个数据集在两个不同的支持集样本实验设置的效果. 在构建查询集时, 从 5 个闭类和 5 个开类中各抽取 15 个样本, 对于闭集和开集场景, 每个样本总计最多 75 个样本. 因此, 每个完整查询集总共有 150 个样本. 开放集损失和开放性学习损失影响的超参数$ \eta $和$\mu $分别设置为1/3, 1/3.

2.4 与先进方法对比

本节在miniImageNet和tieredImageNet上与先进方法作性能的比较并将对比的方法划分为4个组, 分别是FSL (ProtoNet^[8], FEAT^[9]), OSR (OpenMax^[13], CounterFactual^[12]), FSOSR (PEELER, SnaTCHer-F^[16], TANE-ATT^[19], ProCAM, RFDNet, MRM)以及本文所提出的方法 (FDOL, FDOL-CA, FDOL-SA). 其中, ProtoNet、FEAT、OpenMax和CounterFactual的结果引用自TANE^[19], RFDNet的结果是按照ResNet12实现以进行公平比较. 其他方法的结果来源于各自的原始论文, 比较结果见表1. 后续表中加粗的数据为最优值.

表1揭示了以闭集任务为主的FSL方法难以进行开集检测. 尽管FEAT在原型上用变换器增强后, 性能显著优于经典的FSL方法ProtoNet, 但其性能远不如FSOSR方法理想. 具体而言, 本文方法如FDOL在所有基准测试中始终优于FEAT. 在miniImageNet数据集上, 它在1-shot场景中实现了高达1.8%的Acc增加, 在5-shot场景下实现了18.15%的AUROC提升.

在OSR方法领域, 其架构旨在发现未知的, 反事实的开放场景. 在miniImageNet 5-shot配置中, 它的AUROC比FEAT增加了8.4%. 然而, 一个值得注意的限制是, 由于训练数据不足, 它偶尔会对已知类别进行错误分类. 相反, 本文方法在各种情况下的Acc和AUROC指标上始终优于CounterFactual.

至于当前的FSOSR方法, ProCAM在两个数据集5-shot配置上分别实现83.66%和85.64%的最高闭集分类准确度, 但本文方法仍然在其他所有配置的指标上展现显著的优越性, 如FDOL-CA在miniImageNet 1-shot配置上的Acc超过次优方法ProCAM达1.29%, FDOL-SA在miniImageNet 5-shot配置上的AUROC超过次优方法MRM达1.83%. 简而言之, 本文方法在众多FSOSR方法脱颖而出, 它在数据集上较高的AUROC分数突出了它在有效区分已知和未知类别方面的能力, 即使在有限样本的限制下也是如此.

2.5 消融实验

本节的消融实验在tieredImageNet数据集上进行, 在没有特殊说明的情况下, FD算法的类语义注意力模块CSA采用CA. 基线(baseline)是在SnaTCHer方法上增加了开放集损失的实验结果.

(1) 各组成部分消融实验. 表2展示了本文提出的各个模块单独以及相互作用对模型性能的影响. 实验结果显示, 随着各个模块的增加, 它们之间的相互作用促进了模型性能的提升. 特别是在对未知类的区分上, 表现出了明显的改善, 其中AUROC值相比于SnaTCHer方法分别提升了1.24%和1.47%. 这进一步证明了特征解耦的开放性学习可以有效分离特征中的开放性信息, 获得更具紧凑和类别性的特征表示, 增强一致性变换效果, 从而提高模型已知类分类准确度和未知类判定率.

(2) 不同注意力解耦方法的对比. 表3展示了不同注意力解耦方法对两个数据集的性能影响. 与基线相比, 这些注意力机制的特征解耦方式都取得了一定程度的性能提升. 在miniImageNet和tieredImageNet数据集中, 分别是基于SA和CA的注意力特征解耦方式整体上表现最佳. 特别是在tieredImageNet数据集中, CA在5-shot的配置优势明显, 比次优方式SA在闭集分类准确度和AUROC有0.55%和0.98%的提升. 在小样本场景下, 数据稀缺, 相对于复杂的CBAM方法, SA和CA这种相对简单的注意力机制更有利于模型获取类别语义权重信息. 此外, tieredImageNet数据集具有多样的类别和广泛的分布, 不同类别之间的相似度程度比miniImageNet高, 从实验结果看出, CA相比SA在捕获相似度较大的不同类别之间的差异方面表现更为出色.

(3) 开放性损失$ {l_{\rm ol}} $和反开放性分值$ \bar o $消融实验. 表4对比了$ {l_{\rm ol}} $和$ \bar o $对模型性能的影. 一方面, 从第1、3行可知, $ {l_{\rm ol}} $能促进开放性特征的学习, 间接提高模型特征解耦能力, 获得更加必要的类语义信息, 并且在提高模型闭集分类性能有较大的作用, 结合$ {l_{\rm ol}} $的本文方法在1-shot和5-shot配置下有0.89%和0.58%的提升. 另一方面, 从第2、3行可知, 在类预测值上融入$ \bar o $有助于拉大已知类和未知类的差异, 生成差距较大的开放性判定值, 如结合$ \bar o $的本文方法在1-shot和5-shot配置下有0.52%和0.50%的提升.

3 结论

本文提出了一种基于特征解耦思想的特征开放性学习方法, 旨在通过利用解耦后的特征来扩大开集未知类与闭集已知类之间的差异. 为了实现这一目标, 设计了一个解耦模块, 并通过两个分支来促进特征的解耦过程. 首先, 利用解耦后的与闭集类信息无关的特征进行开放性学习, 并结合开放性损失来有效挖掘开放属性, 间接紧凑类别性特征; 其次, 利用解耦后的闭集类信息相关的特征进行度量学习, 以增强模型对类相关信息的提取能力, 进而获取类别性特征. 为了进一步突出已知和未知样本之间的差异, 本文方法将类别性特征的相似度度量值与开放性特征的反开放性分值结合起来作为损失优化的对象. 实验结果验证了本文方法在miniImageNet和tieredImageNet数据集上的有效性. 与其他先进方法相比, 所提出的方法表现出更好的性能和优越性.