辐射源个体识别又称特定辐射源识别(specific emitter identification, SEI), 目标是通过分析和识别辐射源产生的射频指纹特征, 来对不同的辐射源设备进行识别[1]. 射频指纹特征是发射机在物理层层面的基本特征, 很难被伪造, 因此SEI技术被认为是维护无线通信安全的重要技术之一. 通信辐射源个体识别是针对通信调制信号为目标的SEI技术研究, 目前许多通信辐射源个体方法研究已经被应用于商业领域. 例如应用于识别空中交通管制的自动相关监视广播(automatic dependent surveillance-broadcast, ADS-B)系统中的飞机[2,3]; 在物联网领域, 通信辐射源个体识别技术可以提供可靠的设备认证功能来维护物联网网络安全[4,5].
通信辐射源个体识别是一个模式识别问题, 主要分为特征提取和模式分类两个阶段. 如何提取信号的指纹特征是通信辐射源个体识别问题的重点. 随着研究的深入, 单域特征并不能完全代表发射机的射频指纹, 因此越来越多的研究采用基于时频特征提取的方法. 文献[6]提出了一种基于Wigner和Choi-Williams时频分布特征的辐射源识别方法. 文献[7]通过经验模态分解(empirical mode decomposition, EMD)分解信号, 提出了提取能量熵、均值、方差这3种特征基于Hilbert谱的算法, 证明了在单跳和中继及不同信噪场景下的有效性. 但在经验模态分解过程中会存在模态混叠等分解不充分的问题, 因此其在低信噪比下识别效果较差. 文献[8]对信号进行差分处理, 通过变分模态分解(variational mode decomposition, VMD)差分信号, 然后求取对应的希尔伯特谱. 针对希尔伯特谱的稀疏性, 运用改进的全局信息分析模块对辐射源的细微特征进行提取. 文献[9]使用双变量VMD来降噪, 并使用分解后的样本直接作为射频指纹送入复值神经网络. 目前在通信辐射源个体识别的信号时频特征提取方面, EMD、VMD等分解技术与深度学习结合的研究已有许多进展.
经验小波变换(empirical wavelet transform, EWT)技术[10]是由Gilles等在2013年提出的一种结合了小波理论和EMD两者优点的信号处理方法, 能有效地提取信号的时频域特征, 同时具有完备的小波数学模型, 与VMD技术相比拥有更低的算法复杂度. 从频域角度来看, 它等同于构造一组带通滤波器, 根据通信信号的频谱特性将其分解为分布于各个频段的时域模态信号. 但EWT技术对每个信号分解的边界选择是自适应的, 在低信噪比条件下, 对信号频域分割的边界选取会受到噪声的影响, 使得同一批类信号分解的尺度不同, 导致每一层子信号携带原信号对应的不同频谱特征, 因此不能直接将EWT技术应用于通信辐射源个体识别任务中. 固定边界范围经验小波变换(fixed boundary range-based-empirical wavelet transform, FBR-EWT)是一种针对非平稳信号分解的EWT改进算法[11], 可以有效地解决EWT技术在低信噪比条件下面对同一类信号分解时分解尺度不一的情形, 让处理后的数据更适用于神经网络训练. 文献[12]已经应用FBR-EWT技术和深度卷积神经网络对无人机的射频信号进行分类, 通过FBR-EWT技术增强网络对细微特征的敏感度, 从而提高神经网络对个体进行识别的准确性和可靠性. 但与其他分解方法类似, FBR-EWT方法并没有通过分解方法来分离信号成分和指纹特征, 使通信辐射源的指纹特征更容易被分类器识别. 同时其分解边界的选取是按照经验进行等距划分的, 没有理论依据.
为此, 本文根据IEEE 802.11a信号短导码的子载波频率分布情况来提出了一种通过固定频率边界经验小波变换和残差网络对IEEE 802.11a信号进行识别和分类的方法. 来解决OFDM辐射源个体识别任务中指纹特征信息受数据信号分量和信道噪声影响而分类识别率低的问题, 本文工作的主要贡献如下.
(1)根据IEEE 802.11a短导码的子载波频率特性, 设计FFB-EWT方法对短前导进行分解, 提取包含指纹特征信号的空子载波分量, 从而消除信号信息对识别通信辐射源指纹特征时的干扰.
(2)根据噪声的统计特性对各空子载波分量进行相干积累, 提高指纹特征信号的信噪比.
(3)采用双通道ResNet18网络, 嵌入通道注意机制和非局部注意机制相结合的模块, 对经过FFB-EWT分解和相干积累的I/Q信号数据进行特征提取和分类.
1 OFDM辐射源前导射频指纹模型 1.1 OFDM前导信号帧结构OFDM信号中的前导部分通常应用于同步接收端以获得信道估计和同步时序信息. 在IEEE 802.11a协议下, OFDM信号的帧结构由前导码、信令段、数据段3部分组成, 帧结构如图1所示, 前导码由持续时间均为8 μs的短导码和长导码组成, 其中短导码由t1–t10的10个短训练序列组成, 长导码由循环前缀GI2和2个长训练符号组成, 信令段部分为1个OFDM符号, 其包含数据的调制类型、编码速率和数据长度等信息, 数据部分即所要传输的数据信息. 对接收到的OFDM信号与短导码进行互相关计算有:
| d=argmaxd∑D−1C=0|∑D−1n=0r(d+n,C)⋅xp(n)|2 | (1) |
其中, C为载波索引,
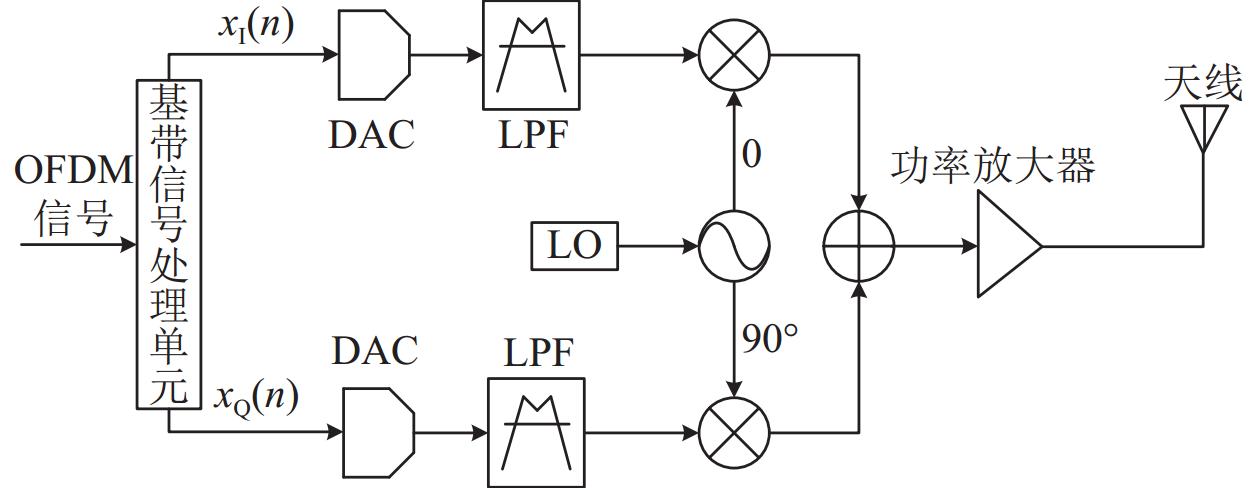
OFDM辐射源指纹特征通常由发射机中的硬件因素产生, 如图2所示为OFDM设备的发机简化模型.

|
图 1 IEEE 802.11a协议信号帧结构 |
|
图 2 OFDM设备的发射机简化模型 |
OFDM信号送入基带信号处理单元, 将信号分为I/Q两路, 分别通过数模转换(digital to analog converter, DAC), 将信号转变为模拟信号, 然后通过低通滤波器(low pass filter, LPF), 滤除掉高频分量, 接着通过混频器对信号进行正交调制, 最后通过功率放大器, 通过天线发出射频信号. 根据文献[2]可以将射频信号建模为:
| RFF(⋅)=Aγ0(1+hPA(˜atx))×exp{iθ+ht(σmTIE)+hΔ(Δn,ΔINL)+hm(ξ)+hp(ρh,ρv)} | (2) |
其中,
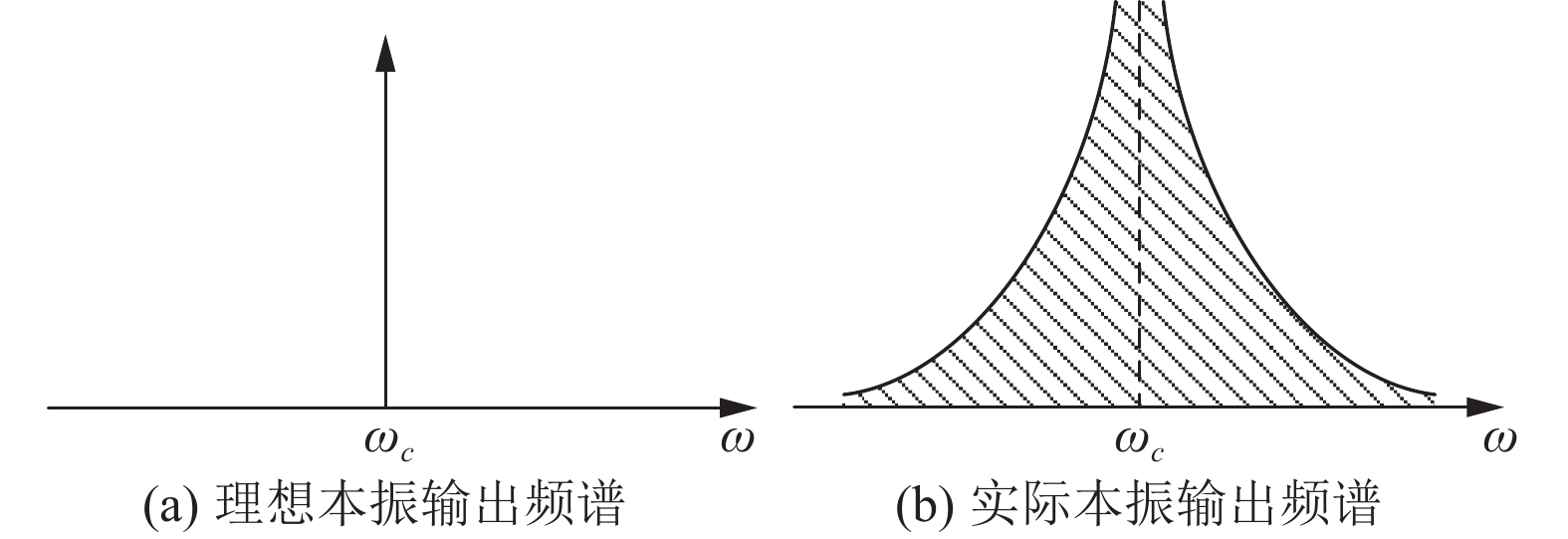
|
图 3 振荡器输出频谱 |
发射设备的本振中相位波动引起的频谱扩展或再生, 在信号混频时, 会使发射信号的频谱展宽. 发射机器件的非线性会与本振相位噪声导致的频谱展宽相互作用, 寄生在OFDM信号中, 可以作为射频指纹特征用于识别. OFDM信号中的短导码由固定的短训练序列生成, 与其他信号成分相比更加稳定, 更容易分离通信信息和指纹特征, 因此从短导码中提取射频指纹更具有可行性.
2 基于FFB-EWT的信号分解算法 2.1 FFB-EWT算法原理本文使用的FFB-EWT多尺度信号分解技术, 将接收的短导码分解为若干时频分量. 在通信系统中, 接收到的I/Q信号经过解调和模数转换后得到两路信号记为
| ˜I(k)=∑N−1n=0I(n)e−j2πnkN | (3) |
其中,
| Bl=2πFl/Fs | (4) |
其中,
| ϕ(k)={1,if|k|⩽Bl−Tlcos[π2B(12τl(|k|−Bl+τl))], ifBl−τl⩽|k|⩽Bl+τl0,Otherwise | (5) |
| ψl(k)={1,ifBl+Tl⩽|k|⩽BI−Tlcos[π2f(12τl+1(|k|−Bl+1+τl+1))],ifBl+1−τl+1⩽|k|⩽Bl+1+τl+1sin[π2f(12τ1(|k|−Bl+τl))],ifBl−τl⩽|k|⩽Bl+τl0,Otherwise | (6) |
其中,
| y1(n)=Re[1N∑N−1k=0(˜I(k)ׯφ(k))ej2πnkN] | (7) |
| yl(n)=Re[1N∑N−1k=0(˜I(k)ׯψl(k))ej2πnkN] | (8) |
其中,
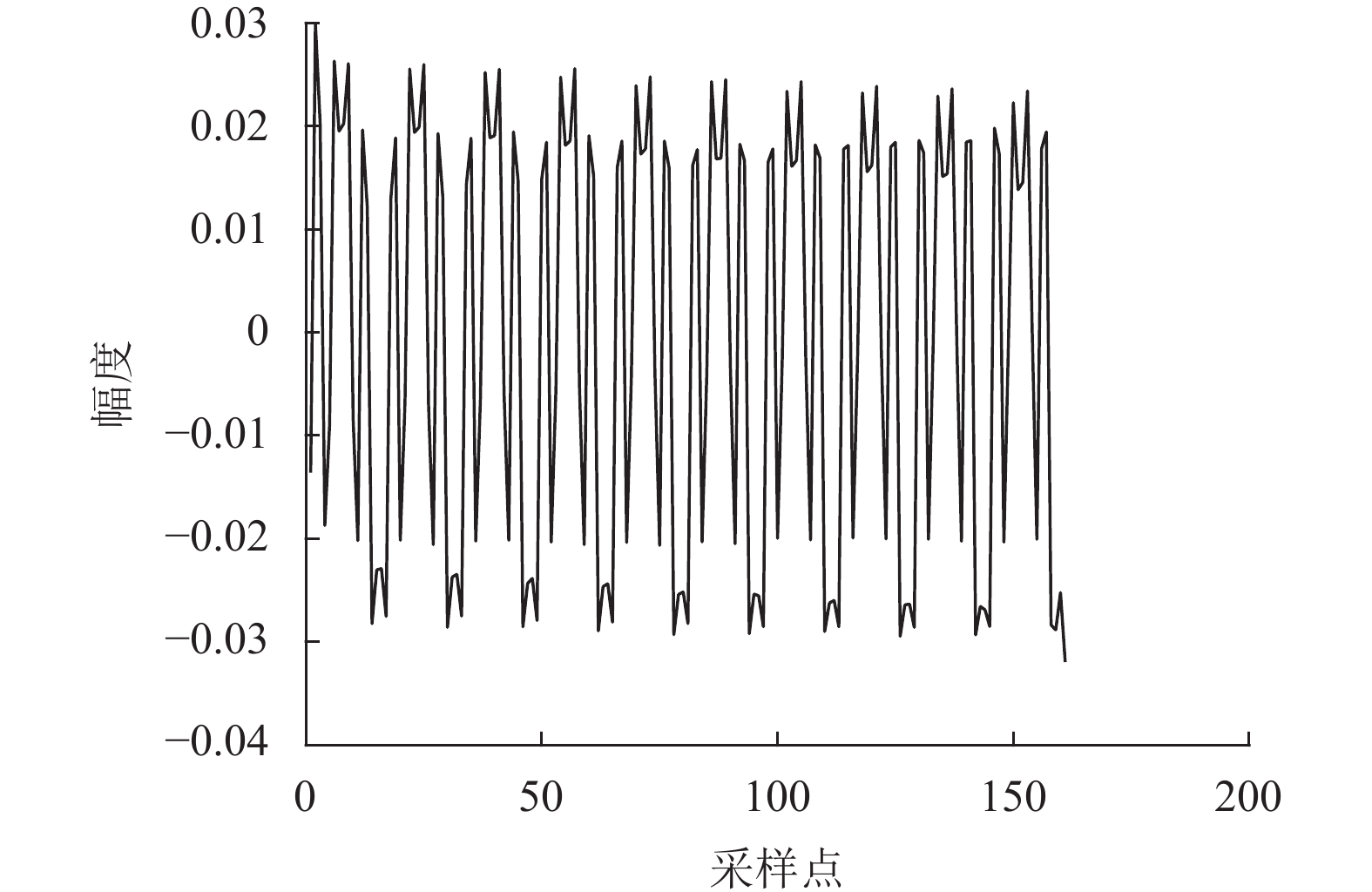
OFDM信号的短导码是根据
|
图 4 实际接收的短导码的时域波形 |
图5中2、4、6、8、10这几层的子载波分量, 携带信号的有效信息. 在指纹特征的提取过程中, 这些信号信息本身就是一种干扰, 影响对指纹特征的提取. 而剩余的空子载波分量中含有因频谱展宽而携带的指纹信息, 因此去除掉分解后包含信息成分的非空子载波分量, 选取剩余的1、3、5、7、9、11、13这7层空子载波分量, 来进行下一步的处理.
3 相邻帧空子载波分量时域相干积累在低信噪比条件下, 通信辐射源信号的细微特征信号易被噪声淹没. 考虑到短导码上附加的辐射源细微指纹信息在相邻帧具有稳态特性, 而噪声没有相干性, 对短导码信号在相邻帧进行积累可以效提高信噪比. 而直接对信号在时域进行积累需要定位到每一帧信号短导码的精确起始位置, 否则即使是微小的偏差, 对相邻帧的短导码进行时域相干积累后, 会对信号的频谱造成影响, 导致FFB-EWT技术不能完整的分离信号成分. 为此本文采用对相邻帧的各层子信号分量在时域进行积累来提高指纹特征信号的信噪比. 假设FFB-EWT分解后的第i层空子载波分量
| yi(n)=ρi(n)+wi(n) | (9) |
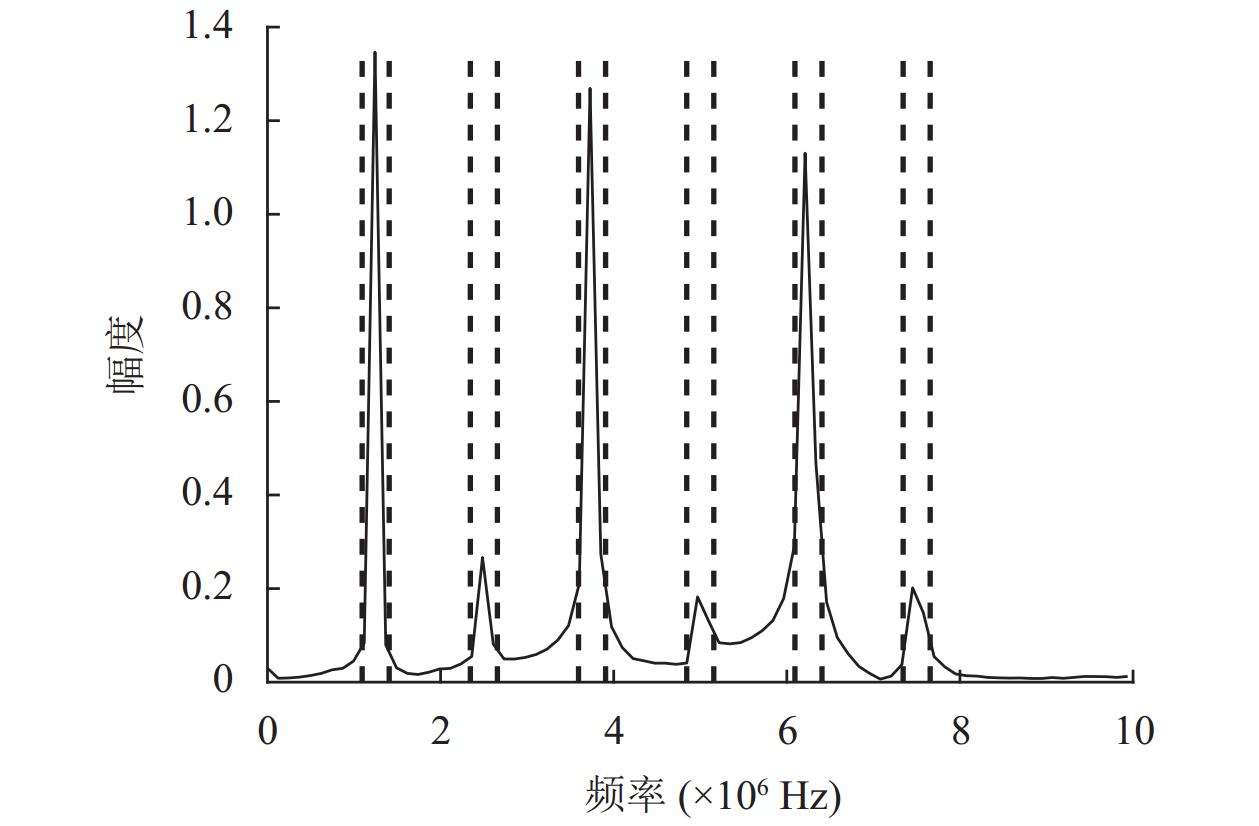
|
图 5 划分固定边界条件后的频谱 |
对M帧的信号各空子载波分量在时域进行积累:
| M∑j=1yij(n)=M∑j=1ρij(n)+M∑j=1wij(n) | (10) |
其中,
残差网络(ResNet)由He等人于2016年提出的[13]. 它引入了残差学习的概念, 通过添加残差块(residual blocks)来解决深层神经网络训练过程中的梯度消失和梯度爆炸问题. ResNet的核心思想是, 通过加入了Shortcut结构, 进行跨层的残差连接, 加快了网络收敛速度, 让卷积网络学习在多个层次上的复用特征, 提高了卷积神经网络在图像分类、目标检测等任务中的识别性能. 残差模块可以简化的定义为:
| yi=F(xi)+xi | (11) |
其中,
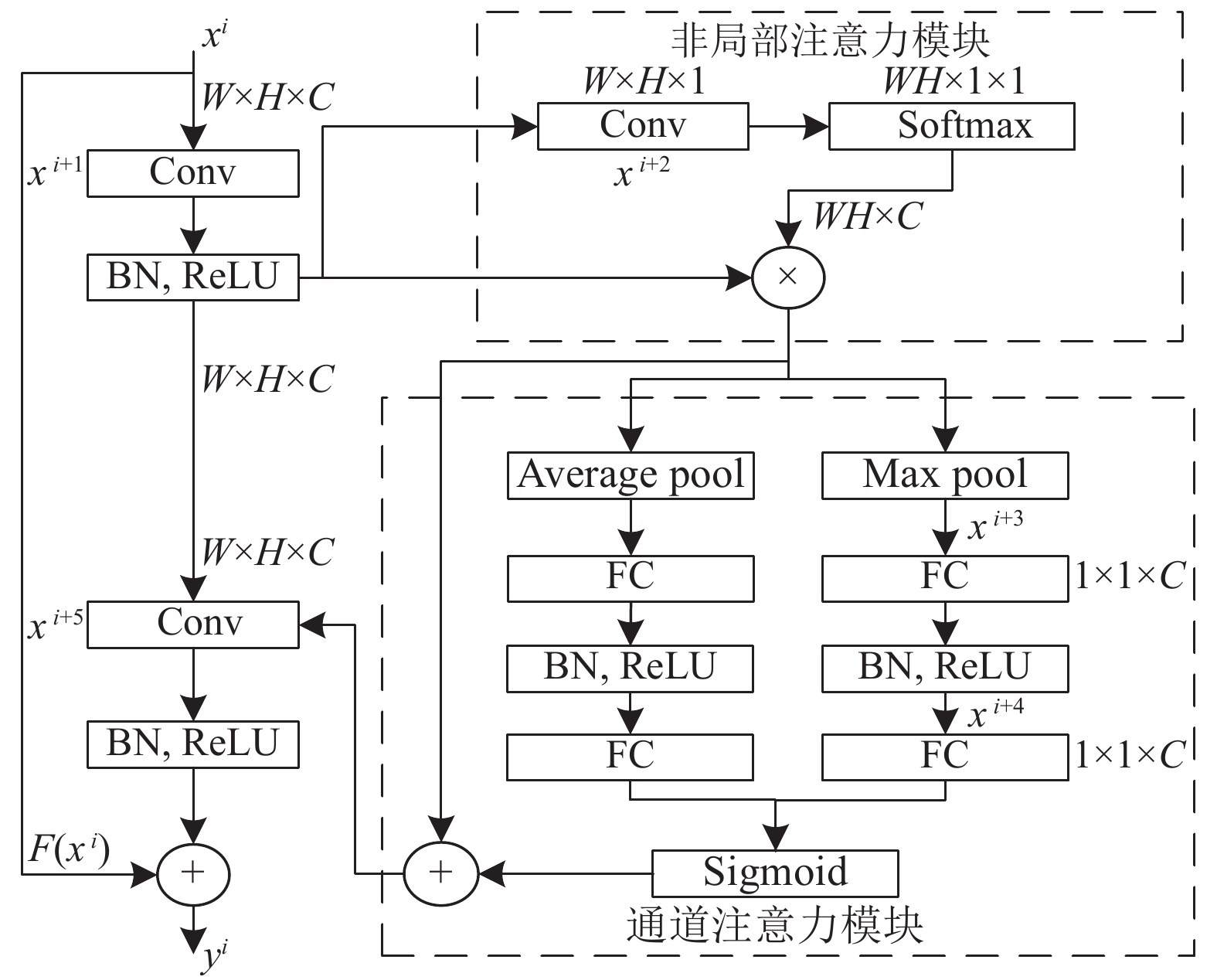
|
图 6 结合非局部注意力和通道注意力的残差模块 |
输入的特征图
在OFDM辐射源个体识别任务当中, 不同频段信号的指纹特征含量不同, 对最终的识别贡献不同, 而NCAB残差模块可以使网络更加关注指纹特征贡献更多的信号分量上的特征, 同时可以弥补残差神经网络的局部感受野的缺陷, 提升网络在低信噪比条件下对指纹特征的提取性能, 最终提高识别率.
4.2 基于双通道的NCAB-ResNet18网络的分类在ResNet系列中, ResNet18相较于ResNet34, ResNet50有较低的网络复杂度, 具体的网络结构见文献[9]. 同时因为经过FFB-EWT分解后的样本尺寸较小, 浅层网络就可以有效提取特征, 因此本文选取ResNet18网络框架作为参考, 将改进的NCAB残差模块嵌入到ResNet18中, 得到NCAB-ResNet18作为主体网络进行特征提取.
在通信系统中I路信号与Q路信号是正交的, 两路信号在时域和频域上呈现通信辐射源不同的指纹特征. 将两路信号的特征融合起来, 可以更全面地利用信号中包含的全部信息, 从而提高识别的准确性和可靠性. 为此本文采用如图7所示的双通道的网络结构.
如图7所示, 将经过FFB-EWT分解和时域相干积累处理后的IQ两路信号分别使用相同参数的NCAB-ResNet18网络来提取特征, 通过最大池化降低特征图的维度, 捕捉特征图中的显著特征. 然后通过Cat操作, 将两路的特征沿同一维度进行串联, 送入全连接网络中将特征进行整合, 最后通过Softmax层进行最终的分类决策输出.
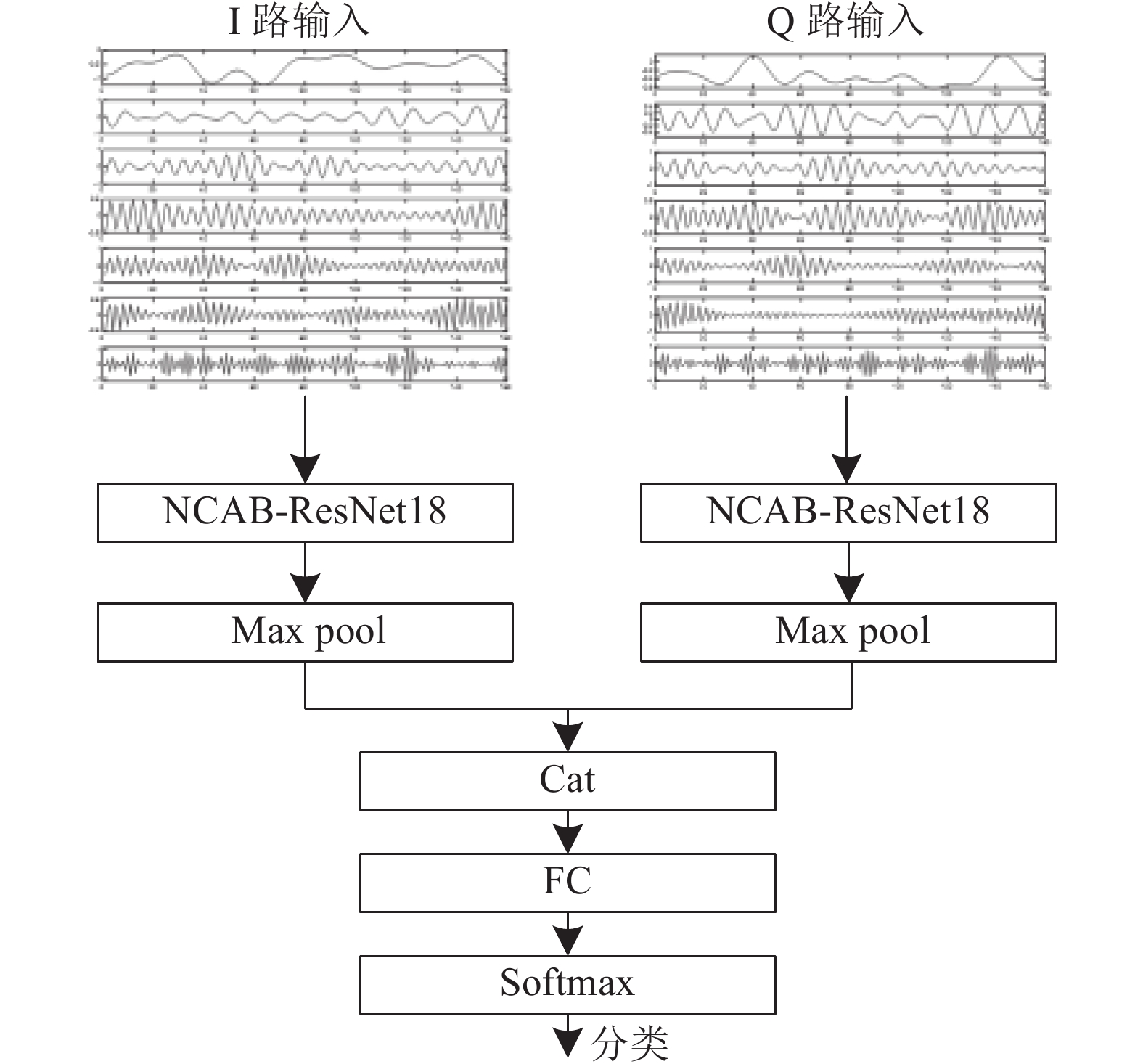
|
图 7 基于双通道的NCAB-ResNet18网络结构 |
5 算法主要流程
本文算法主要处理流程如下.
1) 将采样率为20 MHz的I/Q信号解调为两路实信号, 对接收信号计算短训练序列和信号的互相关, 确定信号起始位置.
2) 使用移动窗口对I路信号和Q路信号的短导码进行对齐切片. 处理后的数据为2×160格式.
3) 对两路信号的输入数据z(n)进行式(12)的标准化处理, 让使对每一路信号中的据样本的均值等于0, 方差为1, 使数据在一个标准的尺度上.
| zn=zn−1NN∑i=1zn√1NN∑i=1(zn−1NN∑i=1zn)2 | (12) |
4) 使用FFB-EWT技术对两路标准化处理后的短导码进行分解, 输入的频率边界为
5) 对每一层子信号与相邻帧同层的空子载波分量进行相干积累. 处理后每个样本的数据格式仍为2×7×160.
6) 将相干积累后的数据样本使用双通道的NCAB-ResNet18网络模型进行训练, 每个通道输入为1×7×160, 在通过NCAB-ResNet18网络模型提取特征后, 进行最大池化对数据降维, 然后将2路特征通过Cat操作进行拼接, 使用Softmax函数进行分类.
7) 根据验证集的实验结果选择最优的网络参数, 用训练好的网络模型去对测试集中样本进行测试, 得到识别结果.
6 实验结果及仿真 6.1 实验条件设置实验所使用的硬件平台为Gen InterCore(TM) i7-12700H CPU, GPU为NVIDIA GeForce RTX 3070 Ti Laptop GPU. 信号处理部分在Matlab 2021a环境下进行, 深度学习网络训练环境为 Python 3.9+PyTorch 1.9.
6.2 数据集处理实验所使用的数据集为开源数据集ORACLE[16], 该数据使用相同型号的URSP作为发射器, 由Matlab WLAN系统工具箱生成信号, 产生具有相同的硬件、协议、物理地址和介质访问控制地址的数据帧, 并使用同一个设备来对信号进行接收. 本文选取6台发射机的信号数据, 信号采样率为20 MHz, 信噪比取值区间[−4, 6] dB, 以2 dB为间隔, 每类提取
为了验证FFB-EWT分解方法的有效性, 与FBR-EWT, EMD, VMD方法进行对比, 同时使用NCAB-ResNet18网络模型在0 dB信噪比条件下进行实验, FFB-EWT分解层数设置为13, FBR-EWT分解层数设置为6, VMD分解层数设置为6, EMD最大迭代次数设置为5, 统计对所有
| 表 1 0 dB信噪比条件不同分解方法对比 |
由表1可知, 除EMD方法外, FFB-EWT, FBR-EWT, VMD方法在0 dB条件下都取得高于了80%的识别准确率, 说明了在使用短导码进行实验的过程中, 网络更容易提取到射频指纹特征. 分解相同层数的VMD方法比FBR-EWT方法的识别准确率高4.60%, VMD方法的处理时间为FBR-EWT方法的处理时间的435.1%. 分析出现这样的结果是因为VMD方法本质是多个自适应的维纳滤波器, 对噪声有更强的鲁棒性, 因此识别精度高于FBR-EWT方法, 但同时计算开销更大. 而本文提出的FFB-EWT方法在去掉含信号信息的子载波分量后进行识别取得了接近VMD方法的识别率, 说明了FFB-EWT方法的有效性. 同时在分解层数更多的情况下所有样本的处理时间只比FBR-EWT多11.3%, 说明了FFB-EWT方法在计算开销不大的同时, 能有效地对信号进行分解, 帮助网络更好地提取出信号中的时频特征.
6.4 对比实验为了验证本文方法对I/Q通信辐射源信号识别的有效性, 本文与其他文献方法进行了对比. 对比文献[12]使用了FBR-EWT对信号进行分解, 并使用深度卷积神经网络进行识别. 文献[17]设计了一种ResNet50-1D网络模型对一维时间序列的IQ数据进行识别; 文献[18]设计一种复数CNN (CV-CNN)网络, 可将复数IQ信号直接输入网络进行识别; 文献[19]使用VGG16的类似网络模型提取I/Q两路的相关特征. 使用以上文献中应用的相关方法与本文方法进行对比实验. 图8为对比实验结果图.
如图8所示, 本文提出的方法在各种信噪比条件下均取得了最高的识别率, 同时随着信噪比逐渐降低, 识别准确率相较别的方法越高. 表2为不同信噪比条件下各个方法的识别准确率.
由表2可知在0 dB条件下文献[17–19]的网络对I/Q信号的前导部分识别准确率分别为68.17%, 79.50%, 76.83%. 与本文使用类似方法对信号先进行FBR-EWT的文献[12]在此信噪比条件下的识别率为81.83%, 而本文方法在0 dB信噪比条件下识别率达到89.33%, 比文献[12]的方法识别率高8.5%, 分析出现的结果一是因为文献[17–19]都是将原始I/Q路信号直接送入神经网络中而本文方法与文献[12]的方法都是在对信号进行时频域分解后送入神经网络中, 这样能放大信号特征, 让网络能更好地提取指纹特征. 二是因为使用FFB-EWT方法能够去掉含有信号信息干扰的子载波. 同时本文使用相邻帧间相同层子载波的相干积累方法, 能有效提高指纹信号的信噪比, 因此在低信噪比条件下能准确提取通信辐射源信号的指纹特征, 说明了本文方法对噪声具有较强的鲁棒性.

|
图 8 对比实验结果图 |
| 表 2 不同信噪比条件下各个方法的识别准确率 (%) |
6.5 消融实验
为了进一步研究对空子载波分量进行相干积累和NCAB-ResNet18带来的影响, 在分别在对子载波不进行积累, 不使用NCAB-ResNet18进行消融实验, 如表3所示为0 dB条件下消融实验的识别率.
由表3可知, 使用ResNet18、NCAB-ResNet18、进行子载波积累的ResNet18、进行子载波积累的NCAB-ResNet18的方法, 在0 dB条件下的进行消融实验的识别结果分别为77.67%、83.33%、81.00%、89.33%. 可以看出使用在对空子载波分量进行积累后, ResNet18和NCAB-ResNet18分别提高了3.33%和11.66%, 在不对空子载波分量进行积累时, NCAB-ResNet18较ResNet18提高了5.66%, 能够体现NCAB-ResNet18在低信噪比条件下对经过FFB-EWT去除信号成分后进行识别辐射源信号的有效性.
| 表 3 0 dB条件下消融实验的识别率 (%) |
7 结论
针对在传统辐射源个体识别方法中OFDM辐射源细微指纹特征信息会受到信号成分和信道噪声的影响导致分类识别率低的问题, 本文对OFDM信号进行FFB-EWT分解, 有效去除信号成分干扰, 通过对空子载波分量进行相干积累, 来提高指纹特征信号的信噪比; 使用通过嵌入非局部注意力机制模块和通道注意力机制模块, 来提升ResNet18的识别性能. 使用双通道的NCAB-ResNet18网络模型来对I/Q两路数据提取特征及分类. 实验表明通过对6个不同辐射源个体在6 dB和0 dB条件下进行识别, 准确率可以达到98.17%和89.33%, 通过对比实验, 使用FFB-EWT和NCAB-ResNet18的OFDM辐射源个体识别方法与其他处理方法相比, 具有识别率高、抗噪性能好的优势.
| [1] |
Fu X, Shi SN, Wang Y, et al. Semi-supervised specific emitter identification via dual consistency regularization. IEEE Internet of Things Journal, 2023, 10(21): 19257-19269. DOI:10.1109/JIOT.2023.3281668 |
| [2] |
Zhang YB, Peng Y, Sun JL, et al. GPU-free specific emitter identification using signal feature embedded broad learning. IEEE Internet of Things Journal, 2023, 10(14): 13028-13039. |
| [3] |
Zha HR, Wang HH, Feng ZM, et al. LT-SEI: Long-tailed specific emitter identification based on decoupled representation learning in low-resource scenarios. IEEE Transactions on Intelligent Transportation Systems, 2024, 25(1): 929-943. DOI:10.1109/TITS.2023.3308716 |
| [4] |
Halder S, Newe T. Radio fingerprinting for anomaly detection using federated learning in LoRa-enabled industrial Internet of Things. Future Generation Computer Systems, 2023, 143: 322-336. DOI:10.1016/j.future.2023.01.021 |
| [5] |
Wu WW, Hu S, Lin D, et al. Radio-frequency fingerprinting for distributed IoT networks: Authentication and QoS optimization. IEEE Systems Journal, 2023, 17(3): 4440-4451. DOI:10.1109/JSYST.2023.3248685 |
| [6] |
Lundén J, Koivunen V. Automatic radar waveform recognition. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(1): 124-136. DOI:10.1109/JSTSP.2007.897055 |
| [7] |
Zhang JW, Wang FG, Dobre OA, et al. Specific emitter identification via Hilbert-Huang transform in single-hop and relaying scenarios. IEEE Transactions on Information Forensics and Security, 2016, 11(6): 1192-1205. DOI:10.1109/TIFS.2016.2520908 |
| [8] |
韦建宇, 彭来献, 俞璐, 等. 基于差分-变分模态分解与全局信息分析网络的辐射源个体识别方法. 信号处理, 2022, 38(10): 2092-2101. |
| [9] |
Jiang Q, Sha J. RF fingerprinting identification in low SNR scenarios for automatic identification system. IEEE Transactions on Wireless Communications, 2024, 23(3): 2070-2081. DOI:10.1109/TWC.2023.3294988 |
| [10] |
Gilles J. Empirical wavelet transform. IEEE Transactions on Signal Processing, 2013, 61(16): 3999-4010. DOI:10.1109/TSP.2013.2265222 |
| [11] |
Panda R, Jain S, Tripathy R, et al. Detection of shockable ventricular cardiac arrhythmias from ECG signals using FFREWT filter-bank and deep convolutional neural network. Computers in Biology and Medicine, 2020, 124: 103939. DOI:10.1016/j.compbiomed.2020.103939 |
| [12] |
Bremnes K, Moen R, Yeduri SR, et al. Classification of UAVs utilizing fixed boundary empirical wavelet sub-bands of RF fingerprints and deep convolutional neural network. IEEE Sensors Journal, 2022, 22(21): 21248-21256. DOI:10.1109/JSEN.2022.3208518 |
| [13] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
|
| [14] |
Wang XL, Girshick R, Gupta A, et al. Non-local neural networks. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 7794–7803.
|
| [15] |
Woo S, Park J, Lee JY, et al. CBAM: Convolutional block attention module. Proceedings of the 15th European Conference on Computer Vision. Munich: Springer, 2018. 3–19.
|
| [16] |
Sankhe K, Belgiovine M, Zhou F, et al. No Radio Left Behind: Radio fingerprinting through deep learning of physical-layer hardware impairments. IEEE Transactions on Cognitive Communications and Networking, 2020, 6(1): 165–78.
|
| [17] |
Gritsenko A, Wang ZF, Jian T, et al. Finding a ‘new’ needle in the haystack: Unseen radio detection in large populations using deep learning. Proceedings of the 2019 IEEE International Symposium on Dynamic Spectrum Access Networks (DySPAN). Newark: IEEE, 2019. 1–10.
|
| [18] |
Agadakos I, Agadakos N, Polakis J, et al. Chameleons’ oblivion: Complex-valued deep neural networks for protocol-agnostic RF device fingerprinting. Proceedings of the 2020 IEEE European Symposium on Security and Privacy (EuroS&P). Genoa: IEEE, 2020. 322–338.
|
| [19] |
Elmaghbub A, Hamdaoui B. LoRa device fingerprinting in the wild: Disclosing RF data-driven fingerprint sensitivity to deployment variability. IEEE Access, 2021, 9: 142893-142909. DOI:10.1109/ACCESS.2021.3121606 |
 2024, Vol. 33
2024, Vol. 33



