1 引言

高维数据由于高维空间中样本之间距离的稀疏性, 导致数据稀疏和冗余, 增加了计算和存储成本, 因此在处理和分析时面临挑战. 作为常用的降维算法之一, 投影学习在高维数据处理和分析中具有重要意义^[1–3]. 通过保留数据的基本信息并将其映射到低维空间, 投影学习可以显著减少数据的冗余和复杂性, 同时保持数据点之间的关键关系. 这简化了问题求解, 提高了计算效率, 并促进了数据可视化和理解^[4].

降维算法的演进经历了从传统线性方法, 如主成分分析 (principal component analysis, PCA)^[5] 和线性判别分析 (linear discriminant analysis, LDA)^[6], 到基于流形学习的非线性方法的过程. 在这个过程中, 出现了一系列基于流形学习的降维算法, 包括等距映射 (isometric mapping, ISOMAP)^[7]、局部线性嵌入 (locally linear embedding, LLE)^[8]和拉普拉斯特征映射 (Laplacian eigenmap, LE)^[9]等. 这些方法致力于将高维数据映射到低维流形空间, 以便更好地捕捉数据中的非线性特征和结构. 然而, 尽管非线性流形学习方法在处理复杂数据结构方面表现出色, 但在样本外推和泛化方面仍然存在挑战. 在一些应用中, 线性投影技术表现突出成为最常用和稳定的方法. 因此, 经典的局部保持投影 (locality preserving projection, LPP)^[10]作为一种线性降维方法, 利用 LE 在原始和嵌入空间之间建立线性映射. 同时, 通过保持样本之间的局部邻域关系, LPP 可以更好地揭示数据的局部结构. 随着研究的深入, 逐渐出现了许多将其他优秀的数据挖掘工具 (如低秩或稀疏属性) 与投影学习相结合的投影学习方法^[11–14].

众所周知, 类似于 LPP 的方法在执行之前需要预定义一个图来描述数据样本之间的局部关联. 显然, 在稀疏高维空间中, 随着欧氏度量逐渐失效, 基于任何假设的任何预定义图都将是徒劳的. 近年来, 提出了许多同时优化图和投影矩阵的方法^[15–18]. 在类内样本之间的亲和度满足二次条件的前提下, Li 等人^[19]研究了全连接的类内图, 并提出了局部自适应判别分析 (locality adaptive discriminant analysis, LADA), 可以很好地揭示潜在的数据流形结构. Pang 等人^[20]提出了同时学习邻居和投影矩阵的方法 (simultaneously learning neighborship and projection matrix, SLNP), 使相似度和邻居成为低维子空间中的变量. 然后通过最小化统一的目标函数获得最佳相似度和投影矩阵. Nie 等人^[21]提出了自适应局部线性判别分析 (adaptive local linear discriminant analysis, ALLDA), 它从数据本身自适应地学习了一个$k$近邻图, 以提取数据的局部连通性. 但在特定情况下, 伴随投影学习的持续优化图可能不会超越预定义图的性能, 主要原因有3点: (1) 特定假设可能导致学习到的亲和度分布与真实数据分布之间存在差异; (2) 当数据在高维空间中稀疏分布时, 仅依赖数据距离进行相似性估计可能无法准确表示数据点之间的真实局部关系; (3) 亲和度的初始估计误差可能导致投影中的方向偏差, 随后在学习过程中引起累积误差.

在流形学习的背景下, 基本假设是数据分布在一个低维流形上, 这意味着该流形的局部区域可以同胚于某个欧几里得空间 (通常是低维空间). 在这些局部区域中, 数据在流形上呈近似线性, 允许在欧几里得空间中使用线性关系对其进行近似. LLE 是一个经典的为此目的设计的流形学习算法, 而邻域保持嵌入(neigh-borhood preserving embedding, NPE)^[22]是一个具有线性投影学习的扩展版本. LLE 和 NPE 使每个样本可以通过其相邻样本的线性组合在低维空间中近似重构, 同时保持数据点之间的局部关系. 然而, 在环境空间(ambient space)中选择$k$个最近邻可能并不总是理想的. 为此, 稀疏保持投影 (sparsity preserving projection, SPP)^[23]利用稀疏编码学习原始数据的稀疏表示, 而表示系数直接描述了数据点之间的局部关系, 实现了有效的特征提取和冗余信息的减少. 考虑到 NPE 和 SPP 在显式判别时的局限性和对损坏样本的脆弱性, 低秩保持嵌入 (low-rank preserving embedding, LRPE)^[24]联合获得所有数据的自表示, 从而能够提取数据集的整体全局结构. 一般来说, 表示学习和投影学习通常被认为是两个不相关的学习过程, 这限制了实现最佳性能的潜力. 因此, 低秩嵌入 (low-rank embedding, LRE)^[25]通过使用鲁棒的低秩表示 (low-rank representation, LRR) 来解决对损坏数据的无监督鲁棒线性降维问题, 同时寻找最佳的 LRR 和最佳子空间. 此外, 扩展近似低秩投影学习(extended approximate low-rank projection learning, EALPL)^[26]和潜在低秩和稀疏嵌入 (latent low-rank and sparse embedding, LLRSE)^[27]与 LRPE 和 LRE 把原始数据用作字典不同, 而是使用投影样本作为字典. 更准确地说, 对于低秩表示学习, 字典是通过利用投影后的样本重构形成的, 从而使噪声效应得以抑制. 近年来, 人们对稀疏和低秩表示揭示数据固有局部结构的能力越来越感兴趣^[28–30].

以上的介绍涵盖了2种代表性的技术. 其中一种源于 LPP 方法, 从预定义的亲和度图演变为动态亲和度图. 另一种是基于 NPE 方法构建的, 从$k$个最近邻线性表示演化为稀疏或低秩表示. 现有的方法往往只沿着其中一条思路开展研究, 难以有效捕捉高维空间中数据的复杂结构. 在本文的工作中, 我们结合了以上2种思路, 创新地提出了一种监督降维方法, 即 LPP_SRL, 它不仅考虑了在欧几里得度量下保持邻域关系, 还结合了稀疏表示, 以促进主成分的提取, 并在环境空间中过滤噪声和冗余特征. 总之, 本文的研究具有以下主要贡献: (1) 本文将基于欧几里得距离的邻域保持和局部稀疏自表示两个模块自适应地纳入一个统一的框架, 丰富了对数据局部拓扑结构的描述, 并克服了传统方法的潜在缺点; (2) 在稀疏自表示模块中, 本文选择重构样本作为字典, 并建立了与投影学习的联合学习模式, 使模型能够在投影学习过程中捕获数据的主要成分, 消除冗余特征, 并消除噪声; (3) 为了优化所提出模型, 我们开发了一个高效的迭代算法, 并在不同场景下对各种公开可用数据集进行了实验, 证明了所提出的算法在降维方面表现出色.

本文第 2 节介绍本文写作中的一些符号, 并简要概述了该领域的相关方法. 接下来, 在第 3 节中, 本文提出一种创新的模型, 讨论了优化过程, 并分析了其计算复杂性. 实验设置和结果在第 4 节详细说明. 最后, 在第 5 节中, 我们总结了全文.

2 相关工作 2.1 符号与定义

假设有一个数据矩阵 $X = [{X_1}, {X_2}, \cdots, {X_c}] = [{x_1}, {x_2}, \cdots, {x_n}] \in {\mathbb{R}^{d \times n}}$, 由$d$维空间中的$n$个样本组成, 其中每个${X_i}$表示属于第$i$个类别的子矩阵. 在降维任务中, 我们的目标是学习一个投影矩阵$Q \in {\mathbb{R}^{m \times d}}$, 有效地将原始样本${x_i} \in {\mathbb{R}^{d \times 1}}$投影到一个$m$维子空间中, 旨在提取最显著的特征, 如下所示:

$ {y_i} = Q{x_i} $

(1)

其中, ${y_i} \in {\mathbb{R}^{m \times 1}}$表示与${x_i}$对应的低维向量表示. 此外, 对于向量$x = [{x_1}, {x_2}, \cdots, {x_n}]$, ${\ell _2}$范数被定义为${\left\| x \right\|_2} = \sqrt {\displaystyle\sum\nolimits_{i = 1}^n {x_i^2} } $. 对于矩阵$X \in {\mathbb{R}^{d \times n}}$, 我们将${\ell _1}$范数、${\ell _{2, 1}}$范数和 Frobenius范数分别定义为$ {\left\| X \right\|_1} = \displaystyle\sum\nolimits_{j = 1}^n {\displaystyle\sum\nolimits_{i = 1}^d {|{x_{ij}}|} } $、${\left\| X \right\|_{2, 1}} = \displaystyle\sum\nolimits_{j = 1}^n {\sqrt {\displaystyle\sum\nolimits_{i = 1}^d {x_{ij}^2} } } $和$\left\| X \right\|_F^2 = \displaystyle\sum\nolimits_{j = 1}^n {\displaystyle\sum\nolimits_{i = 1}^d {x_{ij}^2} } $.

2.2 局部保持投影

LPP 是一种线性降维方法, 旨在保持高维数据的局部邻域, 并确保低维空间中的数据样本投影与其在高维空间中的原始局部关系紧密相符. 一般来说, 其目标函数可以表示为:

$ \underset{Q}{\mathrm{min}}\frac{1}{2}{\displaystyle \sum _{i, j=1}^{n}\Vert Q{x}_{i}-Q{x}_{j}{\Vert }_{2}^{2}}{w}_{ij} $

(2)

其中, $ {w}_{ij}=\mathrm{exp}(-\Vert {x}_{i}-{x}_{j}{\Vert }_{2}^{2}/t) $表示样本${x_i}$和${x_j}$之间的亲和度, 它们彼此是k-最近邻的 (否则, ${w_{ij}} = 0$), $t$是一个可调节参数. 通过简单的数学推导, 可以得到以下等式:

$ \frac{1}{2}{\displaystyle \sum _{i, j=1}^{n}\Vert Q{x}_{i}-Q{x}_{j}{\Vert }_{2}^{2}}{w}_{ij}={\mathrm{tr}}(QXL{X}^{\rm T}{Q}^{\rm T}) $

(3)

其中, $L = D - W$是拉普拉斯矩阵, $D$是度矩阵, 其对角线元素为${d_{ii}} = \displaystyle\sum\nolimits_{j = 1} {{w_{ij}}} $, $W$是亲和矩阵, 其第$(i, j)$个元素表示为${w_{ij}}$. 因此, 通过对式(3) 加上约束, 可以将其转化为式(4):

$ \mathop {\min }\limits_Q {\mathrm{tr}}(QXL{X^{\mathrm{T}}}{Q^{\mathrm{T}}})\;\;\;\;{\text{s.t.}}\;QXD{X^{\mathrm{T}}}{Q^{\mathrm{T}}} = I $

(4)

利用拉格朗日乘子法, 约束问题 (4) 等价于以下广义特征值分解问题:

$ XL{X^{\mathrm{T}}}{q^{\mathrm{T}}} = \alpha XD{X^{\mathrm{T}}}{q^{\mathrm{T}}} $

(5)

其中, $q$是对应于特征值$\alpha $的特征向量, 并且作为行向量组成投影矩阵$Q$. LPP 中的最优投影由与$m$个最小广义特征值对应的$m$个特征向量组成.

2.3 稀疏表示学习

稀疏表示^[31–33]是信号处理和机器学习领域常用的技术之一, 旨在将信号或数据表示为尽可能少的非零元素的线性组合, 有助于从信号中提取关键特征, 降低数据维度, 并展现出了优秀的噪声鲁棒性. 假设要表示的信号是一个向量$x \in {\mathbb{R}^d}$, 字典由矩阵$D \in {\mathbb{R}^{d \times n}}$表示, 其中$d$是信号维度, $n$是字典中原子(基)的数量. 则稀疏表示的数学模型可以描述为:

$ \mathop {\min }\limits_w {\left\| w \right\|_0}\;\;\;\;{\text{s.t.}}\;x = Dw $

(6)

其中, $w \in {\mathbb{R}^n}$是稀疏表示系数向量, $ {\left\| w \right\|_0} $表示$w$的${\ell _0}$范数, 即非零元素的数量. 目标是找到一个稀疏系数向量$w$, 使得信号$x$可以表示为字典$D$中原子的线性组合, 同时最小化$w$的${\ell _0}$范数, 即尽可能少地使用基来表示信号.

然而, 问题 (6) 是一个 NP-hard 问题, 因为计算${\ell _0}$范数是一个非凸优化问题. 为了解决这个问题, 通常使用${\ell _1}$范数作为${\ell _0}$范数的近似, 得到以下近似问题:

$ \mathop {\min }\limits_w {\left\| w \right\|_1}\;\;\;\;{\text{s.t.}}\;x = Dw $

(7)

其中, ${\left\| w \right\|_1}$表示$w$的${\ell _1}$范数, 即其元素的绝对值之和. ${\ell _1}$范数问题是一个凸优化问题, 可以用各种优化方法求解. 在实践中, ${\ell _1}$范数提供了良好的稀疏性, 同时计算效率更高. 此外, 在实际场景中, 我们要考虑到真实数据通常存在噪声. 因此, 模型 (7) 中的条件可以放宽为$x = Dw + e$, 其中$e$表示噪声向量. 然后, 模型 (7) 可以进一步写为:

$ \underset{w}{\mathrm{min}}{\Vert w\Vert }_{1}\;\;\;\;\text{s.t.}\;\Vert x-Dw\Vert \leqslant \epsilon $

(8)

其中, $ \epsilon $是误差容限或误差阈值, 表示原始信号和利用稀疏系数向量$w$和字典$D$复原的信号之间的最大允许误差或偏差.

2.4 稀疏保持投影

SPP 是 LLE 和 NPE 的一种变体, 专注于在将高维数据投影到低维空间时保持数据的稀疏性. LLE、NPE 和 SPP 使用一个共同目标函数, 可以表达为:

$ \underset{Y}{\mathrm{min}}{\displaystyle \sum _{i=1}^{n}\Vert {y}_{i}-{\displaystyle \sum _{j=1}^{n}{w}_{ij}}{y}_{j}{\Vert }_{2}^{2}}\;\;\;\;\text{s.t.}\;Y{Y}^{\rm T}=I $

(9)

其中, $Y = [{y_1}, {y_2}, \cdots , {y_n}] \in {\mathbb{R}^{m \times n}}$是嵌入数据矩阵, 第$i$列表示嵌入数据样本${y_i}$. 对于每个数据样本${x_i}$, LLE 和 NPE 计算其邻域中每个样本的局部重构权重${w_{ij}}$, 使得以下重构误差最小化:

$ \underset{W}{\mathrm{min}}{\displaystyle \sum _{i=1}^{n}\Vert {x}_{i}-{\displaystyle \sum _{j=1}^{n}{w}_{ij}}{x}_{j}{\Vert }_{2}^{2}}\;\;\;\;\text{s.t.}\;{\displaystyle \sum _{j}{w}_{ij}}=1 $

(10)

其中, $W = \{ {w_{ij}}\} _{i, j = 1}^n \in {\mathbb{R}^{n \times n}}$是描述原始数据的邻接属性的权重矩阵. 与 LLE 和 NPE 不同, SPP 的权重矩阵$W$是通过考虑每个样本作为其他样本的稀疏线性组合而构建的, 并且可以一次完成, 即:

$ \underset{{w}_{i}}{\mathrm{min}}\Vert {w}_{i}{\Vert }_{1}\;\;\;\;\text{s.t.}\;\Vert {x}_{i}-X{w}_{i}{\Vert }_{2}^{2}\leqslant \epsilon , \text{ }{\displaystyle \sum _{j}{w}_{ij}}=1 $

(11)

其中, 字典选择为$X$自身. 在使用 SPP 的情况下, 无需预定义每个样本的邻域, 而是由稀疏表示学习引导的自适应机制, 确定哪些样本是样本${x_i}$的邻居.

3 利用潜在稀疏表示学习的增强局部保持投影方法

考虑到现有方法的优点和局限性, 在本节中, 我们将逐步完善所提出的模型 LPP_SRL, 并设计了一个高效的迭代算法来优化它. 此外, 我们还分析了所提出模型的求解算法的计算复杂度.

3.1 模型建立

如第1节所述, 在投影学习过程中学习到的图在许多情景下表现出了良好的性能, 但原始空间中基于欧氏距离定义的图也确实包含了对后续分类任务有益的某些特征信息. 因此, 所提出的模型继承了原始 LPP 如下:

$ \underset{Q}{\mathrm{min}}\frac{1}{2}{\displaystyle \sum _{i, j=1}^{n}\Vert Q{x}_{i}-Q{x}_{j}{\Vert }_{2}^{2}}{w}_{ij} $

(12)

此外, 考虑到特定亲和度假设的适用性可能不够灵活, 我们只利用环境空间中样本的$k$近邻连接信息. 具体来说, 亲和度矩阵$W$定义如下:

$ {w_{ij}} = \left\{ {\begin{array}{*{20}{l}} {1/k, }&{{x_i} \in {N_k}({x_j})} \\ {0, }&{{\text{otherwise}}} \end{array}} \right. $

(13)

其中, ${x_i} \in {N_k}({x_i})$表示样本${x_i}$是${x_j}$同一类中的$k$个最近邻之一.

此外, 我们认为稀疏局部表示能揭示数据样本之间的内在连接. 因此, 得到以下目标函数:

$ \underset{{{\textit{z}}}_{i}}{\mathrm{min}}\Vert {{\textit{z}}}_{i}{\Vert }_{1}+\lambda \Vert {e}_{i}{\Vert }_{1}\;\;\;\;\text{s.t.}\;{x}_{i}=X{{\textit{z}}}_{i}+{e}_{i} $

(14)

其中, ${{\textit{z}}_i}$表示第$i$个样本的表示系数, 而${e_i}$可能包含一些错误或噪声. 令$Z = [{{\textit{z}}_1}, {{\textit{z}}_2}, \cdots , {{\textit{z}}_n}]$和$E = [{e_1}, {e_2}, \cdots , {e_n}]$可以以矩阵形式表示为:

$ \mathop {\min }\limits_Z {\left\| Z \right\|_1} + \lambda {\left\| E \right\|_1}\;\;\;\;{\text{s.t.}}\;X = XZ + E $

(15)

事实上, 式(15) 不能直接与投影学习过程集成, 除非利用表示系数以图的形式描述数据样本之间的连接. 此外, 从现实场景中收集到的数据$X$不可避免地包含噪声, 这意味着直接使用$X$作为字典来学习表示系数可能会受到负面影响. 为了解决这些问题, 我们假设投影空间具有一组正交基向量$\{ {p_1}, {p_2}, \cdots , {p_m}\} $(也可以称为原始数据的主成分), 使用这些基向量上的投影坐标${y_i} = {[{y_{1i}}, {y_{2i}}, \cdots , {y_{mi}}]^{\mathrm{T}}}$重构样本${x_i}$, 如下所示:

$ {x_i} = {p_1}{y_{1i}} + {p_2}{y_{2i}} + \cdots + {p_m}{y_{mi}} + {r_i} $

(16)

其中, 残差向量${r_i}$可能包含一些低级特征或噪声. 令${y_i} = Q{x_i}$, $P = [{p_1}, {p_2}, \cdots , {p_m}]$, $R = [{r_1}, {r_2}, \cdots , {r_m}]$, 式(16) 可以以矩阵形式表示为:

$ X = PQX + R $

(17)

然后, 将式 (17) 替换进方程$X = XZ + E$的右侧, 得到:

$ X = PQXZ + RZ + E $

(18)

其中, $RZ$作为重新组装的残差向量, 可以与$E$合并成为一个矩阵. 结合式(15)和式(18), 得到新的稀疏表示模型如下:

$ \mathop {\min }\limits_Z {\left\| Z \right\|_1} + \lambda {\left\| E \right\|_{2, 1}}{\text{ s}}{\text{.t}}{\text{. }}X = PQXZ + E $

(19)

其中, 用$PQX$替换$X$作为字典可以揭示数据样本之间更本质的连接, 残差矩阵$E$合并了$RZ$和原始的$E$, 范数$ \Vert \cdot{\Vert }_{2, 1} $用于过滤掉特定样本的损坏和离群值.

综合考虑式(12)和式(19)可以实现相互促进学习的目的, 导出最终目标函数如下:

$ \left\{\begin{split} &\underset{P, Q, Z, E}{\mathrm{min}}\frac{1}{4}{\displaystyle \sum _{i, j=1}^{n}\Vert Q{x}_{i}-Q{x}_{j}{\Vert }_{2}^{2}}{w}_{ij}+ {\lambda }_{1}\Vert Z{\Vert }_{1} \\ &\quad+{\lambda }_{2}\Vert E{\Vert }_{2, 1}+\frac{{\lambda }_{3}}{2}\Vert Q{\Vert }_{F}^{2}\\ &\text{s.t.}\;X=PQXZ+E, \text{ }{P}^{\rm T}P=I\end{split} \right.$

(20)

其中, ${\lambda _1}$、${\lambda _2}$和${\lambda _3}$是3个正则化参数, 约束${P^{\mathrm{T}}}P = I$使模型在求解过程中避免平凡解.

3.2 模型优化

在本节中, 我们将通过采用交替方向乘子法 (alternating direction method of multipliers, ADMM) 框架^[34]解决式(20)中的优化问题. 关于 ADMM 在非凸问题上的详细收敛分析可以在文献 [35] 中找到. 为了简化优化过程, 我们首先引入一个辅助变量$B$和一个约束$Z = B$, 使式(20)可分离. 因此, 通过放松原始问题, 问题(20)可以重新表述如下:

$ \left\{\begin{split} &\underset{P, Q, Z, E, B}{\mathrm{min}}\frac{1}{2}{\mathrm{tr}}(QX{L}_{W}{X}^{\rm T}{Q}^{\rm T})+{\lambda }_{1}\Vert B{\Vert }_{1}+{\lambda }_{2}\Vert E{\Vert }_{2, 1}+\frac{{\lambda }_{3}}{2}\Vert Q{\Vert }_{F}^{2}\\ &\text{s.t.}\;X=PQXZ-E, \text{ }{P}^{\rm T}P=I, \text{ }Z=B\end{split} \right.$

(21)

其中, 拉普拉斯矩阵${L_W}$定义为${L_W} = D - (W + {W^{\mathrm{T}}})/2$, $D \in {\mathbb{R}^{n \times n}}$是对角矩阵, 其第$ii$项为$\displaystyle\sum\nolimits_j {({w_{ij}} + {w_{ji}})/2} $.

紧接着, 问题 (21) 的增广拉格朗日函数定义如下:

$ \left\{\begin{split} &\mathcal{L}(P, Q, Z, E, B)\\ &=\frac{1}{2}{\mathrm{tr}}(QX{L}_{W}{X}^{\rm T}{Q}^{\rm T})+{\lambda }_{1}\Vert B{\Vert }_{1}+{\lambda }_{2}\Vert E{\Vert }_{2, 1}\\ &\quad+\frac{{\lambda }_{3}}{2}\Vert Q{\Vert }_{F}^{2}+\langle {C}_{1}, X-PQXZ+E\rangle +\langle {C}_{2}, Z-B\rangle \\ &\quad+\frac{\mu }{2}\left(\Vert X-PQXZ-E{\Vert }_{F}^{2}+\Vert Z-B{\Vert }_{F}^{2}\right)\\ &\text{s.t.}\;{P}^{\rm T}P=I\end{split} \right.$

(22)

其中, $\left\langle {A, B} \right\rangle = {\text{tr}}({A^{\mathrm{T}}}B)$, $\mu $是惩罚参数, ${C_1}$和${C_2}$是两个拉格朗日乘子.

通过使用一些数学技巧, 问题 (22) 可以重新表述为:

$\left\{ \begin{split} &\mathcal{L}(P, Q, Z, E, B)\\ &=\frac{1}{2}{\mathrm{tr}}(QX{L}_{W}{X}^{\rm T}{Q}^{\rm T})+{\lambda }_{1}\Vert B{\Vert }_{1}+{\lambda }_{2}\Vert E{\Vert }_{2, 1}+\frac{{\lambda }_{3}}{2}\Vert Q{\Vert }_{F}^{2}\\ &\quad+\frac{\mu }{2}\left(\Vert X-PQXZ-E+\frac{{C}_{1}}{\mu }{\Vert }_{F}^{2}+\Vert Z-B+\frac{{C}_{2}}{\mu }{\Vert }_{F}^{2}\right)\\ &\quad-\frac{1}{2\mu }\left(\Vert {C}_{1}{\Vert }_{F}^{2}+\Vert {C}_{2}{\Vert }_{F}^{2}\right)\\ &\text{s}\text{.t}\text{. }{P}^{\rm T}P=I\end{split} \right.$

(23)

为了解决问题 (23), 需要交替更新变量$P$、$Q$、$Z$、$E$和$B$.

● 更新$Z$: 给定$B$、$Q$、$P$和$E$值, 关于$Z$的子问题如下:

$ \underset{Z}{\mathrm{min}}\Vert X-PQXZ-E+\frac{{C}_{1}}{\mu }{\Vert }_{F}^{2}+\Vert Z-B+\frac{{C}_{2}}{\mu }{\Vert }_{F}^{2} $

(24)

定义$F = X - E + {C_1}/\mu $, $T = B - {C_2}/\mu $并且让$\partial \mathcal{L}(Z)/ \partial Z = 0$, 我们有:

$ ({X^{\mathrm{T}}}{Q^{\mathrm{T}}}QX + I)Z = {X^{\mathrm{T}}}{Q^{\mathrm{T}}}{P^{\mathrm{T}}}F + T $

(25)

然后, 从式(25)计算出:

$ Z = {({X^{\mathrm{T}}}{Q^{\mathrm{T}}}QX + I)^{ - 1}}({X^{\mathrm{T}}}{Q^{\mathrm{T}}}{P^{\mathrm{T}}}F + T) $

(26)

● 更新$B$: 给定固定的$Z$, 关于$B$的子问题如下:

$ \underset{B}{\mathrm{min}}{\lambda }_{1}\Vert B{\Vert }_{1}+\frac{\mu }{2}\Vert B-J{\Vert }_{F}^{2} $

(27)

其中, $J = Z + {C_2}/\mu $.

$B$可以通过以下方式获得:

$ B = {\Omega _{\frac{{{\lambda _1}}}{\mu }}}(J) $

(28)

其中, $\Omega $是标量缩放算子^[36]. 具体来说, $B$中的每个元素应为:

$ {B_{ij}} = {\text{sgn}}({J_{ij}}) \cdot \max \left(|{J_{ij}}| - \frac{{{\lambda _1}}}{\mu }, {\text{ }}0\right) $

(29)

其中, ${\mathrm{sgn}}$是用于确定实数的符号 (正或负) 的逻辑函数, $\max (\alpha , \beta )$是一个取$\alpha $和$\beta $之间最大值的函数.

● 更新$Q$: 给定$P$、$Z$和$E$, 关于$Q$的问题变为:

$ \begin{split} &\underset{Q}{\mathrm{min}}\frac{1}{2}{\mathrm{tr}}(QX{L}_{W}{X}^{\rm T}{Q}^{\rm T})+\frac{{\lambda }_{3}}{2}\Vert Q{\Vert }_{F}^{2}\\ &\text{ }+\frac{\mu }{2}\Vert X-PQXZ-E+\frac{{C}_{1}}{\mu }{\Vert }_{F}^{2}\end{split} $

(30)

对$\mathcal{L}(Q)$关于$Q$的导函数取零, 即$\partial \mathcal{L}(Q)/\partial Q = 0$, 我们有:

$ Q({\lambda _3}I + X{L_W}{X^{\mathrm{T}}} + \mu XZ{Z^{\mathrm{T}}}{X^{\mathrm{T}}}) = \mu {P^{\mathrm{T}}}F{Z^{\mathrm{T}}}{X^{\mathrm{T}}} $

(31)

其中, $F = X - E + {C_1}/\mu $, 然后, 由式(31) 可计算得到Q:

$ Q = \mu {P^{\mathrm{T}}}F{Z^{\mathrm{T}}}{X^{\mathrm{T}}}{({\lambda _3}I + X{L_W}{X^{\mathrm{T}}} + \mu XZ{Z^{\mathrm{T}}}{X^{\mathrm{T}}})^{ - 1}} $

(32)

● 更新$P$: 给定$Q$、$Z$和$E$, 并删除与$P$无关的项, 关于$P$的子问题如下:

$ \underset{P}{\mathrm{min}}\Vert F-PQXZ{\Vert }_{F}^{2}\;\;\text{s.t.}\;{P}^{\rm T}P=I $

(33)

问题 (33) 是一个正交普鲁克问题 (orthogonal Procrustes problem, OPP)^[37], 其解可以直接从thin SVD 中获得, 即:

$ F{Z^{\mathrm{T}}}{X^{\mathrm{T}}}{Q^{\mathrm{T}}} = U\Sigma {V^{\mathrm{T}}} $

(34)

然后, 我们得到:

$ P = U{V^{\mathrm{T}}} $

(35)

其中, $U$和$V$分别是$F{Z^{\mathrm{T}}}{X^{\mathrm{T}}}{Q^{\mathrm{T}}}$的左奇异向量和右奇异向量.

● 更新$E$: 给定$P$、$Q$和$Z$, 更新$E$的子问题为:

$ \underset{E}{\mathrm{min}}{\lambda }_{2}\Vert E{\Vert }_{2, 1}+\frac{\mu }{2}\Vert X-PQXZ-E+\frac{{C}_{1}}{\mu }{\Vert }_{F}^{2} $

(36)

令$K = X - PQXZ + {C_1}/\mu $, 问题 (36) 等价于:

$ \underset{E}{\mathrm{min}}\frac{{\lambda }_{2}}{\mu }\Vert E{\Vert }_{2, 1}+\frac{1}{2}\Vert E-K{\Vert }_{F}^{2} $

(37)

可以分解为:

$ \underset{{e}_{i}}{\mathrm{min}}\frac{{\lambda }_{2}}{\mu }\Vert {e}_{i}{\Vert }_{2}+\frac{1}{2}\Vert {e}_{i}-{k}_{i}{\Vert }_{2}^{2} $

(38)

其中, ${e_i}$和${k_i}$分别是矩阵$E$和$K$的第$i$列. 问题 (38) 的解^[38]如下:

$ {e}_{i}=\left\{\begin{array}{ll}\left(1-\dfrac{{\lambda }_{2}/\mu }{\Vert {k}_{i}{\Vert }_{2}}\right){k}_{i}, & \Vert {k}_{i}{\Vert }_{2} \gt \dfrac{{\lambda }_{2}}{\mu } \\ 0, & \Vert {k}_{i}{\Vert }_{2}\leqslant \dfrac{{\lambda }_{2}}{\mu } \end{array}\right. $

(39)

● 更新${C_1}$、${C_2}$和$\mu $: ${C_1}$、${C_2}$和$\mu $分别通过以下方式更新:

$\left\{ \begin{gathered} {C_1} = {C_1} + \mu (X - PQXZ - E) \\ {C_2} = {C_2} + \mu (Z - B) \\ \mu = \min (\rho \mu , {\text{ }}{\mu _{\rm max}}) \\ \end{gathered} \right.$

(40)

模型 (20) 的详细优化过程见算法 1.

算法1. 通过ADMM优化模型(20)的算法

输入: 训练样本矩阵$\scriptstyle X \in {\mathbb{R}^{d \times n}}$, 超参数$\scriptstyle {\lambda _1}$, $\scriptstyle {\lambda _2}$, $\scriptstyle {\lambda _3}$, 邻域数量$\scriptstyle k$和投影维度$\scriptstyle m$.

初始化: $\scriptstyle P = \arg {\max _{{P^{\mathrm{T}}}P = I}}{\mathrm{tr}}({P^{\mathrm{T}}}\Sigma P)$, 其中$\scriptstyle \Sigma $是训练样本协方差矩阵; $\scriptstyle Q = {P^{\mathrm{T}}}$, $\scriptstyle Z = B = 0$, $\scriptstyle E = 0$, 并且$\scriptstyle {C_1} = {C_2} = 0$, $\scriptstyle \mu = 0.1$, $\scriptstyle \rho = 1.1$, $\scriptstyle {\mu _{\max}} = {10^8}$且$\scriptstyle \epsilon ={10}^{-6} $.

重复:

1. 使用式(26)更新 $\scriptstyle Z$.

2. 使用式(29)更新 $\scriptstyle B$.

3. 使用式(32)更新 $\scriptstyle Q$.

4. 使用式(35)更新 $\scriptstyle P$.

5. 使用式(39)更新 $\scriptstyle E$.

6. 使用式(40)更新 $\scriptstyle {C_1}$, $\scriptstyle {C_2}$和$\scriptstyle \mu $.

直到: 以下约束条件被满足

$ \scriptsize { \left\{ \begin{array}{l} \Vert X-PQXZ-E{\Vert }_{\infty }\leqslant \epsilon \\ \Vert Z-B{\Vert }_{\infty }\leqslant \epsilon \end{array} \right.}$

输出: 判别投影矩阵$\scriptstyle Q$.

3.3 复杂度分析

在本节中, 对解决所提出模型 LPP_SRL 所涉及的计算复杂性进行了全面分析. 算法 1 涉及几个关键步骤, 其中矩阵求逆是解决$Q$和$Z$所需的主要耗时操作. 对于计算$E$的${\ell _{2, 1}}$范数的优化以及使用${\ell _1}$范数解决$B$, 相对而言计算成本较小, 可以忽略不计. 考虑到矩阵求逆, 求解$Q$的计算复杂度为${\mathrm{O}}({d^3})$, 而求解$Z$的计算复杂度为${\mathrm{O}}({n^3})$. 对于$P$的更新主要由奇异值分解 (singular value decomposition, SVD) 计算所决定, 其复杂度为${\mathrm{O}}({m^3})$^[27]. 总的来说, 算法 1 的计算复杂度为${\mathrm{O}}(\tau ({n^3} + {d^3} + {m^3}))$, 其中$\tau $表示迭代次数. 在实际情况中, 通常有$d \leqslant n$且$m$较小, 因此可以将总计算复杂度的近似估计为${\mathrm{O}}(\tau {n^3})$.

4 实验

在本节中, 我们评估了所提出方法在6个广泛使用的公共数据集上的有效性, 这些数据集收集自不同的场景, 包括: (1) EYaleB^[39]; (2) YTC^[40]; (3) Binalpha (https://cs.nyu.edu/~roweis/data.html); (4) USPS^[41]; (5) Caltech101 Silhouettes^[42]; (6) ETH80^[43]. 为了进行有说服力的比较, 我们将所提方法与一些先进的方法进行比较, 包括 LDA^[6], Supervised LPP (SLPP)^[44], LSDA^[45], OLSDA^[46], FOLPP^[47], LADA^[19], RSLDA^[48], SLNP^[20], ALLDA^[21], SN-TSL^[49], LRPER^[3]. 在本文的实验中, 使用最近邻 (1-NN) 分类器利用欧氏距离对样本进行分类, 并将上述方法的参数调试到最佳范围之内或直接采用作者推荐的值. 此外, 我们针对每个数据集固定了所有参数, 并同时改变训练样本的数量. 为了公平起见, 我们对所有算法在比较实验中进行了 10 次实验, 并计算出平均识别率. 在每一次实验中, 我们随机选择每个类别的一些样本作为训练数据 (#Tr), 同时使用剩余的样本作为测试数据. 为了提高计算效率, 我们首先对样本进行归一化, 即$ {x}_{i}={x}_{i}/\Vert {x}_{i}{\Vert }_{2} $, 然后使用 PCA, 在所有数据集中通过保留 98% 能量来减少数据的维度. 保留 98% 能量指的是仅选择满足$\displaystyle\sum\nolimits_{i = 1}^k {{\lambda _i}} / \displaystyle\sum\nolimits_{i = 1}^n {{\lambda _i}} = 0.98$的最大的$k$个特征值对应的特征向量, 其中${\lambda _i}$表示原始数据的协方差矩阵的第$i$大特征值, $n$是总特征值的数量. 这些选定的向量用于组成 PCA 的投影矩阵进行降维.

4.1 在 Extended Yale B 数据集上的实验

Extended Yale B (EYaleB) 数据集包括从 38 名志愿者那里获取的共 2414 张人脸图像, 每位志愿者提供了 59–64 张具有不同光照条件的图像, 此外, 每个人的一半图像包含不同程度的阴影. 在本文的实验中, 每个样本被调整大小为 32×32 像素, 图1 展示了 EYaleB数据集的一些典型样本. 对于所有的比较算法, 我们随机选择每个人的 10、15、20 和 25 个样本作为训练数据, 剩余的样本用于测试, 从表1 可以明显看出, 所提出的方法与其他监督学习方法相比具有优势.

4.2 在 YTC 数据集上的实验

YouTube-Celebrities (YTC) 数据集包括来自 YouTube 的 47 位名人的1910个视频片段. 这些视频来自真实场景, 展示了在面部表情、外貌和姿势上的显著变化, 同时还包含噪音、错位、低画质和遮挡等问题, 每个视频片段包含 8–400 帧, 每个名人由 1000 多张图像表示. 对于本文的实验, 每位名人的 200 张图像被随机选取为实验数据 (即总共9400张图像), 这些人脸图像被统一调整大小为 30×30 像素, 图2 展示了不同个体的一些人脸图像. 我们随机选择每位名人的 15、20、25 和 30 个样本作为训练数据, 剩余的图像作为测试数据. 表2 所示的实验结果表明, 所提出的方法在所有比较算法中表现最佳.

4.3 在 Binalpha 数据集上的实验

该数据集包含分布在 36 个类别中的 1404 个样本, 每个样本由一个大小为 20×16 像素的二进制图像表示. 值得注意的是, 该数据集不仅包括从“0”到“9”的数字, 还包括大写字母从“A”到“Z”, 因此对分类任务构成了挑战, 图3 展示了一些样本图像. 我们随机选择每个类别的 10、15 和 20 个样本作为训练数据, 剩余的作为测试数据, 此数据集上的平均识别结果如表3 所示, 我们可以发现, 与其他监督学习方法相比, 所提出的方法具有优势.

4.4 在 USPS 数据集上的实验

USPS 数据集是一个手写数字图像集合, 包括从“0”至“9”的 10 类, 该数据集包含共 9289 个图像, 每个类别包含不同数量的样本, 从 708 到 1553 个不等. 为了方便分析, 所有图像都已调整大小为 16×16 像素的灰度图像, 因此样本的原始维度为 256, 图4 展示了数据集中的一些样本, 代表了不同的数字. 在我们的实验中, 我们随机选择每个类别的 10、20、30 和 40 个图像作为训练集, 剩余的作为测试集, 表4 表明, 所提出的方法在比较的算法中获得了最高的准确率.

4.5 在 Caltech101 Silhouettes 数据集上的实验

Caltech101 数据集包含 101 个不同类别的物体图像, 每个类别包含 31–798 张图像, 大多数类别大约有 50 张图像, 该数据集中的每个图像都包含一个高质量的多边形轮廓, 勾勒出场景中的主要对象. 在这里, 我们利用了 Caltech101 Silhouettes 数据集, 它专门关注物体轮廓, 以研究每种方法在形状识别中的性能, 在该数据集中, 轮廓被呈现为填充的黑色多边形, 背景为白色. 该数据集包含来自原始数据集的 8641 个样本, 其中每个样本都是一个大小为 16×16 像素的轮廓图像, 图5 提供了原始 Caltech101 数据集中飞机和雷龙的一些样本. 在本文的实验中, 我们从每个类别中随机提取了 10、15 和 20 个样本, 形成3组训练集, 剩余的样本被作为测试集, 从表5 可以看出, 只有 RSLDA 表现略优于所提出的方法.

4.6 在 ETH80 数据集上的实验

ETH80 数据集包括属于 8 个不同类别的物体图像, 包括苹果、汽车、奶牛、杯子、狗、马、梨和番茄, 每个类别有 10 个对象实例, 并且每个对象实例有来自 41 个不同视角的图片, 图6 展示了 ETH80 数据集中的一些样本. 在本文的实验中, 我们将灰度图像调整大小为 20×20 像素, 并将其转换为 400 维向量, 我们随机选择每个类别的 10、20、30 和 40 个图像作为训练集, 剩余的作为测试集. 从表6 呈现的结果中, 可以明显看出所提出方法的优越性能.

4.7 实验结果与分析

根据表1–表6 中呈现的实验结果, 所提出的方法在包括人脸识别、手写识别、形状识别和物体识别在内的所有6个图像数据集上表现出优越的性能. 这表明了所提出方法的普适性, 并且我们从观察中发现了以下有趣的现象.

(1) 保留高维数据的局部结构通常会产生更好的性能. 例如, LPP 胜过 LDA, 因为 LPP 有效地保留了数据的局部结构, 而 LDA 则忽略了这一点. 此外, FOLPP 比 LPP 具有更强的局部保持能力^[47], 从而得到更高的识别率. 另外, 正如本文前面所讨论的一样, 预定义图方法和自适应优化图方法的性能没有显著差异.

(2) 本文提出的方法和 RSLDA 在所有数据集上都能稳定表现出较高的识别率, 而其他方法则无法保持稳定. 例如, SLNP 在 Binalpha 和 ETH80 数据集中, 以及 SN-TSL 在 Binalpha 数据集中, 表现出较差的识别率. 原因在于所提出的方法和 RSLDA 通过在投影学习过程中考虑数据重建来有效地保留数据的主要成分.

(3) 在大多数情况下, 所提出的方法优于 RSLDA. 这是因为我们的方法不仅保留了基于距离的邻域, 而且自适应地学习了局部稀疏自表示, 丰富了数据的局部拓扑结构的描述. 相比之下, RSLDA 忽略了这个对于有效分类至关重要的结构. 这表明我们方法中的局部保持增强策略的确有助于保持数据的局部内在结构.

(4) 在ETH80数据集上使用 LADA、SLNP 和 ALLDA 时, 需要预先消除全局散布矩阵${S_t}$的零空间, 或者对矩阵${S_t}$的逆矩阵施加正则化扰动. 相比之下, 所提出的方法绕过了这些要求, 并且不需要任何特定的数据预处理步骤, 这说明了所提出方法没有小样本 (small sample size, SSS) 问题.

总之, 实验结果表明了我们所提出的方法在各种图像识别任务中的有效性和泛用性.

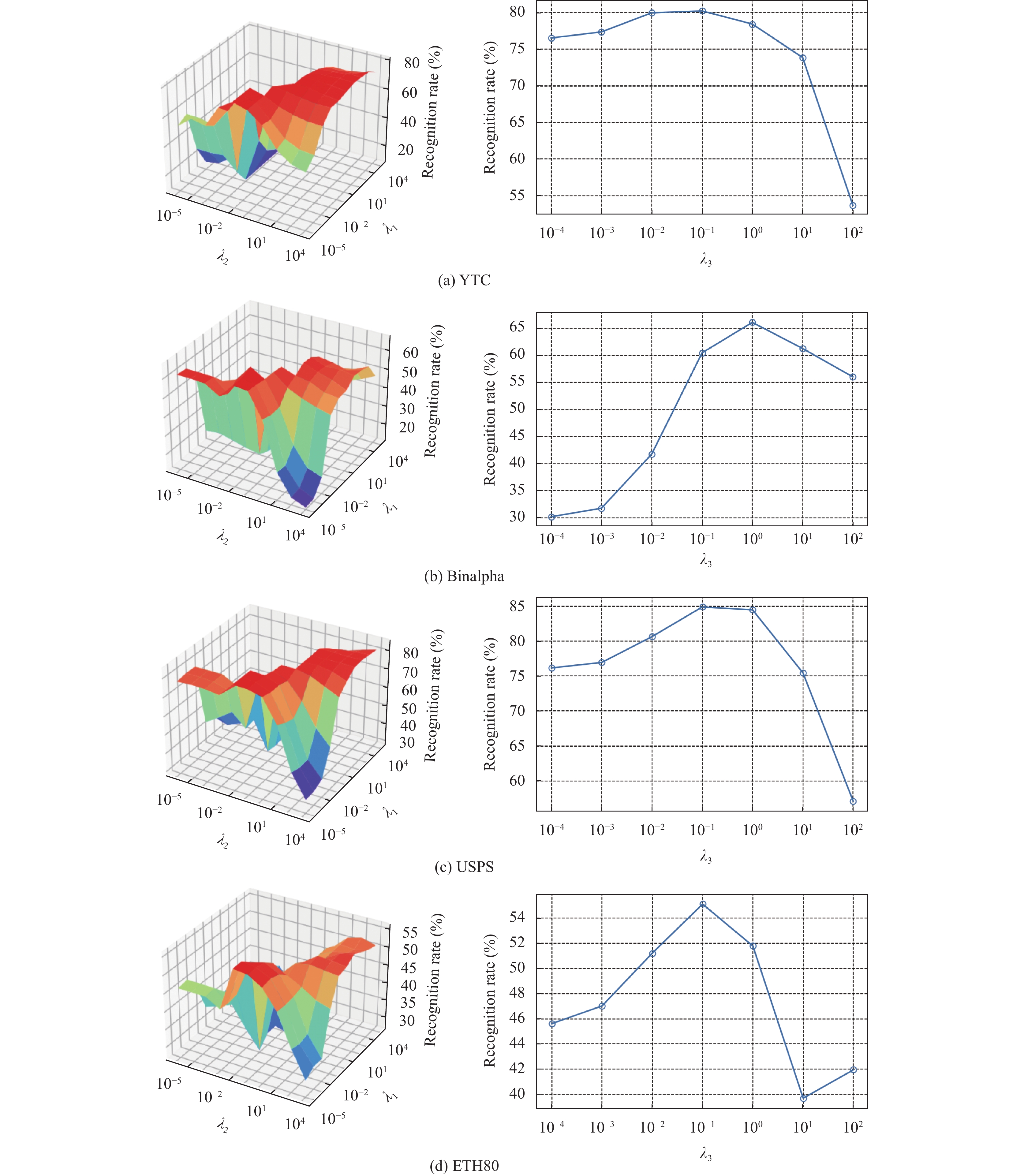
4.8 参数敏感性研究

目标模型(20)的分类性能可能会受到4个可调整参数的影响, 即${\lambda _1}$、${\lambda _2}$、${\lambda _3}$和$k$. 然而, 自适应地选择合适的参数仍然是一个开放问题, 到目前为止尚未提出有效的解决方案.

在本节中, 我们测试不同参数组合下的分类准确率, 来分析这4个参数的影响. 通过实验, 我们观察到${\lambda _3}$和$k$对其他参数的影响较小. 因此, 我们独立确定它们的值. 然而${\lambda _1}$和${\lambda _2}$表现出一定的互相关性, 因此我们进行了网格搜索, 以确定这两个参数的最佳值. 具体来说, ${\lambda _1}$和${\lambda _2}$从$\{ {10^{ - 5}}, {10^{ - 4}}, {10^{ - 3}}, {10^{ - 2}}, 0.1, 1, 10, {10^2}, {10^3}, {10^4}\} $中选择, ${\lambda _3}$从$\{ {10^{ - 4}}, {10^{ - 3}}, {10^{ - 2}}, 0.1, 1, 10, {10^2}\} $中选择, 而$k$从$\{ 1, 2, 3, \cdots, 8, 9\} $和${n_c} - 1$中选择, 其中${n_c}$表示训练集中每个类别的样本数. 图7 展示了在4个数据集上不同参数组合下所提出算法的性能. 对于 YTC 数据集, 在${\lambda _1} \in \{ {10^{ - 5}}, {10^{ - 4}}\} $, ${\lambda _2} \in \{ {10^{ - 2}}, 0.1\} $和${\lambda _3} \in \{ {10^{ - 2}}, 0.1\} $时获得最佳性能. 对于 Binalpha 数据集, 最佳值为${\lambda _1} \in \{ {10^{ - 4}}, {10^{ - 3}}\} $, ${\lambda _2} \in \{ {10^{ - 2}}, 0.1\} $和${\lambda _3} = 1$. 对于 USPS 数据集, 最高识别率在${\lambda _1} \in \{ {10^{ - 5}}, {10^{ - 4}}\} $, ${\lambda _2} \in \{ {10^{ - 2}}, 0.1\} $和${\lambda _3} \in \{ 0.1, 1\} $时获得. 最后, 对于 ETH80 数据集, 当${\lambda _1} \in \{ {10^{ - 5}}, {10^{ - 4}}\} $, ${\lambda _2} \in \{ {10^{ - 2}}, 0.1\} $和${\lambda _3} = 0.1$时, 获得最佳性能. 图8 显示了在 YTC、Binalpha、USPS 和 ETH80 数据集上选择的邻域样本数与识别率之间的关系. 在大多数情况下, $k$的最优值相对较小.

4.9 对维度敏感性的研究

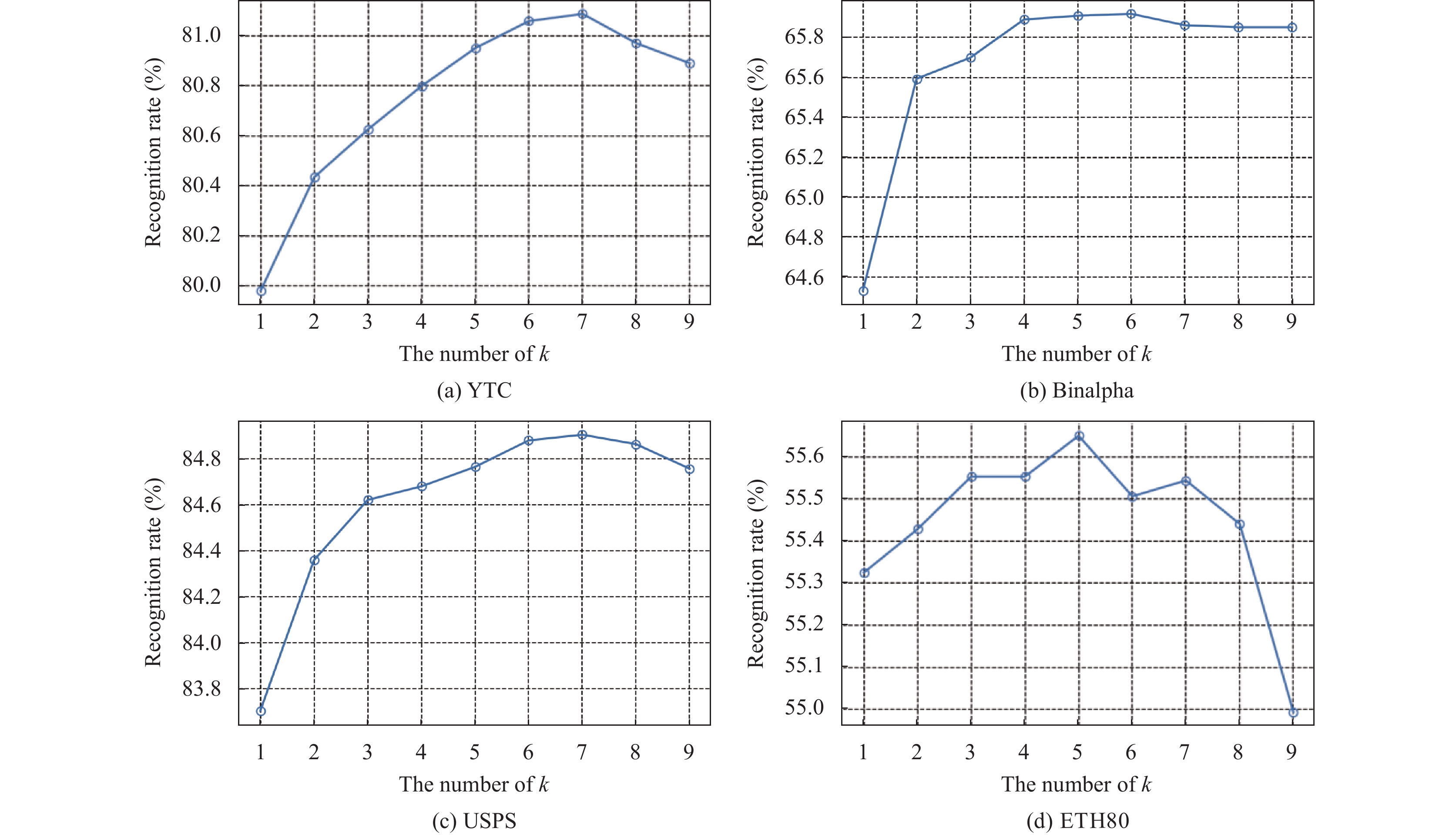
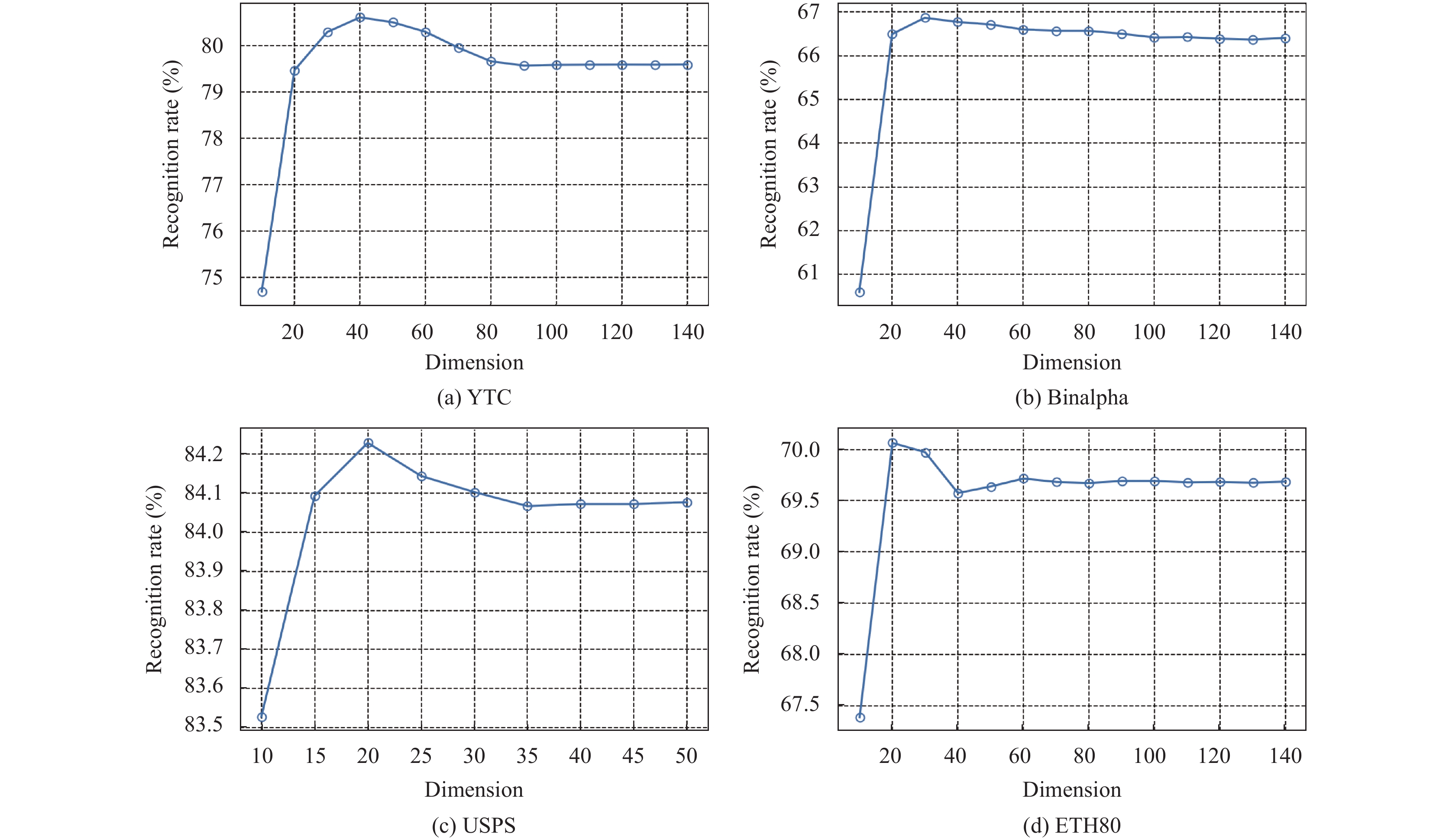
为了进行特征提取, 我们在4个不同的数据集上分别评估了所提出方法在各种维度下的性能. 图9 展示了识别率与降维后维度之间的关系. 从图9中可以观察到, 只要不设定过低的维度, LPP_SRL 在各种特征维度上都能表现出一致且可观的性能. 在表1–表6 的实验结果中, 我们对所有除了 SN-TSL 外的方法设定了统一的子空间维度, 在 EYaleB、YTC、Binalpha、USPS、Caltech101 Silhouettes 和 ETH80 数据集上分别为 80、40、50、25、50 和 20. 对于 SN-TSL, 降维后的维度则始终设置为$c$, 其中$c$对应于训练样本中的类别数.

4.10 收敛性研究

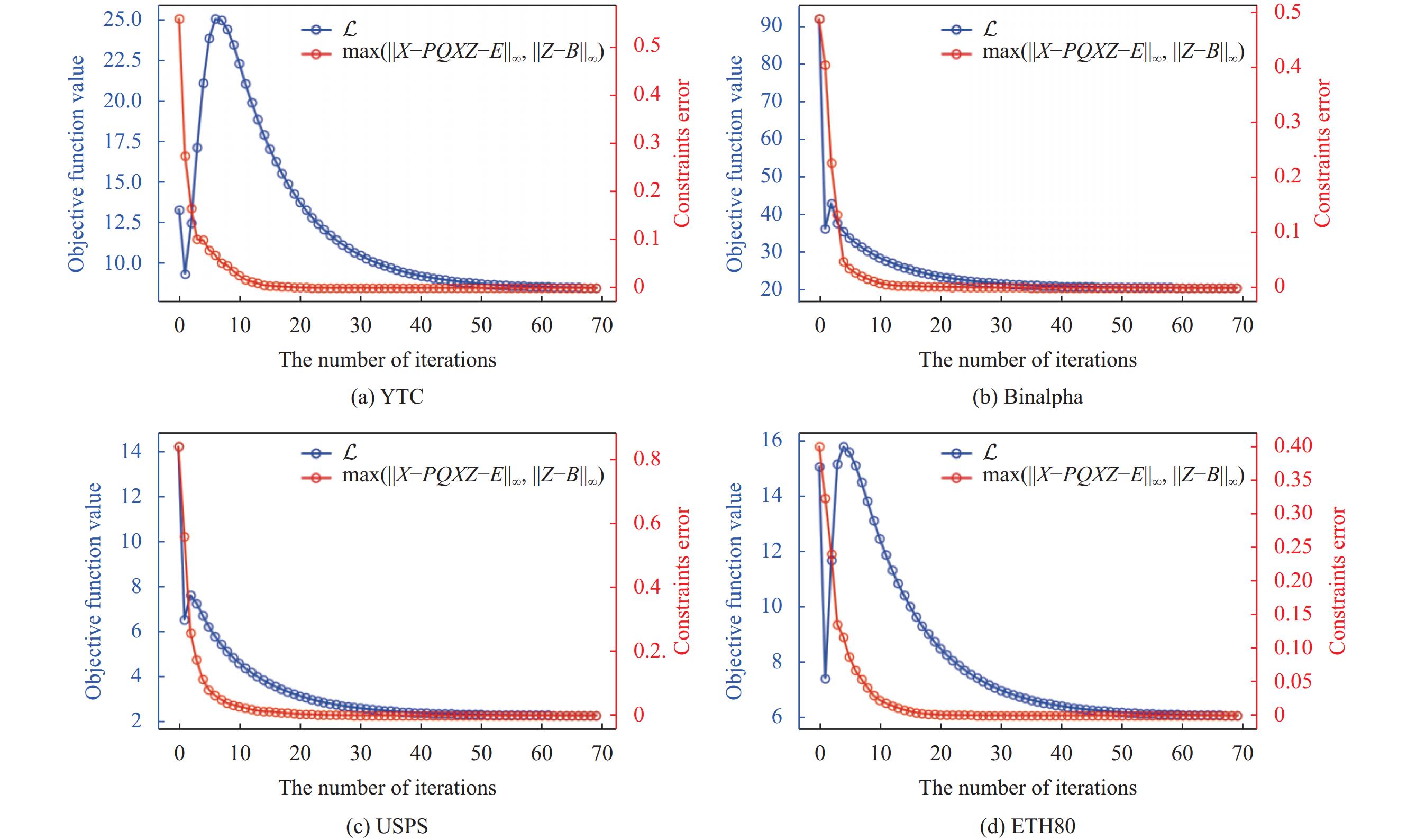
在本节中, 我们从实验的角度展示了所提出方法的收敛性, 在 YTC、Binalpha、USPS 和 ETH80 这4个数据集上进行了实验. 图10 显示了模型在4个数据集的不同迭代次数下的目标函数值和约束误差. 从中可以观察到, 所提出的学习模型 (20) 的目标函数损失和约束误差稳步减小, 并最终趋于稳定. 这一观察结果表明我们设计的优化算法表现出了良好的收敛特性.

5 结论

本文提出了一种监督降维方法, 通过潜在稀疏表示学习增强了局部保持投影的性能. 本文将保持邻域结构和局部稀疏自表示集成到统一框架中, 解决了传统方法的局限性, 并丰富了数据的局部拓扑结构描述.

在稀疏自表示模块中, 本文使用重建样本作为字典, 并将其与投影学习相结合, 以有效捕获数据的主要成分、消除冗余特征和去除噪声. 通过高效的迭代算法和在多个公开可用数据集上的实验, 所提出的方法在降维方面表现出了出色的性能. 对于未来的工作, 我们计划设计一种不基于任何假设的图学习方法, 并进一步将其整合到我们的方法中, 以增强其在不同场景下的泛化能力.