区块链是一种去中心化、无需信任的分布式账本, 允许网络中所有节点通过共识算法和加密算法管理相同的数据[1]. 随着区块链技术的不断进步, 其已被广泛应用于商品溯源[2]、智能交通[3]、物流监管[4]等多个领域. 然而, 这些应用大多基于不同的场景和设计理念, 区块链之间的孤立性、封闭性以及链与链之间的高度异构化, 影响了数据流通和价值转移, 成为阻碍区块链技术广泛发展的瓶颈. 为了解决这一挑战, 跨链技术应运而生[5]. 这种允许不同区块链系统之间进行信息互通的技术, 为多个区块链平台之间的信息流动提供了可能性, 使得多样化的服务得以跨平台提供[6]. 随着跨链技术的发展, 不同区块链系统之间信息互通的需求日益增长, 数据共享和和互操作性已成为常规需求[7]. 例如, 车联网需要车辆间的数据共享, 医疗领域要管理患者医疗数据, 金融领域需要构建更高效透明的支付系统以提升跨境支付和结算的速度, 客户信用评估需要数据计算等[8].
然而在实际的区块链应用中, 账本的公开透明性对链上的数据安全造成了威胁. 在跨链交互过程中, 因涉及多链数据传输与交换, 导致用户个人隐私及交易数据泄露的风险更高, 如何保护跨链数据隐私正成为研究热点之一. 按照康海燕等[9]提出的分类, 区块链的数据隐私主要包括身份隐私和交易隐私两种类型. 身份隐私指区块链系统中用户匿名性问题, 即用户身份信息与区块链账户地址的关联; 交易隐私则指存储在区块链的交易记录及相关信息, 包括交易金额和交易双方信息等. 在跨链系统中, 跨链交易涉及多个不同区块链网络, 不同链系统的架构和实现数据隐私的方式可能存在差异, 也增加了隐私保护问题的复杂性和难度. 本文着重研究跨链场景中的交易隐私问题.
针对上述问题, 学术界对跨链隐私的研究主要集中在同态加密、零知识证明、代理重加密等方面. Cai等[10]提出了一种基于Paillier同态加密的跨链资产交易隐私保护新方法, 在隐私保护过程中利用Paillier同态加密代替哈希加密, 解决了整个跨链交易过程中身份隐私信息泄露的主要问题, 但对于跨链交易金额的隐私安全性有所欠缺. Yang等[11]提出了一种基于零知识证明算法和混币技术的跨链隐私保护协议, 该协议改变了认证机制, 利用组合生成函数来映射交易中的虚拟外部地址, 允许实现快速跨链匿名交易, 但会面临中间人攻击的问题. 薛庆水等[12]提出了一种基于条件代理重加密的跨链数据共享方案, 通过随机选择的公证人执行条件代理重加密, 实现密文由提供者解密转变为请求者解密, 同时确保密钥由提供者生成 , 但存在一定的中心化风险. Yin等[13]提出了Bool网络, 该平台利用多方计算来协作创建支持的每个区块链上的账户, 并利用阈值签名方案来联合签名跨链交易. 但可信执行环境的异构性意味着如果部分可信执行环境芯片遭受侧信道攻击, 仍然存在潜在的安全风险. Li等[14]提出了一个旨在保证交换公平的密钥交换机制, 以及通过CP-SNARK验证机制来确保交易得到确认而不泄露交易细节的方法. 然而, 当一个链的隐私受到侵犯时, 可能会影响到其他链的隐私.
同态加密是一种能够在不解密数据的情况下对密文进行操作的加密技术, 从而对数据隐私起到重要的保护作用. 根据相关研究[15], 同时实现加法和乘法的全同态加密难度较大, 相比之下, 仅实现加法或乘法的其中一个性质的半同态加密算法具有更高的效率, 且适用范围更广. 目前, 常见的半同态加密算法包括RSA、ElGamal和Paillier. 而RSA和ElGamal算法基于乘法同态性质, 这导致了验证交易后余额正确性方面存在一定局限性. 在区块链交易中通常需要验证交易余额, 这种验证涉及加法运算, 故选择具有加法同态属性的Paillier算法更为合适, 因此本文以Paillier算法作为跨链交易隐私保护方案的基础. 密码学算法的安全性取决于密钥管理的严谨性, 私钥的安全管理至关重要. 任何泄露或不当使用都可能导致严重的隐私数据泄露和系统安全威胁. 因此对密钥的安全管理和保护显得尤为重要.
目前主流的公证人机制、哈希锁定机制等跨链技术在实现区块链网络互操作性方面取得了进展, 但都存在局限性. 公证人机制是指引入一个或多个可信实体作为公证人, 以听取和响应链上事件. 可能产生中心化的信任问题和单点故障风险, 拥有较大的权力和控制权, 从而降低系统的公正性和可信度[16–18]. 哈希锁定机制旨在通过设置时间和解锁条件来实现跨区块链交易的安全性和原子性, 但缺乏跨链合约可能导致交易条件泄露, 存在超时和数据传输失败造成资产损失的风险, 所以它的使用场景有限[19]. 中继链则被视作是一种去中心化的公证人机制, 无需第三方介入, 通过链间通信协议和数据传输机制, 在保护用户隐私的同时, 保持交易信息的完整性和可验证性[20]. 通过利用中继链技术, 能够在不同区块链间安全地传输加密信息, 同时通过加密技术保障数据隐私[21]. 本文方案采用中继链进行跨链交互, 主要关注合约层, 通过跨链合约部署实现在链下加密. 跨链合约的主要功能是发起交易, 使用密文作为交易内容, 并通过嵌入智能合约形式构建跨链节点, 即使应用节点彼此不信任, 也能在跨链合约的控制下安全地进行数据交互[22].
基于上述分析, 本文提出了一种基于改进Paillier同态加密和中继链技术的跨链交易数据隐私保护方案, 旨在提高交易数据的隐私性和安全性. 主要工作如下.
(1) 对已有Paillier算法进行了针对浮点数的重新设计. 提出一种支持浮点数的同态加密跨链交易数据隐私保护方案, 实现了对跨链交易金额的隐私保护.
(2) 设计了一种基于Shamir秘密共享的私钥共享机制. 针对改进的Paillier同态加密私钥管理不当或丢失问题. 该机制在实现对私钥份额抗篡改的同时, 有效防止了节点的串谋行为, 确保了同态加密私钥的完整性和安全性.
(3) 对所提出的方案进行了安全性分析和实验验证. 结果表明, 该方案能够有效保护跨链场景下的交易数据隐私.
1 预备知识 1.1 Paillier同态加密本文使用Paillier算法作为同态加密算法来设计方法. 相关的理论知识如下[23–25].
(1) 算法构成
1) 密钥生成. 随机选择两个大素数
| g=1+n,λ=φ(n),u=φ(n)−1modn | (1) |
2) 加密. 对于任意明文消息
| c=gm⋅rn(modn2) | (2) |
3) 解密. 输入密文
| m=L(cλmodn2)⋅μmodn | (3) |
注意解密使用
(2) 同态性
给定两个密文
| c1=Encpk(m1),c2=Encpk(m2) | (4) |
1) 定义密文之间的加法运算
| c1⊕c2=c1c2modn2=(gm1.rn1modn2)(gm2.rn2modn2)=gm1+m2⋅(r1r2)nmodn2 | (5) |
因此
2) 给定
| a⊗c=camodn2=gam⋅(ra)nmodn2=Encpk(a⋅mmodn) | (6) |
因此,
可验证随机函数(verifiable random function, VRF)是一种具有验证性质的随机数生成器, 是一个密钥相关函数, 将输入映射到一个随机的输出, 并且可以生成一个证明, 证明输出确实是由特定的输入和密钥生成的[13].
(1) 参数生成
合约中的参数生成阶段, 一个VRF系统需要生成一对公私钥. 合约中的公钥可以被外部验证者获取合约中使用
| VRF.GenerateKeyPair()→(publicKey, privateKey) | (7) |
(2) 输入与输出
对于合约中的输入input, 通过VRF生成函数生成随机数和相应的证明. 其中, 生成函数接受输入和私钥, 返回随机数和证明:
| VRF.Verify(publicKey, input,randomValue, proof)→ 0/1 | (8) |
(3) 验证
外部验证者通过合约中的公钥、输入、生成的随机数和证明来验证随机数的有效性:
| VRF.Verify(publicKey, input,randomValue, proof)→ 0/1 | (9) |
Shamir秘密共享方案是一种安全的密钥分发方法. 其允许分享者将一个秘密分割成多个私钥份额分配给参与者. 阈值参数为
(1) 选择一个大质数
| f(x)=a0+a1x+a2x2+⋯+at−1xt−1 | (10) |
(2) 通过在多项式
(3) 在原始数据恢复过程中, 获得
| s=t∑j=1f(j)t∏i≠j,i=1k−ij−i | (11) |
在不同区块链系统之间进行交互时, 确保敏感数据不被泄露至关重要. 以金融领域为例, 当银行A需要从银行B中跨链获取客户的存款余额以了解客户在两个银行的总存款额时, 如何在不暴露敏感数据的情况下有效交互显得尤为重要, 因此本文提出了一种支持浮点数的Paillier同态加密隐私保护方案.
2.1 Paillier算法的改进Paillier同态加密的加密过程通过模运算得到密文. 因此, 只能处理整数明文和密文, 而无法对浮点数进行加密. 为了符合银行交易中浮点数运算的特性, 本文提出了一种改进的Paillier同态加密算法, 保留了原算法的加法同态性质, 并支持浮点数的加法运算. 与传统的模运算不同, 本文方案支持使用任意次数的加法运算, 进一步提高了加密算法的灵活性和适用性.
对全局的公钥设置为
(1) 生成密钥过程
1) 将明文和密文划分为明文集合m1–mk和密文集合c1–ck, 用加密算法得到
2) 使用原Paillier算法生成公钥
3) 随机生成浮点数
(2) 明文加密过程
1) 随机选择正整数
| Mt(Mt=(p+1)×Ltp) | (12) |
其中,
2) 根据VRF生成干扰因子
3) 用
| Lci=EncPaillier(ti) | (13) |
4) 获取浮点数
| Rci=gmi×rhti | (14) |
5) 对明文
| ci=(Lci,Rci) | (15) |
(3) 密文解密过程
1) 用
| DecPaillier(Lci)=L(tλimodn2)⋅μ=L((gtirnmodn2)λmodn2)⋅λ−1=λ⋅ti⋅λ−1=ti | (16) |
2) 使用浮点数
| DecPaillier(Rci)=DecPaillier(gmi×rhti)=loggRcihtir=mi | (17) |
(4) 加法同态过程
1) Paillier具备加法同态, 因此有:
| EncPaillier(t1)EncPaillier(t2)=EncPaillier(t1+t2) | (18) |
| EncPaillier(t1)EncPaillier(−t2)=EncPaillier(t1−t2) | (19) |
2)
| gm1×rht1×gm2×rht2=g(m1+m2)×rht1+t2 | (20) |
| gm1×rht1÷gm2×rht2=g(m1−m2)×rht1−t2 | (21) |
3) 对密文
| c3=(Lc3,Rc3)=(EncPaillier(t1+t2),g(m1+m2)×rht1+t2) | (22) |
| c4=(Lc4,Rc4)=(EncPaillier(t1−t2),g(m1−m2)×rht1−t2) | (23) |
4) 对
| t1+t2=DecPaillier(Lc3)=DecPaillier(t1+t2) | (24) |
| DecPaillier(Rc3)=(loggRc3hDecPaillier(Lc3))r=loggRc1ht1+loggRc2ht2r=m1+m2 | (25) |
5) 同理, 对
| t1−t2=DecPaillier(Lc4)=DecPaillier(t1−t2) | (26) |
并将干扰因子
| DecPaillier(Rc4)=(loggRc4hDecPailler(Lc4))r=loggRc1ht1−loggRc2ht2r=m1−m2 | (27) |
原Paillier算法是针对整数的, 本文方案为了支持浮点数运算, 使用浮点数
在明文加密和解密过程中, 干扰因子扮演着重要角色. 干扰因子是一个随机生成的正整数, 在加密时与明文相结合, 使得同样的明文每次加密都会产生不同的密文, 增强了加密的随机性和安全性. 在解密过程中, 干扰因子用于解密密文的一部分, 同时确保只有持有正确的私钥才能解密出明文的小数部分. 干扰因子通过VRF生成, 保证了其随机性和可验证性, 使得外部验证者或智能合约可以验证其有效性, 从而提高了加密的安全性.
2.2 系统模型方案涉及3种实体: 应用链、跨链网关和中继链. 应用链是跨链交易的主体区块链, 能够与其他应用链进行跨链交互, 执行特定的应用业务逻辑. 通过采用统一的跨链数据格式和标准化的跨链合约接入跨链交互中. 跨链网关负责在区块链网络中收集和传播跨链交易, 监控应用链和中继链上的跨链请求, 进行跨链交易转发, 支持应用链与中继链之间的消息交互. 中继链是跨链服务平台, 管理连接的应用链, 提供可信验证和可靠路由等服务, 以支持跨链交易的进行. 系统模型见图1.
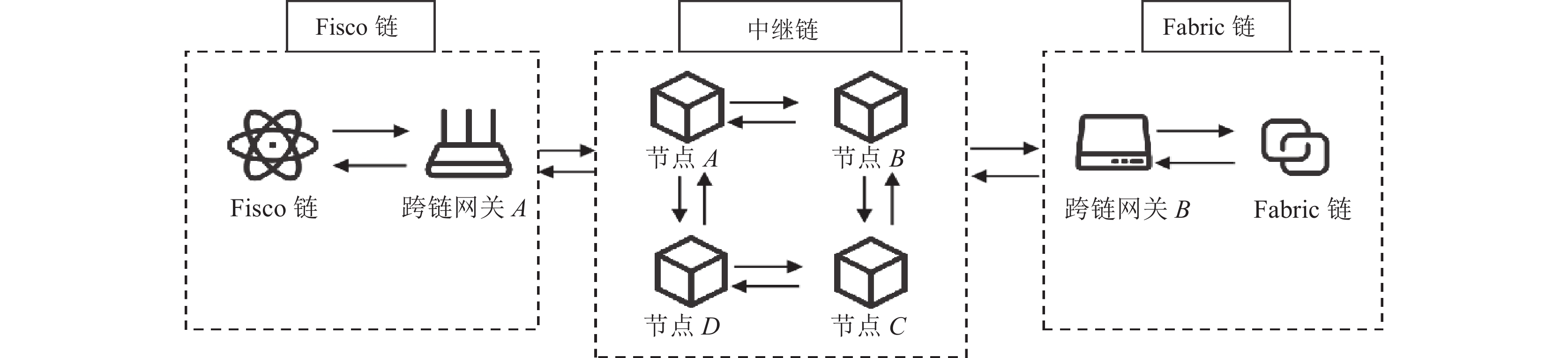
|
图 1 跨链系统模型 |
2.3 方案流程
在本文中银行A选择采用Fisco链, 银行B选择采用Fabric链. 本节给出了基于上述系统模型的隐私保护方案流程. 在第3.2节会比较两种区块链性能.
步骤1: 每个银行部署自己的应用链.
步骤2: 中继链部署.
步骤3: 应用链跨链合约部署.
步骤4: 启动跨链网关.
步骤5: 在成功部署两条应用链后, 发起跨链交易请求. 以id为appchain1的Fabric链和id为appchain2的Fisco链为例, 银行A到银行B的交互过程如下.
(1) 银行A在Fisco链上通过Paillier算法生成的密钥, 加密用户A的金额信息amount, 发起跨链交易
| T1=set(UsernameA,EncPaillier (amountA))={Hash,Status,BlockNumber, Receipt,Timestamp} | (28) |
同理, 银行B在Fabric链上发起跨链交易
| T2=set(UsernameB, EncPaillier (amountB))={Hash,Status,BlockNumber, Receipt,Timestamp} | (29) |
(2) 银行A向银行B发起跨链交易
| T3=get(BitxHubid+Fiscoid+Fiscobrokeraddress,UsernameB)={Hash,Status,BlockNumber,Receipt,Timestamp} | (30) |
(3) 银行B在收到银行A的请求消息后发起交易
| T4=invokeInterchain(srcid,destid,index,type,callFunc,arg,txStatus,isEncrypt)={Hash,Status,BlockNumber,Receipt,Timestamp} | (31) |
(4) 银行B发起交易
| T5=invokeReceipt(srcid,destid,index,type,result,txStatus)={Hash,Status,BlockNumber,Receipt,Timestamp} | (32) |
(5) 银行A通过getData方法发起交易
| T6= getData(UsernameB)={Hash,Status, BlockNumber, Receipt,Timestamp} | (33) |
(6) 银行A对收到的密文进行解密, 并根据改进的Paillier加同态的性质, 对交易金额正确性进行验证, 即验证银行A的当前账户金额加上交易金额是否等于交易完成后的账户余额, 即式(34)是否成立.
| EncPaillier(SumA)=EncPaillier(amountA)+EncPaillier(amountB) | (34) |
在跨链场景中, 中继链需要记录来自不同应用链的请求. 所有跨链交易对于已加入中继链跨链系统的应用链来说都是可见的. 如果应用链用户发起的跨链交易带有隐私数据, 隐私数据很容易泄露. 为防止中继链节点获取私钥并进一步获取交易详细信息, 本文提出在应用链上使用私钥对交易进行加密. 然而这种加密方式存在潜在的风险, 即私钥管理不当或丢失可能导致私钥被泄露, 从而威胁交易的隐私和安全性. 因此引入一种应用链私钥共享机制是必要的. 通过去中心化的方法共同维护同态加密的私钥, 可以有效防止私钥受到单个节点攻击的风险.
在本节中, 使用Shamir秘密共享方案来实现私钥共享. 考虑到节点的不可信, 有可能发送恶意私钥份额, 且节点可能因掉线或离开网络而导致私钥份额丢失. 为了防止串谋行为, 设置了更新Shamir秘密共享方案的机制. 通过这种方式, 即使部分节点受到攻击或处于离线状态, 仍能保证私钥的安全性和可靠性, 确保交易数据的完整性和隐私性. 应用链中的节点充当参与方, 假设应用链共有
步骤1: 在系统初始化的过程中, 密钥生成中心生成私钥
| {fλi(x)=λ×v+h(v)+a1x+a2x2+⋯+at−1xt−1h(v)=a1v+a2v2+a3v3fμi(x)=μ×v+g(v)+b1x+b2x2+⋯+bt−1xt−1g(v)=b1v+b2v2+b3v3 | (35) |
其中,
为了应对可能的恶意节点尝试恢复私钥的情况, 增加了抗篡改机制. 通过验证私钥份额来确保在分发过程中私钥份额未被篡改. 具体而言, 跨链网关在分发过程中为每个私钥份额添加了一个ECDSA数字签名, 有助于阻止恶意节点对密钥进行篡改, 从而加强了系统对私钥管理过程的信任度.
步骤2: 跨链网关对应用链节点
步骤3: 如果发起的交易存在争议或私钥丢失, 跨链网关会执行恢复私钥
(1) 跨链网关收到来自应用链的参与者
| {λ′=∑tj=1fλi(j)∏ti≠j,i=1k−ij−i−h(v)vμ′=∑tj=1fμi(j)∏ti≠j,i=1k−ij−i−g(v)v | (36) |
跨链网关由式(36)通过对私钥份额进行加权和, 重建同态加密私钥
(2) 在动态加入的情况下, 当新的参与者加入时, 无需修改现有参与者的私钥份额, 且秘密多项式
(3) 在动态离开的情况下, 对于参与者的离开, 若不重新计算其他私钥份额, 剩余参与者仍可以用原有的秘密多项式重新构建私钥. 但若离开的参与者私钥份额泄露, 整个私钥可能受到威胁. 此时更新版本号
| {fλi(x)′=fλi(x)+λ×v2−λ×v1+a1v2+a2v22+a3v32−a1v1−a2v21−a3v31fui(x)′=fui(x)+μ×v2−μ×v1+b1v2+b2v22+b3v32−b1v1−b2v21−b3v31 | (37) |
本文方案通过改进Paillier同态加密算法来支持浮点数运算, 对跨链交易金额进行加密, 保护跨链交易数据隐私. 同时基于Shamir秘密共享方案对改进算法的私钥进行管理, 增强了私钥的安全性. 本节对方案进行了分析和验证, 验证方案的安全性和可行性.
3.1 安全性分析定理1. 在改进的Paillier算法私钥未泄露的前提下, 攻击者不能对加密后的密文进行篡改.
证明: 改进的Paillier密文
定理2. 如果应用链用户发起的跨链交易中带有隐私数据, 中继链节点不可能获取私钥并进一步获取交易详细信息.
证明: 在私钥共享机制中, 私钥首先通过Shamir秘密共享方案分割成多个私钥份额, 通过跨链网关分发给应用链节点
本文实验环境为Intel(R) Core(TM) i5-7300HQ CPU, 内存为16 GB的Windows 10系统, 运行操作系统为Ubuntu 20.04 LTS. 采用Fabric链和Fisco链构建底层应用链, 在腾讯云服务器进行部署. 采用BitXHub系统提供的跨链网关进行中继链和应用链之间通信.
本文方案评估跨链系统性能的指标包括同时执行操作的账户个数和改进Paillier算法的执行时间. 主要测试不同操作在跨链系统中所需的处理时间. 将原Paillier算法的执行时间作为基准, 对比本文方案中执行相同类型操作的Paillier算法所需时间. Paillier算法的执行过程包括密钥生成、加密、密文操作和解密. 考虑到密钥生成在方案中运行次数有限, 因此不对其进行测试. 针对测试的银行数据最多为12位整数和2位小数, 根据位数和整数, 浮点数的区别, 进行了
从图2–图4可以看出, 随着整数位数增加, 整数平均加密, 解密和加法运算时间略有波动, 表明算法在处理不同位数的整数数据时能够保持稳定性. 由于本文方案改进的Paillier算法使用可验证随机函数VRF生成干扰因子, 并使用智能合约验证, 使得几乎所有阶段消耗时间都比原Paillier算法长, 但这种延迟时间完全在可接受范围内.
本文方案改进的Paillier算法不仅支持对整数进行同态加密, 还能直接对浮点数进行加解密和同态计算, 无需先将浮点数转换为整数再进行计算, 从而提高了运算效率. 由于不涉及模幂运算, 该算法支持任意次数的加法运算. 在进行多次浮点数的加法操作时, 算法显示出高效性和稳定性. 根据图5所示的实验结果, 浮点数加密、解密和加法运算的平均运行时间并没有随着位数的增加呈现线性增长的趋势, 表明算法对于不同位数的浮点数计算效率相对稳定.
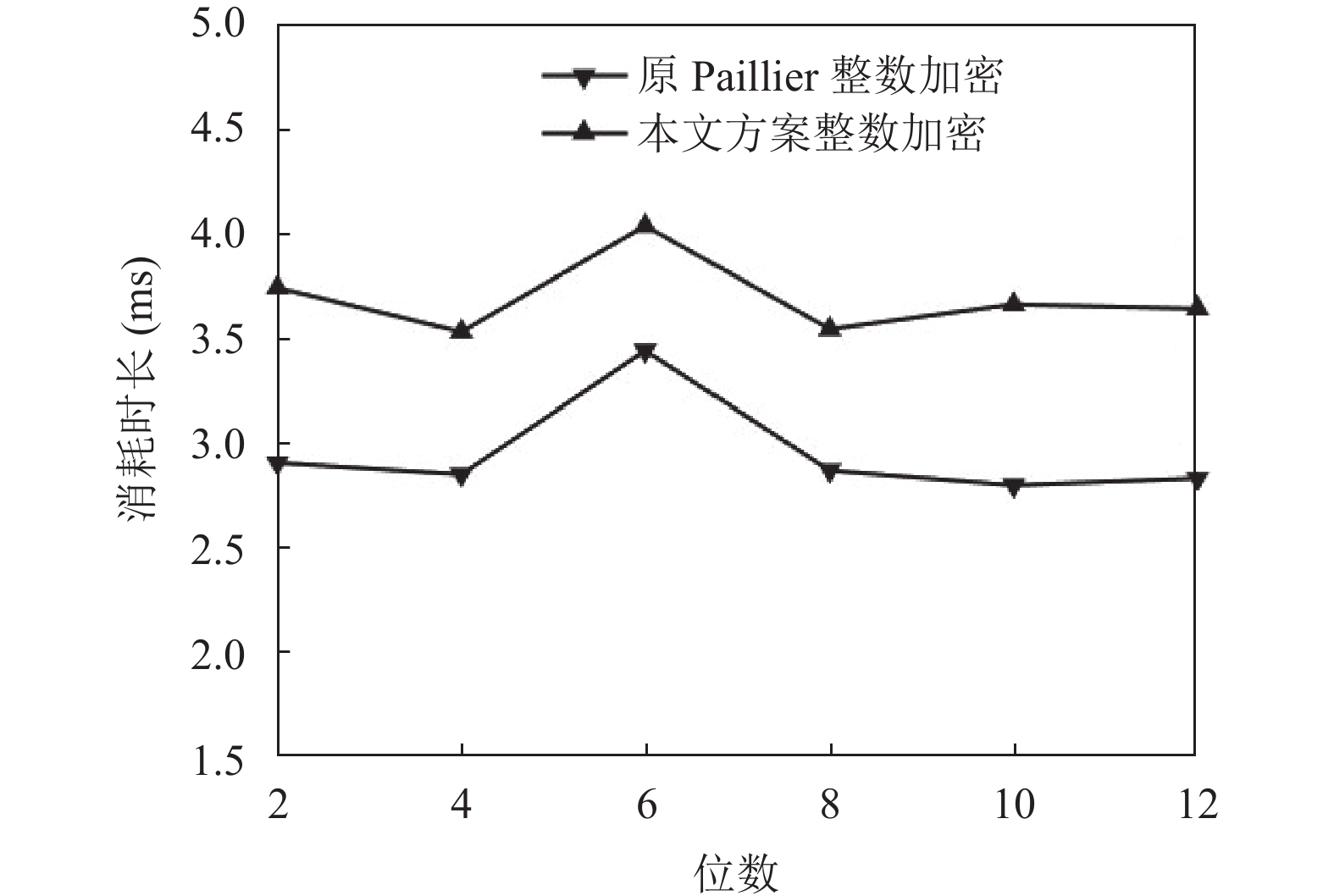
|
图 2 整数平均加密时间 |

|
图 3 整数平均解密时间 |

|
图 4 整数加法运算平均时间 |
本文方案采用Fisco链和Fabric链进行跨链测试. 如图6和图7所示, 随着账户个数的变化, Fisco链上的Paillier算法在吞吐量方面优于Fabric链, 然而跨链交易的吞吐量较低且延迟较高. 随着账户个数的增加, 吞吐量下降, 延迟增加. 在跨链网络中, 跨链交易会引入一定程度的延迟, 但延迟时间完全在可接受的范围内. 总体而言, 本文方案表现出可用性和稳定性, 能够确保数据隐私的同时实现安全的跨链交互. 这使得银行可以获取必要信息而不泄露敏感数据.

|
图 5 浮点数平均运行时间 |
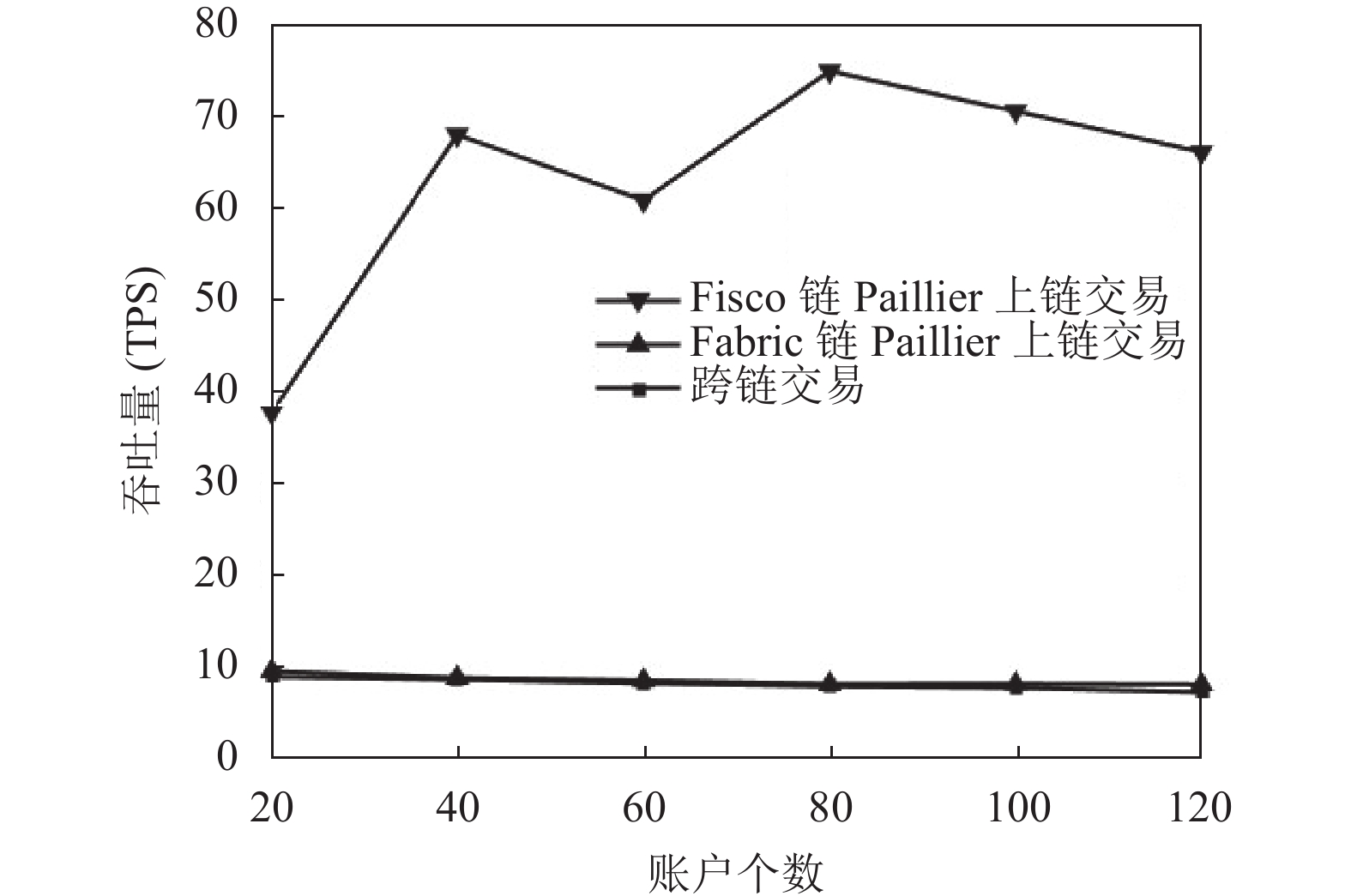
|
图 6 账户个数对吞吐量的影响 |
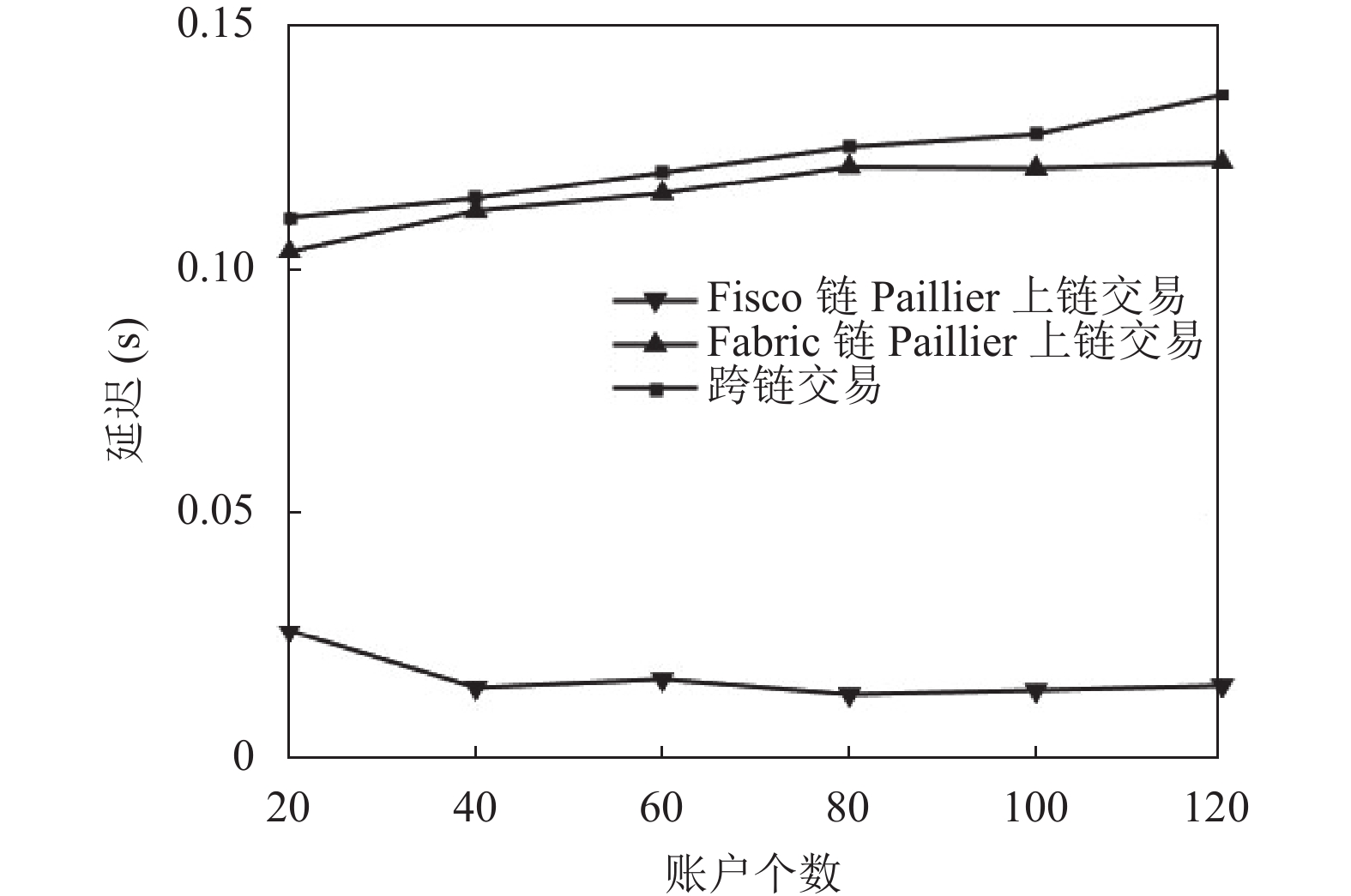
|
图 7 账户个数对延迟的影响 |
4 结论
本文提出了一个基于同态加密的跨链交易数据隐私保护方案. 该方案采用支持浮点数加密的Paillier同态加密算法, 对跨链交易金额进行加密, 使跨链过程中的隐私数据以密文形式出现, 有效确保了交易数据在跨链过程中的隐私安全. 为了防止同态加密私钥管理不当或丢失的情况, 引入了基于Shamir秘密共享的私钥共享机制. 通过使用ECDSA数字签名验证私钥份额, 可以防止其在分发过程中被恶意篡改. 此外, 更新节点加入和离开的份额有助于防止节点串谋, 提升私钥管理的安全性. 安全性分析和实验验证表明, 所提出的方案有效保护了对跨链交易中的隐私数据.
| [1] |
Huang HW, Kong W, Zhou SC, et al. A survey of state-of-the-art on blockchains: Theories, modelings, and tools. ACM Computing Surveys, 2021, 54(2): 44. DOI:10.1145/3441692 |
| [2] |
张帅, 项伟. 基于区块链对溯源数据的多方共享系统. 计算机系统应用, 2022, 31(6): 394-399. DOI:10.15888/j.cnki.csa.008569 |
| [3] |
穆蕾, 安毅生, 肖玉坤. 基于联盟区块链的电动汽车可信充电模型. 计算机系统应用, 2023, 32(2): 119-127. DOI:10.15888/j.cnki.csa.008984 |
| [4] |
肖梦雪, 左力, 徐志锟, 等. 基于区块链的铁路电子提单系统. 计算机系统应用, 2022, 31(9): 145-151. DOI:10.15888/j.cnki.csa.008650 |
| [5] |
李芳, 李卓然, 赵赫. 区块链跨链技术进展研究. 软件学报, 2019, 30(6): 1649-1660. DOI:10.13328/j.cnki.jos.005741 |
| [6] |
何全文, 林庆新, 林晖, 等. 基于跨链的医疗数据安全共享方案. 计算机系统应用, 2023, 32(5): 97-104. DOI:10.15888/j.cnki.csa.009087 |
| [7] |
曾诗钦, 霍如, 黄韬, 等. 区块链技术研究综述: 原理、进展与应用. 通信学报, 2020, 41(1): 134-151. DOI:10.11959/j.issn.1000-436x.2020027 |
| [8] |
祝烈煌, 高峰, 沈蒙, 等. 区块链隐私保护研究综述. 计算机研究与发展, 2017, 54(10): 2170-2186. DOI:10.7544/issn1000-1239.2017.20170471 |
| [9] |
康海燕, 邓婕. 区块链数据隐私保护研究综述. 山东大学学报(理学版), 2021, 56(5): 92-110. DOI:10.6040/j.issn.1671-9352.0.2020.595 |
| [10] |
Cai JY, Zhou Y, Hu TY, et al. PTLC: Protect the identity privacy during cross-chain asset transaction more effectively. Proceedings of the 22nd IEEE International Conference on Software Quality, Reliability, and Security Companion. Guangzhou: IEEE, 2022. 70–78. [doi: 10.1109/QRS-C57518.2022.00019]
|
| [11] |
Yang YH, Bai FH, Yu Z, et al. An anonymous and supervisory cross-chain privacy protection protocol for zero-trust IoT application. ACM Transactions on Sensor Networks, 2024, 20(2): 32. DOI:10.1145/3583073 |
| [12] |
薛庆水, 孙晨曦, 马海峰, 等. 基于条件代理重加密的跨链数据共享方案. 计算机应用研究, 2023, 40(5): 1324-1329. DOI:10.19734/j.issn.1001-3695.2022.09.0478 |
| [13] |
Yin ZY, Zhang BS, Xu JZ, et al. Bool network: An open, distributed, secure cross-chain notary platform. IEEE Transactions on Information Forensics and Security, 2022, 17: 3465-3478. DOI:10.1109/TIFS.2022.3209546 |
| [14] |
Li YX, Weng J, Li M, et al. Zerocross: A sidechain-based privacy-preserving cross-chain solution for monero. Journal of Parallel and Distributed Computing, 2022, 169: 301-316. DOI:10.1016/j.jpdc.2022.07.008 |
| [15] |
Acar A, Aksu H, Uluagac A S, et al. A survey on homomorphic encryption schemes: Theory and implementation. ACM Computing Surveys, 2018, 51(4): 79. DOI:10.1145/3214303 |
| [16] |
蒋楚钰, 方李西, 章宁, 等. 基于公证人组的跨链交互安全模型. 计算机应用, 2022, 42(11): 3438-3443. DOI:10.11772/j.issn.1001-9081.2021111915 |
| [17] |
叶祥翮, 刘学业, 王斌辉, 等. 面向联盟链的分布式公证人跨链模型. 应用科学学报, 2022, 40(4): 567-582. DOI:10.3969/j.issn.0255-8297.2022.04.003 |
| [18] |
郭晓涵, 姚中原, 张勇, 等. 基于改进公证人机制的联盟链跨链隐私保护方案. 计算机应用, 2023, 43(10): 3028-3037. DOI:10.11772/j.issn.1001-9081.2022111641 |
| [19] |
Herlihy M. Atomic cross-chain swaps. Proceedings of the 2018 ACM Symposium on Principles of Distributed Computing. Egham: ACM, 2018. 245–254. [doi: 10.1145/3212734.3212736]
|
| [20] |
Wood G. Polkadot: Vision for a heterogeneous multi-chain framework. White Paper, 2016, 21(2327): 4662. |
| [21] |
叶少杰, 汪小益, 徐才巢, 等. BitXHub: 基于侧链中继的异构区块链互操作平台. 计算机科学, 2020, 47(6): 294-302. DOI:10.11896/jsjkx.191100055 |
| [22] |
郑建辉, 林飞龙, 陈中育, 等. 基于联盟自治的区块链跨链机制. 计算机应用, 2022, 42(11): 3444-3457. DOI:10.11772/j.issn.1001-9081.2021111922 |
| [23] |
张学旺, 黎志鸿, 林金朝. 基于公平盲签名和分级加密的联盟链隐私保护方案. 通信学报, 2022, 43(8): 131-141. DOI:10.11959/j.issn.1000-436x.2022162 |
| [24] |
肖瑶, 冯勇, 李英娜, 等. 基于同态加密的区块链交易数据隐私保护方案. 密码学报, 2022, 9(6): 1053-1066. DOI:10.13868/j.cnki.jcr.000567 |
| [25] |
刁一晴, 叶阿勇, 张娇美, 等. 基于群签名和同态加密的联盟链双重隐私保护方法. 计算机研究与发展, 2022, 59(1): 172-181. DOI:10.7544/issn1000-1239.20200576 |
| [26] |
Ma ZF, Wang JY, Gai KK, et al. Fully homomorphic encryption-based privacy-preserving scheme for cross edge blockchain network. Journal of Systems Architecture, 2023, 134: 102782. DOI:10.1016/j.sysarc.2022.102782 |
 2024, Vol. 33
2024, Vol. 33



