1 引言

比例积分微分(PID)控制算法诞生于20世纪30–40年代, 其简单易实现、鲁棒性强, 在工业过程控制和机器人控制任务中被广泛使用. 然而实际应用中, 其通常需要经过繁琐的参数整定和准确的系统建模保证控制效果. 常见的参数整定方法包括临界比例法和衰减曲线法^[1], 但上述方法都属于离线整定, 依赖于专业人员经验观察, 且参数难以灵活调整. PID控制算法对系统变化敏感, 当系统发生变化时, 往往需要重新调整参数以保持控制性能. 因此, 针对PID控制算法, 搜索最优参数、实时自适应整定参数以及优化提高整体控制性能成为控制领域的重要研究方向.

目前, 许多研究者致力于解决被控对象模型改变后PID控制器需要重新整定参数的问题. 其中, 模糊PID控制器利用模糊逻辑和规则实现了对PID参数的自适应调整, 一定程度上缓解了传统PID参数整定的难题, 并实现了较大范围的有效控制. 徐托等人^[2]设计了基于模糊PID的空气质量测控系统, 成功解决了室内空气质量调节滞后和能耗高的问题. 夏长高等人^[3]针对果树间杂草的清理问题, 设计了基于遗传算法优化的模糊PID控制系统, 实现了利用机械臂对指定位置的杂草清除. 然而, 模糊PID控制器中模糊规则及隶属度函数的设计仍依赖专家经验. 后来, 专家系统因其高效、准确以及可解释性强等优点被也尝试引入自动控制系统. 李哲华等人^[4]针对传统PID控制滞后和稳定性较差的问题, 设计了专家控制规则, 实现了在线修正PID控制器参数, 优化了系统的动态性能和抗干扰性能. 然而, 由于专家系统需要设计大量规则以及依赖相关领域专家来主导, 因此实际应用受限.

为了解决模糊PID控制器和专家PID控制器依赖专家经验的问题, 后来的研究人员又进行了深入的研究. 袁春元等人^[5]通过粒子群优化算法来实现车辆悬架PID控制器的参数整定, 解决了传统PID控制器参数整定需要大量工程经验和试验的问题. 袁建平等人^[6]针对温室系统非线性、强耦合等问题, 提出了一种基于遗传-粒子群优化的BP神经网络PID控制器, 其结合了遗传算法和粒子群算法全局搜索和快速收敛的能力, 对神经网络的权值进行了优化, 实现了对温室环境的有效控制. 上述方法摆脱了对专家经验的依赖, 但是无法实时调整PID控制器参数. 后来, 孙嘉梁等人^[7]基于遗传算法的全局寻优能力对模糊PID控制器中的量化因子和比例因子进行了重新计算, 提高了系统响应速度和鲁棒性. Du等人^[8]提出了基于径向基函数的神经网络PID算法, 实现了控制曝气池中溶解氧浓度的同时在线更新系统部分参数.

近年来, 随着人工智能的迅速发展, 用先进智能技术优化传统控制方法成为当前研究热点之一. 强化学习通过智能体不断地与环境进行交互进行自监督学习, 并根据奖励和惩罚来不断改进策略, 如今已经在机器人控制、游戏竞技^[9]等领域大放异彩. Barzegar等人^[10]提出了一种基于强化学习的空中机器人姿态和高度控制器, 其能主动估计机器人控制器参数, 及时调整姿态和高度. Chen等人^[11]提出了一种基于深度强化学习的速度伺服控制策略, 解决了速度伺服系统的控制参数调节困难、力矩扰动和惯性突变等问题. Wang等人^[12]针对机器人轨迹跟踪问题, 提出了一种结合Q-learning和PID控制的方法, 该方法通过累加强化学习输出和PID控制器输出作来提高了机器人的跟踪精度. 然而, 由于Q-learning算法需要存储大量状态下的最大未来奖励期望, 导致查找和存储时间复杂度很大, 影响控制器的效率. 乔通等人^[13]提出了一种基于Q-learning算法的控制策略, 实现了PID参数自整定, 该策略具有更短的控制周期和更高的稳定性. 后来, Shi等人^[14]针对非线性系统提出了基于深度强化学习的自适应神经模糊PID控制器, 该方法利用了模糊推理系统的优势, 并采用强化学习算法优化参数, 实现了模糊PID控制器增益的自动调整. Yu等人^[15]提出了一种基于强化学习的自适应无模型 SAC-PID 控制方法, 用于移动机器人的自动控制, 相比模糊PID控制, 该方法具有更强的鲁棒性和泛化性. Wang等人^[16]利用深度 Q 网络和PID算法, 实现了有效跟踪移动目标, 解决了特征丢失和稳态误差大的问题. Yang等人^[17]针对车辆排队控制任务基于DDPG算法对传统PID控制器进行了改进, 使其能够适应不同的路况和车辆加减速等情况. 尽管强化学习在如今的机器人控制领域展现出其自身的优势, 但是目前仍旧存在着样本效率低、训练不稳定和探索与利用难以平衡等问题.

本文以移动机器人轨迹跟踪控制问题为背景, 设计了一种基于深度强化学习算法的分层自适应PID控制器(TD3-PID). 具体来说, TD3-PID由上层智能体层和下层的PID控制器组成, 上层智能体通过深度强化学习算法进行训练, 能够实时地观测当前的环境信息和系统状态从而及时调整下层PID控制器的参数和输出补偿量, 以优化整个控制系统的性能, 快速减小误差. 为了验证所提方法的有效性, 本文进行了实物实验, 结果表明本文提出的TD3-PID控制器相较传统的PID控制器有着更好的整体控制性能, 具有快速响应和较小的累积跟踪误差等优点. 此外, 本文提出的方法无需复杂建模, 同时避免了繁琐的参数整定过程.

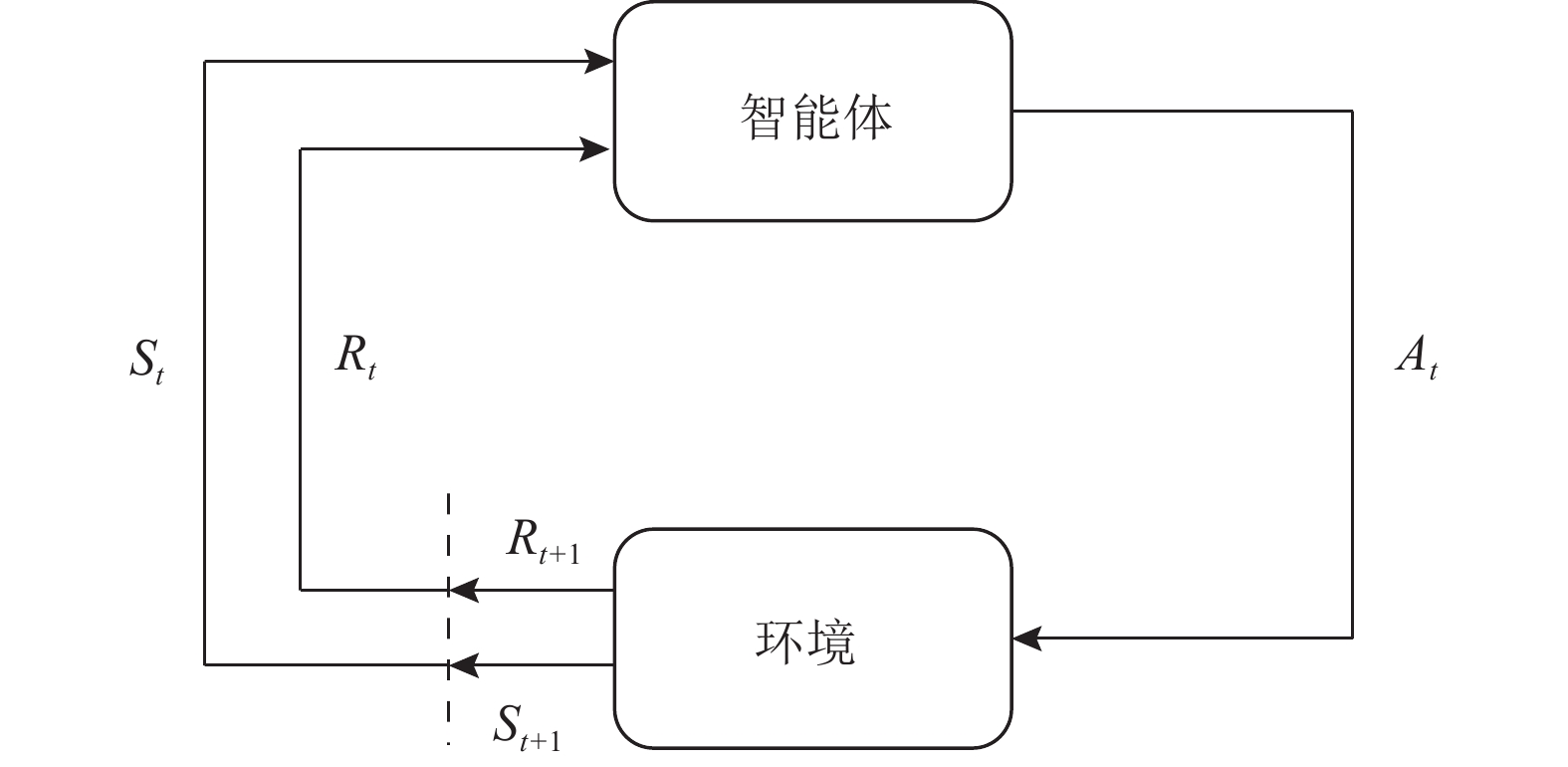
2 相关理论

强化学习是机器学习领域一类特殊的算法, 灵感来源于行为心理学中生物为了趋利避害而采取对自身最有利策略的思想. 强化学习算法的基本思想是基于马尔科夫决策过程(MDP), 通过智能体与环境的交互来学习最优策略π, 从而获得最大的累计回报. 在这个过程中, 环境通过奖励来强化智能体的正确行为, 使其不断改进自身行为模式. 强化学习算法的交互流程如图1所示. 在某个时刻t, 智能体可以观测到环境的状态S_t, 并根据此观测值S_t以及策略函数π(S_t)做出动作决策A_t, 环境受智能体动作的影响会更新自身的状态为S_t+1并给出奖励值R_t给智能体.

在强化学习任务中, 通过上述智能体和环境的不断交互, 会得到一个轨迹表示为(S₀, A₀, R₁, S₁, A₁, R₂, …, S_t). 强化学习的目标是最大化轨迹上的累积回报G_t, 如式(1)所示:

$ G_t=\sum_{t=0}^T \gamma^t R_t, \;\gamma \in[0, 1] $

(1)

其中, T是终止时刻, R_t是在时刻t获得的奖励, γ是折扣因子, γ决定了如何在最近的奖励和未来的奖励间进行折中.

深度强化学习是深度学习和强化学习的结合, 其利用了深度神经网络强大的模型表征能力去拟合、近似强化学习中的状态价值函数V(S)、动作价值函数Q(S, A)以及策略π(S)等. 状态价值函数表示从状态S出发, 遵循策略π能够获得的期望回报. 动作价值函数表示在当前状态S出执行动作A之后, 遵循策略π能够获得的期望回报.

3 深度强化学习分层自适应PID控制器 3.1 算法整体框架

本文基于深度强化学习算法训练了一个分层自适应PID控制器并应用于移动机器人轨迹跟踪任务中, 其完整结构框架如图2所示. 设计的分层自适应控制器下层部分通过PID控制算法直接对被控对象进行控制, 而上层部分通过智能体实时地根据当前观测的环境和系统状态信息及时调整下层控制器的参数以及输出补偿量, 从而提高控制器动态响应性能以及鲁棒性.

由于本文面对的轨迹跟踪任务属于连续控制问题, 因此采用结合了深度确定性策略梯度算法 (DDPG)^[18]和深度双重Q学习(deep double Q-learning)^[19]的双重延迟深度确定性策略梯度算法(TD3)对上层智能体进行训练.

TD3算法基本框架也属于Actor-Critic框架, 具体如图2所示. Actor网络利用策略函数生成行为与环境交互, Critic通过行为价值函数评价Actor网络的表现, 并指导后续行为动作. TD3算法采用了目标网络备份以稳定Critic网络的训练, 并且利用两组相同的神经网络对Actor网络的输出动作进行评估, 以缓解Q值高估的问题. 为了确保训练的稳定性, TD3算法调整了Actor网络的更新频率, 提高了Critic网络的更新频率, 以降低更新策略时的误差. 此外, 算法采用目标策略平滑方法, 通过引入随机噪声ε来减少更新目标值时的Q函数误差的影响.

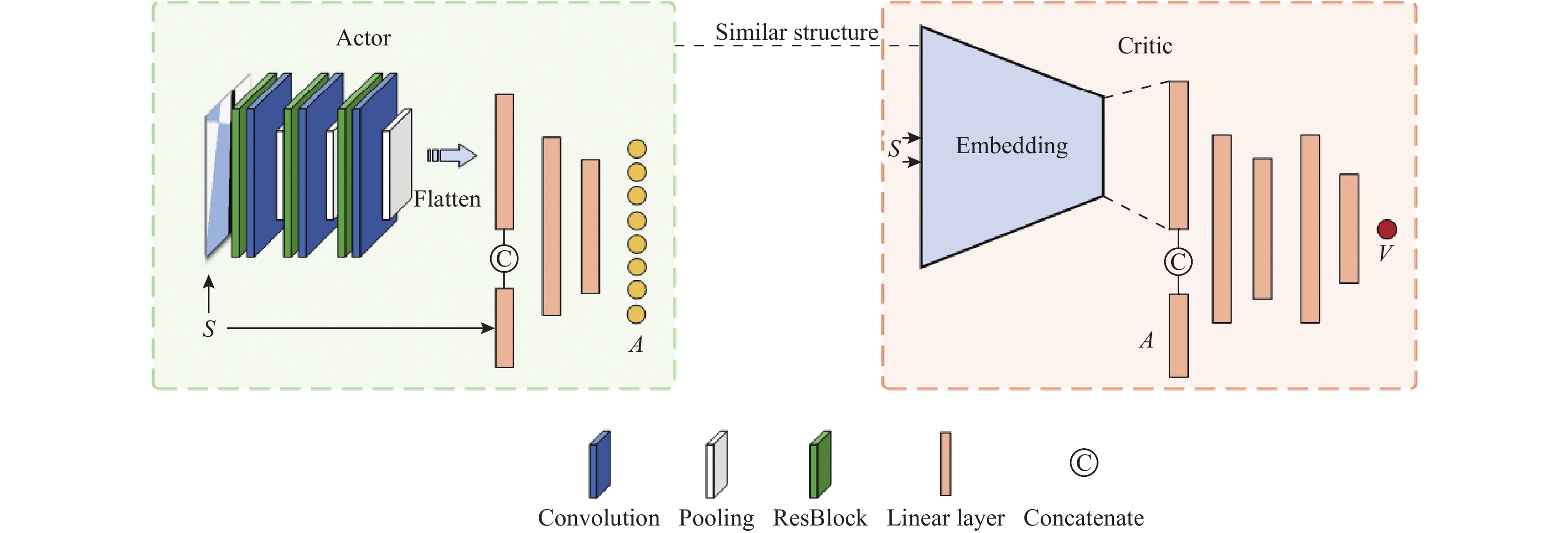
针对本文的移动机器人轨迹跟踪问题, 本文设计的Actor网络和Critic网络结构如图3所示. Actor网络首先对输入图像经过卷积网络进行特征提取并转换为特征向量, 然后与系统状态等信息进行连接, 考虑到轨迹跟踪任务需要保证一定的实时性, 因此没有采取更加复杂的网络结构, 而是经过多个线性层网络后得到输出动作A. 通过Actor网络可以从输入的图像中提取高层次、抽象的特征以提高智能体对环境的感知能力, 并结合系统当前状态以决定采取怎样的动作调整下层控制器参数. Critic网络中部分网络采用了和Actor网络相似的状态编码结构, 通过对输入的状态进行编码然后和动作连接并经过线性层网络得到最终的价值V.

3.2 轨迹跟踪控制方法

本文所提出的TD3-PID应用于轨迹跟踪任务的控制方法如图4所示. 具体来说, 对于每一个时间步, 通过移动机器人前置RGB摄像头获取前方的环境图像I_t, 然后分别送入上层智能体以及下层控制器. 在下层控制器, 首先将环境图像I_t转化为灰度图, 并先后通过均值滤波和阈值分割得到二值化的轨迹图像B_t, 然后通过形态学操作去除轨迹的毛刺和内部空洞, 最后基于霍夫变化进行直线拟合得到轨迹的角度θ和偏移距离d, 并按式(2)计算角度误差e_θ和偏移误差e_d. 其中, W表示图像的宽度.

$ \left\{\begin{aligned} & e_\theta=90^{\circ}-\theta \\ & e_d=\frac{W}{2}-d \end{aligned}\right. $

(2)

接下来, 角度误差和偏移误差也会被送入上层深度强化学习智能体作为当前观测状态中的系统信息. 在上层智能体中主要是通过获取当前的环境和系统状态信息送入图3中的Actor网络得到动作输出作用于下层PID控制器, 从而调整控制器参数和总输出. 下层角度PID控制器和偏移距离PID控制器接收到上层的动作后输出o_θ和o_d, 具体计算公式如式(3)所示:

$ \left\{\begin{split} o_\theta= & \left(\Delta k p_\theta+K p_\theta\right) \times e_\theta^t+\left(\Delta k i_\theta+K i_\theta\right) \sum_{i=0}^t e_\theta^i \\ & +\left(\Delta k d_\theta+K d_\theta\right) \times\left(e_\theta^t-e_\theta^{t-1}\right)+\Delta o u t_\theta \\ o_d= & \left(\Delta k p_d+K p_d\right) \times e_d^t+\left(\Delta k i_d+K i_d\right) \sum_{i=0}^t e_d^i \\ & +\left(\Delta k d_d+K d_d\right) \times\left(e_d^t-e_d^{t-1}\right)+\Delta o u t_d \end{split}\right. $

(3)

其中, $e_\theta^t $和$e_d^t $分别代表t时刻的角度误差和偏移误差, Kp_θ、Ki_θ和Kd_θ是角度PID控制器的初始控制参数, ∆kp_θ、∆ki_θ和∆kd_θ是上层控制器输出的角度PID控制器对应的参数调整量. Kp_d、Ki_d和Kd_d是偏移距离PID控制器的初始控制参数, ∆kp_d、∆ki_d和∆kd_d是上层控制器输出的偏移距离PID控制器对应的参数调整量. ∆out_θ和∆out_d分别表示上层控制器对下层角度PID控制器和偏移距离PID控制器的最终输出补偿量.

通过这种设计, 上层智能体能够在观测到环境图像中出现直线、急弯等特征后可以及时调整控制器参数以应对环境变化, 并在当前系统出现较大偏差等情况时通过增加输出补偿量及时缩减误差, 从而提高控制系统的整体响应性. 此外, 本文通过预设初始控制参数, 可以使得在刚开始进行训练时也获取更多的有效经验

3.3 状态空间及动作空间

为了使得智能体能够观测到足够多的信息来决定采取的输出动作, 状态空间主要包括环境信息和系统状态信息, 其定义如式(4)所示. 其中, I_t是前置摄像头在时刻t采集的环境RGB图像, 作为环境信息. $e_\theta^t $和$e_\theta^{t-1} $分别代表当前时刻和上一时刻的角度误差, $e_d^t $和$e_d^{t-1} $分别代表当前时刻和上一时刻的偏移距离误差, 这些作为系统状态信息供智能体观测.

$ S=\left(I_t, e_\theta^t, e_\theta^{t-1}, e_d^t, e_d^{t-1}\right) $

(4)

由于本文所提方法目标是自适应调整角度PID控制器和偏移距离PID控制器的参数及输出补偿, 因此定义动作空间维度大小为8, 如式(5)所示:

$ A=\binom{\Delta k p_\theta, \Delta k i_\theta, \Delta k d_\theta, \Delta { out }_\theta, }{\Delta k p_d, \Delta k i_d, \Delta k d_d, \Delta { out }_d} $

(5)

其中, ∆kp_θ和∆kp_d分别表示比例环节的调整系数, ∆ki_θ和∆ki_d表示积分环节的调整系数, ∆kd_θ和∆kd_d表示微分环节的调整系数, ∆out_θ和∆out_d表示最终输出量的补偿.

由于PID控制器中比例、积分、微分环节的作用不同, 本文对每个环节的调整系数的数值范围进行了限制, 其中∆kp和∆kd的数值范围较大, 设置为[−c, c], ∆ki的范围设置为[−c/k, c/k], k>1. 这样的设定是为了避免积分作用过强导致系统发生震荡现象而降低训练过程样本的采样效率, 从而使得训练过程缓慢且难以收敛. 同时, 针对∆out, 本文也进行了一些优化处理, ∆out作为输出补偿量, 可以在误差较大时补偿系统输出使得缩短系统的上升时间(第1次到达终值的时间). 此外, 在训练过程中的∆out可以作为一种微弱的随机噪声参与训练, 从而提高自适应控制器的抗干扰性能. 然而, 当系统到达稳态时, ∆out可能会使得系统跳变至非稳态, 因此当系统已经处于稳态时, 则会设置∆out=0自动取消输出补偿. 这一措施旨在确保系统在稳态时不受额外扰动的影响.

3.4 奖励函数

奖励函数是强化学习中至关重要的一个设计环节, 一个好的奖励函数往往决定了训练的收敛速度和最终训练的策略. 在智能体每次执行动作后, 会获得当前的即时奖励, 本方法定义的奖励函数如式(6)所示. 其中, R_c是实时奖励, R_d是到达终态时的奖励.

$ R=R_c+R_d $

(6)

实时奖励R_c定义如式(7)所示, 如果当前误差的绝对值小于阈值L₁, 定义奖励值为$ {{\mathrm{e}}}^{k-\left|{e}_{i}\right|} $, 此时误差越小, 获得的奖励值越大, 并且只要机器人没有跟丢轨迹, 都会获得一定的正向奖励. 如果当前误差绝对值介于阈值L₁和L₂之间, 为了能够尽快缩小系统误差, 额外添加了上次误差的绝对值和本次误差的绝对值之差作为奖励值, 使得当误差缩减的速度与获得的奖励成正比, 其中k、α和β均是超参数.

$ R_c=\left\{\begin{array}{ll} \mathrm{e}^{k-\left|e_i\right|}, & 0 \leqslant\left|e_i\right|< L_1 \\ \alpha\left(\left|e_{i-1}\right|-\left|e_i\right|\right)+\beta \mathrm{e}^{k-\left|e_i\right|}, & L_1 \leqslant\left|e_i\right| \leqslant L_2 \end{array}\right. $

(7)

到达终态ES时的奖励R_d如式(8)所示, 其中C₁和C₂均为常量. 当误差的绝对值大于阈值L₂, 会认为系统误差过大属于进入了异常终止状态ET, 则会给予一个比较大的负值来惩罚智能体. 当到达正常终止状态NT时, 会给予一些额外的正值奖励给智能体. 此外, 针对本文的自适应PID控制器问题, 本文考虑了将绝对误差积分AEI作为评价指标在正常终止态NT时给予智能体一定的额外奖励分数.

$ R_d= \begin{cases}-c_1, & \text { if } {ES}={ET} \\ {\mathrm{e}}^{c_2-A E I}, & \text { if } {ES}={NT}\end{cases} $

(8)

其中, 绝对误差积分AEI定义如式(9)所示:

$ A E I=\int_0^T|{e}(t)| {\mathrm{d}}t $

(9)

4 实验与分析

本文首先对智能体在Pybullet虚拟仿真环境下进行训练, 仿真环境相关设置如图5所示, 每一轮训练最大回合数设置为800. 其中, 本仿真实验环境全部使用Python语言进行编写, 深度学习环境采用PyTorch 1.7.1, 笔记本硬件配置为Intel(R) Core(TM) i7-9750H CPU @ 2.60 GHz, 内存16 GB, 显卡为NVIDIA的RTX2060.

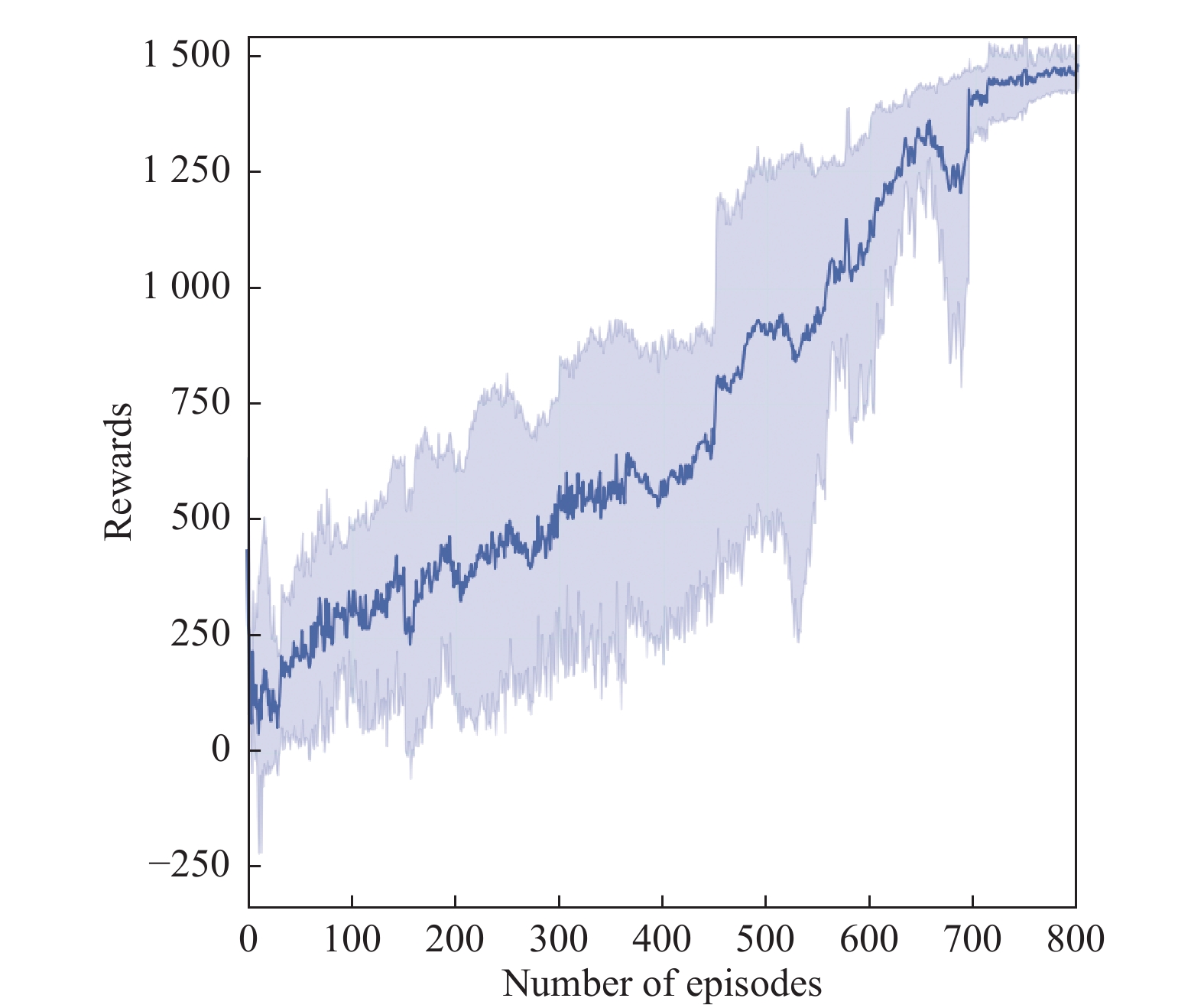
在虚拟仿真环境中, 本文记录了10组训练过程中的平均奖励值变化, 如图6所示, 可以看到所提出的算法具有比较好的收敛速度.

为了验证所提出的算法的有效性, 本文将提出的TD3-PID控制算法和传统PID控制算法、SAC-PID在真实场景下进行了比较实验, 实验平台选择4轮差速移动机器人, 摄像头为Intel RealSense D435i, 实验分别在两种不同类型的轨迹下进行, 具体如图7所示. 除此之外, 通过设置不同的初始角度偏差和初始偏移距离以比较不同初始状态下两个算法的整体控制性能. 实验中各个控制器基础参数均相等, 本文通过衰减曲线法并经过多次实验确定了一组比较好的基础参数 Kp_θ=1.2、Ki_θ=0.02、Kd_θ=2.1、Kp_d=2.7、Ki_d=0.07、Kd_d=2.1. 对于每条轨迹均在不同初始状态下进行5次重复实验, 并记录移动机器人跟踪过程实时的角度误差和距离偏移误差. 结果显示, TD3-PID控制器通过实时观测前方环境状态信息, 如弯道, 从而及时调整控制器参数和补偿输出, 实现了更优的轨迹跟踪控制, 具体如图8和图9所示.

此外, 本文量化了在每条轨迹不同初始状态下进行实验的绝对误差积分的平均值, 如表1和表2所示. 从实验结果可以看出, TD3-PID控制在轨迹1中相比传统PID控制器角度绝对误差积分下降了40.65%, 偏移距离绝对积分误差下降了41.58%, 相比SAC-PID角度绝对误差积分下降了18.15%, 偏移距离绝对积分误差下降了21.88%; 在轨迹2中相比传统PID控制器角度绝对误差积分下降了40.43%, 偏移距离绝对积分误差下降了38.82%, 相比SAC-PID角度绝对误差积分下降了26.95%, 偏移距离绝对积分误差下降了25.94%. 相比传统PDI和SAC-PID, 本文提出的TD3-PID控制算法能够通过及时的观测环境信息(弯道、直线等)以及系统误差信息实时地更新下层控制器参数, 从而在误差较大时能够快速进行响应缩小误差, 在前方将会出现弯道时及时调整参数及补偿来提前应对, 减少滞后, 从而保证整个控制过程具有更小的绝对积分误差. 因此基于本文提出的TD3-PID控制器具有更好的稳定性和快速响应能力, 具有更优的控制性能.

5 总结

本文针对传统PID控制器调参困难、不能够根据当前状态实时调整参数以及滞后等缺点, 提出了一种基于深度强化学习算法的分层自适应控制器, 即TD3-PID, 该控制器能够通过观测当前的环境状态和系统状态实时地调整PID控制器的参数和总输出补偿量, 从而优化系统性能. 通过真实场景实验结果显示, 本文提出的TD3-PID控制器相比传统PID和SAC-PID有着更好的动态性能, 更小的超调量, 并且整体响应的绝对积分误差更小.