2. 西安交通大学 自动化学院, 西安 710049
2. College of Automation, Xi’an Jiaotong University, Xi’an 710049, China
实施双碳政策已经催生了新能源行业的数字化升级, 这一趋势必然推动了新型电力系统的构建. 以新能源为主导来建设电力系统已经成为主要的发展方向[1]. 随着新能源比例的不断提高, 电力系统的转动惯量逐渐减小, 传统的同步稳定性体现出了新的特征[2], 因此, 我们仍然需要持续关注系统的功角稳定性问题. 传统的电力系统暂态稳定方法主要分为时域仿真和直接方法. 时域仿真方法的主要弊端在于其高昂的计算成本, 导致计算效率低, 影响了其实用性. 与之相对, 直接方法是基于李雅普诺夫稳定性理论的电力系统暂态稳定性分析方法. 尽管相对于时域仿真方法而言, 直接方法计算效率更高, 然而在处理复杂的暂态稳定性评估问题时, 其适应性相对较弱. 在这一背景下, 不同于传统方法, 数据驱动的暂态稳定性评估方法摒弃了对特定问题进行建模的需求. 从数据驱动的角度出发, 我们可以将暂态稳定性问题视为一个二分类问题, 即稳定或不稳定[3], 数据驱动的方法通常采用多种人工智能算法, 其中包括长短期记忆网络(LSTM)[4]、门控循环单元(GRU)[5]等技术. 这些先进的数据驱动方法为电力系统暂态稳定性评估提供了更为灵活和高效的解决方案, 避免了传统方法中对系统具体模型的过度依赖.
数据驱动方法以其卓越的非线性预测模型构建和杰出的泛化性能而备受研究者青睐. 在实际应用中, 为了实现更广泛区域的稳定性预测, 需要对不同区域的电网系统进行联合训练. 传统的数据驱动方法需要将所有的训练数据集中存储并且训练, 这种集中式机器学习架构在处理电力系统暂态稳定问题时存在可扩展性有限、易暴露隐私和高管理成本的问题[6]. 例如, 这种集中式方法可能使得整个系统对于恶意入侵和数据篡改变得非常脆弱. 一旦恶意入侵者成功获取对中心数据的控制权, 他们就能够破坏模型的完整性, 从而导致错误的稳定性预测和电力系统不稳定的运行. 随着电力系统日益数字化和互联化, 数据的收集、传输和分析面临越来越严峻的挑战. 恶意入侵和数据篡改可能对电力系统的运行和可靠性产生严重的负面影响. 因此, 我们需要采用更为安全和可靠的机器学习架构, 以应对潜在的威胁.
为了防止所有数据被存放于一个中心服务器, 导致一旦恶意入侵者获取中心数据控制权则极易造成隐私数据泄露的问题, 因此本文引入了联邦学习方法[7], 以提升电力系统稳定性预测的安全性和鲁棒性. 联邦学习是一种分布式机器学习方法, 其允许多个数据持有者在维护其数据隐私性的同时, 共同训练一个全局模型. 这种方法的关键优势在于将模型训练推向数据的分布式位置, 减轻了单一中心化服务器的负担, 同时有效地降低了数据泄漏的风险, 联邦学习的实施允许参与方在本地保留其数据, 并仅共享模型的更新信息, 从而不同地区的电力系统可以合作共同提升稳定性预测模型, 而无需牺牲数据的隐私性. 这种分布式方法有效地缓解了传统集中式机器学习方法中存在的隐私和安全性隐患, 为电力系统的数字化转型提供了更为可行的解决方案. 通过联邦学习, 我们不仅可以维护高水平的安全性和鲁棒性, 还能够更好地应对电力系统面临的复杂挑战, 确保其在数字时代的可持续运行.
在联邦学习中, 各独立联邦学习节点同步进行训练. 每个训练轮次中, 客户端节点提供自身梯度更新, 中央服务器将这些更新进行综合, 从而最终形成全局梯度. 该全局梯度随后广播至所有客户端节点, 以实现迭代训练. 目前, 对这些梯度的聚合通常采用平均方法[8]或其变体[9]来实现.
然而, 尽管联邦学习系统允许参与者在本地保留原始数据, 并没有将所有数据统一存放于中心服务器, 传统的联邦学习方法仍然存在一个巨大漏洞. 由于传统的联邦学习大多采用了由McMahan等人提出的聚合方法(FedAvg)[10], 即将各个客户端节点提供的梯度进行算术平均, 作为该轮训练中的全局模型梯度, 但是参与分布式训练的一些参与者可能是恶意的[11], 或者已经受到某个恶意攻击者的入侵, 导致这些参与者的本地训练数据中包含错误标签或有害样本. 由于没有中央机构能够验证数据的真实性, 这些恶意参与者因此可能破坏受训的全局模型. 在联邦学习中, 如果存在恶意节点, 它们可能会故意污染模型或传播错误信息, 从而破坏整个训练过程[12]. 目前已有的针对分布式人工智能系统的攻击方式包括标签替换(label-flipping). 攻击者通过攻击离线的训练数据库, 修改其中训练数据的标签, 以实现对联邦学习节点的攻击. 此外, Baruch等人提出的“lie”攻击[13] , 是另一种攻击方式, 攻击者只能访问自己的数据, 并且只能对自己的参数进行微小的更改. 这与传统的攻击模型假定攻击者可以对参数进行大量更改的情况有所不同. 由于“lie”攻击只对自己的参数进行微小的更改, 因此它可以绕过大多数现有的防御机制.
本研究着眼于构建分布式电网暂态稳定性判别的联邦学习方案, 以及如何在拜占庭节点数量小于所有客户端节点数量一半的攻击场景下, 提高联邦学习模型的鲁棒性和稳定性.
1 相关研究背景目前在处理联邦学习鲁棒性问题方面, 涌现了一系列算法. 其中, Yin等人[14] 提出的Median-based GD方法将FedAvg方法中的算术平均数替换为中值, 有效抵御了一些极值攻击. 另一种算法是Krum[15,16] 即Kullback-Leibler robust unanimity maximization, 主要用于异常值检测和数据修复, 在处理分布式数据时尤其有用. 该算法通过考虑一致性来确定哪些节点提供的数据是可信的, 以维护整体模型的准确性. 此外, Multi-krum在传统Krum的基础上做了改进, 不再只选择一个节点的梯度来更新全局模型, 而是选择多个安全节点的平均梯度. 相比于Krum方法, Multi-krum方法在全局模型的收敛速度更快, 模型更易训练. 然而, Luis等人[17] 发现在面对label-flipping攻击时, Multi-krum方法在测试准确率方面可能出现大幅度的震荡, 导致全局模型的极其不稳定, 甚至在模型停止训练时可能得到较差的训练结果. 另一方面, El Mhamdi等人[18] 将Krum中对梯度的每一维都选出β个梯度:
| β=n−4f | (1) |
其中, n为客户端节点总数, f为拜占庭节点总数, 这些值是距离每一维梯度的中位数最近的值. 该算法应用于每维空间, 可以识别出某一个变化很大的维度. Li等人[19]则通过引入正则化项提出了一种抵御拜占庭攻击的分布式学习方法, 称为拜占庭鲁棒随机梯度聚合方法(RSA). RSA算法通过聚合各个节点的梯度来更新模型参数, 并在每次迭代中使用正则化项来减轻拜占庭攻击的负面影响. 该算法的收敛速度为:
| O(1k) | (2) |
其中, k是迭代次数, 而优化效果取决于拜占庭节点的数量.
现有Multi-krum算法有诸多限制, 特别是需要提前设定拜占庭节点的数量, 导致在许多恶意节点未知的情况下无法有效使用. 同时, 维度诅咒(curse of dimen-sionality)[20] 的存在使得在神经网络较为复杂的情况下, 距离度量变得不准确, 导致无法准确识别拜占庭节点的问题.
本文建立了分布式电网暂态稳定评估的联邦学习框架, 并提出了一种改进的拜占庭节点识别算法. 通过区域电网各自的神经网络模型联合训练获取暂稳评估联邦学习模型; 进一步采用在线自编码器对各神经网络的梯度进行降维, 将高维数据转换为低维数据, 以规避维度诅咒的问题; 采用密度聚类方法对各节点的梯度进行聚类[21], 实现对恶意节点的检测, 提高联邦学习模型的鲁棒性.
本文提出的算法旨在克服Multi-krum算法的不足之处, 通过降维和密度聚类, 解决距离度量不准确导致的拜占庭节点检测不准确的问题, 同时在未知恶意节点数量的情况下依然能够准确地识别拜占庭节点. 这一改进有望为联邦学习在电力系统暂态稳定性预测中的应用, 提供更高的鲁棒性和可靠性.
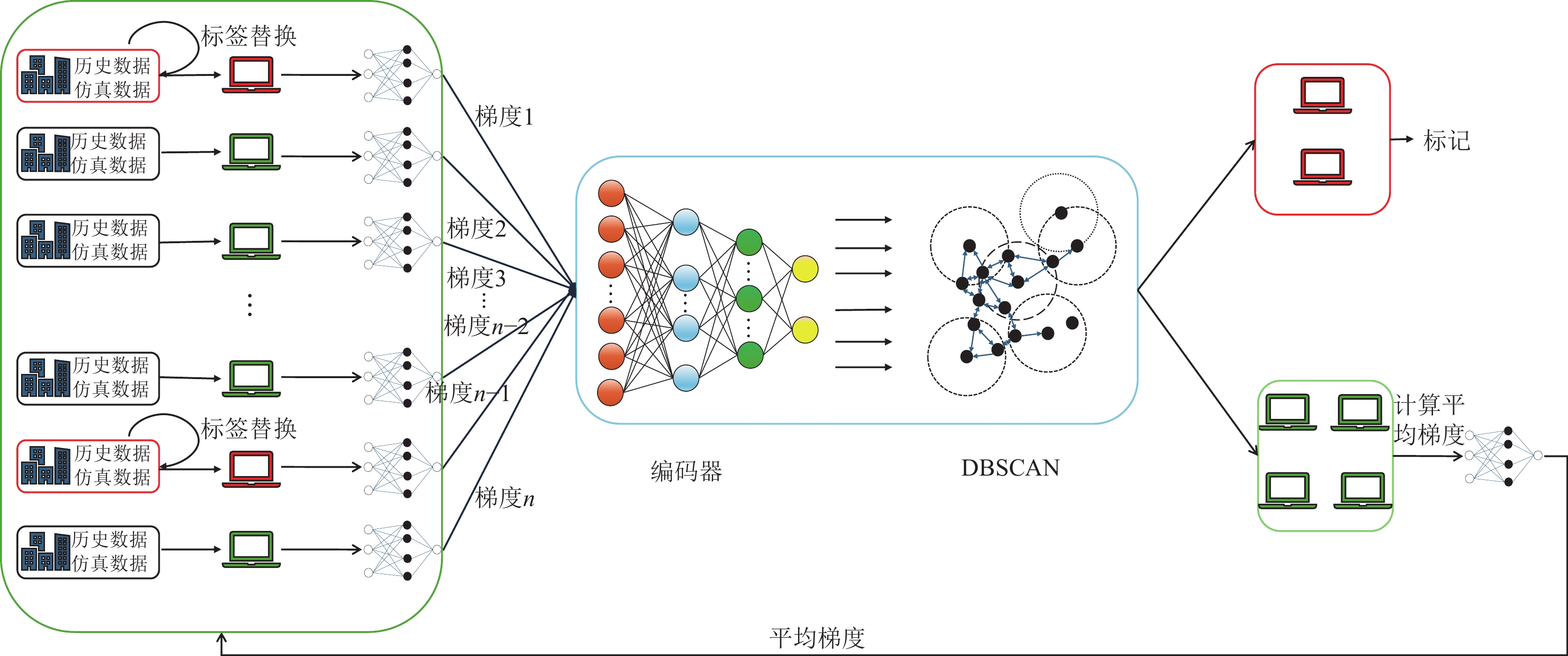
2 基于AE-DBSCAN的拜占庭节点检测方法本文所提出的分布式电网暂稳评估联邦学习及拜占庭节点检测的整体框架如所示. 各个区域电网分别用独立的神经网络模块计算梯度, 基于自编码器进行梯度降维, 采用DBSCAN算法实现拜占庭节点检测, 进一步基于Multi-krum算法进行联合梯度更新, 实现联邦学习模型的训练. 以下分别介绍各个关键模块的细节.
2.1 基于Multi-krum的鲁棒梯度更新现有的拜占庭节点检测算法最常用的是基于Multi-krum的梯度更新方法. Multi-krum是一种应用于提升联邦学习鲁棒性的方法, 广泛应用于联邦学习中的拜占庭节点检测中. Multi-krum的核心思想是在全局模型收集到每个客户端节点的更新后, 首先两两计算各个节点梯度的距离:
| di,j=‖gi−gj‖2 | (3) |
其中,
对于每个梯度选择离他最近的n–f–1个节点的距离相加作为该梯度
| Kr(i)=n−f−1∑j=1di,j | (4) |
计算所有梯度的得分后, 得到得分最小的n–f个作为“安全节点”集合, 计算这n–f个节点的平均梯度:
| g∗i=1n−fn−f∑i=1gi | (5) |
作为全局模型的梯度, 并更新全局模型参数:
| W=W−lr⋅g∗i | (6) |
重复以上步骤直到全局模型收敛, 其中lr表示学习率.
2.2 基于自编码器和密度聚类的恶意节点检测方法Multi-krum算法是一种可行的联邦学习鲁棒性算法, 其通过计算各客户端节点梯度的欧氏距离来判断离群点. 然而, Multi-krum需要在使用前事先知道拜占庭节点的个数, 这限制了其适用场景, 并不适用于电力系统的稳定性判定任务. 同时, 因为电力系统数据通常由PMU采样得到, 往往是高维数据[22], 相应的神经网络也较为复杂. 在这种情况下, 由于维度诅咒的存在, 在高维空间中进行距离度量会变得不准确. 如果直接将复杂神经网络的梯度用于计算欧氏距离, 可能导致距离度量失效, 从而误判离群点. 因此, 在高维空间中且拜占庭节点数量未知的情况下, 如何提高联邦学习的鲁棒性成为迫切需要解决的问题.
本文提出的面向电力系统暂态稳定性的联邦学习拜占庭节点检测算法首先使用自编码器对各个节点的高维梯度进行降维, 避免维度诅咒, 接着将降维后的梯度进行密度聚类, 进而划分出包含异常点的簇, 即检测出拜占庭节点. 提出的算法充分解决了Multi-krum需要在事先知道拜占庭节点的个数以及在高维空间中进行距离度量结果会变得不准确而导致拜占庭节点检测失败的问题.
具体来说, 传统的线性降维方法如主成分分析(PCA)在给定
|
图 1 基于自编码器和密度聚类的恶意节点检测方法 |
本文设计的自编码器(auto-encoder)采用多层前向神经网络结构, 能够提供良好的降维性能[23]. 每个区域电网数据经过门控循环单元(GRU)训练之后的梯度向量x 维数为N. 自编码器包含3层全连接前向神经网络, 包括输入层隐藏层和输出层, 它的输出可以表示为:
| hW,b(x)=(˜x1,˜x2,⋯,˜xN)T | (7) |
与输入
| hW,b(x)=g(f(x))≈x | (8) |
| J(W,b;x,y)=12‖hW,b(x)−y‖2 | (9) |
其中,
在对梯度向量降维之后, 采用DBSCAN进行聚类, 寻找离群点. DBSCAN是一种基于密度的聚类算法, 关键思想是对于每个聚类的对象, 给定半径(Eps)的邻域必须包含至少一定数量的对象(MinPts), 这意味着邻域的基数必须超过某个阈值. 点p的
| NEps={q∈Ddist(p,q)<Eps} | (10) |
其中, D表示数据集合,
| NEps(P)>MinPts | (11) |
其中, Eps和MinPts是用户指定的参数, 分别表示邻域的半径和核心点的
本文提出的拜占庭节点检测方法将自编码器的降维能力与密度聚类DBSCAN进行结合, 在拜占庭节点识别方面, 克服了Multi-krum需要事先知道拜占庭节点数量这一约束条件以及在面对较复杂神经网络时变现出的维度诅咒问题. 拜占庭节点检测的具体流程如下.
(1) 每个客户端节点将自己本轮更新后的神经网络梯度统一发送至中央节点.
(2) 中央节点使用少量训练周期中的客户端节点提供的梯度在线训练自编码器.
(3) 使用自编码器对梯度降维, 提取降维后的数据作为DBSCAN的输入.
(4) 使用DBSCAN对各客户端经过降维后的数据做密度聚类, 选择包含节点数量少的类别为拜占庭节点集合.
(5) 选取非拜占庭节点集合, 使用计算所有梯度平均值的聚合方法获得全局梯度.
(6) 将拜占庭节点标记并在之后的迭代中不使用拜占庭节点提供的梯度.

|
图 2 DBSCAN核心思想示意图 |
在拜占庭节点检测完成之后, 从梯度更新节点集合中剔除相应的拜占庭节点, 应用式(4)–式(6)对联邦学习模型进行梯度更新, 训练直至收敛, 即可获得具有恶意节点鲁棒性的分布式暂稳评估联邦学习模型.
3 实验验证与分析本节基于我国的区域电力系统数据[24]进行了大量实验, 该数据是由中国电力科学研究院提供的适用于功角稳定特性研究的功角稳定机电暂态仿真算例(China electric power research institute-rotor angle stability, CEPRI-RAS)验证了提出的联邦学习模型和拜占庭节点检测算法的有效性. 本研究设置了N–1三相短路总线故障, 并利用BPA对相应的数据进行模拟. 我们选择发电机数据作为原始的瞬态稳定评估即TSA特征. 实验数据划分如表1所示, 其中正负样本的比例为1:1.
设计共15、100个客户端节点和30%、40%的拜占庭节点实验场景, 拜占庭节点分别使用label-flipping的对称标签替换攻击以及100个客户端节点40%拜占庭节点的非对称标签替换攻击, 测试提出方法的有效性. 在本文中对称替换指将所有正负样本的标签全部替换为相反标签, 非对称替换指仅将部分负样本的标签替换为相反标签. 采用区域电力系统197节点的仿真数据开展拜占庭节点的检测即联邦学习鲁棒性的实验, 电力系统接线图如图3所示, 实验数据的具体的描述如表2和表3所示.
| 表 1 仿真数据结构 |

|
图 3 197节点电力系统接线图 |
| 表 2 电力系统数据集描述 |
| 表 3 特征结构 |
实验设备GPU使用NVIDIA GeForce RTX 3060, CPU使用i7-11800H @ 2.30 GHz.
为了测试所提出方法的优越性, 主要在对称替换攻击和非对称替换攻击模型准确率上对比Multi-krum和Median-based GD. 其中Multi-krum设置选取的良性集合大小为n–f, 其中n为客户端节点总数, f为拜占庭节点总数.
每个客户端节点和中央节点使用GRU构建神经网络模型, 包含两个GRU层和一个全连接层. 网络结构如表4所示, 实验使用的自编码器的编码器部分包含3个全连接层, 结构如表5所示.
| 表 4 模型结构设置 |
| 表 5 编码器结构设置 |
3.1 采用label-flipping攻击的对称替换实验
Label-flipping攻击对称替换实验中, 我们将拜占庭节点的所有训练样本倒置, 即所有正样本标签与所有负样本标签互换.
对于本文所提出的方法, 在每个客户端节点采用一个批次的数据训练时, 将训练得到的梯度送入自编码器进行在线训练, 并使用经过在线训练的自编码器对各个节点的梯度进行降维. 在label-flipping攻击场景下进行实验. 在15个客户端节点40%拜占庭的对称替换攻击场景中经过降维之后聚类的各个节点梯度可视化示意图如图4所示. 实验平均准确率对比如图5–图8所示.

|
图 4 100个节点30%拜占庭对称攻击聚类结果 |
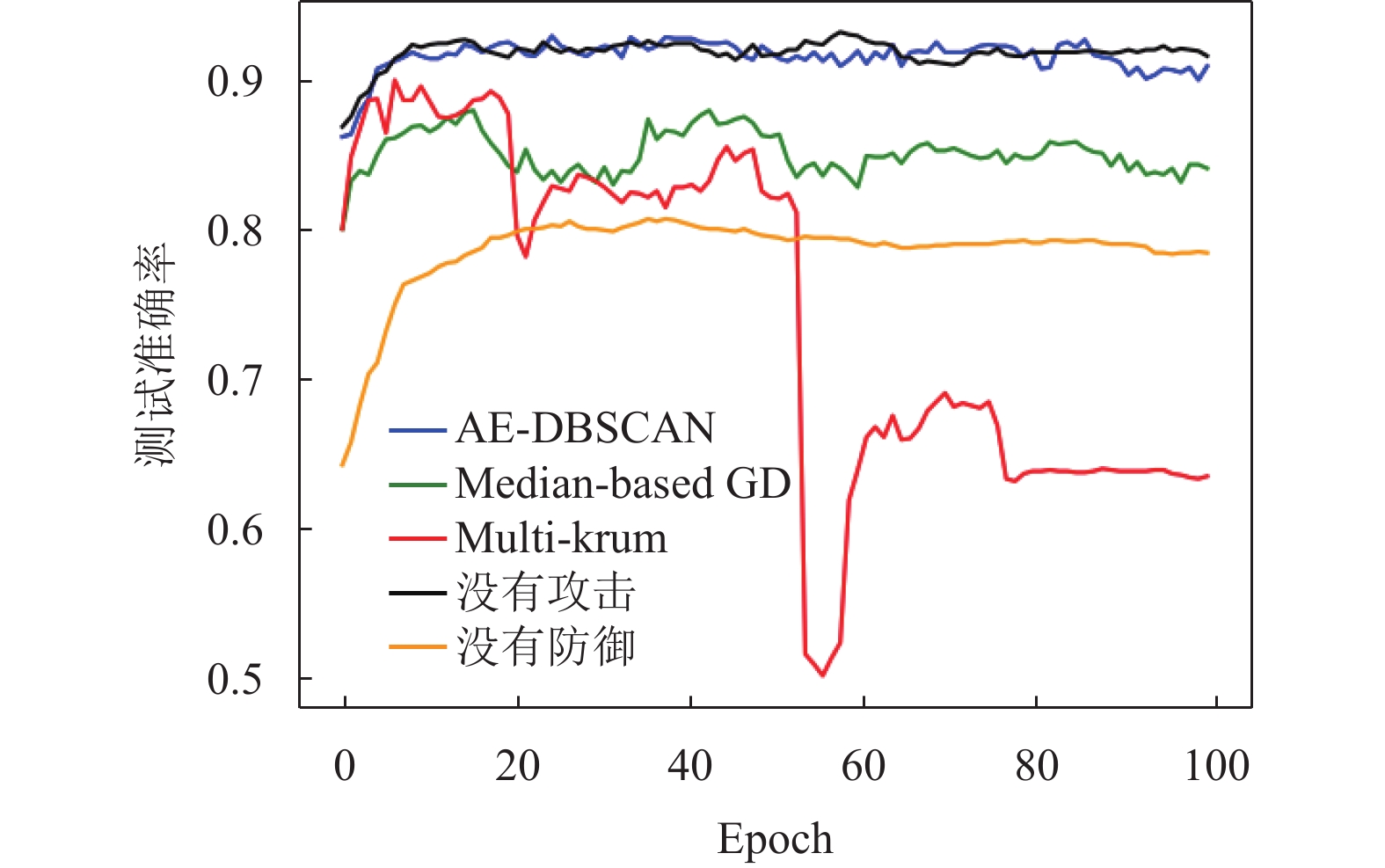
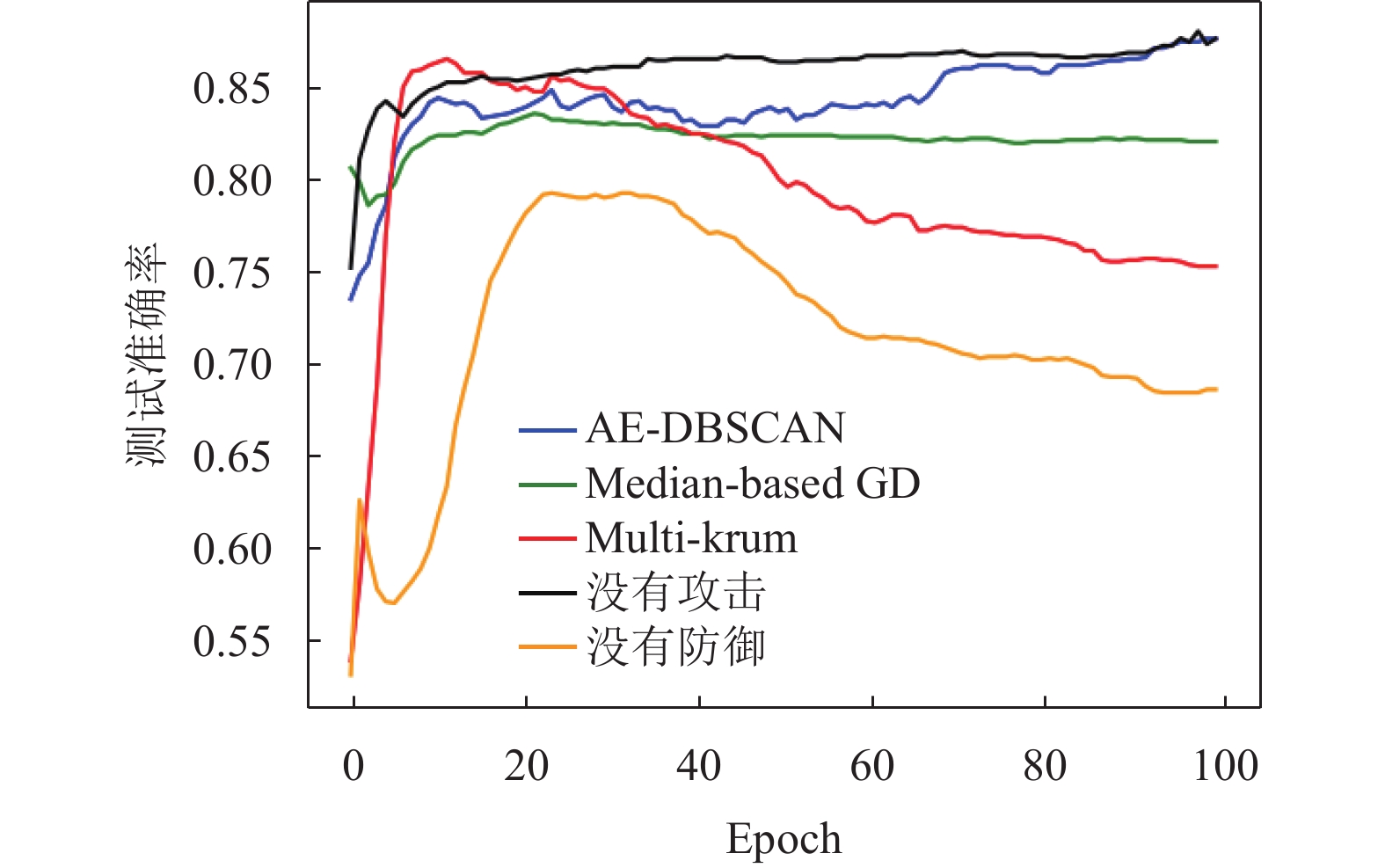
可以看出, 本文提出的拜占庭节点检测和聚合方法在客户端节点遭遇拜占庭节点的label-flipping攻击时, 15个客户端的情况下平均准确率可以达到92%, 100个客户端的情况下平均准确率可以达到87%, 相比于Multi-krum和Median-based GD, 有较大提高, 观察到因为“维度诅咒”的存在, Multi-krum方法在15客户端节点时出现了准确率的震荡, 在100客户端节点时因为距离度量不准确所选取的集合包含大量拜占庭节点, 导致Multi-krum的准确率相比于没有任何防御的朴素FedAvg聚合方法还要低.

|
图 5 15个节点40%拜占庭对称攻击测试准确率 |
|
图 6 15个节点30%拜占庭对称攻击测试准确率 |

|
图 7 100个节点40%拜占庭对称攻击测试准确率 |
表6和表7分别展示了在不同节点数面对不同比例的拜占庭节点攻击时的拜占庭节点检测召回率和精确率, 召回率Recall和精确率Precision可以表示为:
| Recall=TPTP+FN=TPf | (12) |
| Precision=TPTP+FP | (13) |
|
图 8 100个节点30%拜占庭对称攻击测试准确率 |
| 表 6 拜占庭节点检测召回率(%) |
| 表 7 拜占庭节点检测精确率(%) |
实验结果表明, AE-DBSCAN首先通过编码器的降维, 解决了高维数据距离度量不准确的问题, 又通过密度聚类划分出拜占庭节点集合因此在良性节点误判率方面, 相较于Multi-krum有明显提高, 能够更好、更快地识别出拜占庭节点和良性节点, 有助于全局模型更快的收敛.
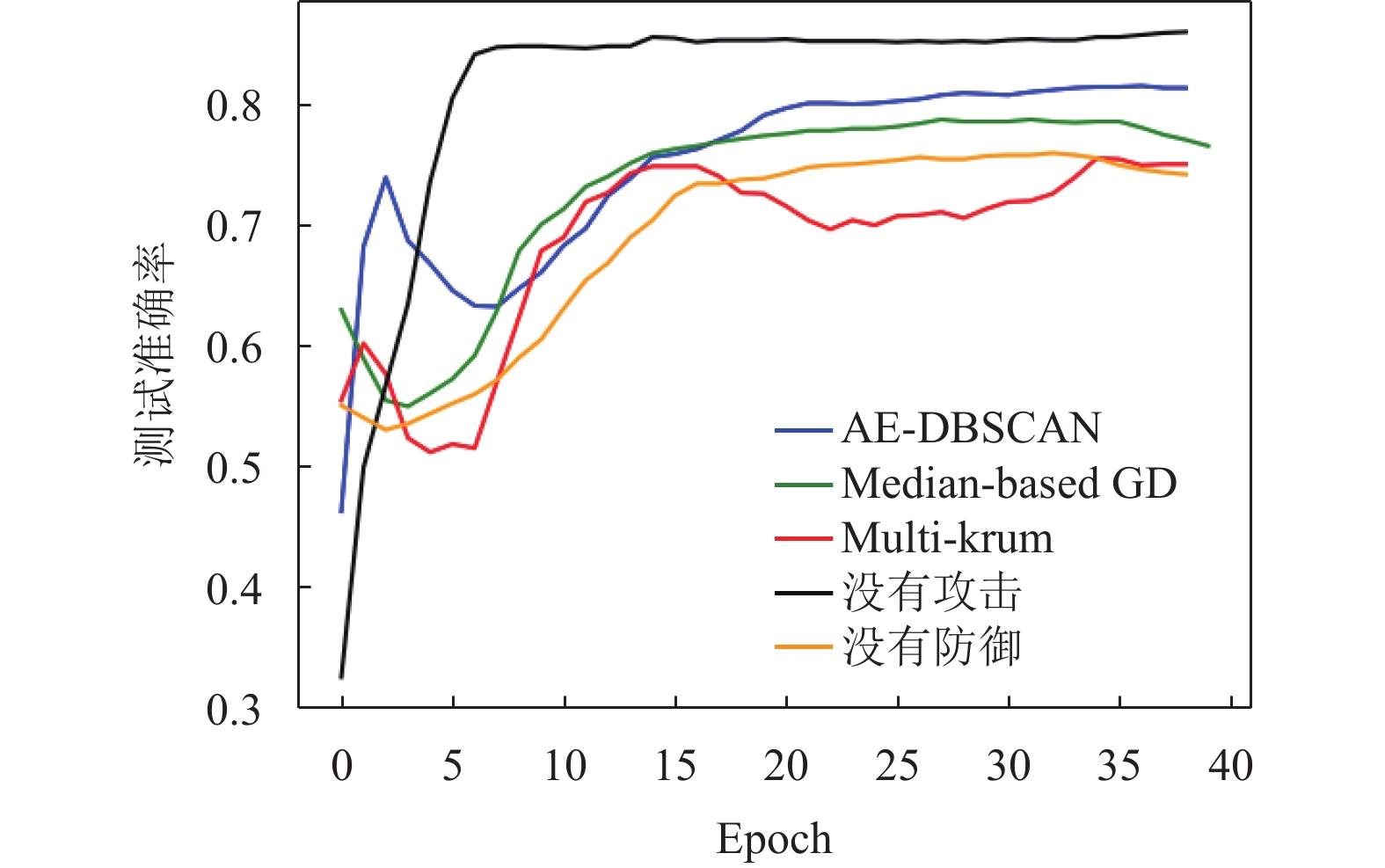
3.2 采用label-flipping攻击的非对称替换实验为了验证所提出方法的普遍适用性, 在非对称场景下进行了实验. 非对称实验中, 我们将所有负样本中55%的标签替换为正样本标签, 正样本不做改变. 在100个客户端, 40%拜占庭节点的情况下进行了实验. 实验结果如图9–图12所示.
|
图 9 100节点40%拜占庭非对称攻击测试准确率 |
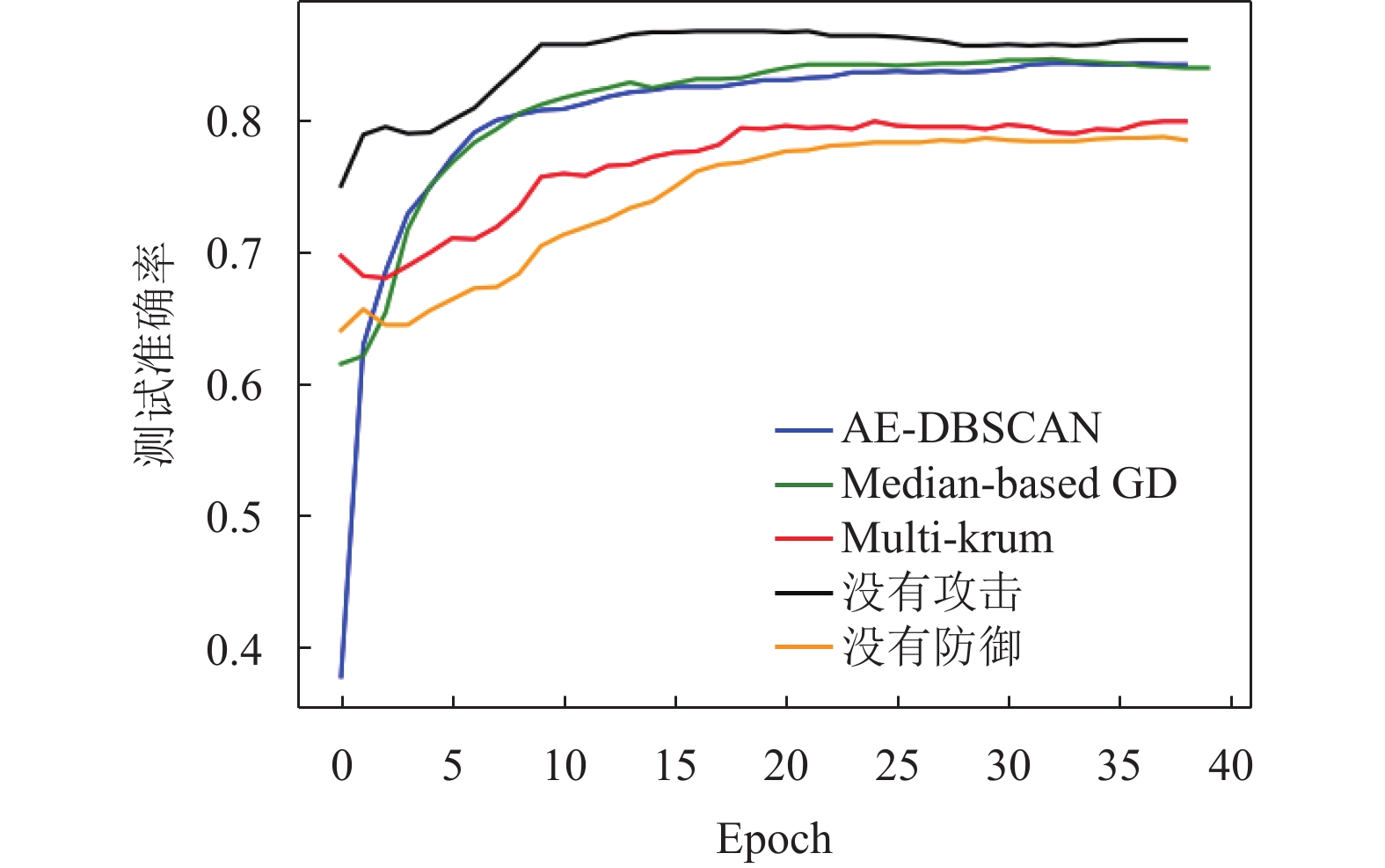
|
图 10 100节点30%拜占庭非对称攻击测试准确率 |

|
图 11 15节点40%拜占庭非对称攻击测试准确率 |
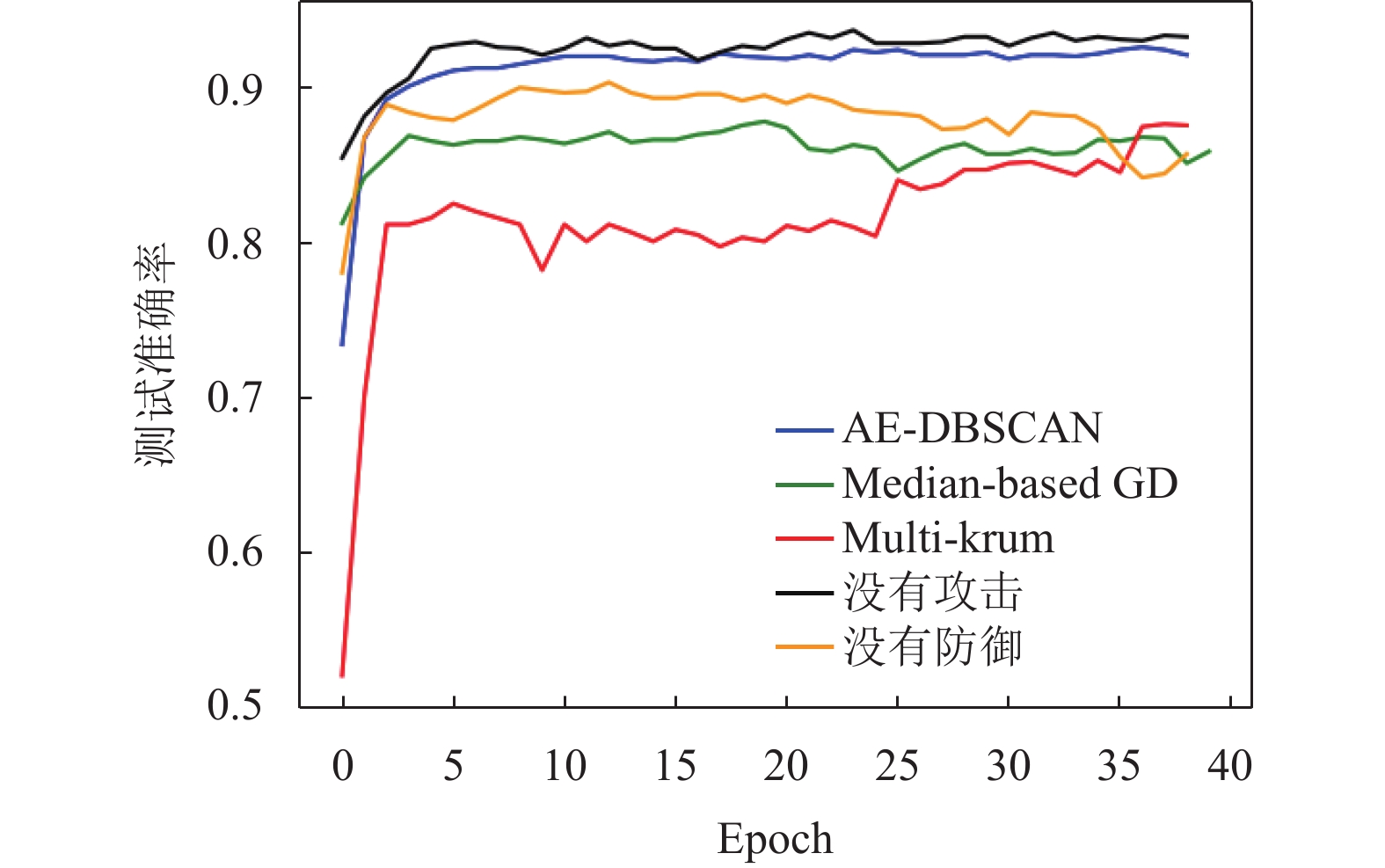
|
图 12 15节点30%拜占庭非对称攻击测试准确率 |
在面对非对称攻击的实验中, 本文所提出的方法相较于Multi-krum和Median-based GD表现出了显著的提高, 并且模型的稳定性明显优于其他方法, 不容易出现准确率的剧烈跳变.
通过对实验结果的分析, 可以观察到在100个节点的情况下, 所提出的AE-DBSCAN算法在面对非对称攻击时, 测试准确率明显高于Multi-krum和Median-based GD. 这一改进的原因在于H-AE-DBSCAN算法充分利用了自编码器的降维特性和DBSCAN的密度聚类优势, 有效地区分了拜占庭节点和良性节点, 从而提高了全局模型的训练效果.
4 结论与展望本文建立了分布式电网暂态稳定评估联邦学习框架, 提出了基于自编码器和DBSCAN的拜占庭节点检测方法, 利用自编码器的降维能力和DBSCAN, 可以直接从多个客户端节点中找到拜占庭节点, 减少拜占庭节点对全局模型的恶意更新, 实现了全局模型更安全的训练, 提高了在电力系统暂态稳定性判定领域使用联邦学习时面对网络攻击的鲁棒性. 通过实验测试数据得到如下结论.
(1)本文提出的基于自编码器和DBSCAN的拜占庭节点检测方法, 在面对label-flipping的对称攻击时, 测试准确度均可以达到87%以上, 相较于Multi-krum和Median-based GD有明显提高. 本文提出的方法可以在第1–2个训练周期中, 将至少90%的拜占庭节点成功检测, 并排除在之后的训练节点之外.
(2)在客户端节点较少的时候, 因为Multi-krum在高维空间的距离估算不准确, 导致全局模型受拜占庭节点影响较为明显, 造成全局模型测试准确率出现较大的震荡或者准确率低于不采用任何防御手段的情况. 本文提出的方法利用自编码器对高维梯度进行降维, 解决了距离计算不准确的问题, 使全局模型的训练结果更加稳定.
| [1] |
别朝红, 潘超琼, 陈叶, 等. 能源转型下新能源电力系统概率风险评估. 西安交通大学学报, 2021, 55(7): 1-11. |
| [2] |
孙华东, 徐式蕴, 许涛, 等. 电力系统安全稳定性的定义与分类探析. 中国电机工程学报, 2022, 42(21): 7796-7808. |
| [3] |
邹逸冰. 人工智能在智能电网中的应用和展望. 中国新通信, 2022, 24(19): 67-69. DOI:10.3969/j.issn.1673-4866.2022.19.024 |
| [4] |
Wang X, Zhou Q, Huang C, et al. A transient stability assessment method using LSTM network with attention mechanism. Proceedings of the 8th IEEE International Conference on Advanced Power System Automation and Protection (APAP). Xi’an: IEEE, 2019. 120–124.
|
| [5] |
Pan FL, Li J, Tan BD, et al. Stacked-GRU based power system transient stability assessment method. Algorithms, 2018, 11(8): 121. DOI:10.3390/a11080121 |
| [6] |
Ren C, Wang TJ, Yu H, et al. EFedDSA: An efficient differential privacy-based horizontal federated learning approach for smart grid dynamic security assessment. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2023, 13(3): 817-828. DOI:10.1109/JETCAS.2023.3293253 |
| [7] |
戴理朋, 杨鑫, 徐茹枝. 联邦学习在电力数据分析中的应用及隐私保护研究. 电力信息与通信技术, 2022, 20(11): 47-56. |
| [8] |
Collins L, Hassani H, Mokhtari A, et al. FedAvg with fine tuning: Local updates lead to representation learning. Proceedings of the 36th International Conference on Neural Information Processing Systems. New Orleans: Curran Associates Inc., 2022. 768.
|
| [9] |
Pillutla K, Kakade SM, Harchaoui Z. Robust aggregation for federated learning. IEEE Transactions on Signal Processing, 2022, 70: 1142-1154. DOI:10.1109/TSP.2022.3153135 |
| [10] |
McMahan B, Moore E, Ramage D, et al. Communication-efficient learning of deep networks from decentralized data. Proceedings of the 20th International Conference on Artificial Intelligence and Statistics. Fort Lauderdale: PMLR, 2017. 1273–1282.
|
| [11] |
张世文, 陈双, 梁伟, 等. 联邦学习中的攻击手段与防御机制研究综述. 计算机工程与应用, 2024, 60(5): 1-16. |
| [12] |
Alotaibi A, Rassam MA. Adversarial machine learning attacks against intrusion detection systems: A survey on strategies and defense. Future Internet, 2023, 15(2): 62. DOI:10.3390/fi15020062 |
| [13] |
Baruch M, Baruch G, Goldberg Y. A little is enough: Circumventing defenses for distributed learning. Proceedings of the 33rd International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2019. 775.
|
| [14] |
Yin D, Chen YD, Kannan R, et al. Byzantine-robust distributed learning: Towards optimal statistical rates. Proceedings of the 35th International Conference on Machine Learning. Stockholm: PMLR, 2018. 5650–5659.
|
| [15] |
Blanchard P, El Mhamdi EM, Guerraoui R, et al. Machine learning with adversaries: Byzantine tolerant gradient descent. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 118–128.
|
| [16] |
Colosimo F, de Rango F. Median-krum: A joint distance-statistical based Byzantine-robust algorithm in federated learning. Proceedings of the 2023 International ACM Symposium on Mobility Management and Wireless Access. Montreal: ACM, 2023. 61–68.
|
| [17] |
Luis MG, Co KT, Lupu EC. Byzantine-robust federated machine learning through adaptive model averaging. arXiv:1909.05125, 2019.
|
| [18] |
El Mhamdi EM, Guerraoui R, Rouault S. The hidden vulnerability of distributed learning in Byzantium. Proceedings of the 35th International Conference on Machine Learning. Stockholm: PMLR, 2018. 3521–3530.
|
| [19] |
Li LP, Xu W, Chen TY, et al. RSA: Byzantine-robust stochastic aggregation methods for distributed learning from heterogeneous datasets. Proceedings of the 33rd AAAI Conference on Artificial Intelligence. Honolulu: AAAI, 2019. 1544–1551.
|
| [20] |
Chandra NK, Canale A, Dunson DB. Escaping the curse of dimensionality in Bayesian model-based clustering. Journal of Machine Learning Research, 2023, 24(144): 1-42. |
| [21] |
Wang HX, Lu N, Luo H, et al. Self-supervised clustering with assistance from off-the-shelf classifier. Pattern Recognition, 2023, 138: 109350. DOI:10.1016/j.patcog.2023.109350 |
| [22] |
Wang GZ, Guo JB, Ma SC, et al. Data-driven transient stability assessment using sparse PMU sampling and online self-check function. CSEE Journal of Power and Energy Systems, 2023, 9(3): 910-920. |
| [23] |
Li PZ, Pei Y, Li JQ. A comprehensive survey on design and application of autoencoder in deep learning. Applied Soft Computing, 2023, 138: 110176. DOI:10.1016/j.asoc.2023.110176 |
| [24] |
徐式蕴, 李宗翰, 赵兵, 等. 新型电力系统标准算例(1): 功角稳定CSEE-RAS. 中国电机工程学报, 2024: 1–14. [doi: 10.13334/j.0258-8013.pcsee.230534]
|
 2024, Vol. 33
2024, Vol. 33



