2. 上海第二工业大学 智能制造与控制工程学院, 上海 201209
2. School of Intelligent Manufacturing and Control Engineering, Shanghai Polytechnic University, Shanghai 201209, China
复杂生产流程车间的优化调度研究对于实现智能制造[1–3]具有重要推动作用. 有限缓冲区流水车间调度问题(flow shop scheduling problem with limited-buffer, FSSP_LB)是对传统的置换流车间调度问题(PFSP)的一种扩展. 近年来, 已经引起了广泛的关注[4,5].
缓冲区约束通常存在于各种生产行业中, 由于机器中间缓冲区或生产温度的限制, 使得工件加工完成后被阻塞在当前机器上. 在阻塞情况下, 前一台机器会保持当前已完成的作业, 直到下一台机器或缓冲区可用[6,7]. 产品属性的影响也会导致阻塞现象. 例如, 在钢铁制造中, 有两个关键的阶段: 加热和轧制钢板. 铸块在煤坑中加热到很高的温度后, 被送到轧制钢板磨坊轧制. 由于加热设备的停止和开启需要很长时间, 为了提高效率和节省成本, 在设备运行时, 希望加工过程是连续的, 此时的铸块加工过程可以被考虑为缓冲区容量为0的流水车间调度问题.
为了解决阻塞约束问题, 许多工业生产工厂已经开始采用优化作业排序策略以提高生产效率. 高效的作业调度算法对于企业提高生产效率有重要的推动作用[3], 针对有限缓冲区流水车间调度问题, Liang等[8]提出了自适应差分进化算法来解决以最大时间和最大工作延迟为目标的双目标优化问题问题. Bai等[9]研究了一个具有有限缓冲区的非排列双代理流水车间调度问题, 任务随着时间的推移而释放, 并提出了一种混合粒子群优化(HPSO)算法来寻求高质量的解决方案. Kazemi Esfeh等[10]提出了一种新的数学模型来解决存在中间缓冲区、预算和人力资源等约束的柔性流水车间问题. Janeš等[11]探讨了有限缓冲条件下混合流水车间中产品批次的订单和批次大小的确定问题, 并开发了一种基于改进的稳态遗传算法的调度方法对问题进行求解并取得了良好的效果. 徐震浩等[12]针对缓冲区空间和时间同时受限的流水车间调度问题, 以最小化完工时间为优化目标, 提出一种改进的离散帝国竞争算法求解.
近年来, 随着能源价格的持续走高, 考虑节能减排的绿色制造浪潮正在全球范围内兴起, Lu等[13]以最小化完工时间和总能耗(TEC)为目标, 针对具有有限缓冲的分布式置换流水车间节能调度问题进行了研究, 并提出了一种基于Pareto的协同多目标优化算法进行求解. Jiang等[14]建立了针对有限缓冲区的混合整数线性规划模型, 该模型考虑最小化总加权延迟和总加工能耗两个目标. 在基于分解的多目标进化算法框架下开发了一种高效的多目标优化算法. 取得了良好的效果. Yaurima-Basaldua等[15]针对复杂的多阶段、多产品、多机器和批量生产环境, 考虑完成时间和能耗为优化目标, 提出了基于非支配排序遗传算法双目标算法, 实验结果表明, 与实际生产相比, 它可以节省48%的生产时间和47%的电力消耗. Han等[16]提出了一种将基于模拟退火算法、Hopfield神经网络算法与局部调度规则相结合的新方法对缓冲区柔性流水车间进行了研究.
蒲公英优化算法(dandelion optimization algorithm, DOA)由Zhao等[17]于2022年提出, 通过模拟蒲公英种子依靠风长距离飞行的过程对问题进行优化求解, 作者在CEC2017测试集上, 将蒲公英优化算法与9种先进的元启发式算法进行比较, 对算法的优化精度、稳定性、收敛性和延展性等进行了评估. 实验结果表明, 与已有算法相比, 蒲公英优化算法具有较好的优化能力和较强的鲁棒性. 本文将蒲公英优化算法的应用拓展到车间调度问题当中, 首先建立了以完工时间和完工能耗为目标函数的有限缓冲区流水车间调度模型, 设计了适应于调度问题的双层编码机制表示问题的解. 之后通过引入一种种群初始化策略, 提高初始种群的多样性, 在算法迭代过程中, 基于编码染色体设计了实数交叉策略和变邻域搜索策略, 弥补了原始蒲公英算法局部搜索能力较差的缺点, 提高了改进算法的开发能力. 最后, 通过仿真实验和算法比较, 验证了所提IDOA算法的有效性.
1 问题描述与模型考虑缓冲区容量限制和机器加工档位的流水车间调度问题(flow shop scheduling problem with limited buffers and machine processing gears, FSSP_LBMPG), 可以描述如下: 有
| 表 1 符号及其含义 |
给出本文问题模型目标函数计算公式如下:
| {Cπ11=tπ11=Tπ11/vπ11Cπi1=Cπi−11+Tπi−11/vπi−11,i=2,⋯,B1+1Cπ1j=Cπ1(j−1)+Tπ1j/vπ1j,j=1,⋯,mCπi1=max | (1) |
则最大完工时间计算公式为:
| {C_{\max }} = {C_{{\pi _n}m}} | (2) |
总能耗的计算公式为:
| \begin{split} E = & {E_{\rm cost}} + {E_{\rm idle}} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{P_{j{v_{ij}}}}} } \times {T_{ij}}/{v_{ij}} \\ &+\sum\limits_{i = 2}^n {\sum\limits_{j = 1}^m {{{P'_j}}} } \times ({C_{{\pi _i}j}} - {C_{{\pi _{i - 1}}j}} - {T_{{\pi _i}j}}/{v_{ij}}) \end{split} | (3) |
s.t.
| \sum\limits_{j = 1}^m {{x_{ilj}}} = 1, \forall i, l | (4) |
| \sum\limits_{i = 1}^n {{x_{ilj}}} = 1, \forall l, j | (5) |
| \sum\limits_{s = 1}^S {{y_{ijs}}} = 1, \forall i, j | (6) |
| {t}_{ij}={T}_{ij}\times {\displaystyle \sum _{s=1}^{S}({y}_{ijs}}/{S}_{s})\text{, }\forall i, j | (7) |
| {C}_{ij+1}-{C}_{ij}\geqslant {t}_{ij}\text{, }j=1, 2, \cdots, m-1, \forall i | (8) |
| {C}_{lj}-{C}_{l-1j}\geqslant {\displaystyle \sum _{i=1}^{n}({x}_{ilj}\times {t}_{ij}})\text{, }l\geqslant 2, \forall i, j | (9) |
| {x}_{ilj}\in \{0, 1\}, \forall i, l, j | (10) |
| {y}_{ijs}\in \{0, 1\}, \forall {i}, j, s | (11) |
其中, 式(1)、式(2)为完工时间的计算公式, 式(3)为总能耗的计算公式. 式(4)阐述了不同机器之间不得协同加工工件的规定. 式(5)说明了不同工件不能在同一台机器上同时进行加工的限制. 式(6)表明在工件的工序加工过程中, 机器的加工档位是固定的. 式(7)表示工件在机器上的实际加工时间的计算方法. 式(8)规定了工件的加工工艺路线是固定的. 式(9)明确了在同一台机器上, 在同一时刻只能有一个工件进行加工. 式(10)和式(11)为0-1变量约束.
2 改进蒲公英优化算法 2.1 蒲公英算法基本流程蒲公英算法由Zhao等[17]在2022年提出, 算法主要模拟蒲公英种子依靠风进行长距离飞行的过程, 成熟之后的蒲公英种子要进行3个阶段: 在上升阶段蒲公英种子在风速的作用下上升, 到达一定高度后, 进入下降阶段, 直到最终随机落地, 生长出新的蒲公英. DOA算法模拟了这个过程并引入了Brownian运动和Levy飞行描述种子的运动轨迹.
(1)上升阶段
在晴天, 蒲公英在风速的影响下被随机吹到各个位置, 风速越大, 飞得越远, 在这种情况下, 蒲公英个体的位置更新公式为:
| x_i^{t + 1} = x_i^t + \alpha \times {v_x} \times {v_y} \times \ln Y \times (x_{rand}^t - x_i^t) | (12) |
其中,
| \ln Y = \left\{ \begin{gathered} \frac{1}{{y\sqrt {2\pi } }}{{\mathrm{e}}^{\left[ { - \frac{1}{{2{\sigma ^2}}}{{(\ln y)}^2}} \right]}}, y \geqslant 0 \\ 0, \qquad\qquad\qquad\;\;\; y< 0 \\ \end{gathered} \right. | (13) |
其中,
| \alpha = rand \times \left(\frac{1}{{{T^2}}}{t^2} - \frac{2}{T}t + 1\right) | (14) |
其中,
| {v_x} = \frac{1}{{{{\mathrm{e}}^\theta }}} \times \cos \theta , {v_y} = \frac{1}{{{{\mathrm{e}}^\theta }}} \times \sin \theta | (15) |
其中,
雨天, 蒲公英种子无法上升, 而是在当前位置周围盘旋, 此时的位置更新公式为:
| \left\{ \begin{split} & x_i^{t + 1} = x_i^t \times k \\ & k = 1 - rand \times q \\ & q = \frac{1}{{{T^2} - 2T + 1}}{t^2} - \frac{2}{{{T^2} - 2T + 1}}t + 1 + \frac{1}{{{T^2} - 2T + 1}} \end{split} \right. | (16) |
其中,
| x_i^{t + 1} = \left\{ \begin{gathered} x_i^t + \alpha \times {v_x} \times {v_y} \times \ln Y \times (x_{rand}^t - x_i^t), rand < 1.5 \\ x_i^t \times k{, \qquad\qquad\qquad\qquad\qquad\quad\;\;{\mathrm{else}}} \\ \end{gathered} \right. | (17) |
其中,
(2)下降阶段
通过模拟蒲公英种子的下降阶段增强算法的勘探能力, 此阶段算法通过引入Brownian运动和采用上升阶段后的平均位置信息, 使得种群朝着更有潜力的区域发展, 此阶段个体的位置更新公式为:
| x{'}_i^{t + 1} = x_i^{t + 1} - \alpha \times \beta (x_{\rm mean}^{t + 1} - \alpha \times \beta \times x_i^{t + 1}) | (18) |
其中,
(3) 落地阶段
在前两个阶段的基础上, 蒲公英种子随机选择降落地点, 随着迭代的逐步进行, 算法有望收敛到全局最优解. 落地阶段蒲公英个体利用当前精英个体的位置, 在其局部邻域中搜索, 位置更新公式为:
| x{'}_i^{t + 1} = x_{\rm elite}^t + Levy(\lambda ) \times \alpha \left(x_{\rm elite}^t - x{'}_i^{t + 1} \times \frac{{2t}}{T}\right) | (19) |
其中,
| Levy(\lambda ) = s \times \frac{{w \times \sigma }}{{{{\left| {{r_1}} \right|}^{\frac{1}{\gamma }}}}} | (20) |
其中,
| \sigma = {\left(\frac{{\Gamma (1 + \gamma ) \times \sin \left(\dfrac{{\pi \gamma }}{2}\right)}}{{\Gamma \left(\dfrac{{1 + \gamma }}{2}\right) \times \gamma \times {2^{(\frac{{\gamma - 1}}{2})}}}}\right)^{\frac{1}{\gamma }}} | (21) |
蒲公英优化算法通过上升、下降、落地3大策略, 大大提高了算法的搜索能力, 能够搜索到更多的存在潜在最优解的区域, 具有良好的探索性能. 付出的代价是算法的开发能力较差, 由于算法全局探索和局部开发能力不平衡, 导致算法收敛时间长. 为了提高蒲公英优化算法求解流水车间调度问题时的综合性能, 本文提出一种改进蒲公英优化算法(improved dandelion optimization algorithm, IDOA), 改进算法首先建立一种双层编码机制, 分别用来求解工件排序子问题和档位选择子问题. 采用对数函数计算方法以统一完工时间及加工能耗之间的量纲. 引入初始化机制, 提高初始种群的多样性, 提高算法的全局搜索能力. 种群迭代过程中, 在原有蒲公英算法上升、下降、落地3大搜索策略的基础上, 设计了基于机器档位选择编码向量的实数交叉策略与结合交换、插入、逆序3种邻域结构的变邻域搜索策略, 弥补了原始蒲公英算法局部搜索能力较差的缺点, 提高了改进算法的开发能力.
2.2.1 编码与解码本文建立的考虑缓冲区容量限制的流水车间调度问题需要确定工件在机器上的加工顺序与机器选择的加工档位2个子问题. 为此, 本文建立一种双层编码机制, 每个解决方案都由2个部分组成, 分别是工件排序编码向量和机器档位选择编码向量. 这2个向量都是由随机生成的0–1之间的数字组成, 工件排序向量的长度与车间需加工的总工件数相等, 机器档位选择向量长度为
在对编码向量进行解码计算目标函数值时, 首先通过ROV转换将工件排序编码向量从实数域转换到整数域, 机器档位选择编码向量通过计算向量值乘以机器可选档位数再向上取整, 计算得到的值即为对应档位中选择的加工档位, 需要注意的是, 本文设计的机器档位编码按照工件顺序进行编码而与工件排序编码无关. 如图1所示为一个拥有5个工件, 5台加工机器, 每台加工机器具备3个加工档位[1, 1.2, 1.4]的案例示意图, 
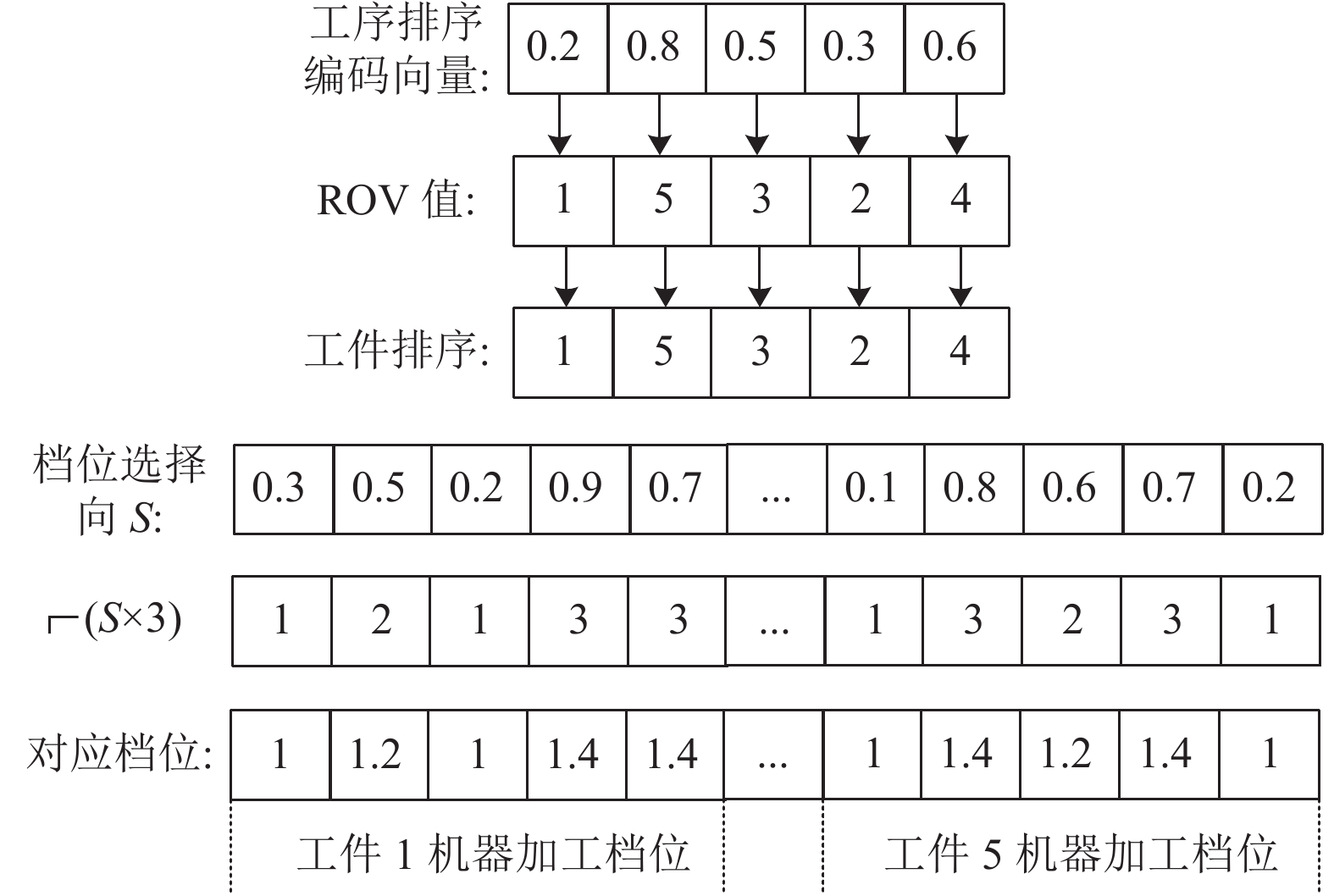
|
图 1 编码解码示意图 |
如图2所示为在不同缓冲区约束条件下, 使用主动调度的解码方式, 对图1中的编码向量进行解码之后的甘特图示意图, 图2(a)为缓冲区容量限制为0时, 解码得到调度方案的完工时间值为27.5, 图2(b)为缓冲区容量限制为无限大时, 解码得到调度方案的完工时间值为25.25, 缓冲区容量越小, 机器在加工工件时为避免违反缓冲区容量约束, 工件在机器上的加工完成时间可能越晚, 从而影响最终的加工完成时间.
2.2.2 适应度函数为比较不同解决方案之间的优劣关系, 采用对数函数统一能耗和完工时间之间的量纲, 并通过归一化方法将多目标调度问题转换为单目标调度问题, 适应度函数的计算公式为:
| f(X) = {\lambda _1} \times {\lg}C + {\lambda _2} \times {\lg}E | (22) |
其中,
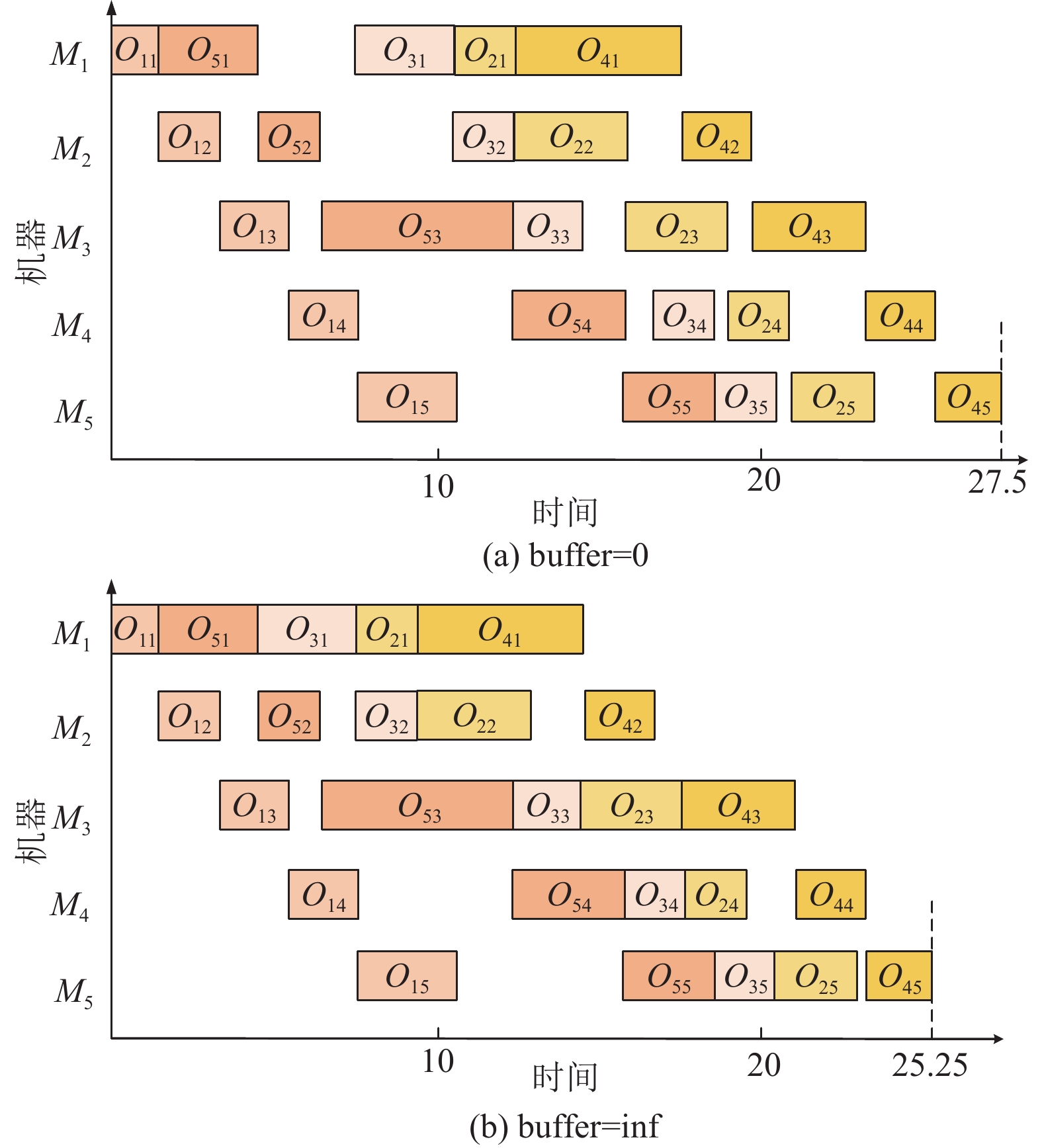
|
图 2 不同缓冲区解码示意图 |
2.2.3 种群初始化
为了提高初始种群的多样性从而增强算法的全局探索能力, 本文采用随机初始化的方法产生工件排序向量编码, 对于机器档位编码, 考虑降低能耗与降低完工时间的影响, 机器档位编码种群中1/10的个体选择最高的加工档位进行加工以降低解决方案的完工时间, 最大化机器利用率, 属于用能耗换加工效率. 1/10的初始种群个体选择最低的加工档位以降低能耗的影响, 通过延长加工时间, 降低生产能耗. 其余种群中的初始个体采用随机初始化的方法产生机器档位选择编码种群. 通过以上方式, 既达到了提高初始解质量的目的, 在对机器加工档位选择编码向量进行实数交叉变异策略之时, 能够进行更加充分地搜索, 增强算法搜索能力.
2.2.4 实数交叉策略本文设计的编码方案包括工序排序编码向量和机器加工档位选择编码向量两部分, 针对工序排序编码向量, 原蒲公英优化算法利用上升、下降、落地3大搜索策略, 对工序排序编码向量进行充分的搜索, 然而在这个阶段机器加工档位选择编码向量并没有参与到搜索过程当中, 因此本文针对机器档位选择编码向量, 设计了一种基于实数编码的交叉策略, 选择不同的机器加工档位可能会提升解的质量, 从而在蒲公英种群迭代过程中, 使算法对解空间进行更高效搜索, 提高算法的探索能力, 搜索到更多的可能存在最优解的区域.
本文基于实数对机器档位选择编码向量进行交叉产生实数子代, 从而在算法迭代过程中, 产生的子代向量可以继续参与到原蒲公英优化算法的进化策略当中, 而不需要再将ROV值转换为蒲公英优化算法进化过程中需要的实数值, 基于实数的交叉策略的具体步骤为: 随机生成一个与机器档位选择编码向量长度相等的只包含整数0, 1值的数组
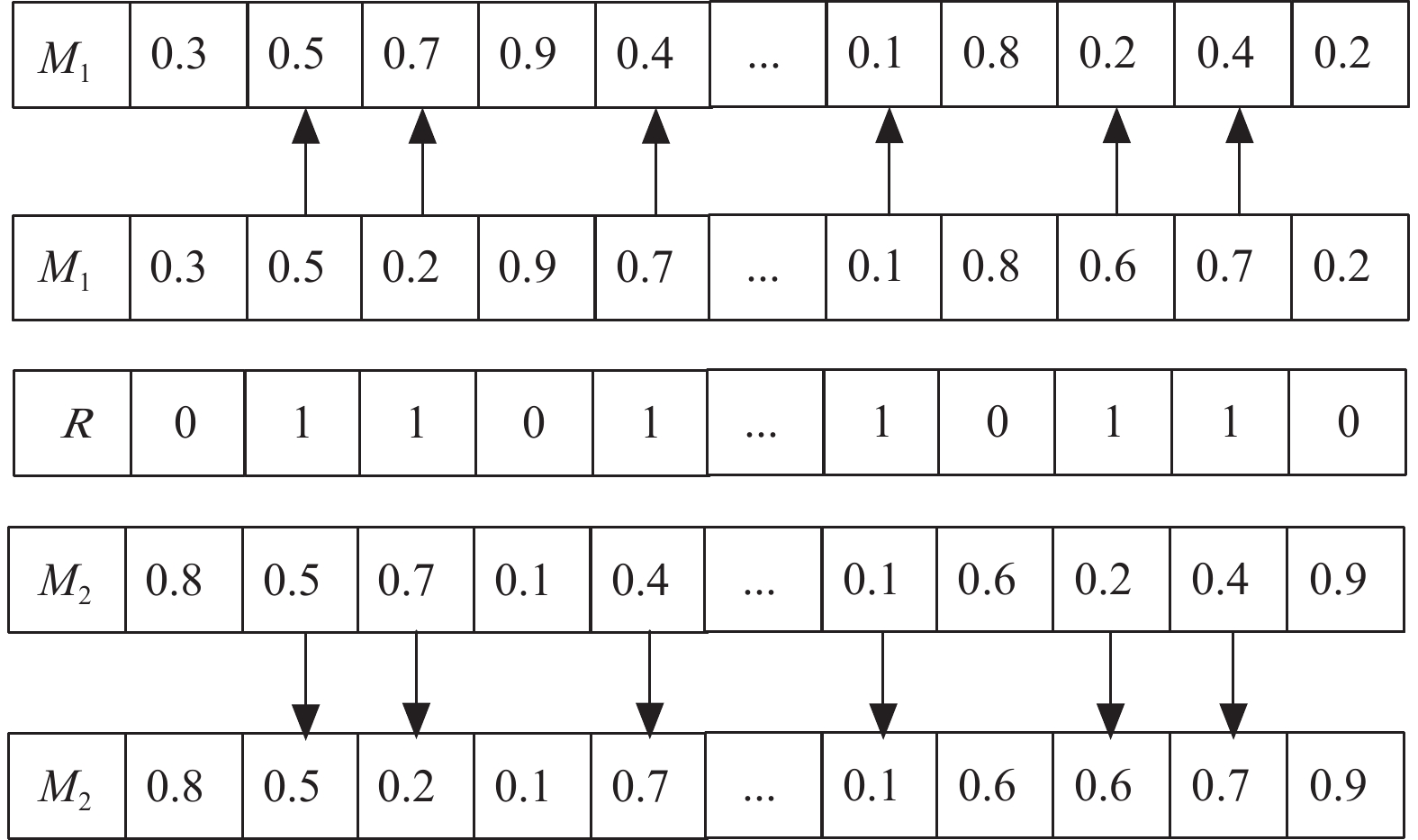
|
图 3 实数交叉示意图 |
2.2.5 变邻域搜索策略
为进一步提高算法的开发能力, 本文在基于机器档位选择编码向量的实数交叉策略的基础上, 针对工件排序编码向量, 进一步提出一种基于实数编码的变邻域搜索策略以提高解的质量, 增强改进算法的局部搜索能力. 邻域策略包括: (1)交换邻域, 随机产生工件排序编码向量长度范围内的两个不相等的正整数, 交换对应整数位置上的值. (2)插入邻域, 随机产生工件排序编码向量长度范围内的两个不相等的正整数, 将第1个整数位置上的值插入到第2个整数位置后方. (3)逆序邻域, 将两个整数中间位置上的值逆序. 通过变邻域搜索操作, 算法在潜在最优解区域周围能够进行更加充分的搜索, 从而大大提升了算法的开发能力. 邻域结构示意图如图4所示.
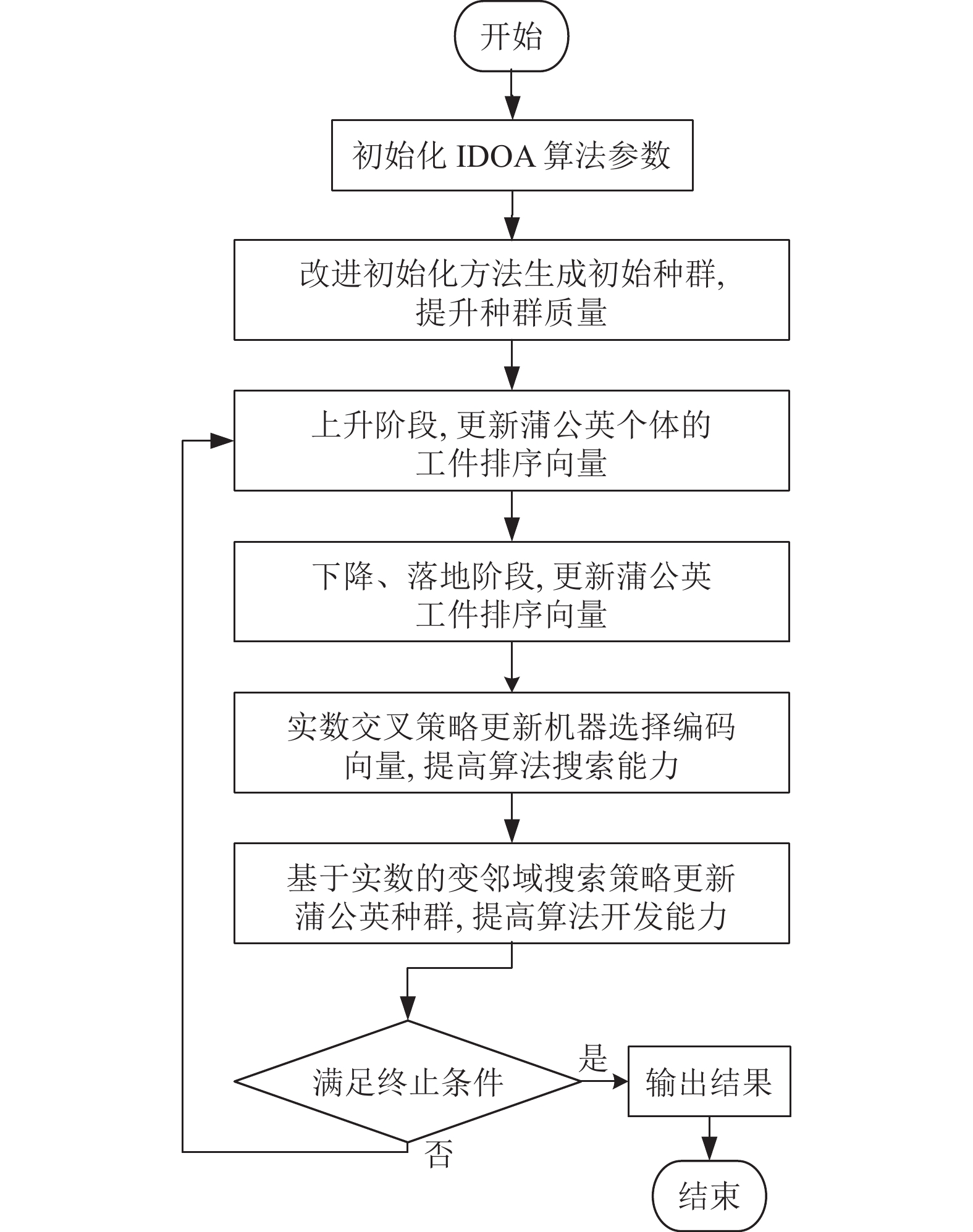
2.2.6 算法基本流程改进蒲公英优化算法的基本流程如图5所示.
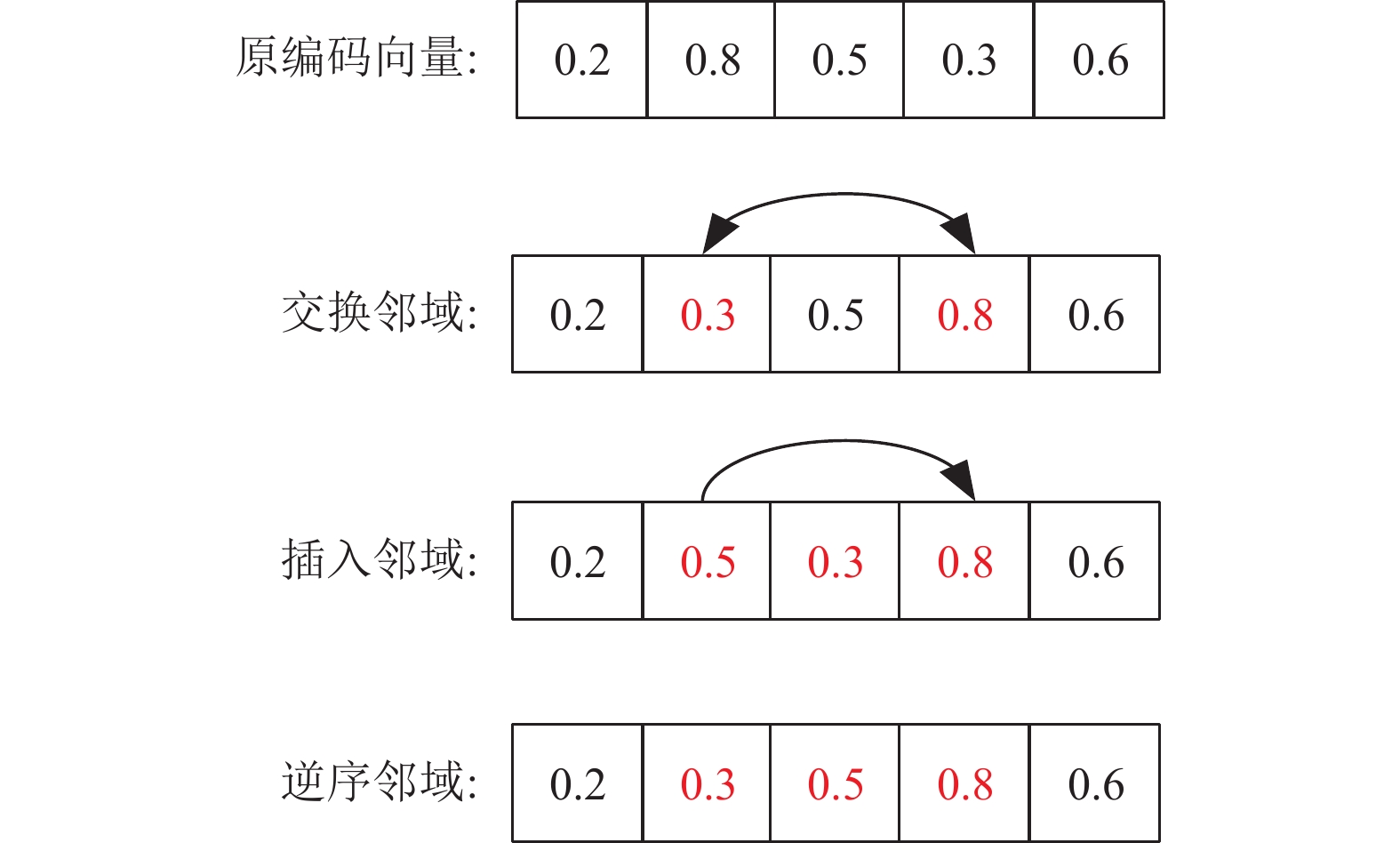
|
图 4 变邻域搜索示意图 |
|
图 5 改进蒲公英优化算法流程图 |
3 仿真实验
为了验证算法性能, 本文基于典型的10个流水车间调度问题设计测试算例, 即Reeves系列测试集rec01, rec03, …, rec19. 参考文献[18]中有关机器加工档位的设定, 本文中的机器加工档位值设置为S={S1, S2, S3}={1, 1.2, 1.4}, 机器加工功率
为了验证本文所提改进策略对于算法效果的提升, 采用缓冲区等于1的测试集对IDOA和DOA进行对比, 同时为了降低随机性的影响, 算法在每个算例上均运行10次, 使用Best表示算法在不同算例下10次求解结果中, 适应度函数的最优值. Avg表示算法在不同算例下10次求解结果的平均值. 算法种群规模设为100, IDOA实数交叉概率设为0.8, 如表2所示为算法在不同算例下分别运行20代、50代、100代后适应度函数的指标值. 从表2可以看出, 在所有4类规模的10个测试算例上, 本文的改进蒲公英优化算法在最优值指标和平均值指标上均取得了较原始蒲公英优化算法更好的解, 这是因为DOA算法虽然具有良好的勘探能力, 但当DOA算法寻找到潜在最优解周围区域时, 由于缺少良好的局部开发能力, 导致算法在潜在最优解周围收敛速度很慢, 而本文提出的IDOA算法, 当寻找到潜在最优解周围时, 通过改进的实数交叉策略和变邻域搜索策略, 改进算法可以进行更加充分且有效的有针对性的搜索, 大大提高了算法的局部搜索能力, 增强了算法的性能.
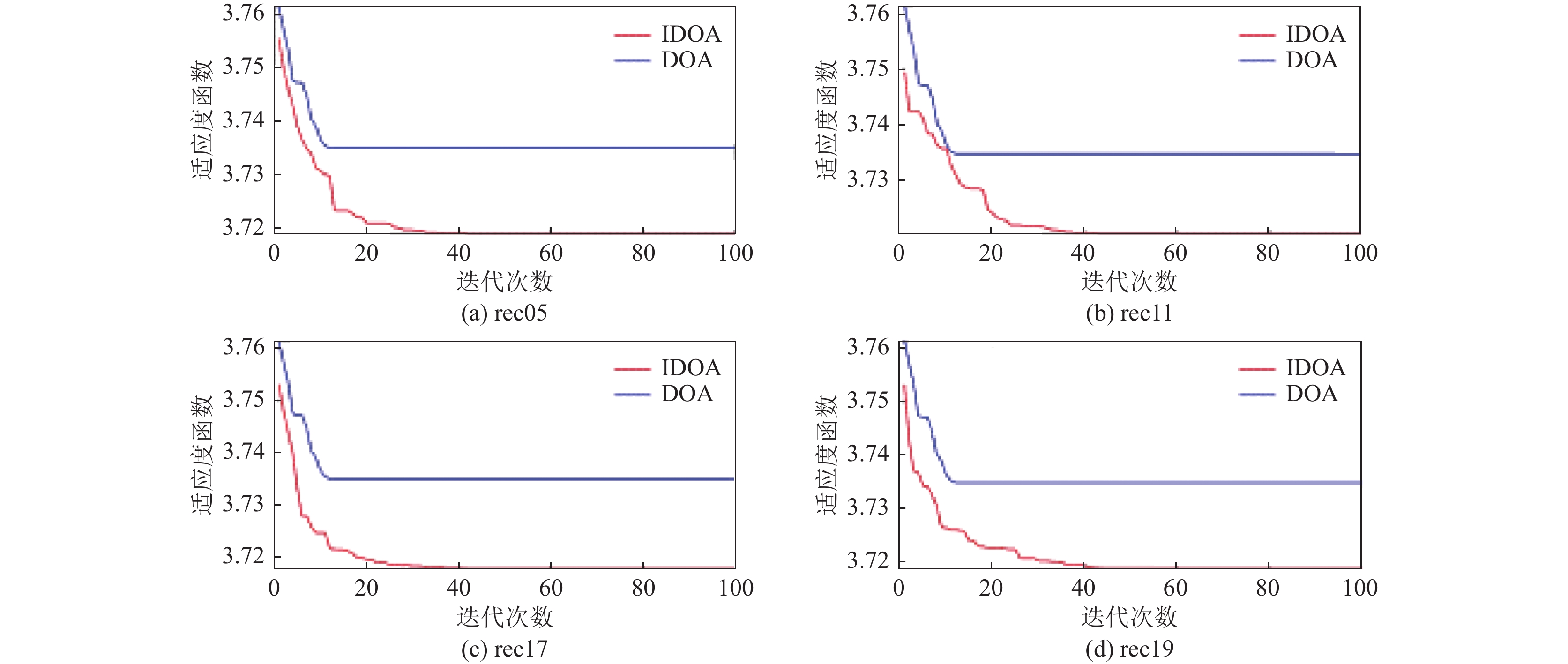
从算法收敛性能看, 如图6所示为DOA算法和IDOA算法在4个算例上运行的最优值收敛曲线图, 从图6中可以看出在刚开始迭代时, IDOA最优解的质量明显优于DOA算法, 证明了本文提出的初始化机制对于提高初始种群质量的有效性, 随着算法的迭代运行, DOA算法虽然比IDOA算法收敛速度更快, 但是寻找到的最优解的质量要明显劣于IDOA算法, 侧面印证了原始DOA算法开发能力较弱的问题, 从而导致算法过早收敛于局部最优解.
| 表 2 IDOA与DOA的对比结果 |
|
图 6 IDOA与DOA收敛曲线图 |
3.2 IDOA与其他优化算法的对比
为验证算法性能, 将IDOA算法与广泛应用于车间调度问题的遗传算法(GA)、模拟退火算法(SA)以及双层变异迭代贪婪算法(IGDLM)[20]进行比较. GA、SA、IDOA算法的种群规模设为100, 迭代次数设为100, 遗传算法的交叉概率为0.8, 变异概率设为0.1. 模拟退火算法初始温度设为50, 最低温度设为1E–6, 降温速率设为0.99. IGDLM算法参考文献[20]进行参数取值. 同样进行10次重复实验以降低随机性的影响, 算法对比结果如表3所示.
| 表 3 IDOA、GA、SA、IGDLM在不同缓冲区容量下的对比结果 |
从表3可以看出, 本文所提的IDOA在对比结果中的优化效果明显优于遗传算法、模拟退火算法和双层变异迭代贪婪算法, 在所有的测试算例上, 不论是求解的最优值, 还是10次求解结果的平均值, IDOA均取得了比对比算法更优的结果. 双层变异迭代贪婪算法虽然在求解本文的考虑机器档位和缓冲区容量的流水车间调度问题时效果要略优于模拟退火算法和遗传算法, 但是由于缺乏良好的勘探策略, 影响了算法整体的求解效果.
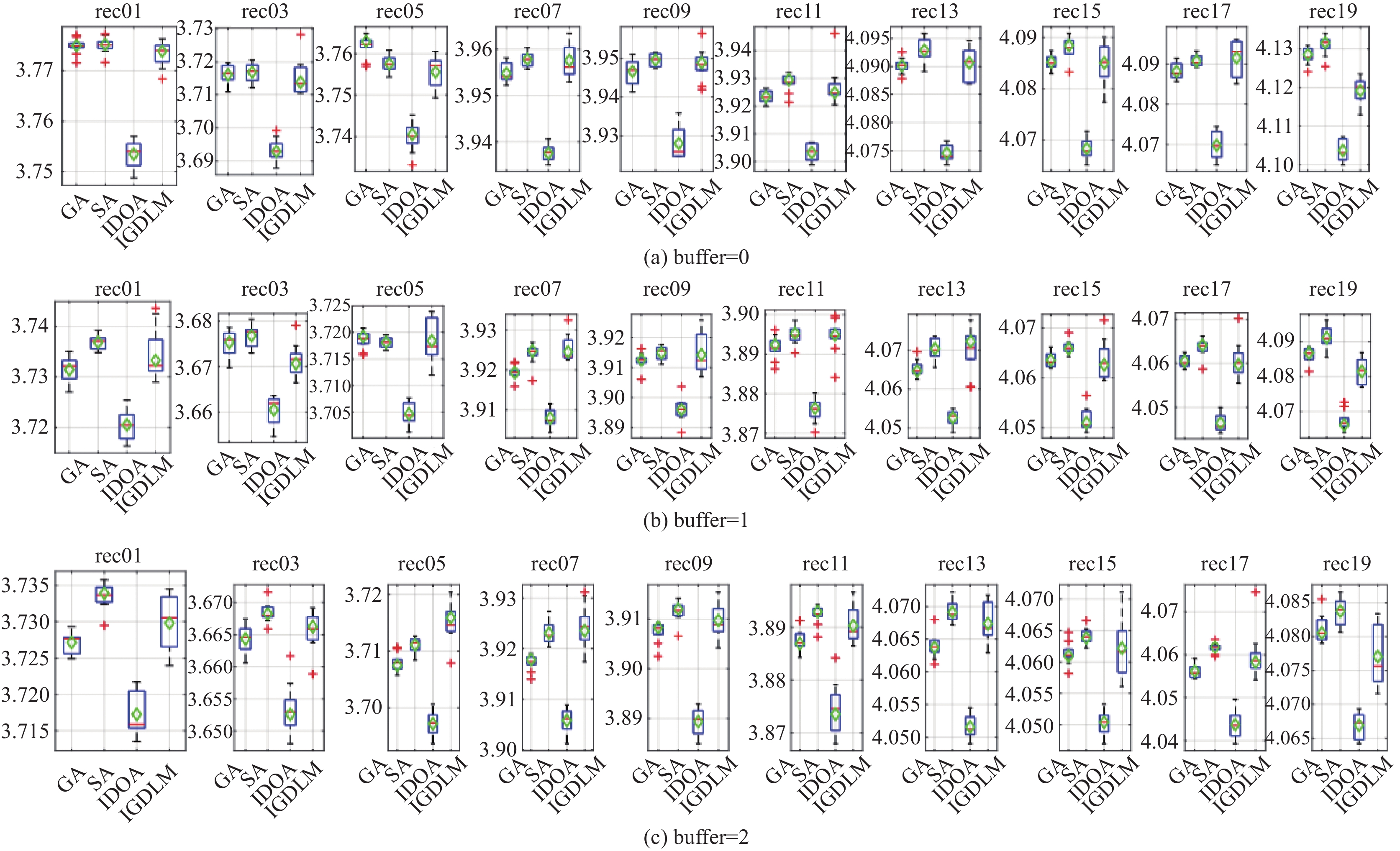
算法收敛性对比如图7–图9. 图7为不同缓冲区容量下的算法对比箱线图, 绿色菱形表示10次求解结果的平均值.
|
图 7 不同缓冲区下算法对比箱线图 |

|
图 7 不同缓冲区下算法对比箱线图(续) |
|
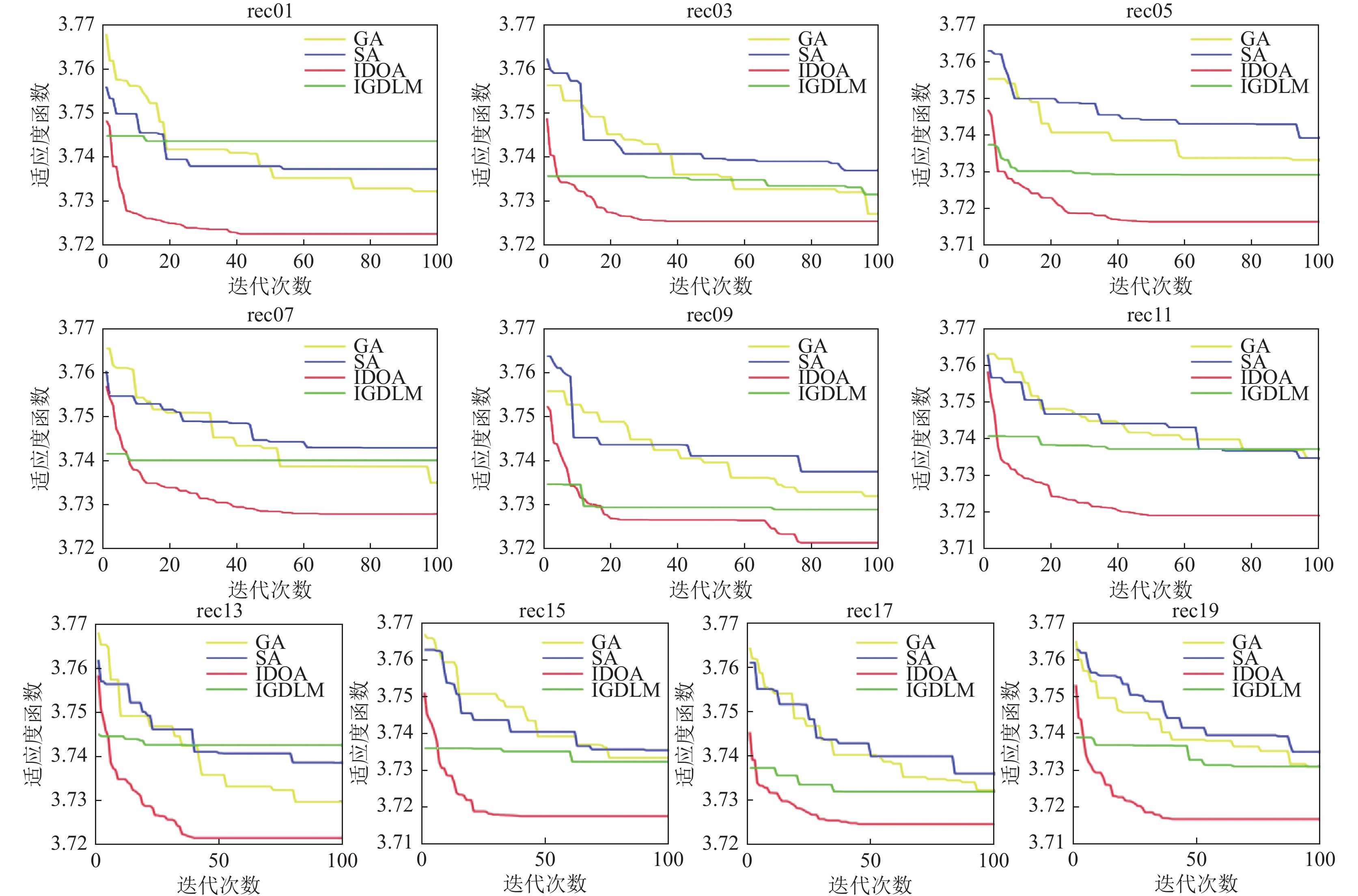
图 8 收敛曲线对比 |
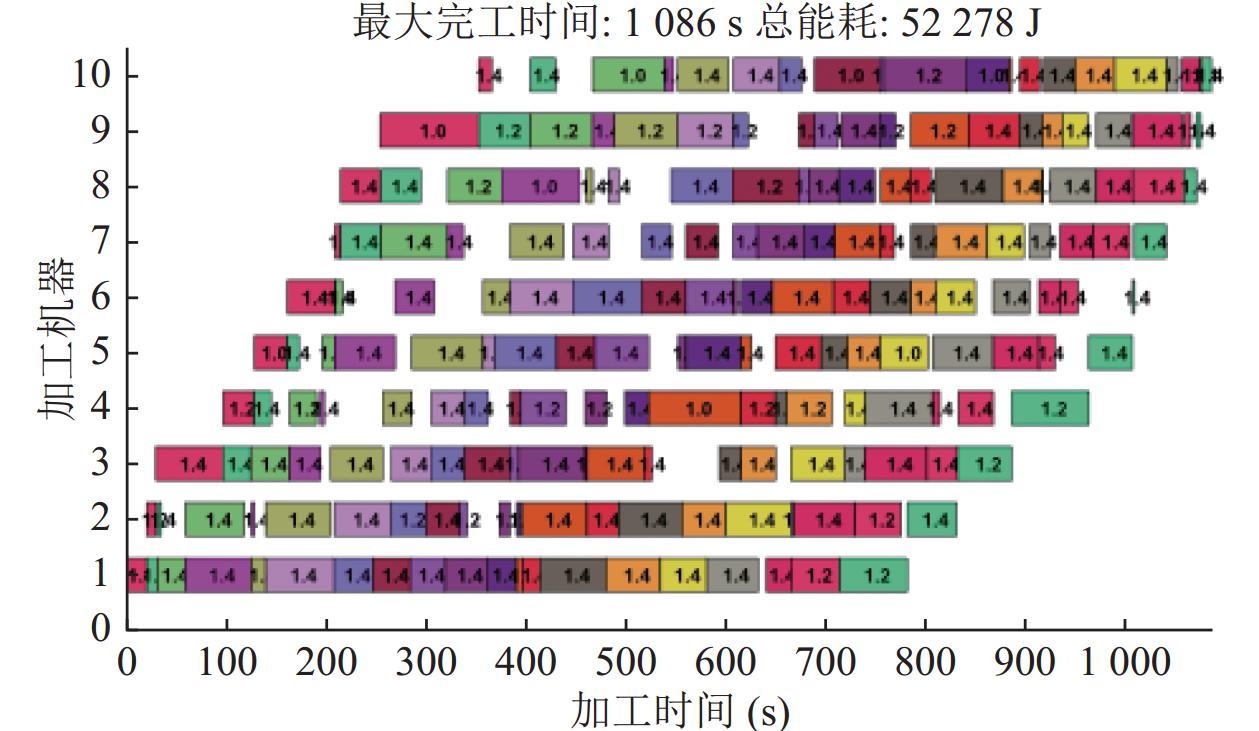
图8所示为算法在缓冲区容量为1时运行的最优值收敛曲线图, 从图8中可以看出, 在求解稳定性上, IDOA算法性能要差于对比算法, 但IDOA算法在求解质量上要远优于对比的遗传算法、模拟退火算法与双层变异迭代贪婪算法. 验证了IDOA算法在求解本文提出的FSSP_LBMPG问题时的有效性. 如图9所示为IDOA算法在rec11算例下求得的最优结果的甘特图, 算法求得的工序排序结果为[14 16 9 18 19 1 12 10 7 20 4 13 2 8 3 5 11 15 17 6], 甘特图中矩阵上的数字表示工件选择的机器加工档位.
|
图 9 甘特图 |
4 结语
通过考虑机器加工过程中加工档位和加工时间、加工能耗之间的关系, 本文建立了以最小化完工时间和最小化能量消耗为目标函数的考虑缓冲区容量限制和机器加工档位的流水车间调度模型, 并提出一种改进蒲公英优化算法对模型进行求解, 改进算法在原有蒲公英优化算法上升、下降、落地3大进化策略的基础上, 进一步提出了一种种群初始化机制以提高初始种群的质量, 加快搜索速度. 算法迭代过程中, 提出了针对机器档位编码的实数交叉策略以及变邻域搜索策略, 弥补了原始DOA算法局部搜索能力差, 开发性能疲弱的缺点, 大大提高了算法的性能. 最后通过在测试算例上将IDOA与DOA算法, IDOA与GA、SA、IGDLM算法进行对比分析验证了IDOA算法在求解本文所提出的问题时的有效性和鲁棒性.
| [1] |
Qin M, Wang RS, Shi ZS, et al. A genetic programming-based scheduling approach for hybrid flow shop with a batch processor and waiting time constraint. IEEE Transactions on Automation Science and Engineering, 2021, 18(1): 94-105. DOI:10.1109/TASE.2019.2947398 |
| [2] |
Meng T, Pan QK, Wang L. A distributed permutation flowshop scheduling problem with the customer order constraint. Knowledge-based Systems, 2019, 184: 104894. DOI:10.1016/j.knosys.2019.104894 |
| [3] |
Qin HX, Han YY, Wang YT, et al. Intelligent optimization under blocking constraints: A novel iterated greedy algorithm for the hybrid flow shop group scheduling problem. Knowledge-based Systems, 2022, 258: 109962. DOI:10.1016/j.knosys.2022.109962 |
| [4] |
轩华, 郑倩倩, 李冰. 带不相关并行机的阻塞FFP的混合遗传算法. 计算机工程与设计, 2021, 42(4): 949-956. DOI:10.16208/j.issn1000-7024.2021.04.008 |
| [5] |
温廷新, 关婷誉. 考虑能耗和运输的有限缓冲区混合流水车间调度. 系统仿真学报, 2024, 36(6): 1344–1358. [doi: 10.16182/j.issn1004731x.joss.23-0343]
|
| [6] |
Han X, Han YY, Zhang B, et al. An effective iterative greedy algorithm for distributed blocking flowshop scheduling problem with balanced energy costs criterion. Applied Soft Computing, 2022, 129: 109502. DOI:10.1016/j.asoc.2022.109502 |
| [7] |
Aqil S, Allali K. Two efficient nature inspired meta-heuristics solving blocking hybrid flow shop manufacturing problem. Engineering Applications of Artificial Intelligence, 2021, 100: 104196. DOI:10.1016/j.engappai.2021.104196 |
| [8] |
Liang J, Wang P, Guo L, et al. Multi-objective flow shop scheduling with limited buffers using hybrid self-adaptive differential evolution. Memetic Computing, 2019, 11(4): 407-422. DOI:10.1007/s12293-019-00290-5 |
| [9] |
Bai DY, Liu TY, Zhang YC, et al. Scheduling non-permutation flowshop with finite buffers and two competitive agents. Computers & Industrial Engineering, 2023, 177: 108939. |
| [10] |
Kazemi Esfeh M, Shojaie AA, Javanshir H, et al. Flexible flow shop scheduling problem with reliable transporters and intermediate limited buffers via considering learning effects and budget constraint. Complexity, 2022, 2022: 1253336. |
| [11] |
Janeš G, Ištoković D, Jurković Z, et al. Application of modified steady-state genetic algorithm for batch sizing and scheduling problem with limited buffers. Applied Sciences, 2022, 12(22): 11512. DOI:10.3390/app122211512 |
| [12] |
徐震浩, 王程, 顾幸生. 基于DICA的存储受限流水车间调度. 华东理工大学学报(自然科学版), 2018, 44(4): 563–572. [doi: 10.14135/j.cnki.1006-3080.20170627003]
|
| [13] |
Lu C, Huang YX, Meng LL, et al. A Pareto-based collaborative multi-objective optimization algorithm for energy-efficient scheduling of distributed permutation flow-shop with limited buffers. Robotics and Computer-integrated Manufacturing, 2022, 74: 102277. DOI:10.1016/j.rcim.2021.102277 |
| [14] |
Jiang SL, Zhang L. Energy-oriented scheduling for hybrid flow shop with limited buffers through efficient multi-objective optimization. IEEE Access, 2019, 7: 34477-34487. DOI:10.1109/ACCESS.2019.2904848 |
| [15] |
Yaurima-Basaldua VH, Tchernykh A, Villalobos-Rodríguez F, et al. Hybrid flow shop with unrelated machines, setup time, and work in progress buffers for bi-objective optimization of tortilla manufacturing. Algorithms, 2018, 11(5): 68. DOI:10.3390/a11050068 |
| [16] |
Han ZH, Han C, Lin S, et al. Flexible flow shop scheduling method with public buffer. Processes, 2019, 7(10): 681. DOI:10.3390/pr7100681 |
| [17] |
Zhao SJ, Zhang TR, Ma SL, et al. Dandelion optimizer: A nature-inspired metaheuristic algorithm for engineering applications. Engineering Applications of Artificial Intelligence, 2022, 114: 105075. DOI:10.1016/j.engappai.2022.105075 |
| [18] |
胡蓉, 董钰明, 钱斌. 基于探路者算法的绿色有限缓冲区流水线调度. 系统仿真学报, 2021, 33(6): 1384-1396. DOI:10.16182/j.issn1004731x.joss.20-0077 |
| [19] |
Lei DM, Zheng YL, Guo XP. A shuffled frog-leaping algorithm for flexible job shop scheduling with the consideration of energy consumption. International Journal of Production Research, 2017, 55(11): 3126-3140. DOI:10.1080/00207543.2016.1262082 |
| [20] |
秦浩翔, 韩玉艳, 陈庆达, 等. 求解阻塞混合流水车间调度的双层变异迭代贪婪算法. 控制与决策, 2022, 37(9): 2323-2332. DOI:10.13195/j.kzyjc.2021.0607 |
 2024, Vol. 33
2024, Vol. 33



