2. 兰州工业学院 经济管理学院, 兰州 730030
2. School of Economics and Management, Lanzhou Institute Technology, Lanzhou 730030, China
在中国史前彩陶文化中, 甘肃彩陶因其未曾间断的文化传承, 在漫长的历史进程中形成了独特的文化体系和区域特色, 占据了我国彩陶文化中的重要地位. 甘肃彩陶的纹样丰富多彩, 器形结构独特优美, 尤其是马家窑文化出土的彩陶, 代表着中国彩陶艺术的最高成就, 被誉为新石器时代“彩陶之冠”. 当前对甘肃彩陶的研究主要聚焦于纹样演变[1]、艺术鉴赏[2]以及制作工艺解析[3]等方面, 而针对甘肃彩陶进行数字化研究的尝试尚未广泛展开. 数字化研究面临的首要问题是缺乏甘肃彩陶数据集. 其次, 近年来图像风格迁移研究通常对图像提取不同层级特征, 帮助算法衡量图像之间内容和风格差异, 进而实现将一幅图像的风格迁移为另一幅图像的艺术效果, 由于彩陶纹理的复杂多样性以及色彩层次的相近性, 使充分捕捉其纹理特征成为一大难题. 此外, 神经风格迁移一直以纹理迁移为主, 但几何变化也是风格的组成部分, 当只关注图像的色彩和纹理等方面的风格时, 最终输出会保持内容图像的原始几何形状不变, 这使得输出图像很容易被辨认为对原始图像简单添加“滤镜”. 随着逐渐认识到几何变化的重要性, 大多研究都围绕面部图像迁移为漫画[4]和文本图像迁移为艺术字体[5]展开, 而甘肃彩陶具有特有的曲线和器型, 当其在几何形状上与其他物体存在显著差异时, 难以直接进行外形上的风格化处理.
为了解决以上问题, 本文构建了一个甘肃彩陶数据集, 并设计了一个甘肃彩陶风格迁移模型GPST (Gansu painted pottery style transfer)与几何风格迁移方法DST[6]和LWST[7]不同, GPST利用彩陶和目标对象的掩膜图像生成了一个神经扭曲场, 将目标对象的几何形状迁移到甘肃彩陶图像上. 实验结果表明, 在对彩陶进行大规模几何扭曲变形时, GPST能够产生令人满意的结果, 实现了对甘肃彩陶进行数字化创新的首次成功尝试, 迁移效果如图1所示. 本文的工作主要概括为以下3个方面.
(1)针对甘肃彩陶几何风格迁移任务缺乏数据集的问题, 本文构建了一个甘肃彩陶数据集, 该数据集包括彩陶图像的JPG格式文件以及相应的分割掩膜, 填补了甘肃彩陶数据集的空白.
(2)针对当彩陶和目标对象之间存在较大几何差异时, 直接通过风格迁移很难进行精确扭曲变形的问题, 本模型将掩膜图像作为输入, 以减少图像之间的差异, 同时引入了位置嵌入模块和特征增强模块来提高特征的质量, 从而改善扭曲场的变形效果.
(3)为验证GPST模型的有效性, 本文进行了大量实验, 实验结果表明, 该模型在彩陶迁移效果和定量评估指标方面均取得了显著的提升.

|
图 1 彩陶风格迁移效果图 |
1 相关工作 1.1 文创产品设计
文化创意产品的设计过程, 是一种将文化元素和创意思维紧密结合, 并以现代化的形式体现在产品设计之中的创作活动. 在这一过程中, 如何将地域历史文化元素与文化创意设计相融合, 以促进传统文化和文化创意产业的发展, 已成为文化创意产品设计的重要研究内容. 以深度学习为核心的图像艺术风格迁移技术已经在文化创意产品设计创新中得到了应用, 例如Zhu等人[8]提出的CycleGAN可以将图像从一种风格转换为另一种风格, 并同时保留其关键属性特征, 这对设计创意的产生和发展起到了积极的促进作用. Li等人[9]提出了一种基于深度学习和感性工学的产品概念生成方法框架, 用以生成具有情感偏好的产品概念图. Pagán等人[10]展示了图像识别技术在文化遗产、创意产业和设计创新方面的应用. Wu等人[11]将虚拟现实等新数字技术引入到竹编工艺品的保护和传承中, 促进了竹编产品的创新设计. 然而, 在传统文化工艺品创新设计领域, 有关风格迁移的研究仍然相对较少. 鉴于甘肃彩陶在传统文化遗产中的重要性, 本文研究了一种在保持甘肃彩陶纹理风格不变的情况下进行几何风格迁移的方法.
1.2 几何风格迁移几何形状是视觉风格的基本方面, 自2016年Gatys等人[12]首次运用深度学习进行风格迁移任务以来, 风格迁移一直侧重于使用艺术图像对内容图像进行纹理风格迁移, 几乎完全忽略了几何形状. 近年来越来越多的研究者开始认识到, 运用神经风格迁移对物体进行富有想象力的几何变形是非常有必要的. 尽管与几何风格迁移相关的文献数量远不及纹理风格迁移, 但这并不影响几何风格迁移的重要性.
卷积神经网络由于能够提取强大的特征, 因此在几何匹配中得到了普及. Rocco等人[13]提出了用于几何匹配的卷积神经网络结构, 通过在网络中嵌入几何匹配模块, 可以实现对图像的几何结构进行调整, 从而实现几何风格的迁移, 后来Kim等人[14]、Ham等人[15]、Liu等人[7]分别在此基础上做出各种改进. 有一些方法是用于专门的语义类别, 比较流行的是面部漫画[4,16,17]、艺术字体[5,18,19]等. 这些方法在语义相似的图像之间有很好的表现, 但无法处理两个不同类别的对象进行大规模的扭曲变形. DST[6]可以通过NBB[20]来匹配内容图像和目标样本之间的点实现任意的扭曲变形, Liu等人[7]提出学习从4D特征间距离阵列到非参数化的2D扭曲场的映射实现变形, 这些方法虽然不再局限于单个的领域, 但也仅限于同类级别的扭曲. 还有一类研究是针对3D对象实现几何形状的迁移. 例如, 通过在神经笼[21,22]上施加形变操作, 将源形状的一系列姿态自动转移到目标形状[23], 以及预测一个部分感知的仿射变换场, 实现自然地扭曲源形状以模仿目标形状的整体几何风格[24]. 这两种方法是对特定的3D数据集或场景进行的设计, 在处理不同类型的数据时存在一定的局限性, 不适合实时性要求较高的应用场景. 与上述方法相比, GPST能够实现甘肃彩陶与各种类别对象之间的大规模扭曲变形, 创造众多融入了甘肃彩陶这一传统文化元素的文化创意产品外观候选, 其输出的图像结果在视觉外观方面表现出色, 对协助设计师的工作具有实际应用价值.
2 本文方法 2.1 甘肃彩陶几何风格迁移模型本文提出一个新的甘肃彩陶几何风格迁移模型GPST, 该模型主要由几何扭曲网络和扭曲损失两部分组成. 受到光流估计方法RAFT[25]的启发设计了几何扭曲网络, 该网络具有两个输入: (1)要进行迁移的源图像, 即甘肃彩陶图像
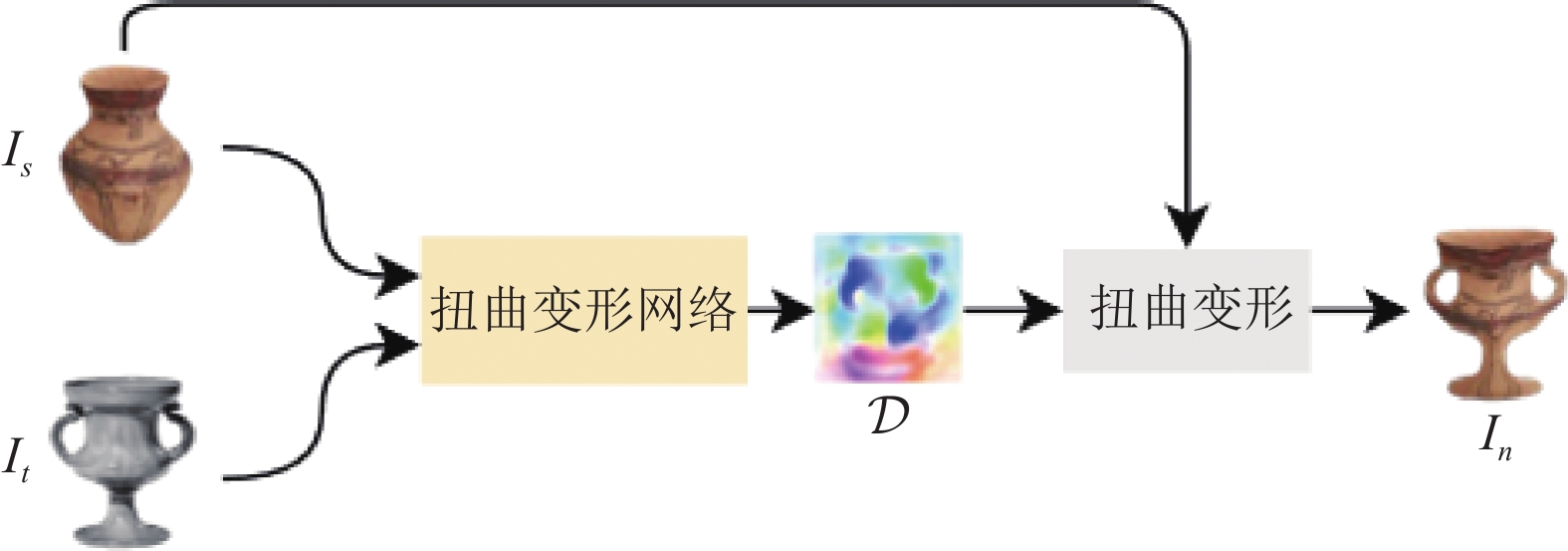
|
图 2 彩陶风格迁移模型 |
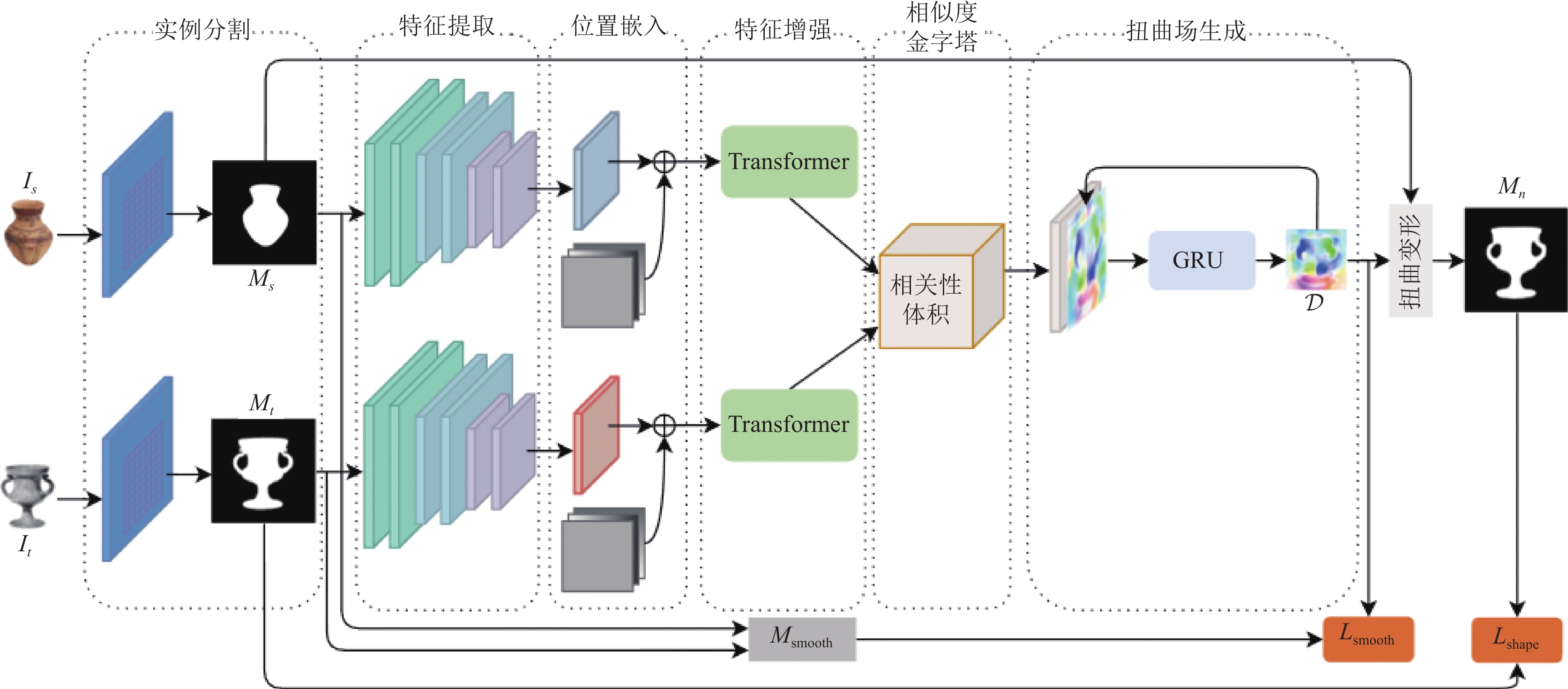
|
图 3 模型网络结构图 |
2.2 大规模几何扭曲网络
几何扭曲网络主要有6个组件, 分别为掩膜提取、特征提取、位置嵌入、特征增强、视觉相似度计算以及扭曲场生成. 下面将详细阐述这些组件的细节.
(1)掩膜提取
当两个RGB图像在语义上没有关联, 或者在形状上差异很大时, 很难直接扭曲它们来匹配形状, 但是两个掩膜图像之间的差异远低于RGB图像, 于是本文选择将掩膜图像输入到模型中进行训练. 为此采用一个预训练的对象实例分割网络ResNeXt101+FPN+Mask R-CNN[26]来获得彩陶和目标产品的分割掩膜, 表示为:
(2)特征提取
使用卷积网络从输入的掩膜图像
(3)位置嵌入
掩膜图像与RGB图像有着根本的不同, 通常以二值图像的形式呈现, 其中每个像素只包含一个二值值. 由于缺少颜色信息, 两个掩膜图像中存在许多的相似点, 所以
| {F′s=Fs+EposF′t=Ft+Epos | (1) |
其中,
(4)特征增强
为了获得尽可能精确的变形扭曲场, 关键在于获得更加高质量的特征. 由于甘肃彩陶具有独特的几何特性, 模型在对掩膜图像提取特征时, 本身提取到的特征质量并不高, 因此又在模型中引入了一个定制的Transformer来进一步考虑特征
| {ˆFs=T(F′s,F′t)ˆFt=T(F′t,F′s) | (2) |
其中,
传统的Transformer架构[28]是基于全局来计算注意力的, 因此计算复杂度十分高. 为了提高效率减少计算量, 本模型采用了Swin Transformer[30]的移位局部窗口注意策略, 将注意力的计算限制在每个窗口内. Swin Transformer使用固定的窗口大小, 而本研究将特征分割成固定数量的局部窗口, 使窗口大小与特征大小相适应. 具体来说, 将特征尺寸为
(5)视觉相似度计算
在得到彩陶图像和目标产品图像的特征张量后, 通过构建图像特征之间的完整相关性体积来计算视觉相似度. 本研究使用点积相似度衡量, 对两张图像两两像素之间进行点积相似度的计算, 表示为
| Cijkl=∑hˆFs(ijh)⋅ˆFt(klh) | (3) |
其中,
接下来, 将彩陶图像中每个像素点
| N(x′)r={x′+dx|dx∈Z2,‖dx‖1⩽r} | (4) |
其中,
(6)扭曲场生成
该模块根据RAFT中的迭代更新来计算扭曲场. 默认将初始扭曲场设置为0, 利用GRU模块以及卷积操作, 计算出相对于上次迭代过程输出的扭曲场的残差值, 然后与上次迭代过程输出的扭曲场进行相加用作补偿. 模块中还利用卷积操作学习上采样权值, 使当前
| D={Dr}Rr=1=Giu(T(Gf(M(Is))+Epos,Gf(M(It))+Epos),T(Gf(M(It))+Epos,Gf(M(Is))+Epos)) | (5) |
其中,
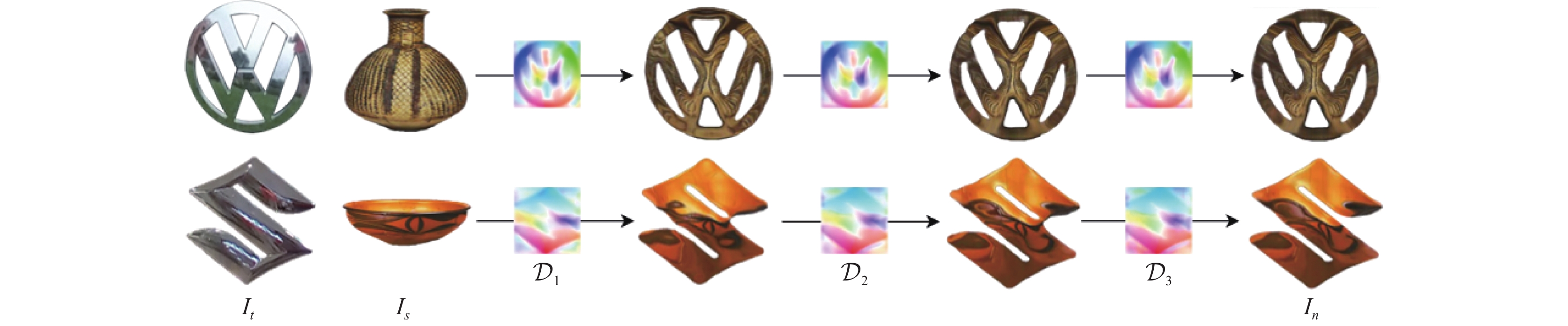
|
图 4 扭曲场迭代示意图 |
2.3 扭曲损失
本文采用无监督的学习方式训练几何扭曲网络, 并将感知损失与形状一致性损失的结果对比发现, 使用感知损失时甘肃彩陶的迁移效果并没有得到明显提升, 如图5所示. 因此在模型中引入形状一致性损失和平滑正则化, 下面将对这两个方面的内容进行详细阐述.
(1)形状一致性损失
基于式(5)得到扭曲场
| Lshape=∑Rr=1αr‖Dr(M(Is))−M(It)‖ | (6) |
其中, 用
(2)平滑正则化
形状一致性损失只是使掩膜之间在几何形状上匹配, 不能限制采样方向, 因此还会在最终生成的产品图像上发生图像域混乱变形的现象. 为了进一步限制扭曲场的采样方向, 保持彩陶图像内容上的细节, 本文按照从边缘到边缘采样的变形规则提出了掩膜平滑度正则化, 并将其加入扭曲场中目标对象边缘的两侧. 首先模型要生成一个平滑度掩膜, 其公式表示为:
| Msmooth=(M(Itedge)\& M(Is))|(M(Is)⊕M(It)\& M(It)) | (7) |
其中, |、
| Lsmooth=∑Rr=1βrLsmooth(Dr,M) | (8) |
其中,
| Lsmooth(Dr,M)=1∑i,jMij∑i,jMij(‖Dri+1,j−Dri,j‖2+‖Dri,j+1−Dri,j‖2+‖Dri+1,j+1−Dri,j‖2+‖Dri+1,j−1−Dri,j‖2) | (9) |

|
图 5 损失函数对比 |
通过对扭曲场
| Lall=Lshape+γLsmooth | (10) |
其中, 用
为了解决风格迁移任务中缺少甘肃彩陶数据集的问题, 本文构建了一个专门的甘肃彩陶数据集. 首先通过爬虫技术从甘肃省博物馆官网收集了

|
图 6 甘肃彩陶数据集部分图像 |
为了丰富目标对象数据集, 本文从多个来源选择一系列图像构建了新的数据集, 包括从VOC2012数据集[32]选取的飞机、汽车、瓶子等图像, 从Vehicle Logos数据集挑选的车标图像, 以及选自纽约大都会艺术博物馆收藏的一些真实瓷器和花瓶等艺术品图像[33], 共计

|
图 7 目标对象数据集部分图像 |
本文用彩陶图像和目标图像来训练几何扭曲网络. 由于几何扭曲场是通过迭代生成的, 每个后续扭曲场相对前一个都产生更大的扭曲变形效果, 因此增加权重
为了证明GPST模型能够创造出有良好视觉外观的甘肃彩陶文创产品, 本文将其与其他几种先进的方法进行了比较, 并进行了定性和定量的评估. 此外, 还进行了消融实验, 以验证GPST模型中部分组件对几何风格迁移的重要性. 本文的所有实验结果均在相同的超参数条件下训练产生的, 详细实验过程和结果如下.
3.2.1 定性比较本文将GPST模型与经典的几何风格迁移方法LWST[7]和DST[6], 以及纯纹理风格迁移方法AdaIN[35]进行了定性比较, 图8展示了相应的输出结果. 将甘肃彩陶迁移成为一些品牌商标以及工艺品的外形, 可以很明显地看到几何扭曲的有效性. 几何风格迁移方法DST是让两幅图像成对的关键点之间的特征相似度最大化, 通过一组匹配的关键点来引导形状变形. LWST是通过计算一个非参数化的向量场来扭曲变形输入的内容图像. 上述两种方法只能学习小规模的扭曲场, 当彩陶与目标对象在语义和几何形状上存在较大差异时, 需要进行大规模的几何扭曲, 无法取得较好的结果. 纯纹理方法AdaIN并没有捕捉到风格特征中除了纹理之外的形状变化, 它只是很好地保持了彩陶的纹理特征和目标产品的颜色分布. 相比之下, 本文提出的GPST模型在彩陶与目标对象之间存在较大的语义和几何形状差异时, 依然能够捕捉到目标对象的几何风格, 获得一个大规模的扭曲场, 使彩陶能够很好地匹配目标对象的几何形状. 同时, 观察到彩陶的纹理风格也得到了很好的迁移, 结果保持了彩陶纹理内容的完整性.
3.2.2 定量比较平均交并比(mean intersection over union, MIoU)是一种常用的图像语义分割性能评估指标, 用于衡量预测结果与真实结果之间的重叠程度, 可以用它来评估模型的几何扭曲性能. 如表1所示, 与LWST、DST和FGTP[36]相比, 本文的模型取得了更高的MIoU分数, 表明本模型将彩陶变形后与目标对象的几何形状更加匹配.
3.2.3 用户感知为了进一步验证模型输出与目标对象的风格接近程度, 本研究进行了一个相似性调查实验. 实验中, 100名参与者每人都可以看到3幅图片, 其中一幅图片来自目标对象, 另外两幅图片随机来自于LWST、DST和GPST的输出结果. 这3幅图像两两搭配组成3对组合, 并且以随机顺序并排展示. 参与者被要求选择出他们认为最相似的一对图像, 然后统计了认为模型输出的图像与目标对象更相似的次数, 以及认为两个模型输出图像彼此更相似的次数, 并将数据整理成了百分比的形式. 如图9所示, 参与者中有85%认为本文的GPST方法更接近目标对象, 而其他方法最多只有29%. 此外, 最多还有77%的人认为模型之间生成的图像更相似.

|
图 8 不同模型对比实验结果 |
| 表 1 MIoU分数 |
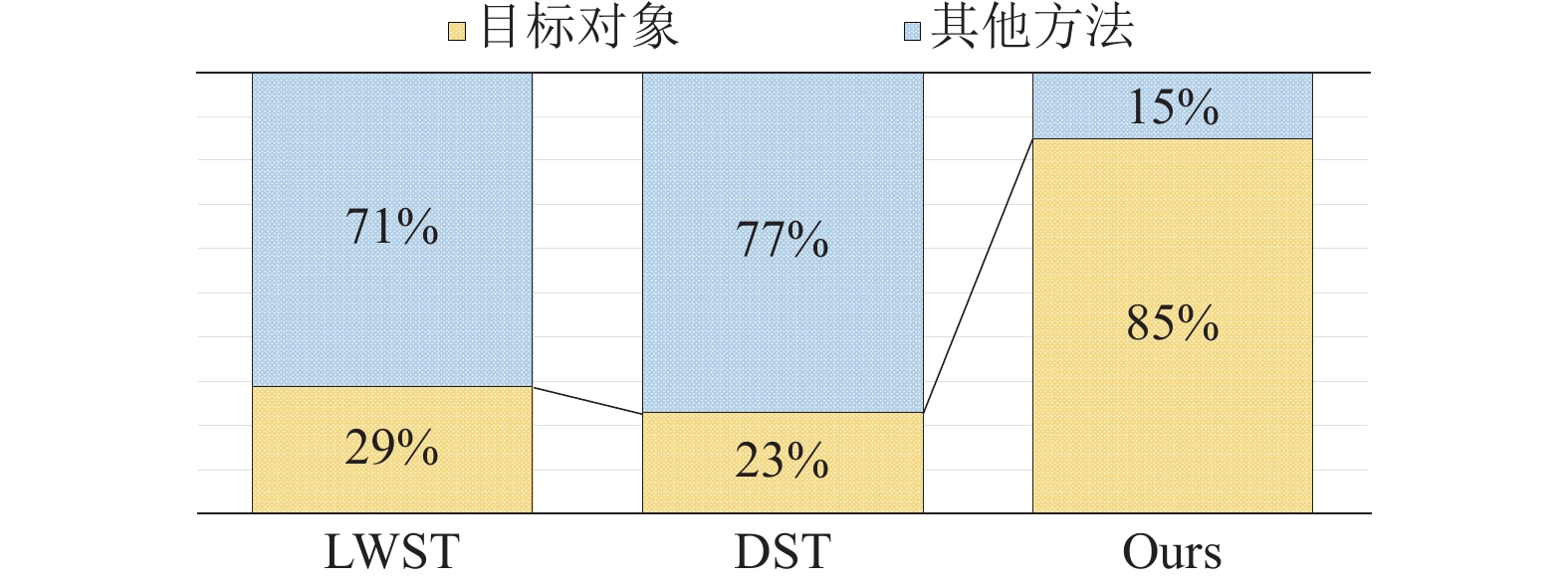
|
图 9 主观相似度 |
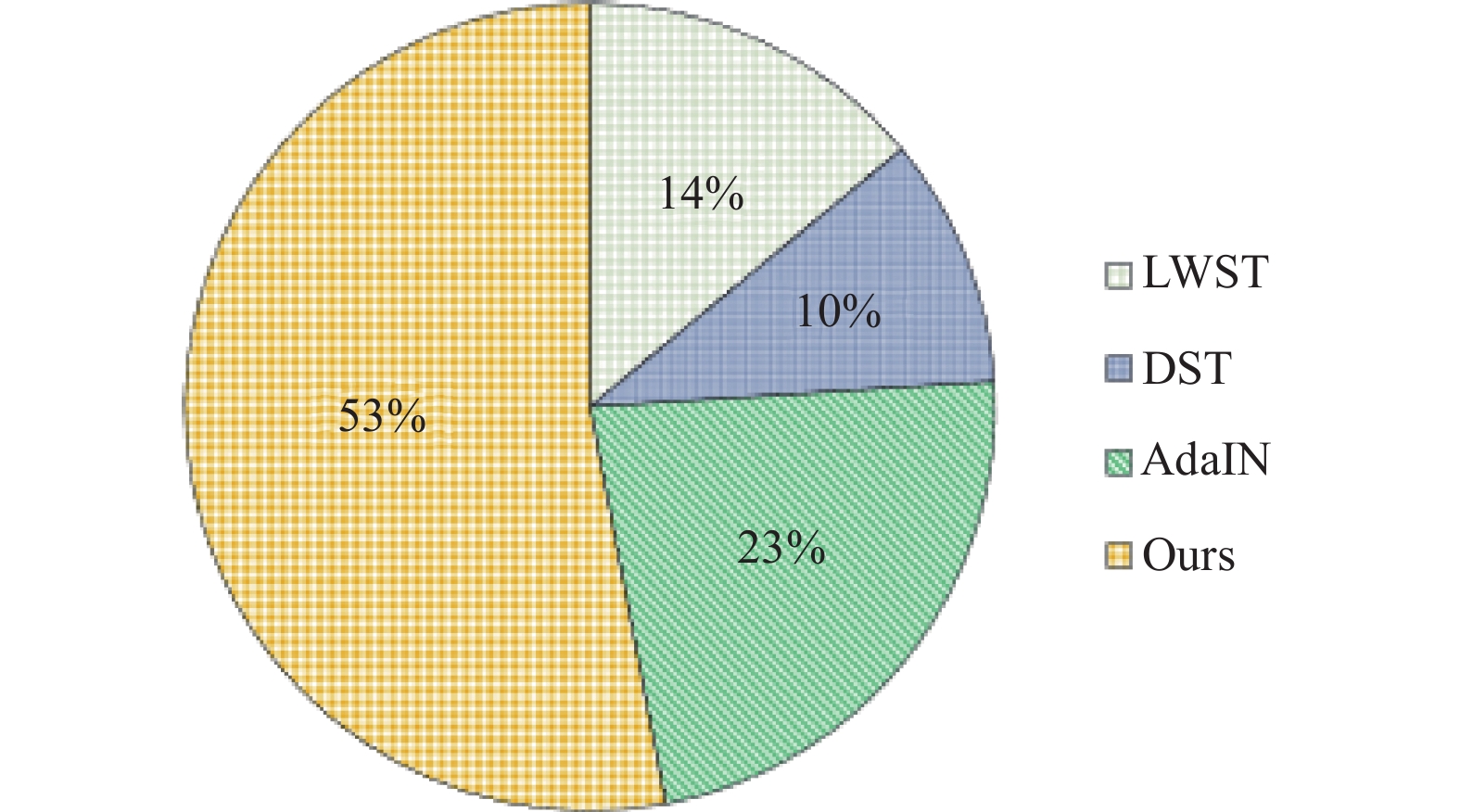
风格迁移的效果如何是一种人类的主观感受, 为了衡量这种主观感受, 本研究又进行了一个问卷调问卷调查. 实验选择10幅甘肃彩陶图像作为内容图像, 10幅目标对象图像作为风格图像. 每份问卷随机抽取15组内容风格对. 对于每一组, 将本文GPST生成的风格化图像与其他3种具有代表性的方法生成的图像以随机顺序向参与者并排展示, 并要求参与者投票选出他们最喜欢的结果. 实验共收集了100份参与者的调查问卷, 计算了每种方法的投票百分比, 如图10所示以饼状图的形式展示了结果, 可以看到GPST的风格化结果更受欢迎, 获得了更高的投票百分比.
|
图 10 用户偏好结果 |
3.2.4 消融实验
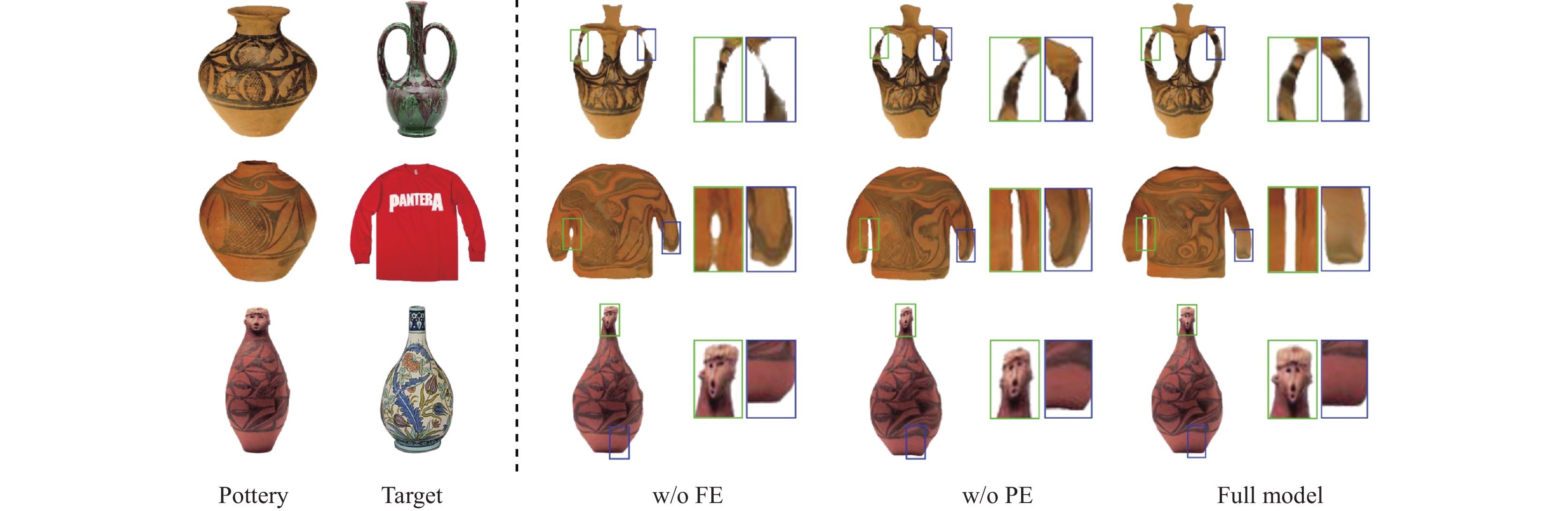
为了验证特征增强模块和位置嵌入模块的有效性, 本文进行了一系列消融实验. 在实验中, 分别展示了不包含特征增强模块的模型(w/o FE)、不包含位置嵌入模块的模型(w/o PE)以及同时包含这两个模块的完整模型(Full model)的输出结果, 并同时展示了输出结果的部分细节对比, 实验结果如图11所示.
在w/o FE中, 由于缺少了特征增强模块, 导致彩陶和目标对象的特征没有得到增强, 它们之间的相互依赖关系变得较弱. 从图中可以看到, 生成的图像结果与目标对象相比存在彩陶变形不完整和彩陶纹理迁移后结果不和谐的问题. 而在w/o PE中, 由于缺少了位置嵌入模块, 相邻位置之间的相关性减弱了. 虽然彩陶的变形结果较为完整, 但在保持彩陶的细节和结构方面存在一定的不足.
|
图 11 消融实验结果对比图 |
在Full model中, 可以观察到具有特征增强模块和位置嵌入模块的GPST模型在对彩陶进行风格迁移时, 彩陶的纹理和几何形状的细节保持具有更好的可控性, 能够产生更出色的结果.
4 结束语本文构建了一个全新的甘肃彩陶数据集, 并基于光流估计的思想, 首次提出一种用于甘肃彩陶的几何风格迁移模型GPST. 该模型的目标是即使在甘肃彩陶与目标对象的几何形状存在较大差异时, 也能通过学习一种扭曲变形网络, 将目标对象的几何外形迁移到甘肃彩陶上. 通过引入位置嵌入和特征增强模块, 获取了更高质量的风格特征, 并采用形状一致性损失函数和平滑正则化项, 实现了更好的扭曲变形效果, 提高了模型的性能. 实验结果表明, GPST在大规模几何变形方面明显优于以往的方法, 在保持彩陶细节方面取得了较好的结果, MIoU分数也有了显著提高.
有关甘肃彩陶的几何风格迁移研究工作相对较少, 该领域仍面临一系列挑战, 还有许多问题值得深入探究. 未来的研究可以考虑进一步改进网络结构, 优化相关损失函数, 增加对彩陶的外形和纹理的关注机制, 同时降低模型的训练成本, 以提高彩陶风格迁移效果的效率和质量.
| [1] |
王立夫, 周侠. 从氏族融合到农业的象征——马家窑文化彩陶中三种主要纹饰的演变及其意旨蠡测. 中国陶瓷, 2022, 58(10): 78-84. |
| [2] |
李彦英. 试析人头形器口陶瓶. 中国陶瓷, 2020, 56(5): 80-83. |
| [3] |
Dammer E, Hein A, Spataro M. An exploration of potential raw materials for prehistoric pottery production in the Tao River Valley, Gansu Province, China. Geoarchaeology, 2024, 39(2): 122-142. DOI:10.1002/gea.21984 |
| [4] |
Shi YC, Deb D, Jain AK. WarpGAN: Automatic caricature generation. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach, IEEE, 2019. 10754–10763.
|
| [5] |
Zhu XY, Lin MG, Wen KH, et al. Deep deformable artistic font style transfer. Electronics, 2023, 12(7): 1561. DOI:10.3390/electronics12071561 |
| [6] |
Kim SSY, Kolkin N, Salavon J, et al. Deformable style transfer. Proceedings of the 16th European Conference on Computer Vision. Glasgow: Springer, 2020. 246–261.
|
| [7] |
Liu XC, Yang YL, Hall P. Learning to warp for style transfer. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 3701–3710.
|
| [8] |
Zhu JY, Park T, Isola P, et al. Unpaired image-to-image translation using cycle-consistent adversarial networks. Proceedings of the 2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017, 2242–2251.
|
| [9] |
Li X, Su JN, Zhang ZP, et al. Product innovation concept generation based on deep learning and Kansei engineering. Journal of Engineering Design, 2021, 32(10): 559-589. DOI:10.1080/09544828.2021.1928023 |
| [10] |
Pagán EA, del Mar Gaitán Salvatella M, Pitarch MD, et al. From silk to digital technologies: A gateway to new opportunities for creative industries, traditional crafts and designers. The SILKNOW case. Sustainability, 2020, 12(19): 8279. DOI:10.3390/su12198279 |
| [11] |
Wu J, Guo LC, Jiang JL, et al. The digital protection and practice of intangible cultural heritage crafts in the context of new technology. E3S Web of Conferences, 2021, 236: 05024. DOI:10.1051/e3sconf/202123605024 |
| [12] |
Gatys LA, Ecker AS, Bethge M. Image style transfer using convolutional neural networks. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 2414–2423.
|
| [13] |
Rocco I, Arandjelovic R, Sivic J. Convolutional neural network architecture for geometric matching. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 39–48.
|
| [14] |
Kim S, Lin S, Jeon S, et al. Recurrent Transformer networks for semantic correspondence. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 6129–6139.
|
| [15] |
Ham B, Cho M, Schmid C, et al. Proposal flow: Semantic correspondences from object proposals. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(7): 1711-1725. DOI:10.1109/TPAMI.2017.2724510 |
| [16] |
Yang S, Jiang LM, Liu ZW, et al. Pastiche master: Exemplar-based high-resolution portrait style transfer. Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022. 7683–7692.
|
| [17] |
Han FZ, Ye SQ, He MM, et al. Exemplar-based 3D portrait stylization. IEEE Transactions on Visualization and Computer Graphics, 2023, 29(2): 1371-1383. DOI:10.1109/TVCG.2021.3114308 |
| [18] |
Yang S, Wang ZY, Wang ZW, et al. Controllable artistic text style transfer via shape-matching GAN. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 4441–4450.
|
| [19] |
Zhu AN, Yin ZH, Iwana BK, et al. Text style transfer based on multi-factor disentanglement and mixture. Proceedings of the 30th ACM International Conference on Multimedia. Lisboa: ACM, 2022. 2430–2440.
|
| [20] |
Aberman K, Liao J, Shi MY, et al. Neural best-buddies: Sparse cross-domain correspondence. ACM Transactions on Graphics, 2018, 37(4): 69. |
| [21] |
Ju T, Schaefer S, Warren J. Mean value coordinates for closed triangular meshes. Seminal Graphics Papers: Pushing the Boundaries, 2023, 2: 25. |
| [22] |
Joshi P, Meyer M, DeRose T, et al. Harmonic coordinates for character articulation. ACM Transactions on Graphics, 2007, 26(3): 71-es. DOI:10.1145/1276377.1276466 |
| [23] |
Wang YF, Aigerman N, Kim VG, et al. Neural cages for detail-preserving 3D deformations. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 72–80.
|
| [24] |
Yin KX, Gao J, Shugrina M, et al. 3DStyleNet: Creating 3D shapes with geometric and texture style variations. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021. 12436–12445.
|
| [25] |
Teed Z, Deng J. RAFT: Recurrent all-pairs field transforms for optical flow. Proceedings of the 16th European Conference on Computer Vision. Glasgow: Springer, 2020. 402–419.
|
| [26] |
He KM, Gkioxari G, Dollár P, et al. Mask R-CNN. Proceedings of the 2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017. 2980–2988.
|
| [27] |
Carion N, Massa F, Synnaeve G, et al. End-to-end object detection with Transformers. Proceedings of the 16th European Conference on Computer Vision. Glasgow: Springer, 2020. 213–229.
|
| [28] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 6000–6010.
|
| [29] |
Sun JM, Shen ZH, Wang YA, et al. LoFTR: Detector-free local feature matching with Transformers. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 8918–8927.
|
| [30] |
Liu Z, Lin YT, Cao Y, et al. Swin Transformer: Hierarchical vision Transformer using shifted windows. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021. 9992–10002.
|
| [31] |
Jaderberg M, Simonyan K, Zisserman A, et al. Spatial Transformer networks. Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2015. 2017–2025.
|
| [32] |
Liu YY, Tian Y, Chen YH, et al. Perturbed and strict mean teachers for semi-supervised semantic segmentation. Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022. 4248–4257.
|
| [33] |
Wu SZ, Makadia A, Wu JJ, et al. De-rendering the world’s revolutionary artefacts. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 6334–6343.
|
| [34] |
Kingma DP, Ba J. Adam: A method for stochastic optimization. Proceedings of the 3rd International Conference on Learning Representations. San Diego: ICLR, 2015.
|
| [35] |
Huang X, Belongie S. Arbitrary style transfer in real-time with adaptive instance normalization. Proceedings of the 2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017. 1510–1519.
|
| [36] |
Xue MH, Ito Y, Nakano K. An art font generation technique using Pix2Pix-based networks. Bulletin of Networking, Computing, Systems, and Software, 2023, 12(1): 6-12. |
 2024, Vol. 33
2024, Vol. 33



