2. 中国科学技术大学 国际金融研究院, 合肥 230026;
3. 合肥工业大学 数学学院, 合肥 230609
2. International Institute of Finance, University of Science and Technology of China, Hefei 230026, China;
3. School of Mathematics, Hefei University of Technology, Hefei 230609, China
由于互联网的普及, 信息过载在人们的日常生活中是一个日益严重的问题. 推荐系统是缓解信息过载、方便用户寻求所需信息、增加应用服务提供方流量和收入的有效解决方案, 是现代信息系统中最普遍的以用户为中心的人工智能应用之一. 基于隐式反馈数据的协同过滤技术在推荐系统中非常重要. 协同过滤[1]是构建商业推荐系统最常用的技术之一, 只使用用户对物品的显式反馈或隐式反馈数据而不使用用户或物品的其他属性信息, 能够从海量物品中快速筛选出与用户相关的个性化物品推荐列表. 显式反馈数据包含用户对物品的打分, 如用户对电影的评分, 隐式反馈数据则通常只包含用户对物品的点击记录[2]. 由于在许多应用程序和网站中通常只有少部分用户会提供明确的打分, 显式反馈数据的收集有一定困难, 用户覆盖度也低于隐式反馈数据, 与此同时, 通过记录用户的点击链接、点击加入收藏等行为, 则可以更容易地收集到隐式反馈数据[2].
隐式反馈数据是由观测而不是随机实验收集来的, 存在多种偏差, 包括曝光偏差和从众偏差. 曝光偏差是指用户只接触到系统所推荐的一小部分物品, 导致观测数据存在遗漏和偏向; 从众偏差则发生于用户倾向于与群体中的其他人保持一致所以违背自身偏好进行点击的情况[3]. 当存在曝光偏差时, 用户和物品的相关概率的估计有偏; 当存在从众偏差时, 用户与物品相关这一事件包含用户在被曝光该物品时会违背自身偏好从众点击该物品和用户偏好该物品两个事件. 因此, 单纯估计用户与物品的相关概率并不是用户对物品的偏好概率的无偏估计.
根据综述和文献检索结果, 已知的去偏领域的研究对曝光偏差关注较多, 较少关注从众偏差, 而且较少同时对这两种偏差进行去偏, 少数能够去偏多种偏差的算法需要一个难以获得的无偏数据集作为辅助信息[3]. 在不考虑数据偏差的情况下盲目拟合数据将导致算法的推荐结果偏离用户的真实偏好. 对用户偏好的偏离随着反复的采集数据和训练迭代参数而逐渐被反馈回路放大, 会导致推荐结果中的偏向性逐渐加强, 从而损害用户对推荐服务的满意度和信任[4].
针对曝光偏差这一问题, Saito等人提出逆倾向加权方法[5], 假设用户对物品的点击概率是曝光概率和用户与物品相关概率之积, 证明经过该方法加权的经验损失是其提出的理想损失的无偏估计量. 逆倾向加权方法对曝光偏差有一定的无偏性质, 已被灵活应用到许多算法中用于去偏, 包括许多基于神经网络的协同过滤推荐算法. 例如, Gupta等人[6]在Truong等人[7]的基于变分自编码器的相关概率估计算法的基础上, 用训练集中物品被点击的频次估计物品的流行度, 用逆倾向加权方法去偏. 但该方法没有考虑从众偏差问题, 而隐式反馈数据中经常存在从众偏差, 这会导致基于逆倾向加权方法估计出的用户与物品的相关概率和用户对物品的偏好概率之间存在差异[3,4].
为了进一步满足推荐系统精准命中用户偏好的需要, 本文的目标是提出一个对曝光偏差和从众偏差双重去偏的协同过滤推荐算法, 利用隐式反馈数据估计用户对物品的偏好概率, 从而使得推荐算法能够根据用户偏好对物品进行排序.
传统协同过滤算法和矩阵分解算法对线性交互进行建模, 难以捕捉用户和物品之间的非线性关系[7,8]. 为了突破上述局限性, 人们开始研究基于具有非线性复杂建模能力的神经网络的协同过滤推荐算法. 同时, 隐式反馈数据有着稀疏的特点, 而自编码器便于拟合非线性关系, 而且可以将稀疏数据编码为尽量保留原始信息的降维向量, 在近年的一些研究中已被应用于协同过滤推荐算法的构建, 与几种竞争方法相比, 其性能有很大的改进[2,7,9,10]. Khawar等人[11]学习物品间的相关性作为先验信息指导构建一个参数量更小的稀疏连接的自编码器, 但这样的先验是基于观察性而不是实验性的历史数据得到的, 而且只提取其中的显著相关的组而没有提取其他信息, 可能加剧观察到的数据中存在的偏差问题. Lee等人[2] 针对隐式反馈数据提出BISER算法和自逆倾向加权方法, 以双塔自编码器在参数迭代过程中输出的用户与物品的相关概率估计作为倾向得分的估计, 对曝光偏差进行去偏, 取得了比其对比算法更优的推荐效果, 但没有考虑其他偏差对反馈数据的影响. Wu等人[12]通过引入额外的输入节点, 允许在输入层加入用户侧的额外信息的表示向量, 以基于用户的去噪自编码器结合构造的正样本去除曝光偏差. 但该算法的重构目标只有被加入增强噪声的输入而没有原始输入的隐式反馈数据.
对比学习能够同时从原始的输入数据和加入增强噪声的输入数据中学习, 通过抽取自监督信号, 能够有效地缓解隐式反馈数据的数据稀疏问题, 而且在自监督学习的生成、对比和预测这3类范式中具有轻量级和设计灵活的优点[13,14]. InfoNCE损失是最流行的对比学习损失之一, 而且有更好的理论支持: 最小化InfoNCE对比损失相当于最大化正样本之间的互信息的下界; 此外, Wang等人[15]证明, 渐近地, 经过采用InfoNCE损失的对比学习, 能够加强正例对的表示向量的接近度、诱导表示向量均匀分布在单位超球面上, 一定程度上可以防止表示崩塌并保存更多的信息.
已有一些研究采用InfoNCE对比损失, 设置对比学习辅助任务以去除推荐系统中的数据偏差. Yu等人[14]提出SimGCL算法, 通过向图节点的表示向量添加均匀噪声的方法实现数据增强从而利用InfoNCE对比损失进行训练, 并通过实验说明, 优化InfoNCE对比损失不仅能够加快参数梯度下降的收敛, 而且能带来更均匀的特征表示, 特征表示的均匀程度与去除流行度偏差的能力存在一定的正相关. 热门商品更有可能被用户看到, 因此, “流行度偏差”是“曝光偏差”的另一种形式[3]. Zhou等人[16]用对比学习去除隐式反馈数据的曝光偏差, 实验表明, 与按倾向分数或物品流行度采样相比, 用等概率随机采样的数据增强方法设置对比学习辅助任务能带来更好的推荐效果. 该算法从反事实的角度设置对比学习辅助任务以去偏曝光偏差, 但没有同时考虑和去偏从众偏差等其他偏差.
综合考虑隐式反馈数据的曝光偏差、从众偏差以及数据稀疏问题, 本文提出了一种适用于稀疏隐式反馈数据的双重去偏协同过滤算法. 算法通过我们提出的双重逆倾向加权方法和对比学习辅助任务去偏输入双塔自编码器的隐式反馈数据中包含的两种偏差, 估计用户对物品的偏好概率. 本文的主要工作和贡献如下.
(1)针对逆倾向加权方法[5]去偏曝光偏差但没有考虑从众偏差的问题, 分析曝光偏差和从众偏差的存在机理, 我们提出同时去偏两种偏差的双重逆倾向加权方法, 并证明经过该方法加权的经验损失是理想的以偏好概率为标签的损失的无偏估计量.
(2)虽然理论上已经证明双重逆倾向加权方法的去偏作用, 但它仍然需要准确的倾向分数的估计来保证. 我们设置一个去偏曝光偏差和从众偏差的自监督对比学习辅助任务, 与自编码器的偏好概率估计任务联合训练, 得到双重去偏的偏好概率估计, 进而依照自蒸馏的思想, 以训练过程中偏好概率的估计作为倾向得分.
(3)通过在双塔自编码器上整合上述两种双重去偏方法, 我们提出了一种适用于稀疏隐式反馈数据的双重去偏协同过滤推荐算法, 能够从用户和物品的双重视角学习, 同时对曝光偏差和从众偏差去偏. 在两组隐式反馈协同过滤场景的公开的有偏训练集和无偏测试集上的实验结果表明, 相较于对比算法, 我们的算法表现出了更优的推荐性能. 消融实验表明, 我们提出的双重逆倾向加权方法和对比学习辅助任务对推荐效果都有贡献.
本文的其余部分组织如下. 第 2 节介绍本文的问题设置. 第 3 节介绍双重去偏协同过滤算法的具体内容. 第 4 节用两个现实数据集进行对比实验、消融实验并讨论实验结果. 第 5 节总结全文.
2 问题设置给定N个用户的集合
为了更形式化地表达隐式反馈数据中曝光偏差的影响机理, Saito等人[5]引入了关于相关事件和曝光事件是否发生的两个随机变量矩阵.
| P(Yui=1)=P(Oui=1)⋅P(Rui=1)=ωui⋅γui | (1) |
上面的定义只考虑了曝光偏差, 但从众偏差和曝光偏差一样, 会与真实的用户偏好一同体现在点击记录中, 影响推荐的效果. 为了减少从众偏差的负面影响, 本文继承Saito等人的假设, 并进一步假设用户与物品相关这一事件是用户在被曝光该物品时会违背自身偏好从众点击该物品和用户偏好该物品两个事件的和事件. 为此, 引入偏好矩阵
| P(Yui=1)=P(Oui=1)⋅(P(Bui=1)+P(Cui=1))=ωui⋅(βui+ξui) | (2) |
从而有:
| βui=P(Yui=1)ωui−ξui | (3) |
在现实的推荐系统应用场景中,
本文的目标是用隐式反馈数据
针对曝光偏差和从众偏差问题, 本文提出能够利用稀疏隐式反馈数据估计用户对物品的偏好概率的双重去偏协同过滤推荐算法. 算法的执行流程如图1.
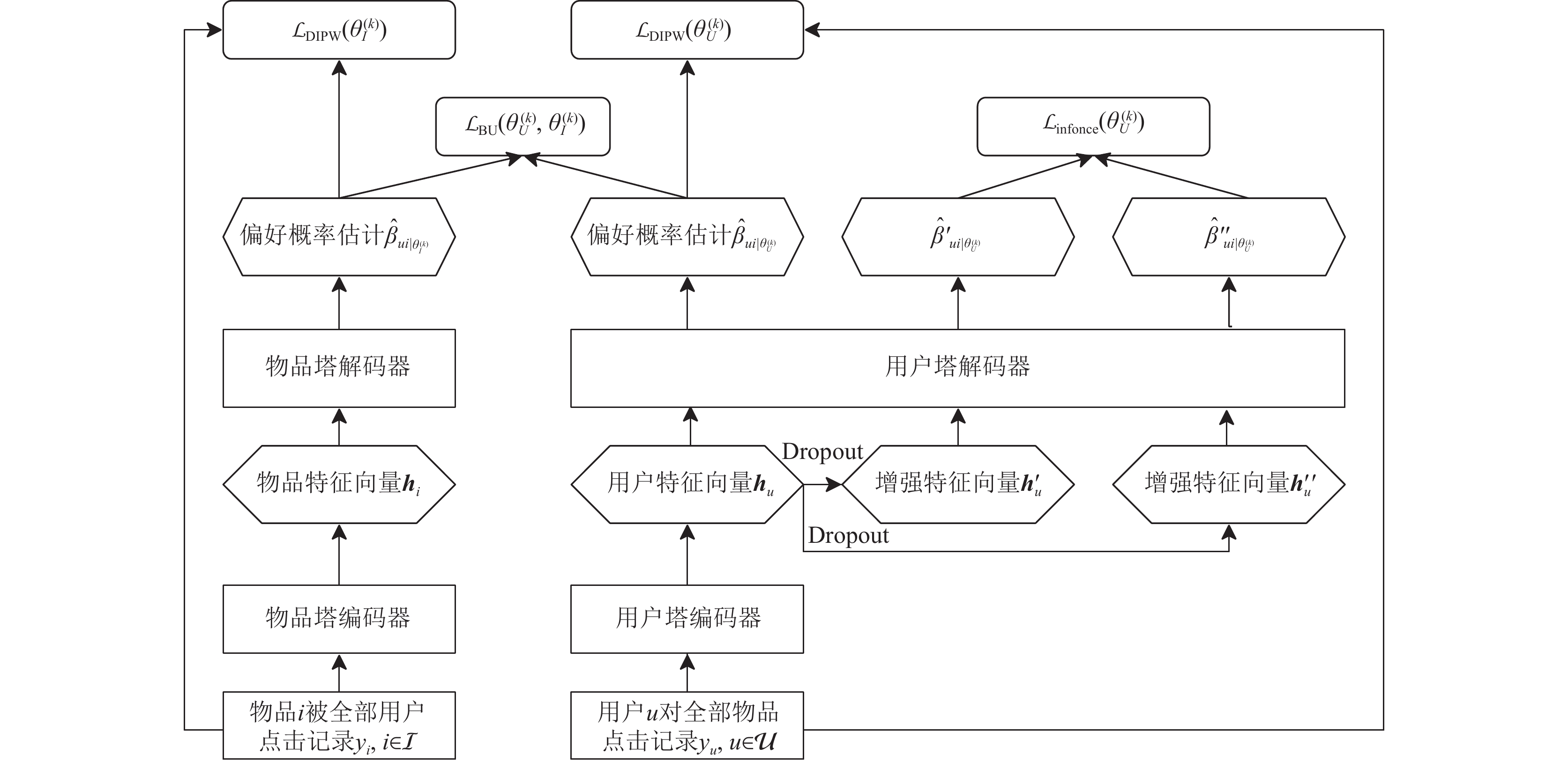
|
图 1 算法整体流程图 |
算法采用的神经网络结构是两个并行的自编码器, 分别是图中左边第1列的物品塔和右边的用户塔, 每个自编码器由编码器和解码器组成; 两个自编码器分别从用户和物品的角度学习, 由双边正则损失
交叉熵损失是常用的用于更新自编码器神经元参数的经验损失,但没有考虑曝光偏差和从众偏差的影响, 因此, 为了对两种偏差进行去偏, 使得自编码器的输出能够作为用户对物品的偏好概率的估计, 我们为其设置了两个损失, 包括经过双重逆倾向加权的交叉熵重构损失
由于自编码器适合较小的批训练数据大小(batchsize), 而我们的对比学习辅助任务需要大于1的批训练数据大小来提供负样本, 为得到最优效果, 我们只限制用户塔的批训练数据大小大于1, 只对用户塔设置对比学习辅助任务. 综上, 可以形式化表示物品塔的损失如式(4), 用户塔的损失如式(5):
| L(θ(k)I)=LDIPW(θ(k)I)+λBLBU(θ(k)U,θ(k)I) | (4) |
| L(θ(k)U)=LDIPW(θ(k)U)+λBLBU(θ(k)U,θ(k)I)+λCLLinfonce(θ(k)U) | (5) |
其中, 参数
自编码器有着神经网络便于拟合非线性关系的优点, 能够在重构输入的同时将输入的稀疏数据编码为降维的特征向量, 近年来也被应用于协同过滤推荐算法领域, 以它对点击记录的重构输出作为所求概率的估计. 结合之后两个章节将介绍的两个双重去偏方法, 本文将它对输入的隐式反馈
进一步, 为从用户和物品的双方角度进行学习以及缓解双重逆倾向加权方法在实践中的高方差问题[3,5], 本文使用两个并行的自编码器分别从用户和物品双方的角度编解码, 并用一个双边正则损失约束两个自编码器给出数值接近的偏好概率估计.
两个自编码器分别称为用户塔和物品塔. 用户塔的一个输入是一个用户对全部M个物品的点击记录, 对用户
用户塔的自编码器如式(6)、式(7):
| hu=Sigmoid(Wue⋅yu+bue) | (6) |
| ˆβu∣θU=Sigmoid(Wud⋅hu+bud) | (7) |
物品塔的自编码器如式(8)、式(9):
| hi=Sigmoid(Wie⋅yi+bie) | (8) |
| ˆβi∣θI=Sigmoid(Wid⋅hi+bid) | (9) |
其中,
两塔的自编码器的重构损失都是经过双重逆倾向加权的交叉熵损失, 将在后文介绍, 如式(17). 除此之外, 鉴于隐式反馈数据的稀疏性, 我们加入额外的先验知识以帮助自编码器收敛到合理的参数, 并缓解逆倾向加权方法的高方差问题. 我们认为, 对于已经有点击的用户-物品对, 两塔的偏好概率估计应该接近. 为此, 在发生点击的用户-物品对集合
| LBU(θ(k)U,θ(k)I)=1|˜D|∑(u,i)∈˜D(ˆβui|θ(k)U−ˆβui|θ(k)I)2 | (10) |
其中,
用随机梯度下降法训练至收敛后, 得到两塔的参数
| ˆβui∣θ=ˆβui∣θU+ˆβui∣θI2 | (11) |
Saito等人提出的逆倾向加权方法只考虑了曝光偏差, 目标是从隐式反馈中估计用户-物品相关概率[5]. 当存在从众偏差时, 用户与物品相关这一事件包含用户在被曝光该物品时会违背真实意愿从众点击该物品和用户偏好该物品两个事件. 因此, 单纯估计用户与物品的相关概率并不是用户-物品偏好概率的无偏估计. 本文的目标是估计用户-物品偏好概率, 希望推荐系统更精准命中用户偏好. 所以理想中的损失应该促使输出拟合偏好概率
| Lideal2(θ)=−1|D|∑(u,i)∈D(βuilog(ˆβui|θ)+(1−βui)log(1−ˆβui|θ)) | (12) |
| Lunbiased2 (θ)=−1|D|∑(u,i)∈D(yui˜ωuilog(ˆβui|θ)+(1−yui˜ωui)log(1−ˆβui|θ)) | (13) |
其中,
| ˜ωui≜ωuiyuiyui−ωuiξui | (14) |
从而由式(2)可得:
| E[yui˜ωui]=E[yuiωui−ξui]=E[yui]ωui−ξui=P(Yui=1)ωui−ξui=βui | (15) |
从而可以证明, 采用双重逆倾向加权方法的损失的期望等于理想中的以用户对物品的偏好概率作为标签的损失, 如式(16):
| E[Lunbiased2 (θ)]=−1|D|∑(u,i)∈D(E[yui]˜ωuilog(ˆβui|θ)+(1−E[yui]˜ωui)log(1−ˆβui|θ))=−1|D|∑(u,i)∈D(βuilog(ˆβui|θ)+(1−βui)log(1−ˆβui|θ))=Lideal2 (θ) | (16) |
为了估计
| LDIPW(θ(k))=−1|D|∑(u,i)∈D(yuiˆβui|θ(k)log(ˆβui|θ(k))+(1−yuiˆβui|θ(k))log(1−ˆβui|θ(k))) | (17) |
由于自逆倾向加权方法是将迭代过程中自编码器的重构输出作为倾向分数, 用额外的双重去偏辅助任务促使自编码器的重构输出尽快收敛于准确的偏好概率估计可以在进一步去偏的同时加快算法整体的收敛速度, 因此, 我们在用户塔上增加一个以去偏为目的的对比学习辅助任务. 第一, 通过dropout[17]数据增强的对比学习训练, 可以避免算法过度依赖部分数据, 从而避免算法过度依赖存在从众偏差的数据. 第二, 曝光偏差导致的数据缺失不应当影响我们对用户的刻画, 通过经验损失的设置人为地拉近同一个用户经过dropout数据增强和解码得到的两个偏好概率估计、推远不同用户的偏好概率估计, 我们把这一先验知识传递给算法, 结合InfoNCE损失促使表示向量在超球面上的均匀分布的作用, 提高算法对曝光偏差的鲁棒性.
对用户塔的一个输入向量
| {hu=Sigmoid(Wue⋅yu+bue)h′u=dropout(hu∣p)h″u=dropout(hu∣p) | (18) |
再将两个数据增强后的特征向量
| {ˆβ′u|θ(k)U=Sigmoid(Wud⋅h′u+bud)ˆβ″u|θ(k)U=Sigmoid(Wud⋅h″u+bud) | (19) |
为了使算法对有缺失的数据做有意义的输出, 认为同一个用户的特征向量做两次数据增强和解码得到的两个估计向量的余弦相似度应该较大, 不同用户的估计向量的余弦相似度应该较小. 采用InfoNCE经验损失表达这种约束, 如式(20) [18,19]:
| Linfonce(θ(k)U)=−1bu∑u∈{1,⋯,bu}logexp(s(^β′u|θ(k)U,ˆβ″u|θ(k)U))∑v∈{1,⋯,bu},v≠uexp(s(ˆβ′u|θ(k)U,ˆβ′v|θ(k)U)) | (20) |
其中,
本节我们在公开实际数据集Yahoo!R3[20]和Coat[21]上验证算法的效果.
Yahoo!R3[20]是在音乐推荐场景下收集的用户给歌曲的评分的数据集. 训练集收集了用户在雅虎音乐服务中的正常交互的评分, 可以被认为是受到数据偏差影响的数据, 包括
Coat[21]是用户对衣物的评价数据集, 它覆盖290个用户和300件衣物, 每个用户首先被分配一个网页商店, 被要求选择最想购买的24件衣物给出评分, 得到训练集. 之后要求用户对随机选出的16件衣物给出评分, 得到测试集.
因为这两个数据集的训练集收集自真实场景, 很可能包含从众偏差、曝光偏差等语义偏差, 而测试集给出的物品是等概率随机选出的, 用户一定会对它们给出评分, 可以认为是无偏的, 所以这两个数据集是在受控环境下评估去偏推荐算法的理想选择[2]. 已知的其余公开数据集则没有提供由随机实验得到的测试集, 所以我们遵循历史研究[2,5]的实验设置, 将这两个评分范围是1–5分的显式反馈数据集转换为隐式反馈数据集使用, 具体做法是, 将4分或更高的评分视为有正反馈, 其余评分被视为无正反馈. 经过这样的预处理后, Yahoo!R3的训练集中有
对于测试集中的每个用户, 我们计算对该用户最推荐的K个物品, 并计算3个推荐系统中的常用指标: 归一化折扣累积增益(NDCG@K)、均值平均精度(MAP@K)和召回率(Recall@K). 考虑到测试集中每个用户评分的物品数量有限, 其中表示出偏好的物品数量一定少于评分物品的数量, 而且我们希望用户偏好的物品尽可能被排在推荐列表的最前面, 而不是靠集中在推荐列表偏后的位置的更多的偏好物品带来更高的得分, 所以K设置得太大时上述指标体现推荐性能的意义有限. 我们使用K=1, 3, 5来计算评估指标, 评估估计概率最大的K个物品的推荐准确性. 具体的评估指标计算方法遵循RelMF[5]中的定义.
4.2 对比实验我们将本文提出的算法与适用于隐式反馈数据的传统推荐算法MF[22]、使用自编码器的UAE[10]、IAE[10], 以及去偏推荐算法RelMF[5]、CJMF[23]、MACR[24]、BISER[2]进行比较. 由此, 我们在去偏方面比较采用逆倾向加权和因果推断两类方法的算法, 在网络结构设计方面比较传统的MF[22]、使用自编码器的UAE[10]和IAE[10] , 以及使用其他神经网络结构的MACR[24]. 后面用DUCF (dual unbiased collaborative filtering)表示我们提出的算法. 国内外相关研究中还有一些算法消除隐式反馈数据中的偏差, 但部分算法[25,26]需要无偏数据参与训练, 因此没有选为对比算法.
(1) 矩阵分解(MF)[22]: 经典推荐算法, 通过用户和商品特征向量矩阵的乘积估计相关概率.
(2) 相关性矩阵分解(RelMF)[5]: 使用启发性函数估计物品的流行度作为逆倾向分数, 并做阈值裁剪减小方差.
(3) 基于用户的自编码器(UAE)[10]: 接收不同的用户与一组固定的物品的交互记录, 使用自编码器学习非线性的物品-物品相关性.
(4) 基于物品的自编码器(IAE)[10]: 接收不同的物品与一组固定的用户的交互记录, 使用自编码器学习非线性的用户-用户相关性.
(5) 组合联合学习矩阵分解(CJMF)[23]: 基于逆倾向加权方法, 引入一个联合训练框架, 使用多个子网络估计倾向得分和相关概率. 对于我们的数据集, 我们将子网络的数量设置为8个.
(6) 模型无关因果推理(MACR)[24]: 使用因果图通过反事实推理的方法去偏流行度对于推荐的影响. 具体实现时使用LightGCN[27]算法.
(7) 双边自去偏自编码器(BISER)[2]: 接受隐式反馈数据, 两个自编码器以自逆倾向加权方法去偏, 双边自编码器估计的平均作为估计概率输出
我们采用Lee等人[2]随论文提供的代码实现用于比较的算法. 实验采用AdaGrad优化器, 采取5个数据批次的早停和最多500轮的迭代轮次限制. 基于自编码器的算法的编码器的全连接层的神经元个数h在{50, 100, 200, 400}中, 两塔的批数据大小
在两个数据集上的实验结果见表1, 其中加粗部分表示最优结果.
| 表 1 真实无偏测试集上各算法的效果 |
首先, 总体而言, 我们的DUCF算法的推荐效果优于对比的算法, 在Coat数据集上提升较大, 相比推荐效果次好的算法, NDCG@5、MAP@5和Recall@5这3个指标分别提升5.94%、5.71%和9.20%, 而在提升相对较小的Yahoo!R3数据集上, NDCG@5、MAP@5和Recall@5这3个指标也分别有1.95%、2.11%和1.88% 的提升, 这说明我们的算法在有偏训练集上能够更好地去除偏差、学习无偏的用户对物品的偏好概率, 因为无偏测试集上更好的表现表明偏差被更好地去偏, 或者至少, 我们提出的算法比对比算法对于数据偏差更具鲁棒性.
从每个评估指标来看, 相比基线算法, 更高的归一化折扣累积增益、均值平均精度指标说明我们的算法能够将用户偏好的物品排在推荐列表中更靠前的位置; 更高的召回率说明我们的算法能够筛选出更多用户偏好的物品.
其次, 矩阵分解算法MF表现较弱, 分析原因可能在于数据集的规模较小, 不足以帮助我们找到合适的算法参数以及去偏超参数, 容易欠拟合, 而且MF没有进行去偏. 由8个子网络集成的CJMF与其他基于MF的算法包括MF和RelMF相比, 取得了更好的推荐效果. 这也侧面验证了子网络的集成效应在隐式反馈数据上的正面作用, 而我们的对比学习辅助任务中采用的dropout数据增强也有类似的集成效应.
最后, 基于矩阵分解的去偏推荐算法RelMF、CJMF在两个数据集上的表现通常优于传统矩阵分解算法MF; 基于自编码器的去偏推荐算法BISER在两个数据集上的表现优于未做去偏的自编码器推荐算法UAE、IAE, 这可能意味着去除训练数据中的偏差可以改善用户体验. MACR和使用单个自编码器的UAE、IAE在对比算法中也表现出了竞争力. 相比于CJMF、UAE、IAE、MACR等, 我们的算法不仅能从用户和物品双边角度进行学习, 而且采用对比学习和双边正则损失帮助参数收敛, 以及两种双重去偏方法同时对曝光偏差和从众偏差去偏, 表现出更优的效果.
4.3 重要超参数影响分析我们讨论本文算法的重要超参数, dropout保留概率p对算法效果的影响. 在本节的实验中, 我们保持其他条件不变, 并逐步调整dropout保留概率p的值, 以探索它如何影响推荐的性能. 实验选取该参数的集合为{0.1, 0.3, 0.6, 0.9}. 由于Yahoo!R3数据集较大, 实验耗时较长, 我们选择在Coat数据集上进行实验. 由于实际应用中的推荐列表一般可以达到5的长度, 所以选择综合了准确和排序顺序的常用指标NDCG@5作为比较指标. 结果如图2所示.
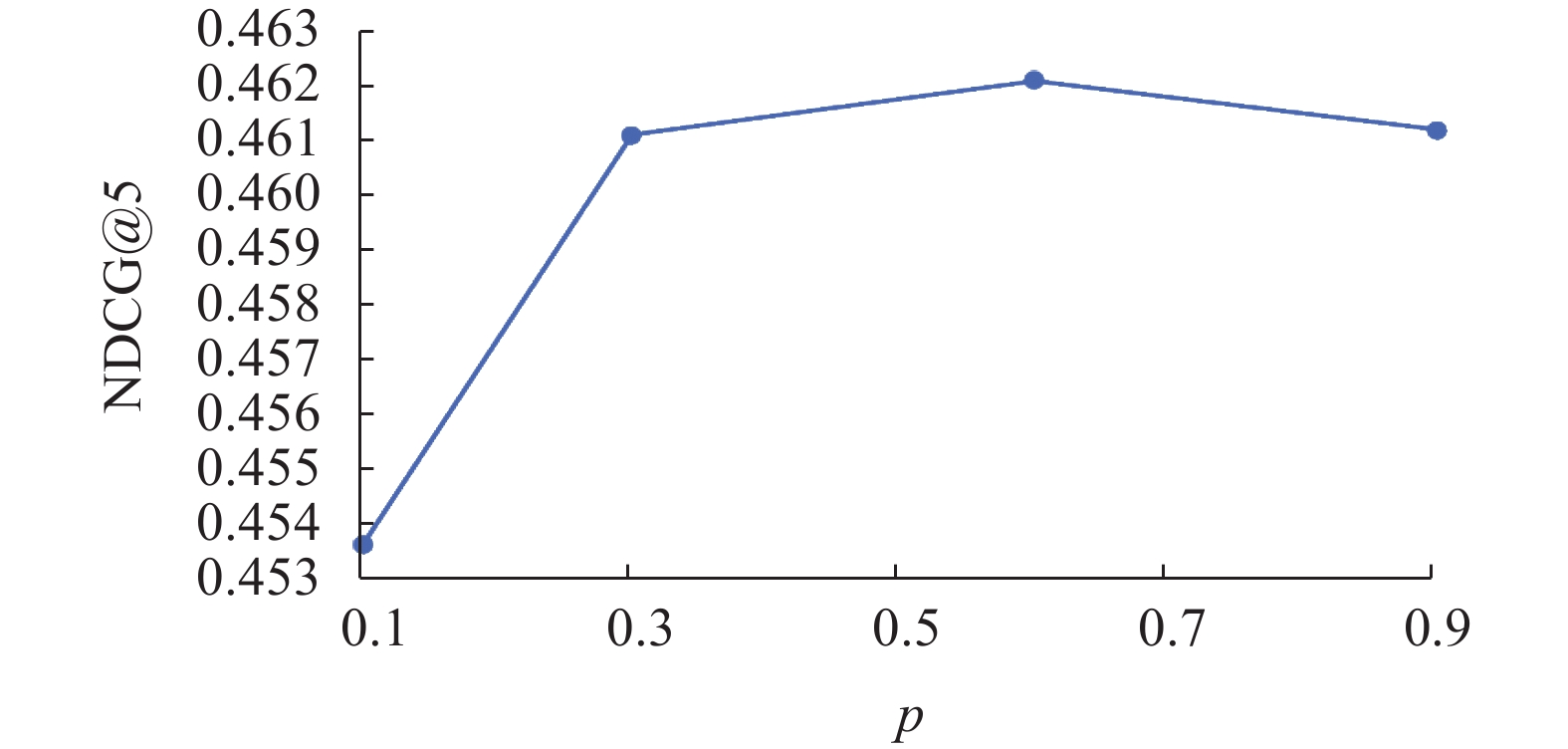
|
图 2 dropout保留概率p对 NDCG@5 的影响 |
从图2中可以看出, 不同的dropout保留概率p对推荐效果存在影响, Coat数据集上DUCF算法的NDCG@5指标值随着dropout保留概率p的变大先上升再下降, 在p=0.6时达到最大, 在p=0.1时最小. 分析其原因可能是, p过小时, 大部分神经元被丢弃, 特征向量变得稀疏, 对比学习辅助任务只能在稀疏向量上学习, 更难学到有意义的表示. 在p>0.3之后, 指标的变化并不大, 我们进行的更细粒度的实验也支持这一观察, 这可能是因为相比于数据增强的程度, InfoNCE经验损失促使表示向量在超球面上的均匀分布的作用对向量表示和去偏的效果有更大的影响.
4.4 消融实验为了进一步验证本文算法和各个子方法的有效性, 我们在Coat数据集上进行消融实验, 分别测试算法的每一部分的贡献, 结果如表2所示. 从表2中可以看出, 如果不使用双重逆倾向加权或者不使用对比学习辅助任务来去偏, 那么效果都会低于本文提出的完整算法. 这是因为双重逆倾向加权方法可以同时对曝光偏差和从众偏差进行去偏; 对比学习辅助任务利用InfoNCE经验损失引入先验知识, 促使表示向量在超球面上的均匀分布的作用和dropout带来的集成效应, 同样可以对两种数据偏差进行去偏、提高算法对数据偏差的鲁棒性.
| 表 2 消融实验 |
5 结论与展望
针对隐式反馈数据中存在的曝光偏差、从众偏差和数据稀疏的问题, 为了估计用户对物品的偏好概率, 使推荐系统能够更精准地命中用户偏好, 本文提出了一种同时去偏曝光偏差和从众偏差的双重去偏协同过滤推荐算法. 算法通过我们提出的双重逆倾向加权方法和对比学习辅助任务去偏输入双塔自编码器的隐式反馈数据中包含的两种偏差, 估计用户对物品的偏好概率.
本文采用衣物推荐和歌曲推荐两个现实推荐场景的公开数据集, 在去偏测试集上进行效果验证, 对比了传统推荐算法和一些已知表现较好的去偏推荐算法, 并进行了消融实验验证方法每一部分的作用. 结果表明, 本文提出的方法具有较好的效果, 能够提高推荐的准确度、将用户偏好的相关物品排在更靠前的位置、对用户偏好的物品集有更高的召回率.
在信息爆炸、物质极大丰富的时代背景下, 用户面临海量选择, 需要提高信息接收效率、探索潜在需求; 应用服务提供方对需求和偏好各异的用户需要进行个性化精准推荐以提高用户满意度和收益, 而推荐系统在不断地推荐、观测记录、迭代训练的循环中加剧偏差. 影响用户和应用服务提供方双方的利益. 本文提出的算法易于部署应用, 能够去偏多种成因和形式的数据偏差, 利用更容易采集、数据量更大的隐式反馈数据, 取得更好的推荐效果.
| [1] |
Linden G, Smith B, York J. Amazon.com recommendations: Item-to-item collaborative filtering. IEEE Internet Computing, 2003, 7(1): 76-80. |
| [2] |
Lee JW, Park S, Lee J, et al. Bilateral self-unbiased learning from biased implicit feedback. Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval. Madrid: ACM, 2022. 29–39.
|
| [3] |
Chen JW, Dong HD, Wang X, et al. Bias and debias in recommender system: A survey and future directions. ACM Transactions on Information Systems, 2023, 41(3): 67. |
| [4] |
邱阳. 面向推荐系统数据偏差的去偏方法研究 [硕士学位论文]. 合肥: 中国科学技术大学, 2023.
|
| [5] |
Saito Y, Yaginuma S, Nishino Y, et al. Unbiased recommender learning from missing-not-at-random implicit feedback. Proceedings of the 13th International Conference on Web Search and Data Mining. Houston: ACM, 2020. 501–509.
|
| [6] |
Gupta S, Oosterhuis H, de Rijke M. A deep generative recommendation method for unbiased learning from implicit feedback. Proceedings of the 2023 ACM SIGIR International Conference on Theory of Information Retrieval. Taipei: ACM, 2023. 87–93.
|
| [7] |
Truong QT, Salah A, Lauw HW. Bilateral variational autoencoder for collaborative filtering. Proceedings of the 14th ACM International Conference on Web Search and Data Mining. ACM, 2021. 292–300.
|
| [8] |
Wu L, He XN, Wang X, et al. A survey on accuracy-oriented neural recommendation: From collaborative filtering to information-rich recommendation. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(5): 4425-4445. |
| [9] |
Kerley CI, Cai LY, Tang YC, et al. Batch size go big or go home: Counterintuitive improvement in medical autoencoders with smaller batch size. Proceedings of SPIE 12464, Medical Imaging 2023: Image Processing. San Diego: SPIE, 2023. 124640H.
|
| [10] |
Sedhain S, Menon AK, Sanner S, et al. AutoRec: Autoencoders meet collaborative filtering. Proceedings of the 24th International Conference on World Wide Web. Florence: ACM, 2015. 111–112.
|
| [11] |
Khawar F, Poon L, Zhang NL. Learning the structure of auto-encoding recommenders. Proceedings of the 2020 Web Conference. Taipei: ACM, 2020. 519–529.
|
| [12] |
Wu Y, DuBois C, Zheng AX, et al. Collaborative denoising auto-encoders for top-N recommender systems. Proceedings of the 9th ACM International Conference on Web Search and Data Mining. San Francisco: ACM, 2016. 153–162.
|
| [13] |
Jing MY, Zhu YM, Zang TZ, et al. Contrastive self-supervised learning in recommender systems: A survey. ACM Transactions on Information Systems, 2024, 42(2): 59. |
| [14] |
Yu JL, Yin HZ, Xia X, et al. Are graph augmentations necessary? Simple graph contrastive learning for recommendation. Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval. Madrid: ACM, 2022. 1294–1303.
|
| [15] |
Wang TZ, Isola P. Understanding contrastive representation learning through alignment and uniformity on the hypersphere. Proceedings of the 37th International Conference on Machine Learning. JMLR.org, 2020. 1–11.
|
| [16] |
Zhou GL, Huang CK, Chen XC, et al. Contrastive counterfactual learning for causality-aware interpretable recommender systems. Proceedings of the 32nd ACM International Conference on Information and Knowledge Management. Birmingham: ACM, 2023. 3564–3573.
|
| [17] |
Srivastava N, Hinton G, Krizhevsky A, et al. Dropout: A simple way to prevent neural networks from overfitting. The Journal of Machine Learning Research, 2014, 15(1): 1929-1958. |
| [18] |
Gao TY, Yao XC, Chen DQ. SimCSE: Simple contrastive learning of sentence embeddings. Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing. ACL, 2021. 6894–6910.
|
| [19] |
Yao TS, Yi XY, Cheng DZ, et al. Self-supervised learning for large-scale item recommendations. Proceedings of the 30th ACM International Conference on Information & Knowledge Management. ACM, 2021. 4321–4330.
|
| [20] |
Marlin BM, Zemel RS. Collaborative prediction and ranking with non-random missing data. Proceedings of the 3rd ACM Conference on Recommender Systems. New York: ACM, 2009. 5–12.
|
| [21] |
Schnabel T, Swaminathan A, Singh A, et al. Recommendations as treatments: Debiasing learning and evaluation. Proceedings of the 33rd International Conference on Machine Learning. New York: PMLR, 2016. 1670–1679.
|
| [22] |
Hu YF, Koren Y, Volinsky C. Collaborative filtering for implicit feedback datasets. Proceedings of the 8th IEEE International Conference on Data Mining. Pisa: IEEE, 2008. 263–272.
|
| [23] |
Zhu ZW, He Y, Zhang Y, et al. Unbiased implicit recommendation and propensity estimation via combinational joint learning. Proceedings of the 14th ACM Conference on Recommender Systems. ACM, 2020. 551–556.
|
| [24] |
Wei TX, Feng FL, Chen JW, et al. Model-agnostic counterfactual reasoning for eliminating popularity bias in recommender system. Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining. ACM, 2021. 1791–1800.
|
| [25] |
Chen JW, Dong HD, Qiu Y, et al. AutoDebias: Learning to debias for recommendation. Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval. ACM, 2021. 21–30.
|
| [26] |
Zheng Y, Gao C, Li X, et al. Disentangling user interest and conformity for recommendation with causal embedding. Proceedings of the 2021 Web Conference. Ljubljana: ACM, 2021. 2980–2991.
|
| [27] |
He XN, Deng K, Wang X, et al. LightGCN: Simplifying and powering graph convolution network for recommendation. Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval. New York: ACM, 2020. 639–648.
|
 2024, Vol. 33
2024, Vol. 33



