基于多层空间特征融合的三维人体姿态估计

引用本文

梁桉源, 肖学中. 基于多层空间特征融合的三维人体姿态估计. 计算机系统应用, 2024, 33(8): 250-256.http://www.c-s-a.org.cn/1003-3254/9602.html

Liang AY, Xiao XZ. 3D Human Pose Estimation Based on Multi-layer Spatial Feature Fusion. Computer Systems and Applications, 2024, 33(8): 250-256(in Chinese).http://www.c-s-a.org.cn/1003-3254/9602.html

基于多层空间特征融合的三维人体姿态估计

梁桉源, 肖学中

南京邮电大学计算机学院, 南京 210023

收稿日期：2024-02-26; 修改日期：2024-03-28; 采用时间：2024-04-10; csa 在线出版时间：2024-06-28

通讯作者：梁桉源, E-mail: 1228153458@qq.com.

摘要：在三维人体姿态估计任务当中, 人体关节之间的连接关系形成了一种复杂的拓扑结构, 利用图卷积网络对该结构进行建模, 可以有效捕捉局部关节间的联系; 尽管不相邻关节之间没有直接的物理连接, 但由于人体的运动和姿态受到生物力学约束以及人体关节之间的协同作用, 利用Transformer编码器建立关节之间的上下文关系, 可以更好地推断出人体姿态; 在大模型的背景下, 如何在保证模型性能的同时, 降低参数量, 也显得尤为重要. 针对上述问题, 设计了一个基于图卷积和Transformer的多层空间特征融合网络模型(MLSFFN), 在使用相对少量的参数基础上, 有效地融合了局部和全局空间特征. 实验结果表明, 本文提出的方法在仅需2.1M参数量的情况下, 在Human3.6M数据集上达到了49.9 mm的平均每关节误差(MPJPE). 此外, 模型在MPI-INF-3DHP数据集上也展示出了较强的泛化能力.

关键词: 多层空间特征融合三维人体姿态估计图卷积网络 Transformer 轻量型

3D Human Pose Estimation Based on Multi-layer Spatial Feature Fusion

LIANG An-Yuan, XIAO Xue-Zhong

School of Computer Science, Nanjing University of Posts and Telecommunications, Nanjing 210023, China

Abstract: In the task of 3D human pose estimation, the complex topology formed by the connection relationship between human joints presents a challenge. Effective capture of the connections between local joints is possible through modeling this structure with a graph convolutional network. Although non-adjacent joints lack direct physical connections, Transformer encoders establish contextual relationships between joints, which is crucial for better human posture inference due to the biomechanical constraints influencing human motion and pose, as well as the synergistic interaction of human joints. Balancing model performance with a reduction in the number of parameters is of particular importance for large-scale models. To tackle these challenges, a multi-layer spatial feature fusion network model (MLSFFN) based on graph convolution and Transformer is designed. This model proficiently fuses local and global spatial features with a relatively minimal parameter set. Experimental results demonstrate that the proposed method achieves a mean point per joint error (MPJPE) of 49.9 mm on the Human3.6M dataset with only 2.1M parameters. Moreover, the model demonstrates a robust generalization capability.

Key words: multi-layer spatial feature fusion 3D human pose estimation graph convolutional network (GCN) Transformer lightweight

人体姿态估计(human pose estimation, HPE)在计算机视觉领域一直是研究热点, 尤其在三维人体姿态估计方面, 对人机交互、康复治疗以及增强现实等应用领域产生深远影响. 在过去几年中, 基于深度学习的三维人体姿态估计方法取得了显著的进展, 但是实现对三维人体姿态的精确估计仍然是一个具有挑战性的问题.

基于单帧视频的三维人体姿态估计的关键在于空间特征的提取及处理, 其效率与准确度直接决定了模型的性能表现. 当前, 图卷积网络(graph convolutional network, GCN)与Transformer模型成为处理此类问题的两种主流技术, 它们分别通过图结构和自注意力机制进行空间特征的深度挖掘. 然而, 源自频谱卷积的原始GCN存在一个重要问题, 即权重共享卷积. 在原始的GCN模型中, 每个节点都通过相同的转换矩阵进行转换, 然后邻近特征将被聚合, 用以传输到下一层^[1]. 但这种权重共享方法并不能有效捕捉到人体关节的复杂信息, 因为人体运动的灵活性和速度会随着关节的变化而变化. 此外, 其中还存在着3D HPE中关节间非局部依赖性的问题^[2–5]. Transformer中的自注意力机制能够捕捉特征的全局信息. 在3D HPE中, 自注意力机制能够帮助关节与其他关节建立联系, 从而获得全局依赖性. 这种全局依赖性适合模拟关节间的相似性关系, 因为它能够随着输入姿态的变化而进行相应的调整.然而, 纯粹的Transformer模型也有其局限性, 它可能会忽视人体骨骼中的物理信息^[6].

大多数现有的研究往往只依赖于其中一种技术, 忽略了GCN与Transformer间可能存在的互补优势. 此外, 如何有效自适应局部和全局空间特征的权重也是一个重要问题. 局部和全局空间特征在模型处理过程中扮演着不同的角色, 缺乏适应性的权重调整可能会导致模型处理这两种特征的能力不足, 进一步影响模型性能. 而且Transformer编码器的参数量呈指数级增长, 对模型的计算效率和存储需求也提出了严峻的挑战. 因此, 如何在保证模型性能的前提下, 更加合理地设计模型结构以减少参数量, 成为当前研究的一个重要任务.

为了克服上述这些问题, 同时充分利用人体骨骼中关节的局部和非局部关系, 我们提出了一种新的架构. 这种架构将GCN和Transformer编码器两个独立的模块交替使用, 混合并利用局部和全局依赖性的信息. 在这种架构下, GCN模块和Transformer编码器可以交互地进行信息处理, 使得模型在处理关节间的复杂关系时, 既保留了局部的精细信息, 又捕捉到了全局的依赖性, 从而提高了模型的性能和准确度.

本文的主要贡献包括: 提出了一种新颖的结构设计, 将GCN和Transformer编码器设计成6层结构, 交替混合提取局部和全局空间特征后, 使用SE模块进一步突出重要的空间特征, 在使用相对少量参数的同时提升了模型的效果. 并且在Human3.6M数据集中进行了大量实验, 结果表明, 本文提出的模型MLSFFN在各项指标上均优于与之比较的7个模型, 并在MPI-INF-3DHP数据集上进一步验证其泛化性.

1 相关工作

三维人体姿态估计是计算机视觉领域的一个重要研究方向, 它的目标是从二维图像或视频中估计出人体的三维关键点信息. 这个问题具有很大的挑战性. 因为人体姿态的变化非常复杂, 而且图像的投影会导致深度信息的丢失. 本文研究的内容是单视角单人三维人体姿态估计, 根据是否使用二维姿态结果作为中间表示, 可以分为直接估计法和二维提升到三维两种方法. 本节回顾了基于深度学习的单视角单人三维人体姿态估计的一些相关工作.

1.1 基于直接估计的方法

直接估计法即直接从二维图像中推断出三维人体姿态, 而不需要中间估计2D姿态表示. 早期的工作应用了回归范式来直接估计三维人体姿态. Li等人^[7]最初将端到端的方法与深度神经网络相结合, 通过关节检测器和关节回归器的结合进行3D HPE. 与早期的研究相比, 现在有许多单阶段方法将热图表示应用到3D HPE中. 例如, Pavlakos等人^[8]提出了一种单阶段方法, 该方法在体素空间中预测三维热图, 并提出了一个粗到细的预测方案以减少大的三维热图代价.

1.2 基于二维提升到三维的方法

随着深度学习的发展, 二维人体姿态估计已经相对成熟. 使用现有的二维人体姿态估计模型来估计二维姿态, 然后将二维姿态作为中间表示, 进一步提升到三维姿态已经成为当下一种流行的三维人体姿态估计方法. 得益于先进的二维姿态检测器的卓越性能, 二维提升到三维的方法通常优于直接估计方法. GAT^[9]使用自注意力机制学习每个节点的权重以聚合邻域信息. aGCN^[10]与GAT的工作方式相同, 通过自注意力机制学习邻接节点的权重. 区别在于aGCN使用不同的激活函数和转换矩阵. 尽管GAT和aGCN通过聚合邻接节点来提升效果, 但有限的感受野仍然是一个具有挑战性的问题. 为了获得全局感受野, Zhao等人^[11]提出了语义图卷积, 使用non-local模块^[12]来学习二维关节之间的关系. Lin等人^[13]修改了标准的Transformer编码器并调整了编码器层的维度. 然而, 这种交互忽略了上述的相邻关节的局部空间特征信息. 由于人体姿态可以表示为图结构, 其中关节是节点, 骨骼是边, 因此图卷积网络(GCN)已经被广泛应用到二维提升到三维的姿态估计任务当中. Ge等人^[14]使用堆叠沙漏网络从图像中提取特征, 这些特征被重塑为图结构. 通过图卷积网络提取的特征预测三维网格, 然后用于预测3D姿态. Xu等人^[3]提出了图沙漏网络并采用SE Block^[15]来融合从图沙漏网络的不同层次提取的特征. STCFormer^[16]引入了时空交叉注意力模块, 通过串联多个STC模块, 并融入了一种新型的结构增强位置嵌入(SPE), 以深化模型对人体结构的理解. 这种结构增强位置嵌入通过对邻近关节进行时空卷积, 精准捕获关节的局部结构特征, 并通过部分感知嵌入明确每个关节所属的具体部位. GraFormer^[6]为了建模非邻近节点间隐含的高阶连接关系, 引入了ChebGConv块以在非邻近节点间交换信息, 从而获得更大的感受野. AMPose^[17]通过两个独立的模块串联混合局部和全局依赖的信息来捕获人体骨骼中的全局和局部信息.

在本文中, 我们对AMPose基线模型进行了优化, 将图卷积和Transformer编码器设计成多层来交叉融合局部和全局空间特征, 并用SE Block进一步突出重要的空间特征, 从而用少量的参数基础上, 能够获得与原模型三维人体姿态估计接近的估计效果.

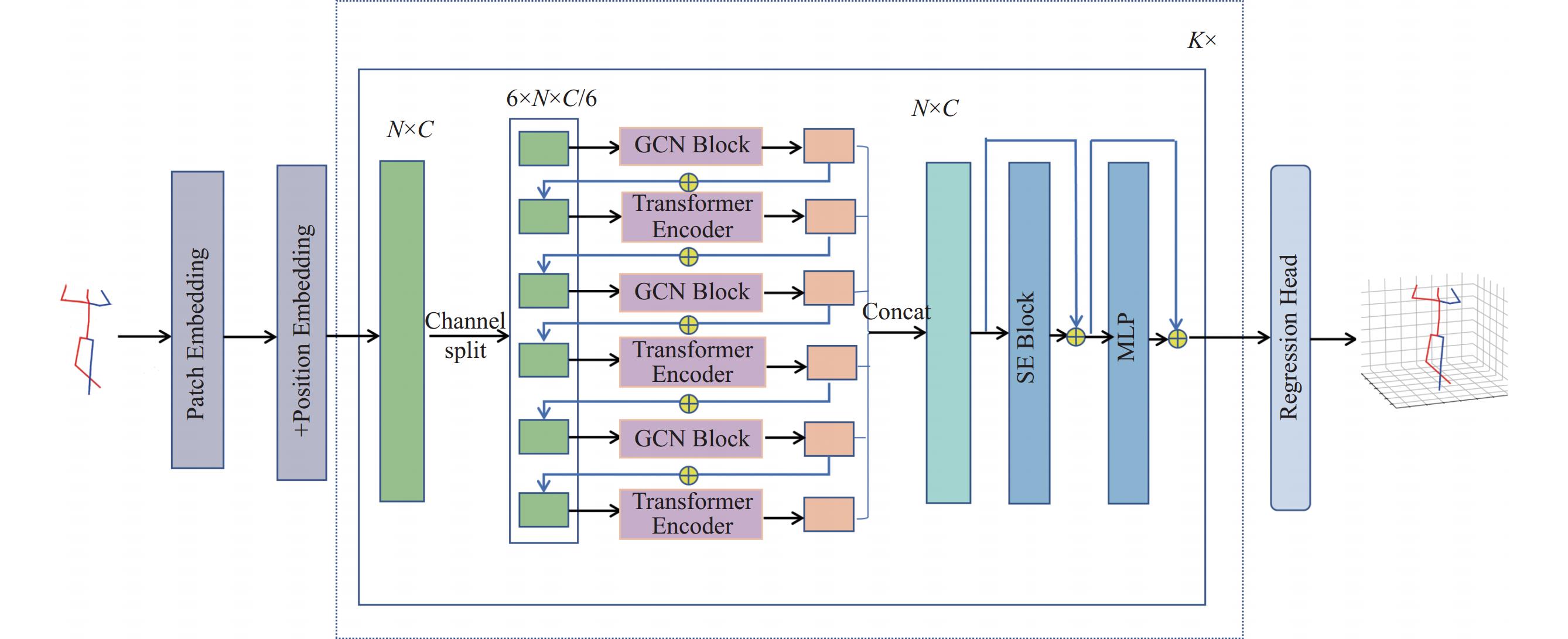
2 基于多层空间特征融合的模型

如图1所示, 本文提出的模型MLSFFN的网络结构主要包括GCN模块、Transformer编码器和SE模块3部分. 首先用成熟的二维姿态估计器估计出输入图片的二维关键点坐标$X \in {R^{N \times 2}}$, 然后通过Patch Embedding将映射到高维向量空间$X' \in {R^{N \times C}}$, 其中是N关节的数量, C是通道维度. 然后我们将网络模型中学习得到的位置矩阵${E_{\rm pos}} \in {R^{N \times C}}$嵌入到$X'$中, 得到嵌入特征向量${X^\ell }$. 接下来, ${X^\ell }$被均匀分成6部分: $ {X}_{1}^{\ell }、{X}_{2}^{\ell }、{X}_{3}^{\ell }、{X}_{4}^{\ell }、{X}_{5}^{\ell }、{X}_{6}^{\ell } $. 它们都具有相同的维度$C' = C{\text{/}}6$, 并根据$X_i^\ell $中的$i$送入对应的第$i$层的模块. 这些模块从多个语义层次构建人体关节和身体空间特征. 然后将每一层的输出向量${Y^\ell }$拼接起来获得向量${Y^\ell } \in {R^{N \times C}}$, 再将向量$Y_i^\ell $输入SE模块进行权重自适应, 突出重要的空间特征. 最后输入到多层感知机中, 再使用线性层回归头来估计出三维坐标$Y \in {R^{N \times 3}}$. 图卷积网络模块、Transformer编码器和SE模块的结构将在以下章节介绍.

图 1 MLSFFN的网络结构

2.1 GCN模块

人体骨架的图结构可以表示为$G = (V, A)$, 其中V是N个关节点的集合, $A \in {\{ 0, 1\} ^{N \times N}}$是邻接矩阵, 代表关节之间的连接关系. 给定输入$X_i^\ell \in {R^{N \times \mathcal{C}'}}$以通过GCN Block将相邻关节的空间特征聚合, 当$i - 1$时, 具体公式如下:

$ {\mathrm{GCN}}(X_i^\ell ) = {\tilde D^{ - 1/2}}\tilde A{\tilde D^{ - 1/2}}X_i^\ell W $

(1)

$ Y_i^\ell = X_i^\ell + {\mathrm{GCN}}(\sigma ({\mathrm{GCN}}(X_i^\ell ))) $

(2)

当$i \in \{ 3, 5\} $时, 先将第i层的输入向量与第$i - 1$层的输出向量$\tilde X_i^\ell $相加获得向量$\tilde X_i^\ell $, 即$\begin{array}{*{20}{r}} {\tilde X_i^\ell = X_i^\ell + Y_{i - 1}^\ell } \end{array}$, 然后再将$\tilde X_i^\ell $输入到GCN Block中, 具体公式如下:

$ {\mathrm{GCN}}(\tilde X_i^l) = {\tilde D^{ - 1/2}}\tilde A{\tilde D^{ - 1/2}}\tilde X_i^lW $

(3)

$ Y_i^\ell = \tilde X_i^l + {\mathrm{GCN}}(\sigma ({\mathrm{GCN}}(\tilde X_i^l))) $

(4)

其中, $\tilde A = A + I$, $\tilde D$是关节点的度的对角矩阵, W是权重矩阵, $Y_i^\ell $表示第i层对应的GCN Block的输出, ${\sigma}$表示GELU激活函数.

2.2 Transformer编码器

缩放的点积注意力: 缩放的点积注意力通常被定义为一个自注意力函数, 这个函数将Query (Q)矩阵, Key(K)矩阵, Value (V)矩阵作为输入. 其中$Q, K, V \in {R^{{N_j} \times {N_d}}}$, ${N_j}$表示关节的数量, ${N_d}$表示通道的数量. 为了避免Q和K的乘积过大, 引入${\sqrt N _d}$作为归一化因子. 自注意力的计算公式如下:

$ Attention(Q, K, V) = \mathit{Softmax}\left(\frac{{Q{K^{\mathrm{T}}}}}{{\sqrt N }}\right)V $

(5)

当输入特征${\mathbf{Z}} \in {R^{{N_j} \times {N_d}}}$经过可学习的变换矩阵${W^Q}, {W^K}, {W^V} \in {R^{{N_d} \times {N_d}}}$的变换后, 可以得到Q、K、V, 也就是:

$ Q = Z{W^Q}, K = Z{W^K}, V = Z{W^V} $

(6)

多头自注意力(multi-head self attention, MSA)层: 多头自注意力是多个自注意力函数的拼接. 每个头部独立地处理部分输入特征. 多个头的拼接结果会通过${W^{\rm out}}$进行变换. 多头自注意力公式如下:

$ \begin{array}{*{20}{c}} {}&{\mathit{MSA}(Q, K, V) = {Concat}(hea{d_1}, \cdots , hea{d_{{N_h}}}){W^{\rm out}}} \end{array} $

(7)

其中, $hea{d_{in}} = Attention({Q_{in}}, {K_{in}}, {V_{in}}), $$in \in [1, \cdots , {N_h}]$, 而${W^{\rm out}} \in {R^{{N_d} \times {N_d}}}$是可训练的参数矩阵, ${N_h}$是注意力头的数量.

在本文中, 当$i \in \{ 2, 4, 6\} $时, 先将第i层的输入向量$X_i^\ell $与第i–1层的输出向量$Y_{i - 1}^\ell $相加获得向量$\tilde X_i^t$, 即$ \tilde X_i^\ell = X_i^\ell + Y_{i - 1}^\ell $, 然后再将$\tilde X_i^\ell $输入到Transformer Encoder中, 具体公式如下:

$ hea{d_t} = \mathit{Softmax}\left( {\frac{{{Q^\ell }{K^{{\ell ^{\mathrm{T}}}}}}}{{\sqrt {C'} }}} \right){V^\ell }, \;\;t \in \{ 1, \cdots , h\} $

(8)

$ \mathit{MSA}(\tilde X_i^\ell ) = ({hea{d_1}}, {head}_{2}, \cdots, {head}_{h}){W}^{\rm out} $

(9)

$ \tilde Y_i^\ell = \tilde X_i^\ell + LN(\mathit{MSA}(\tilde X_i^\ell )) $

(10)

其中, h是注意力头的数量, ${Q^\ell }, {K^\ell }, {V^\ell }$分别是Query、Key、Value矩阵, 它们是通过$\tilde X_i^\ell $线性变换得到的, $\tilde Y_i^\ell $表示第i层对应的Transformer Encoder的输出.

2.3 SE模块

如图2所示, SE模块具体包括全局池化层、全连接层、ReLU激活函数以及Scale操作. 将每一层的输出向量$Y_i^\ell $拼接起来后获得的向量${Y^\ell } \in {R^{N \times C}}$到SE模块, 在引入少量的参数的基础上, 显式建模卷积特征通道之间的相互依赖关系, 提高网络的表征能力, 通过权重自适应有选择性地突出人体建模中的重要的特征, 抑制不太重要的特征, 最后输出与输入向量${Y^\ell }$同等维度的向量.

图 2 SE模块

3 实验

本节描述了实验中所用到的数据集、评估指标、消融实验等. 在Human3.6M数据集上与其他基线方法进行了对比, 并通过消融实验证明了本文设计出的模型结构的有效性. 最后, 在MPI-INF-3DHP数据集上进行测试, 进一步证明该方法的泛化能力.

3.1 数据集

本文提出的模型在两个公共数据集上进行了测试: Human3.6M和MPI-INF-3DHP.

Human3.6M: 是三维人体姿态估计中最常见的数据集之一, 由360万张图像组成, 通过4台高分辨率逐行扫描相机以每秒50帧的速率捕获视频数据. 该数据集包括17个场景, 其中11名专业演员(6男5女)参与各种活动, 包括讨论、吸烟、拍照、打电话等. 在本文中, 将对象1、5、6、7、8归入训练集, 而将对象 9和11划分为测试集.

MPI-INF-3DHP: 是一个具有挑战性的数据集, 图像包括了室内和室外环境. 该数据集包含130多万帧图像, 由14个摄像角度记录8位参与者的8类活动. 在本文中通过在 MPI-INF-3DHP 的测试集上进行测试来进一步评估模型的泛化能力.

3.2 评估指标

对于Human3.6M数据集, 通常采用MPJPE (mean per joint position error)和P-MPJPE (procrustes MPJPE)作为评价指标. MPJPE指估计的关节和地面真值之间的平均欧氏距离, 单位为mm, MPJPE也称为Protocol #1. P-MPJPE是先进行刚性变换后, 再计算MPJPE. 通常将P-MPJPE称为Protocol #2. 而对于MPI-INF-3DHP数据集, 通常采用正确关键点的百分比(PCK)、AUC、Outdoor、GS、noGS作为评价指标.

3.3 实验参数设置

本文提出的模型MLSFFN是一种两阶段方法, 即基于二维提升到三维的方法. 首先将图像输入到成熟的二维姿态估计模型中, 本方法采用的二维姿态估计模型是级联金字塔网络(cascaded pyramid network, CPN). 然后MLSFFN以二维关节坐标作为输入生成三维姿态坐标. 本文将模型的深度 K 设置为 3, 编码后的向量通道大小C设置为240, 多头注意力的头数设置为8. 在本文提出的模型MLSFFN中, 将batch-size设置为 512, 迭代次数为50. 学习率最初设置为0.0001, 每5个epoch后学习率以0.95倍指数衰减, 优化器采用的Adam优化器.

3.4 实验结果对比

从表1可以看出, MLSFFN与基线方法AMPose相比, 仅使用了原模型将近1/9的参数量和不到1/10的浮点运算次数, 就实现了和AMPose差不多的P1和更优的P2值. 这表明MLSFFN在保持性能的同时, 显著提高了模型的效率和轻量化程度.

表 1 MLSFFN与AMPose在参数量和浮点运算次数上的对比

表2、表3展示了本文提出的方法与其他方法在Human3.6M数据集上的表现.

表 2 MLSFFN与其他方法在Human3.6M上Protocol #1 (MPJPE)和Protocol #2 (P-MPJPE)的对比

表 3 MLSFFN与其他方法在Human3.6M上不同动作的MPJPE的对比

从表2和表3可以看出, 本文提出的方法相比于其他基线方法, 在打电话、拍照等多个动作场景下具有更好的表现. 当使用CPN估计得到的二维关键点作为输入时, MLSFFN在MPJPE (49.1 mm)和 P-MPJPE (38.9 mm) 下都取得了最佳结果. 此外, 使用ground truth 二维关节作为输入时, MLSFFN也表现很好, 平均每关节误差达到了36.7 mm. 为了进一步评估MLSFFN的泛化能力, 在Human3.6M上训练MLSFFN, 并在 MPI-INF-3DHP上进行测试. 如表4中所示, MLSFFN使用少量的参数保持了在MPI-INF-3DHP上与AMPose相近的性能, 并且在PCK、AUC、Outdoor等3个指标上优于其他基线模型.

表 4 MLSFFN与其他方法在MPI-INF-3DHP上的性能对比

3.5 消融实验

为了评估MLSFFN在模型设计结构上的有效性, 本文在Human3.6M数据集上进行了消融实验, 针对不同设计结构、参数和分层的层数进行了参数量和模型效果的对比. 实验结果如表5和表6所示.

表 5 在Human3.6M上不同结构的性能对比

表 6 在Human3.6M上不同层数和参数的性能对比

结果表明, MLSFFN相比于单个GCN模块、单个Transformer模块、并行设计、串行设计、多层空间特征融合(不包括SE模块), 本文设计的结构可以在使用的少量参数量的基础上, 模型获得最优的性能. 并且进一步在层数和参数的选择上进行了实验对比, 当层数为6, 模型深度k为3时, 模型效果最优.

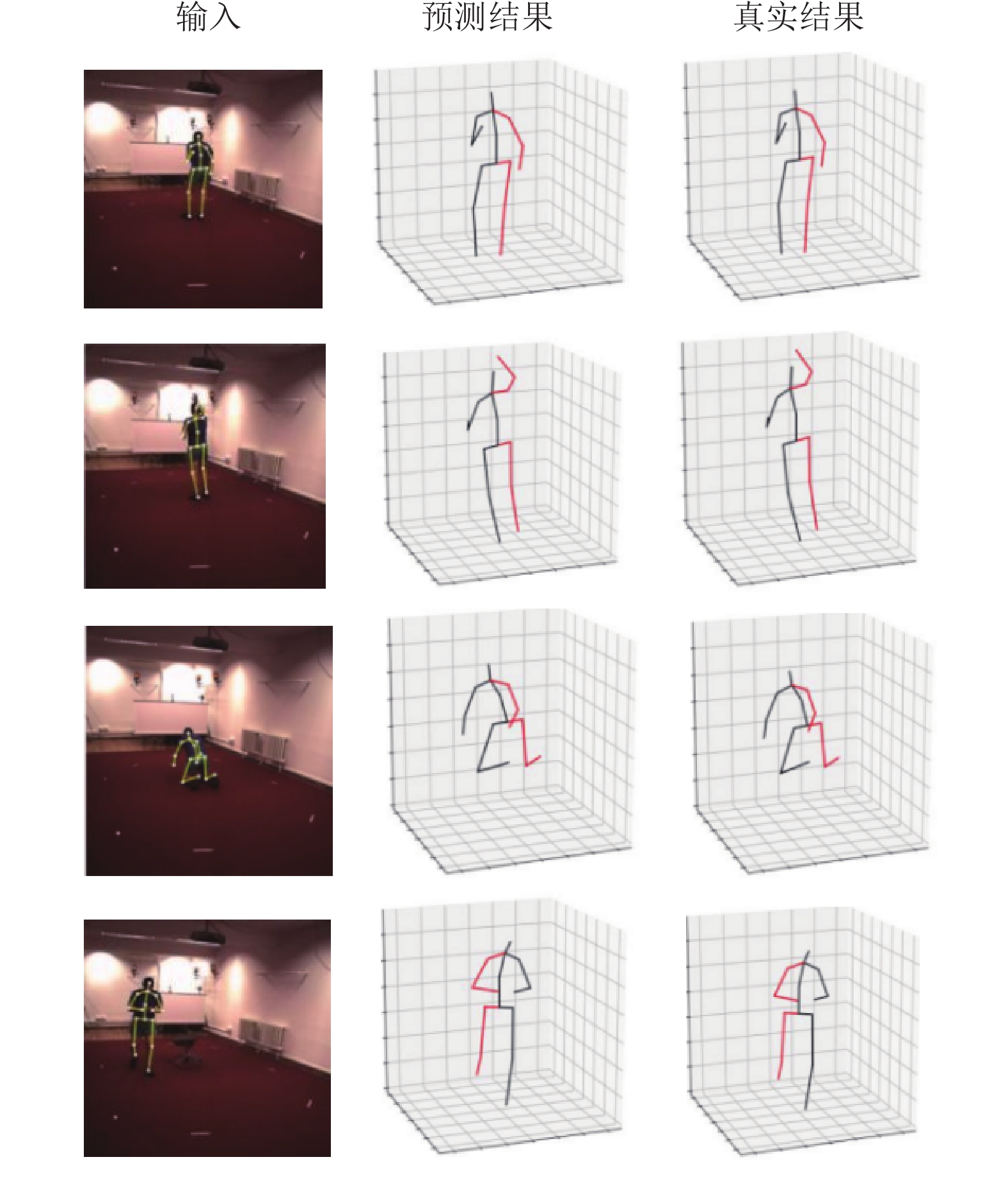
3.6 定性结果

图3展示了本文提出的模型MLSFFN在Human3.6M上的定性结果. 采用Human3.6M数据集中的视频帧作为输入, 利用本文提出的模型对视频帧中的人体姿态进行估计, 得到了图3中的预测结果. 为了验证本文算法的准确性, 将预测结果与三维地面真值(ground truth)进行了对比分析. 经过比较, 发现估计值与真实值之间的差异极其微小, 也进一步证明了我们算法的有效性.

图 3 MLSFFN在Human3.6M上的定性结果

4 总结

本文基于基线模型AMPose进行了优化, 提出了一种新颖的架构MLSFFN. 人体关节之间的关系可以分为两种: 非物理连接和物理连接关系在MLSFFN中, 分别由Transformer编码器和GCN对关节关系模块化. 其中, Transformer 编码器用于处理每个关节与所有其他关节的连接关系, 而 GCN用于捕获人体相邻关节的信息. 通过Transformer编码器和GCN模块进行6层空间特征交互融合, 再通过SE模块突出其中重要特征的权值, 有效提取了关节间的空间特征信息. 在提升模型性能的同时, 一定程度上降低了参数量. 本文所提出的方法在Human3.6M和 MPI-INF-3DHP数据集上与基线模型进行了对比. 实验结果表明, MLSFFN在准确性和参数量方面表现出更好的性能.

参考文献

[1]	Kipf TN, Welling M. Semi-supervised classification with graph convolutional networks. Proceedings of the 5th International Conference on Learning Representations. Toulon: ICLR, 2017. 1–14.
[2]	Cai YJ, Ge LH, Liu J, et al. Exploiting spatial-temporal relationships for 3D pose estimation via graph convolutional networks. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 2272–2281.
[3]	Xu TH, Takano W. Graph stacked hourglass networks for 3D human pose estimation. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 16100–16109.
[4]	Liu KK, Ding RQ, Zou ZM, et al. A comprehensive study of weight sharing in graph networks for 3D human pose estimation. Proceedings of the 16th European Conference on Computer Vision. Glasgow: Springer, 2020. 318–334.
[5]	Zou ZM, Tang W. Modulated graph convolutional network for 3D human pose estimation. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021. 11457–11467.
[6]	Zhao WX, Wang WQ, Tian YJ. GraFormer: Graph-oriented Transformer for 3D pose estimation. Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022. 20406–20415.
[7]	Li SJ, Chan AB. 3D human pose estimation from monocular images with deep convolutional neural network. Proceedings of the 12th Asian Conference on Computer Vision. Singapore: Springer, 2015. 332–347.
[8]	Pavlakos G, Zhou XW, Derpanis KG, et al. Coarse-to-fine volumetric prediction for single-image 3D human pose. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 1263–1272.
[9]	Veličković P, Cucurull G, Casanova A, et al. Graph attention networks. arXiv:1710.10903, 2017.
[10]	Yang JW, Lu JS, Lee S, et al. Graph R-CNN for scene graph generation. Proceedings of the 15th European Conference on Computer Vision (ECCV). Munich: Springer, 2018. 690–706.
[11]	Zhao L, Peng X, Tian Y, et al. Semantic graph convolutional networks for 3D human pose regression. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 3420–3430.
[12]	Wang XL, Girshick R, Gupta A, et al. Non-local neural networks. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 7794–7803.
[13]	Lin K, Wang LJ, Liu ZC. End-to-end human pose and mesh reconstruction with Transformers. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 1954–1963.
[14]	Ge LH, Ren Z, Li YC, et al. 3D hand shape and pose estimation from a single rgb image. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 10825–10834.
[15]	Hu J, Shen L, Sun G. Squeeze-and-excitation networks. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 7132–7141.
[16]	Tang ZH, Qiu ZF, Hao YB, et al. 3D human pose estimation with spatio-temporal criss-cross attention. Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Vancouver: IEEE, 2023. 4790–4799.
[17]	Lin HX, Chiu Y, Wu PY. AMPose: Alternately mixed global-local attention model for 3D human pose estimation. Proceedings of the 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Rhodes Island: IEEE, 2023. 1–5.
[18]	Ci H, Wang CY, Ma XX, et al. Optimizing network structure for 3D human pose estimation. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 2262–2271.
[19]	Li H, Shi BW, Dai WR, et al. Hierarchical graph networks for 3D human pose estimation. Proceedings of the 32nd British Machine Vision Conference 2021. BMVC, 2021. 1–14
[20]	Lutz S, Blythman R, Ghosal K, et al. Jointformer: Single-frame lifting Transformer with error prediction and refinement for 3D human pose estimation. Proceedings of the 26th International Conference on Pattern Recognition (ICPR). Montreal: IEEE, 2022. 1156–1163.
[21]	Zeng AL, Sun X, Yang L, et al. Learning skeletal graph neural networks for hard 3D pose estimation. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021. 11416–11425.
[22]	Liu RX, Shen J, Wang H, et al. Attention mechanism exploits temporal contexts: Real-time 3D human pose reconstruction. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 5063–5072.