2. 中国科学技术大学 苏州高等研究院, 苏州 215004
2. Suzhou Institute for Advanced Research, University of Science and Technology of China, Suzhou 215004, China
移动群智感知(mobile crowdsensing, MCS)[1]是一种经济高效的大规模数据采集方法, 已被应用于环境监测[2]、交通管理[3]、城市感知等多个领域. 通常来说, MCS系统需要招募一批工人, 利用他们携带的移动设备在一些感知区域收集数据. 在许多实际应用中, 可用的工人是有限的, 而任务分布在大规模区域, 招募足够的工人同时完成所有任务是不可行的. 因此, 有人提出了稀疏MCS[4], 即从感知区域的子集收集数据, 然后推理剩余数据. 然而, 实际应用中, 有两个因素限制稀疏MCS的性能: (1) 工人的不足或分布不均可能导致一些关键区域的数据采集不足. (2) 数据的时效性不足会增加系统误差. 越新鲜的数据越有价值, 比如在智能交通方面, 实时的道路状况能帮助人们更好地分析交通拥堵状况; 在应急响应方面, 事故和自然灾害的新鲜数据有助于人们及时做出对应的应急响应.
在本文中, 我们重点讨论考虑工人的数量以及对数据新鲜度敏感的稀疏MCS场景. 考虑一个分布在许多感知区域的持续的数据收集任务, 例如在十字路口收集交通信息或在特定地点测量空气质量指数. 每个感知区域都会不断产生数据, 稀疏MCS平台负责招募工人收集这些区域的最新数据. 由于预算和工人数量的限制, 平台只能招募有限的工人执行部分感知任务. 此外, 由于感知时间不同, 不同工人收集到的数据可能表现出不同的新鲜度. 为了衡量数据的新鲜度, 我们采用信息年龄(age of information, AoI)[5,6]指标, 它被定义为自最新数据收集以来所经过的时间. 然而, 在稀疏MCS中考虑AoI将在工人选择和数据推理方面带来两个新的挑战.
第1个挑战是设计准确的数据推理模型, 以在稀疏数据量下捕捉数据的时空关系. 在时间维度上, 只有AoI可用于辅助数据推理. 每个区域数据的AoI会随着时间的推移而不断变化, 并依赖于工人选择策略. 复杂的模型在稀疏MCS的小数据量场景下容易过拟合[7], 这使得基于AoI准确捕捉数据中的时间关系更加具有挑战性. 现有工作没有考虑该因素, 如Wang等人使用时空压缩感知算法补全数据[8], 难以捕捉数据的长期依赖关系. Wang等人使用了Transformer模型推理数据[2], 但没有考虑数据新鲜度的影响.
第2个挑战是设计高效的工人选择策略, 选择合适的工人收集数据, 以最大限度地降低感知数据的平均AoI并提高推理精度. 在稀疏MCS的在线场景中, 不是每个时刻所有区域都有可用的工人, 存在重要区域没有工人或者工人分布不均匀的情况. 在预算限制下, 我们需要精心挑选部分贡献度更大的工人. 现有的工作大多考虑的是离线的工人选择场景[9], 没有考虑更实际的工人实时到达的在线场景.
为了应对上述挑战, 我们提出一个名为“轻量级年龄敏感的数据感知和推理(simplified AoI-aware sensing and inference, SASI)”的框架. 该框架基于先知秘书算法来确定工人选择策略, 选择的工人收集数据后送入简化的数据推理模型推理全局数据.
2 稀疏移动群智感知模型和问题定义 2.1 系统模型本文主要研究一个连续时间的稀疏MCS系统. 该系统由任务请求者、大量工人、一组目标感知区域和云端服务平台组成. 任务请求者向平台发出数据收集服务, 平台招募工人在目标感知区域收集数据, 工人收集到数据后将数据上传回平台, 平台接收到数据后进行一系列的数据处理和分析工作, 并将结果返回给任务请求者. 在本文中, 每个时刻平台最多只选择一个工人从其所在的感知区域收集数据. 为简化表述, 我们将每次工人招募视为一轮数据收集. 此外, 由于感知数据是持续生成的, 由于存储空间有限, 平台只能保留从感知区域收集到的最新若干条数据. 让Mt代表平台在t时间的数据副本. 同时, 平台维护一个数据推理模型, 以推理未被选中进行数据收集的感知区域的数据. 此外, 平台还需要花费一定的成本来招募每个工人并存储数据副本. 我们将所有感知区域表示为一个集合N={1, 2, …, n}.
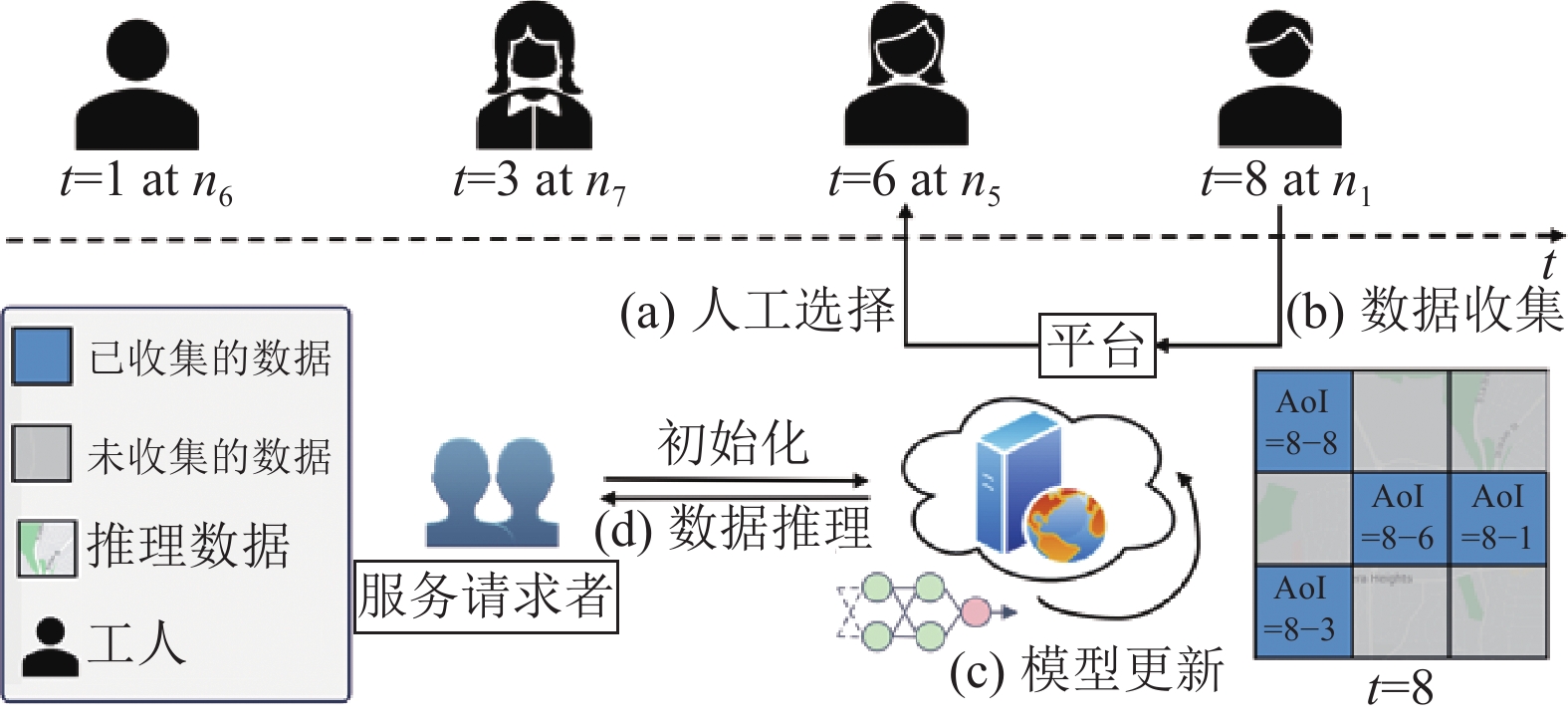
工作流程介绍如下. 首先, 服务请求者向平台提交数据收集请求. 然后, 平台招募工人逐轮收集数据. 如图1所示, 每一轮可分为4个阶段: 工人选择、数据收集、数据推理和模型更新, 具体如下.
|
图 1 稀疏移动群智感知系统总体结构图 |
工人选择: 在第1阶段, 对于连续在线到达的工人流, 平台会选择招募一名工人从感知区域ni收集数据, 其成本被表示为ci. 如图1所示, 平台在t=8时选择工人, 工人在其所在的区域n1进行数据采集.
数据收集: 在第2阶段, 工人收集数据并上传到平台. 平台将存储接收到的数据, 并更新感知区域对应的AoI值(在第1.2节中定义). 之后, 工人将收到佣金. 在图1的示例中, 工人对应的佣金等于c1. n1的AoI值从8下降到0, 而其他感知区域的AoI值则随着时间的推移呈线性增长.
数据推理: 我们使用数据推理模型来推理未采集的数据. 在图1的示例中, 除了左上方的感知区域是最新收集的数据外, 其余区域的数据都是推理出来的. 然后, 将推理结果发送给服务请求者.
模型更新: 最后, 推理模型利用收集到的数据进行实时更新. 经过一轮轮的更新, 模型变得更加精确.
2.2 AoI模型为了衡量数据的新鲜度, 我们将Δi(t)定义为区域ni的瞬时AoI, 它可以通过最近一次更新后的时间来计算. 更新策略指明了每次由工人上传哪个感知区域的数据. 我们将πi(t)定义为二进制变量, 表示感知区域ni的数据是否在时间t上传, 而π(t)={0, 1, 0, …, 0}表示所有感知区域的更新策略. 为便于解释, 我们假定Δi(t)在更新发生后下降为0, 即时间为t. Δi(tm)的演变过程可描述为:
| Δi(tm)={tm−tm−1+Δi(tm−1),ifπi(tm)=00,ifπi(tm)=1 | (1) |
其中, tm是数据在第m轮(m≥1)上传到平台的时间. 特别地, 当m=1时, tm–1=0, Δ(tm–1)=0. 此外πi(tm)表示在tm时是否选择收集区域ni的数据.
2.3 问题定义在上述稀疏MCS系统中, 平台逐轮收集数据. 给定预算限制B和持续时间T, 我们的目标是在线选择一组工人在目标感知区域收集数据, 使得感知数据的平均AoI和数据推理损失最小化, 形式化如下:
| {min1NT∑t=1N∑i=1Δi(tm)+T∑t=1βL(tm)s.t.{ˆM=f(M)wj∈W,k∑wj=1πjcj⩽B | (2) |
其中, β是为平衡平均AoI和推理损失之间的权重因子. 这里, M表示存储在平台中的原始数据, 而
为了解决上述问题, 我们提出轻量级年龄敏感的数据感知和推理(simplified AoI-aware sensing and inference, SASI)框架, 该框架的设计旨在实现轻量且高效的推理模型, 同时考虑数据的新鲜度作为感知决策和数据推理的重要因素. 具体而言, 该框架主要以强化学习算法深度Q-learning网络(DQN)为基础. 我们将框架抽象为一个强化学习(RL)代理, 其根据已有数据(状态)选择一个行动(工人), 以最小化AoI和推理损失(奖励). 因此, RL代理能够招募工人收集数据, 并根据环境反馈学习有效的策略, 以及根据当前状态预测未来. 总体而言, SASI包括两个模块: 工人选择和数据推理.
一方面, 工人选择是由代理的策略网络结合秘书算法决定的. 具体来说, 代理的策略网络本质上是从状态空间到行动空间的函数映射. 鉴于在我们的场景中, 行动空间对应于出现在某个感知区域的工人, 因此可以使用分类器来表示. 这种情况下, 我们使用Transformer神经网络来表示代理的策略网络, 它可以考虑不同区域之间的全局关系, 再结合秘书算法对于每个到来的工人做出决策. 更多详情参见第2.1节.
我们还将数据推理模块设置为Transformer神经网络. 它将当前状态下所有感知区域的数据作为输入, 并在下一个时间步返回所有区域的推理结果. 我们在输入中嵌入了位置信息和AoI, 因此神经网络可以有效捕捉时空信息, 并且针对稀疏MCS的小数据量场景, 我们改进了精简的模型, 从而实现精确推理. 更多细节将在第2.2节中详细阐述.
在代理与环境的交互过程中, 代理利用数据推理模型对所有感知区域进行推理. 基于工人选择的策略网络, 它决定实际招募哪个区域的工人收集数据, 该区域称为区域X. 然后, 代理将收集到的数据与X区域推理数据之间的误差以及所有区域的AoI结合起来, 形成奖励. 该奖励用于优化策略网络和数据推理模型, 使代理能够改进有效的策略.
3.1 工人选择我们要解决的第1个难题是选择哪个工人收集数据, 以获得最大的未来奖励. 首先, 对于每个即将到来的工人, 我们首先从历史记录和即将到来的工人中进行一次抽样. 然后, 我们利用强化学习根据工人对数据推理的贡献估计值和先知秘书策略选择合适的工人.
3.1.1 模型定义不同工人所在的感知区域的数据对于数据推理的具有不同的贡献度. 例如, 来自AoI较大区域的信息往往相对过时, 对提高数据推理的准确性贡献较小. 因此, 应优先考虑选择AoI较高区域的工人. 由于数据的空间相关性, 最好招募位置分散的工人收集数据, 以提高信息量. 我们使用强化学习来解决这个问题, 因为它不仅考虑了过去的信息, 还考虑了未来的奖励.
我们将“基于AoI的工人贡献度估计”问题抽象为一个RL代理, 该代理根据已收集的数据(状态)选择一个区域(行动), 以最小化AoI和推理损失(奖励).
状态: 表示当前采集的数据和相应的AoI值. 状态空间用矩阵Sm×2表示, 每行对应一个感知区域, 每列代表状态空间的一个元素. 其中第1列是最新采集的若干感知区域数据yi; 第2列是区域i数据的AoI Δi.
因此, 状态空间可以表示为:
| S=[y,Δ] | (3) |
行动: 指的是决定在当前一轮中选择哪个工人进行数据采集. 因此, 行动空间可以定义为所有可能的工人所在感知区域的集合
| R=−1NN∑i=1Δi(t)−βL(t) | (4) |
奖励: 用来表示一个行动的好坏. 由于我们的目标是最小化平均AoI和推理损失, 因此可以将奖励定义为式(2)第1个子式的负值, 如下所示.
代理的目标是学习一种策略, 将每个状态映射为最佳行动, 以最大化预期累积奖励. 该策略由一个深度神经网络表示, 该网络将状态作为输入, 并输出行动空间的概率分布. 代理根据该分布选择概率最高的行动, 采用探索-利用策略, 在利用当前最佳行动和探索新行动之间取得平衡, 从而不断改进策略.
3.1.2 秘书算法在在线场景中, 工人不断到来, 我们需要实时决定选择或者不选择一个工人. 因为我们有预算限制B, 因此可以将问题抽象为从连续到来的Y个工人中选择k个, 使得对数据推理的贡献度最高, 且花费满足式(2)第3个子式. 我们将工人wi的贡献定义如下:
| f(wi)=R | (5) |
其中, R是基于第2节的定义模型的行动获得的奖励.
传统的秘书问题从y个工人里选出一个最佳工人, 解决策略是: 对于某些整数r, 其中1≤r≤y. 先面试前r人, 都不聘请他们, 在之后的n–r人中, 如果任何一人比前面的人都更佳, 便聘请他. 在我们的情景中, 我们将这一概念扩展到选择k个工人[10]. 因此, 我们将Y个工人分为Y/k段, 并使用秘书问题算法从每段中选择最佳的一个工人. 此外, 我们引入先知秘书问题思想[11], 构造样本工人集, 利用工人历史记录学习一个工人贡献分布. 这种方法的优点在于, 我们不再直接丢弃每段的前r个工人, 而是通过历史数据集中的抽样来做出决策, 从而提高数据利用率.
3.2 数据推理SASI 的推理模块是基于Transformer实现的. 它从当前状态下的所有感知区域获取输入数据, 并在随后的时间步中对所有区域进行推理. 值得注意的是, 由于在输入中嵌入了位置信息和AoI, 它能有效捕捉时空信息, 并且Transformer善于捕捉长期关系, 这些是我们选择它做推理模型的理由. 更重要的是, 稀疏MCS场景下的数据量相对于训练有着复杂结构和大量参数的Transformer模型来说是不足的, 训练不充分可能会带来过拟合的问题, 因此本文中我们对传统Transformer模型做了大量简化, 使得在小数据量场景下能训练出更加高效准确的模型.
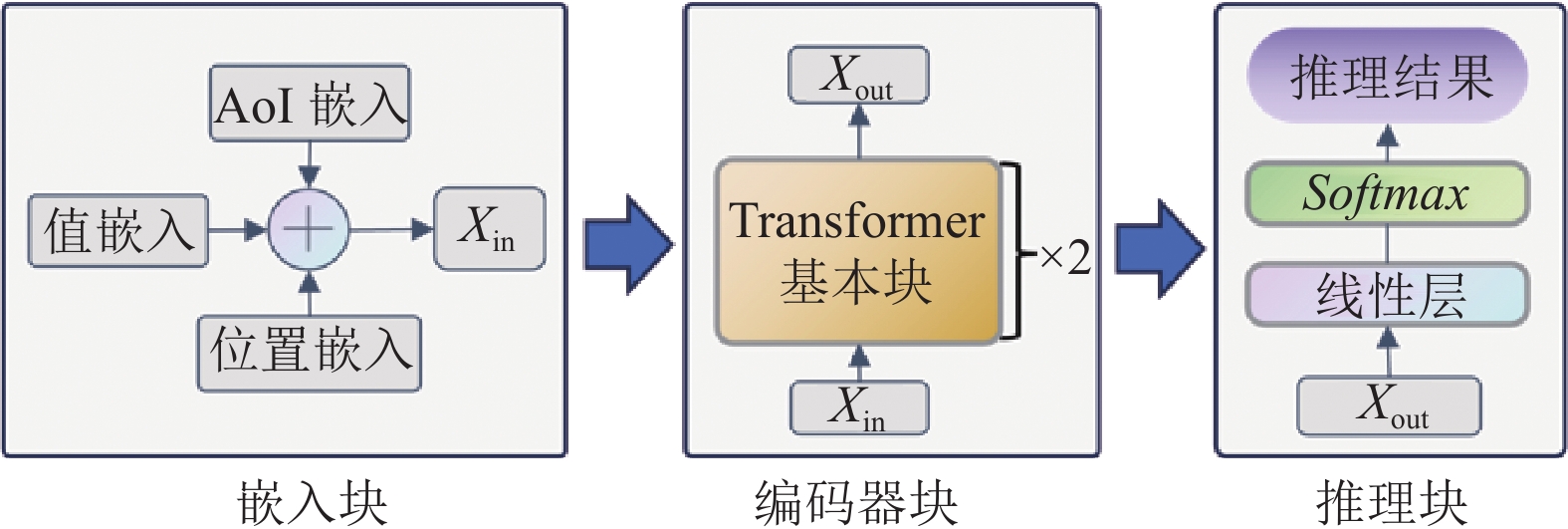
3.2.1 整体结构和改进思路SASI是基于传统Transformer的轻量级数据推理模型. 它由3大块组成: 嵌入块、编码器块和推理块. 如图2所示, 嵌入块由位置嵌入、AoI 嵌入和值嵌入3部分信息组成. 编码器块由两个基本块组成, 每个基本块包含一个多头注意力层和一个前馈层. 推理块包含了一个线性层和Softmax函数. 图2中从左到右是数据流的流向. 我们将原始数据通过嵌入块获得时空编码特征, 然后将其送入编码器块学习数据间时空关系, 最后送入推理块推理下一次应收集的感知区域的数据值.
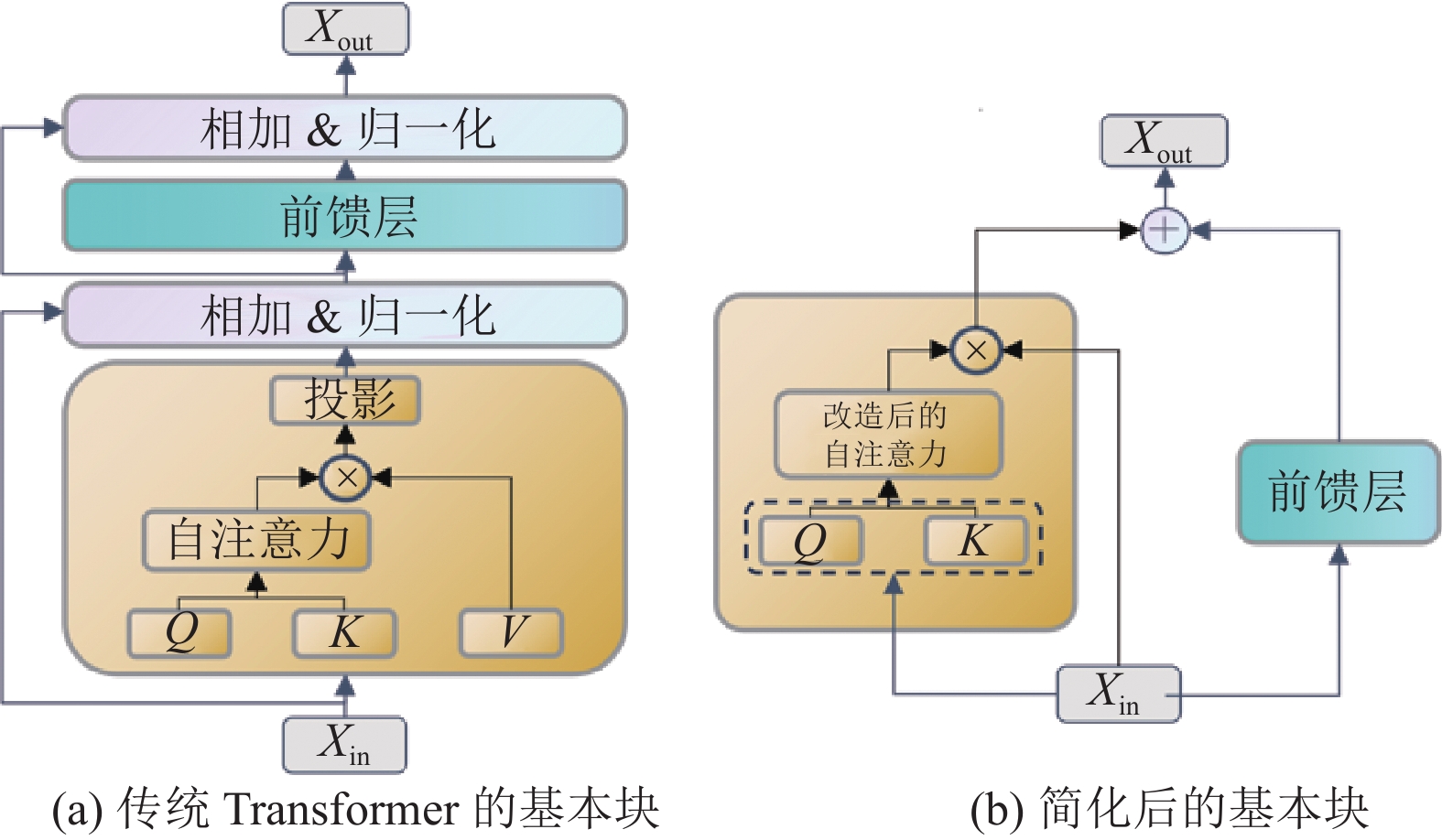
为了应对稀疏数据场景下的复杂模型过拟合, 我们针对图2中的编码器块中的基本块进行简化. 传统的Transformer一般遵循一个设计规范, 即首先构造一个基本块, 这个基本块通常由注意力层、MLP层、残差连接和归一化层等组件构成, 它们以特定方式进行精确的排列组合, 随后对基本块进行堆叠形成最终的Transformer模型, 如图3(a)所示. 这种复杂性导致了架构的脆弱性, 看似微小的变化都会大大降低训练速度, 或导致模型无法训练. 而结合信号传播理论和广泛的消融实验的最新研究, 我们发现可以在不降低训练速度和模型表现的情况下移除Transformer许多块组件, 包括残差连接、投影或值向量参数、顺序子块和归一化层. 并且, 深度缩放研究[12]表明, 当模型深度增加时, 性能得到提升. 说明简化的模块不仅训练速度更快, 而且能有效利用更深层次的额外容量.
|
图 2 AoI敏感的推理模型 |
|
图 3 推理模型基本块简化前后对比 |
除此之外, 我们没有采用经典的Transformer编码器-解码器架构, 原因有两个. 首先, 我们的推理任务需要固定长度的输出, 这可以由编码器有效处理. 因此, 在这种情况下不需要使用解码器来处理非固定长度的序列到序列输出. 其次, 在数据规模相对较小的稀疏MCS场景中, 参数量较多但数据量有限的解码器可能会导致过拟合, 降低训练效率. 因此, 我们利用Transformer编码器直接将输入序列编码为固定长度的特征向量, 然后将其输入多层感知器进行回归预测.
3.2.2 嵌入块在稀疏MCS中, 离散或连续数据存在于不同的向量空间. 因此, 我们采用嵌入技术将信息映射到相同的矢量空间, 将其表示为固定长度、相同的数量级的低维连续矢量. 我们将3种类型的信息嵌入到编码器输入中: 二维位置嵌入、AoI嵌入和值嵌入.
在值嵌入方面, 我们采用线性神经网络将感知任务中的离散或连续数值映射到d维向量中. 至于二维位置嵌入, 我们分别嵌入每个感知区域的经度和纬度. 在 AoI 嵌入中, 我们将每个感知区域的AoI映射为一个d维向量. 然后, 我们将4个向量汇总, 得到感知区域的最终嵌入向量
编码器模块由3个基本块组成, 每个基本块包括两层: 多头注意力层和前馈层. 接下来介绍对基本块的简化, 包括移除残差连接、投影和值向量参数、顺序子块和归一化层, 如图3(b)所示.
首先, 自注意力的残差连接可以被移除. 矩阵的秩反映了流经网络的信号的维数. 从数学的角度解释, 如果注意力矩阵的秩显著降低, 则意味着该矩阵变得更接近于低维子空间, 发生了秩坍塌[13], 从而失去了捕捉稀疏MCS场景里复杂的数据时空相关性的能力. 先前有工作已经证明, 直接移除自注意力的残差连接会导致模型训练发生秩坍塌现象[13], 导致可训练性变差[14], 因此需要对自注意力进行修改. Transformer原有的注意力机制可以使用下面的矩阵形式表现:
| A(X)=Softmax(XWQ(XWK)T√dk)XWV | (6) |
其中, WQ、WK、WV分别为查询、键和值的权值矩阵, dk为键的维数, 用于缩放Softmax函数中的点积. 使用Value-SkipInit[15]来修改自注意力矩阵来缓解信号退化:
| A′(X)=(αIT+βA(X)) | (7) |
可训练标量α和β分别初始化为1和0, IT是单位矩阵, 这里的关键在于通过初始化自注意力矩阵, 鼓励输入信息相对于其他信息更加关注于自身的变化, 从而在更深的网络前向传播时实现更好的信号传递. 这种策略只能在网络初始化阶段使用.
但是, 无法忽略的一点是, 移除注意力子块中的残差连接会直接导致网络整体的训练速度下降. 根据研究[15]表明, 如果将更新参数限制在初始化的投影和值向量上, 就可以更好的恢复跳连的效果.
第二, 将投影和值向量参数移除. 如果去掉数值和投影参数, 会简化Transformer 的内部结构. 将这些矩阵设置为恒等式本质上将Transformer 的相关组件转换为线性层, 从而降低了它们需要执行的操作的复杂性. 通过将值矩阵WV和投影矩阵WP设置为单位矩阵, 大大简化了自注意力机制. 新的公式变成:
| Attenidentify(X)=Softmax(QKT√dk)X | (8) |
其中, Q和K是查询矩阵和键矩阵, 通常计算为Q=XWQ和K=XWK. 在这种情况下, 不使用值矩阵V, 而是使用输入矩阵X本身. 将Softmax函数应用于Q和K的标量点积, 并将结果乘以X. 同样的, 在计算多头注意力矩阵时也不再使用投影矩阵P. 在这里, 移除投影和值向量参数, 使计算变成线性操作, 降低了注意力机制的复杂性. 从方程中消除WV和WP减少了大约13%的可训练参数数量, 从而获得更快的收敛速度.
第三, 将MLP 子块的残差连接移除. 对于MLP层的残差连接优化, 一个很直接的做法就是采用并行子块设计, 同时计算MHA和MLP层的输出结果, 随后对它们进行加权求和, 这种方式在一些大型Transformer模型中以及得到验证, 从数学形式上定义, 并行MLP层的计算过程如下:
| Xout=αcombXin+βFFMLP(Norm(Xin))+βSAMHA(Norm(Xin)) | (9) |
其中, αcomb、βFF和βSA是可训练的参数, 分别控制输入、MLP和MHA块对输出的贡献比例. Norm表示在MLP和MHA块处理之前应用于输入的规一化函数. MLP和MHA块并行处理相同的归一化输入, 它们的输出与缩放后的输入求和后得到Xout. 默认情况下, 残差连接权重αcomb=1, MLP和MHA权重βFF=βSA=1. 与按顺序计算子块的标准基础块相比, 通过并行处理MHA和MLP块, 训练速度提高了15%.
第四, 将归一化层移除. 在基础块每个子块中都会使用归一化层作为后处理, 如果能去除归一化层, 就可以得到最简单的标准块. 从信号传播初始化的角度来看, 归一化操作可以隐含的削减上一子块(残差分支)的权重, 而这种效果也可以在残差连接过程通过明确降低残差分支的权重来实现, 或者使用前面改造后的线性自注意力来代替. 由于在前面修改过程中考虑到了这些机制(如降低MLP的权重βFF和使用改造后的线性自注意力), 因此无需再进行归一化处理.
4 实验分析 4.1 实验描述为了评估SASI框架的性能, 我们在真实世界的数据集上进行了综合评估, 比如北京36个固定站点收集的空气质量数据[16], 包括了PM2.5、CO、SO2和NO2的测量值. 我们选择了该数据集的一个子集, 其中包含169 950条记录, 代表2013年2月8日–2014年2月8日期间每天和每小时记录的各空气质量参数的测量值. 每个数据条目包括站点ID、采集时间戳和4个空气质量参数的值. 此外, 还有一个站点数据集, 提供了站点 ID、站点名称、纬度和经度.
上述数据集最初是从静态监测站获得的. 实际上, 这些数据也可以通过手机收集. 因此, 在实验中, 我们提出了一个合理的假设, 即稀疏MCS的工人可以利用其移动设备中的传感器来收集空气质量和交通数据.
4.2 对比算法为全面了解数据推理和工人选择之间的相互作用, 我们首先对数据推理部分进行了单独实验, 然后在数据推理策略固定的情况下对工人选择部分进行了实验.
在数据推理模块, 我们选择了5种算法作比较方法. KNN-T和KNN-S利用从k条时间和空间最近的数据记录中获取的数据的加权平均值, k设置为5. LR是一种统计模型, 模拟时空和数据间的关系, 学习率设定为 0.01. 时空矩阵补全算法(spatio-temporal matrix completion, STMC)[8]利用数据时空关系, 使用数学方法对数据进行补全. U-SAI (unabridged SAI)是SASI中数据推理未简化版本模型的算法简称, 推理模型采用了传统的Transformer, 其基本块如图3(a)所示.
在工人选择模块, 我们固定数据推理策略为简化的Transformer模型, 使用4种工人选择算法作比较方法. 随机策略(RAND)随机选择工人, 在空间维度能提供有价值的信息. 传统秘书策略(TSS)[10]是不带有先知数据池、利用秘书问题算法来动态选择最佳解决方案的方法. 近最优线下策略(NOS)是一种在离线场景中接近最佳性能的方法.
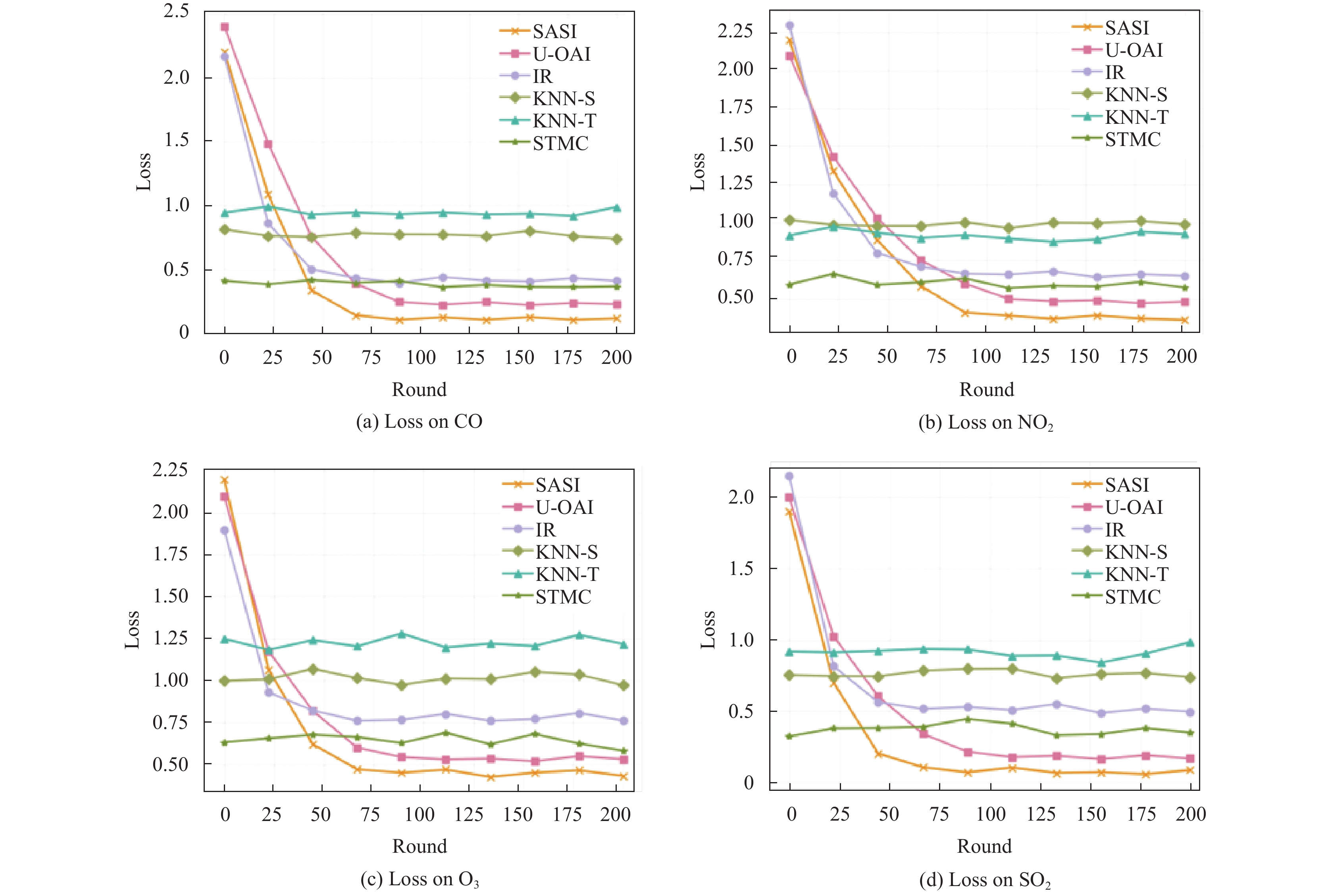
4.3 实验结果 4.3.1 数据推理我们评估了算法在4个数据集的数据推理损失, 如图4所示. 从推理损失来看, 我们的SASI算法获得了最低的推理损失. 对比算法中损失从低到高依次是U-SAI、STMC、LR和KNN算法. 由于SASI和U-SAI的深度学习模型能更好地抓住数据的时空关系, 因此优于STMC、LR和KNN算法; 此外, SASI相比于U-SAI参数量减少了13%, 更适合稀疏MCS的小规模数据, 表现出了比U-SAI更好的推理结果.
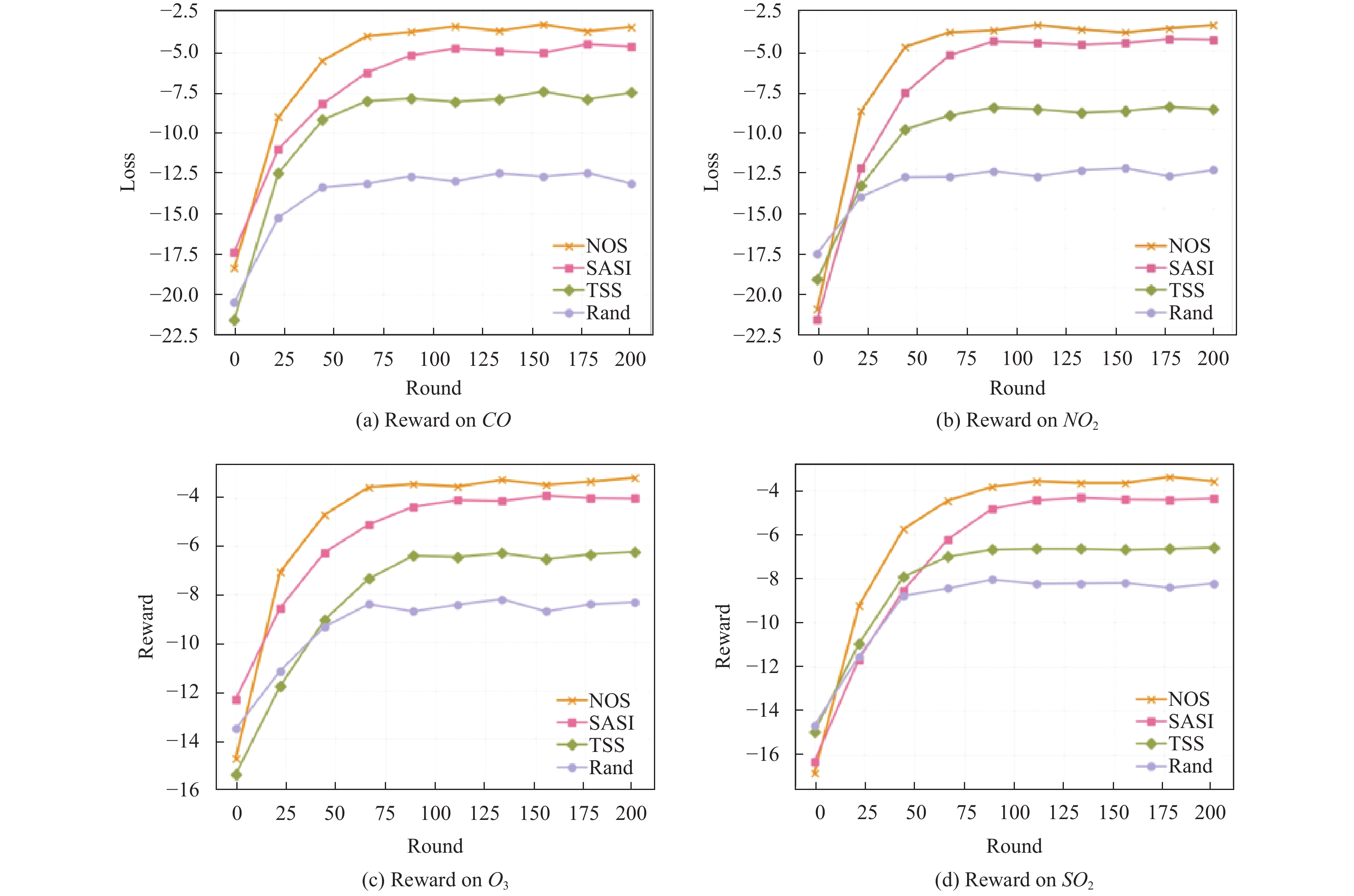
4.3.2 工人选择我们从奖励的角度评估了工人选择算法的性能, 奖励由AoI和推理损失组成. 评估结果如图5所示. 我们设置平衡系数为0.02, 工人平均成本为2, 预算约束B为400, 评估了在4个不同数据集上的效果. 可以看出, 最初由于冷启动阶段的数据量有限, 所有算法的奖励都很差. 随着收集数据和在线更新, 所有算法性能都有所提高. 其中, NOS是拥有完全信息的理想情况, 因此奖励最高. 除了NOS之外, 我们的SASI由于其基于历史信息能在在线场景中做出合适决策的优势, 在所有数据集上获得了更优的奖励.
|
图 4 不同数据推理算法在不同数据集上的损失 |
|
图 5 不同工人选择算法在不同数据集上的回报 |

|
图 5 不同工人选择算法在不同数据集上的回报(续) |
5 结论与展望
本文针对稀疏MCS中的工人选择和数据新鲜度展开研究, 提出了轻量级年龄敏感的数据感知和推理(SASI)框架. SASI框架通过合适的工人选择和数据推理优化信息年龄和推理准确性, 应对了预算约束和工人不足的挑战, 并通过模型精简应对小数据量的问题. 实验结果表明, SASI在性能上优于几种基准算法.
| [1] |
Capponi A, Fiandrino C, Kantarci B, et al. A survey on mobile crowdsensing systems: Challenges, solutions, and opportunities. IEEE Communications Surveys & Tutorials, 2019, 21(3): 2419-2465. |
| [2] |
Wang E, Liu WT, Liu WB, et al. Spatiotemporal urban inference and prediction in sparse mobile crowdsensing: A graph neural network approach. IEEE Transactions on Mobile Computing, 2023, 22(11): 6784-6799. |
| [3] |
Xue JZ, Xu YT, Wu W, et al. Sparse mobile crowdsensing for cost-effective traffic state estimation with spatio-temporal transformer graph neural network. IEEE Internet of Things Journal, 2024, 11(9): 16227-16242. DOI:10.1109/JIOT.2024.3356554 |
| [4] |
Zhao ST, Qi GZ, He TJ, et al. A survey of sparse mobile crowdsensing: Developments and opportunities. IEEE Open Journal of the Computer Society, 2022, 3: 73-85. DOI:10.1109/OJCS.2022.3177290 |
| [5] |
Kaul S, Yates R, Gruteser M. Real-time status: How often should one update? Proceedings of the 2012 IEEE INFOCOM. Orlando: IEEE, 2012. 2731–2735.
|
| [6] |
Yates RD, Sun Y, Brown DR, et al. Age of information: An introduction and survey. IEEE Journal on Selected Areas in Communications, 2021, 39(5): 1183-1210. DOI:10.1109/JSAC.2021.3065072 |
| [7] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 6000–6010.
|
| [8] |
Wang LY, Zhang DQ, Yang DQ, et al. SPACE-TA: Cost-effective task allocation exploiting intradata and interdata correlations in sparse crowdsensing. ACM Transactions on Intelligent Systems and Technology, 2018, 9(2): 20. |
| [9] |
Xie K, Tian JZ, Xie GG, et al. Low cost sparse network monitoring based on block matrix completion. IEEE Conference on Computer Communications. Vancouver: IEEE, 2021. 1–10.
|
| [10] |
Liu WB, Yang YJ, Wang E, et al. Dynamic online user recruitment with (non-) submodular utility in mobile crowdsensing. IEEE/ACM Transactions on Networking, 2021, 29(5): 2156-2169. DOI:10.1109/TNET.2021.3083955 |
| [11] |
Ehsani S, Hajiaghayi M, Kesselheim T, et al. Prophet secretary for combinatorial auctions and matroids. Proceedings of the 29th Annual ACM-SIAM Symposium on Discrete Algorithms. New Orleans: SIAM, 2018. 700–714.
|
| [12] |
He B, Hofmann T. Simplifying transformer blocks. arXiv:2311.01906, 2023.
|
| [13] |
Dong YH, Cordonnier JB, Loukas A. Attention is not all you need: Pure attention loses rank doubly exponentially with depth. Proceedings of the 38th International Conference on Machine Learning. PMLR, 2021. 2793–2803.
|
| [14] |
Noci L, Anagnostidis S, Biggio L, et al. Signal propagation in Transformers: Theoretical perspectives and the role of rank collapse. Proceedings of the 36th Conference on Neural Information Processing Systems. New Orleans, 2022.
|
| [15] |
He B, Martens J, Zhang GD, et al. Deep Transformers without shortcuts: Modifying self-attention for faithful signal propagation. Proceedings of the 11th International Conference on Learning Representations. Kigali: OpenReview.net, 2023.
|
| [16] |
Zheng Y, Liu FR, Hsieh HP. U-air: When urban air quality inference meets big data. Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Chicago: ACM, 2013. 1436–1444.
|
 2024, Vol. 33
2024, Vol. 33



