空间大数据是带有位置信息的大规模数据, 对其进行分析和利用能够为企业、政府和个人提供非常有价值的信息服务, 辅助做出更明智的空间决策. 推动空间大数据技术的发展, 对我国建设智慧城市、发展智能交通与优化城市资源配置具有重大意义. 空间选址是空间大数据领域的基本应用, 旨在根据用户与设施的空间数据从给定的候选位置集合中选择最优的一个或一组位置, 使得决策最优化或用户收益最大化. 随着GPS定位技术、移动网络技术的兴起, 以及智能设备的普及, 基于位置的服务(location-based service, LBS)迅速发展并得到广泛的应用, 网络上积累了大量带有位置和文本信息的空间文本数据. 近年来, 空间关键字查询[1]在时空数据领域得到了广泛的关注. 具体地, 给定空间位置和一系列关键字, 空间关键字查询将返回满足特定查询条件的一个或多个空间文本对象. 例如, 检索国家图书馆1 km内具有关键字“咖啡”“烤鸡”“意大利面”的所有餐厅(即空间文本对象).
Choudhury等人[2]进一步借鉴反向最近邻思想提出面向空间文本对象的选址问题MaxBRSTkNN, 即从候选位置中选出最优的位置, 能够影响最多空间文本对象. 其中影响是由空间邻近程度和文本相似程度共同决定, 愈接近且越相似影响力越大. 例如打算从候选位置集合里选最优位置开一家意大利餐厅(“意大利”和“餐厅”为文本), 上述选址方法可以挖掘出附近喜欢意大利菜顾客最多的候选位置.
空间文本选址问题应用领域十分广泛. 针对个人用户推荐服务设施, 比如为推荐最称心的餐厅就餐或最舒适的酒店入住等; 针对企业和组织提供合理的决策, 在商业领域, 能够为超市选择具有最多潜在客户的店址, 为物流企业选择交通便利的最佳仓储位置等; 在交通领域, 可以帮助组织规划更加合理的公交站或地铁站位置等; 在城市规划领域, 能够帮助城市管理者优化城市布局, 提高土地利用率等.
空间文本选址问题应用领域十分广泛. 针对个人用户推荐服务设施[3], 比如为推荐最称心的餐厅就餐或最舒适的酒店入住等; 针对企业和组织提供合理的决策, 在商业领域[4], 能够为超市选择具有最多潜在客户的店址, 为物流企业选择交通便利的最佳仓储位置等; 在交通领域[5], 可以帮助组织规划更加合理的公交站或地铁站位置等; 在城市规划领域[6], 能够帮助城市管理者优化城市布局, 提高土地利用率等.
尽管现有方法一定程度解决了空间文本选址问题, 但仍存在以下3方面局限. 首先, 在线消费平台的迅速发展积累了大量用户评价数据(如Yelp、大众点评等). 用户通过这些平台选择服务设施时往往会根据过往用户评价等级(通常表示为1–5星)进行筛选, 比如通过Yelp优先选择用户评级高的酒店住宿(或餐厅就餐). 显然, 空间文本选址问题应当考虑服务设施的用户评级. 其次, 传统空间文本选址中用户只会被对其影响力最大的服务设施影响, 当设施间影响力相差不大时, 该模型与真实世界中用户可能同时受到多个设施影响[7]的情况并不一致. 最后, 位置影响力的计算未考虑周边其他同类服务设施的竞争. 比如当设施A和设施B都能服务顾客时, 二者必然产生同行竞争[8]. 传统方法非此即彼的影响模式并不完全符合现实情况.
为更合理地在同行竞争环境中结合用户评级因素做出选址决策, 本文提出了新的空间文本竞争选址问题CoSTUR (competitive spatio-textual location selection based on user rating), 首次同时将用户评级和同行竞争因素纳入空间文本选址的考虑范围, 用于从候选位置集合中选择最优的前k个, 使它们相比剩余候选, 综合文本相关性、距离远近、评级高低等因素, 在设施竞争环境中能够影响更多的用户. 其中, 现有设施和候选位置均具备位置、文本和用户评级属性, 每个用户具有位置和文本信息. CoSTUR问题所选择的最优k个位置可用于企业和组织进一步决策.
为了解决CoSTUR问题: 首先, 借鉴Liu等人[8]对同类竞争设施间均分影响力的思想, 在此基础上结合用户评级完善竞争影响力的定义. 其次, 利用可权衡的影响力阈值摆脱了顾客只能受单个设施影响的假设局限. 阈值越大时, 设施对潜在顾客的影响估计就越准确; 反之, 设施可能影响的潜在顾客数量则越大. 最后, 构建了基于aR-tree[9]的索引结构TaR-tree, 其通过文本相似性将树节点的信息向父节点聚合, 进而实现空间性与文本的共同检索. 利用阈值设计了一个基于用户受影响范围的新剪枝策略, 结合TaR-tree结构建立基于范围查询和空间联合思想的两种解决方案. 相比基线算法, 所设计的方法能够提升近一个量级的计算效率.
本文的贡献总结如下.
• 提出了一个新的空间文本选址问题CoSTUR, 首次将设施的同行竞争和用户对设施的评级因素融入到空间文本选址问题当中.
• 设计了一个基于用户受影响的空间范围剪枝策略, 结合文本信息构建新的类似aR-tree的索引结构实现范围查询和空间联合两种解决方案.
• 在真实和合成数据集上的实验结果表明, 所提出的优化算法能够显著提高计算效率.
1 问题定义 1.1 基本概念空间文本数据由空间位置
定义1 (空间相关性
| S(u,o)=1−d(u.loc,o.loc)Dmax | (1) |
其中,
定义2 (文本相关性
| T\left( {u, o} \right) = \frac{{|u.des \cap o.des|}}{{|u.des \cup o.des|}} | (2) |
定义3 (空间文本相关性
| P\left( {u, o} \right) = \alpha S\left( {u, o} \right) + \left( {1 - \alpha } \right)T\left( {u, o} \right) | (3) |
其中,
真实世界中用户可能同时受多个设施影响, 因此, 为摆脱传统空间文本选址问题中顾客只受单个设施影响假设的局限, 本文引入影响阈值
定义4 (对象影响用户). 给定一个用户
值得一提的是, 阈值
定义5 (对象影响力
基于定义4可定义对象间是否存在竞争关系.
定义6 (对象间竞争关系). 两个对象
定义7 (用户竞争集
基于对象间竞争关系, 借鉴文献对同类竞争设施间均分影响力的思想, 定义影响平分模型.
定义8 (平分影响力
此时想建立新的设施获利, 就需要考虑与现有设施集
进一步考虑在竞争的基础上增加用户评级给影响力计算带来的变化. 由于每个用户对影响值的贡献为1, 换句话说, 一个用户受到的总影响值表征为1, 考虑到用户评级通常以1–5星进行从劣到优的评价, 故将对象的用户评级
定义9 (竞争尺度
此时, 可以定义结合设施间竞争和设施用户评级的综合竞争影响值.
定义10 (综合竞争影响值
| score\left( {o, O} \right) = \sum\nolimits_{u \in {S_{inf }}\left( o \right)} {\frac{{o.rat}}{{comp\left( {u, O} \right)}}} | (4) |
其中,
| score\left( {c, O \cup \left\{ c \right\}} \right) = \sum\nolimits_{u \in {S_{inf }}\left( c \right)} {\frac{{c.rat}}{{comp\left( {u, O \cup \left\{ c \right\}} \right)}}} | (5) |
其中,
定义11 (CoSTUR). 给定具有空间位置、文本描述和评级的已有设施集合
本研究通过影响阈值的设置, 不仅解决了现有方案中用户只能被唯一设施影响的局限, 也可以帮助选址决策者在更高质量的用户影响估计和更多可能的潜在用户间做出权衡. 针对同类设施间竞争影响力的公式化定义, 完善了融入用户评级对竞争的影响. 接下来, 本文将着力解决在给定用户集合和候选位置集合基数较大时计算代价升高的问题. 本文实验中的用户、已有设施和候选位置等数据集取自New York真实数据集和基于London的合成数据集.
2.1 基线方法根据前文中问题的公式化定义, 解决CoSTUR最直接的方法是检索所有的用户和现有设施, 找到影响每个用户的用户竞争集, 然后再同样扫描并利用式(5)判断每个候选位置的综合竞争影响值. 过程中需要根据
基线算法使用HashMap
算法1. Baseline
输入:
输出: top-
1 Initialize
2 for
3 for
4 Calculate
5 if
6
7 end if
8 end for
9 end for
10 for
11 for
12 Calculate
13 if
14
15 end if
16 end for
17 end for
18 return top-k c in
为降低基线算法线性扫描的复杂度, 本节分别提出基于范围查询(range query)和空间连接(spatial join)思想的两个优化算法, 结合索引结构和剪枝策略提升计算效率.
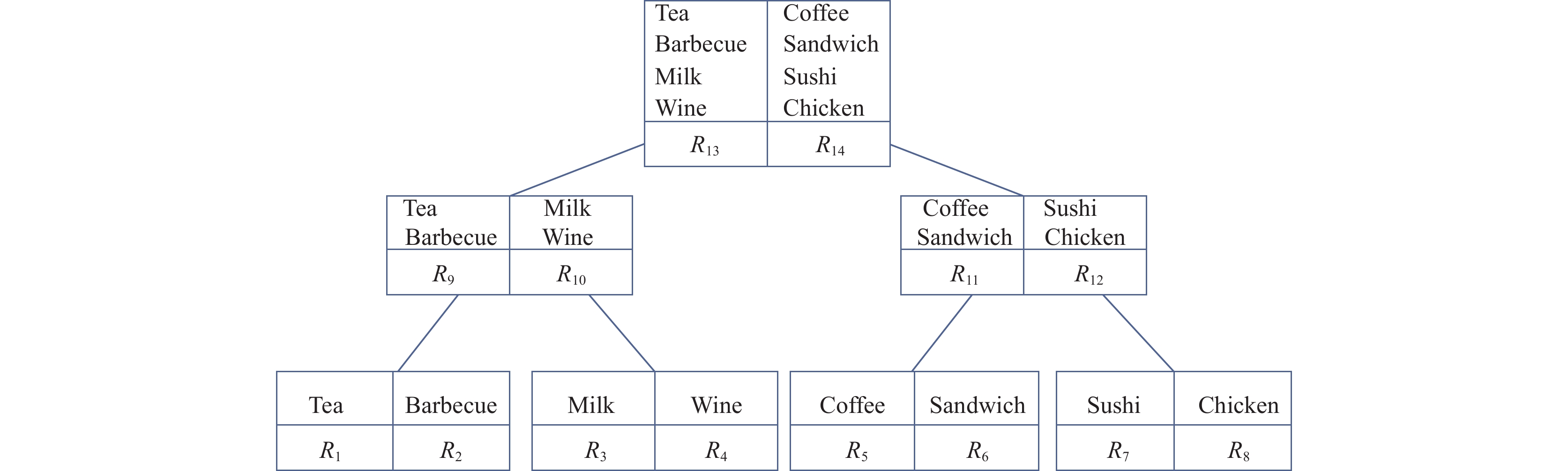
空间范围聚集索引结构aR-tree能将节点空间和附带属性进行聚合, 以提升联合检索效率, 该优点适于CoSTUR问题. 图1显示了基于aR-tree构建的索引结构TaR-tree, 它融合了空间和文本属性. 其中, TaR-tree每个节点由聚合空间信息的MBR (minimum bounding rectangle)及聚合文本信息的并集(便于计算Jaccard相似性)组成. 叶子节点的父节点将所包含子节点的位置构造成MBR; 非叶子节点的父节点则将所包含子节点的多个MBR囊括为更大的MBR. TaR-tree将子节点的文本属性逐级向父节点并集聚合, 直至根节点. 遍历TaR-tree的过程中, 可以同时处理空间和文本信息.
|
图 1 TaR-tree示例 |
2.2.1 基于range query方法
影响阈值
| d = {D_{\max }}\left[ {1 - \frac{{\tau - \left( {1 - \alpha } \right)T}}{\alpha }} \right] | (6) |
式(6)的具体推导如下(为便于理解, 此处用户与设施之间的距离、空间和文本相关性分别简写为
|
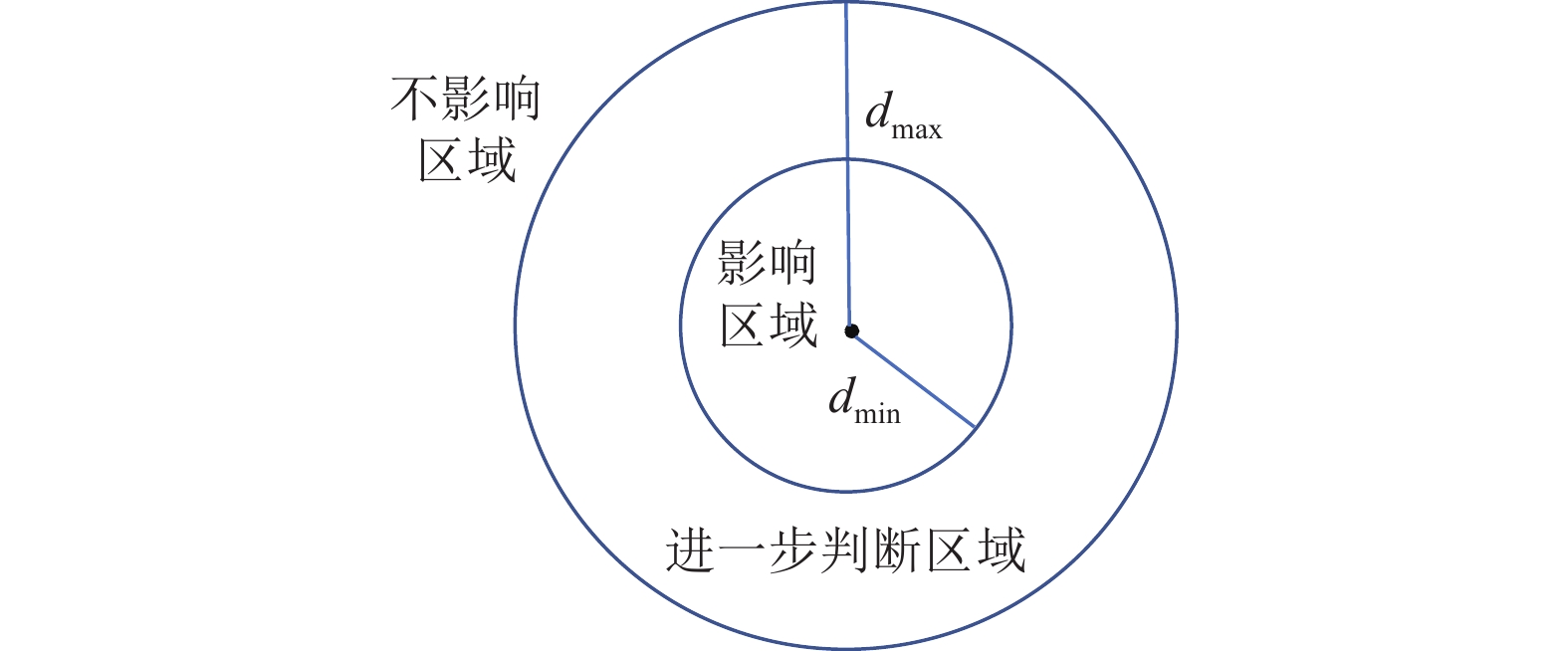
图 2 用户受影响范围示意 |
根据上述用户必然受影响和必然不受影响区域, 可以结合TaR-tree索引结构进行范围查询. 在用户必然受影响区域内的设施将参与竞争, 而在必然不影响范围内的设施可以直接剪枝. 在上述两个范围间(圆环区域)的设施, 仍需通过定义4进行计算, 若大于阈值
鉴于此, 提出基于范围查询(range query)的解决方案. 由于现有设施
算法2. RangeQuery
输入:
输出: top-
1 Initialize
2 for
3 Calculate
4 Build
5
6 for
7 if
8
9 end if
10 end for
11 end for
12 for
13 Build TaR-tree
14
15 for
16 if
17
18 end if
19 end for
20 end for
21 return top-k c in
RangeQuery算法基线算法使用HashMap
空间连接(spatial join)[11]的核心思想是在不同空间数据集间根据空间谓词进行“连接”操作, 即当两个空间对象间存在如相交(intersect)、包围(enclose)等谓词关系时, 可以进行join匹配.
根据空间连接思想, 可以将设施集(候选集)和用户集视为要进行连接的双方, 参照范围查询思路, 可以使用定义4的阈值判定作为谓词进行匹配. 为更有效地进行数据集空间连接遍历, 用户集也构建为TaR-tree, 利用树的剪枝过程优化计算性能. 该方法将从设施集(候选集)和用户集两棵TaR-tree的根结点开始同时执行深度优先遍历. 若两树中间节点的聚合空间文本相关性大于阈值
按照空间连接阈值判定遍历的逻辑, 遍历结束后可以得到所有对象
引理1 (综合竞争影响值上界). 对于
证明: 当
| score\left( {c, F \cup \left\{ c \right\}} \right) = \frac{{c.rat}}{{f.rat + c.rat}} | (7) |
由于
当
以此类推, 当有更多设施影响
结合空间连接思想和引理1设计了SpatialJoin算法, 具体流程如算法3所示. 与前文两种算法类似, SpatialJoin算法也使用HashMap
算法3. SpatialJoin
输入:
输出:
1 Build TaR-trees
2 Initialize
3
4
5 for pop
6 if
7 break
8 Calculate
9 if
10 if
11 pop
12 insert
13 end if
14 else insert
15 end if
16 return
接下来利用空间连接函数
本节对前述各解决方案的计算复杂度进行理论分析, 其中定义4的计算作为原子操作.
基线方法Baseline采用线性扫描方法遍历用户集、候选位置集和已有设施集, 方法的时间复杂度为
在结合TaR-tree、
SpatialJoin算法利用TaR-tree之间的空间连接思想. 首先构建用户集与候选集TaR-tree需要
容易看出RangeQuery算法和SpatialJoin算法的时间复杂度明显低于基线方法.
3 实验论证与分析 3.1 实验设置 3.1.1 实验数据集本文实验中的用户、已有设施和候选位置等数据集取自New York真实数据集和基于London的合成数据集. 其中后者是由真实POI设施位置随机捕获一组POI文本数据的方式合成, 数据特征如表1所示. 所选数据集为不同国家区域的开源数据集, 有助于体现本文研究方法和实验结果的普适性.
| 表 1 数据集基本信息 |
经数据抽样, 用户和设施间空间相关性和文本相关性均值分别在0.7和0.1附近, 差距较大. 为使空间相关性和文本相关性的
以下解决方案将在本节进行评估, 实验采用Python语言编码, 环境为Windows 10 (64位), Intel(R) i5-13600KF 3.5 GHz, 内存16 GB.
实验分别评估本文第2.1节Baseline算法, 第2.2.1 RangeQuery算法, 第2.2.2节SpatialJoin算法.
3.2 实验结果 3.2.1 阈值验证影响阈值
如图3(a)所示, SpatialJoin性能在London数据集上提升更理想, 这很大程度上取决于其计算复杂度优势. 图3(b)中New York数据集上情况则相对复杂. 当影响阈值

|
图 3 阈值 |

|
图 3 阈值 |
3.2.2 用户数量
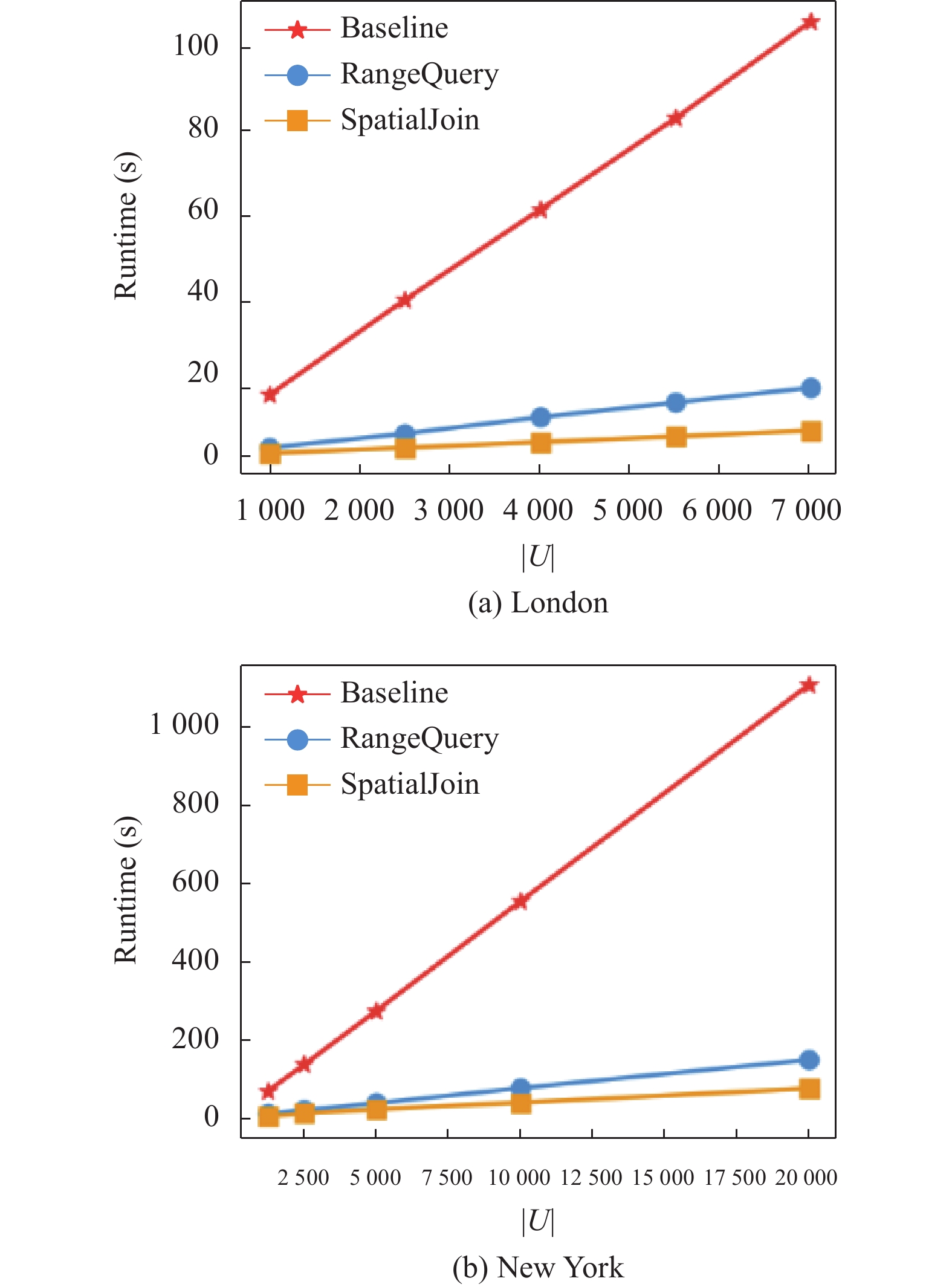
接下来针对输入用户数据集规模
将候选位置
本部分的实验着眼于验证
|
图 4 用户数量 |
|
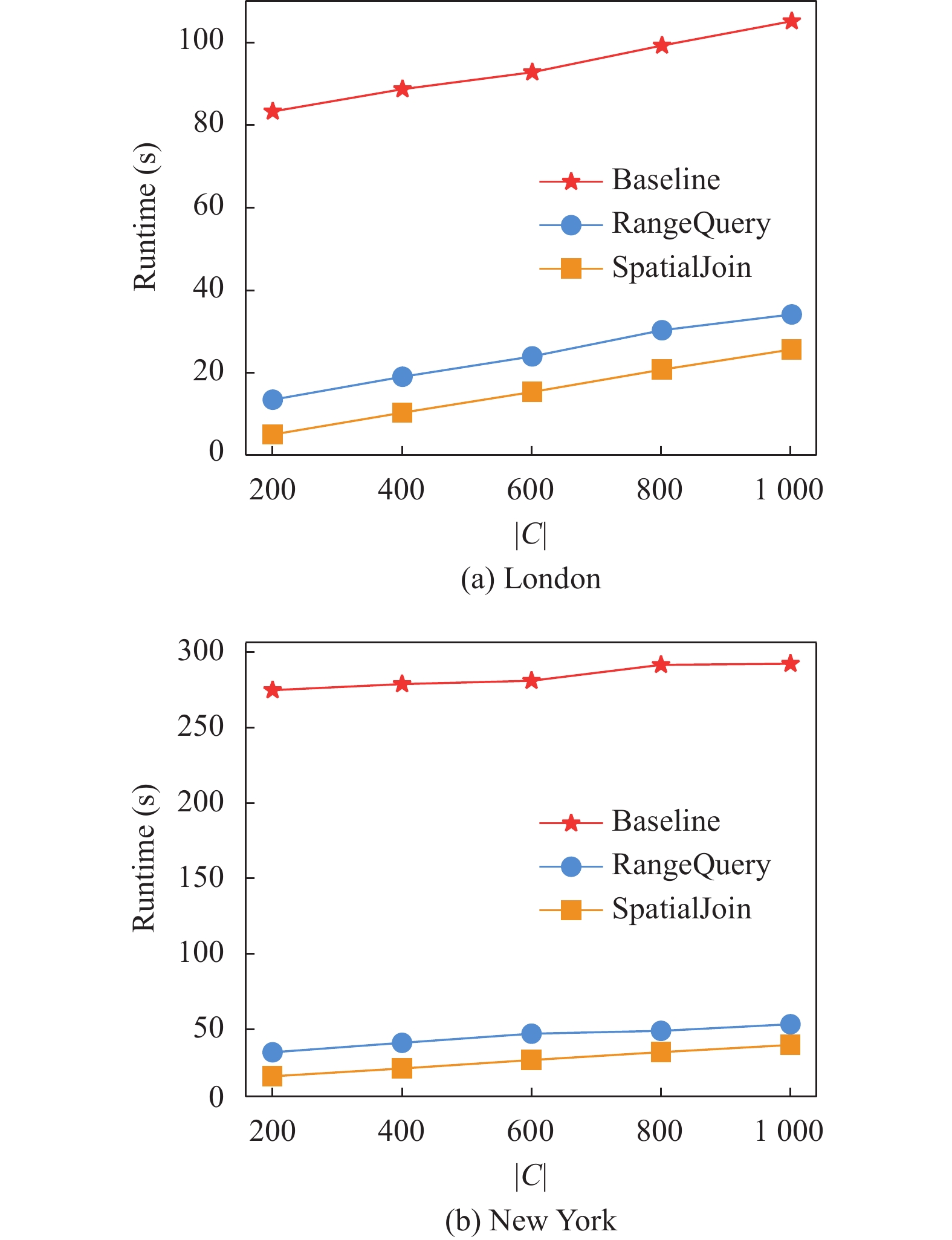
图 5 候选位置 |

|
图 6 |
4 相关研究
空间文本位置选择问题: Ahmed等人[12]提出反向空间top-k关键字查询(RSK), 并采用网格索引划分数据集, 其中每个网格存储关键字频率表, 本文的索引结构设计也借鉴了其思想. Choudhury等人[2]提出了MaxBRSTkNN查询的经典空间文本选址模型, 为本研究的选址模型提供了理论支撑. 文献[13]是对Choudhury等人[2]研究的扩展, 提出了一种最大化双色反向空间文本最近邻查询(MaxST), 并在有阻碍和无阻碍空间中, 为对象寻找最佳位置和一组关键字. Chen等人[14]将研究扩展至路网环境, 其反向top-k关键字的位置查询(RTkKL)旨在找到最大空间区域, 以便将查询对象包含在任何top-k空间关键字查询的结果中. 该研究的路网场景与本文模型不相符, 但可考虑作为未来的研究方向. 上述研究解决了各自应用场景中的问题, 然而均未考虑设施之间的竞争因素, 难以直接用于应对CoSTUR问题的挑战.
设施竞争位置选择问题: 传统的竞争性选址问题[15]假设一家新公司将入驻存在现有公司运营的市场, 其最佳选址期望在竞争中争夺最大的市场份额. Revelle[16]引入新的竞争选址问题, 它在现有设施的基础上增加了新设施, 使新设施群的影响力最大化扩展. 其中若两个设施捕获同一对象, 则会平分对它的影响, 这与CoSTUR依据的经典竞争影响模型相同, 但该模型其未考虑设施评级. Huang等人[17]基于最大影响力模型考虑现有设施对选址的影响, 影响关系的定义以最近邻为基础. Liu等人[8]将竞争问题扩展到运动对象, 使用影响关系剪枝规则和影响值剪枝规则来加速查询过程. 现有竞争选址研究尽管有些也采用和本文相同的竞争影响模型, 但均未考虑设施和对象的文本因素, 也缺少对设施评级的应对, 方法不适用CoSTUR问题.
5 结束语本文引入一个称为CoSTUR的新型空间文本位置选择问题, 并提供了两种有效且高效的解决方案. 相比于经典空间文本选址问题, CoSTUR问题综合考虑了用户可以同时被多个设施影响、同类设施间存在竞争, 及用户评级对竞争的影响等因素. 该问题在现实世界中应用广泛, 如城市规划、市场营销、LBS等. 提出的其中一种算法基于范围查询思想, 通过构建必然影响/不影响的两个新剪枝距离范围, 结合空间文本索引TaR-tree, 能够有效解决问题. 另一种方法建立在空间连接思想上, 利用一个新的分值上界简化计算过程. 在真实及合成数据集上的大量实验证明了所提方法的有效性和高效性.
| [1] |
Chan HKH, Liu SX, Long C, et al. Cost-aware and distance-constrained collective spatial keyword query. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(2): 1324-1336. |
| [2] |
Choudhury FM, Culpepper JS, Sellis T, et al. Maximizing bichromatic reverse spatial and textual k nearest neighbor queries. Proceedings of the VLDB Endowment, 2016, 9(6): 456-467. DOI:10.14778/2904121.2904122 |
| [3] |
Lv Z, Shang KY, Huo HW, et al. RASK: Range spatial keyword queries on massive encrypted geo-textual data. IEEE Transactions on Services Computing, 2023, 16(5): 3621-3635. DOI:10.1109/TSC.2023.3289654 |
| [4] |
Wang L, Yu ZW, Yang DQ, et al. Efficiently targeted billboard advertising using crowdsensing vehicle trajectory data. IEEE Transactions on Industrial Informatics, 2020, 16(2): 1058-1066. DOI:10.1109/TII.2019.2891258 |
| [5] |
Darwish TSJ, Bakar KA, Kaiwartya O, et al. TRADING: Traffic aware data offloading for big data enabled intelligent transportation system. IEEE Transactions on Vehicular Technology, 2020, 69(7): 6869-6879. DOI:10.1109/TVT.2020.2991372 |
| [6] |
Priyadarshini I, Kumar R, Alkhayyat A, et al. Survivability of industrial internet of things using machine learning and smart contracts. Computers and Electrical Engineering, 2023, 107: 108617. DOI:10.1016/j.compeleceng.2023.108617 |
| [7] |
Wang M, Li H, Cui JT, et al. PINOCCHIO: Probabilistic influence-based location selection over moving objects. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(11): 3068-3082. DOI:10.1109/TKDE.2016.2580138 |
| [8] |
Liu P, Wang M, Cui JT, et al. Top-k competitive location selection over moving objects. Data Science and Engineering, 2021, 6(4): 392-401. DOI:10.1007/s41019-021-00157-1 |
| [9] |
Papadias D, Kalnis P, Zhang J, et al. Efficient OLAP operations in spatial data warehouses. Proceedings of the 7th International Symposium on Spatial and Temporal Databases. Redondo Beach: Springer, 2001. 443–459.
|
| [10] |
Yiu ML, Dai XY, Mamoulis N, et al. Top-k spatial preference queries. Proceedings of the 23rd IEEE International Conference on Data Engineering. Istanbul: IEEE, 2007. 1076–1085.
|
| [11] |
Qiao BY, Hu B, Zhu JH, et al. A top-k spatial join querying processing algorithm based on spark. Information Systems, 2020, 87: 101419. DOI:10.1016/j.is.2019.101419 |
| [12] |
Ahmed P, Eldawy A, Hristidis V, et al. Reverse spatial top-k keyword queries. The VLDB Journal, 2023, 32(3): 501-524. DOI:10.1007/s00778-022-00759-9 |
| [13] |
Choudhury FM, Culpepper JS, Bao ZF, et al. Finding the optimal location and keywords in obstructed and unobstructed space. The VLDB Journal, 2018, 27(4): 445-470. DOI:10.1007/s00778-018-0504-y |
| [14] |
Chen ZJ, Wang X, Liu WY. Reverse keyword-based location search on road networks. GeoInformatica, 2022, 26(1): 201-231. DOI:10.1007/s10707-021-00440-3 |
| [15] |
Plastria F. Static competitive facility location: An overview of optimisation approaches. European Journal of Operational Research, 2001, 129(3): 461-470. DOI:10.1016/S0377-2217(00)00169-7 |
| [16] |
Revelle C. The maximum capture or “sphere of influence” location problem: Hotelling revisited on a network. Journal of Regional Science, 1986, 26(2): 343-358. DOI:10.1111/j.1467-9787.1986.tb00824.x |
| [17] |
Huang J, Wen ZY, Pathan M, et al. Ranking locations for facility selection based on potential influences. Proceedings of the 37th Annual Conference of the IEEE Industrial Electronics Society. Melbourne: IEEE, 2011. 2411–2416.
|
 2024, Vol. 33
2024, Vol. 33



