2. 北京化工大学 经济管理学院, 北京 100029
2. School of Management and Economics, Beijing University of Chemical Technology, Beijing 100029, China
在现代分子细胞遗传学领域, 荧光原位杂交技术(fluorescence in situ hybridization, FISH)[1]因其在可视化特定DNA序列方面的卓越表现, 成为一项备受关注且广泛应用的技术. 特别是在染色体畸变研究领域, FISH技术在乳腺癌、肺癌、淋巴癌等实体肿瘤的辅助诊断中展现出巨大潜力. 被特定荧光探针标记的DNA在FISH荧光显微图像中常以荧光斑点形式出现[2], 这为获取图像中斑点的位置、数量和聚集度等客观数据提供了可能. 通过斑点检测技术, 可实现对荧光斑点的像素级定量分析, 为实体肿瘤的辅助诊断提供可靠且高效的技术支持, 且能有效地节省人力资源. 面向显微图像的斑点检测算法在各类文献中已有大量研究[3–14], 但现有的斑点检测算法在辅助临床诊断方面仍存在挑战, 主要源于样本制备和CCD成像等阶段的多种因素, 图像存在高噪声且背景复杂, 斑点出现粘连并呈现多样形态, 同时非斑点结构的存在对检测精度产生显著影响.
传统斑点检测算法模拟荧光图像形成过程, 构建适应点扩散函数(PSF)的函数模型, 考虑图像噪声类型采用相应降噪技术, 调节参数针对不同斑点形状和大小, 以实现斑点检测.
斑点增强滤波法(spot enhancing filter, SEF)是由Sage等人[3]提出的一种用于显微图像斑点检测的方法, 利用Laplacian of Gaussian (LoG)核增强图像中的斑点、抑制噪声. 然而SEF方法中LoG核宽的选取与斑点尺寸相关, 难以实现多尺度斑点的准确检测. 为此, Jaiswal等人[4]提出了multi-scale spot enhancing filter (MSSEF), 明显改善斑点粘连区域的检测效果, 但对于噪声干扰较严重的FISH荧光图像, MSSEF难以确保检测结果的准确性. 另一种方法由Basset等人[5]提出, 名为具有自动选择尺度的高斯拉普拉斯图像的自适应阈值(ATLAS), 通过选择与图像中的光斑大小相对应的最佳尺度降低漏检率, 但最优尺度往往难以获得. Acosta等人[6]提出基于选定尺度的多尺度斑点分割算法, 该方法能够有效提取出类高斯核的斑点, 但仍无法应对FISH荧光图像中的非斑点结构干扰. Marsh等人[7]提出的Hessian斑点算法基于尺度空间中的局部曲率定义边界, 完全独立于算法参数, 且斑点中心和边界可扩展至亚像素精度. Zhang等人[8]提出的多尺度方差稳定变换(MSVST)算法可用于信噪比极低的图像数据, 处理Poisson-Gaussian混合噪声效果显著, 但算法复杂度较高, 且无法去除非斑点结构的干扰. 而Ren等人[9]利用多尺度二阶各向异性高斯定向导数实现斑点检测, 可描述斑点形状. Big-FISH[10]是一个用于分析单分子荧光原位杂交(smFISH)图像的Python软件包, 它能够进行斑点检测和细胞与细胞核的分离.
基于深度学习的斑点检测方法通过使用卷积核以数据驱动的方式自动提取目标特征. DetNet[11]在U-Net基础上使用残差主干优化信息流, 去除跳跃连接以削减参数量, 在一定程度上减轻了网络负担. DeepSpot网络[12]设计了上下文融合模块, 通过学习全面、互补的特征来实现在可变强度和高噪声水平RNA斑点图像下的斑点检测, 并利用残差卷积优化特征信息. deep-Blink方法[13]将注意力机制融入U-Net, 在不同背景亮度水平和斑点质量的单分子荧光显微镜图像中实现准确、高通量的斑点检测和定位, 具有出色的斑点检测性能. SE-Res-UNet方法[14]在高密度和低信噪比下具有优秀的斑点检测和定位性能. 以上深度学习方法主要侧重于斑点的精确定位, 无法对斑点进行像素级定量分析, 且其鲁棒性和泛化能力受限于训练数据集的数量与标签质量. FISH荧光图像的复杂性导致数据采集和标注过程繁琐, 构建合适的训练样本集成本高, 针对本文工况中背景干扰严重且存在非斑点结构干扰的情况, 处理效果欠佳.
在现有文献基础上, 各种方法如MSSEF、MSVST、Big-FISH等均在斑点检测领域发挥着重要作用, 但在特定场景下仍存在局限性. 本文针对FISH荧光图像的特殊挑战, 研究并改进基于传统的斑点检测算法. 首先, 采用小波多尺度求和去除噪声、提升图像质量; 随后利用多尺度LoG算子增强目标斑点信号、抑制不相关的背景; 最后, 使用二阶单边高斯核抑制非斑点结构干扰, 得到最终斑点检测结果. 该方法适用于低信噪比、背景干扰严重且存在非斑点结构干扰的FISH荧光显微图像, 具备较高检测精度.
1 荧光显微图像斑点检测方法 1.1 小波多尺度求和去噪荧光显微图像的噪声主要是Poisson型光子散射噪声和加性Gaussian型读取量化噪声[15]. 针对荧光图像存在的噪声, 使用基于B3样条([1,4,6,4,1]/16)的à trous小波[16]对原图像
| Wi(x,y)=Ii−1(x,y)−Ii(x,y) | (1) |
| I0(x,y)=IK+K∑i=1Wi(x,y) | (2) |
其中,
| ˜Wi={Wi,0,Wi⩾tiWi<ti | (3) |
其中,
| MAD(Wi)=median(abs(Wi−median(Wi))) | (4) |
定义第
| ID=IK+K∑i=2˜Wi(x,y) | (5) |
本文在对荧光显微图像进行去噪时, 进行了3层分解, 根据式(5), 利用WMA去噪后的图像
| ID=I3+˜W2+˜W3 | (6) |
经过降噪处理后, 图像仍存在背景干扰, 需对斑点区域进行增强. 高斯拉普拉斯算子(LoG)已被广泛应用于斑点检测与增强[3,4], 针对LoG算子尺度计算问题, 首先对斑点进行数学建模. 荧光显微图像斑点在图像上表现近似为二维高斯函数, 二维高斯核的定义为:
| g(x;σ)=12πσ2exp(−xTx2σ2) | (7) |
其中,
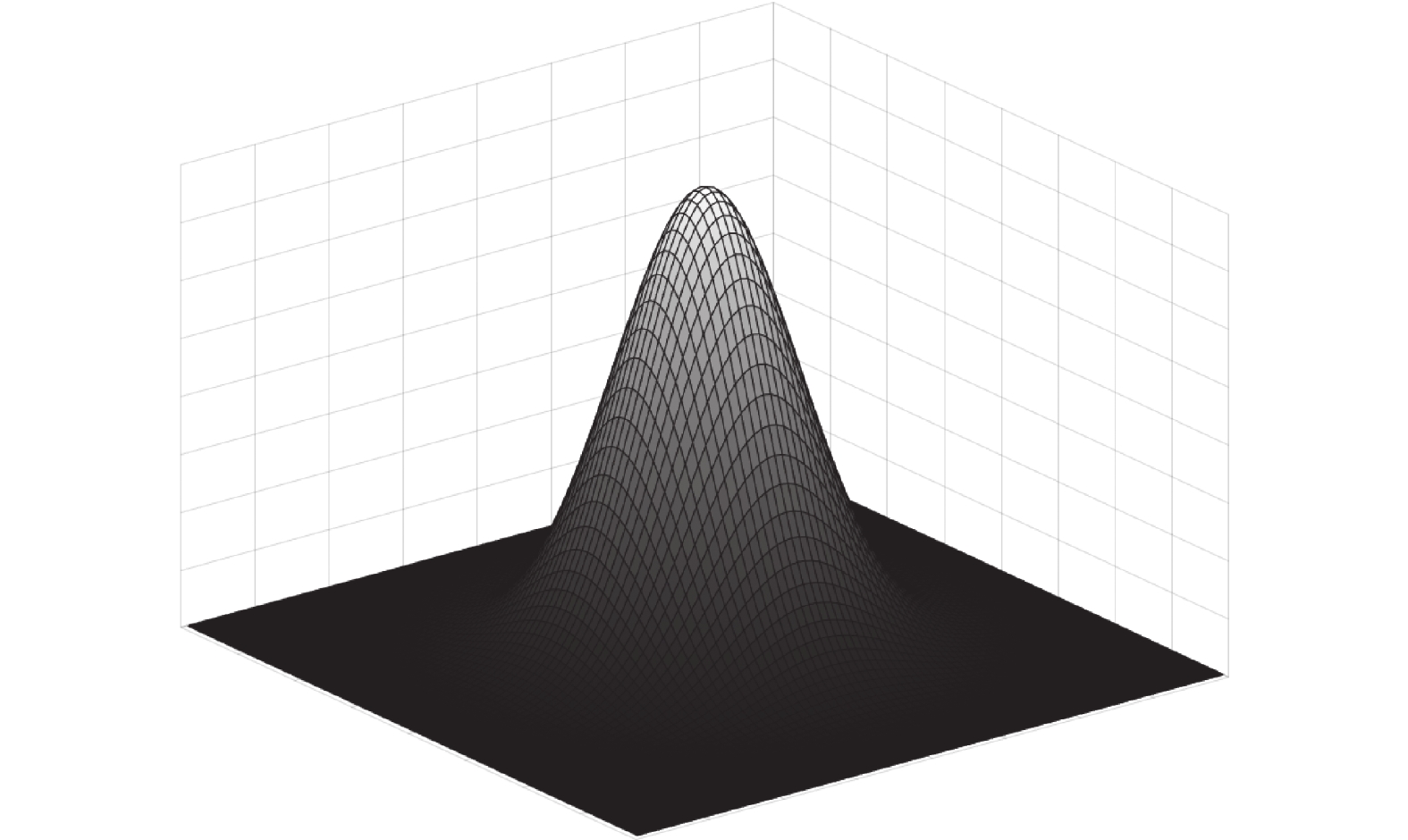
|
图 1 二维高斯核示意图 |
则斑点数据可建模为:
| Λ0(x;x0,ω0,p0,b0)=p0exp(−(x−x0)T(x−x0)2ω20)+b0 | (8) |
其中,
| Λ0(x;ω0,p0,b0)=p0exp(−xTx2ω20)+b0 | (9) |
设斑点的像素半径为
| r0≈3ω0 | (10) |
特定像素半径的斑点与特定尺度的LoG算子卷积后, 能够得到较强的响应, 规范化后的LoG算子[19]数学建模由式(11)给出:
| ∇2gL(x;σ)=−1⋅σ2⋅(∂2g(x;σ)∂x2+∂2g(x;σ)∂y2)=−x2+y2−2σ22πσ4exp(−xTx2σ2) | (11) |
如图2所示为LoG算子示意图, 图2(a)和图2(b)分别为三维可视化图像与平面二维图像.
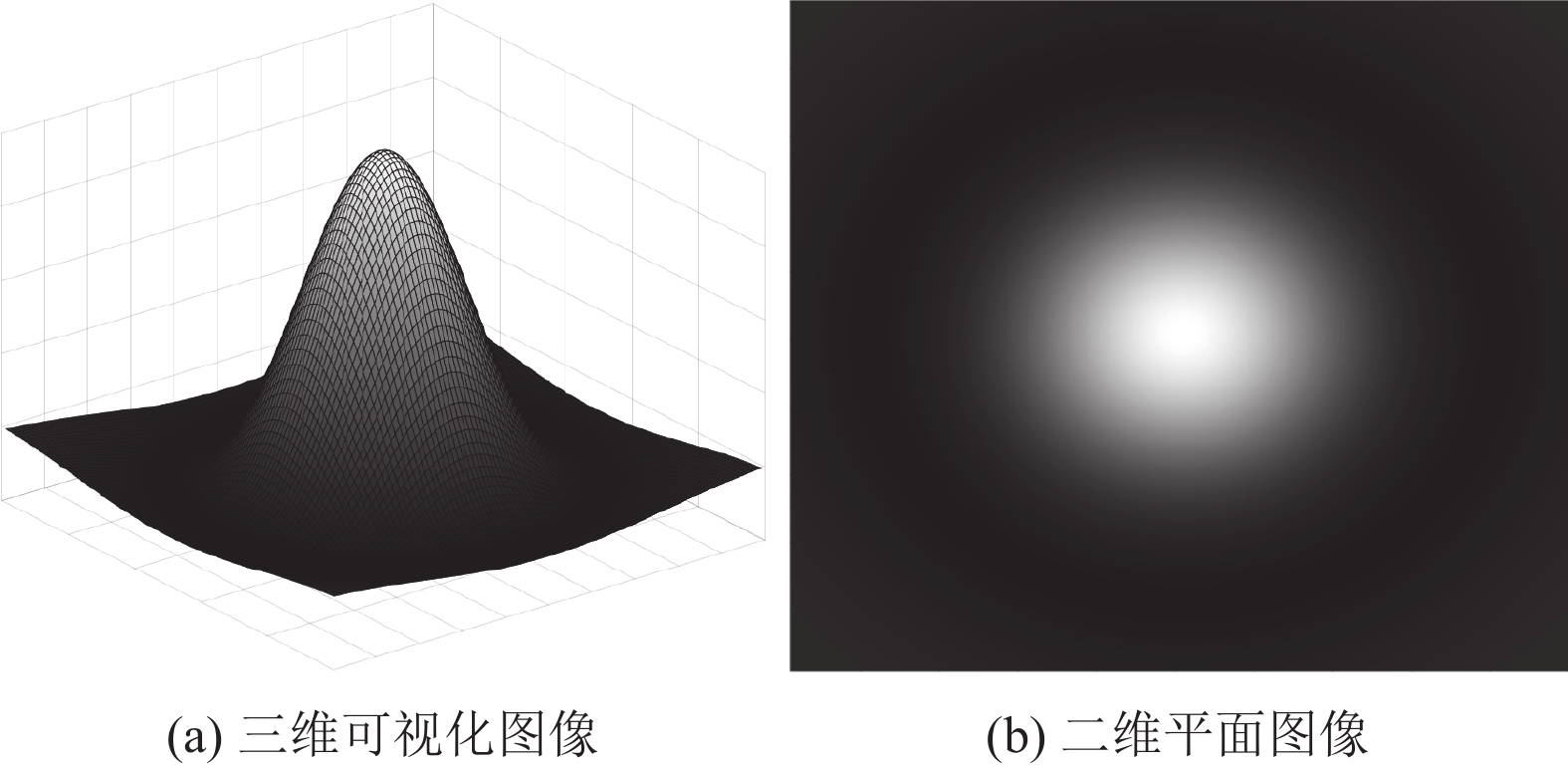
|
图 2 LoG示意图 |
本文将式(11)进行缩放后, 得到式(12), 具体原因将在后文给出.
| ∇2gn(x;σ)=2⋅∇2gL(x;σ)=−x2+y2−2σ2πσ4exp(−xTx2σ2) | (12) |
得到斑点的数学建模以及LoG算子后, 将两者卷积可以得到具体的响应值:
| L0(x;σ)=Λ0(x;ω0,p0,b0)∗∇2gn(x;σ)=2p0ω20σ2⋅x2+y2−2(ω20+σ2)−(ω20+σ2)3exp(−xTx2(ω20+σ2)) | (13) |
设
| L0(0;σ)=4p0ω20σ2(ω20+σ2)2 | (14) |
为求取当
| ∂L0(0;σ)∂σ=8p0ω20σω40−σ4(ω20+σ2)4 | (15) |
令式(15)为0, 求得
| L0(0;σ∗)=p0 | (16) |
刚好对应式(9)中的斑点强度, 这就是式(12)对式(11)缩放的原因. 综上所述, LoG算子的尺度选择对应如式(17):
| σ∗=r0/3 | (17) |
为了增强不同像素半径的斑点, 需要使用多个尺度的LoG算子对图像进行卷积, 设斑点半径集为
| L(x)=max | (18) |

|
图 3 多尺度LoG斑点增强示例图 |
1.3 二阶单边高斯核抑制非斑点结构
由于相机的动态范围有限以及人工操作失误等因素, 一些荧光显微图像会产生强度超过大部分斑点的非斑点结构, 如图4所示, 其半径远大于正常斑点的半径, 产生强边缘干扰影响斑点检测, 使得误检率提升. 二阶单边高斯核(unilateral second-order Gaussian, USG)[20]已被用于重叠斑点的分离, 根据其设计思想, 本文使用该算法来抑制非斑点结构.
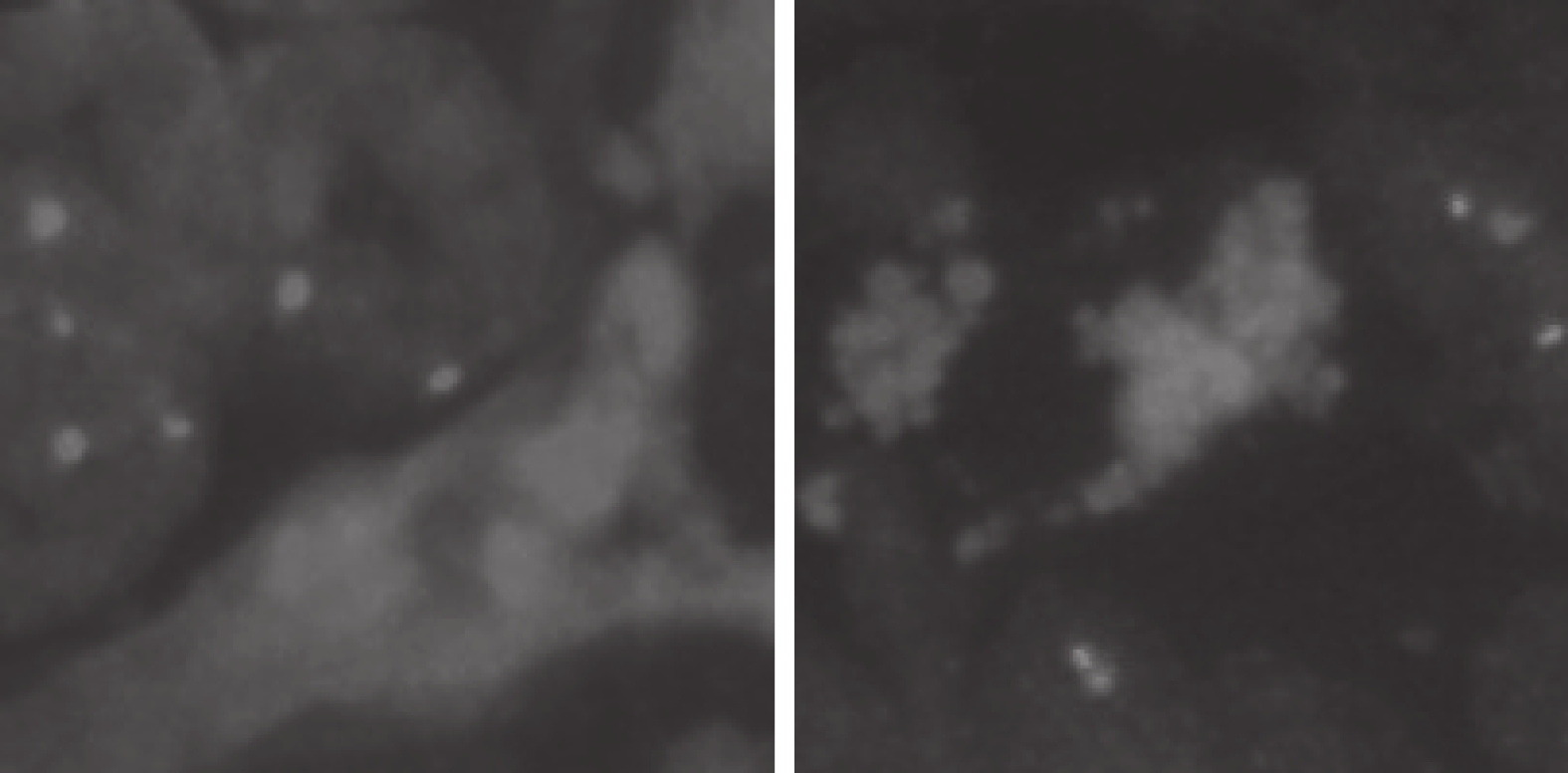
|
图 4 强边缘干扰示意图 |
规范化后的二阶高斯核的定义为式(19), 其示意图如图5所示, 图5(a)为三维可视化图像, 图5(b)为平面可视化图像.
| {g''_L}\left( {{{x}};\sigma } \right) = - 1 \cdot {\sigma ^2} \cdot \frac{{{\partial ^2}g\left( {{{x}};\sigma } \right)}}{{\partial {x^2}}} | (19) |
具有方向性的二阶高斯核数学建模如下:
| \begin{gathered} g''_n\left( {{{x}};\sigma , \theta } \right) = \\ - 2 \cdot \frac{{{{\left( {\left[ {\cos \theta , \sin \theta } \right]{{x}}} \right)}^2} - {\sigma ^2}}}{{{\text π} {\sigma ^4}}}\exp \left( { - \frac{{{{{x}}^{\mathrm{T}}}R_\theta ^{\mathrm{T}}{R_\theta }{{x}}}}{{2{\sigma ^2}}}} \right) \\ \end{gathered} | (20) |
其中,
| {R_\theta } = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta } \\ { - \sin \theta }&{\cos \theta } \end{array}} \right] | (21) |
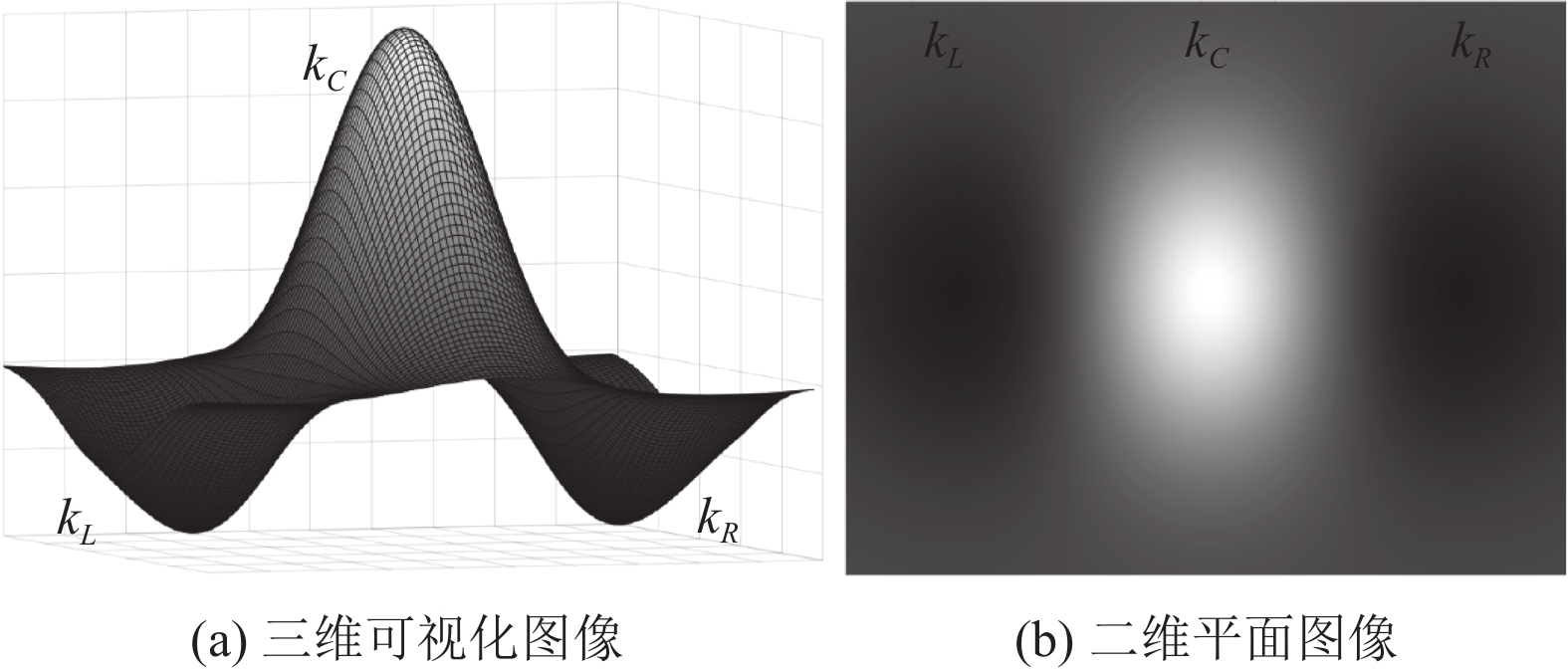
|
图 5 二阶高斯核示意图 |
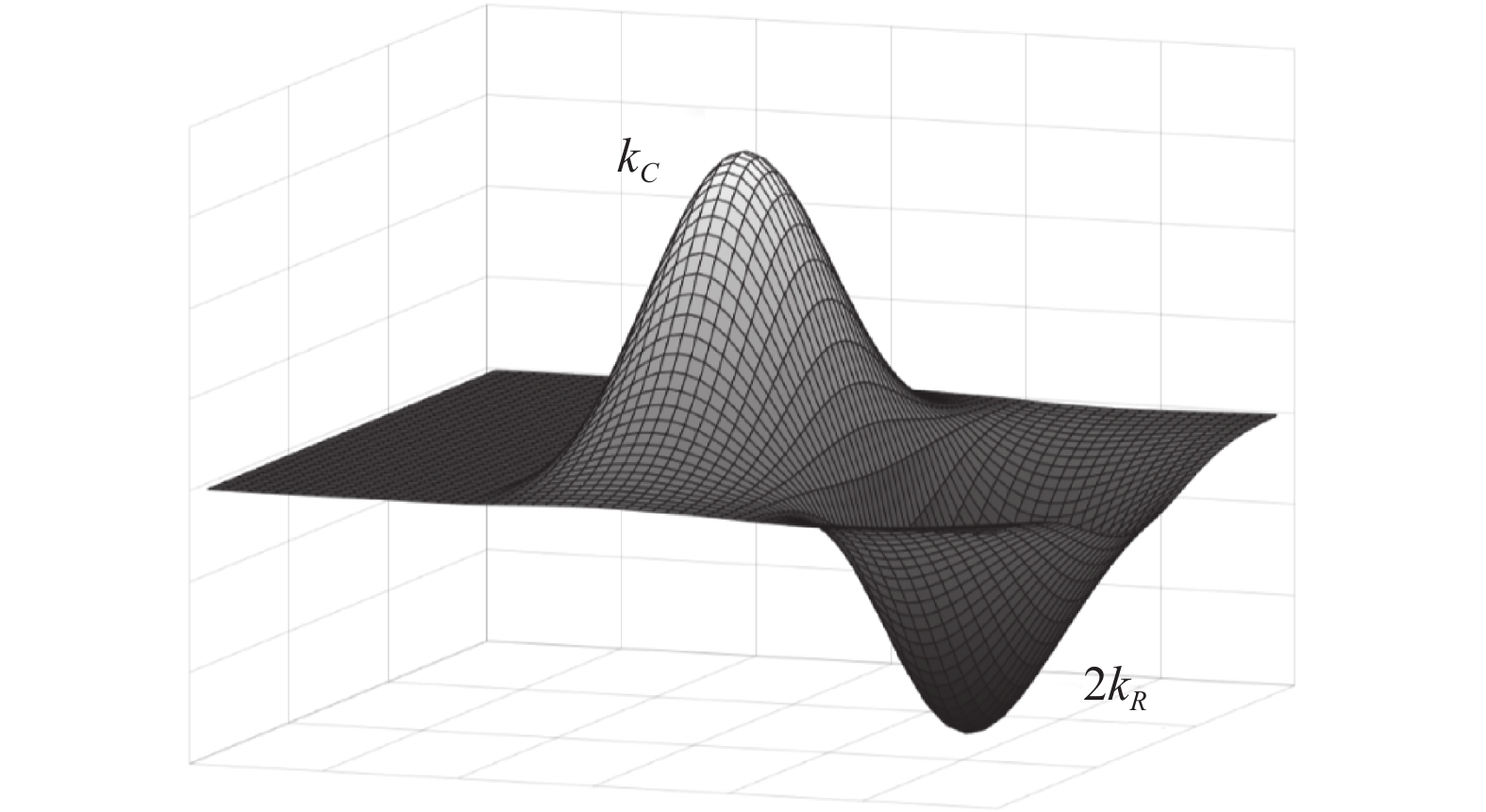
如图5所示, 二阶高斯核在空间上被划分为3个部分, 即中心部分
| {k_C}\left( {{{x}};\sigma , \theta } \right) = \left\{ {\begin{array}{*{20}{l}} {g''_n\left( {{{x}};\sigma , \theta } \right), } \\ {0, } \end{array}} \right.\begin{array}{*{20}{l}} {{\mathrm{if}}\; - \sigma < {\sigma _\theta } < \sigma } \\ {{\mathrm{otherwise}}} \end{array} | (22) |
| {k_R}\left( {{{x}};\sigma , \theta } \right) = \left\{ {\begin{array}{*{20}{l}} {g''_n\left( {{{x}};\sigma , \theta } \right), } \\ {0, } \end{array}\begin{array}{*{20}{l}} {{\mathrm{if}}\;{\sigma _\theta } \geqslant \sigma } \\ {{\mathrm{otherwise}}} \end{array}} \right. | (23) |
| {k_L}\left( {{{x}};\sigma , \theta } \right) = \left\{ {\begin{array}{*{20}{l}} {g''_n\left( {{{x}};\sigma , \theta } \right), } \\ {0, } \end{array}\begin{array}{*{20}{l}} {{\mathrm{if}}\;{\sigma _\theta } \leqslant - \sigma } \\ {{\mathrm{otherwise}}} \end{array}} \right. | (24) |
其中,
二阶高斯核度量了中心区域和其两侧区域之间的局部对比度, 传统的二阶高斯核函数通常会导致方向信息的丢失, 因其总是将中心部分与两侧区域捆绑在一起. 为了充分利用局部对比度的方向信息, 对单边二阶高斯核进行如下设计:
| u\left( {{{x}};\sigma , \theta } \right) = {k_C}\left( {{{x}};\sigma , \theta } \right) + 2 \cdot {k_R}\left( {{{x}};\sigma , \theta } \right) | (25) |
单边二阶高斯核示意图如图6所示.
从原理上讲, 显著的斑点在所有方向上都具有正的局部对比度, 这使得斑点可与其余结构区分开来. 与非斑点结构相比, 斑点在所有方向上的最小局部对比度仍是正的. 在给定的尺度下, 使用USG核来测量区域在所有方向上的局部对比度, 然后选择最小值作为响应, 实现抑制非斑点结构. 通过式(26)可获得USG核的最终响应:
| U\left( {{x}} \right) = \mathop {\max}\limits_{\sigma \in {S_u}} \left( {\mathop {\min}\limits_{\theta \in {D_u}} \left( {U\left( {{{x}};\sigma , \theta } \right)} \right)} \right) | (26) |
其中,
|
图 6 单边二阶高斯核示意图 |

|
图 7 单边二阶高斯核图像 |
1.4 斑点区域提取
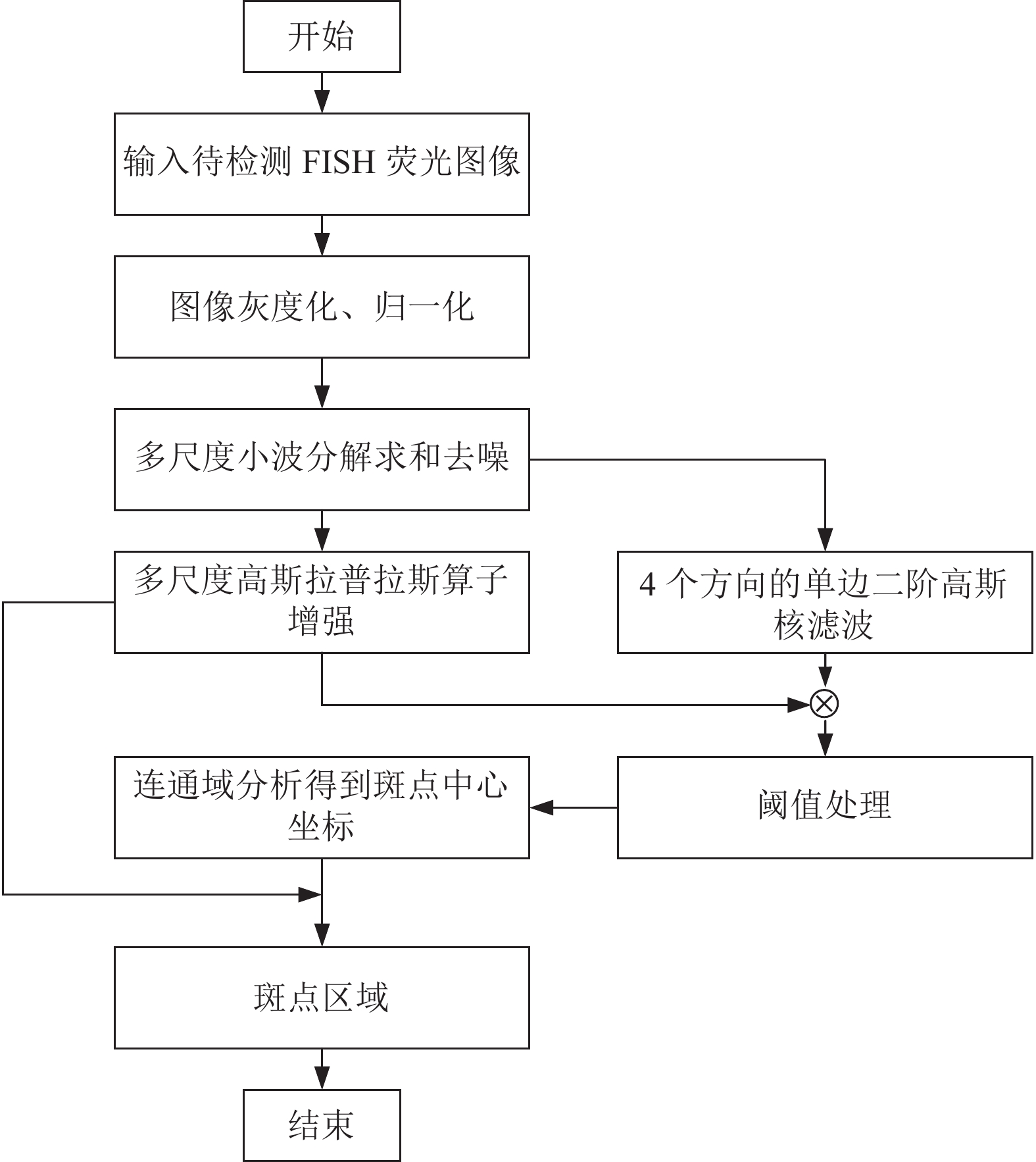
为实现对斑点的像素级分析, 得到斑点整个区域, 算法具体流程图如图8所示. 输入图像后, 首先对其进行预处理, 并使用小波多尺度求和算法对图像进行降噪处理, 然后对降噪后的图像分别使用多尺度高斯拉普拉斯算子和4个方向的单边二阶高斯核算子, 得到增强后的响应平面
| LU\left( {{x}} \right) = L\left( {{x}} \right) \cdot U\left( {{x}} \right) | (27) |
此时,
对
为了评估本文斑点检测算法的检测准确性, 实验主要对自建数据库一共83张进行测试, 其中根据斑点数量、成像质量、背景与噪声的干扰程度以及是否有非斑点结构干扰, 将数据库分为简单、一般、复杂工况, 数据库详情见表1, 具体图像示例如图9所示.
将本文算法与其他7种方法对比, 本文所有测试是在Windows 10, CPU主频为3.2 GHz, 内存为16 GB下进行的, 其中本文算法利用C++语言在Visual Studio 2022平台实现, 其余算法编程环境为PyCharm 2021和Matlab 2021.
|
图 8 荧光显微图像斑点提取流程图 |
2.2 评估指标
FISH荧光显微图像中所需提取的正确斑点由多个专业医师综合评定, 称之为金标准. 斑点检测是一个区分斑点和背景的二进制分类问题, 因此检测结果会出现3种情况: 真阳性(TP), 检测结果符合金标准; 假阳性(FP), 检测结果不符合金标准; 假阴性(FN), 未被检测出的金标准斑点. 为方便统计, 若金标准中心点6个像素半径内有斑点检测到, 则判定此斑点被正确检测, 反之漏检. 借由TP、FP和FN可有效评估算法的性能优劣,
| F = \frac{{2 \times {P_{{\mathrm{precision}}}} \times {P_{{\mathrm{recall}}}}}}{{{P_{{\mathrm{precision}}}} + {P_{{\mathrm{recall}}}}}} | (28) |
| {P_{{\mathrm{precision}}}} = \frac{{TP}}{{TP + FP}} | (29) |
| {P_{{\mathrm{recall}}}} = \frac{{TP}}{{TP + FN}} | (30) |
| 表 1 自建数据库信息 |

|
图 9 自建数据集中各工况图像示例 |
2.3 实验结果
由于本文数据库中图像分辨率较为统一, 其中2448×2048的图像也将它缩放到1360×1024, 则所需提取斑点的像素半径可以统计得到
1) MSSEF[4]: 尺度集
2) MSSIS[6]: 尺度集
3) THB[7]: 尺度集
4) MSVST[8]: 分解层数
5) SAOG[9]: 尺度集
6) BFSH[10]: 尺度集
7) 本文方法: 小波分解层数
其中, 前4种方法可以得到斑点区域, SAOG算法可以通过椭圆估计斑点形状, BFSH和SRUN[14]算法只能对斑点进行定位, SRUN深度学习算法使用模拟数据集训练, 不同算法选取最优结果, 再与金标准比对, 统计得到最终结果如表2所示, 其中加粗部分为
| 表 2 不同工况下的不同算法的检测性能 |
从表2中可看出: 简单工况下, 所有算法均能获得很好的检测效果, 性能差异可忽略不计; 一般工况下, MSSEF、MSSIS、MSVST等算法的提取率能够保持在较高水平, 但准确率下降较为严重, 这是因为图像噪声以及背景干扰加重, 使得误检率上升, 本文算法指标均优于其他算法; 复杂工况下, SAOG、BFSH、SRUN等算法指标大幅下降, 主要是因为干扰进一步加重, 且增加了非斑点结构, 对于较弱斑点难以检测到, 对于非斑点结构容易检测到其边缘部分, 但本文算法
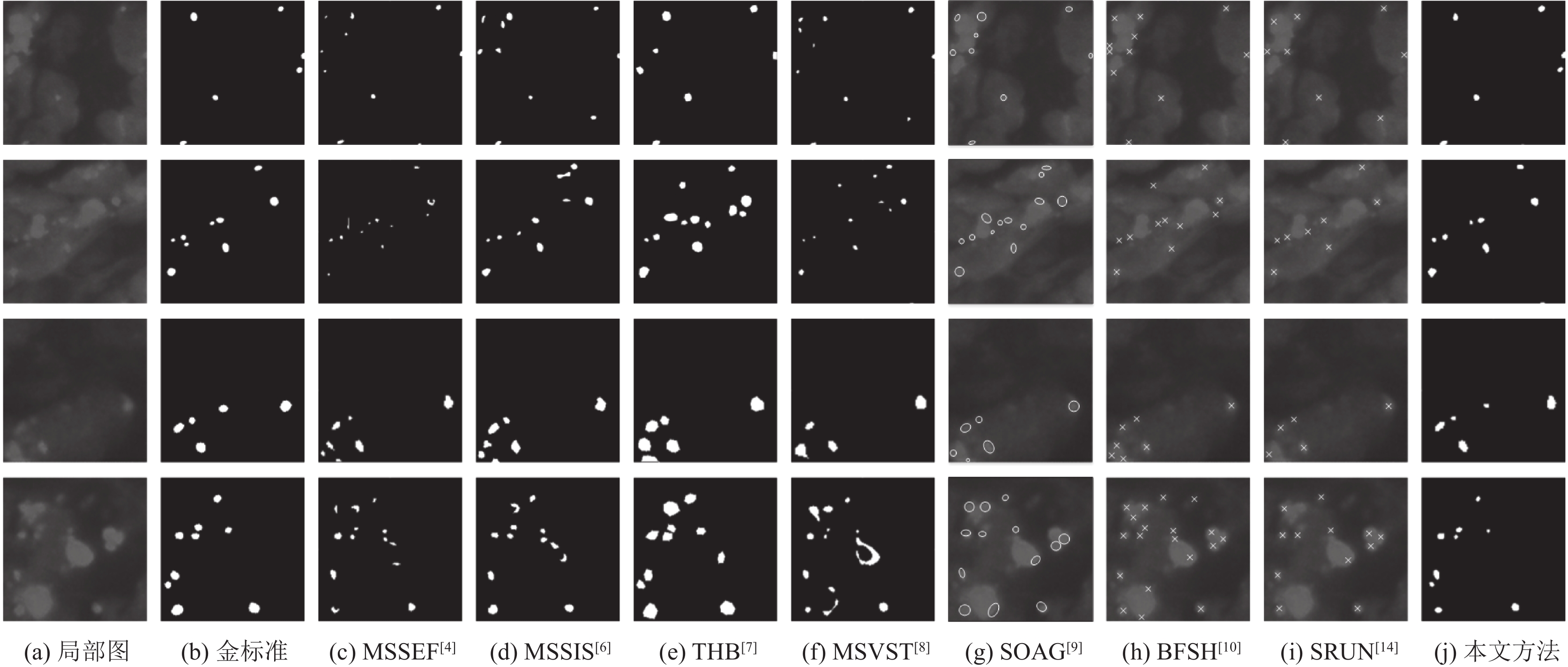
为进一步体现算法的优劣, 选择复杂工况中一张极具代表性的图像更直观的体现提取结果差异. 如图10所示为FITC-3荧光显微图像, 该图具有高噪声、斑点与背景对比度较低、背景干扰较为严重, 且具有非斑点结构干扰, 斑点检测难度较高, 易产生漏检与误检. 选取该图4个局部区域对各种算法进行测试, 最终测试结果如图11所示, 其中SAOG算法结果能用椭圆估计斑点形状, BFSH、SRUN算法只能得到斑点中心坐标, 在图中用×表示.

|
图 10 FITC-3荧光图像示例 |
|
图 11 复杂工况图像示例 |
从图11中可得到, 大多数算法如SRUN、MSSEF、MSVST方法均能够检测到大部分斑点, 但一些非斑点结构也被误检, 其中大多为高亮区域的边缘部分, 由于尺度限制, 在这些边缘上容易产生较高的响应, 从而高亮的部分边缘容易被提取到, 造成最终的准确率下降, THB算法具有较高的准确率, 但很难提取出边缘模糊、强度较弱的斑点, 使得提取率较低, SRUN深度学习方法依靠数据驱动, 得到的指标较为均衡, 但针对本文工况, 难以剔除非斑点结构的干扰.
本文方法兼顾了准确率与提取率, 能够提取到较弱强度的斑点, 且能够抑制非斑点结构的干扰, 使得最终
算法的时效性也是一项重要指标, 使用不同算法对自建数据库的83张图像进行平均耗时测试, 最终结果由表4所示, 由于本算法包含降噪、增强、非斑点结构抑制多个步骤, 所需时间略高于其他算法, 但总体平均时间在0.5 s以内, 在不同工况下的性能表现均优于其他算法.
| 表 3 不同算法对FITC-3图像的检测性能 |
| 表 4 不同算法耗时 |
3 结论与展望
本文提出一种面向FISH荧光显微图像的斑点检测算法, 该传统算法对于低信噪比、背景干扰严重且存在非斑点结构干扰的图像表现出良好的性能. 实验结果验证了算法在自制FISH荧光图像库上的优越性, 其平均
| [1] |
Kwon S. Single-molecule fluorescence in situ hybridization: Quantitative imaging of single RNA molecules. BMB Reports, 2013, 46(2): 65-72. DOI:10.5483/BMBRep.2013.46.2.016 |
| [2] |
Ahmed WM, Leavesley SJ, Rajwa B, et al. State of the art in information extraction and quantitative analysis for multimodality biomolecular imaging. Proceedings of the IEEE, 2008, 96(3): 512-531. DOI:10.1109/JPROC.2007.913556 |
| [3] |
Sage D, Neumann FR, Hediger F, et al. Automatic tracking of individual fluorescence particles: Application to the study of chromosome dynamics. IEEE Transactions on Image Processing, 2005, 14(9): 1372-1383. DOI:10.1109/TIP.2005.852787 |
| [4] |
Jaiswal A, Godinez WJ, Eils R, et al. Tracking virus particles in fluorescence microscopy images using multi-scale detection and multi-frame association. IEEE Transactions on Image Processing, 2015, 24(11): 4122-4136. DOI:10.1109/TIP.2015.2458174 |
| [5] |
Basset A, Boulanger J, Salamero J, et al. Adaptive spot detection with optimal scale selection in fluorescence microscopy images. IEEE Transactions on Image Processing, 2015, 24(11): 4512-4527. DOI:10.1109/TIP.2015.2450996 |
| [6] |
Acosta BMT, Basset A, Bouthemy P, et al. Multi-scale spot segmentation with selection of image scales. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). New Orleans: IEEE, 2017. 1912–1916. [doi: 10.1109/ICASSP.2017.7952489]
|
| [7] |
Marsh BP, Chada N, Gari RRS, et al. The Hessian blob algorithm: Precise particle detection in atomic force microscopy imagery. Scientific Reports, 2018, 8(1): 978. DOI:10.1038/s41598-018-19379-x |
| [8] |
Zhang B, Fadili JM, Starck JL. Wavelets, ridgelets, and curvelets for Poisson noise removal. IEEE Transactions on Image Processing, 2008, 17(7): 1093-1108. DOI:10.1109/TIP.2008.924386 |
| [9] |
Ren J, Yu WY, Guo JP, et al. Second-order anisotropic Gaussian directional derivative filters for blob detection. arXiv:2305.00435, 2023.
|
| [10] |
Imbert A, Ouyang W, Safieddine A, et al. FISH-quant v2: A scalable and modular tool for smFISH image analysis. RNA, 2022, 28(6): 786-795. DOI:10.1261/rna.079073.121 |
| [11] |
Wollmann T, Ritter C, Dohrke JN, et al. DetNet: Deep neural network for particle detection in fluorescence microscopy images. Proceedings of the 16th IEEE International Symposium on Biomedical Imaging (ISBI 2019). Venice: IEEE, 2019. 517–520. [doi: 10.1109/ISBI.2019.8759234]
|
| [12] |
Bouilhol E, Savulescu AF, Lefevre E, et al. DeepSpot: A deep neural network for RNA spot enhancement in single-molecule fluorescence in-situ hybridization microscopy images. Biological Imaging, 2022, 2: e4. DOI:10.1017/S2633903X22000034 |
| [13] |
Eichenberger BT, Zhan YX, Rempfler M, et al. deepBlink: Threshold-independent detection and localization of diffraction-limited spots. Nucleic Acids Research, 2021, 49(13): 7292-7297. DOI:10.1093/nar/gkab546 |
| [14] |
余永建, 王越, 李寰, 等. 融合通道层注意力机制的UNet的衍射极限荧光点检测和定位. 激光与光电子学进展, 2023, 60(14): 1412004. DOI:10.3788/LOP230718 |
| [15] |
吴坚. 近膜区域荧光显微图像中亚细胞目标的斑点检测、融合事件识别和三维形态重建 [博士学位论文]. 杭州: 浙江大学, 2016.
|
| [16] |
Starck JL, Murtagii F, Bijaoui A. Multiresolution support applied to image filtering and restoration. Graphical Models and Image Processing, 1995, 57(5): 420-431. DOI:10.1006/gmip.1995.1036 |
| [17] |
Sadler BM, Swami A. Analysis of multiscale products for step detection and estimation. IEEE Transactions on Information Theory, 1999, 45(3): 1043-1051. DOI:10.1109/18.761341 |
| [18] |
Kong H, Akakin HC, Sarma SE. A generalized Laplacian of Gaussian filter for blob detection and its applications. IEEE Transactions on Cybernetics, 2013, 43(6): 1719-1733. DOI:10.1109/TSMCB.2012.2228639 |
| [19] |
Lindeberg T. Feature detection with automatic scale selection. International Journal of Computer Vision, 1998, 30(2): 79-116. DOI:10.1023/A:1008045108935 |
| [20] |
Wang G, Lopez-Molina C, De Baets B. Automated blob detection using iterative Laplacian of Gaussian filtering and unilateral second-order Gaussian kernels. Digital Signal Processing, 2020, 96: 102592. DOI:10.1016/j.dsp.2019.102592 |
 2024, Vol. 33
2024, Vol. 33



