目前互联网技术不断发展, 在线教育已经成为一种越来越受欢迎的学习方式. 然而在线教育平台中有着海量的学习资源, 如何为学生自适应推荐符合自身学习情况的个性化学习资源, 注重弱点帮助学生更加高效地学习[1]. 让每个学生都能够得到专属的学习计划和教学资源, 实现个性化教学. 个性化学习[2]是智慧教育领域重要的课题, 实现这个过程最重要的是实时追踪学生知识状态. 知识追踪(knowledge tracing, KT)任务旨在利用学生历史的学生数据进行分析, 实时有效地追踪学生知识状态, 并且预测学生未来的表现, 是实现智慧教育的重要基础. 此外知识追踪还可以帮助教师实现更加精准地评估和反馈, 从而提高教学质量和效果, 实现在线教育的智能化.
随着深度学习因其强大的表征能力被应用于各类研究中, 基于深度学习的知识追踪模型被大量提出, 模型的性能优于传统的知识追踪. 深度知识追踪模型(deep knowledge tracing, DKT)[3]基于循环神经网络(recurrent neural network, RNN)[4]进行建模任务, 使用隐藏层来表示学生的知识状态. 最近几年, 图神经网络(graph neural network, GNN)[5]已成为一种有效的分析图结构数据的方法, 并在KT领域中得到广泛应用. KT领域的研究受GNN启发, 基于GNN的知识追踪(graph-based knowledge tracing, GKT)[6], 它构建了知识点关系图, 并将知识追踪任务转化为GNN中的时间序列节点级分类问题. 通过这一方法, 我们能够更加有效地捕捉知识点之间的关联, 从而提高知识追踪的准确性和效率. 基于联合图卷积网络的深度知识追踪(joint graph convolutional network based deep knowledge tracing, JKT)[7]通过练习与练习、知识点与知识点的关系构建多维关系图, 并将其与练习-知识点关系融合. 基于双图对比学习的知识追踪(bi-graph contrastive learning based knowledge tracing, Bi-CLKT)[8]采用了全局双层和局部双层结构的对比学习, 分别应用图级和节点级的GCN来提取练习与练习、概念与概念的关系信息. 图结构可以有效地捕捉题目之间的潜在关系, 在一定程度上丰富了题目的表示形式. 对于如何准确表示题目和知识点之间关系信息以及可解释性问题一直是研究的重点内容.
上述知识追踪研究在KT领域中取得了显著进展, 但它们仍面临一些缺陷. 首先, 在知识追踪任务中, 知识点之间的关系往往非常复杂, 简单的同构图仅使用题目-知识点无法准确刻画这些关系. 另外一些研究忽略了两者的关系, 其次, 在整个学习过程中学习和遗忘是同时存在的, 遗忘会对学生知识状态产生影响. 一些研究忽略了学生的遗忘行为或者考虑得不够全面.
针对上述问题, 本文提出一种融合知识点关系的深度记忆网络知识追踪模型(HRGKT). 本文的主要创新和贡献包括以下几个方面.
(1)引入知识点关系图来有效地捕捉知识点之间的复杂关系, 建模学生答题序列中知识点之间的高阶关系.
(2)应用教育学理论中的学习和遗忘曲线等概念建立一个综合模型, 用于捕捉随着时间的变化学生对知识点掌握程度的改变.
(3)在4个真实的数据集上进行实验, 证明该模型在性能预测方面优于现有模型.
本文第1节回顾与知识追踪相关的研究工作. 第2节介绍一些重要的定义和符号. 第3节详细介绍模型各个模块. 在第4节中, 详细阐述相关的实验结果, 并对其进行分析. 最后, 在第5节中, 给出研究结论并展望未来的研究方向.
1 相关工作 1.1 知识追踪在本节中首先回顾知识追踪的相关工作, 其次对所使用的方法进行介绍. 在知识追踪领域主要有两种方法, 一种是传统的基于隐马尔可夫模型[9]的知识追踪, 另外一种是基于深度学习的知识追踪[10]. 传统的方法主要为贝叶斯知识追踪BKT[11], 是构建学生学习序列模型中最常用的方法. BKT将学生知识状态定义为二元组(掌握, 未掌握), 通过HMM更新学生知识状态进而预测学生未来表现. 模型未考虑学生个体差异以及遗忘行为, 知识点之间是相互独立的. 针对以上问题, Pardos等人[12]考虑学生的个体差异, 初始掌握知识点的概率是不同的, 在BKT的基础上进行扩展, 改进了BKT. BKT以及BKT的扩展具有相对比较简单, 解释性强的优点, 但是仅将知识状态表示为二元组不符合实际认知状态, 还具有一定的局限性.
深度知识追踪DKT模型首先将深度学习技术应用于知识追踪领域, 其核心思想在于将学生的练习和响应嵌入作为模型的输入数据. 通过利用循环神经网络RNN中的隐藏层, DKT能够有效地表示学生的知识状态, 从而精准地预测他们在未来的学习表现. DKT存在重构和预测波动问题, Yeung等人[13]定义重构误差和波度测量, 将原始损失函数增强为正则化损失函数, 解决了上述两个问题. Chen等人[14]将知识点之间的先决条件引入知识追踪, 更准确地预测学生未来表现. Wang等人[15]把练习之间的关系表示成练习关系图, 将练习之间的关系信息融入学生知识状态建模中. Su等人[16]通过双向长短期记忆网络(bi-directional long short-term memory, BiLSTM)自动捕捉练习文本每个练习的语义, 充分利用练习文本中丰富的信息. 但是基于RNN的深度知识追踪使用隐藏层表示学生整个知识状态, 无法表示每个知识点的状态, 可解释性差. 动态键值记忆网络知识追踪模型(dynamic key-value memory networks for knowledge tracing, DKVMN)[17]受到记忆增强网络的启发使用一个静态矩阵Mk来存储知识点, 一个动态矩阵Mv来存储知识点状态, 实时追踪每个知识点状态. Ai等人[18]在DKVMN的基础上, 人工设计静态矩阵Mk中知识点信息, 支持输入更多特征来获得更高的性能. Minn等人[19,20]将学生能力考虑在内, 根据学生能力进行动态分组追踪学生的表现, 并随着时间的推移定期进行重新评估. 琚生根等人[21]针对现有模型可能无法直接处理包含多个知识点的题目以及可解释性不足问题, 提出了一种多知识点融合嵌入的深度知识追踪模型(deep knowledge tracing model based on embedding of fused multiple concepts, MCAKT).
总的来说, 深度学习在知识追踪领域的应用能够精准地捕捉学生的知识状态, 并且能有效预测学生未来的答题表现. 但是模型忽略了题目涵盖知识点中复杂的高阶关系以及遗忘行为, 或者考虑得不够全面. 模型还有着一定的局限性, 还存在改进的空间, 进而可以提高模型的预测准确性和可解释性.
1.2 图注意力网络图注意力网络(graph attention network, GAT)[22]是一种用于处理图结构数据的深度学习模型. 传统的图神经网络通常使用固定的邻居采样策略或基于图拉普拉斯算子进行特征传播, 而GAT引入了注意力机制来动态地对节点之间的关系进行建模. 它通过学习每个节点与其邻居节点之间的权重分配, 从而捕捉到不同节点之间的重要性差异.
如图1所示, 在GAT中其核心思想是通过自适应地计算每个邻居节点对当前节点的重要性权重, 然后根据这些权重对邻居节点的特征进行加权汇聚. 具体而言, GAT利用一个前馈神经网络来计算每个节点对应的注意力系数, 然后将注意力系数与邻居节点的特征进行加权求和, 得到当前节点的表示. 这种机制使得GAT能够更好地捕捉到图中全局和局部之间的关系, 提高了模型的表达能力.
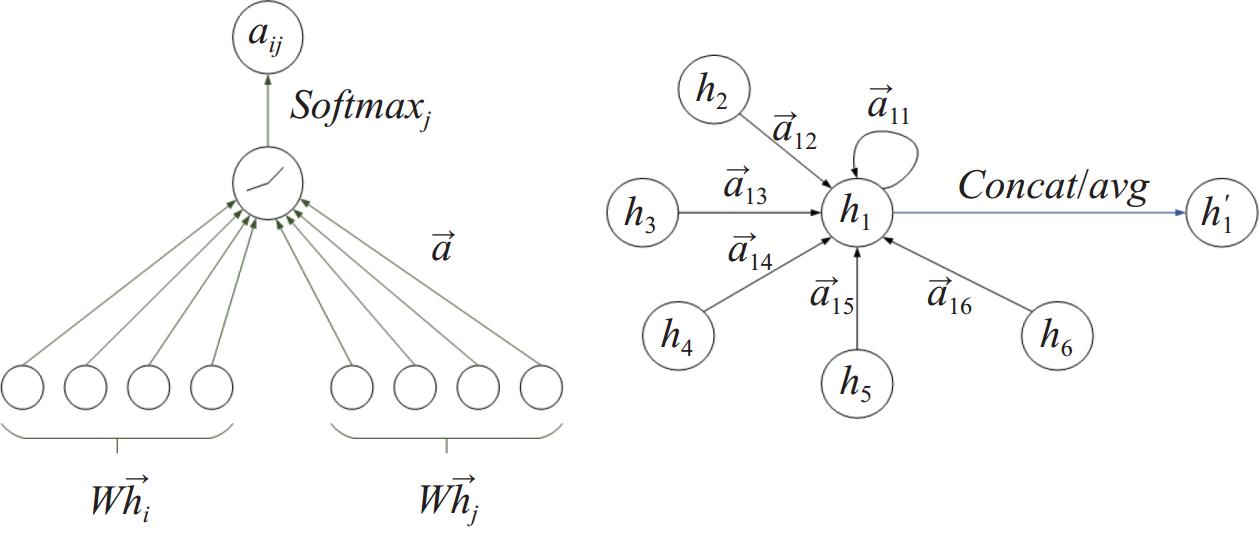
|
图 1 GAT框架结构 |
2 问题定义
在本节中, 首先介绍KT相关的任务, 然后给出知识点关系图涉及的一些定义并给出它们的解释.
2.1 KT任务KT任务的核心在于实时、精准地追踪学生的知识状态, 基于其历史学习数据, 进而对学生未来的答题表现进行预测. 这一任务的实现有助于更全面地掌握学生的学习进展, 并为教育评估提供有力支持. 在KT中每个学生的答题序列由一系列题目和回答组成, 假设Q表示题目集合, K表示知识点集合. 定义学生的答题序列为, 其中表示学生交互的第t个题目. 表示学生相应的题目回答情况, 1表示回答正确, 0表示回答错误. 给定学生以上的答题序列, 实现实时追踪学生的知识状态, 并且预测学生未来t+1时刻题目的答题表现.
通过图2中的学生学习历史过程例子可以更直观清楚地说明KT的任务. 如何根据他们的历史作答结果通过知识追踪来精确地追踪每个人的知识水平, 进而为每个人推荐符合自身学习情况的题目、老师为每个学生制定专属的学习计划以及进行智能学情诊断[23]等.
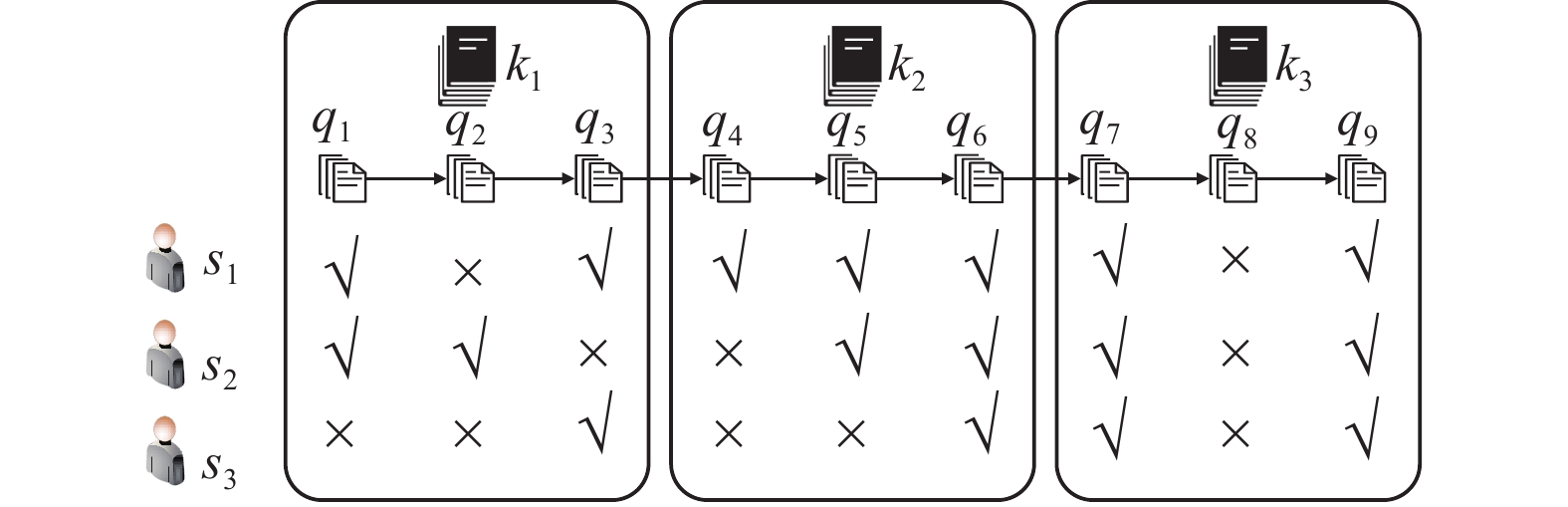
|
图 2 学生学习历史过程 |
2.2 知识点关系图
学生在答题过程中, 题目、知识点之间存在着关系. 如图3所示, 将学生答题记录中的题目和知识点之间的关系进行表示. 图中题目q2包含知识点k1和k3, 因此k1和k3通过题目q2产生了关系.
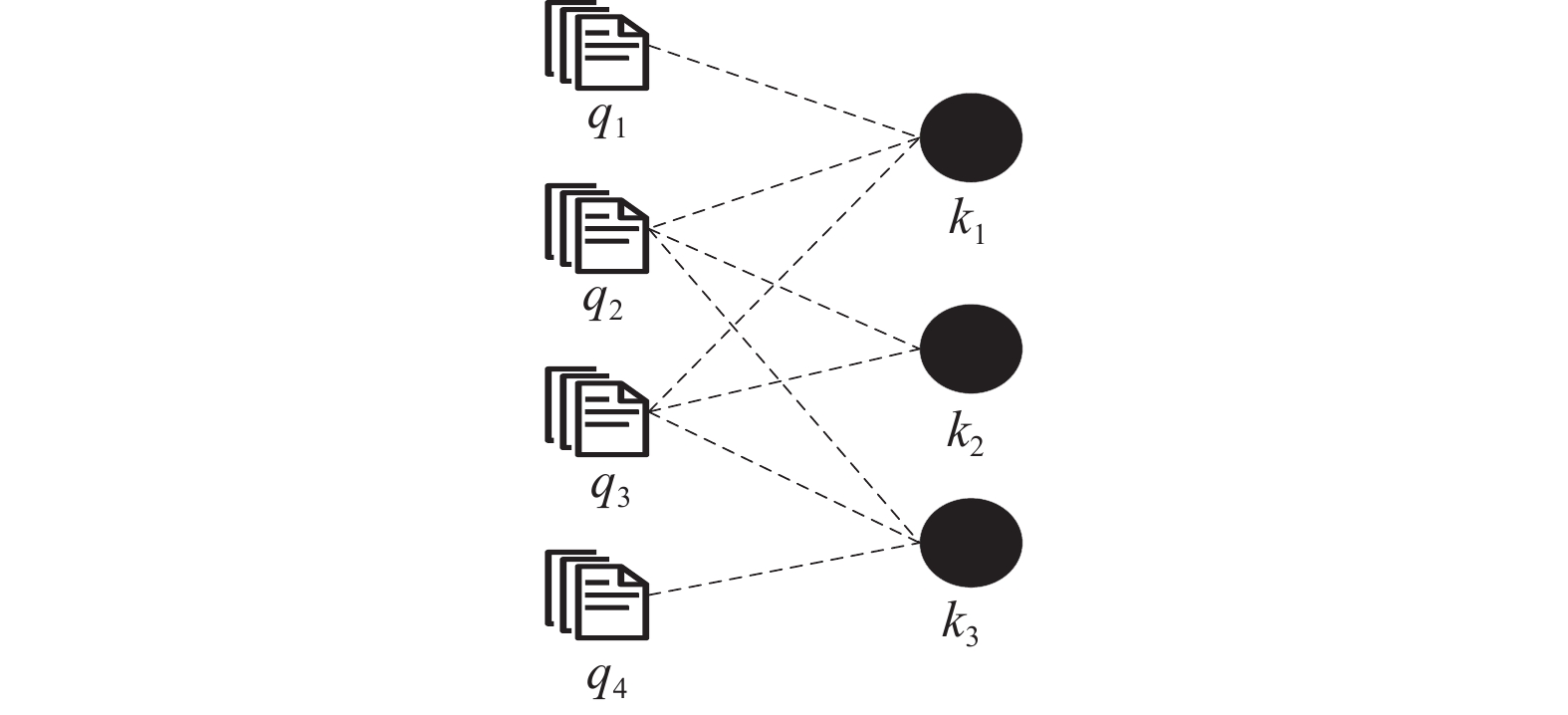
|
图 3 题目知识点关系图 |
因此在知识点关系图中, 节点是所有的知识点, 每条边关系是知识点与题目的一阶邻居知识点产生, 也就是一个题目包含的所有知识点都有关系信息. 如图中q2包含的k1, k2, k3, 3个节点在知识点关系图中存在边的关系.
为了精准将知识点之间存在的关系, 定义知识点集合为
教育学理论艾宾浩斯遗忘曲线[24,25]表明, 学生的知识遗忘受到重复学习的次数和时间间隔的影响, 时间间隔包括顺序时间间隔和重复学习相同知识点时间间隔. 此外, 学生对知识点的掌握程度也会对其遗忘产生影响[26]. 因此考虑以下4个影响知识遗忘的因素.
具体影响遗忘的3个因素示例如图4所示. 上次学习的时间间隔(sequential learning interval, SLI), SLI表示当前学习时间距离上次学习产生的时间间隔. 最近知识点时间间隔(knowledge learning interval, KLI), KLI表示当前作答题目与含有相同知识点的相关题目距离的最近时间. 知识点重复学习次数(number of repetitive studies, NRS), NRS表示整个学习过程中学习过知识点的次数. 知识点原本掌握程度(knowledge mastery level, KML), KML表示学生对某个知识点本身的掌握程度.
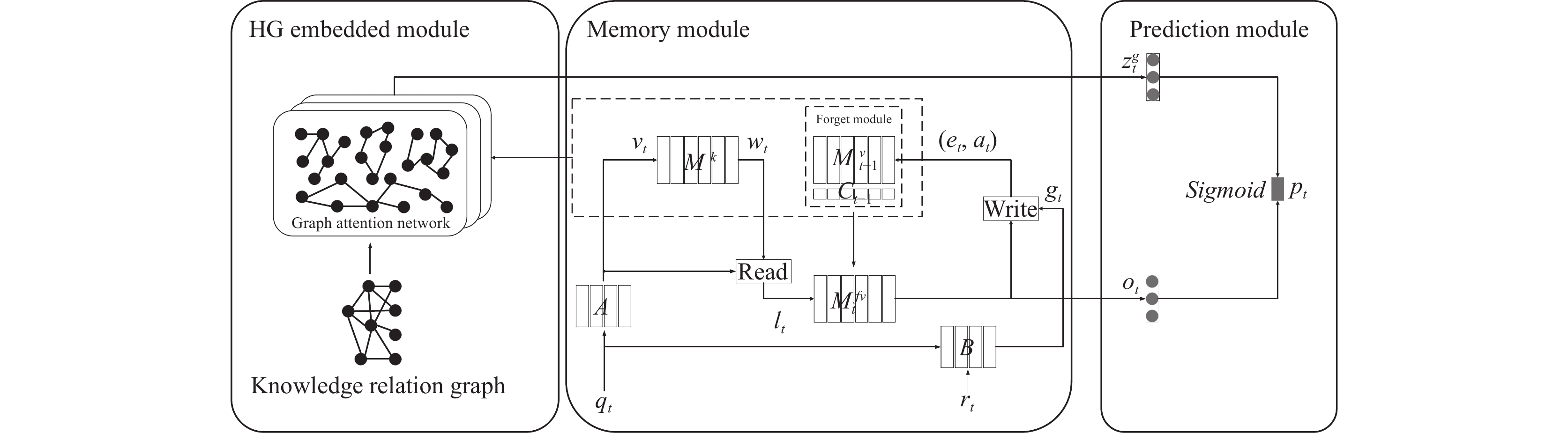
3 融合知识点关系的深度记忆网络知识追踪模型本节详细介绍融合知识点关系的深度记忆网络知识追踪模型HRGKT. HRGKT框架图如图5所示, 由HG嵌入模块、记忆网络模块以及预测模块3个模块组成. 其中, HG嵌入模块用于学习HG中知识点之间的关系信息以及两者的高阶关系信息. 另外HG模块还能通过知识点关系图动态地捕捉知识点关系信息. 记忆网络模块主要是跟踪学生知识状态的动态变化, 分为知识点嵌入模块、知识点状态模块、学习模块以及遗忘模块. 预测模块使用HG模块中的知识点关系嵌入矩阵以及记忆网络模块中的知识状态预测学生正确回答题目的概率. 由此, HRGKT模型可以更加全面、准确地了解学生的知识状态, 提供更好的学习指导和帮助.
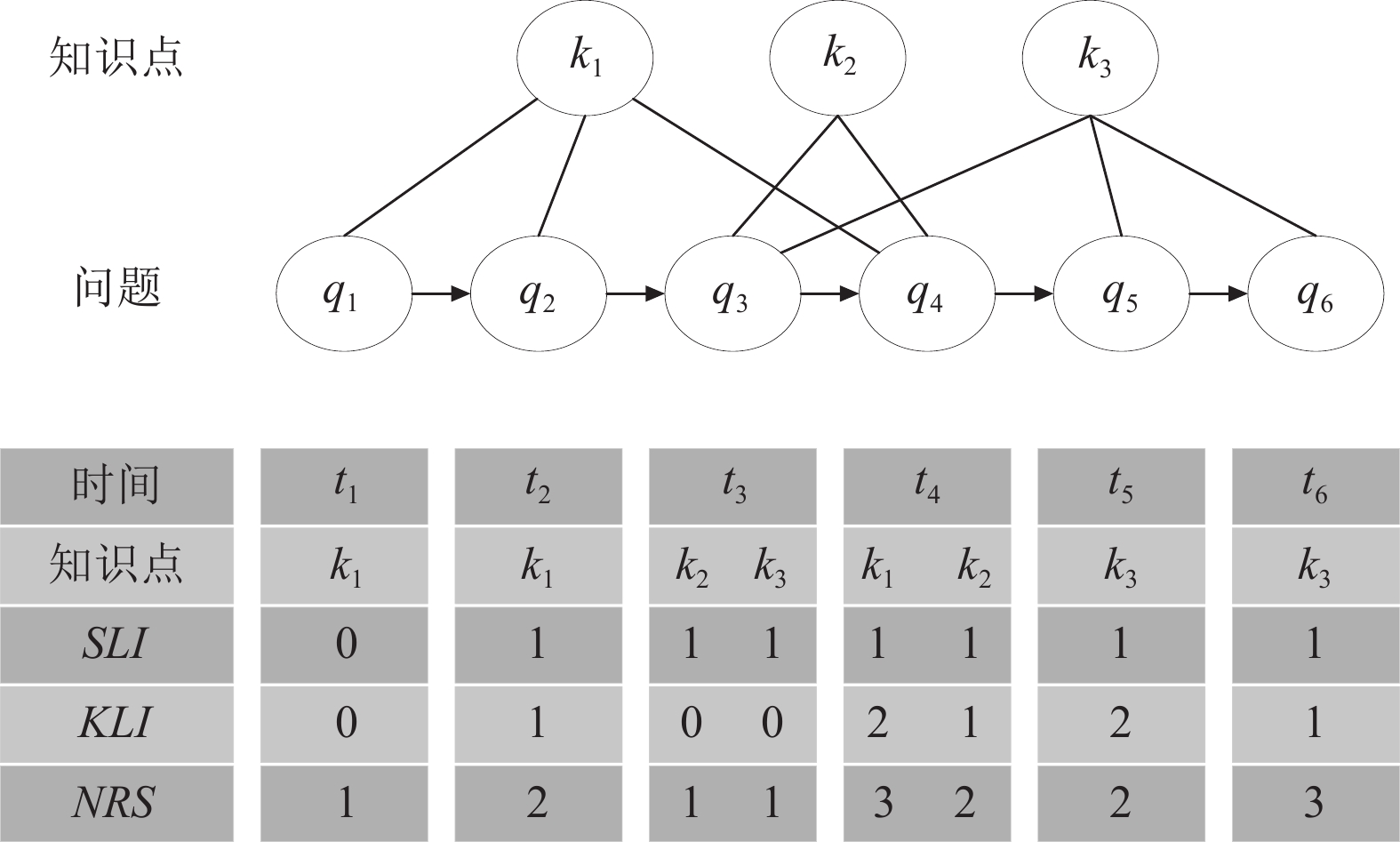
|
图 4 影响遗忘的3个因素 |
3.1 HG嵌入模块
本模块使用GAT捕捉HG中题目知识点之间的高阶关系信息. 知识点之间的高阶关系是知识点关系图中知识点与其二阶邻居等多阶关系信息. 知识点的邻居则属于同一题目涵盖的所有知识点. HG模块只关注知识点的关系状态.
因为某一个知识点状态变化会影响与其有关系的知识点状态的变化. 所以采用GAT获取知识点关系图HG中各个知识点的高阶关系信息, 来捕捉知识点之间变化的相互影响关系. 根据第2.2节中的HG图计算每个知识点之间的注意力系数, 使用自注意力机制用于所有知识点, 使用共享权重矩阵用于邻居节点, 使用激活函数获得知识点之间的关系系数. 具体过程如式(1):
| nij=LeakyReLU(W⋅[Wt⋅ti‖Wt⋅tj]) | (1) |
其中, ||表示连接操作, ·表示内积操作. 对
| aij=Softmax(nij)=exp(nij)∑k∈Niexp(nik) | (2) |
其中, Ni表示节点ti的相邻知识点的数量, aij表示知识点ti与邻居知识点tn的注意力权重. 另外多头注意力层的引入, 为稳定学习注意力权重提供了有效手段. 通过M个独立的注意力机制, 每个中心节点的权重得以精确计算, 进而产生M个注意层面. 然后, 对这些注意层面进行平均处理, 并经过激活函数的转换, 最终生成知识点的最终表示, 具体的过程如式(3):
| t(h)i=σ(1MM∑m=1∑j∈Niamij⋅Wmt⋅tn) | (3) |
为了让知识点表示更加全面, 通常会设置多个图注意力层进行训练. 经过h层的图注意力层训练后, 每个中心节点能够获取到h阶邻居节点的信息. 通过多层图注意力的训练, 节点能够更好地捕捉到图结构中的重要关系和特征[27].
|
图 5 HRGKT模型框架图 |
3.2 记忆网络模块
本模块旨在学习知识追踪任务中知识点的嵌入表示, 计算题目与知识点之间的知识相关权重. 另外考虑学生学习过程中的学习行为以及遗忘行为对学生知识状态进行维护, 动态地追踪学生的知识状态.
3.2.1 知识点嵌入模块知识点嵌入模块用来学习知识点的表示, 该模块为每个知识点存储一个嵌入向量, 将其表示为一个矩阵
| wt(i)=Softmax(vTtMk(i)) | (4) |
遗忘模块用来表示学生遗忘行为对知识状态产生的影响, 通过4个遗忘因素分别对不同的知识点进行遗忘处理. 根据第2.4节中提出影响遗忘的4个因素, 将3个SLI, KLI, NRS影响遗忘的因素进行连接, 组合成向量
以上遗忘因素
| fet(i)=Sigmoid(WT1Ft(i)+b1) | (5) |
然后将
| fat(i)=tanh(WT2Ft(i)+b2) | (6) |
其中,
根据记忆擦除向量与记忆更新向量对t–1时刻的知识状态进行遗忘处理得到t时刻开始学习时的知识状态
| Mfvt(i)=Mvt−1(i)(1−fet(i))(1+fat(i)) | (7) |
知识点状态模块用来表示学生知识点的状态, 该模块使用
| lt=N∑i=1wt(i)Mfvt(i) | (8) |
其中,
| ot=tanh(W[lt,vt]+b) | (9) |
学习模块根据学生不同的答题结果实时追踪学习过程知识状态的变化, 进而更新学生知识的状态. 将学生开始学习的知识状态
| et=Sigmoid(We⋅gt+be) | (10) |
其中,
| ˜Mfvt+1(i)=Mfvt(i)[1−wt(i)et] | (11) |
在擦除以上信息后, 使用添加信号
| at=tanh(Wa⋅gt+ba) | (12) |
最后计算t时刻答完题之后未经过遗忘的学生知识状态, 具体计算公式如式(13):
| Mvt+1(i)=˜Mfvt+1(i)+wt(i)at | (13) |
预测模块是对学生未来的答题表现进行预测, 本质上就是考查学生对题目所含知识点的掌握情况. 为了预测输入题目
另外还要考虑与题目涵盖知识点相关的知识点对答题结果的影响[28]. 计算图摘要向量
| zgt+1=tanh(Wz(K∑i=1wt+1(i)H(i))T+bz) | (14) |
其中,
最后将来自记忆网络模块的组合向量
| pt+1=Sigmoid(Wp[ot+1,zgt+1]+bp)⋅δ(qt+1) | (15) |
其中,
在模型训练过程中, 主要的参数包括题目嵌入矩阵A、答题结果嵌入矩阵B、神经网络中的权重与偏置, 以及知识点矩阵
为了更好地训练模型, 本文中建立了一个联合训练框架, 以实现模型参数的最优化. 一方面首先为了能更好获取知识点关系图中知识点关系信息, 使用内积的方式来评估图中节点之间的关系. 具体过程如式(16). 其中
| ˆbij=σ(tTi,tn) | (16) |
为了让节点之间关系更加符合真实结果构建交叉熵损失函数来保持两者关系如式(17)所示:
| L1=|T|∑i=1|T|∑j=1−(bijlogˆbij+(1−bij)log(1−ˆbij)) | (17) |
另一方面通过使用Adam方法最小化模型对预测值
| L2=−∑(rtlogpt+(1−rt)log(1−pt)) | (18) |
最后针对预训练问题, 知识点信息目标和知识追踪目标进行联合优化, 其中
| L=λ1L1+λ2L2 | (19) |
本节主要介绍HRGKT模型的伪代码, 伪代码如算法1所示.
算法1. HRGKT算法训练过程
输入: 学生答题历史记录以及知识点关系图HG.
输出: 学生未来答题表现.
1. 初始化权重、偏置参数和嵌入矩阵
2. For each epoch
3. 式(3)计算知识点的关系信息
4. one-hot编码题目嵌入, 式(4)计算知识点相关向量
5. 式(7)计算经过遗忘后的掌握状态
6. 式(8)计算知识点掌握状态
7. 式(9)计算组合向量
8. 式(14)计算图摘要向量
9. 式(15)预测学生答题表现概率
10. 式(13)更新知识点状态矩阵
11. 计算损失函数, 更新参数
12. end for
4 实验与分析在本节中描述了进行的实验以验证HRGKT模型方法的有效性. 在4个真实的在线教育数据集上比较了HRGKT与5个基准模型的性能. 最后进行两个消融实验, 以观察HRGKT模型核心模块的有效性.
4.1 数据集本文的实验是在4个经典的公开知识追踪数据集上进行的. 数据集为ASSISTments2009, Statics2011, ASSISTments2012, Synthetic-5. 这些数据集的详细统计数据见表1, 其中Student表示学生数量, Question表示题目数量, Knowledge表示知识点数量, Records表示答题总数.
ASSISTments2009数据集是通过ASSISTments在线教育平台在2009–2010年期间收集而来的, 共有
| 表 1 数据集统计信息 |
4.2 实验基准
为了评估HRGKT的性能, 需要与其他基准模型进行比较. 对5个基准模型进行介绍, 所有模型的参数按照研究者提供的最佳参数进行设置, 基准模型的详细信息如下.
DKT[3]使用RNN对学生的知识状态进行建模. DKT是第1个使用深度学习来实现知识追踪任务的模型.
Bi-CLKT[11]采用了全局双层和局部双层结构的对比学习, 分别应用图级和节点级的GCN来提取练习与练习和概念与概念的关系信息.
DKVMN[19]使用一个键值矩阵来追踪学生各个知识点的知识状态, 实时追踪各个知识点.
LFKT[26]将学生的遗忘行为考虑在内, 综合考虑了4个遗忘影响因素, 模拟学生学习过程中的遗忘行为.
DKT+forget[29]在DKT的基础上通过增加从题目回答序列中计算出的遗忘特征, 考虑学生的遗忘行为扩展了DKT模型.
4.3 评价指标与实验设置在实验中, 采用AUC (area under the curve)评价指标来评估模型的性能. ROC曲线全称为接收者操作特征曲线, 它是以假阳性率(FPR)作为横坐标, 真阳性率(TPR)作为纵坐标进行绘制的. 当ROC曲线越趋近于左上角时, 意味着分类模型的性能表现越佳. AUC的值等于ROC曲线下的面积, AUC的值越大, 说明模型的性能越好.
本文模型是在内存32 GB, Intel Core i7, RTX 3060的主机上进行实验. 模型将数据集随机划分为3个部分: 训练集、验证集和测试集. 其中, 70%的数据被用作训练集, 20%的数据被用作测试集, 10%的数据被用作验证集. 训练集用于模型的训练, 验证集用于超参数的调整, 而测试集则被用于评估模型的性能表现.
模型使用TensorFlow框架, 在实验中采用5折交叉验证的方法来评估模型的性能表现, 使用零均值随机高斯分布初始化记忆矩阵和嵌入矩阵. 超参数设置如下, 最大训练次数500次, 使用Adam梯度下降算法优化模型的参数, 学习率为0.001. 训练的批次大小一般设置为64, 知识点表示和知识点掌握水平表示向量维度设置为
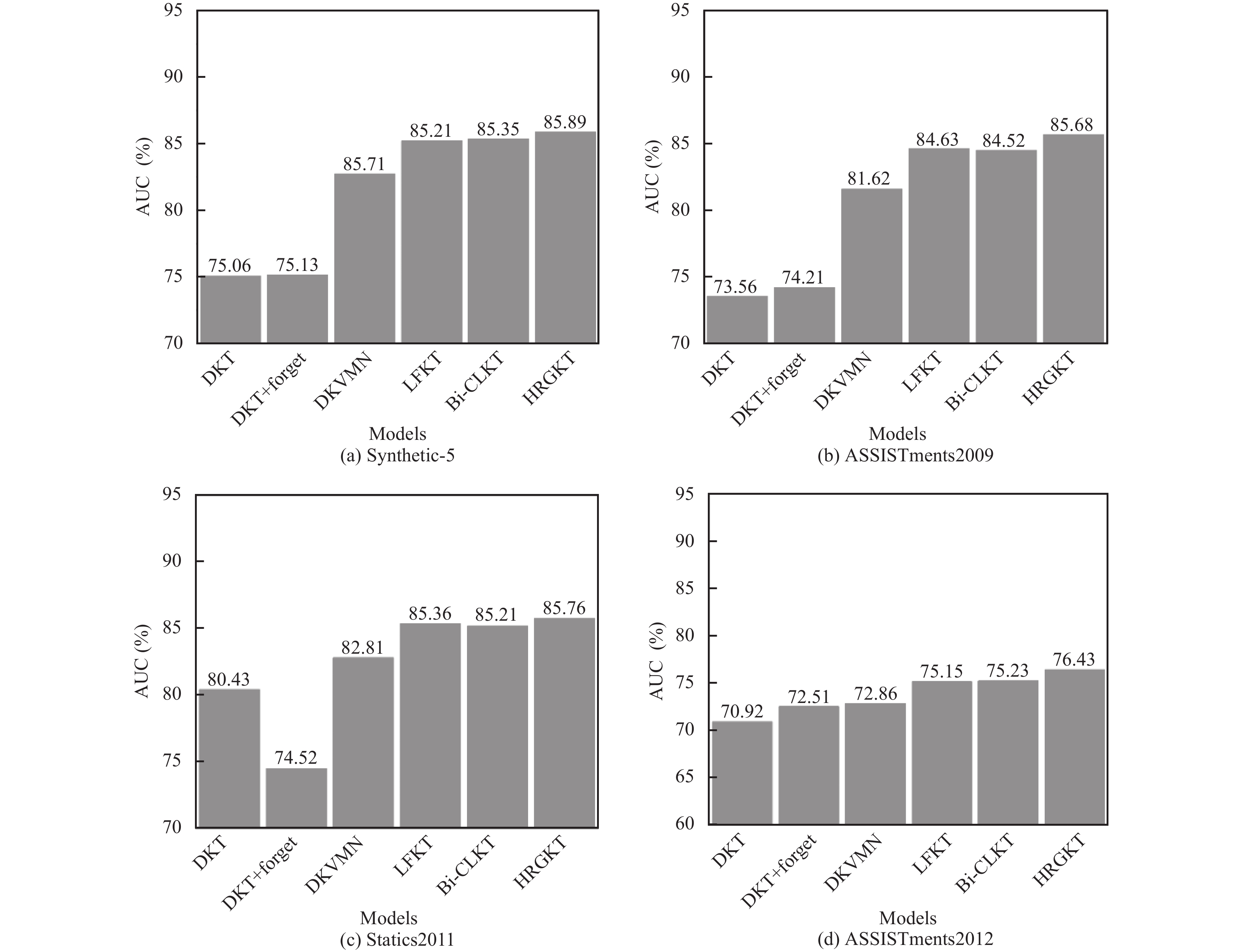
本节比较了5种模型在4个公开数据集上的AUC结果, 如表2、图6所示. 根据给出的表2、图6可以看到HRGKT在4个数据集上的AUC值均优于其他5种模型. 在4个数据集上分别实现AUC平均改善1.0%, 0.4%, 1.2%和0.5%.
| 表 2 不同数据集上AUC的比较 |
|
图 6 模型在不同数据集上的AUC对比 |
结果表明, HRGKT模型分别使用了HG模块的图结构特征以及遗忘特征, 在预测学生未来表现方面性能是优于现有模型的. 与DKT, DKT+forget, DKVMN, LFKT, Bi-CLKT相比, DKT两个特征都没有使用, DKT+forget, LFKT只使用遗忘特征, DKVMN仅使用记忆网络没有考虑其余特征, Bi-CLKT仅使用知识点图关系信息, 所以HRGKT在性能上有着更大的优势.
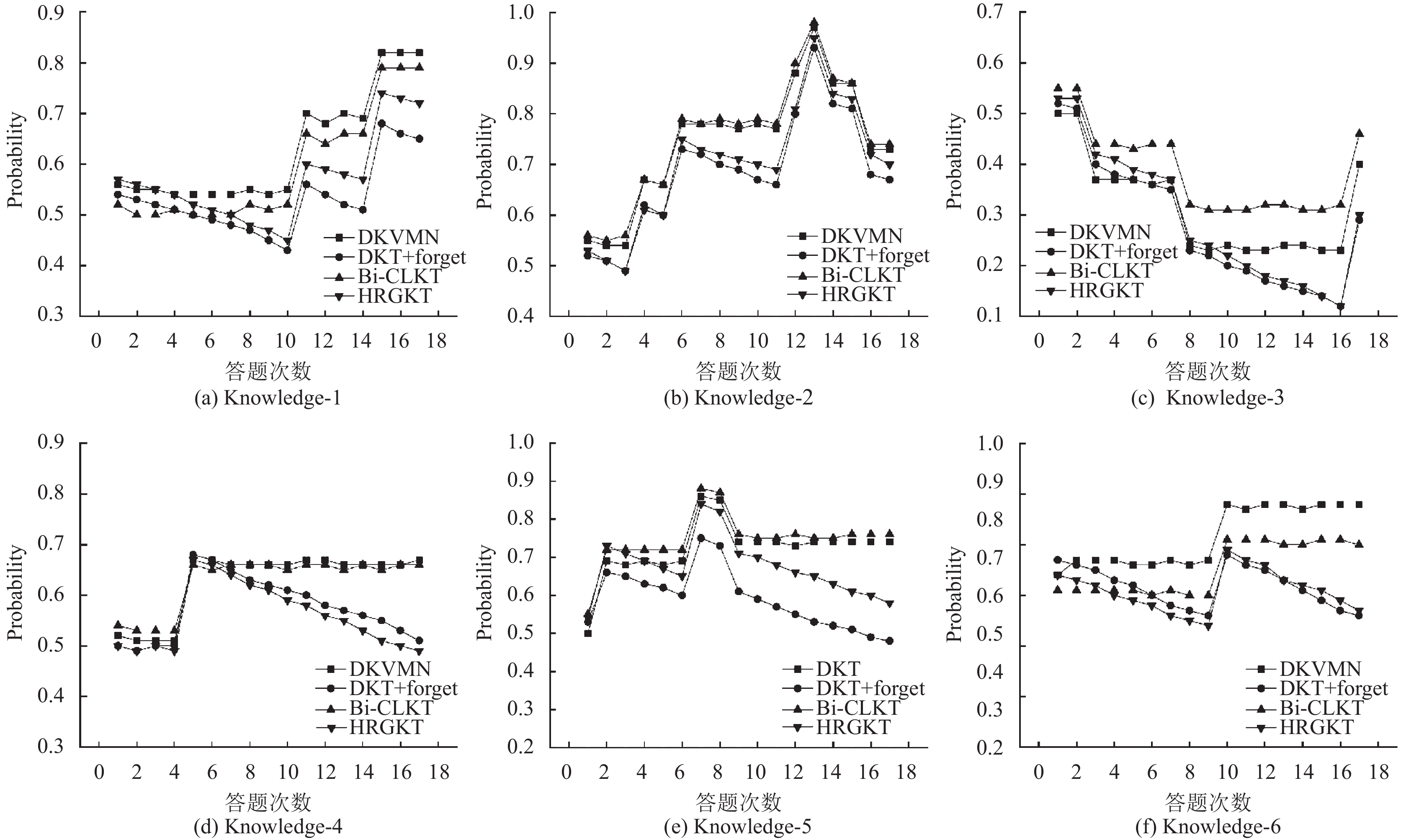
实验对单个学生的知识状态预测进行了可视化比较, 在数据集ASSISTments2012中随机抽取了1名学生作答的16道题目, 其中这16道题目包含6个知识点. 学生的作答序列为Hi={(5, 1), (3, 0), (2, 1), (4, 1), (2, 1), (5, 1), (3, 0), (5, 0), (6, 1), (1, 1), (2, 1), (2, 1), (2, 0), (1, 1), (2, 0), (3, 1)}. 为了方便处理将知识点id进行了重新编号, 作答序列中每一个元组第1项表示知识点id, 第2项表示作答结果. 由图7可知6个知识点状态变化, 其中横坐标代表学生的答题次数, 通过4种模型对学生知识点掌握程度进行追踪.
|
图 7 不同模型知识点状态输出结果图 |
可以从图7(b)中看出在t=3时刻学生正确回答题目后, 学生在下一时刻对该知识点的掌握程度有所提升. 在t=13时刻错误回答题目后, 在下一时刻该知识点的掌握程度会有明显的下降, 结果证明6种模型均可以模拟学生学习过程中的学习行为. 在图7(d)中学生在t=4时刻正确回答题目后, 在之后的时间里没有再对该知识点进行继续的学习. 从图7(d)中可以看出, 在后续的时间里, DKVMN和Bi-CLKT这些模型对于某个知识点的掌握状态预测有些微小波动, 但变化不大. 然而, 当使用DKT+forget和HRGKT这两种模型时, 学生对该知识点的掌握状态呈现持续下降的趋势, 并且变化比较大. 这个结果表明, HRGKT模型能够模拟学生学习过程中由于遗忘而导致的知识状态变化, 并跟踪这些变化过程.
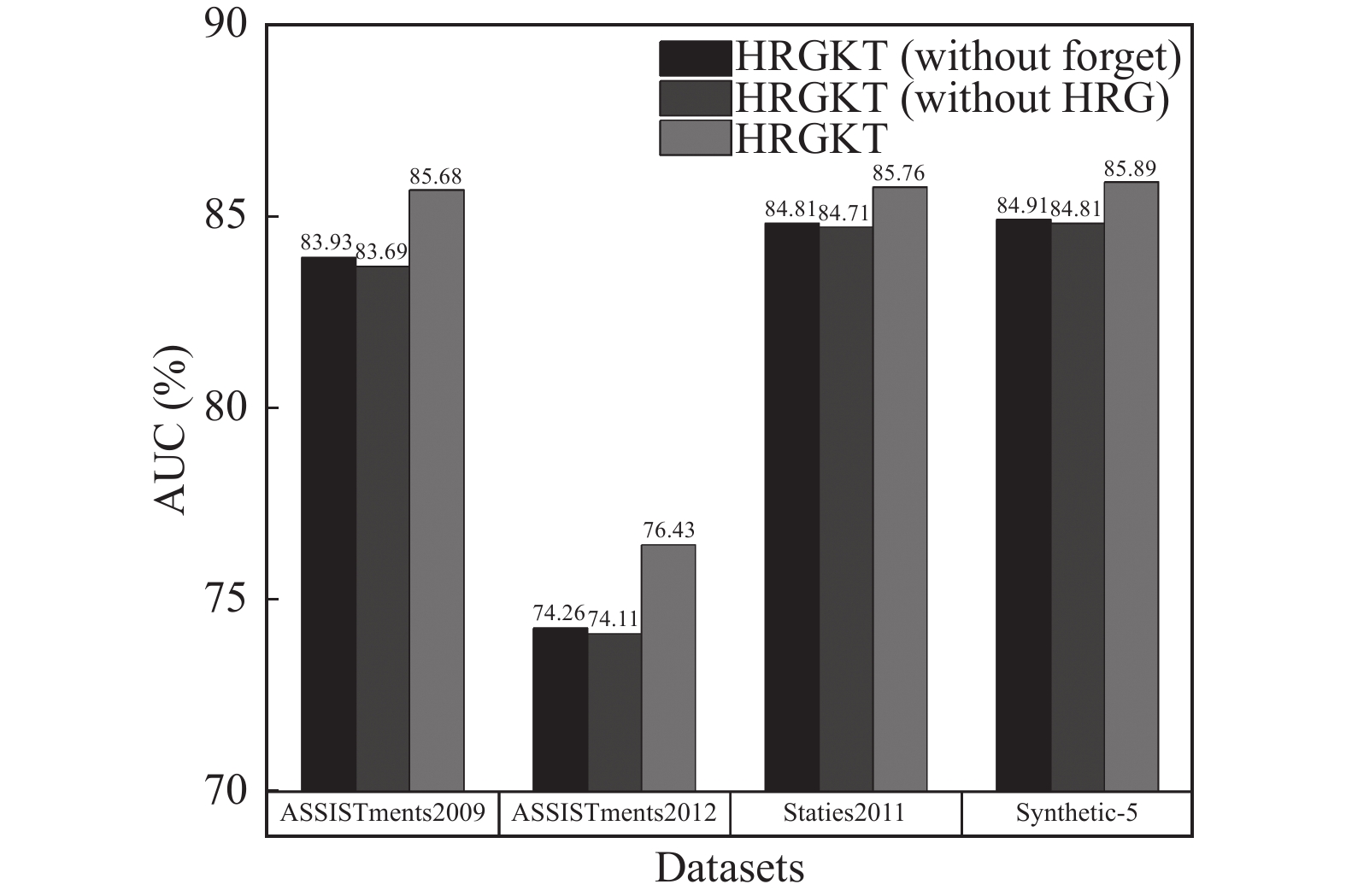
4.5 消融实验本节进行了消融实验来验证HRGKT中HG模块和遗忘模块的性能. 表3和图8分别表示不同HRGKT不同变体在4个数据集上AUC的值.
从表3以及图8中可以看出HRGKT (basic)的AUC是最低的, 这是因为该模型没有使用HG模块与遗忘模块, 不考虑题目知识点之间的信息以及学生的遗忘行为. HRGKT (without forget)忽略学生的遗忘行为, 其预测性能较HRGKT有所降低. 这表明影响遗忘的因素对准确追踪学生知识状态是有效的, 遗忘行为会对学生知识状态产生影响. HRGKT (without HRG)忽略知识点两者之间的关系信息, 模型的预测表现不如HRGKT模型, 并且有所下降. 结果说明HG模块捕获的题目知识点之间的关系信息能够有效提高模型的准确性.
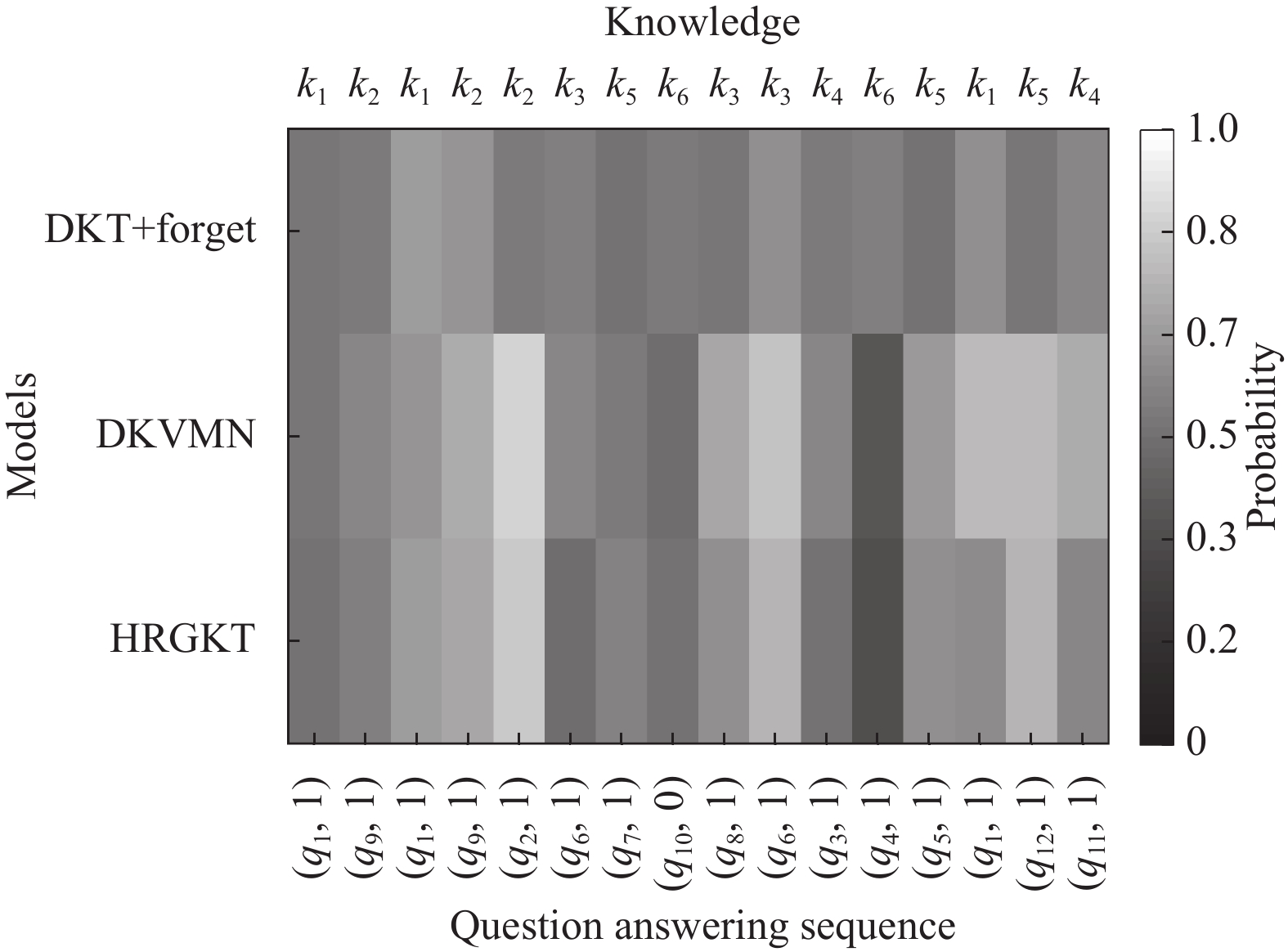
为了验证遗忘模块的有效性, 本文对DKT+forget, DKVMN和HRGKT模型对知识状态的预测进行对比. 如图9所示从ASSISTments2009随机抽取一名学生回答的12个题目, 其中涵盖6个知识点. 从图9中t=10时刻因为遗忘因素KLI=4和NRS=2, 所以DKT+forget对知识点k3预测结果较低. 与DKT+forget相比, 因为HRGKT能够捕获t=9时刻的q8和t=10时刻的q6有着相同的知识点, 所以遗忘因素KLI=1和NRS=3, k3的遗忘概率低于DKT+forget. 在t=13, t=15时刻DKT+forget对k5的预测概率较低, 这是因为q5和q12是第1次出现在答题序列中无法捕获两个题目之间含有相同知识点的关系. 另外在t=11时刻学习了k4知识点之后中间没有再学习k4知识点, 在t=16时刻HRGKT比DKVMN有着更低的预测概率, 这是因为DKVMN没有考虑遗忘因素. 因此可以证明遗忘模块在知识追踪中是十分有效的.
| 表 3 HRGKT变体在不同数据集上的AUC值 |
|
图 8 HRGKT变体在不同数据集上AUC的对比 |
|
图 9 不同模型知识状态对比结果图 |
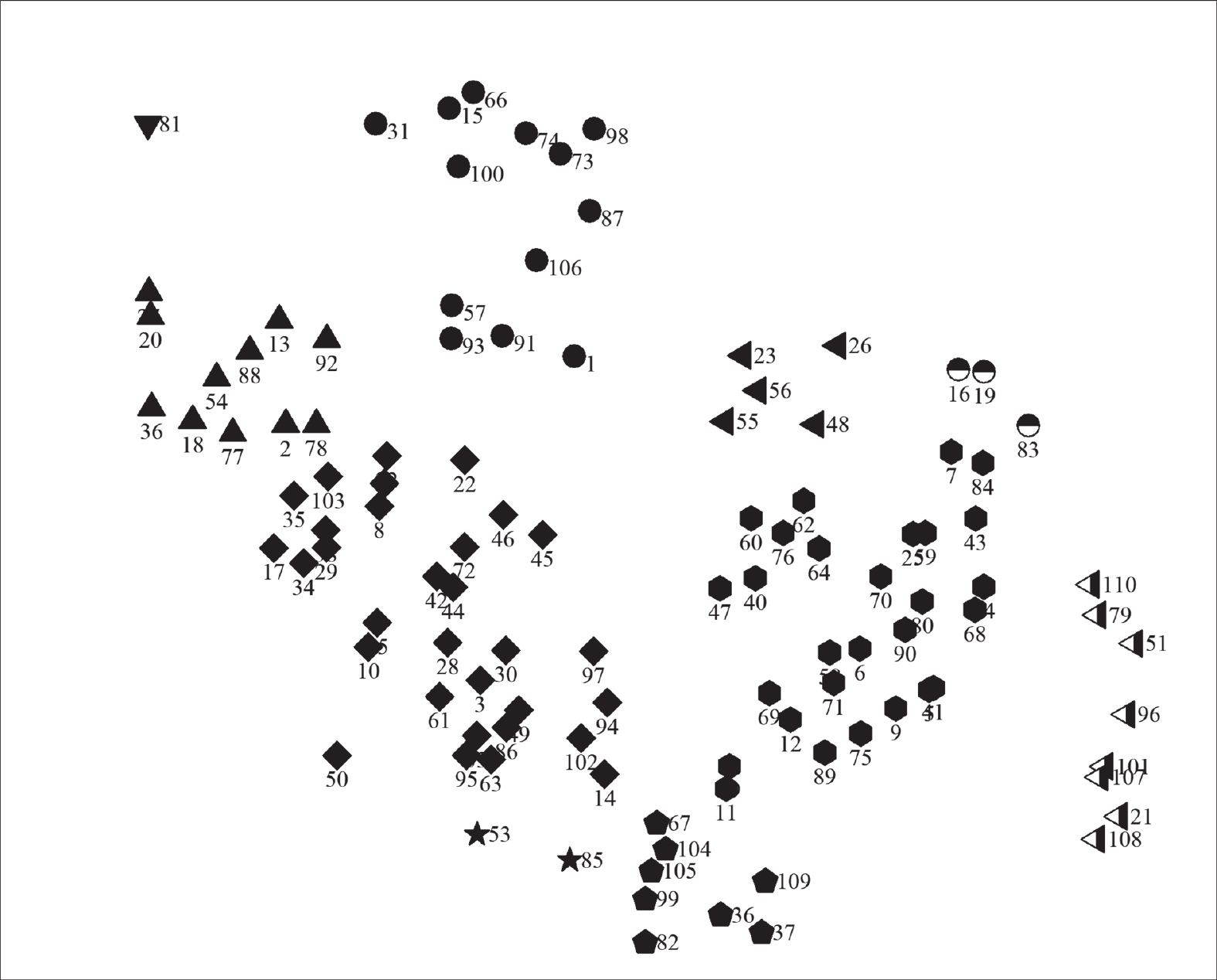
为了验证HG模块在知识追踪中的有效性, 对数据集中110个知识点进行聚类, 使用相同的图标表示相似的知识点, 为了方便表示将知识点重新编号结果如图10所示.
|
图 10 ASSISTments2009数据集聚类图 |
在图10中知识点被分为10个类别, 圆形的集群表示数学中与方程相关的知识点, 比如其中{15, 31, 66, 100}分别表示两步以上的方程解法、根据图表写出线性方程、根据情况写出线性方程、线性方程. 半色圆的集群{16, 19, 83}分别表示两个不同事件的概率、单一事件的概率、了解概率的概念, 通过描述可以知道该集群是对概率相关的知识点. 由此可见HG模块能够很好地对题目知识点进行分类, 能够较好地获取题目知识点以及两者之间的关系信息, 可以证明该模块在知识追踪中的有效性.
5 总结本文将知识点之间的关系信息用知识点关系图表示并且使用GAT提取两者的高阶关系信息. 另外还综合考虑了影响遗忘的4个因素, 提出了融合知识点关系的深度记忆网络知识追踪模型HRGKT. 在HRGKT中, 使用GAT对邻居信息进行聚合, 以得到知识点关系表示. 其次考虑学生学习过程中的遗忘行为更加准确地表示学生知识状态, 有效预测学生未来的答题表现. 最后通过实验可知, HRGKT模型在4个真实公开的数据集上证明了模型的有效性.
在未来的研究中将针对以下方面进行研究. 题目, 知识点和学生之间的关系往往非常复杂, 简单的同构图仅使用题目-知识点无法准确刻画这些异构关系, 如何将这些异构关系信息充分利用. 另外知识点之间存在先决关系等, 如何将这些关系融入模型也是未来研究工作的重点.
| [1] |
Injadat M, Moubayed A, Nassif B, et al. Systematic ensemble model selection approach for educational data mining. Knowledge-based Systems, 2020, 200: 105992. DOI:10.1016/j.knosys.2020.105992 |
| [2] |
Ingkavara T, Panjaburee P, Srisawasdi N, et al. The use of a personalized learning approach to implementing self-regulated online learning. Computers and Education: Artificial Intelligence, 2022, 3: 100086. DOI:10.1016/j.caeai.2022.100086 |
| [3] |
Piech C, Bassen J, Huang J, et al. Deep knowledge tracing. Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2015. 505–513.
|
| [4] |
Williams RJ, Zipser D. A learning algorithm for continually running fully recurrent neural networks. Neural Computation, 1989, 1(2): 270-280. DOI:10.1162/neco.1989.1.2.270 |
| [5] |
Gori M, Monfardini G, Scarselli F. A new model for learning in graph domains. Proceedings of the 2005 IEEE International Joint Conference on Neural Networks, 2005, Montreal: 729-734. |
| [6] |
Nakagawa H, Iwasawa Y, Matsuo Y. Graph-based knowledge tracing: Modeling student proficiency using graph neural network. Proceedings of the 2019 IEEE/WIC/ACM International Conference on Web Intelligence. Thessaloniki: IEEE, 2019. 156–163.
|
| [7] |
Song XY, Li JX, Tang YF, et al. JKT: A joint graph convolutional network based deep knowledge tracing. Information Sciences, 2021, 580: 510-523. DOI:10.1016/j.ins.2021.08.100 |
| [8] |
Song XY, Li JX, Lei Q, et al. Bi-CLKT: Bi-graph contrastive learning based knowledge tracing. Knowledge-based Systems, 2022, 241: 108274. DOI:10.1016/j.knosys.2022.108274 |
| [9] |
Eddy SR. Hidden Markov models. Current Opinion in Structural Biology, 1996, 6(3): 361-365. DOI:10.1016/S0959-440X(96)80056-X |
| [10] |
王宇, 朱梦霞, 杨尚辉, 等. 深度知识追踪模型综述和性能比较. 软件学报, 2023, 34(3): 1365-1395. DOI:10.13328/j.cnki.jos.006715 |
| [11] |
Corbett AT, Anderson JR. Knowledge tracing: Modeling the acquisition of procedural knowledge. User Modeling and User-adapted Interaction, 1994, 4(4): 253-278. |
| [12] |
Pardos ZA, Heffernan NT. KT-IDEM: Introducing item difficulty to the knowledge tracing model. Proceedings of the 19th International Conference on User Modeling, Adaptation, and Personalization. Girona: Springer, 2011. 243–254.
|
| [13] |
Yeung CK, Yeung DY. Addressing two problems in deep knowledge tracing via prediction-consistent regularization. Proceedings of the 5th Annual ACM Conference on Learning at Scale. London: ACM, 2018. 5.
|
| [14] |
Chen PH, Lu Y, Zheng VW, et al. Prerequisite-driven deep knowledge tracing. Proceedings of the 2018 IEEE International Conference on Data Mining (ICDM). Singapore: IEEE, 2018. 39–48.
|
| [15] |
Wang ZW, Feng XQ, Tang JL, et al. Deep knowledge tracing with side information. Proceedings of the 20th International Conference on Artificial Intelligence in Education. Chicago: IEEE, 2019. 303–308.
|
| [16] |
Su Y, Liu QW, Liu Q, et al. Exercise-enhanced sequential modeling for student performance prediction. Proceedings of the 32nd AAAI Conference on Artificial Intelligence. New Orleans: AAAI Press, 2018. 297.
|
| [17] |
Zhang JN, Shi XJ, King I, et al. Dynamic key-value memory networks for knowledge tracing. Proceedings of the 26th International Conference on World Wide Web. Perth: International World Wide Web Conferences Steering Committee, 2017. 765–774.
|
| [18] |
Ai FZ, Chen YS, Guo YC, et al. Concept-aware deep knowledge tracing and exercise recommendation in an online learning system. Proceedings of the 12th International Conference on Educational Data Mining. Montréal: International Educational Data Mining Society (IEDMS), 2019. 240–245.
|
| [19] |
Minn S, Yu Y, Desmarais MC, et al. Deep knowledge tracing and dynamic student classification for knowledge tracing. Proceedings of the 2018 IEEE International Conference on Data Mining (ICDM). Singapore: IEEE, 2018. 1182–1187.
|
| [20] |
Minn S, Desmarais MC, Zhu FD, et al. Dynamic student classiffication on memory networks for knowledge tracing. Proceedings of the 23rd Pacific-Asia Conference on Knowledge Discovery and Data Mining. Macao: Springer, 2019. 163–174.
|
| [21] |
琚生根, 康睿, 赵容梅, 等. 多知识点融合嵌入的深度知识追踪模型. 软件学报, 2023, 34(11): 5126-5142. DOI:10.13328/j.cnki.jos.006724 |
| [22] |
Zhang S, Tong HH, Xu JJ, et al. Graph convolutional networks: A comprehensive review. Computational Social Networks, 2019, 6(1): 11. DOI:10.1186/s40649-019-0069-y |
| [23] |
Abdelrahman G, Wang Q. Learning data teaching strategies via knowledge tracing. Knowledge-based Systems, 2023, 269: 110511. DOI:10.1016/j.knosys.2023.110511 |
| [24] |
Ebbinghaus H. Memory: A contribution to experimental psychology. Annals of Neurosciences, 2013, 20(4): 155-156. |
| [25] |
Murre JMJ, Dros J. Replication and analysis of Ebbinghaus’ forgetting curve. PLoS One, 2015, 10(7): e0120644. DOI:10.1371/journal.pone.0120644 |
| [26] |
李晓光, 魏思齐, 张昕, 等. LFKT: 学习与遗忘融合的深度知识追踪模型. 软件学报, 2021, 32(3): 818-830. DOI:10.13328/j.cnki.jos.006185 |
| [27] |
董永峰, 黄港, 薛婉若, 等. 融合IRT的图注意力深度知识追踪模型. 计算机科学, 2023, 50(3): 173-180. DOI:10.11896/jsjkx.211200134 |
| [28] |
Abdelrahman G, Wang Q. Deep graph memory networks for forgetting-robust knowledge tracing. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(8): 7844-7855. |
| [29] |
Nagatani K, Zhang Q, Sato M, et al. Augmenting knowledge tracing by considering forgetting behavior. Proceedings of the 2019 World Wide Web Conference. San Francisco: ACM, 2019. 3101–3107.
|
 2024, Vol. 33
2024, Vol. 33



