1 引言

近年来, 云计算技术发展迅猛^[1], 云存储作为云计算的重要服务之一, 为使用者提供了海量的存储空间, 却只需付出与配套硬件相比极小比重的代价^[2], 因此备受青睐^[3]. 当购买云存储服务后, 云存储服务器为用户提供存储空间, 同时使用者可凭借租赁凭证访问远程数据. 对于云平台而言, 可通过自定规则完成数据的整合与管理, 若使用者提供访问规则, 云平台也应满足. 以上内容是云存储服务可访问性与灵活性的体现. 同时, 在规则完善的前提下, 借助云平台可实现用户数据的共享, 当前的医疗数据共享大多借助云平台实现.

医疗数据是病人在医院或健康机构产生的各种数据, 包括诊疗、体检等数据, 病人可以从相应机构获取并下载至本地^[4]. 医疗数据共享, 指数据可被获得许可的其他人员查看. 比如外地医生等, 医疗数据共享使看诊医生快速地获取到病人的过往病历, 促进医疗数据共享便于实现诊疗快速化^[5]. 当数据持有者将自己的医疗数据上传至云端与他人共享时, 访问用户无需向医疗机构申请, 而是直接与数据持有者交互, 避免了经由医疗机构申请访问的繁琐流程, 实时性更强. 尽管借助云存储完成医疗数据共享具备数据获取快捷, 成本低等显著优势^[6], 但因用户丧失了外包数据的物理控制, 加之云服务提供商(cloud service provider, CSP)的不可信性, 远程数据的完整性与正确性无法确定. 例如, 因遭受自然灾害、黑客攻击等不可抗因素, CSP上存储的用户数据被迫丢失; 为节省存储空间, CSP主动丢弃一些不常访问的数据. 这些因素导致的数据丢失都违背了用户选择云存储服务的初衷, 会使用户对云存储服务丧失信心^[7], 因此, 有必要对云端数据定期执行完整性验证^[8–12].

数据共享意味着会有多人访问数据, 但访问数据的用户并非可以完全信任. 例如: 目前有许多医院推出了网上看诊平台, 由于平台的开放性, 会有大量的潜在用户访问平台提供的病例. 未获得访问权限的用户试图非法查看共享数据; 获得查看权限的用户不满足当前权限, 妄图修改数据. 由于医疗数据的特殊性, 需要约束访问医疗数据用户的行为. 另外, 群组的访问规则应当是灵活的, 如为新加入的用户明确访问权限, 为离组用户撤销访问权限. 因此除对云端共享数据的完整性验证问题展开讨论外, 共享数据的访问权限也应明确. 综上, 针对共享医疗数据的完整性验证问题, 需从数据校验与文件访问的安全性两个角度出发展开研究.

本文针对云存储共享医疗数据场景, 在保证医疗数据完整性的基础上, 解决群组用户访问共享数据的权限分配和管理问题, 贡献总结如下.

(1)为便于访问权限分配, 共享医疗数据持有者向申请用户分配授权标识符, 哈希函数的抗碰撞性保证授权标识符不会被伪造. 为便于访问权限管理, 引入可信实体群管理者. 群管理者无需本地保存用户权限信息便可验证群组用户的权限, 极大地节省了存储代价. 考虑到医疗共享数据的私密性, 委托群管理者定期检测群组用户的行为, 及时发现并剔除恶意用户, 增加系统安全性并降低群组开销.

(2)医疗数据在上传至CSP前会进行加密操作, 可保证第三方审计者在完整性验证阶段无法通过暴力破解的方式获取到任何信息, 保证了数据机密性. 安全性分析部分证明了本方案的正确性, 以及用户删除安全性. 实验分析证明了方案的可行性和高效性.

1.1 相关研究

数据完整性验证技术可对云端外包数据的正确性与完整性进行验证. 最初的完整性校验技术采用将云端文件全部下载至本地再执行验证的形式, 验证准确率最高但成本巨大. Ateniese等人^[13]在2007年提出了数据可持有性验证(provable data possession, PDP)方案, 用户不需在验证阶段将所有外包文件下载到本地, 只需随机抽样部分数据块执行校验即可, 极大地降低了通信开销, 同时以很高的概率保证数据的完整性. 随后, 为减轻用户验证的负担与计算代价并支持公开审计, 委托第三方审计员(third party auditor, TPA)代替用户进行完整性验证的方案被提出^{[6–9,12,14–19]}.

群组数据共享作为云存储的重要应用, 也被广泛讨论. Wang等人^[12]首先提出了支持保护群组用户隐私的公开完整性审计方案. Wang等人^[14]也提出验证者无法破解签名者身份的群组共享数据公开审计方案, 但随着群组用户数量的增加, 验证开销也随之增长, 不适合用户较多的情形. Shen等人^[2]针对共享多副本加密医疗数据, 设计了数据完整性验证方案.

考虑到群组用户可能是动态的, 一旦有用户撤销离组, 其参与签名的共享数据将无法被验证的问题, Wang等人^[15]采用代理重签名技术提出相应方案, 但在用户删除阶段只针对撤销用户对签名数据块产生的影响进行了讨论, 未考虑撤销用户与CSP合谋的情形. 基于保证前向安全性的群签名方案, 付安民等人^[16]假设群组中可能存在多个管理者, 构造了多管理者情形下支持用户撤销的完整性验证方案. 在该方案中, 多管理者需同时在本地保存所有加入过群组的成员信息, 诸如撤销用户信息, 并根据已撤销用户的撤销密钥计算出一个变量, 通过比较用户撤销密钥与该变量是否有公因数来判断用户是否已离组, 但此时若有未被撤销的用户的撤销密钥是任一已撤销用户撤销密钥的因数, 则会产生误判, 导致无辜用户被迫离组. Zhang等人^[17]的方案让每个群组用户都需要根据自己的私钥生成验证标签, 被撤销的群组用户将无法获取合法的私钥, 因此被撤销用户无法继续生成合法的验证标签. 并且在撤销用户后被撤销用户产生的验证标签, 只需更换未被撤销用户的密钥, 有效地降低了用户撤销的计算开销, 但未明确被撤销用户的管理措施, 且云端数据验证开销较大. He等人^[18]在实现云数据全动态的基础上支持群组中的用户撤销. Deng等人^[19]提出让群管理员和群组用户共同生成验证标签, 让审计者无法获取生成标签的用户身份, 引入用户信息表记录合法用户, 由于用户信息表为顺序表, 确定用户为合法用户的计算复杂度为${\mathrm{O}}(n)$, 开销较大. Li等人^[20]讨论在线共享文件的动态操作问题, 一旦某一用户被撤销, 便剥夺该用户编辑和更改文件的权力, 使共享文件不被恶意篡改, 并保护群组用户的隐私. Yang等人^[21]基于无证书密码体制, 构造了支持用户撤销的共享数据完整性验证方案. 上述方案针对群组被撤销用户无法继续对共享数据生成完整性验证标签, 以及撤销成本问题进行了研究, 但均未提出高效地区分正常群组用户和被撤销用户的措施, 也未实现用户访问授权.

因此, 在群组共享云医疗数据的场景下, 通过借鉴上述方案, 提出了支持群用户授权管理的共享数据完整性审计方案.

1.2 文章结构

本文第2节介绍基础知识. 第3节方案描述. 第4节详细介绍支持组用户授权管理的医疗数据完整性验证方案. 第5节分析所提方案的安全性. 第6节进行性能评估. 第7节全文总结.

2 基础知识 2.1 双线性映射

假设${G_1}, {G_2}$均为阶为$q$的乘法循环群, $g$是${G_1}$生成元, 双线性映射$e:{G_1} \times {G_1} \to {G_2}$满足以下性质.

(1) 双线性: 对任意$u, v \in {G_1}$和$\forall a, b \in Z_p^*$, 都有$ e({u^a}, {v^b}) = e{(u, v)^{ab}} $;

(2) 非退化性: $ e(g, g) \ne 1 $;

(3) 可计算性: 存在可以有效计算出$e$的方法.

2.2 离散对数问题

离散对数(discrete logarithm, DL)问题: 设$a \in Z_p^*$, 已知$g, {g^a} \in {G_1}$, 求$a$.

DL假设: 对于攻击者A, 在多项式时间内求解出离散对数问题的概率可忽略的, 表示为:

$ \Pr [A(g, {g^a}) = (a):a\xleftarrow{R}Z_p^*] \leqslant \varepsilon $

2.3 计算Diffie-Hellman问题

计算Diffie-Hellman (computational Diffie-Hellman, CDH)问题: 已知$g, {g^a}, {g^b} \in {G_1}$, 求${g^{ab}}$.

CDH假设: 对于攻击者A, 在多项式时间内求解出CDH问题的概率可忽略的, 表示为:

$ \Pr [A(g, {g^a}, {g^b}) = ({g^{ab}}):a, b\xleftarrow{R}Z_p^*] \leqslant \varepsilon $

3 方案描述 3.1 方案模型

图1为方案模型图, 共包含数据持有者(data owner, DO)、群管理者(group administrator, GA)、云存储提供者(cloud service provider, CSP)、群组用户(group member, GM)和第三方审计员(third party auditor, TPA)这5个实体, 具体描述如下.

(1) DO: 云存储医疗数据的拥有者. 职责有: 1)向用户发放注册密钥(register secret key, RSK)和授权标识符; 2)委托GA对群组用户进行管理; 3)委托GA保存完整性验证结果.

(2) GA: GA需要进行4项工作: 1)为群组用户分配访问密钥(access secret key, ASK); 2)记录并管理用户的身份信息; 3)委托TPA执行完整性验证, 并定期记录完整性验证结果; 4)定期监测群组用户访问文件的行为, 撤销恶意用户访问权限, 并更新撤销用户表.

(3) CSP: 云服务提供者, 不可信实体. 为DO提供数据存储服务, 在完整性验证阶段根据完整性质询内容提供完整性证据.

(4) GM: 拥有合法RSK的用户被视为群组用户, 从GA获取合法的访问密钥后访问云存储医疗数据. 群组用户如果出现下述恶意行为: 1)长时间不访问数据. 2)执行DO未授权的操作. 会被GA认定为恶意用户, 身份信息ID会记录至撤销用户表. 长时间不访问的用户可能是不需访问数据的用户, 或是可能与攻击者合谋的用户. 撤销掉这部分用户的权限有助于增加方案安全性, 同时可以减轻GA监测用户行为的负担.

(5) TPA: 第三方审计员, 可信实体. 执行远程云存储医疗数据的完整性校验工作.

3.2 算法介绍

方案包含6个算法: Setup、RSKeyGen、ASKeyGen、TagGen、ProofGen、ProofVerify, 简介如下.

Setup: 该算法由DO和GA在建立系统时执行. DO输入自己的身份信息$I{D_0}$得到并公开系统参数$pub$和主公钥mpk. GA秘密地选择自己的密钥${x_A} \in Z_p^*$.

RSKeyGen: 该算法由DO执行. 输入用户的$ID \in Z_p^*$, 输出$(ID, {U_{ID}}, {\omega _s}, {\textit{RSK}}{_{ID}})$. 其中${U_{ID}}$是用户的匿名身份; ${\omega _s} \in Z_p^*$为授权标识符; ${\textit{RSK}}{_{ID}}$为用户的注册密钥.

ASKeyGen: 该算法由GA执行. 输入群组用户的$(ID, {\omega _s}, {\textit{RSK}}{_{ID}})$, 输出$({\textit{ASK}}{_{ID}}, {\textit{SK}})$. 其中${\textit{ASK}}{_{ID}}$为群组用户的访问密钥; ${\textit{SK}}$为解密医疗数据的密钥.

TagGen: 该算法由DO执行. 输入公开参数pub和加密医疗数据$file = \{ {m_i}\} _{i = 1}^n, {m_i} \in Z_p^*$, 输出标签集$T = \{ {T_i}\} _{i = 1}^n$.

ProofGen: 该算法由CSP执行. 输入完整性质询chal, 输出完整性证据P.

ProofVerify: 该算法由TPA执行. 输入完整性质询chal、完整性证据P、公开参数pub, 如果验证通过输出1, 否则输出0.

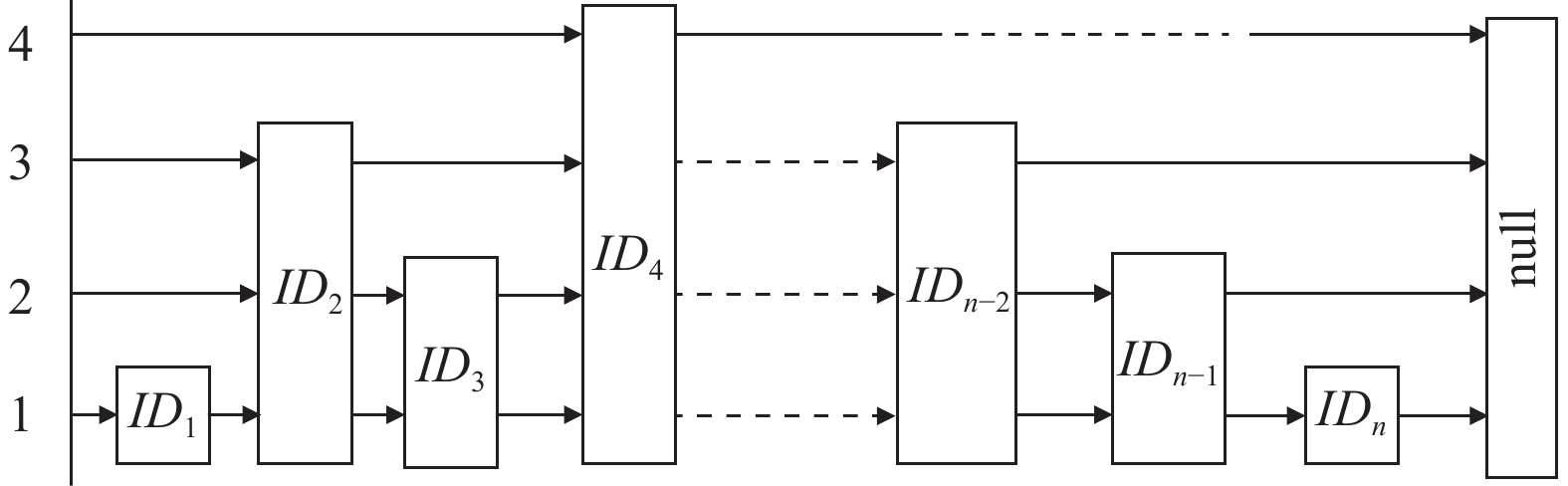
4 具体方案 4.1 撤销用户表

本方案添加由GA本地保存并维护的撤销用户表, 用来记录恶意用户. 因为方案中设定, GA会将有恶意行为的群组用户认定为恶意用户, 并将恶意用户的ID加入撤销用户表. 为保证GA不再给恶意用户分配ASK, 在给申请ASK的用户分配ASK前, GA需要先查找撤销用户表来确定用户是否属于恶意用户. 综上, 需要采用支持快速查找和插入操作的数据结构对撤销的用户进行记录. 因此撤销用户表选用跳表^[22]实现, 其结构如图2所示. 图中的方块代表撤销用户表中的一个节点, 节点中记录恶意用户的ID, 并按用户ID的数字大小从左到右排列.

引入该结构会增加GA的存储负担, 但是为了系统的安全性是必要的. 本方案中撤销用户的计算开销可以达到${\mathrm{O}}(\log n)$, 而文献[19]的方案计算复杂度为${\mathrm{O}}(n)$.

4.2 方案详细步骤

图3为方案流程图. 方案具体步骤描述如下.

(1)初始化阶段(Setup和TagGen算法)

1) DO: 执行Setup算法. 选择两个阶均为p的乘法循环群${G_1}, {G_2}$, g是${G_1}$的生成元. DO选定密码哈希函数$H:{\{ 0, 1\} ^*} \to {G_1}$, 双线性映射$e:{G_1} \times {G_1} \to {G_2}$. 选定随机值${\mu _1}, {\mu _2}, \cdots , {\mu _n}, {f_1}, {f_2}, \cdots , {f_n} \in {G_1}$. 挑选主密钥$msk = {x_0} \in Z_p^*$, 计算主公钥$mpk = {g^{{x_0}}}$. 保密存储主密钥msk, 公布主公钥mpk和公开参数$pub = ({G_1}, {G_2}, g, p, e, H, {\mu _1}, \cdots , {\mu _n}, {f_1}, \cdots , {f_n})$.

2) GA: 执行Setup算法. 选择随机数${x_A} \in Z_p^*$作为自己的密钥. 创建记录撤销用户ID的撤销用户表L, 初始设为空.

3) DO: 秘密选择文件加密密钥${\textit{SK}} \in Z_p^*$, 用对称加密算法加密医疗数据F, F加密后得到加密医疗数据file. 将file分块为$\{ {m_i}\} _{i = 1}^n$, 其中${m_i} \in Z_p^*$, 同时设置文件标识符$name \in Z_p^*$. 运行TagGen算法为每个数据块${m_i}$计算验证标签$ {T_i} = {g^{{x_0}}} \cdot H{(name||i)^{{m_i}}} $. 随后, 将加密密钥SK与GA通过安全信道共享, 再将加密医疗数据$file = \{ {m_i}\} _{i = 1}^n$和标签集$T = \{ {T_i}\} _{i = 1}^n$发送至CSP, 并删除本地数据.

(2)用户请求阶段(RSKeyGen和ASKeyGen算法)

1)方案设定DO能为用户分配两种权限: a) DO若正在看病, DO判定现在申请权限的用户为看病的医生, 则赋予该用户查看、修改的权限; b)不属于a)中的用户, 只会赋予查看的权限. 这样可以最大限度地减少用户对医疗数据的操作, 提高方案安全性. 用户发送自己的身份信息ID向DO申请注册密钥${\textit{RSK}}{_{ID}}$. DO收到用户申请后, 先判断是否为该用户分配访问权限, 若要分配则继续下一步, 否则拒绝用户请求.

2) DO: 运行RSKeyGen算法, 秘密选择随机数$a \in Z_p^*$, 计算并公开$\delta = {g^a}$. 为用户分配授权标识符${\omega _s} \in Z_p^*$, 当${\omega _s}$为全0比特串时, 代表用户拥有查看、修改医疗数据的权限; 当${\omega _s}$为全1比特串时, 代表此用户只有查看医疗数据的权限. 利用下式计算并发送用户相关信息, 并分别发送$(ID, {U_{ID}}, {\omega _s}, {\textit{RASK}}{_{ID}})$和$({U_{ID}}, {\omega _s}, {\textit{RSK}}{_{ID}})$至GA和用户:

$ \left\{\begin{split} &{U_{ID}} = H(name||ID) \\ &{\textit{RSK}}{_{ID}} = {g^{{x_0}}} \cdot {\left(\prod\nolimits_{i = 1}^n {{\mu _i}} \right)^a} \cdot H{(({U_{ID}}||name) \oplus {\omega _s})^{{x_0}}} \end{split} \right.$

3)用户收到${\textit{RSK}}{_{ID}}$后成为群组用户. 群组用户向GA发送$({U_{ID}}, {\omega _s}, {\textit{RSK}}{_{ID}})$申请访问密钥${\textit{ASK}}{_{ID}}$. GA查找撤销用户表L, 判断用户ID是否存在于L中. 若存在, 则证明该用户是被GA认定的恶意用户, 拒绝用户请求; 否则, 继续下一步骤.

4) GA: 通过式(1)验证用户提供的注册密钥是否有效:

$ \begin{split} e({\textit{RSK}}{_{ID}}, g)\mathop = \limits^? & e(mpk, g) \cdot e\left(\prod\nolimits_{i = 1}^n {{\mu _i}} , \delta \right) \\ & \cdot e(H(({U_{ID}}||name) \oplus {\omega _s}), mpk) \end{split} $

(1)

若验证未通过, 则要求用户重传$({U_{ID}}, {\omega _s}, {\textit{RSK}}{_{ID}})$. 验证通过则继续. 本次验证可以确保${\textit{RSK}}{_{ID}}$的合法性以及${\omega _s}$的正确性.

5) GA: 运行ASKeyGen算法, 设置时间参数${t_{ID}} \in Z_p^*$, 控制用户访问时间. 随机选择秘密随机数$b \in Z_p^*$, 计算并公开$\eta = {g^{b \cdot {x_A}}}({t_{ID}}, {\textit{ASK}}{_{ID}})$, 并利用下式为该用户产生访问密钥${\textit{ASK}}{_{ID}}$.

$ \begin{split} {\textit{ASK}}{_{ID}} =& {g^{{x_0}}} \cdot {\left({\prod\nolimits_{i = 1}^n \mu _i}\right)^a} \cdot H{(({U_{ID}}||name) \oplus {\omega _s})^{{x_0}}} \\ & \cdot H{\left({\left(\prod\nolimits_{i = 1}^n {{f_i}} \right)^b}\right)^{{x_A}}} \\ \end{split} $

6) GA本地保存, 并将${\textit{ASK}}{_{ID}}$与文件加密密钥SK返回给用户.

(3)数据访问阶段

群组用户可凭$({\omega _s}, {\textit{RSK}}{_{ID}}, {\textit{ASK}}{_{ID}}, {\textit{SK}})$访问CSP中的医疗数据. 群组用户必须在${t_{ID}}$失效前完成数据访问. 一旦时间参数${t_{ID}}$失效, 若仍需访问数据, 群组用户必须重新向GA申请访问密钥ASK, 此做法可极大确保群组用户合理且必要地访问和使用共享医疗数据, 保护医疗数据的隐私性, 另外强调重新授权ASK的过程无需DO参与.

同时, GA必须定期监测群组用户的行为. 群组用户在访问医疗数据过程中, 若出现下述行为: (1)长时间不访问数据. (2)执行DO未授权的操作. GA将出现上述行为的群组用户认定为恶意用户, 并执行下述操作.

1)令本次认定所有的恶意用户的时间参数${t_{ID}}$无效, 并将该用户的ID添加到L中.

2)重新选择随机数$b \in Z_p^*$, 更新$\eta = {g^{b \cdot {x_A}}}$.

由于时间参数${t_{ID}}$无效, 恶意用户将立即丧失文件的访问权, 并且因其ID被记录在撤销用户表L中, GA将不会再为其发放新的ASK.

(4)完整性验证阶段(ProofGen和ProofVerify算法)

DO将加密医疗数据上传至云后, GA需要定期委托TPA进行完整性验证.

1) TPA选择包含c个随机数的集合$R = \{ i\} , i \in Z$并且$1 \leqslant i \leqslant n$.

2) TPA针对每个$i \in R$, 选择随机数${v_i} \in Z_p^*$.

TPA发送完整性质询$chal = {\{ i, {v_i}\} _{i \in R}}$至CSP.

CSP收到完整性质询后执行ProofGen算法.

1) CSP计算$\lambda = \displaystyle\sum\nolimits_{(i, {v_i}) \in Q} {{v_i}} {m_i}$, $\sigma =\displaystyle \prod\nolimits_{(i, {v_i}) \in Q} {{T_i}^{{v_i}}} $.

2) CSP返回完整性证据$P = \{ \lambda , \sigma \} $给TPA.

TPA收到$P$后, 执行ProofVerify算法, 验证式(2), 如果等式成立, TPA向GA发送1表示通过验证; 如果等式不成立, TPA向GA发送0表示验证未通过. 其中$e(mpk, g)$可以提前计算.

$ \begin{split} & e(\sigma , g)\mathop =\limits^? e{(mpk, g)^{\sum\nolimits_{(i, {v_i}) \in Q} {{v_i}} }} \cdot e\left(\prod\nolimits_{(i, {v_i}) \in Q} {H(name||i), g} \right)^\lambda \end{split} $

(2)

5 安全性分析

定理1 (正确性). 本方案满足以下正确性:

(1) RSK正确性: 可以通过式(1)验证${\textit{RSK}}{_{ID}}$的正确性.

(2) 权限分配正确性: 只有提供正确的授权标识符${\omega _s}$, ${\textit{RSK}}{_{ID}}$才能通过GA的验证.

(3) 完整性验证正确性: 可以通过式(2)验证完整性证据P的正确性.

证明: (1)根据双线性映射的性质, ${\textit{RSK}}{_{ID}}$的验证公式推导如下:

$ \begin{split} & e({\textit{RSK}}{_{ID}}, g) \\ & = e({g^{{x_0}}} \cdot {\left(\prod\nolimits_{i = 1}^n {{\mu _i}} \right)^a} \cdot H{(({U_{ID}}||name) \oplus {\omega _s})^{{x_0}}}, g) \\ & = e({g^{{x_0}}}, g) \cdot e\left({\left(\prod\nolimits_{i = 1}^n {{\mu _i}} \right)^a}, g\right) \cdot e(H{(({U_{ID}}||name) \oplus {\omega _s})^{{x_0}}}, g) \\ & = e({g^{{x_0}}}, g) \cdot e{\left(\prod\nolimits_{i = 1}^n {{\mu _i}} , g\right)^a} \cdot e{(H(({U_{ID}}||name) \oplus {\omega _s}), g)^{{x_0}}} \\ & = e({g^{{x_0}}}, g) \cdot e\left(\prod\nolimits_{i = 1}^n {{\mu _i}} , {g^a}\right) \cdot e(H(({U_{ID}}||name) \oplus {\omega _s}), {g^{{x_0}}}) \\ & = e(mpk, g) \cdot e\left(\prod\nolimits_{i = 1}^n {{\mu _i}} , \delta \right) \cdot e(H(({U_{ID}}||name) \oplus {\omega _s}), mpk) \end{split} $

在用户请求阶段, 只有${\textit{RSK}}{_{ID}}$通过了GA验证, 用户才能申请到访问密钥${\textit{ASK}}{_{ID}}$. 否则, GA会拒绝并通知用户重传${\textit{RSK}}{_{ID}}$.

(2)只有用户给GA提供了正确的${\omega _s}$, 用户的RSK才能通过GA的验证. 由式(1)可知, 若${\omega _s}$被更改, 则式(1)右边哈希函数的输出会改变, 使得式(1)不成立, 因此用户无法通过伪造${\omega _s}$改变自己的权限. 同时群管理员不需为完成验证用户权限而保存多余的用户信息.

(3)在完整性验证阶段, TPA验证完整性证据的等式推导如下:

$ \begin{split} & e(\sigma , g) \\ & = e\left(\prod\nolimits_{(i, {v_i}) \in Q} {{T_i}^{{v_i}}} , g\right) \\ & = e\left(\prod\nolimits_{(i, {v_i}) \in Q} {{{({g^{{x_0}}} \cdot H{{(name||i)}^{{m_i}}})}^{{v_i}}}} , g\right) \\ & = e\left(\prod\nolimits_{(i, {v_i}) \in Q} {{g^{{x_0}}}^{ \cdot {v_i}}} , g\right) \cdot e\left(\prod\nolimits_{(i, {v_i}) \in Q} {H{{(name||i)}^{{m_i}}}^{ \cdot {v_i}}} , g\right) \\ & = e{({g^{{x_0}}}, g)^{\sum\nolimits_{(i, {v_i}) \in Q} {{v_i}} }} \cdot e{\left(\prod\nolimits_{(i, {v_i}) \in Q} {H(name||i)} , g\right)^{\sum\nolimits_{(i, {v_i}) \in Q} {{m_i} \cdot {v_i}} }} \\ & = e{(mpk, g)^{\sum\nolimits_{(i, {v_i}) \in Q} {{v_i}} }} \cdot e{\left(\prod\nolimits_{(i, {v_i}) \in Q} {H(name||i)} , g\right)^\lambda } \end{split} $

定理2 (用户撤销安全性). 在本方案中, 非群组用户和被撤销的恶意用户都无法访问DO的医疗数据.

证明: 用户若想要访问医疗数据, 首先需要执行用户请求阶段的操作. 用户先向DO发送自己的身份信息ID获取注册密钥${\textit{RSK}}{_{ID}}$, 用户获得${\textit{RSK}}{_{ID}}$后成为群组用户. 之后群组用户需从GA申请访问密钥${\textit{ASK}}{_{ID}}$和时间参数${t_{ID}}$.

用户需凭$({\omega _s}, {\textit{RSK}}{_{ID}}, {\textit{ASK}}{_{ID}}, {\textit{SK}})$向GA申请访问医疗数据, GA先确定时间参数${t_{ID}}$的有效性, 只有当${t_{ID}}$有效时GA才会继续验证用户${\textit{RSK}}{_{ID}}$和${\textit{ASK}}{_{ID}}$的正确性. GA检查用户${\textit{RSK}}{_{ID}}$的正确性来确定该用户拥有DO生成的${\textit{RSK}}{_{ID}}$, 该步骤是为了确定该用户是经过DO授权的群组用户. 之后GA检查群组用户${\textit{ASK}}{_{ID}}$的正确性, 只有能通过${\textit{ASK}}{_{ID}}$正确性验证的用户才是合法群组用户, 该步骤是为了保证该群组用户不是恶意用户. 只有通过了上述验证, 用户才能访问医疗数据. 否则, GA会拒绝该用户的访问请求.

若该用户是非群组用户(没有有效的${t_{ID}}$, 合法的${\textit{RSK}}{_{ID}}$和${\textit{ASK}}{_{ID}}$, 或是恶意用户(没有有效的${t_{ID}}$和合法的${\textit{ASK}}{_{ID}}$), 则均无法通过上段所述GA的验证. 因此无法访问DO的医疗数据.

定理3 (完整性验证安全性). 只有CSP拥有完整的医疗数据, 才能生成可通过TPA验证的完整性证据.

证明: 我们提出了一系列游戏并借助随机喻言模型证明. 若CSP未完整保存DO的数据, 但提供了可以通过TPA验证的完整性证据, 那么我们可以通过知识提取器与CSP的交互提取出所有被挑战的数据块.

游戏0:

(1)挑战者C运行Setup算法, 得到公共参数pub、主密钥msk和主公钥mpk, 并将pub、mpk发送给攻击者A.

(2)攻击者A选取一系列数据块m₁, …, m_n, 发送给挑战者C询问这些数据快对应的验证标签T₁,…, T_n.

(3)挑战者C随机发送完整性质询chal给攻击者A, 攻击者A返回完整性证据P. 如果这个证据通过了验证者的验证, 则攻击者A胜利.

游戏1: 以游戏0为基础, 挑战者C会保存在游戏0步骤(2)中被挑战的验证标签. 如果攻击者A提供了在游戏0步骤(2)中没有挑战过的数据块的验证标签, 挑战者C终止游戏并宣布攻击者A胜利.

分析: 假设$P = \{ \lambda , \sigma \} $是一个由诚实的CSP提供的可以通过完整性验证的完整性证据, 根据完整性验证正确性, 有式(3)成立.

$ \begin{split} e(\sigma , g) =& e{(mpk, g)^{\sum\nolimits_{(i, {v_i}) \in Q} {{v_i}} }} \cdot e{\left(\prod\nolimits_{(i, {v_i}) \in Q} {H(name||i), g} \right)^\lambda } \end{split} $

(3)

若攻击者A提供了不同于P的证据$ P' = \{ \lambda ', \sigma '\} $通过了验证, 则式(4)成立:

$ \begin{split} e(\sigma ', g) = e{(mpk, g)^{\sum\nolimits_{(i, {v_i}) \in Q} {{v_i}} }} \cdot e{\left(\prod\nolimits_{(i, {v_i}) \in Q} {H(name||i), g} \right)^{\lambda '}} \end{split} $

(4)

显然$\lambda ' \ne \lambda $, 否则$\sigma ' = \sigma $, 与游戏2矛盾. 因此定义$\Delta \lambda = \lambda ' - \lambda \ne 0$, 如果在游戏1中挑战者C会以不可忽略的概率终止游戏, 那么可以构造出能求解CDH问题的模拟器. 给定$g, {g^a}, h \in {G_1}$, 模拟器的目标是输出${h^a}$. 因为${G_1}$是乘法循环群且g是${G_1}$生成元, 所以一定有$x \in Z_p^*$, 使得${g^x} = h$. 随机选择$b \in Z_p^*$, 令$ {g^{ax}}{h^b} = \prod\nolimits_{(i, {v_i}) \in Q} {H(name||i)} $. 式(4)除以式(3)得:

$ \begin{split} e(\sigma '/\sigma , g) &= e{\left(\prod\nolimits_{(i, {v_i}) \in Q} {H(name||i)} , g\right)^{\lambda ' - \lambda }} \\ & = e{({g^{ax}}{h^b}, g)^{\Delta \lambda }} \end{split} $

可得$\sigma '/\sigma = {({g^{ax}}{h^b})^{\Delta \lambda }}$, 所以有${h^a} = {g^{ax}} = {(\sigma '/\sigma )^{\frac{1}{{\Delta \lambda }}}} \cdot {h^{\frac{1}{b}}}$.

综上, CDH问题无解的概率和$b = 0$的概率相同. $b = 0$的概率是$1/p$, $p$是大素数, 所以这个概率是可忽略的. 如果攻击者A赢得游戏0和游戏1的概率有不可忽略的差距, 那么可以构造出能以不可忽略的概率解决CDH问题的模拟器, 这与我们的假设是矛盾的.

游戏2: 在游戏1的基础上, 挑战者C会保存一个用来记录所有攻击者A查询过的数据块的列表. 如果在第(3)步, 攻击者A提供了包含未询问过的数据块的$\lambda $, 挑战者C会终止游戏, 并宣布攻击者A成功.

分析: 从游戏1的分析得$\sigma ' = \sigma $, 因此定义$\Delta \lambda = \lambda ' - \lambda $.

给定$g, h \in {G_1}$, 构造的模拟器的目标是计算出满足$h = {g^a}$的$a$, 模拟器随机选择$b \in Z_p^*$, 设置${g^x}{h^b} = \prod\nolimits_{(i, {v_i} \in \mathbb{Q})} {H(name||i)} $.

由式(3)和式(4)可得:

$ \begin{gathered} e{(mpk, g)^{\sum\nolimits_{(i, {v_i}) \in Q} {{v_i}} }} \cdot e{\left(\prod\nolimits_{(i, {v_i}) \in Q} {H(name||i), g} \right)^\lambda } = e(\sigma ', g) \\ = e(\sigma , g) = e{(mpk, g)^{\sum\nolimits_{(i, {v_i}) \in Q} {{v_i}} }} \cdot e{\left(\prod\nolimits_{(i, {v_i}) \in Q} {H(name||i), g} \right)^{\lambda '}} \\ \end{gathered} $

有$\prod\nolimits_{(i, {v_i}) \in Q} {H{{(name||i)}^\lambda }} = \prod\nolimits_{(i, {v_i}) \in Q} {H{{(name||i)}^{\lambda '}}} $, 之后$1 = (\prod\nolimits_{(i, {v_i}) \in Q} {H(name||i){)^{\Delta \lambda }}} = {({g^x}{h^b})^{\Delta \lambda }}$. 因为$\Delta \lambda \ne 0\;(\text{mod} q)$, 否则有$\lambda = \lambda '\;(\text{mod} q)$, 因此可得$h = {g^{ - x/b}}$, 则DL问题的结果为$ - x/b$.

因为b有$1/q$的概率是0, q是大素数, 因此$1/q$是可以忽略的, DL问题有解的概率为$1 - 1/q$. 这与DL假设相矛盾. 这代表如果攻击者A取得游戏2和游戏3成功的概率有不可忽略的差距, 则可以构造出能够解决DL问题的模拟器. 综上可得, 可以忽略上述游戏之间的差异.

最后, 我们构造一个知识提取器, 通过选择固定的c个数据块${m_i}$, 并为每个数据块选择不同的系数${v_i}$. 知识提取器对这c个数据块${m_i}$向诚实的CSP发起挑战, 每挑战一次重新选择数据块系数, 共挑战c次, 通过合法的证据中的$\lambda $, 最后能够得到c个相互独立的关于c个数据块${m_i}$的线性方程组, 如式(5):

$ \left\{ {\begin{array}{*{20}{c}} {{\lambda _1} = {v_{11}}{m_1} + {v_{12}}{m_2} + \cdots + {v_{1c}}{m_c}} \\ {{\lambda _2} = {v_{21}}{m_1} + {v_{22}}{m_2} + \cdots + {v_{2c}}{m_c}} \\ \vdots \\ {{\lambda _c} = {v_{c1}}{m_1} + {v_{c2}}{m_2} + \cdots + {v_{cc}}{m_c}} \end{array}} \right. $

(5)

通过求解线性方程组, 知识提取器可以获取c个数据块${m_i}$. 这代表只要CSP通过TPA的完整性验证, CSP一定完好无损地存储了DO的医疗数据.

定理4. 即使TPA参与完整性证据的验证, 也无法知悉用户医疗数据的内容.

证明: TPA收到CSP返回的完整性证据是$P = \{ \lambda , \sigma \} $, 因为$\lambda = \sum\nolimits_{(i, {v_i}) \in Q} {{v_i}} {m_i}$中${m_i}$是医疗数据数据块的密文形式. 因此, 如果TPA出于好奇想要获取数据, 对相同的c个数据块发出c次不同的挑战, 那么TPA可以得到${\lambda _j} = \displaystyle\sum\nolimits_{(i, {v_i}) \in Q} {{v_{ji}}} {m_i}, 1 \leqslant j \leqslant c$, 即如式(5)所示线性方程组.

但在本方案中, 求解上述线性方程组的结果是加密后的医疗数据. 因为TPA没有解密密钥SK, 所以TPA无法通过上述操作获取DO的医疗数据.

6 性能评估 6.1 性能分析

$Mul$表示执行一次乘法运算的时间, $Exp$表示执行一次模幂运算的时间, $Hash$表示执行一次哈希运算的时间, $Add$表示执行一次加法运算的时间, $Pair$表示计算一次双线性映射的时间, $|p|$和$|q|$分别代表${G_1}$和$Z_q^*$中单个元素的大小, $|id|$表示数据块索引的大小.

表1中列出了本方案与文献[17]和文献[19]在不同阶段的计算开销. 在标签生成阶段, 由于本文方案生成标签的模幂运算较少, 因此对应的计算开销少于文献[17]. 文献[19]中由于标签生成需要GM和群组用户共同完成, 需要更复杂的计算. 在完整性验证阶段, 本方案与文献[17]证据生成的计算过程基本相同, 文献[19]需在本方案基础上计算更多参数, 因此计算开销更大. 在证据验证阶段, 本文比文献[17]和文献[19]的计算开销都小. 用户撤销阶段, 以撤销一个用户的计算开销为例. 本方案执行用户撤销操作后, 受到影响的群组用户只需向GA申请就可以得到更新的访问密钥${\textit{ASK}}{_{ID}}$. 文献[19]不需更改密钥, 由GM在本地更新用户信息表即可. 而文献[17]中未被撤销用户凭借服务器发送的信息, 执行一次加法操作后才可以获得新密钥.

表2中列出本方案与文献[17]和文献[19]在不同阶段的通信开销. 在标签生成阶段, 本方案和文献[17]的通信开销均为$n|p| + n|q|$比特, 而文献[19]中标签由群管理员与群组用户共同生成. 在完整性验证阶段, 通信开销包括完整性质询chal和收到的完整性证据P, 3个方案中chal的大小均为$c|p| + c|id|$比特, 本方案和文献[17]中P的大小均为$|p| + |q|$比特, 文献[19]则需要传输更多数据. 在用户撤销阶段, 本方案中需要更新${\textit{ASK}}{_{ID}}$的用户只需向GA发送请求, 即可得到新的${\textit{ASK}}{_{ID}}$, ${\textit{ASK}}{_{ID}}$大小为$|p|$比特; 而文献[17]用户发送申请后, 收到管理者发送的信息大小为$|p| + |q|$比特. 文献[19]撤销群组用户后, 正常群组用户无须更新任何信息, 而是需要GM更新在本地保存的用户信息表.

6.2 实验结果

仿真实验对方案的可行性进行了评估, PC硬件配置Intel Core i5处理器, 8 GB内存. 实验使用Java语言, 调用JPBC库, 设置${G_1}$中元素大小为512比特, $Z_q^*$中元素大小为160比特. 仿真实验假定共享医疗数据大小为20 MB, 共由1 000 000个数据块组成, 每个阶段实验均执行多次取平均值.

(1)标签生成阶段

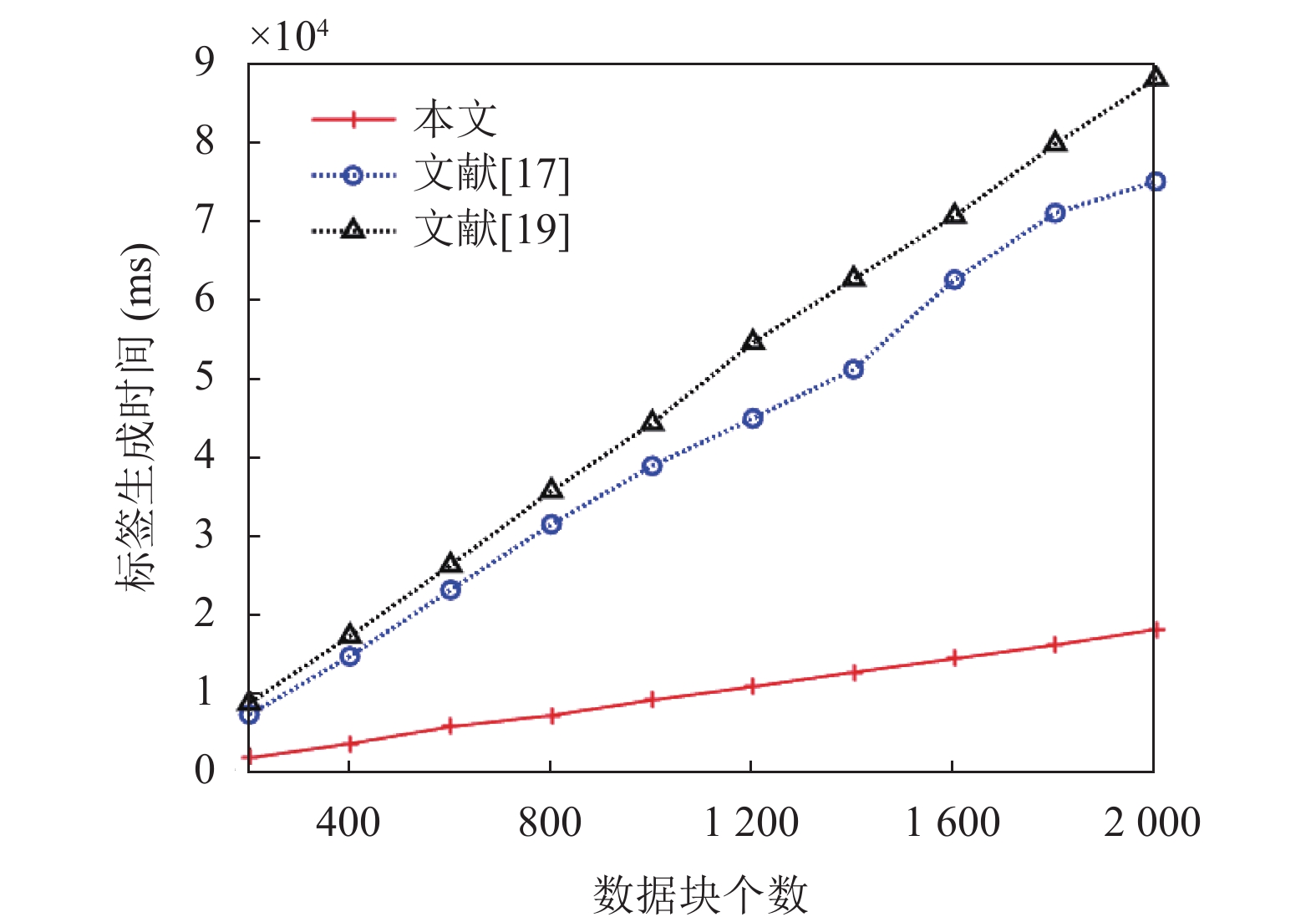
为评估标签生成阶段的性能, 以200为间隔, 计算TagGen算法的性能, 每个实验分别运行20次后取平均值, 与文献[17]和文献[19]做对比, 对比结果如图4所示. 本方案的开销比其他方案都更小.

(2)密钥生成

图5中给出系统产生RSK和ASK的计算开销, 以10为间隔, 用户数从10增长到100, 每次实验执行20次取平均值.

(3)完整性验证阶段

完整性验证阶段包括证据生成和证据验证两部分. 实验中以100为间隔, 挑战从0到1 000个数据块, 每次执行20次取平均值.

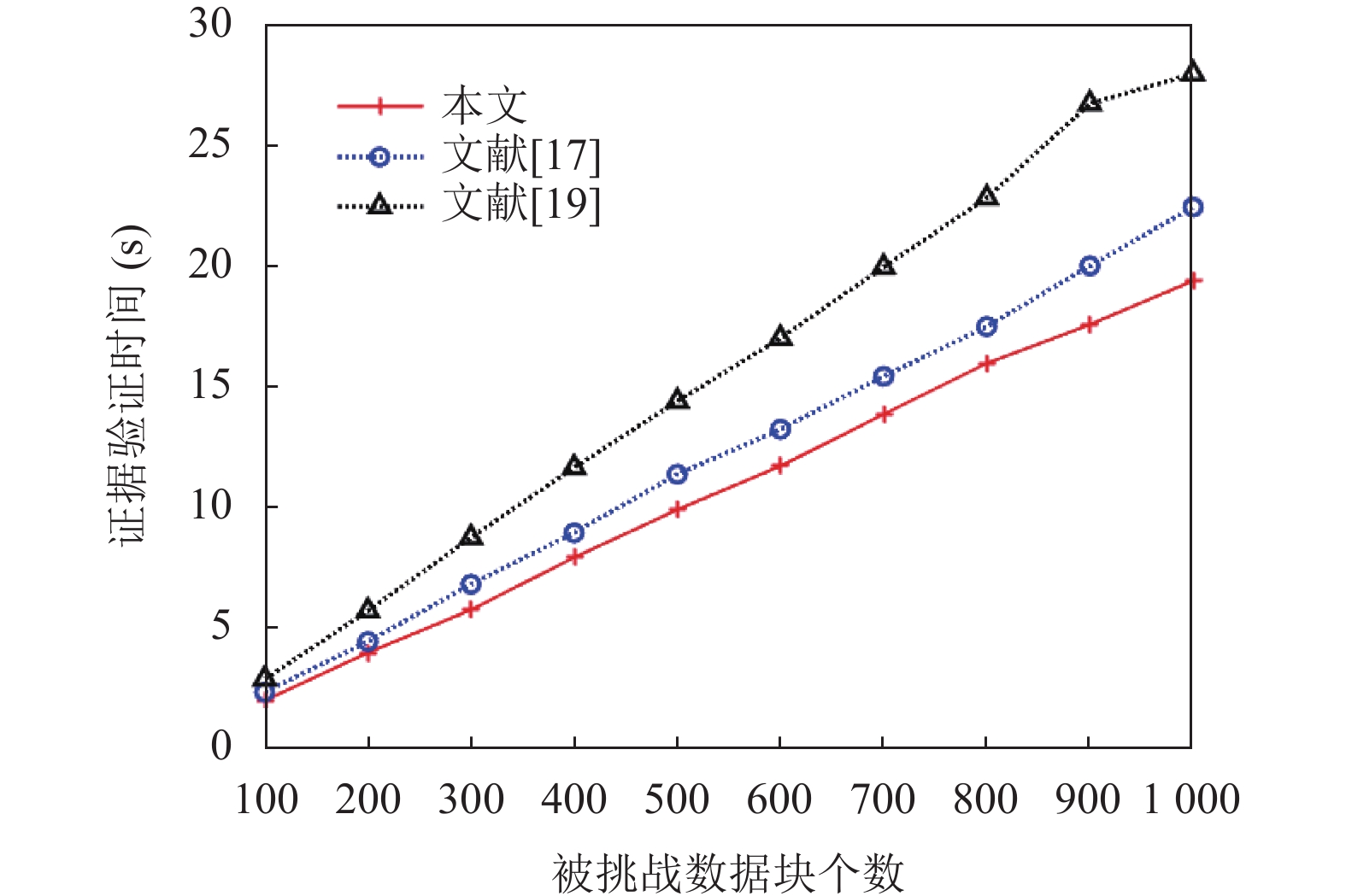
图6为证据生成的计算开销对比, 本方案和文献[17]证据生成计算开销接近, 而文献[19]需要更大计算量. 图7为本文方案与文献[17]方案证据验证的计算开销对比, 可以看出本方案的计算开销较小.

7 结束语

通过云存储服务共享医疗数据, 可以实现诊疗快速化, 但云医疗数据脱离了用户的完全控制, 可能由于各种原因造成损坏, 并且群组用户访问共享数据时也可能越权操作. 因此, 为同时保证云共享医疗数据的完整性和规范访问数据群组用户的行为, 在共享云存储医疗数据的场景下, 提出了同时支持用户访问权限分配和高效撤销恶意用户的数据完整性验证方案. 最后的安全性分析和仿真实验, 分别证明本方案具有较好的安全性和高效性.