2. 中国科学技术大学 数学科学学院, 合肥230026;
3. 中国科学院 吴文俊数学重点实验室, 合肥 230026;
4. 合肥国家实验室, 合肥230088
2. School of Mathematical Sciences, University of Science and Technology of China, Hefei 230026, China;
3. Wu Wen-tsun Key Laboratory of Mathematics, Chinese Academy of Sciences, Hefei 230026, China;
4. Hefei National Laboratory, Hefei 230088, China
聚类算法[1,2]根据数据之间的相似性对数据进行分组, 主要目的是最大化属于同一簇的数据之间的相似性和属于不同簇的数据之间的不相似性. 在现实生活中, 聚类是数据挖掘[3]、图像处理[4,5]、社交网络[6]、生物信息学[7]等领域的一个活跃的研究课题, 还在医学等方面具有重要的作用[8]. 针对不同的应用, 已经提出了各种聚类算法, 如基于层次、划分、模型、网格和密度的算法, 文献[9,10]对各种聚类算法进行了详细描述.
国内外也有很多基于图的聚类算法被提出. 例如文献[11,12]通过构造 k最近邻图, 也有算法[13,14]利用最小生成树(MST)进行聚类. Zahn [13]提出的基于最小生成树的聚类算法将不一致边定义为那些权重明显大于子树中邻近边的平均权重的边.
针对不同的应用场景, 已经提出了广泛的聚类算法. 然而, 由于问题的多样性和数据分布的复杂性, 这些算法并不总是令人完全满意. 基于划分的聚类算法是最基本的聚类方法, 其中K-means算法[15]是划分聚类算法中的经典代表. 该算法简单易用, 倾向于将数据聚类成球形, 但对于具有任意形状的簇来说显然不足够. 尽管如此, 识别具有任意形状的簇在聚类算法的应用中仍然是一项非常重要的任务. 最小生成树聚类算法不受簇边界的几何变化影响, 因此簇边界的形状对算法性能的影响很小, 这使我们能够克服经典聚类算法通常面临的问题. 基于密度的聚类算法一直是聚类算法研究的重点. DPC算法[16]是一种非常有影响力的聚类算法, 尽管在各种数据上表现良好, 但它不能正确处理不同部分密度不同的数据集. 尽管许多聚类算法已经被提出许多年, 但对能够处理上述问题的新的聚类算法的需求仍在继续. 为了克服这些问题, 本文对DPC算法和MST算法进行了改进和扩展, 提出了能够在密度不均匀、形状复杂的数据集上表现优异的聚类算法DPMST.
对国内外研究现状进行分析, 发现大部分聚类算法在处理具有复杂流形分布的数据集方面存在问题, 而在实际应用中, 复杂流形分布是普遍存在的一种结构, 因此复杂流形数据集的聚类分析具有重要的实际意义. 最小生成树聚类算法可以识别复杂的流形簇, 但功能较弱; 密度峰值聚类 (DPC) 算法功能强大, 但对流形结构的适用性较低.
本文针对最小生成树聚类算法和 DPC 算法存在的问题进行研究, 将密度峰与最小生成树聚类算法相结合, 用标签传播提高聚类质量, 提出了基于局部密度峰和标签传播的最小生成树聚类算法(DPMST). 该算法主要在以下3个方面做了改进: 一是利用DPC 算法思想的优点来寻找局部密度峰. 局部密度峰是具有局部最大密度的点, 它保留了原始数据集的分布结构,有助于在局部密度峰上有效构建最小生成树, 减少噪声点的影响, 从而提高算法性能; 二是采用基于共享邻的距离权值, 利用局部密度峰之间的邻域信息, 以更合适的方式表示它们之间的距离, 更有效地识别无效边; 三是引入标签传播机制, 提高聚类结果的质量.
1 相关工作我们提出的算法是在最小生成树聚类算法和DPC算法的基础上改进的, 先介绍两种算法, 再进行研究分析.
1.1 最小生成树聚类算法基于最小生成树的聚类算法流程: 首先构造数据集的无圈加权图, 再创建最小生成树, 计算所有边的均值与方差, 不断去除不一致的边, 直到满足某些终止条件, 则算法结束, 得到一组连通子图即为聚类结果.
最近几年, 在基于MST的聚类算法中, Zhou等提出AMST算法[17], 通过使用新的有效性指标来定义任意形状的簇. 在他们的工作中, 有效性指标被用来确定最佳的簇数量并评估最终的簇. 类似的, Halim等使用新的内部有效性指标[18], 用于改进生成的簇. Saar等提出的算法[19]的目标是克服去除不一致的边和处理异常值这两个问题, 他们的主要贡献是使用一种被称为临界距离的方法来定义最优簇. Zhong等[20]结合了K-means算法和MST算法, 首先利用K-means算法将数据集划分为k个分区, 然后用最小生成树来构建簇.
理想状态是簇间分离良好, 不一致的边就是最长的边, 但是事实上噪声点的出现使得去掉最长边未必能得到正确的聚类结果. 因此, 在最小生成树聚类中如何有效构建最小生成树、有效识别无效边和降低噪声点的干扰是研究中面临的主要问题.
1.2 密度峰值聚类算法密度峰值聚类(DPC)算法要画出关于局部密度和相对距离的决策图, 找出局部密度和相对距离都较大的数据点, 从而很容易得到簇中心.
DPC算法至提出后一直流行, 近年来, 许多学者都在努力改进DPC. Li等提出的KS-FDPC算法[21]采用了分区合并策略, 通过将数据划分为多个子簇, 可以降低高密度点对后续分配点的影响范围. Zhao等提出DPC-FWSN算法[22]将k最近邻与模糊邻域相结合, 得到一个最近邻模糊核函数以此重新定义局部密度. DPC-PPNNN算法[23]通过引入自然最近邻域和概率传播的思想, 实现了非参数聚类过程.
DPC算法在许多数据集上表现出色, 具有显著的优点. 然而, 该算法也存在一些局限性. 首先, 其聚类过程相对简单, 主要是通过最近距离原则将每个点分配到相应的簇中心所在的簇, 这使得它在处理复杂数据结构时可能不适用. 其次, DPC算法仅适用于每个簇都有密度峰且各簇之间密度差异较小的简单数据集. 当数据集具有流形结构时, DPC算法的适用性会大大降低.
我们尝试利用DPC算法的优点和最小生成树聚类算法来设计一种新的聚类算法. 尽管DPC算法在全局聚类上可能不够可靠, 但它能够在局部数据子集中实现高纯度聚类. 因此, 本文将使用局部密度峰来改进最小生成树聚类算法.
1.3 分析最小生成树聚类算法可以识别形状不规则的簇, 问题在于如何有效构建最小生成树、识别无效边和降低噪声点干扰.
密度峰值聚类算法原理简单, 功能强大, 但对复杂数据结构的适用性较低.
我们结合两种算法的优点, 针对上述问题, 做出以下改进.
一是利用 DPC 算法思想的优点来寻找局部密度峰. DPC 算法可以在局部数据子集中实现高纯度. 局部密度峰包含了一定的局部信息, 保留了原始数据集的分布结构. 我们提出用家族树来捕获数据中的潜在结构, 这有助于反映数据中最近邻之间的密度优势. 通过将数据集划分为多个家族树, 可以更好地获得复杂的数据结构. 每个家族树都包含一个局部密度峰, 在此基础上可以有效构造最小生成树, 从而减少噪声点干扰, 提高算法性能.
二是采用基于共享邻的距离权值. 基于共享邻的距离权值充分利用邻域信息, 能够缩小在密集区域的局部密度峰间的距离, 扩大由稀疏区域连接的局部密度峰间的距离, 从而更准确地表示局部密度峰间的距离. 当使用基于共享邻的距离构造最小生成树时, 以一种更合适的方式表示了局部密度峰之间的距离, 更有效地识别无效边.
三是标签传播. 标签传播通过转移矩阵将簇主干的强标签传播到其余点, 并根据得到的标签矩阵重新分配标签. 标签传播可以增强强标签, 削弱弱标签, 以细化错误的标签, 这种改进策略可以提高聚类结果的质量.
2 改进的算法本节将详细介绍我们提出的算法, 即基于局部密度峰和标签传播的最小生成树聚类算法(DPMST).
我们将介绍一些重要的概念, 再基于这些概念描述基于局部密度峰和标签传播的最小生成树聚类算法(DPMST)的详细流程, 该算法包括3个阶段: 识别局部密度峰, 构造最小生成树, 以及标签传播.
2.1 识别局部密度峰局部密度峰是在局部密度最大的数据点, 识别它要先计算局部密度, 再构造家族树(family tree), 数据集将被划分为多个家族树, 每个家族树都有一个根节点(root), 即局部密度峰.
局部密度的计算通过下面几个定义说明.
定义1 (k最近邻). k最近邻是距离数据点最近的k个邻居的集合. 给定数据点
定义2 (相互最近邻MNN). 若数据点p属于数据点q的k最近邻并且数据点q属于数据点p的k最近邻, 那它们互为相互最近邻(mutual nearest neighbor):
| MNN(p)={q|p∈NNk(q)且q∈NNk(p)} | (1) |
定义3 (局部密度函数). 给定数据点
| ρ(xi)=|MNN(xi)| | (2) |
通过局部密度, 再构造家族树. 家族树的定义如下.
定义4 (家族树). 构造家族树的思想是在k个最近邻的意义上找到每个数据点的父节点
| P(xi)={argminxj∈higher(xi)distij,ifhigher(xi)≠∅none,otherwise | (3) |
| higher(xi)={xj|xj∈NNk(xi),ρ(xj)>ρ(xi)} | (4) |
其中, dist是一个
数据集构造家族树的思想是在k个最近邻的意义上找到每个数据点的父节点, 并将没有父节点的数据点识别为树的根节点(root), 即局部密度峰. 数据集将被划分为多个家族树, 每个家族树都有一个局部密度峰, 在局部密度峰上构造最小生成树, 降低了噪声点的干扰, 提高了算法的性能.
2.2 构造最小生成树局部密度峰在数据集上并非均匀分布, 这是由数据集的分布情况决定的. 因此, 使用欧氏距离来衡量局部密度峰之间的距离是不合适的. 我们采用基于共享邻的距离[24,25]权值(SW)来度量局部密度峰间的距离. 首先需要介绍一些与局部密度峰相关的概念.
定义5 (局部密度峰的成员MLDP). 局部密度峰, 也就是家族树的根节点(root)可以代表所在的家族树上的数据点, MLDP是局部密度峰所在家族树上的数据点的集合. 对于局部密度峰p, 它的成员是被p代表的数据点:
| MLDP(p)={a∈X∣root(a)=p} | (5) |
定义6 (局部密度峰的邻域NLDP). 对于一个局部密度峰h, 它的邻域是h所有成员的k 最近邻的并集:
| NLDP(h)=⋃a∈MLDP(h)NNk(a) | (6) |
定义7 (局部密度峰之间的共享邻SLDP). 两个局部密度峰p和q的共享邻是它们邻域的交集:
| SLDP(p,q)=NLDP(p)∩NLDP(q) | (7) |
基于共享邻的距离权值的定义如下.
定义8 (基于共享邻的距离权值SW). 对于局部密度峰p和q, 它们的基于共享邻的距离权值计算为:
| SW(p,q)={d(p,q)|SLDP(p,q)|×∑o∈SLDP(p,q)ρ(o),if |SLDP(p,q)|≠0maxd×(1+d(p,q)),otherwise | (8) |
其中, d(p, q) 是局部密度峰 p和q之间的欧氏距离, maxd为所有局部密度峰之间欧氏距离的最大值.
基于共享邻的距离权值SW的定义可以看出, 在密集区域紧密相连的局部密度峰的SLDP集合中会有许多数据点, 局部密度之和也很大, 所以分母很大, 能够缩短由密集区域紧密相连的局部密度峰间的距离; 在稀疏区域, 分隔的局部密度峰的SLDP集合中会有很少的数据点, 局部密度之和也很小, 所以分母很小, 能够放大被稀疏区域分隔的局部密度峰间的距离.
利用局部密度峰之间的邻域信息, 能够以一种更合适的方式表示了局部密度峰间的距离. 从下面的例子中可以清楚地看出这一点.
从图1中可以看出, 点 P与点H的距离较近, 但并不在同一个簇中, 点 H与点O距离较远, 但在同一簇中. 在数据经过归一化处理之后, 计算欧氏距离和基于共享邻的距离权值SW.

|
图 1 示例 |
从表1可以直观地看出, 点 P与点H的距离被放大了, 点H与点O的距离被缩小了. 在欧氏距离中, 点H与点O距离大约是点 P与点H距离的两倍, 而在SW距离中, 点H与点O距离大约是点 P与点H距离的二分之一. SW距离可以缩短由密集区域紧密相连的局部密度峰间的距离, 放大被稀疏区域分隔的局部密度峰间的距离, 以一种更合适的方式表示了局部密度峰间的距离, 用这个距离权值能更有效地构造最小生成树, 识别无效边.
| 表 1 距离对比 |
通过Prim算法用SW距离权值来构造最小生成树. 然后, 反复删除权值最大边, 每删除一次, 簇的数目增加一个(若目标簇数c, 需要删除c–1条边), 得到给定数目的簇. 举例如图2, 假设目标簇数为3, 该最小生成树需要删除2条边, 按权值需要删除BC边和CF边, 删除后可以看出BE在同一簇, AC在同一簇, DF在同一簇, 这样就分成了3个簇.
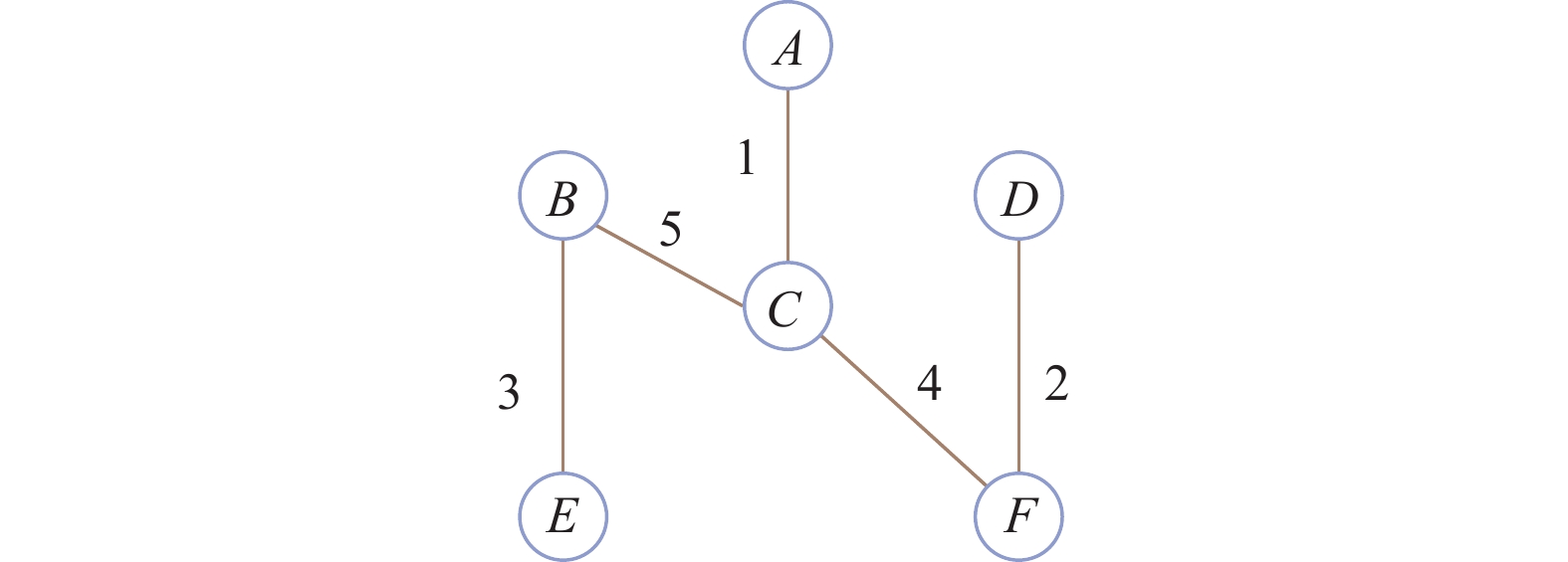
|
图 2 最小生成树例子 |
数据点根据所在的簇分配相应的标签, 所有的数据点都有一个标签. 每个局部密度峰和其邻居被定义为一个簇的主干部分, 主干的标签是强标签, 确定之后保持不变, 某些位于边界和重叠区域的数据的标签是弱标签, 之后可能会再变动标签.
2.3 标签传播这一步的目的是使用强标签的簇主干为某些弱标签的数据点重新分配标签. 标签传播这一步要先把局部密度峰的确定性标签分配给其邻居, 每个局部密度峰和其邻居被定义为一个簇的主干部分, 主干的标签是强标签, 确定之后保持不变, 然后簇主干部分的标签通过转移矩阵传播到其余点, 根据得到的标签矩阵为某些位于边界和重叠区域的数据重新分配标签. 标签传播增强强标签, 削弱弱标签, 以细化错误的标签, 提高聚类质量. 具体流程如下.
首先, 计算转移矩阵, 我们定义了一个加权图G=(V, E, W), 其中顶点V对应数据集X, 权值为:
| Wi,j=exp(d(xi,xj)2σ2i,j) | (9) |
其中,
上述的权值是使用一个全连通的图来定义的. 一般来说, 全连通图并不继承数据点的自然结构, 使用全连通图也会增加计算的复杂度. 因此, 一个更好的方法是连接一个基于k最近邻的图, 其中每个节点只连接到它的邻居, 节省计算成本.
基于k最近邻的权值:
| W(NNk)i,j={Wi,j,if xj∈NNk(xi)0,otherwise | (10) |
然后通过对权值进行归一化, 也就是权值除以行和, 定义一个转移矩阵:
| Pi,j=W(NNk)i,j∑h∈VW(NNk)i,h | (11) |
将数据分为有标记点和未标记点. 已标记的数据点指的是定义为簇主干的数据点, 也就是局部密度峰和其邻居, 其余的数据点被认为是未标记的. 请注意, 每个数据点都与一个标签相关联. 初始标签矩阵定义为:
| Y0=[Y(l);Y(u)]∈Rn×c | (12) |
其中,
在每次迭代中, 未标记的点更新其标签如下:
| Yt+1=Ft∗Yt | (13) |
| F0=P, Ft+1={P,if t=0P(Ft+YtYTt)PT,if t>0 | (14) |
直到标签矩阵不再发生变化, 迭代停止. 在每次迭代中, 那些初始标记的数据点可能会被分配不同的标签. 因此, 它们的标签需要重置如下:
| Y(l)t+1=Y(l)0 | (15) |
通过上述过程, 簇主干部分的强标签通过转移矩阵传播到其余点, 我们根据最终得到的标签矩阵为某些弱标签的数据点重新分配新标签, 得到最终的聚类结果.
大多数标签分配是单步操作的, 因此如果某个数据点被错误地分配了标签, 由于缺乏细化策略, 这个错误会传播到其他节点. 为了解决这个问题, 我们提出通过迭代过程更新标签. 数据点的标签根据标签传播后的标签矩阵进行更新, 给某些位于边界和重叠区域的数据重新分配真标签. 这种策略将数据的局部结构与标签空间相关性相结合, 特别是对边界点以及流形区域, 可以提高聚类结果的质量.
以上就是基于局部密度峰和标签传播的最小生成树聚类算法的整个流程.
基于局部密度峰和标签传播的最小生成树聚类(DPMST)的具体步骤如算法 1 所示.
算法1. 基于局部密度峰和标签传播的最小生成树聚类
输入: 数据集
输出: 聚类标签
for each
Calculate MNN(
Calculate
end for
root←
for each
Compute
If
root←root
end for
root 即局部密度峰
for each 局部密度峰 p do
Compute MLDP(p) (见定义5)
Compute NLDP(p) (见定义6)
end for
for each pair of 局部密度峰 p and q do
Compute SLDP(p, q) (见定义7)
Compute SW(p, q) (见定义8)
end for
edge←构造最小生成树(局部密度峰, SW)
k=1
while k<c do
Cut the longest edge
k=k+1
end while
Assign labels according to the cluster in which they are located
Assign the label of cluster centers to their nearest neighbors to form cluster backbones
Compute transition matrix P (见式(11))
for 迭代次数t=1 to T do
Compute label matrix
end for
Reassign new labels to certain data points according to the resulting label matrix
2.4 DPMST算法分析DPMST算法第1步识别局部密度峰: 计算局部密度, 为数据集构造家族树, 在 k 个最近邻的意义上找到每个数据点的父节点, 并将没有父节点的数据点识别为树的根节点(root), 即局部密度峰. 局部密度峰包含了一定的局部信息, 保留了原始数据集的分布结构. 用家族树来捕获数据中的潜在结构, 可以反映数据中最近邻之间的密度优势. 数据集被划分为多个家族树, 有助于获得复杂的数据结构. 一个数据集将被划分为多个家族树, 每个家族树都有一个局部密度峰, 在局部密度峰上能有效构造最小生成树, 降低噪声点的干扰, 提高算法的性能.
DPMST 算法第 2 步构造最小生成树: 计算局部密度峰之间 SW 距离权值, 使用 SW 距离权值来构造最小生成树, 反复删除最长边, 直到找到给定数量的簇, 根据所在的簇分配标签. 使用基于共享邻的距离构造最小生成树, 能够更有效地识别无效边.
DPMST 算法第 3 步标签传播: 把局部密度峰的确定性标签分配给其邻居, 即簇的主干部分, 计算转移矩阵, 然后簇主干部分的强标签通过转移矩阵传播到其余点, 数据点的标签根据标签传播后的标签矩阵进行更新. 这种策略可以提高聚类结果的质量.
3 实验在本节中, 我们将详细介绍并分析实验结果, 以证明基于局部密度峰和标签传播的最小生成树聚类算法 (DPMST)的有效性.
3.1 实验指标和设置我们选择了7种经典的聚类算法与DPMST算法比较, 包括 DPC[16]、MST[26]、K-means[15]、DBSCAN[27]、AP[28]、谱聚类(SC)[29]和 BIRCH[30]. 为了更客观地反映各种算法的实际结果, 我们进行参数调优, 从而确保比较的是它们的最佳性能.
为验证我们的DPMST算法在各种数据集上的有效性, 我们选取了3种评价指标, 评价指标均保留4位小数. 本文采用了调整兰德指数(ARI)、标准化互信息(NMI)和 Fowlkes-Mallows 指数(FMI)对聚类算法的有效性进行评估, 3种评价指标的满分为1, 指标值与聚类效果成正比.
3.2 实验结果在本节中, 我们选取几个广泛应用于检验聚类算法性能的人工数据集进行分析. 这些数据集具有点、簇分布与数目上的差异, 能够对比各种聚类算法在不同场景的效果. 我们选择的人工和真实数据集的情况如表2所示.
真实和人工数据集源于UCI network data repository和GitHub中. 真实数据集大多来源于生物和医学领域.
8个人工数据集上的聚类评价指标得分在表3显示, 得分最高的评价指标用粗体标记, 可以看到, 在大多数情况下, 我们的算法DPMST获得的得分最高.
8个人工数据集都是便于可视化的 2维数据, 因此本文对8个人工数据集都以图表的形式展示了聚类结果, 绘制图所使用软件是PyCharm.
| 表 2 实验数据集 |
如图3所示, spiral 是一个具有 3 个簇且低密度的数据集, 数据点构成了彼此交叉缠绕的螺旋形曲线.可以看到我们的算法DPMST、MST、DBSCAN和谱聚类算法在此数据集上表现良好, 而 K-means 算法仅考虑数据点之间的距离特性, 无法处理环绕的流线形数据, 效果最差.
jain是一个具有 2 个簇的数据集, 图4中数据点形成上下两环形, 上面的簇密度低, 下面的簇密度高. 可以看到只有我们的算法DPMST能够正确识别所有簇, 密度聚类算法性能不佳的原因是两个簇的密度差异太大. 而K-means不适合用于具有流线形状的数据集.
在图5中, 我们可以看到2d-4c-no9数据集有4个簇, 其中一个簇有非常高的密度. 我们的算法DPMST和DPC算法较为成功地检测到了所有的簇, 聚类效果最佳. K-means和BIRCH效果稍微差一些.
我们的算法DPMST和其他算法在Aggregation上的表现如图6所示. 可以看出, 我们的算法可以正确地检测到该数据集, K-means不能这样做, 因对K-means来说Aggregation数据集有些复杂.
图7显示了Compound数据集上的结果. 我们的算法与MST算法各具优势, 可以正确地检测大部分簇, 还可以识别噪声点. DBSCAN擅长识别噪声, 但它也将许多数据点错误地归类为噪声. DPC和K-means不能识别有噪声的簇.
| 表 3 人工数据集上聚类指标对比 |
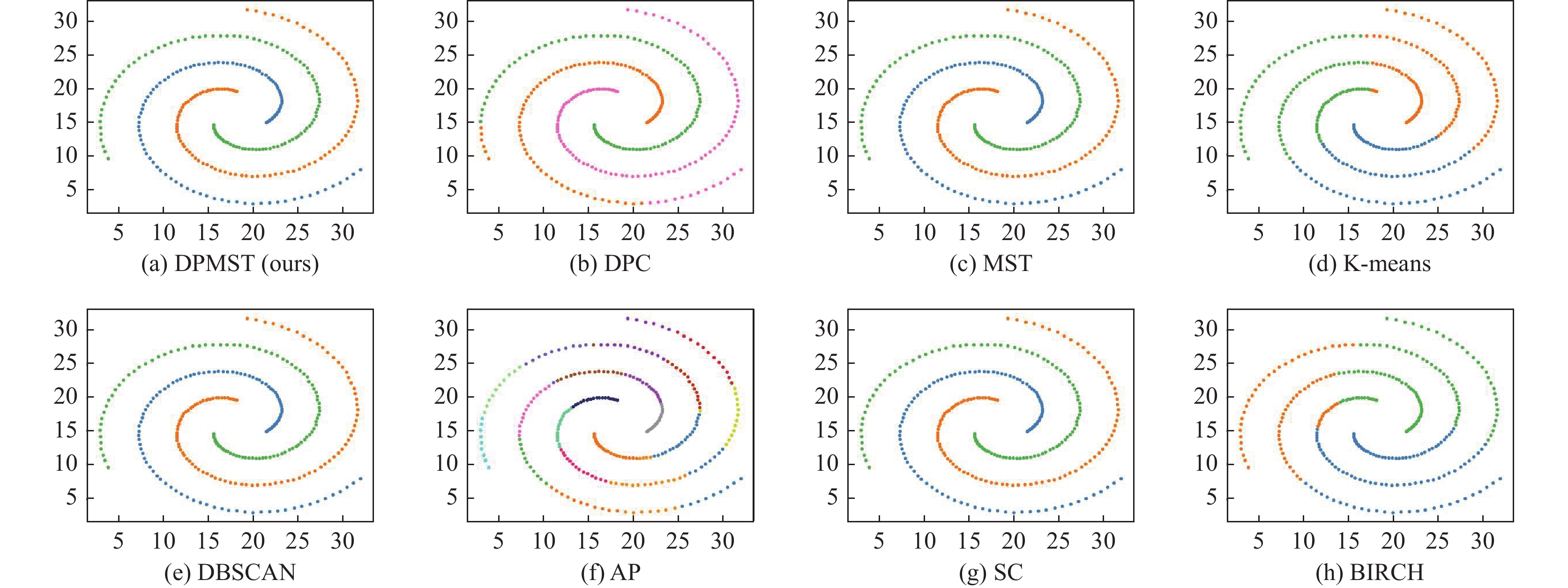
|
图 3 spiral 数据集聚类结果 |

|
图 4 jain 数据集聚类结果 |

|
图 5 2d-4c-no9 数据集聚类结果 |

|
图 6 Aggregation 数据集聚类结果 |

|
图 7 Compound 数据集聚类结果 |
在图8中, 我们可以看到zelink1数据集有3个簇, 形状像同心圆, 最中间的圆心密度高, 其余两簇密度逐渐降低. 我们的算法DPMST成功地检测到了所有的簇, 聚类效果最佳.
在图9中, Half kernel是一个具有两个簇且高密度的数据集, 数据点形成两个弧形簇. 在使用8种聚类算法对它们进行聚类时, 我们的算法DPMST在 Half kernel数据集上具有最佳的聚类结果, 其次是 MST算法.
如图10所示, Moon数据集有4个簇, 数据点形成4个弧形簇. 我们的算法DPMST可以正确识别所有簇, 而其余密度聚类算法将个别点识别为了离群点, 因此没有获得较好表现.

|
图 8 zelink1 数据集聚类结果 |

|
图 8 zelink1 数据集聚类结果(续) |

|
图 9 Half kernel 数据集聚类结果 |
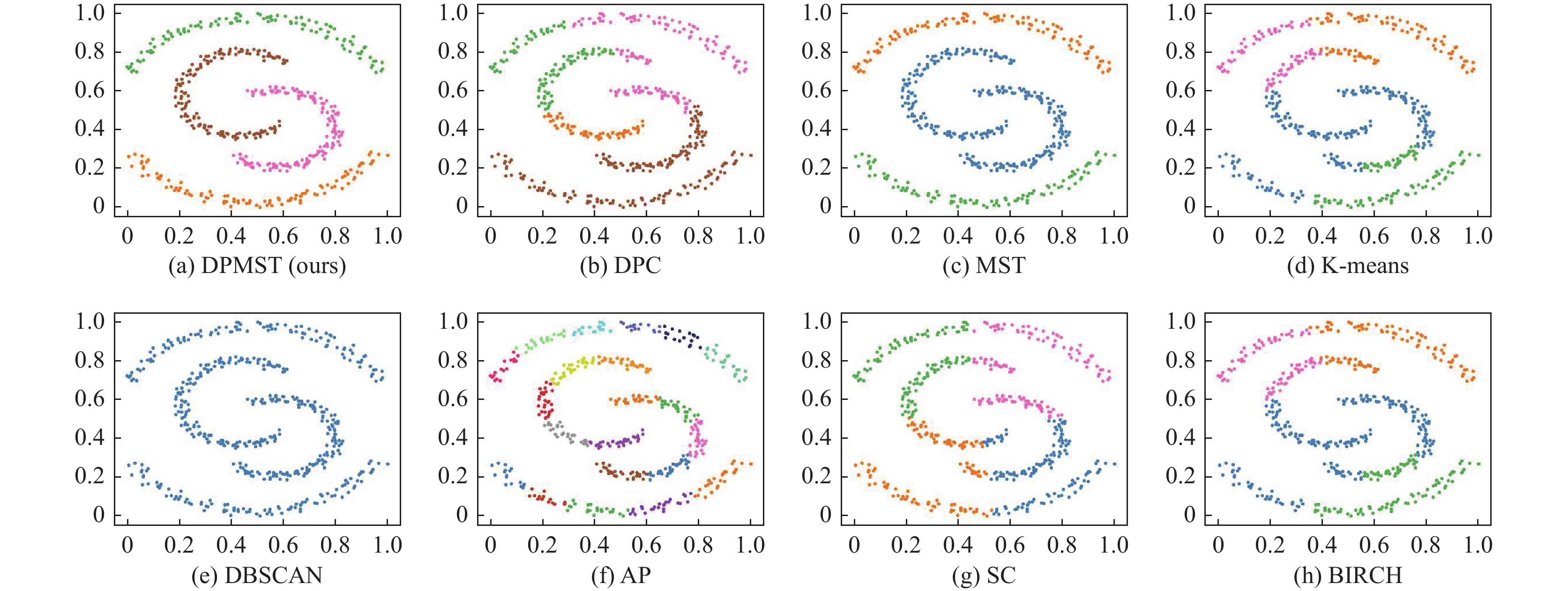
|
图 10 Moon 数据集聚类结果 |
从8个人工数据集的结果可以看出, 本文提出的算法具有非常好的性能, 能聚类任意形状的簇, 具有较好的鲁棒性, 通过调节参数可以对密度差异大的数据实现较好的聚类, 对流形数据也有非常好的效果.
为证明我们算法DPMST在实践中的有效性, 进一步选取8个真实数据集开展实验, 这些数据集的数量、属性以及簇数各不相同, 相较于前面的人工数据集更加复杂. 通过表4中的实验结果可以发现, 在密度不均匀、形状复杂的真实数据集上表现优异的聚类算法DPMST大部分情况下优于其他7种聚类算法. 因此, 我们认为 DPMST算法具有一定的有效性和实用性, 可以在实际应用(例如生物和医学领域)中发挥作用.
| 表 4 真实数据集上聚类指标对比 |
4 结论
本文提出了一种聚类算法DPMST. 算法过程有以下步骤: 首先, 计算局部密度, 为数据集构造家族树, 识别局部密度峰; 其次, 计算SW距离权值, 构造最小生成树, 反复删除最长边, 直到找到给定数量的簇, 根据所在的簇分配标签; 最后, 标签传播, 计算转移矩阵, 簇主干的标签通过转移矩阵传播到其余点, 数据点的标签根据标签传播后的标签矩阵进行更新.
本文提出的改进后的算法 DPMST, 利用 DPC 算法思想的优点来寻找局部密度峰, 在局部密度峰上能有效构造最小生成树, 降低噪声点的干扰. 该算法构造最小生成树时使用基于共享邻的距离, 其以一种更合适的方式表示了局部密度峰之间的距离, 更有效地识别无效边. 标签传播将数据的局部结构与标签空间相关性相结合, 可以提高聚类结果的质量.
人工和真实数据集的实验结果表明, DPMST算法在密度不均匀、形状复杂的数据集上能够达到较为理想的聚类效果, 通过调节参数可以达到不同的聚类效果, 算法性能良好, 总体聚类性能优于其他对比算法, 具有一定的实用价值. 但是, DPMST算法仍需要输入参数, 这意味着该算法不能排除人为因素的干扰, 这对该算法在实际问题中的应用带来了一定的挑战, 因此, 在后续工作中我们将考虑参数的自适应.
| [1] |
Michalski RS, Stepp RE. Learning from observation: Conceptual clustering. In: Michalski RS, Carbonell JG, Mitchell TM, eds. Machine Learning. Berlin: Springer, 1983. 331–363. [doi: 10.1007/978-3-662-12405-5_11]
|
| [2] |
Berkhin P. A survey of clustering data mining techniques. In: Kogan J, Nicholas C, Teboulle M, eds. Grouping Multidimensional Data. Berlin: Springer, 2006. 25–71. [doi: 10.1007/3-540-28349-8_2]
|
| [3] |
Han JW, Kamber M, Pei J. 数据挖掘: 概念与技术. 范明, 孟小峰, 译. 第3版, 北京: 机械工业出版社, 2012.
|
| [4] |
杨传慧. 图像聚类及其在图像检索中的应用研究 [硕士学位论文]. 南京: 南京师范大学, 2013.
|
| [5] |
肖宇. 聚类分析及其在图像处理中的应用 [博士学位论文]. 北京: 北京交通大学, 2012.
|
| [6] |
Niu YY, Kong DT, Liu LG, et al. Overlapping community detection with adaptive density peaks clustering and iterative partition strategy. Expert Systems with Applications, 2023, 213: 119213. DOI:10.1016/j.eswa.2022.119213 |
| [7] |
Petegrosso R, Li ZL, Kuang R. Machine learning and statistical methods for clustering single-cell RNA-sequencing data. Briefings in Bioinformatics, 2020, 21(4): 1209-1223. DOI:10.1093/bib/bbz063 |
| [8] |
唐东明. 聚类分析及其应用研究 [博士学位论文]. 成都: 电子科技大学, 2010.
|
| [9] |
孙吉贵, 刘杰, 赵连宇. 聚类算法研究. 软件学报, 2008, 19(1): 48-61. DOI:10.3724/SP.J.1001.2008.00048 |
| [10] |
Jain AK, Murty MN, Flynn PJ. Data clustering: A review. ACM Computing Surveys, 1999, 31(3): 264-323. DOI:10.1145/331499.331504 |
| [11] |
Karypis G, Han EH, Kumar V. Chameleon: Hierarchical clustering using dynamic modeling. Computer, 1999, 32(8): 68-75. DOI:10.1109/2.781637 |
| [12] |
Franti P, Virmajoki O, Hautamaki V. Fast agglomerative clustering using a K-nearest neighbor graph. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(11): 1875-1881. DOI:10.1109/TPAMI.2006.227 |
| [13] |
Zahn CT. Graph-theoretical methods for detecting and describing gestalt clusters. IEEE Transactions on Computers, 1971, C-20(1): 68-86. DOI:10.1109/T-C.1971.223083 |
| [14] |
Wang XC, Wang XL, Wilkes DM. A divide-and-conquer approach for minimum spanning tree-based clustering. IEEE Transactions on Knowledge and Data Engineering, 2009, 21(7): 945-958. DOI:10.1109/TKDE.2009.37 |
| [15] |
Lloyd S. Least squares quantization in PCM. IEEE Transactions on Information Theory, 1982, 28(2): 129-137. DOI:10.1109/TIT.1982.1056489 |
| [16] |
Rodriguez A, Laio A. Clustering by fast search and find of density peaks. Science, 2014, 344(6191): 1492-1496. DOI:10.1126/science.1242072 |
| [17] |
Zhou RY, Shu LJ, Su Y. An adaptive minimum spanning tree test for detecting irregularly-shaped spatial clusters. Computational Statistics & Data Analysis, 2015, 89: 134-146. DOI:10.1016/j.csda.2015.03.008 |
| [18] |
Halim Z, Uzma. Optimizing the minimum spanning tree-based extracted clusters using evolution strategy. Cluster Computing, 2018, 21(1): 377-391. DOI:10.1007/s10586-017-0868-6 |
| [19] |
Şaar F, Topcu AE. Minimum spanning tree-based cluster analysis: A new algorithm for determining inconsistent edges. Concurrency and Computation: Practice and Experience, 2022, 34(9): e6717. DOI:10.1002/cpe.6717 |
| [20] |
Zhong CM, Malinen M, Miao DQ, et al. A fast minimum spanning tree algorithm based on K-means. Information Sciences, 2015, 295: 1-17. DOI:10.1016/j.ins.2014.10.012 |
| [21] |
Li C, Ding SF, Xu X, et al. Fast density peaks clustering algorithm based on improved mutual K-nearest-neighbor and sub-cluster merging. Information Sciences, 2023, 647: 119470. DOI:10.1016/j.ins.2023.119470 |
| [22] |
Zhao J, Wang G, Pan JS, et al. Density peaks clustering algorithm based on fuzzy and weighted shared neighbor for uneven density datasets. Pattern Recognition, 2023, 139: 109406. DOI:10.1016/j.patcog.2023.109406 |
| [23] |
Zuo WD, Hou XM. An improved probability propagation algorithm for density peak clustering based on natural nearest neighborhood. Array, 2022, 15: 100232. DOI:10.1016/j.array.2022.100232 |
| [24] |
程东东. 基于局部核心点的聚类算法与度量研究 [博士学位论文]. 重庆: 重庆大学, 2018.
|
| [25] |
靳文星, 王电钢, 张哲敏. 基于局部密度的最小生成树聚类算法及其在电力大数据的应用. 四川电力技术, 2021, 44(4): 16-19, 49. DOI:10.16527/j.issn.1003-6954.20210404 |
| [26] |
VanderPlas J. mst_clustering: Clustering via Euclidean minimum spanning trees. Journal of Open Source Software, 2016, 1(1): 12. DOI:10.21105/joss.00012 |
| [27] |
Ester M, Kriegel HP, Sander J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise. Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining. Portland: ACM, 1996. 226–231. [doi: 10.5555/3001460.3001507]
|
| [28] |
Fukunaga K, Hostetler L. The estimation of the gradient of a density function, with applications in pattern recognition. IEEE Transactions on Information Theory, 1975, 21(1): 32-40. DOI:10.1109/TIT.1975.1055330 |
| [29] |
Shi JB, Malik J. Normalized cuts and image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8): 888-905. DOI:10.1109/34.868688 |
| [30] |
Zhang T, Ramakrishnan R, Livny M. BIRCH: An efficient data clustering method for very large databases. ACM SIGMOD Record, 1996, 25(2): 103-114. DOI:10.1145/235968.233324 |
 2024, Vol. 33
2024, Vol. 33



