随着流体力学应用的不断推进及超级计算机的快速发展, 对CFD所模拟的问题复杂度、网格规模以及求解精度的需求也越来越高. 因此, 大规模并行CFD模拟已经成为迫切需求[1].
从微观角度对CFD数值模拟的方法主要有分子动力学方法(molecular dynamics, MD)和LBM. LBM是一种基于分子运动理论的CFD方法[2], 它由介观运动方程发展而来. LBM将流体视为连续的Boltzmann方程的一种特殊离散形式[3], 并利用简化的运动学方程将流场转化为格点, 通过计算格点上微观粒子的碰撞和迁移过程, 来模拟整个流体的运动行为. LBM的通信机制仅涉及相邻格点, 易于并行化处理. 在神威加速计算架构上对LBM进行优化是服务于工业计算的重要方向.
近年来, 高性能计算迅速发展[4], 异构体系结构已经成为高性能计算机的主流趋势. 已经有许多LBM并行计算的研究成果, 主要采用CUDA[5]或者OpenCL[6]在GPU上实现LBM并行计算, 而在MIC上主要使用Intel Offload实现LBM并行计算. 例如, 文献[7]中对LBM开源代码openLBMflow进行了CPU+MIC的异构协同并行实现和优化, 并使用了2 048个节点进行可扩展性测试, 但强扩展性测试结果与理想值有一定的差距. 文献[8]中基于SYCL编程模型对开源多相流数值模拟软件openLBMflow实现跨平台异构并行模拟, 但该研究仅测试了小规模的数值模拟计算. 文献[9]实现了Palabos软件在新一代神威超算上的移植与优化, 为解决神威处理器从核LDM空间无法存储三维迭代计算所需数据的问题, 将一次三维迭代计算变为多次二维迭代计算, 为解决数据依赖导致无法并行的问题, 将碰撞和流动过程拆分, 实现了百万核心规模的并行计算, 但并行效率仅达40%.
尽管上述研究方法推动了LBM并行计算的发展, 但对于LBM的并行仍有数据依赖性强及并行效率低的问题. 本文基于神威加速计算架构(Sunway accelerate computing architecture, SACA), 采用D3Q19网格模型, 通过区域分解、数据重构、SIMD向量化及双缓冲等优化方法实现了LBM程序的多级并行, 有效解决了LBM在异构并行计算机上出现的数据依赖及并行效率低的问题, 在百万核心的并行规模下测试
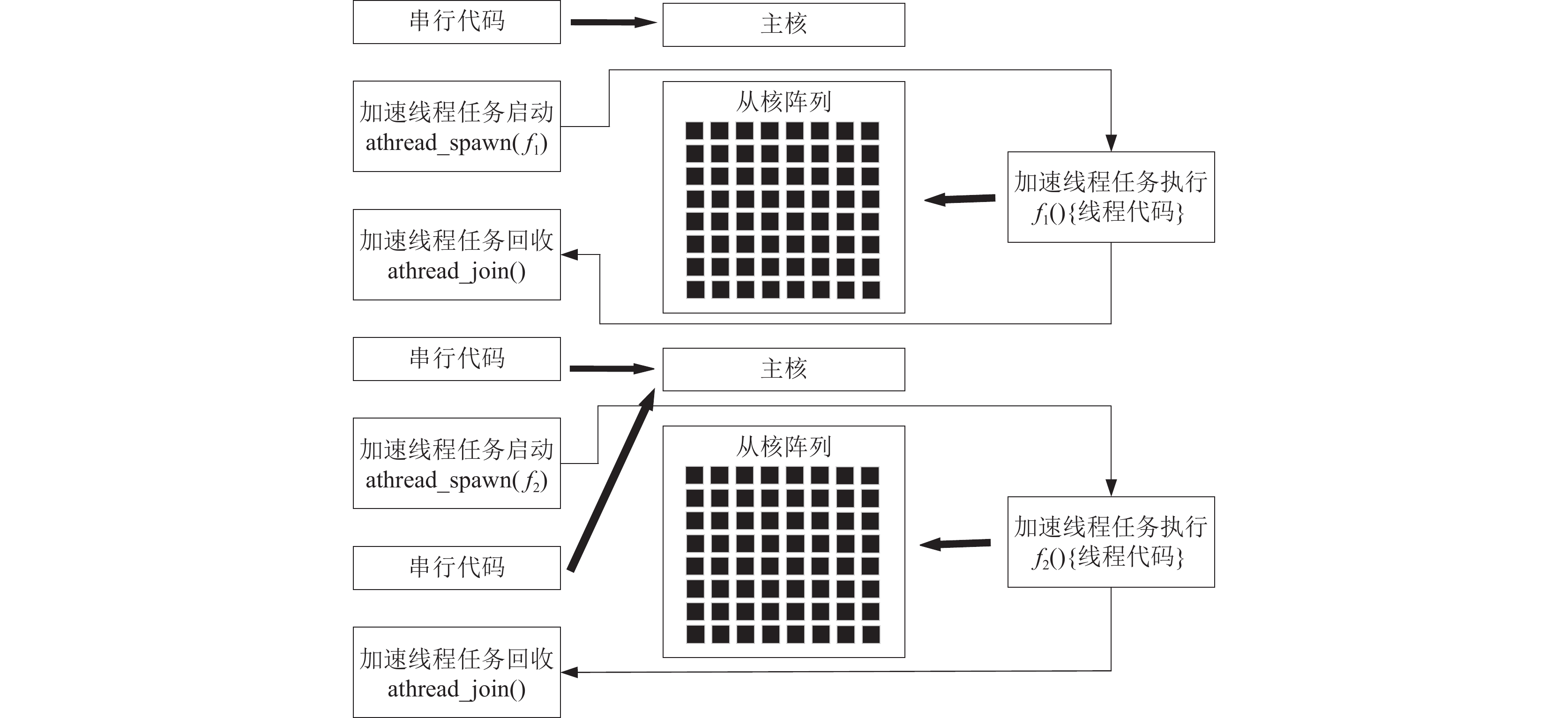
SACA继承和发展了“神威•太湖之光”体系架构[10], 是基于SW26010Pro和互联网络芯片构建的. SW26010Pro处理器[9]集成了6个核组(core group, CG), 每个CG包括一个运算控制中心(management processing element, MPE)和一个8×8运算核心阵列(computing processing elements, CPEs), 从核的局部存储空间(local direct memory, LDM)为256 KB, 从核通过直接存储器(direct memory access, DMA)方式批量访问主存. CPEs任意两个运算核心可以进行寄存器通信. 为适应SW26010Pro架构, SACA采用异构加速编程模式. 如图1所示, 主核程序使用Athread线程库的相关接口对加速线程任务进行管理, 根据接口功能的不同, 加速线程任务将会在CPE上执行. 线程任务启动后, MPE可以继续运行其他串行代码.
|
图 1 SACA代码组成 |
1.2 LBM基本理论分析
Boltzmann方程是描述流体分子分布函数的时间和空间演化的方程. LBM是一种基于Boltzmann方程从介观尺度描述流体系统的方法. 在使用LBM进行数值模拟时, 计算空间被离散为网格, 流体被建模为由粒子组成的系统, 这些粒子位于网格上, 并根据碰撞和迁移规则在网格上移动. 通过对网格上粒子的行为进行统计分析, 推导出描述流体宏观行为的运动规律. LBM的核心是演化方程, 公式为:
| fi(r+eiδt,t+δt)−fi(x,t)=Ωi | (1) |
该方程描述了粒子在空间和时间上的演化过程. 其中
在LBM中粒子按照碰撞和迁移的规则运动, 演化方程可以分为以下两个部分:
| f∗i(r,t)=fi−1τ[fi(r,t)−feqi(r,t)] | (2) |
| fi(r+eiδt,t+δt)=f∗i(x,t) | (3) |
其中, 式(2)为碰撞过程, 式(3)为迁移过程,
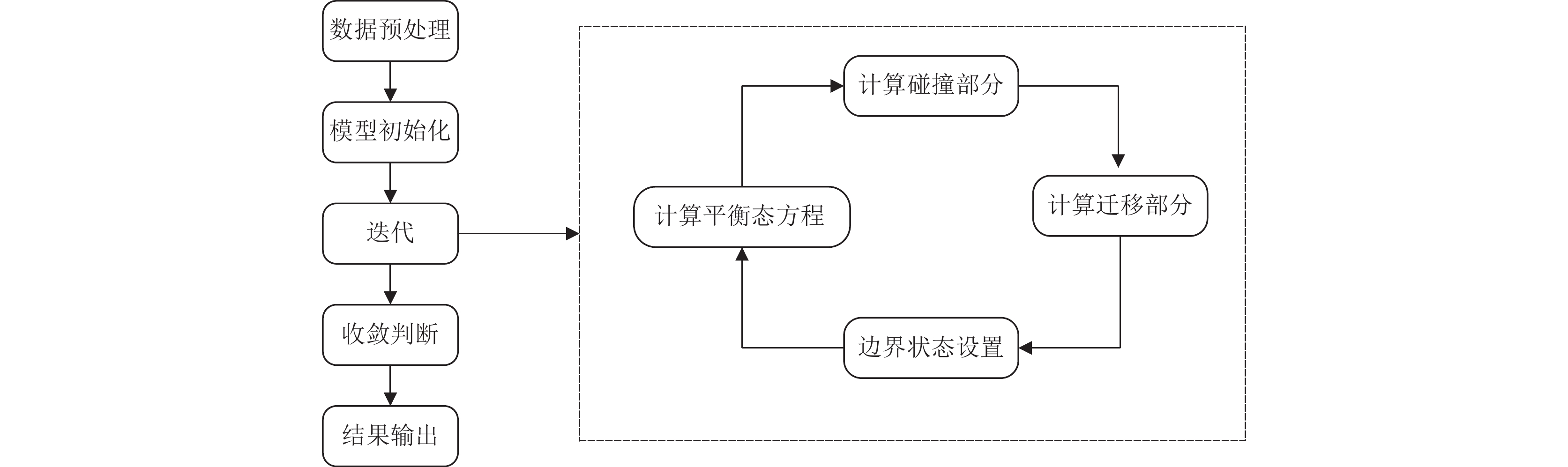
LBM计算流体力学过程中主要涉及两个主要计算密集的过程, 即碰撞过程和迁移过程[11]. 在计算粒子的碰撞过程中, 计算所需数据在粒子的网格点上. 因此, 碰撞过程并行计算时, 不涉及进程间通信, 每个处理器只需获取当前格点的数据即可执行计算, 而计算粒子的迁移过程, 则需要邻居格点的相关数据来完成计算, 这导致了迁移过程的并行计算中存在一定的数据依赖性. 因此, 本文的研究重点是实现LBM碰撞和迁移过程的多级并行计算, 降低迁移过程数据依赖, 提高并行效率. LBM的主要计算过程如图2所示.
|
图 2 LBM计算流体力学的实现流程 |
1.3 LBM并行化分析
本文选取的是经典案例圆柱绕流, 测试的网格规模为
| 表 1 圆柱绕流各个热点函数计算时间占比(%) |
由表1可以看出, LBM算法模拟中主要耗时部分是碰撞和迁移, 因此, 对于这两部分的并行计算对程序的加速至关重要. 碰撞和迁移部分相对独立, 分开并行计算更为合适[12,13]. 因此, 本文按照从核LDM的大小实现循环分裂, 再将外层的多层循环合并, 从而提高从核的并行度.
式(3)表明, 计算LBM迁移过程需要读取网格节点上碰撞之后的分布函数. 一个格点的计算需要周围邻居格点的相关数据, 且与周围格点的数据交换会对下一个格点获取的数据产生影响. 由以上分析可知, 迁移过程存在数据依赖, 实现并行计算比碰撞过程更为复杂. 文献[4]基于CUDA设计了LBM迁移过程的并行算法, 通过模型降维、数据定位等方法成功解决了迁移计算中数据依赖问题. 但该研究仅基于单GPU设计并行算法, 多GPU情况下的并行效率还是未知的. 本文基于SW26010Pro的特殊架构, 在迁移过程从核并行计算时, 采用数据重排及数据复用方案, 有效减少了从核访问主存的次数, 从而提高了访存效率.
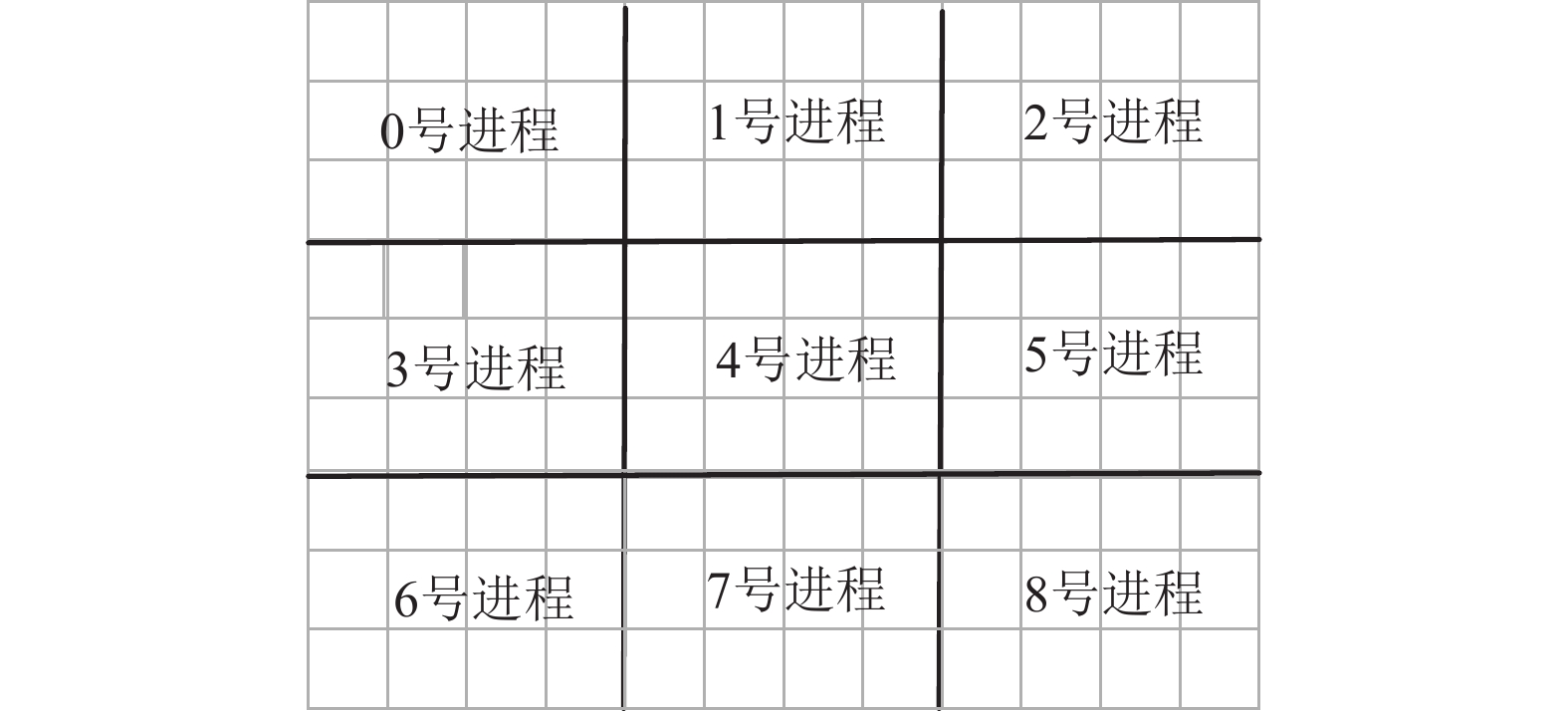
2 LBM多级并行策略 2.1 计算区域划分及负载均衡为了实现LBM的并行计算, 本文将计算区域分解成多个子域, 每个进程负责计算其中一个子域. 在计算区域边界处设置通信缓冲区, 用以存储邻居格点的数据. 对于三维的计算网格, 通常分为单向、双向和三向划分方式. 根据文献[3]的研究成果可知, 二维划分时由于通信时间占比的减少, 能够获得较高的加速比及并行效率. 因此, 二维划分相对于一维划分更有优势. 三维划分的并行度高, 但子域间相互重叠的部分复杂, 大规模运行时进程间的通信开销更大[14]. 基于以上分析, 本文采用二维区域划分的分解策略, 二维网格划分示意图如图3所示.
|
图 3 二维网格划分示意图 |
图3中, 以4号进程为例, 该进程负责的计算区域需要分别与1、3、5、7号进程进行边界数据交换, 为了避免通信过程中出现死锁、资源竞争及消息乱序问题, 进程间MPI通信过程如图4所示.

|
图 4 基于MPI进程之间的通信过程 |
由图4可知, 基于MPI实现LBM进程间通信主要通过如下4个步骤.
(1)向1号进程发送通信缓冲区中的数据, 接收7号进程通信缓冲区中的数据;
(2)向7号进程发送通信缓冲区中的数据, 接收1号进程通信缓冲区中的数据;
(3)向3号进程发送通信缓冲区中的数据, 接收5号进程通信缓冲区中的数据;
(4)向5号进程发送通信缓冲区中的数据, 接收3号进程通信缓冲区中的数据.
2.2 主要函数从核实现碰撞和迁移两部分的数据分块是实现从核并行的前提, 算法1给出了LBM碰撞和迁移过程的伪代码, 其中, domainX、domainY、domainZ分别代表X、Y、Z维的维度.
算法1. LBM碰撞和迁移过程的伪代码
1 for(int i = 0; i < domainX; i++ ){
2 for(int j = 0; j < domainY; j++ ){
3 for(int k=0 ; k<domainZ; k++){
4 for(int d = 0; d < 19; d++ ){
5 …
6 }
7 …
8 collision(x, y, z);
9 streaming(x, y, z);
10 …
11 }
12 }
13 }
本文在网格划分时, 由于X维和Y维的维度比较小, 在从核计算时, 对X或Y维进行数据分割, 会导致并行度较低. 因此, 为了提高程序的并行度及从核的负载均衡, 本文按照从核LDM大小对Z维循环进行分裂, 将数据合理地分配到64个从核中, 并将X、Y维的外层循环进行合并, 算法2为循环分裂与合并的伪代码.
算法2. 循环分裂与合并的伪代码
1 int block = …;
2 if(domainZ < block){
3 kend = …;
4 }else{
5 if(domainZ%block==0){
6 kend = …;
7 }else{
8 kend = …;
9 }
10 }
11 for(int i = 0; i < domainX * domainY * domainZ; i += 64 ){
12 athread_get(…)
13 for(int d = 0; d < 19; d++ ){
14 …
15 }
16 …
17 collision(i);
18 streaming(i);
19 …
20 athread_put(…)
21 }
2.3 数据重组在LBM算法中, 热点函数进行从核并行时存在如下问题: 因为SACA属于异构架构, 且热点函数计算过程中需要整体网格上的所有数据分量, 从而需要多次的数据传输. 因此, 本文根据从核LBM设计合理的内存使用方式, 尽可能减少数据传输的次数.
在核心计算段由于从核局存空间有限且数据分量是离散存储的, 显然无法一次将所有相关数据拷入从核LDM, 因此, 本文建立了面向众核架构的数据结构重构模型, 即在从核并行之前将计算所需的数据保存到新的数据结构中, 数据结构的设计流程如图5所示, 其具体模型如下.
(1)遍历碰撞和迁移的计算过程, 找到计算相关的数据;
(2)针对碰撞和迁移过程的相关数据建立新的数据结构;
(3)在从核并行之前, 根据原拓扑关系, 将相应的数据映射到新的数据结构中对应的成员变量;
(4)在碰撞及迁移从核并行计算时用新的数据结构代替旧的数据结构.

|
图 5 数据结构的重新设计 |
在数据重构之后, 考虑到各个从核的负载均衡问题, 将数据合理分割到64个从核中, 使所有从核同步计算, 在一定程度上避免负载不均衡带来的延迟.
2.4 双缓冲模式优化在数据重构之后, 一定程度上减少了从核访问主存的次数, 针对LBM的从核并行计算部分, 首先, 从核通过DMA将计算数据加载到LDM上. 然后, 从核开始计算. 最后, 从核通过调用线程库将计算结果写回主存. 然而, 这个过程是串行执行的, 包含多次读写操作, 对从核并行性能产生了一定影响. 因此, 为了优化此过程, 本文采用了双缓冲模式. 双缓冲模式本质上是一种并行流水技术, 能够实现从核计算与主从核之间通信的相互重叠, 从而提升计算速度. 具体而言, 通过在从核LDM空间上申请两倍通信数据大小的存储空间, 实现了存放两份同样大小且互为对方缓冲的数据.
双缓冲数据流程图如图6所示, 在双缓冲模式中, 对于每个从核, 将网格数据划分为多个子块, LBM单迭代步从核并行计算中, 需要多个轮次的子块加载、计算、写回. 除了第1个子块的加载和最后一个子块的写回外, 其余子块的计算和通信存在重叠过程, 在一定程度上减少了主从核之间的通信开销, 提高了LBM从核并行的性能.
2.5 数据复用在LBM迁移过程中单个格点数据的更新需要自身及周围邻居格点的数据, 而这些数据仅在最低维连续, 大多数数据是离散存储的. 因此, 从核需要通过多次DMA读取这些数据, 从核导致访存主存的次数过多. 针对以上情况, 本文设计了数据复用方案, 例如, Y维的计算则需要(Y–1)、Y、(Y+1)维的27个方向的速度分量, 而计算(Y+1)维时, 则需要Y、(Y+1)、(Y+2)维的相关数据, Y、(Y+1)维的18个方向的速度分量可以复用Y维计算时的数据, 复用数据率占总数据的66.7%. 使用数据复用方案, 迁移过程的计算流程如图7所示, 该优化方法可进一步减少主从数据传输次数, 提高并行效率.

|
图 6 从核缓冲优化流程图 |

|
图 7 使用数据复用方案迁移过程的计算流程 |
LBM迁移的计算流程如算法3所示.
算法3. LBM迁移的计算流程
1 for(lp=my id; lp<loopend; lp=lp+64){
2 …
3 pre=0; cur=1; next=2;
4 DMA_get();//从主核读取数据
5 for(j= 2:j< ny–l; j++){
6 DMA_get;//get j+1
7 …
8 for(k=1; k <=LEN; k++){
9 DMA_put();//将数据写回主核
10 next=(next+1) % 3;
11 cur=(next+2) % 3;
12 pre=(next+1) % 3;
13 }
14 }
2.6 向量化SW26010Pro是一种支持256位定点计算的处理器, 在LBM算法中, 碰撞过程利用处理器的256位向量寄存器进行向量化计算. 单指令多数据流(single instruction multiple data, SIMD)[15]使用一条指令操作多个数据, 从而实现数据并行. 考虑到向量寄存器的特性及程序中的数据类型, 本文主要使用doublev4进行向量化计算, 通过SIMD指令可以一次将4个double类型的数据加载到一个doublev4向量寄存器中进行计算.
LBM碰撞过程需要处理19个方向的数据, 这会出现方向维度上的边界对齐问题, 并且方向维度并不是最低维度, 导致数据在内存中的存储不连续. 为了解决这两个问题, 本文采取了以下方法: 首先, 将方向维度从19扩展为20, 对计算核心和计算数据进行调整. 其次, 为了实现高维度循环的向量化计算, 本文对向量数据进行重排, 将离散存储的数据调整为连续存储. 以对碰撞过程的n维数据做SIMD优化为例, 对n维数据调整的过程及相关伪代码如算法4.
算法4. n维数据调整过程
1 for(int n=0; n<LEN; n+=4)
2 {
3 simd_load(V1, &nodes[n][0]);
4 simd_load(V2, &nodes[n+1][0]);
5 simd_load(V3, &nodes[n+2][0]);
6 simd_load(V4, &nodes[n+3][0]);
7 V1L=simd_vshuffle(V2, V1, 0x44);
8 V1H=simd_vshuffle(V2, V1, 0xee);
9 V2L=simd_vshuffle(V4, V3, 0x44);
10 V2H=simd_vshuffle(V4, V3, 0xee);
11 VVl=simd_vshuffle(V2L, V1L, 0x88);
12 VV2=simd_vshuffle(V2L , V1L, 0xdd);
13 VV3=simd_vshuffle(V2H, V1H, 0x88);
14 VV4=simd_vshuffle(V2H, V1H, 0xdd);
15 }
首先, 使用simd_load()函数进行扩展数据类型与标准类型之间的映射操作, 将256位标准类型的数据从向量要求的对界内存地址映射到扩展类型变量; 其次, 使用simd_vshuffle()函数实现浮点向量元素按照地址高低排序. 碰撞过程向量化如图8所示, 向量化后, VV1、VV2、VV3、VV4向量计算, 相当于4次n循环计算, 充分发挥了SIMD指令的并行计算能力, 提高程序的性能.

|
图 8 碰撞过程向量化示意图 |
3 实验分析
本文基于SW26010Pro完成LBM的加速计算. 由于各过程包含不同的方案, 且代码量很大, 通过使用国家超级计算无锡中心开发的插装统计工具SWGPTL及SWLU对具体的代码进行详细的性能分析及评估, 性能测试指标主从加速比
| sn=TsTn | (4) |
其中,
本文测试了圆柱绕流案例的并行效果, 其网格规模为
|
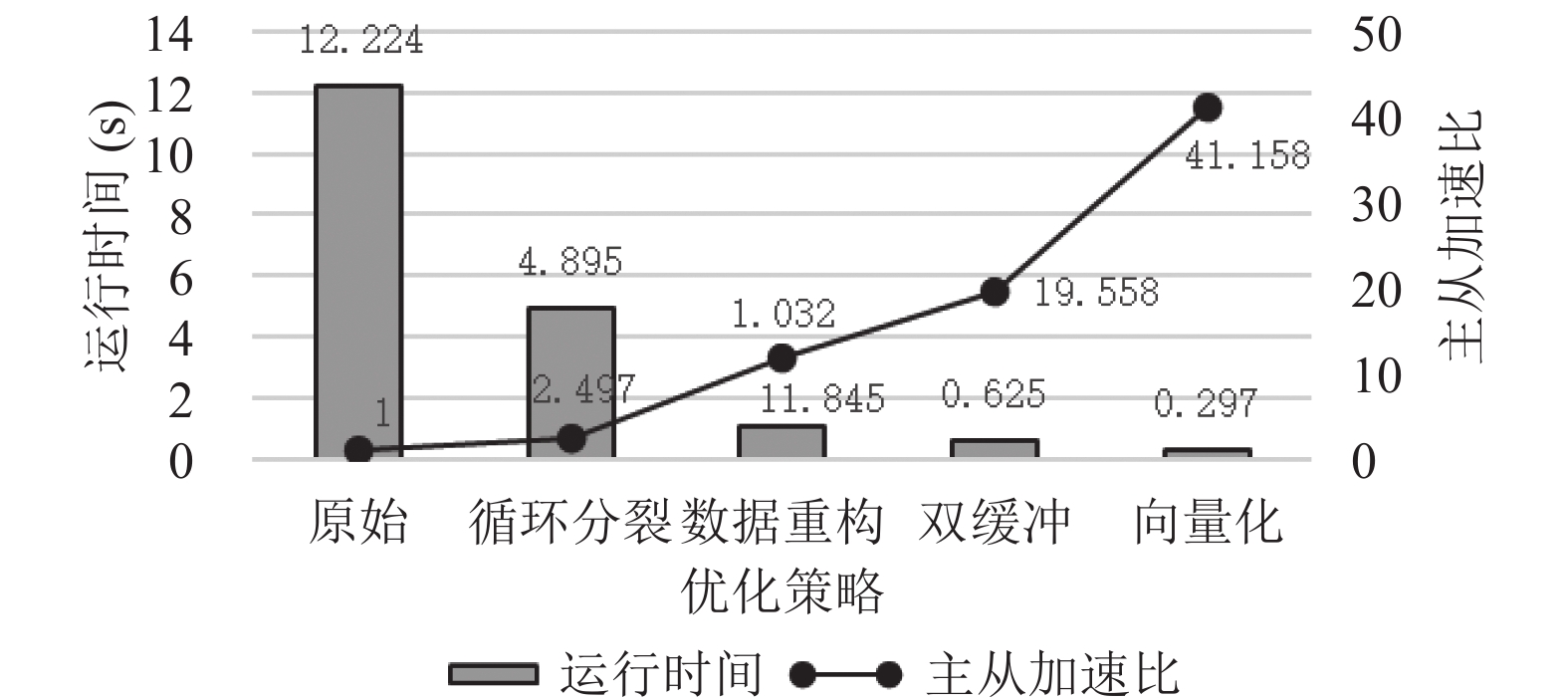
图 9 碰撞过程的计算时间及主从加速比 |
|
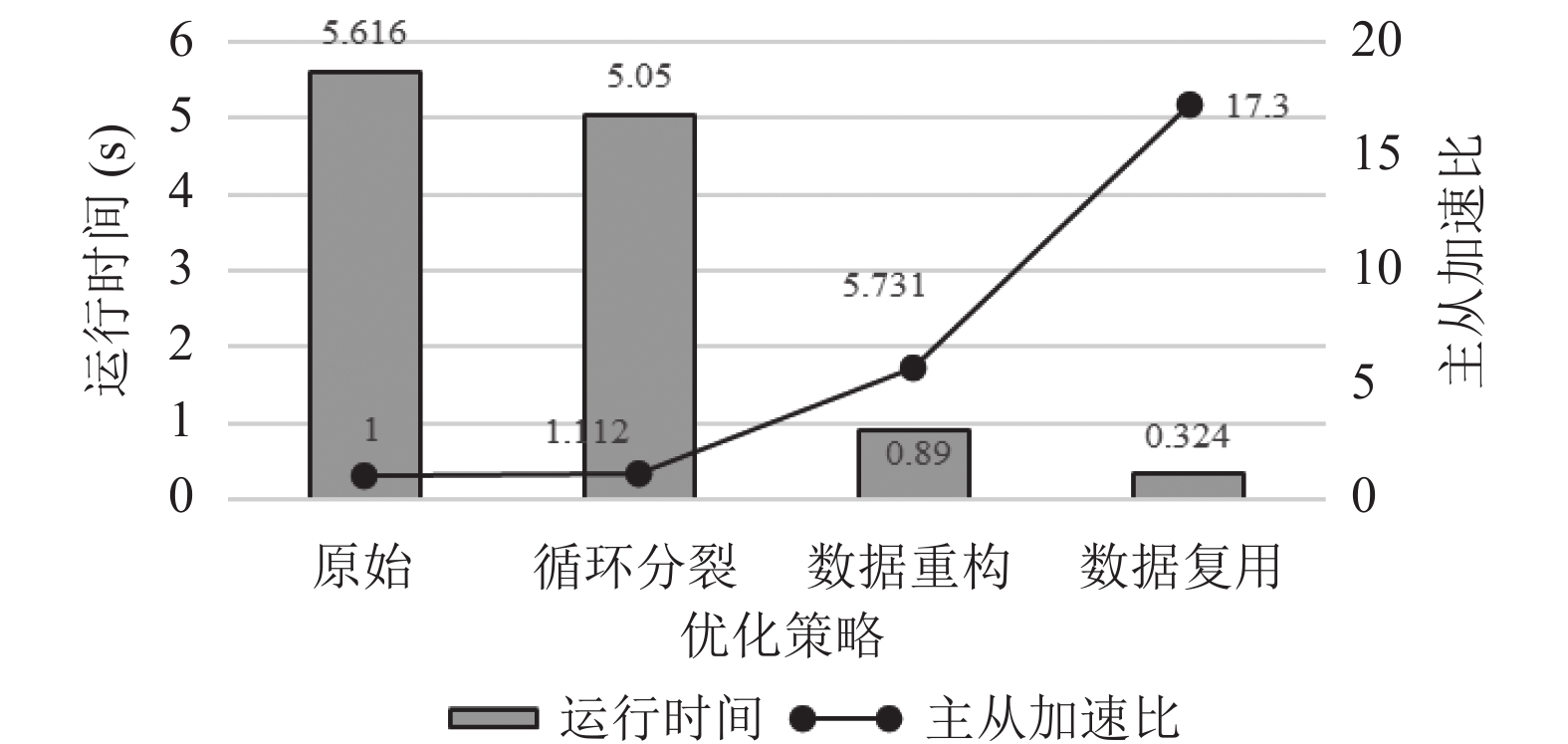
图 10 迁移过程地计算时间及主从加速比 |
由图9可知, 碰撞过程经过循环分裂、数据重构、双缓冲优化及向量化后, 平均主从加速比达到61.737, 而仅通过循环分裂将任务合理地划分到众核计算, 平均加速比仅为2.497, 加速效果并不明显, 这是因为在计算碰撞过程时, 所需的数据并未连续存储, 导致从核多次访问主存, 主从核之间的通信时间过长, 从而导致主从加速效果不理想. 但经过数据重构与双缓冲优化后, 极大地减少了从核访问主存的次数, 此时平均主从加速比可以达到19.558. 本次实验对碰撞过程使用了SIMD向量化优化, 由于在向量化时对方向维进行扩充, 因此, 损耗了一些时间, 与向量化优化前相比, 可以加速3.157倍, 加速效果在合理范围内.
由图9可知, 迁移过程经过循环分裂、数据重构及数据复用后, 平均主从加速比达到17.3, 从图9及图10中可以看出, 迁移过程仅通过循环分裂将任务划分到从核上计算, 平均主从加速比仅为1.112, 几乎没有加速, 这是迁移过程中数据依赖导致的结果, 而经过数据重构及数据复用优化方案加速效果有了明显提高, 从而为大规模数据模拟过程中出现的数据依赖提供了解决思路.
3.2 强扩展测试针对并行算法的强扩展性这一问题, 本文对方腔流案例进行测试, 网格规模为
| 表 2 方腔流强扩展性测试 |
表2的测试结果显示, 在百万核心的规模下进行数值模拟, 仍具有较理想的加速比, 并行效率可以达到60%以上, 提高了LBM计算流体力学的并行模拟能力, 为LBM大规模计算流体力学提供了并行思路.
4 结论与展望本文基于SW26010Pro处理器, 实现LBM算法的多级并行. 通过数据重构、循环分裂、SIMD及数据复用等优化方案实现了LBM在神威加速平台的计算, 达到了较好的优化效果, 碰撞过程的平均主从加速比可以达到61.737, 迁移过程的主从加速比可以达到17.3. 同时, 本文基于方腔流案例做了强扩展测试, 百万核心的并行效率可以达到60.5%以上. LBM算法的迁移过程在神威加速平台的数据依赖部分还有待完善, 下一步将对网格做降维处理, 进一步降低数据的离散型, 从而降低通信开销.
| [1] |
Vinuesa R, Brunton SL. Enhancing computational fluid dynamics with machine learning. Nature Computational Science, 2022, 2(6): 358-366. DOI:10.1038/s43588-022-00264-7 |
| [2] |
Astoul T, Wissocq G, Boussuge JF, et al. Lattice Boltzmann method for computational aeroacoustics on non-uniform meshes: A direct grid coupling approach. Journal of Computational Physics, 2021, 447: 110667. DOI:10.1016/j.jcp.2021.110667 |
| [3] |
Chaaban M, Heider Y, Markert B. A multiscale LBM-TPM-PFM approach for modeling of multiphase fluid flow in fractured porous media. International Journal for Numerical and Analytical Methods in Geomechanics, 2022, 46(14): 2698-2724. DOI:10.1002/nag.3423 |
| [4] |
Phillips JC, Hardy DJ, Maia JDC, et al. Scalable molecular dynamics on CPU and GPU architectures with NAMD. The Journal of Chemical Physics, 2020, 153(4): 044130. DOI:10.1063/5.0014475 |
| [5] |
De Luca P, Galletti A, Ghehsareh HR, et al. A GPU-CUDA framework for solving a two-dimensional inverse anomalous diffusion problem. Parallel Computing: Technology Trends. IOS Press, 2020. 311. [doi: 10.3233/APC200056]
|
| [6] |
Takizawa H, Shiotsuki S, Ebata N, et al. OpenCL-like offloading with metaprogramming for SX-Aurora TSUBASA. Parallel Computing, 2021, 102: 102754. DOI:10.1016/j.parco.2021.102754 |
| [7] |
Li D, Xu CF, Wang YX, et al. Parallelizing and optimizing large-scale 3D multi-phase flow simulations on the Tianhe-2 supercomputer. Concurrency and Computation: Practice and Experience, 2016, 28(5): 1678-1692. DOI:10.1002/cpe.3717 |
| [8] |
丁越, 徐传福, 邱昊中, 等. 基于SYCL的多相流LBM模拟跨平台异构并行计算研究. 计算机科学, 2023, 50(11): 32-40. DOI:10.11896/jsjkx.230300123 |
| [9] |
柳安军, 殷洪辉, 王利, 等. 基于新一代神威超算的计算流体力学Palabos软件的并行优化. 计算机科学, 2022, 49(10): 66-73. DOI:10.11896/jsjkx.220100089 |
| [10] |
Duan XH, Zhang M, Liu WG, et al. Tuning a general purpose software cache library for TaihuLight’s SW26010 processor. CCF Transactions on High Performance Computing, 2020, 2(2): 164-182. DOI:10.1007/s42514-020-00031-y |
| [11] |
何强, 李永健, 黄伟峰, 等. 基于MPI+OpenMP混合编程模式的大规模颗粒两相流LBM并行模拟. 清华大学学报(自然科学版), 2019, 59(10): 847-853. |
| [12] |
陶颖军. 基于OpenCV的人脸识别应用. 计算机系统应用, 2012, 21(3): 220-223. DOI:10.3969/j.issn.1003-3254.2012.03.051 |
| [13] |
王振华, 张鑫月, 刘智翔, 等. 遥感地物分割的改进格子玻尔兹曼并行模型. 遥感信息, 2021, 36(4): 1-6. DOI:10.3969/j.issn.1000-3177.2021.04.001 |
| [14] |
吕小敬, 刘钊, 褚学森, 等. 面向超大规模并行模拟的LBM计算流体力学软件. 计算机科学, 2020, 47(4): 13-17. DOI:10.11896/jsjkx.191000010 |
| [15] |
莫尚丰, 周振芬, 胡勇华, 等. 基于FT-M7002的复数域行向量矩阵乘法移植与优化. 计算机科学, 2023, 50(S2): 839-844. DOI:10.11896/jsjkx.220900277 |
 2024, Vol. 33
2024, Vol. 33



