优化是指在给定的限制条件下, 采用技术手段寻求某一问题的最佳解决方案^[1]. 现今对优化问题的求解方法主要有数学方法和元启发式算法等. 传统数学方法在求解小规模优化问题时, 具有简单快速, 求解精度高等优点, 但是对于高维复杂问题, 容易出现“维度灾”现象, 且计算时间大大延长. 相较于传统的数学方法, 元启发式算法不局限于特定的问题结构和假设^[2]. 这类算法通过运用启发式规则和自适应机制, 能够灵活地搜索解空间, 克服维度灾难, 并在相对较短的时间内找到接近最优的解^[3]. 因此, 元启发式算法在实践中被广泛应用^[4–7]. 群智能优化算法是一类模拟自然界中生物的生存行为而产生的元启发式算法^[8]. 其基本理论是利用群体之间的合作与信息交流, 以及生物自身的进化等来达到寻优的目的. 该类算法因其鲁棒性强, 实现简单, 优化精度高等优点, 受到了众多学者的关注研究^[9]. 近年来, 涌现出了许多性能卓越的新型群智能算法, 比如: 麻雀优化算法(sparrow search algorithm, SSA)^[10], 蜣螂优化算法(dung beetle optimization, DBO)^[11], 灰狼优化算法(grey wolf optimization, GWO)^[12], 鲸鱼优化算法(whale optimization algorithm, WOA)^[13], 哈里斯鹰优化算法(harris hawks optimization, HHO)^[14], 沙丘猫群优化算法(sand cat swarm optimization, SCSO)^[15]等.

人工鱼群算法(artificial fish swarm algorithm, AFSA)是李晓磊博士提出的一种模拟鱼类基本行为的仿生算法^[16]. 鱼类一般通过移动聚集在营养物质最丰富的区域, 根据此现象, 对鱼群的觅食、聚群、追尾、随机行为进行仿真, 从而达到算法全局寻优的目的. 该算法实现简单, 对初始值不敏感, 具有较强的鲁棒性. 但是, AFSA也存在后期收敛精度低、可能陷入局部极值等缺点. 因此, 许多文献提出了改进方法. 比如, 文献[17]引入可变视野, 对人工鱼移动策略做出改进, 并且模仿遗传算法中的变异操作对种群进行更新, 在一定程度上避免了算法陷入局部极值. 文献[18]引入反向解调整鱼群的行为, 并采用自适应视野和步长策略, 平衡全局搜索和局部搜索, 最后运用高斯变异机制, 对劣质解进行改进, 使得算法的鲁棒性和寻优精度得到了一定的提升. 文献[19]结合引力搜索算法提出一种改进的人工鱼群算法, 并应用于模拟机运动洗出优化, 实验结果表明, 改进算法具有较为优秀的求解性能, 适合求解实际优化问题.

上述文献都在一定程度上改进了AFSA的寻优性能, 但是在跳出局部最优、收敛速度和精度等方面, AFSA仍有较大的提升空间. 因此, 本文提出一种自适应差分变异的人工鱼群算法(adaptive and differential mutation artificial fish swarm algorithm, ADMAFSA). 改进算法在人工鱼的移动行为中引入反向学习机制, 避免了原始随机行为的盲目性, 提高了种群的多样性. 为降低算法陷入局部最优的可能性, 改进算法借鉴差分进化算法的变异机制, 每次迭代完成后对较差人工鱼进行变异. 此外, 算法采用自适应视野和步长, 在迭代前期保证全局搜索, 在迭代后期缓慢精准地向最优区域收敛. 在6个基准测试函数和8个CEC2019函数上的实验结果验证了改进算法的有效性. 最后将ADMAFSA应用于求解齿轮系设计这种实际优化问题上.

1 人工鱼群算法(AFSA)

ASFA通过模拟鱼类基本行为实现群智能优化目标. 鱼类一般通过移动聚集在营养物质最丰富的区域, 据此, 对鱼群的觅食、聚群、追尾、随机行为进行仿真, 从而达到算法全局寻优的目的. 设置单条人工鱼的状态为向量${{X}} = ({x_1}, {x_2}, \cdots , {x_D})$, 将当前人工鱼${{X}}$对应的食物浓度记为$Y = f(X)$, 其中$Y$为目标函数值. 两条人工鱼$i$与$j$之间的距离表示为${d_{ij}} = \left\| {{X_i} - {X_j}} \right\|$, 算法中的其他参数包括人工鱼的拥挤度因子$\delta $, 视野$visual$, 步长$step$, 尝试次数$try\_number$. 其中视野$visual$和步长$step$分别决定人工鱼所能搜索的最大范围以及每次移动的距离. 算法包括觅食、聚群、追尾、随机行为, 下面对几种行为进行详细描述.

1.1 觅食行为

在求最小值问题中, 当前人工鱼X_i在视野visual范围内(即d_ij<visual)进行随机搜索, 找到位置X_i, 若Y_i>Y_j, 说明状态j优于状态i, 人工鱼按式(1)向X_j移动一步, 否则重新随机选择X_j. 如果连续尝试try_number次后仍未找到满足条件的X_j, 则执行随机行为.

$ {X_{i\mid {\rm next}}} = {X_i} + Rand() \times \mathit{step} \times \frac{{{X_j} - {X_i}}}{{\left\| {{X_j} - {X_i}} \right\|}} $

(1)

1.2 聚群行为

统计当前人工鱼X_i视野范围内的鱼群总数目n_f, 如果该n_f条人工鱼的中心位置人工鱼X_c满足式(2), 说明中心位置X_c处食物浓度较高且周围人工鱼不太拥挤, 因此, 按式(3)向X_c进行移动. 否则, 执行觅食行为.

$ {Y_c}\cdot{n_f} \lt \delta \cdot {Y_i} $

(2)

$ {X_{i \mid {\rm next} }} = {X_i} + Rand() \times \mathit{step} \times \frac{{{X_c} - {X_i}}}{{\left\| {{X_c} - {X_i}} \right\|}} $

(3)

1.3 追尾行为

搜索当前人工鱼X_i视野范围内食物浓度最高的位置X_max, 如果X_max满足式(4), 说明位置X_max处食物浓度较高且周围人工鱼不太拥挤, 因此, 按式(5)向X_max进行移动. 否则, 执行觅食行为.

$ {Y_{\max }}\cdot{n_f} \lt \delta \cdot {Y_i} $

(4)

$ {X_{i\left| {\rm next} \right.}} = {X_i} + Rand() \times \mathit{step} \times \frac{{{X_{\max }} - {X_i}}}{{\left\| {{X_{\max }} - {X_i}} \right\|}} $

(5)

1.4 随机行为

随机行为是指人工鱼X_i在当前视野范围内(即d_ij<visual)随机搜索, 选择一个位置并向其移动. 如式(6)所示.

$ {X_{i\left| {\rm next} \right.}} = {X_i} + Rand() \times visual $

(6)

2 自适应差分变异的人工鱼群算法

标准AFSA算法具有实现相对简单, 对参数不敏感, 并行化能力强等优点, 但是相对于其他高效的优化算法, AFSA的收敛速度和精度可能较差. 因此, 本文提出一种改进的AFSA, 以期在合理的计算时间内找到高质量的最优解. 下面对算法的主要改进机制进行详细描述.

2.1 自适应视野和步长

AFSA算法使用固定视野和固定步长, 这有利于算法前期迅速向较优区域收敛, 但是在迭代后期, 由于视野值和步长值过大, 鱼群执行觅食行为和随机行为频繁, 从而无法更精准地找到全局最优解. 针对以上问题, 本文引入可变视野和可变步长. 鱼群的视野$ visual $和步长$ step $按式(7)随着迭代次数的递增呈线性减小, 保证算法在迭代前期进行全局搜索, 在迭代后期实现在极值点周围的精细寻优.

$ \left\{ \begin{gathered} visual = visua{l_{\max }} - (visua{l_{\max }} - visua{l_{\min }})/{d_{\max }} \times d \\ {\mathit{step}} = {\mathit{step}_{\max }} - ({\mathit{step}_{\max }} - {\mathit{step}_{\min }})/{d_{\max }} \times d \\ \end{gathered} \right. $

(7)

其中, $ visua{l_{\max }} $、$ visua{l_{\min }} $分别为设置的视野最大值、最小值; $ {d_{\max }} $为最大迭代次数, $ d $表示当前迭代次数; $ {\mathit{step}_{\max }} $、$ {\mathit{step}_{\min }} $分别为设置的步长最大值、最小值.

2.2 改进的随机行为

由上文可知, 在觅食行为中, 若连续尝试$ try\_number $次后仍未找到满足条件的$ {{{X}}_j} $则执行随机行为. 因此, 当执行随机行为时, 算法有较大可能陷入了局部极值. 考虑到随机行为具有一定的盲目性, 算法不能保证总是向更优位置移动, 本文对随机行为引入反向学习机制. 反向学习机制的基本思路是: 当个体远离系统最优解时, 其反向个体接近系统最优解的可能性就会大大增加^[20]. 根据以上思想, 人工鱼群将按式(8)进行随机行为. 改进后的随机行为将反向解纳入迭代过程中, 扩大了寻优空间, 从而增加了种群的多样性, 避免了算法早熟收敛.

$ {X_{i\left| {\rm next} \right.}} = (X_j^U + X_j^L) - {X_{ij}} $

(8)

其中, $ X_j^U $、$ X_j^L $分别为种群搜索空间第$ j $维的最大值和最小值.

2.3 差分变异操作

为了提高算法的求解效率和解的质量, 本文结合差分进化算法的变异策略对部分人工鱼进行更新. 具体操作为: 公告牌不再只存放每次迭代的最优值, 而是存放质量前100%m×N_p个较优值, 其中N_p为种群数量. 每次迭代时更新公告牌, 如果公告牌累计$ Max\_time $次未更新, 则考虑算法可能陷入局部最优, 种群进行随机初始化, 否则, 按照一定比例$ \theta $选取本次迭代产生的最差N_p×θ条人工鱼, 并对其按式(9)执行变异操作.

$ {V_{i, g}} = {F_1} \cdot (X_{{\mathrm{best}}, g}^p - {X_{i, g}}) + {F_2} \cdot ({X_{i, g}} - {X_{i - 1, g}}) $

(9)

其中, $X_{{\rm{best}}, g}^p $为随机选取的本次迭代中质量前$ 100{\text{%}} p \times {N_p} $的人工鱼, $ {F_1} $、$ {F_2} $为变异算子, $ {X_{i - 1, g}} $为经过排序后, $ {X_{i, g}} $前面的一条人工鱼.

2.4 ADMAFSA算法的步骤及流程

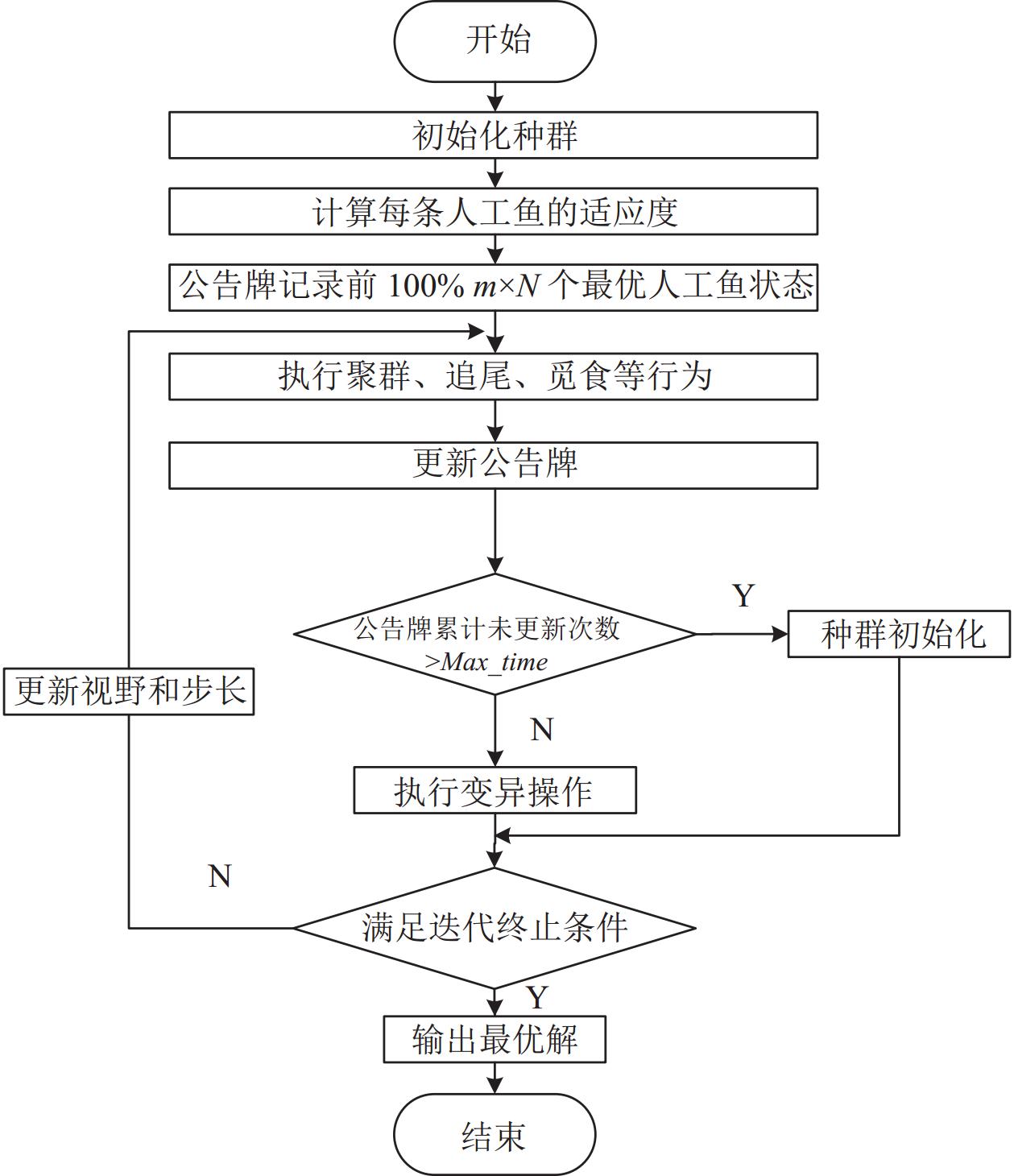
ADMAFSA算法的流程图如图1所示.

步骤1. 随机初始化种群, 种群中人工鱼条数N_p. 计算每条人工鱼的目标函数值, 将质量前100%m×N_p个最优值写入公告牌. 设置算法参数初始值: 拥挤度因子$\delta $, 最大尝试次数$ try\_number $, 视野范围$ visual $, 步长$ step $.

步骤2. 执行人工鱼的追尾、聚群、觅食行为. 如果连续执行超过$ try\_number $次觅食行为, 则执行随机行为.

步骤3. 计算新个体的目标函数值, 对公告牌进行更新.

步骤4. 判断公告牌未更新的次数, 如果公告牌累计$ Max\_time $次未更新, 则种群进行随机初始化, 否则按照一定比例选取此次迭代生成的最差N_p×θ条人工鱼进行变异.

步骤5. 判断是否达到迭代终止条件, 如果是则算法结束, 输出最优解. 否则更新视野和步长, 返回步骤2继续迭代循环.

3 实验仿真与结果分析 3.1 实验环境

为保证算法对比的公平性, 本文所有实验均在64位Windows 10系统, 处理器为Intel i5-8265U 1.60 GHz CPU环境下, 用Matlab R2020a实现.

3.2 与其他AFSA变体对比

为验证改进算法的有效性, 本文对ADMAFSA和AFSA, 改进的人工鱼群算法(modified artificial fish swarm algorithm, MAFSA)^[17], 反向自适应高斯变异的人工鱼群算法(opposite adaptive and gauss mutation artificial fish swarm algorithm, OAGMAFSA)^[18]进行仿真测试, 采用6个经典测试函数进行比较分析. 测试函数如下.

(1) 单峰函数Sphere, 其全局最优值为0, 其中$ {x_i} \in [ - 5.12, 5.12] $.

$ f(x) = \sum\limits_{i = 1}^D {x_i^2} $

(2) 阶跃函数Step, 其全局最优值为0, 其中$x_i \in $$[-100,100] $.

$ f(x) = \sum\limits_{i = 1}^D {\left[ {{{\left( {\left\lfloor {{x_i} + 0.5} \right\rfloor } \right)}^2}} \right]} $

(3) 复杂多峰函数Rastrigin, 其全局最优值为0, 其中$ {x_i} \in [ - 5.12, 5.12] $.

$ f(x) = \sum\limits_{i = 1}^D {\left[ {x_i^2 - 10\cos \left( {2\text{π} {x_i}} \right) + 10} \right]} $

(4) 复杂多峰函数Griewank, 其全局最优值为0, 其中${x_i} \in [ - 600, 600]$.

$ f(x) = \frac{1}{{4000}}\sum\limits_{i = 1}^D {x_i^2 - \prod\limits_{i = 1}^D {\cos \left( {\frac{{{x_i}}}{{\sqrt i }}} \right)} } + 1 $

(5) 复杂多峰函数Ackley, 其全局最优值为0, 其中${x_i} \in [ - 32, 32]$.

$ \begin{split} f(x) =& - 20\exp \left( { - 0.2\sqrt {\frac{1}{D}\sum\nolimits_{i = 1}^D {x_i^2} } } \right) \\ &-\exp \left( {\frac{1}{D}\sum\nolimits_{i = 1}^D {\cos \left( {2\text{π} {x_i}} \right)} } \right) + 20 + {\mathrm{e}} \end{split} $

(6) 复杂多峰函数Schaffer, 其全局最优值为0, 其中${x_i} \in [ - 100, 100]$.

$ f(x) = \sum\limits_{i = 1}^{D - 1} {{{\left( {x_i^2 + x_{i + 1}^2} \right)}^{0.25}}} \left[ {{{\sin }^2}\left( {50{{\left( {x_i^2 + x_{i + 1}^2} \right)}^{0.1}}} \right) + 1} \right] $

测试算法设置维度n=15, 最大迭代次数${{{d}}_{\max }}$=2000, 拥挤因子$\delta $=0.618, 种群数目N_p=100. 其他参数设置为: 视野最大值$visua{l_{\max }} = (ub - lb)/4$, 视野最小值$ visua{l_{\min }} $=0.001, 步长最大值${\mathit{step}_{\max }} = visua{l_{\max }}/8$, 步长最小值${\mathit{step}_{\min }=0.0002}$, $m$=0.1, $\theta $=0.05, $p$=0.05, $ Max\_time $=20. 对比算法参数设置可参考相关文献. 为了使结果更具准确性, 实验中所有算法均在每个测试函数下独立运行30次, 30次运行结果的最优值、平均值和标准差如表1所示, 每个函数的最佳测试结果用黑体表示.

根据表1的实验结果可知, 与其他几种算法相比, ADMAFSA的收敛精度得到明显提升. 对于阶跃函数Step, AFSA、MAFSA、OAGMAFSA和ADMAFSA均能求出其全局最优解0. 在其余5个测试函数的实验中, 改进算法ADMAFSA能够准确求出函数Sphere、Rastrigin、Griewank、Schaffer的全局最优值0. 其中Sphere为单峰函数, Rastrigin和Griewank为多峰函数, Schaffer为有无数极值点的函数. 在求解Ackley函数时, 虽未求得全局最优值0, 但是相较于其他3种算法, ADMAFSA的最优值、平均值和均差均最小, 验证了新算法中引入的机制的有效性. 在6个测试函数中, ADMAFSA的均差均为最小且为0, 说明ADMAFSA具有较好的鲁棒性. 综上所述, ADMAFSA与其他AFSA变体相比, 算法的收敛精度与稳定性更高.

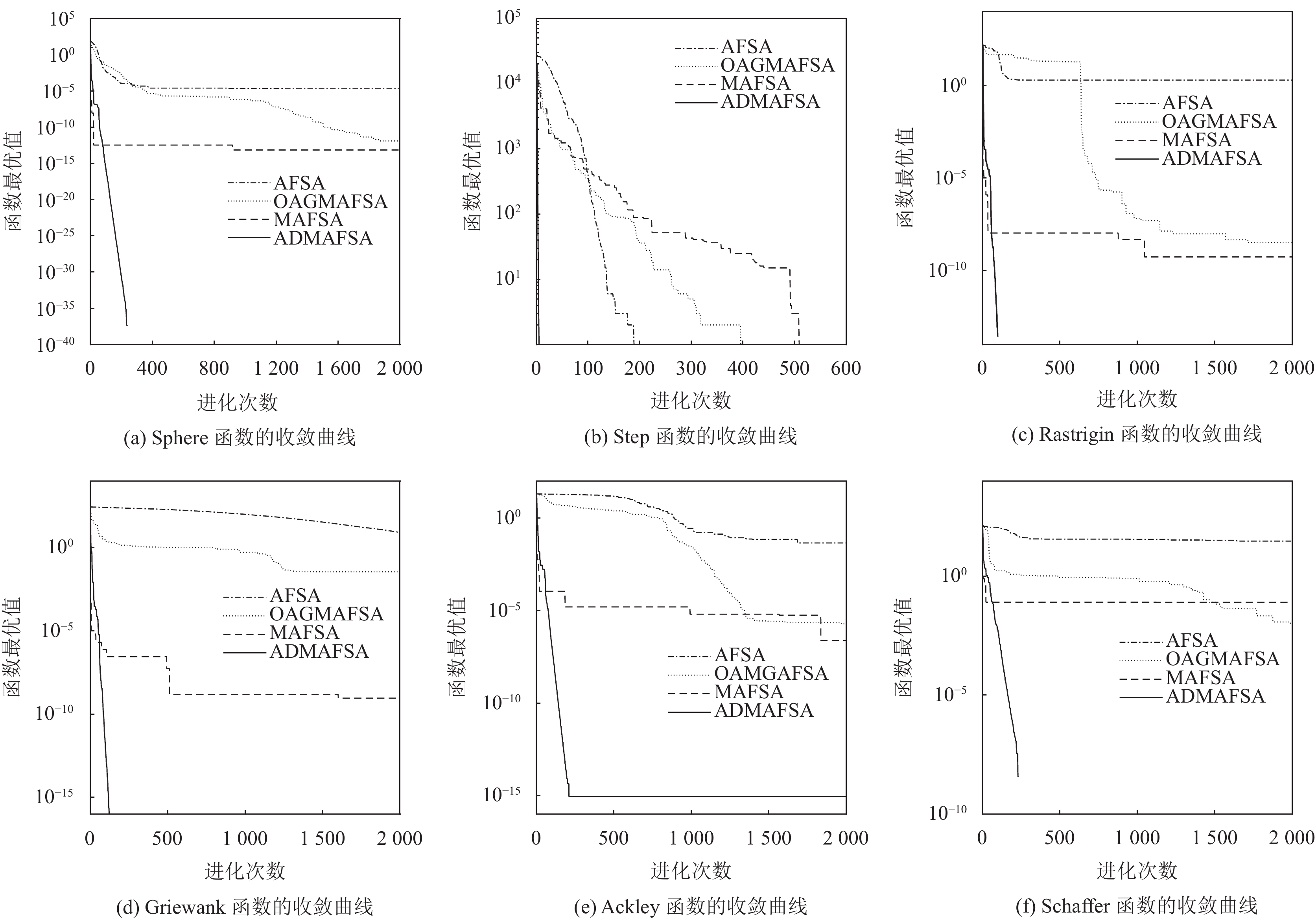
为研究ADMAFSA的收敛能力, 本文将ADMAFSA与其他几种算法在测试函数迭代过程中的收敛情况进行比较. 图2为AFSA、OAGMAFSA、MAFSA和ADMAFSA迭代2000次的对比曲线图. 可以看出, ADMAFSA能够迅速收敛, 在进化500代之内就能找到全局最优位置. 由此可见, 改进算法通过引入变异机制, 能够不断调整和改进劣质解, 从而提高了搜索效率.

由于AFSA在进化过程中保持视野和步长不变, 所以在迭代后期不能保证收敛精度. 且算法没有设置陷入局部最优解的解决方法, 导致优化过程中出现搜索停滞现象. OAGMAFSA过于依赖反向解, 当陷入局部极值时, 如果其反向解的质量也较差, 则跳出该区域具有一定的困难. MAFSA引入可变视野, 在迭代后期, 算法有足够的潜力进行精细寻优. 并且调整移动策略为: 当发现比自身当前状态更好的解时, 直接移动到该位置, 不再进行随机移动, 促进了鱼群向极值点位置快速收敛. 另外, MAFSA按照一定的概率进行变异, 相较于AFSA, 一定程度避免了算法早熟. 然而该算法设置固定的步长, 不利于算法协调全局搜索和局部搜索. 相比较而言, ADMAFSA采用的变异机制、反向学习策略、自适应视野和步长方法能够使算法稳定且快速收敛, 波动性较小.此外, ADMAFSA设置算法陷入局部最优的警戒值, 一旦算法达到该警戒值, 便会触发种群随机初始化操作, 对改善算法性能起到了良好的效果.

3.3 与其他智能算法对比

为进一步测试本文所提算法的优化效果, 将ADMAFSA与麻雀优化算法SSA、灰狼优化算法GWO、蜣螂优化算法DBO这3种新型智能优化算法进行比较. 实验采用8个CEC2019测试函数进行评估, 函数具体信息见表2. 所有测试算法设置种群数量30, 最大迭代次数设为500. 30次的独立运行结果如表3所示, 每个函数优化结果的最佳平均值用黑体表示. 根据实验结果可知, ADMAFSA在大部分基准测试函数上都优于其他3种算法或者基本相当, 仅在函数f₇上, 略低于SSA算法. 此外, 问题求解维度的增加对于ADMAFSA的优化精度和稳定性影响较小. 对于单峰测试函数f₁–f₄以及多峰函数f₅和f₈, ADMAFSA算法均能求得其全局最优值0, 并且30次运行结果的标准差都为0. 从而验证了改进算法不仅在求解精度方面更为突出, 稳定性上也具有一定的优势.

3.4 齿轮系设计问题

在本节中采用齿轮系设计问题, 通过与SSA、GWO、DBO、WOA、SCSO对比最佳寻优结果, 检验ADMAFSA算法在求解工程设计问题的优化性能.

齿轮设计问题的优化目标是通过合理设计4种齿轮的齿数, 使得转动比成本最小化, 通常被描述为带有不等式约束的优化模型^[21]. 如式(10)所示. 其中T_a、T_b、T_d、T_f分别代表4个不同齿轮的齿数.

$ \left\{ \begin{gathered} {{{x}}_i} = [{T_a}, {T_b}, {T_d}, {T_f}] \\ \min f(x) = {\left(\frac{1}{{6.931}} - \frac{{{T_b} \cdot {T_d}}}{{{T_a} \cdot {T_f}}}\right)^2} \\ {x_i} \in {N_ + },\qquad \;\;i = 1, 2, 3, 4 \\ 12 \leqslant {x_i} \leqslant 60,\;\; i = 1, 2, 3, 4 \\ \end{gathered} \right. $

(10)

表4为6种算法各独立运行30次的最优解及对应的各参数取值, 其中黑体表示本文算法的优化结果. 实验设置各算法最大迭代次数100次, 种群数量为30. ADMAFSA求解的最优设计方案中, 目标函数最小值为2.7009×10⁻¹², 最优设计参数为[43, 16, 19, 49]. 相比于其他5种算法, 本文所提算法求解精度更高. 因此, ADMAFSA算法适用于求解带约束条件的工程设计问题.

4 结论与展望

针对AFSA算法收敛精度低, 易陷入局部最优等问题, 本文使用可变视野和步长, 动态地调整寻优范围, 平衡了全局搜索和精细寻优的能力; 引入反向学习机制, 将反向解纳入迭代过程中, 扩大了寻优空间, 从而避免了算法陷入局部极值; 并且采用差分变异策略, 使质量较差的鱼群学习历史最优解, 降低了算法早熟收敛的可能性, 最终提出了ADMAFSA. 为验证ADMAFSA的有效性和可行性, 对6个基准测试函数和8个CEC2019函数进行仿真测试, 实验结果表明, ADMAFSA能够摆脱局部极值的限制, 在兼顾算法的稳定性和准确性的前提下, 提高算法的寻优精度和搜索效率. 最后将改进算法应用于齿轮系设计问题, 进一步验证了ADMAFSA算法有较强的收敛能力, 在解决工程实际问题中也具有良好的潜力. 未来的工作是将改进算法应用于求解多目标工程问题.