1 引 言

集装箱码头作为链接水陆集装箱运输方式的缓冲地, 是集装箱运输过程中的核心枢纽和关键节点^[1–3]. 然而, 相邻港区内传统集装箱码头采取的各自为政, 独立生产的运营模式在当前行业背景和未来前景下都不容乐观, 现实中表现为: 服务同质化、资源闲置利用率不足和恶性压价普遍化, 对港口物流高质量健康发展十分不利, 故推进区域港口一体化发展是促进港口产业提质增效、化解过剩产能、优化资源配置的重要举措, 也是从根本上落实我国交通部“一省一港”的物流资源整合的重要举措, 对建设国际一流港口和服务经济社会发展具有重要意义^[4]. 针对以上行业发展动态, 国内外众多码头运营商开始寻求港区内码头协同调度合作, 通过整合码头作业资源, 将各码头作业子系统联合决策, 寻求港口降本增效的工程实践辅助决策方案^[5–9]. 本文以码头作业的时空二重性特性作为切入点, 面向多码头协同作业, 在系统工程和计算物流的指导思想下, 对同一地区内多集装箱码头异构多作业空间资源的联合作业与集成调度优化进行了初步探索.

具体来看, 多集装箱码头是典型的分布式、异构、邻近物流枢纽组成的层次化物流处理单元集群, 从计算思维^[10]抽象和自动化视角来看, 隶属于同一港口集团的相邻联合作业的多集装箱码头本质上是异构集装箱码头集群物流广义计算系统(heterogeneous container terminal farm logistics generalized computation system, HCTF-LGCS). 泊位和堆场对于单一集装箱码头装卸作业系统(container terminal handling system, CTHS)和HCTF-LGCS, 皆是核心作业空间, 也是其最宝贵的生产运作资源. 对于单一码头而言, 无论是泊位指派问题(berth allocation problem, BAP)^[11–13]还是堆场分配问题(yard allocation problem, YAP)^[14–16]均是国内外相关研究的热点与难点, 且两者的协同分配与联合调度无论是理论研究还是生产实践中均日益被重视^[17–20], 然而HCTF-LGCS中BAP和YAP的联合探讨目前还较少.

有鉴于此, 我们从分布式、并行、异构、可重构计算的角度去探讨战术和执行层面多集装箱码头泊位-堆场一体化计划调度(multiple container terminal tactical berth and yard incorporate integrative scheduling, MCT-TBY-IIS). MCT-TBY-IIS是传统单一集装箱码头泊位-堆场联合计划问题的自然延伸. 后者是单一前沿(多个泊位)-单一堆场(多个箱区)计划调度, 而MCT-TBY-IIS是其面向多码头的拓展, 本质上是多前沿(多个泊位簇)-多堆场(多个箱区群)的协同计划调度, 也更符合同一组织内邻近码头作为综合交通物流枢纽的行业发展和服务实践需求, 然而因为MCT-TBY-IIS独有的、超高的非线性、耦合性、级联性、动态性和计算复杂度, 无论是理论研究还是生产实践中的相关探讨均还较少.

于是, 本文基于计算的本质, 在计算物流和群集智能的建模优化框架下, 对HCTF-LGCS中的MCT-TBY-IIS进行探讨. MCT-TBY-IIS旨在分析HCTF-LGCS中的泊位簇-箱区群的协同分配优化机理和联合作业策略机制, 研究计算物流和群集智能概念体系下的分布式、异构和可重构泊位簇和箱区群的资源分配方法, 构建MCT-TBY-IIS计算模型, 定义其优化策略, 实现干支线船舶及其装卸集装箱在多码头的联合作业和高效运营, 确保各航班的船期表和配载图的顺利执行, 同时帮助集装箱港口减排增效, 提高资源利用率和整体吞吐量.

2 多集装箱码头泊位与堆场联合调度运筹建模 2.1 建模优化思想

经过10年的探索与凝练, 笔者在2015年的第54届 IEEE Annual Conference on Decision and Control (CDC 2015)初步提出了“计算物流”的定义: 计算物流是基于计算理论和相似理论, 通过提取、转化和运用计算机科学和自动化控制理论的基础概念、思想原理、决策框架、控制机制和调度算法规划、设计、实现、测试和评估复杂物流系统, 并在不同管理层次上计划、控制、调度和决策其相关物流服务过程的一种方法, 它为复杂物流系统的设计、构建、执行、管理和改善提供了一条统一、定量、通用的敏捷高效解决途径^[21].

计算物流为复杂物流系统的规划运营、生产计划、运作调度和资源分配提供了一个既可独立应用^[22,23], 又可以与其他人工智能方法^[24]有机结合的思想方法和解决方案. 在以往的研究中, 计算物流多用于单一大型物流枢纽的生产调度与控制决策中^[25]. 现在我们将其应用于邻近物流枢纽集群的生产运作中, 以期望为约束条件更繁复、计算复杂度更高和管理决策运营目标更多元化的HCTF-LGCS提供敏捷高效的运筹模型与调度策略. 面向问题的探索是计算物流的核心思想之一, 本文面向MCT-TBY-IIS问题, 基于计算物流, 对HCTF-LGCS进行抽象建模和资源分配自动化设计, 进而针对MCT-TBY-IIS问题设计面向层次嵌套结构的两阶段改进帝国竞争算法(hierarchical nesting oriented two-stage improved imperialist competitive algorithm, HNO-TSI-ICA)对其进行求解.

2.2 多码头泊位与堆场联合调度的提出

泊位和堆场是单一CTHS生产运作的重要组成部分, BAP和YAP决定了到港集装箱船舶在码头前沿岸线的靠泊位置、停靠时间以及进出口箱在堆场中堆存位置和停留窗口, 从而确定集装箱船舶靠泊顺序、在港作业时间节点以及集卡行驶路径, 并最终通过码头装卸作业效率直接决定了CTHS的整体运营水平.

MCT-TBY-IIS则较单一码头BAP和YAP的协同优化更进一步, 其在一定程度上是多CTHS作业的缩影和内核, 因为集装箱码头集群的两大主要作业区域内运作空间资源的计划、分配、调度和协同均被囊括其中. 单一CTHS运行时就存在并行、协调、竞争、博弈和同/异步协同等多种关系^[26], 所以MCT-TBY-IIS更是一个高度复杂的超高维空间动态离散事件调度过程, 且其问题复杂度会随着港口布局、码头规模和计划周期的增加而迅速攀升, 极难在既定时间内获得高质量的多目标优化满意解. 同时, MCT-TBY-IIS也是考虑泊位水深约束和出口集装箱可转港作业的多码头动态连续泊位分配问题(multi-terminal dynamic and continuous berth allocation problem, MDC-BAP)^[27]向多码头前/后方堆场的拓展和延伸, 两者之间既有联系又有演进. 从计算复杂性理论的角度来看, 就MCT-TBY-IIS而言, 问题的复杂性不是码头指派问题(terminal allocation problem, TAP)的求解(因为相邻码头的数量往往有限), 而是单一码头中前沿泊位与堆场箱区的协同优化. 具体来讲, MCT-TBY-IIS的重中之重是单一CTHS内BAP与YAP的协调与优化. BAP与YAP的联合求解性能是TAP解析的基础, 它直接决定了MCT-TBY-IIS的满意解质量.

在CTHS的生产运作中, 支持系统运转的组件主要包括前沿泊位、岸桥、内集卡、堆场堆存空间、场桥、堆高机等, 它们围绕班轮和集装箱(两者为码头最根本的服务对象)实施面向集装箱码头的物流广义计算(container terminal oriented logistics generalized computation, CTO-LGC)^[23], 系统组件与服务对象间存在明显的相互制约与动态约束, 这使得BAP和YAP在时间维度和空间维度上都表现出高度耦合性. 生产实践中, 班轮预计/实际到港时间、出口集装箱预存进场选择堆存位置等又在很大程度上决定集装箱船对靠泊位置的偏好, 场桥与集卡的分配与调度也在一定程度上决定堆场作业环境中的拥堵程度, 且影响过程在绝大多数情况下都是双向的, 这就表明在战术决策和作业执行层面上整个系统运作皆是动态波动的.

鉴于MCT-TBY-IIS的非确定性多项式时间完备(non-deterministic polynomial-time complete, NPC)问题属性(强非线性和高复杂性)以及TAP、BAP和YAP三者的深度耦合性, 传统的运筹学、精确算法极难对其进行求解和分析, 甚至当前应用最广泛的商业求解器在可接受的时间范围内也难以得到最优解或较理想解, 于是计算物流和元启发式算法被期望联合用于MCT-TBY-IIS的建模优化. 在阐明MCT-TBY-IIS的建模之前, 我们先进一步分析对BAP和YAP协同优化的理解. 在MCT-TBY-IIS的探讨中, MDC-BAP与多码头周期滚动堆场分配(multi-terminal periodic and rolling yard allocation problem, MPR-YAP)之间的协同程度是可以界定分类的, 本文中通过定义耦合深度描述MDC-BAP与MPR-YAP之间的协同程度: 浅层耦合(shallow coupling)、中等耦合(moderate coupling)、深度耦合(deep coupling). 通过MDC-BAP最优泊位分配方案然后确定MPR-YAP堆场分配计划或者通过MPR-YAP最优堆场分配计划确定MDC-BAP码头泊位分配方案为MDC-BAP与MPR-YAP的浅层耦合; 深度耦合指的是MDC-BAP与MPR-YAP在单个决策时间窗口内始终相互约束和统筹安排, 并随着计划周期的向前滚动作业持续决策. 介于浅层耦合和深度耦合之间的即为MDC-BAP与MPR-YAP的中等耦合, 可以有多种形式. 上述MDC-BAP与MPR-YAP耦合深浅的定义, 是进一步展开对MCT-TBY-IIS的理解分析的根本, 同时它也是面向MCT-TBY-IIS优化设计的框架与基础, 至关重要.

2.3 问题描述

单一码头BAP与YAP联合求解是经典BAP的延伸, 而MCT-TBY-IIS是泊位与堆场联合调度问题在港口集团统一协调背景下的进一步延伸, 也可以认为是MDC-BAP的扩展. 在MDC-BAP中, 码头岸线为顺岸式配置, 船舶动态到港且在计划期开始前能够得知所有集装箱船的预计到港时间、预计挂靠码头编号、进出口集装箱量、计划离港时间, 所有码头内部均有专用堆场, 内部堆场根据集装箱性质分为出口重箱区、出口空箱区、进口重箱区、进口空箱区4个箱区, 码头内部集装箱通过内集卡完成水平运输.

按照港口实际运行状况, MCT-TBY-IIS中集装箱船舶及其运输集装箱在港作业时间节点大致如图1所示, 出口箱在集装箱班轮到港前预存至出口箱堆场, 当船舶到港后, 根据泊位分配计划中实际开始作业时间与实际挂靠码头位置停靠码头开始作业, 岸桥、内集卡、场桥根据堆场作业空间分配计划装卸、运输集装箱, 当集装箱船作业完成后, 进口箱在进口箱堆场留存一段时间后由外集卡提箱最终离开港口, 这也是集装箱和集装箱船在港作业的基本流程.

MCT-TBY-IIS的求解包括3个基本目标: 一是确定船舶挂靠码头和码头岸线停靠位置, 二是确定集装箱船挂靠码头开始作业时刻, 三是确定计划周期内随船作业集装箱在堆场箱区中的贝位和箱位分配. MCT-TBY-IIS中前两个目标与MDC-BAP基本相同, 因此MCT-TBY-IIS可以拆分为MDC-BAP和MPR-YAP两个部分单独讨论后再集成求解, 两部分都具有明显的时空二重性. MDC-BAP已经在我们以往的研究中详细讨论过^[27], 接下来主要讨论MCT-TBY-IIS中的MPR-YAP, 然后和MDC-BAP集成, 从而实现对MCT-TBY-IIS的建模与优化.

码头堆场空间分配是一个动态迭代决策的过程, 在面向单一码头的泊位与堆场联合分配决策中, 可以简单认为泊位分配经过一次决策, 而堆场空间分配经历多次决策, 码头堆场分配决策次数与MDC-BAP计划周期长度、堆场分配决策时间周期长度直接相关. 上述堆场分配策略也是典型的BAP和YAP中度耦合形式之一. 为便于讨论, 本文做如下简化: 堆场空间分配动态决策过程通过滚动计划的形式确定进出口箱在堆场中的堆存空间, 出口箱的滚动计划始于该计划周期内第1艘到港船到港时刻前的某一时刻, 止于最后一艘离港船的离港时刻; 类似地, 进口箱的滚动计划始于第1艘到港船到港时刻, 止于最后一艘离港船离港时刻后的某一时刻.

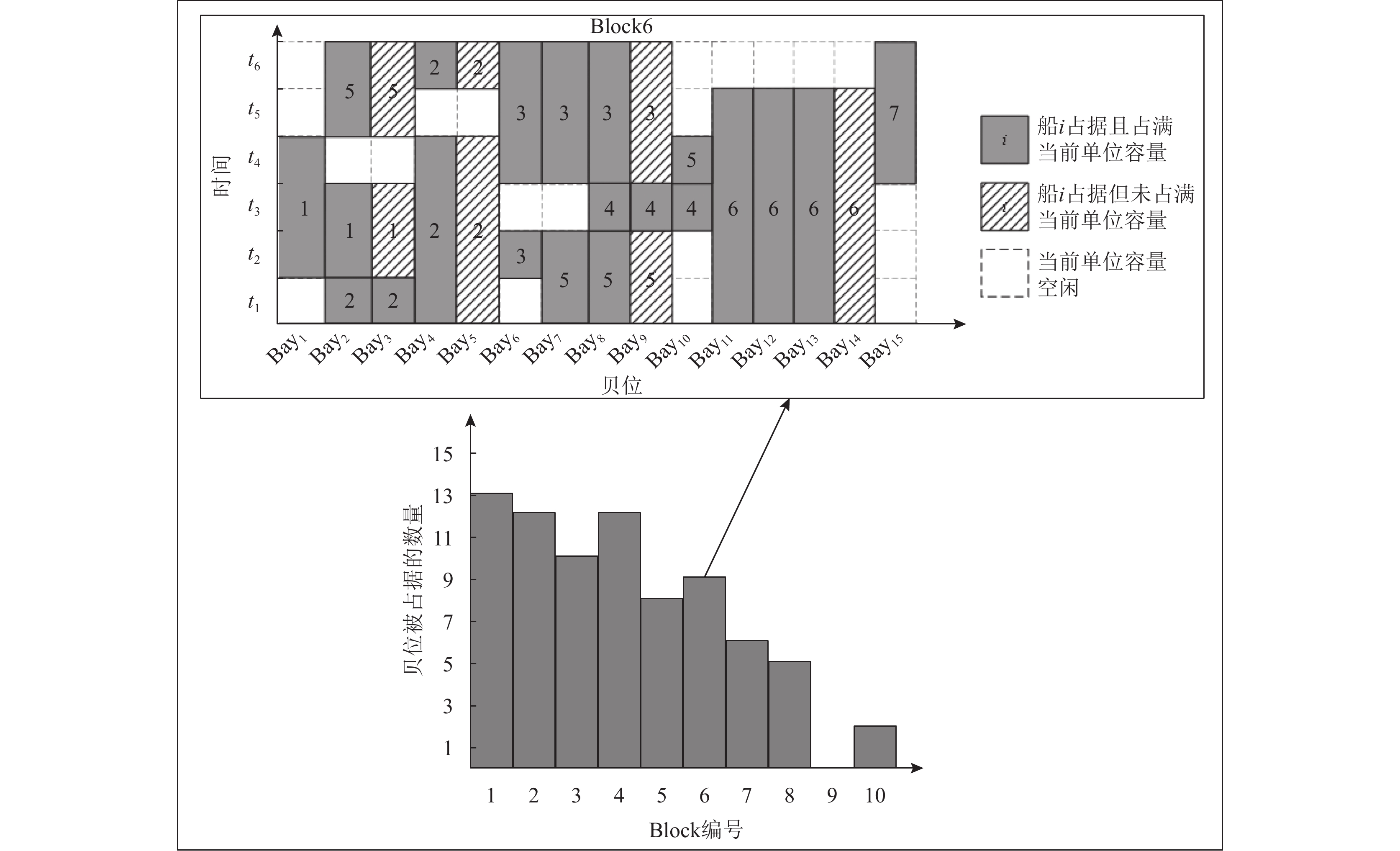
MDC-BAP与多背包问题有诸多相似性, 在我们以往的工作中已经将MDC-BAP抽象为一种多背包问题的变种进行建模分析. 类似地, 同样基于计算物流, 利用多背包问题的变种对MCT-TBY-IIS中的MPR-YAP组件进行运筹建模. 在堆场分配单决策时间周期内, 确定当前决策时间片段中所有船舶进出口箱在堆场箱区的堆存空间包括两个步骤: 确定进出口箱预存于箱区的哪几个Block、确定进出口箱预存于Block中的哪几个贝位, 这个过程可以抽象为多背包问题中的选择背包、放入背包行为, 唯一存在差异的是, 原始多背包问题中背包的容量是连续变化的, 而基于堆场作业空间抽象出的多背包问题中背包的容量变化是离散的, 具体可见图2 (进出口箱混堆模式).

图2是某一码头堆场在第i个决策时间周期中街区(Block)内贝位被占据情况图(假设当前码头堆场箱区有10个Block, 每个Block内有15个贝位), 并且将Block6在滚动决策开始以来的贝位分配情况(上半部分)作了详细展示; 上半部分中, 由虚线围成的小格子数量代表背包容量, 一个小格子代表当前背包的一个单位容量, 每个单位容量可能有3种状态. 图2描述了MCT-TBY-IIS中一个码头的堆场作业抽象分析, 其他码头可作同理分析. 综合多码头背景下泊位与堆场协同调度与决策过程, 基于计算物流, 将MCT-TBY-IIS抽象为多重多背包问题进行研究及设计求解算法.

显然, MCT-TBY-IIS不仅需要评价泊位分配方案的优劣, 还需要评价堆场作业空间分配方案的好坏, 因此MCT-TBY-IIS是一个多目标优化问题, 本文选用一个综合效用函数对多目标优化的各部分线性加权来对MCT-TBY-IIS总体优化的目标进行明确定量评估. 下面给出MCT-TBY-IIS的具体运筹规划模型.

2.4 模型假设与参数介绍 2.4.1 运筹模型假设条件

首先为了更好地描述研究对象和建立合理高效的多目标混合整数非线性规划模型(multi-objectives mixed integer nonlinear programming model, MOMI-NLPM), 本文在MDC-BAP所建立的假设条件之上^[27], 针对MPR-YAP, MCT-TBY-IIS增加了以下假设.

(1)仅考虑当前计划周期内的船舶靠泊作业和对应待作业集装箱的堆场箱区分配;

(2)不考虑在堆场取箱过程中因为翻箱而增加的计算复杂度;

(3)各街区内单个贝位能且仅能被一艘到港船舶的进出口箱占用;

(4)码头前沿岸桥和堆场场桥都能为到港船舶实现持续、稳定的集装箱装卸和堆码作业, 内集卡在船舶装卸船作业过程中数量充足且不会因水平运输作业造成码头内的交通拥堵;

(5)根据码头的生产运营实践, 对于挂靠港口船舶的送取箱作业有严格的时间窗口要求: 出口集装箱的进港时间有严格的时间限制, 即出口箱有明确的最短和最长预存时间限制. 同样鉴于堆场资源的稀缺性, 进口集装箱也有最短和最长的堆场留存时间限制. 为建模方便, 本文将集装箱船舶停靠前沿岸线时刻即是集装箱装卸开始时刻, 集装箱船舶装卸结束时刻即为船舶离港时刻.

2.4.2 模型参数与决策变量

在MDC-BAP所建立的模型参数和决策变量之上, 面向MPR-YAP的探索, MCT-TBY-IIS增加了堆场部分的相关参数和变量介绍.

(1)基础参数

T: 集装箱船装卸作业的所有时间区段集合, T={1, …, t}, 其中t为船舶当前作业所处的时间区段;

T₁: 船舶到港前允许待装箱进场预存的所有时间区段集合, T₁={1, …, t₁};

T₂: 船舶离港后允许待提箱在场留存的所有时间区段集合, T₂={1, …, t₂};

EB_eh: 出口重箱区内所有子街区eh的编号;

EB_ee: 出口空箱区内所有子街区ee的编号;

IB_ch: 进口重箱区内所有子街区ch的编号;

IB_ce: 进口空箱区内所有子街区ce的编号;

EBB_eh-hb: 出口重箱子街区eh内贝位hb的编号;

EBB_ee-eb: 出口空箱子街区ee内贝位eb的编号;

IBB_ch-hb: 进口重箱子街区ch内贝位hb的编号;

IBB_ce-eb: 进口空箱子街区ce内贝位eb的编号;

X_B: 子街区B的X轴坐标;

Y_B: 子街区B的Y轴坐标;

NEH_i: 船i需从出口重箱区装载的出口重箱数量;

NEE_i: 船i需从出口空箱区装载的出口空箱数量;

NCH_i: 船i需对进口重箱区卸载的进口重箱数量;

NCE_i: 船i需对进口空箱区卸载的进口空箱数量;

NB: 子街区中贝位的数量;

NHC: 重箱区贝位堆存集装箱的最大数量;

NEC: 空箱区贝位堆存集装箱的最大数量;

w₁: 目标函数中码头泊位调度过程中产生的作业成本所占的权重;

w₂: 目标函数中堆场内集卡运输集装箱产生的作业成本所占的权重.

(2)决策变量

Pt_i: 船i出口集装箱在船舶到港前提前预存时长;

Rt_i: 船i进口集装箱在船舶离港后堆场留存时长;

SPt_i: 船i待装船出口集装箱开始预存作业时刻;

ERt_i: 船i已卸船进口集装箱结束堆存作业时刻;

$\zeta _{ieh}^1$: 若船i占用出口重箱区街区eh, 则$\zeta _{ieh}^1 = 1$, 否则为0;

$\zeta _{iee}^2$: 若船i占用出口空箱区街区ee, 则$\zeta _{iee}^2 = 1$, 否则为0;

$\eta _{ich}^1$: 若船i占用进口重箱区街区ch, 则$\eta _{ich}^1 = 1$, 否则为0;

$\eta _{ice}^2$: 若船i占用进口空箱区街区ce, 则$\eta _{ice}^2 = 1$, 否则为0;

$\sigma _{ieh {\text{-}} hb}^1$: 若船i占用出口重箱区街区eh内的贝位hb, 则$\sigma _{ieh {\text{-}} hb}^1 = 1$, 否则为0;

$\sigma _{iee {\text{-}} eb}^2$: 若船i占用出口空箱区街区ee内的贝位eb, 则$\sigma _{iee {\text{-}} eb}^2 = 1$, 否则为0;

$\varphi _{ich {\text{-}} hb}^1$: 若船i占用进口重箱区街区ch内的贝位hb, 则$\varphi _{ich {\text{-}} hb}^1 = 1$, 否则为0;

$\varphi _{ice {\text{-}} eb}^2$: 若船i占用进口空箱区街区ce内的贝位eb, 则$\varphi _{ice {\text{-}} eb}^2 = 1$, 否则为0;

NC_ieh-hb: 船i在出口重箱区街区eh贝位hb被分配到的箱量;

NC_iee-eb: 船i在出口空箱区街区ee贝位eb被分配到的箱量;

NC_ich-hb: 船i在进口重箱区街区ch贝位hb被分配到的箱量;

NC_ice-eb: 船i在进口空箱区街区ce贝位eb被分配到的箱量.

(3)辅助决策变量

$K_{i{t_1}}^1$: 若船i的集装箱在t₁时刻占用出口箱堆场, 则$K_{i{t_1}}^1 = 1$, 否则为0;

$K_{i{t_2}}^2$: 若船i的集装箱在t₂时刻占用进口箱堆场, 则$K_{i{t_2}}^2 = 1$, 否则为0;

$\mu _{i{t_1}eh {\text{-}} hb}^1$: 若船i在t₁时刻存放在出口重箱区街区eh贝位hb的出口重箱数量;

$\mu _{i{t_1}ee {\text{-}} eb}^2$: 若船i在t₁时刻存放在出口空箱区街区ee贝位eb的出口空箱数量;

$\nu _{i{t_2}ch {\text{-}} hb}^1$: 若船i在t₂时刻存放在进口重箱区街区ch贝位hb的进口重箱数量;

$\nu _{i{t_2}ce {\text{-}} eb}^2$: 若船i在t₂时刻存放在进口空箱区街区ce贝位eb的进口空箱数量;

$ehs{t_{ieh {\text{-}} hb{t_1}}}$: 若船i在t₁时刻占用出口重箱区街区eh贝位hb, 则$ehs{t_{ieh {\text{-}} hb{t_1}}} = 1$, 否则为0;

$ees{t_{iee {\text{-}} eb{t_1}}}$: 若船i在t₁时刻占用出口空箱区街区ee贝位eb, 则$ees{t_{iee {\text{-}} eb{t_1}}} = 1$, 否则为0;

$chs{t_{ich {\text{-}} hb{t_2}}}$: 若船i在t₂时刻占用进口重箱区街区ch贝位hb, 则$chs{t_{ich {\text{-}} hb{t_2}}} = 1$, 否则为0;

$ces{t_{ice {\text{-}} eb{t_2}}}$: 若船i在t₂时刻占用进口空箱区街区ce贝位eb, 则$ces{t_{ice {\text{-}} eb{t_2}}} = 1$, 否则为0.

2.5 多码头泊位与堆场联合调度运筹规划模型 2.5.1 运筹模型目标函数

MCT-TBY-IIS模型是在MDC-BAP的模型基础之上, 将港区内多个码头堆场作业状况融入到运筹规划中, 进一步拓展了同一港区内多个码头中异构、可重构作业空间资源集群(泊位与堆场)的协同分配, 以寻求港口物流作业过程中更加系统的资源配置与协同优化. MCT-TBY-IIS是单一港口集团背景下的多个码头上泊位指派与堆场分配的联合优化, 究其根本属于分布式、异构和可重构作业空间分配的强耦合、深级联、高复杂的集成调度优化问题.

在以往对单一集装箱码头的BAP和YAP集成调度中, 众多学者通常从船舶或集卡总等待时间^[17]、集卡行驶总距离^[28]、码头作业总加权成本^[29]等几个角度构建了目标函数进行探讨. 综合MCT-TBY-IIS的问题构成以及服务码头-前沿泊位-后方堆场三者作业间的强耦合性, 本文认为码头作业总加权成本能够从多个角度有效评价协同调度方案的优劣, 较适合作为MCT-TBY-IIS的目标函数. 将MCT-TBY-IIS目标函数细化后可分为码头前沿作业总成本和堆场集卡作业总成本, 其中, 多码头泊位作业总成本在文献[29]中已详细介绍, 本节主要介绍码头堆场集卡水平运输作业总成本.

内集卡运输集装箱船i的进出口集装箱产生的运输成本需考虑船i到子街区的曼哈顿距离和箱量, 因此由船i产生的集卡运输成本TTTC_i的来源包括出口重箱区(式(1))、出口空箱区(式(2))、进口重箱区(式(3))、进口空箱区(式(4))这4个部分.

$ TTC_i^1 = TC\cdot\sum\limits_{eh = 1} {\sum\limits_{hb = 1} {\zeta _{ieh}^1\cdot\sigma _{ieh {\text{-}} hb}^1\cdot N{C_{ieh {\text{-}} hb}}\cdot(|{X_{eh}} - {x_i}| + {Y_{eh}})} } $

(1)

$ TTC_i^2 = TC\cdot \sum\limits_{ee = 1} {\sum\limits_{eb = 1} {\zeta _{iee}^2\cdot\sigma _{iee {\text{-}} eb}^2\cdot N{C_{iee {\text{-}} eb}}\cdot(|{X_{ee}} - {x_i}| + {Y_{ee}})} } $

(2)

$ TTC_i^3 = TC\cdot\sum\limits_{ch = 1} {\sum\limits_{hb = 1} {\eta _{ich}^1.\varphi _{ich {\text{-}} hb}^1\cdot N{C_{ich {\text{-}} hb}}\cdot(|{X_{ch}} - {x_i}| + {Y_{ch}})} } $

(3)

$ TTC_i^4 = TC\cdot\sum\limits_{ce = 1} {\sum\limits_{eb = 1} {\eta _{ice}^2\cdot\varphi _{ice {\text{-}} eb}^2\cdot N{C_{ice {\text{-}} eb}}\cdot(|{X_{ce}} - {x_i}| + {Y_{ce}})} } $

(4)

$ TTT{C_i} = TTC_i^1 + TTC_i^2 + TTC_i^3 + TTC_i^4 $

(5)

因此, 港口堆场集卡作业总成本F₂计算公式如式(6)所示:

$ {F_2} = \sum\limits_{q = 1} {\sum\limits_{i = 1} {{m_{iq}}\cdot TTT{C_i}} } $

(6)

虽然码头前沿作业目标函数与堆场作业目标函数都是从港口运作成本的角度评价调度方案的优劣, 但从前期先验结果来看两者具有不同的数量级, 因此需要对两部分的结果进行归一化处理. 本文选择log对数函数进行归一化, 计算公式如式(7)所示. 选择log对数函数有两方面原因: 一方面算法迭代过程中两部分目标结果具有明显的单调性且都大于0; 另一方面两部分目标结果在数量级上相差不大, 符合log对数函数归一化应用的条件和环境. $\lg x_{\max}$是一个先验经验值, 反映子目标函数的最大数量级.

$ {x'} = \frac{{\lg x}}{{\lg{x_{\max}}}} $

(7)

综上所述, 由港口码头作业总成本$ F'_1 $和堆场集卡作业总成本$ F'_2 $可得MCT-TBY-IIS目标函数的计算公如式(8)所示. 权重参数w₁和w₂基本满足数量级较大的子目标函数权重更大, 从物流运作成本的角度考虑是较为可行的.

$ \left\{ \begin{gathered} F = {w_1}\cdot F'_1 + {w_2}\cdot F'_2 \\ {w_1} = \frac{{\lg{x_{1\max}}}}{{\lg{x_{1\max}} + \lg{x_{2\max}}}} \\ {w_2} = 1 - {w_1} \\ \end{gathered} \right. $

(8)

2.5.2 调度模型约束条件

除MDC-BAP中所提约束条件外^[27], 面向MPR-YAP的探讨, MCT-TBY-IIS新增了如下约束:

$ {\textit{SP}}{t_i} = {y_i} - P{t_i} , \;i \in V $

(9)

$ ER{t_i} = {y_i} + (EC{V_i} + IC{V_i})/OT + R{t_i} ,\; i \in V $

(10)

$ {\textit{SP}}{t_i} \leqslant {t_1}\cdot K_{i{t_1}}^1 + M\cdot(1 - K_{i{t_1}}^1) \lt {y_i} $

(11)

$ F = {w_1}\cdot F'_1 + {w_2}\cdot F'_2 ,\; i \in V, {t_1} \in {T_1} $

(12)

$ \begin{split} & {y_i} + (EC{V_i} + IC{V_i})/OT \lt {t_2}\cdot K_{i{t_2}}^2 + M\cdot (1 - K_{i{t_2}}^2) \leqslant ER{t_i} ,\\ & i \in V, {t_2} \in {T_2} \end{split} $

(13)

$ \sum\limits_{{t_2} \in {T_2}} {K_{i{t_2}}^2} = ER{t_i} - {y_i} - (EC{V_i} + IC{V_i})/OT + 1,\; i \in V, {t_2} \in {T_2} $

(14)

$ \sum\limits_{eh = 1} {\sum\limits_{hb = 1} {\zeta _{ieh}^1\cdot N{C_{ieh {\text{-}} hb}} = NE{H_i}} } ,\; i \in V $

(15)

$ \sum\limits_{ee = 1} {\sum\limits_{eb = 1} {\zeta _{iee}^2\cdot N{C_{iee {\text{-}} eb}} = NE{E_i}} } ,\; i \in V $

(16)

$ \sum\limits_{ch = 1} {\sum\limits_{hb = 1} {\eta _{ich}^1\cdot N{C_{ich {\text{-}} hb}} = NC{H_i}} } ,\; i \in V $

(17)

$ \sum\limits_{ce = 1} {\sum\limits_{eb = 1} {\eta _{ice}^2\cdot N{C_{ice {\text{-}} eb}} = NC{E_i}} } ,\; i \in V $

(18)

$ K_{i{t_1}}^1 \leqslant \mu _{i{t_1}eh {\text{-}} hb}^1 \leqslant NHC, \;i \in V, {t_1} \in {T_1} $

(19)

$ N{C_{ieh {\text{-}} hb}} \geqslant \mu _{i{t_1}eh {\text{-}} hb}^1 - NHC\cdot(1 - K_{i{t_1}}^1),\; i \in V, {t_1} \in {T_1} $

(20)

$ K_{i{t_1}}^1 \leqslant \mu _{i{t_1}ee {\text{-}} eb}^2 \leqslant NEC, \;i \in V, {t_1} \in {T_1} $

(21)

$ N{C_{iee {\text{-}} eb}} \geqslant \mu _{i{t_1}ee {\text{-}} eb}^2 - NEC\cdot(1 - K_{i{t_1}}^1),\; i \in V, {t_1} \in {T_1} $

(22)

$ K_{i{t_2}}^2 \leqslant \nu _{i{t_2}ch {\text{-}} hb}^1 \leqslant NHC,\; i \in V, {t_2} \in {T_2} $

(23)

$ N{C_{ich {\text{-}} hb}} \geqslant \nu _{i{t_2}ch {\text{-}} hb}^1 - NHC\cdot(1 - K_{i{t_2}}^2),\; i \in V, {t_2} \in {T_2} $

(24)

$ K_{i{t_2}}^2 \leqslant \nu _{i{t_2}ce {\text{-}} eb}^2 \leqslant NEC, \;i \in V, {t_2} \in {T_2} $

(25)

$ N{C_{ice {\text{-}} eb}} \geqslant \nu _{i{t_2}ce {\text{-}} eb}^2 - NEC\cdot(1 - K_{i{t_2}}^2), \;i \in V, {t_2} \in {T_2} $

(26)

$ \sum\limits_{i \in V} {\sum\limits_{{t_1} \in {T_1}} {ehs{t_{ieh {\text{-}} hb{t_1}}}} } \leqslant NB,\; i \in V, {t_1} \in {T_1} $

(27)

$ \sum\limits_{i \in V} {\sum\limits_{{t_1} \in {T_1}} {ees{t_{iee {\text{-}} eb{t_1}}}} } \leqslant NB, \;i \in V, {t_1} \in {T_1} $

(28)

$ \sum\limits_{i \in V} {\sum\limits_{{t_2} \in {T_2}} {chs{t_{ich {\text{-}} hb{t_2}}}} } \leqslant NB, \;i \in V, {t_2} \in {T_2} $

(29)

$ \sum\limits_{i \in V} {\sum\limits_{{t_2} \in {T_2}} {ces{t_{ice {\text{-}} eb{t_2}}}} } \leqslant NB, \;i \in V, {t_2} \in {T_2} $

(30)

约束(9)给出了SPt_i、y_i、Pt_i这3个变量之间的关系; 约束(10)定义了ERt_i、y_i、Rt_i这3个变量之间的关系; 约束(11)、(12)通过确定了船i的出口集装箱占用出口箱堆场的时间段; 约束(13)、(14)通过确定了船i的进口集装箱占用进口箱堆场的时间段; 约束(15)–(18)表示船i在堆场不同箱区暂存的箱量与船i的装卸箱量相等; 约束(19)、(20)确定了船i占用出口重箱区街区eh贝位hb的时间段以及时间区段t₁内贝位hb暂存的箱量范围; 约束(21)、(22)确定了船i占用出口空箱区街区ee贝位eb的时间段以及时间区段t₁内贝位eb暂存的箱量范围; 约束(23)、(24)确定了船i占用进口重箱区街区ch贝位hb的时间段以及时间区段t₂内贝位hb暂存的箱量范围; 约束(25)、(26)确定了船i占用进口空箱区街区ce贝位eb的时间段以及时间区段t₂内贝位eb暂存的箱量范围; 约束(27)–(30)保证决策时间周期内各类箱区内街区被占用的贝位不超过最大贝位数. 上述约束从时空两个方面确保了MCT-TBY-IIS (尤其是MPR-YAP)运筹规划模型与码头生产实践相符.

3 多码头泊位堆场联合调度优化框架与算法 3.1 面向计算思维的帝国竞争算法

帝国竞争算法(imperialist competitive algorithm, ICA)是由Atashpaz-Gargari等人于2007年提出的一种基于群体的随机优化搜索算法, 与其他受生物行为启发的群集智能算法不同, ICA受社会行为启发, 是通过模拟殖民地同化机制和帝国竞争机制而形成的一种优化方法^[30].

作为群集智能的典型代表之一的ICA本质上也可以认为是计算思维在复杂适应系统(complex adaptive system, CAS)和多智能体系统(multi-agent system, MAS)中的应用与延伸, 是在对国家智能体集群动态交互网络(dynamic interactive network, DIN)分析的基础上, 引入同化、竞争、协作、乃至生物进化等机制, 形成的一系列新的进化计算算法^[31]. 从计算思维和计算本质的抽象视角来看, ICA引入的上述演化机制均可以认为是一种广义的“计算”, 进而通过这些广义计算的机械化与自动化来产生国家智能体种群相变和涌现机制, 实现在高维复杂问题空间中的高效搜索与问题求解. ICA已经被应用于大规模组合优化问题进行探索求解, 尤其是生产调度、智能制造、物流配送与资源分配的探讨^[32–35], 但目前ICA应用于集装箱码头生产服务任务调度与资源分配中的探索还较少^[27], 用于MPR-YAP和MCT-TBY-IIS的相关探讨还未有发现.

与此同时, 计算物流是计算思维面向复杂物流系统(complex logistics system, CLS)的应用与拓展, 更具体来看, 计算物流是计算思维在物理世界中, 面向物流工程与管理领域中大规模与超大模型组合优化问题的迁移、定制、修正和整合. 于是我们在计算思维的方法框架下, 面向CLS、CAS和MAS对MCT-TBY-IIS展开面向问题的探索.

3.2 面向MCT-TBY-IIS的ICA设计

如前所述, 在MCT-TBY-IIS中, MDC-BAP和MPR-YAP之间的协同求解程度包括浅层耦合、中等耦合、深度耦合3种模式, 本文力求在求解代价、计算复杂度、计划可用性和资源利用效率之间取得平衡, 故采用中等耦合模式设计MOMI-NLPM模型优化算法. 鉴于MCT-TBY-IIS中MDC-BAP和MPR-YAP之间的强耦合性, 在计算物流和群集智能概念框架下, 面向MCT-TBY-IIS问题探索指导思想下, 其求解算法应是一种在ICA中嵌套ICA的群集智能优化算法架构, 即面向层次嵌套结构的二阶段改进帝国竞争算法(hierarchical nesting oriented two-stage improved imperialist competitive algorithm, HNO-TSI-ICA), 这是一个典型的面向计算物流模型设计的群集智能优化算法. 因为面向问题的探索由始至终一直贯穿于HNO-TSI-ICA的算法设计中, 其寻优结构主要是为了适配MCT-TBY-IIS超高维多重多背包问题空间特性, 所以求解算法整体具有一定的计算复杂度, 但鉴于MCT-TBY-IIS的高度非线性、级联性、耦合性和复杂性, HNO-TSI-ICA的算法结构仍是可接受且合理的. 上述面向MCT-TBY-IIS的HNO-TSI-ICA智能算法计算流程如图3所示.

从图3可知, 面向MCT-TBY-IIS的HNO-TSI-ICA的智能优化框架虽然是基于ICA类算法, 但是其本质却与计算物流相似, 都具有典型的面向问题探索的内涵, 且寻优搜索机制紧紧围绕MCT-TBY-IIS的非线性、耦合性和复杂性展开. 图3中, t₁指ICA类算法构件1 (imperialist competitive algorithm class algorithmic component 1, ICA-CAC-1)的当前迭代次数, T₁指ICA-CAC-1的最大迭代次数. 类似地, t₂指ICA类算法构件2 (imperialist competitive algorithm class algorithmic component 2, ICA-CAC-2)的当前迭代次数, T₂指ICA-CAC-2的最大迭代次数. ICA-CAC-1为计划周期内到港船舶确定其在哪个码头靠泊及其在各个码头的靠泊作业计划, ICA-CAC-2在ICA-CAC-1给出的MDC-BAP既定满意解下, 为当前滚动时间周期内挂靠船舶的进出口集装箱集合确定多码头间运输(inter-terminal transportation, ITT)成本较优的预存箱区及贝位(Block+Bay).

与此同时, HNO-TSI-ICA蕴含的MCT-TBY-IIS中等耦合特性也能在图3中发现其特征. ICA-CAC-1确定的MDC-BAP高质量满意解是当前迭代次数下种群中的最优个体解, 在整个面向MCT-TBY-IIS问题空间的HNO-TSI-ICA中, ICA-CAC-1是不断演化的, 是演化主轴, 驱动复合算法向前求解模型的; 而ICA-CAC-2在ICA-CAC-1的一次迭代过程中会完成整个寻优搜索生命周期并被持续调用. 假设算法1单次迭代的最大计算复杂度为O(N), 算法2单次迭代的最大计算复杂度为O(n), MDC-BAP计划周期长度为L, MPR-YAP滚动决策周期长度为l, 计划周期内到港集装箱船数量为VN, 则面向MCT-TBY-IIS的求解算法单次迭代的最大计算复杂度为{O(N)+4VN$\left\lceil {L/l} \right\rceil $O(n)}. 由此可见, HNO-TSI-ICA的计算复杂度中求解MPR-YAP的堆场作业空间分配的ICA-CAC-2贡献度最大. 于是HNO-TSI-ICA的总体计算复杂度主要由计划期内集装箱船数量、MDC-BAP计划周期长度和MPR-YAP滚动决策周期长度的相对比值、ICA-CAC-2计算复杂度3个参数共同决定.

在HNO-TSI-ICA的搜索寻优体系下, 外层框架每次迭代得到的TAP和BAP联合指派计划都作为一个备选方案进行存储, 并在达到最大外层迭代次数后通过一个加权函数评估所有TAP、BAP和YAP备选方案的优劣, 并输出最优的码头指派、泊位分配和堆场调度统筹规划方案. HNO-TSI-ICA相对于通过确定TAP/BAP后来求解YAP, 或者通过求解TAP/YAP后来确定BAP的TAP、BAP和YAP统筹规划计算模型, 面向HNS-TSI-ICA设计的嵌入元启发式寻优算法架构中码头前沿泊位与后方堆场的多资源协同运作会更加自然和紧密, 也更有利于MOMI-NLPM和HNO-TSI-ICA组合在港口生产实践中的应用.

3.3 HNS-TSI-ICA的主要构件设计

HNS-TSI-ICA中的主要构件ICA-CAC-1和ICA-CAC-2均采用我们在以往研究中详细定义的ICA及其两阶段改良变种, 即面向0-1背包问题的二进制帝国竞争算法(binary imperialist competitive algorithm, BICA)^[36], 面向帝国兴替的双同化帝国竞争改进算法(double-assimilation of prosperity and destruction oriented improved imperialist competitive algorithm, DPDO-IICA)^[37]和改进二阶段帝国竞争算法(two-stage improved imperialist competitive algorithm, TSI-ICA)^[27]以及标准ICA. 面向MDC-BAP的ICA-CAC-1的设计与应用已经在文献[27]中进行了详细阐述, 下面对ICA-CAC-2如何应用到MPR-YAP中进行简述.

与ICA-CAC-1一样, ICA-CAC-2可以选用4种算法, 即ICA、DPDO-IICA、BICA和TSI-ICA, 算法的搜索寻优方式已经基本确定, 没有确定的主要是算法如何应用到MPR-YAP中, 其中最重要的是面向类ICA的MPR-YAP问题解空间如何构建, 即MPR-YAP如何编码映射到ICA及其变种算法中. 对于所有的4种ICA类算法, 面向MPR-YAP进行问题探索时, 均采用整数编码方式, 编码串的长度n由当前船舶在当前滚动决策周期内待分配预存堆场箱区空间的集装箱所需的最少贝位数决定; 编码串上基位的取值$x \in {\text{[}}1, B{\text{]}}$, (对于同一艘到港船舶, 对应4个相应的字符串), 且其中B是不同类型箱区(Zone)中街区(Block)的数量, 即Agent采用动态变长字符串. 考虑到MDC-BAP和MPR-YAP集成调度的超高计算复杂度, 对MPR-YAP解空间的大小作一定程度的简化, 使ICA-CAC-2仅搜索尚有贝位(Bay)空闲的街区, 即B的取值是面向不同箱区中作业空间分配的实际情况动态变化的, 这是一个资源动态计划、分配、占用、回收、再分配和再回收的资源循环调度过程. ICA-CAC-2编码串长度和编码串上基位取值都是面向计划期内滚动时间节点的当前时刻取值的, 是一个动态变化、实时映射、高度复杂的自学习、自组织、自适应的演化过程.

4 生产实例与实验分析 4.1 多码头联合生产实例

探讨MCT-TBY-IIS采用与文献[27]中相同的测试算例, 同为根据我国东南沿海某港口集团下辖码头A和B的实际运作情况生成, 挂靠集装箱港口的集装箱船舶规格与运营数据亦与文献[27]相同, 均符合实际班轮到港分布与作业特征. 码头A和码头B堆场的相关数据依据现实堆场布局特征抽象, 具有合理性、可信性且基本符合我国沿海主流堆场实际作业特征, 是中国东南沿海大中型集装箱码头的典型代表.

两个码头堆场的主体均被分成4类箱区, 分别是出口重箱区、出口空箱区、进口重箱区、进口空箱区, 每类箱区由若干个街区(Block)组成, 每个Block内部包括一定数量的贝位(Bay). 集装箱通过明确其所在的Block和Bay进而确定其在堆场中的箱位(Slot). 重箱区贝位容量为40标箱(twenty-foot equivalent unit, TEU), 空箱区贝位容量为60 TEU, 不同码头堆场街区内贝位的数量也有一定的差异, 码头A堆场街区的贝位数量为50个, 码头B堆场街区的贝位数量为60个. 值得一提的是, 码头A和码头B的堆场布局都为不规则设计, 这更符合现实的堆场布局, 图4和图5形象地展示了码头A和码头B的主体平面布局, 其中码头A的纵深为648 m, 码头B的纵深为780 m.

本文选用文献[27]中计划周期为7天和10天的算例LE1-LE8作为MCT-TBY-IIS测试算例, 下面对未提及的作业流程及相关指标作简要介绍. 挂靠港口班轮装卸的进出口集装箱中, 进口箱量与出口箱量的比例为1:2, 其中75%的集装箱为重箱, 25%为空箱; 出口箱在班轮到港前的6–48 h内随机进场预存至出口箱堆场, 进口箱在船舶离港后的6–48 h内由外集卡随机提箱离开进口箱堆场, 堆场分配的决策时间周期确定为2 h.

MCT-TBY-IIS计划周期内集装箱船的出口箱从第1艘到港船实际到港时刻的前48 h开始占用出口箱堆场, 到最后离港船实际离港时刻全部离开出口箱堆场; 计划周期内集装箱船的进口箱从第1艘到港船实际到港时刻开始占用进口箱堆场, 并在最后一艘船舶离港时刻之后的48 h全部离开进口箱堆场. 上述堆场作业流程与进出口箱占用堆场时间指标基本符合生产实践中我国大部分沿海集装箱码头的生产经营现状. 面向LE1–LE8的8个测试算例, 我们在高端工作站(Intel Core i9-13900 处理器, 内存128 GB)运行IBM ILOG CPLEX商业求解器, 设置运行时间100 h, 每个实例运行10次, 无一能获得满意解, 更不用说最优解了. 上述计算实验充分说明了MCT-TBY-IIS超高的非线性、耦合性和复杂性.

4.2 模型求解与结果分析

本节选取在MDC-BAP中表现最好的算法DPDO-IICA作为外层框架算法ICA-CAC-1, 并分别结合ICA、DPDO-IICA、BICA、TSI-ICA构建面向MCT-TBY-IIS问题探索的嵌入式DPDO-IICA算法, 命名为DPDO-IICA_ICA、DPDO-IICA_DPDO-IICA、DPDO-IICA_BICA和DPDO-IICA_TSI-ICA, 收集4个算法在LE1–LE8算例上求解码头集群的平均加权作业总成本(average weighted total operation cost, AWTOC)、码头前沿泊位分配平均作业成本(average operating cost of berth allocation, AOCBA)和内集卡水平运输平均作业成本(average operating cost of horizontal transferring for yard trailers, AOCHT), 其测试结果如表1所示.

从表1可以了解到, 改进ICA作为ICA-CAC-2应用于嵌入式DPDO-IICA决策堆场作业空间分配计划时均优于经典ICA, 表现在AOCHT指标均相对较优, 说明改进ICA在求解堆场作业空间分配问题上的改进也是较为有效的. 从AOCBA作业指标来看, 基于不同ICA-CAC-2的嵌入式DPDO-IICA在相同算例的结果均不相同, 这能够证明本文所设计的HNS-TSI-ICA算法架构中ICA-CAC-1与ICA-CAC-2间的耦合关系明确存在, 这也从一个侧面表明MDC-BAP与MPR-YAP之间的强耦合性, 嵌入式DPDO-IICA在演化过程中前沿与堆场作业子系统间持续相互传递当前迭代次数下搜索到的较优决策计划, 并在外层框架ICA-CAC-1的驱动下, 从满意解池中输出加权全局最优的协同调度计划, 表1中的实验结果较好符合上述预期与分析过程. 同时由上可知, HNS-TSI-ICA算法架构虽然较精确求解算法(如CPLEX中的分支定界算法)能够部分克服MCT-TBY-IIS的超高计算复杂度, 但仍然无法确保在允许的时间范围内获得问题的最优解.

按照AWTOC、AOCBS和AOCHT指标的结果对4种嵌入式DPDO-IICA进行排名以评价算法间性能的强弱, DPDO-IICA_ICA、DPDO-IICA_DPDO-IICA、DPDO-IICA_BICA、DPDO-IICA_TSI-ICA这4个算法的排名为: 3.50、2.90、1.35、2.25. 故可粗略认为DPDO-IICA+BICA组合求解本文中MCT-TBY-IIS的相对性能是最强的. 当前实验的结果和分析过程表明HNO-TSI-ICA能够为求解MCT-TBY-IIS提供柔性且高效的智能优化算法架构及类ICA算法构件.

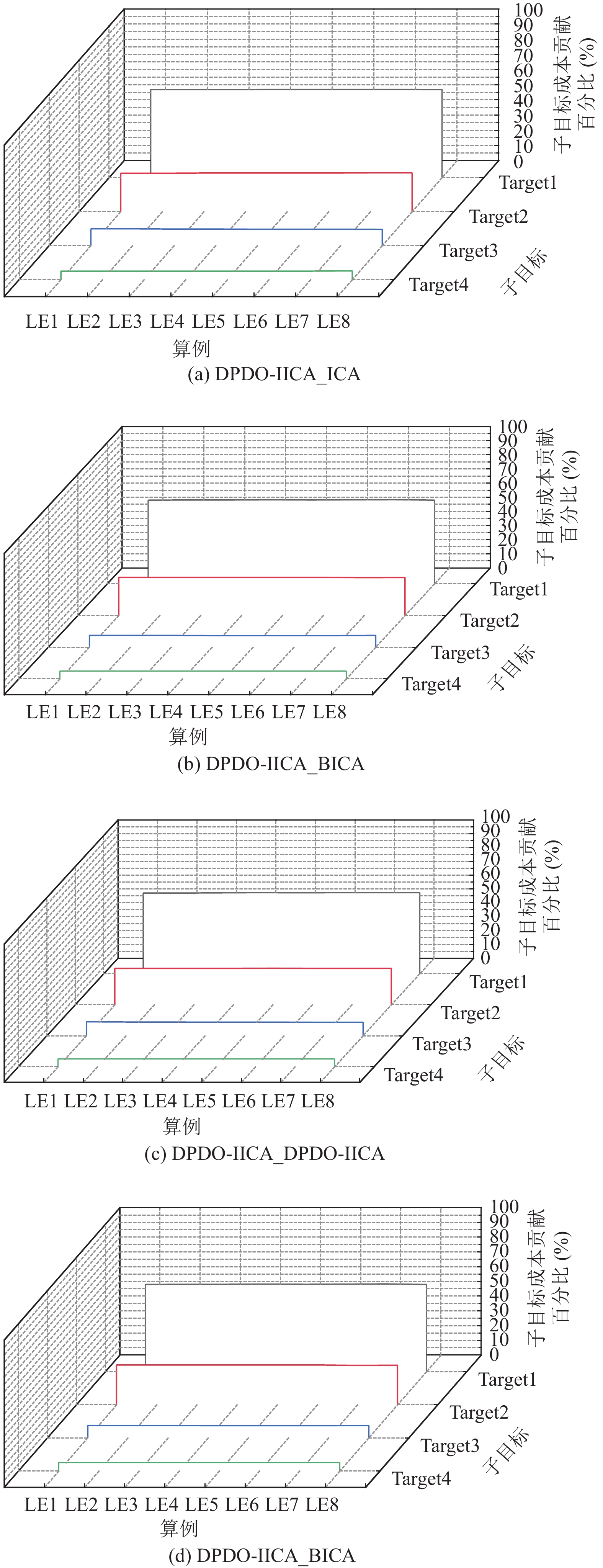
为进一步分析MCT-TBY-IIS协同调度计划中堆场作业成本子目标的二级子目标(出口重箱区集装箱水平运输成本-Target1、出口空箱区集装箱水平运输成本-Target2、进口重箱区集装箱水平运输成本-Target3、进口空箱区集装箱水平运输成本-Target4)在不同算例上对堆场作业成本子目标的贡献情况, 收集上述4种嵌入式DPDO-IICA算法在测试算例上求解结果的堆场作业二级子目标成本对堆场作业总成本的贡献百分比如图6所示.

从图6中能够发现4个算法求解结果的二级子目标成本贡献度在不同/相同计划周期中, 面向不同作业负荷的算例上均未发生较明显的变化, 说明堆场作业子系统中各二级目标成本的结构较为稳定, 基本不受计划周期内港口负荷和计划周期长度的影响. 其中, 出口箱区集装箱水平运输成本贡献度稳定在83%上下, 重箱区集装箱运输成本贡献度稳定在69%左右. 图6的相关结论和分析对于港口在战术和执行决策层面优化资源配置、降本增效、提升效率提供了有意义且值得借鉴的思路和依据.

在MCT-TBY-IIS问题中, 衔接多码头间泊位与堆场协同作业的纽带之一是集装箱船舶预挂靠码头与实际挂靠码头存在事实上的偏差, 文献[27]中已经基于计算物流和ICA, 面向泊位协同分配验证了MDC-BAP的可行性与先进性. 本文更进一步, 从MCT-TBY-IIS中堆场作业空间分配子问题上进一步验证了多码头协同调度模式的先进性与必要性. 这些充分证明了MCT-TBY-IIS研究的必要性与迫切性, 也为我国“一省一港”整合思路高效落地提供运筹优化的技术支撑.

4.3 面向问题探索的集成计算优化设计范式

于是, 在HNO-TSI-ICA优化框架下, 面向MCT-TBY-IIS问题的探索, 本节选取DPDO-IICA+TSI-ICA的算法组合, 以初步探讨计算物流与群集智能相结合的面向问题探索的运筹集成计算优化设计范式(operations integrated computation optimization design paradigm for problem-oriented exploration, OIC-ODP-POE)的可行性、可用性与可信性.

与此同时, 我们也采用多码头独立生产模式对各码头的泊位与堆场协同分配展开探讨, 以便进一步说明MCT-TBY-IIS的性能优越性. 对于各单一码头的泊位和堆场联合调度, 我们借鉴文献[27]的研究结论, 采用面向连续泊位的先到先服务调度算法(first come first served scheduling algorithm for continuous berths with subtle granularity, FCFS-CBSG)和TSI-ICA的算法组合进行求解. 码头独立生产模式按照船舶预挂靠码头计划进行靠泊作业, 并依次得到单码头上的泊位调度方案和对应的堆场作业空间分配计划, 其中FCFS-CBSG主要应用于单码头动态连续泊位调度问题, 按照启发式规则依次为当前码头上的到港船舶确定它们在时空图中的位置.

DPDO-IICA+TSI-ICA的ICA算法组合旨在面向不同的算例, 得到集装箱码头联合作业模式下, 高质量的加权最优调度计划, 即使无法证明上述作业空间资源分配计划中的堆场作业空间调度方案一定是所有堆场作业空间调度方案中的最优方案, 但是若该方案仍优于码头独立生产模式, 则一定能够通过“有且不仅有一个解的结论”证明多码头堆场作业系统联合作业模式能够优于码头独立生产模式.

分别从LE1-LE8中各选取一个具有代表性的实例作为研究算例, 收集码头联合作业与独立生产模式下算例求解结果的堆场作业总成本如表2所示. 从表2能够发现MPR-YAP联合作业模式在LE4、LE5、LE6、LE8上表现优于独立生产模式, 遵循存在一个联合作业计划优于独立生产计划, 则前者优于后者的结论能够在MCT-TBY-IIS的堆场作业空间分配子问题上得到印证, 即从MPR-YAP来看, MCT-TBY-IIS仍具有先进性, 并且表现为计划周期内船舶规模越大, 联合作业模式表现越好, 即在大任务负载情况下, MCT-TBY-IIS更为适用, 这一结论也基本符合联合作业模式中MDC-BAP上的表现^[27]. 这也从一个侧面说明同一集装箱港口应当何时采用多码头联动的生产服务模式.

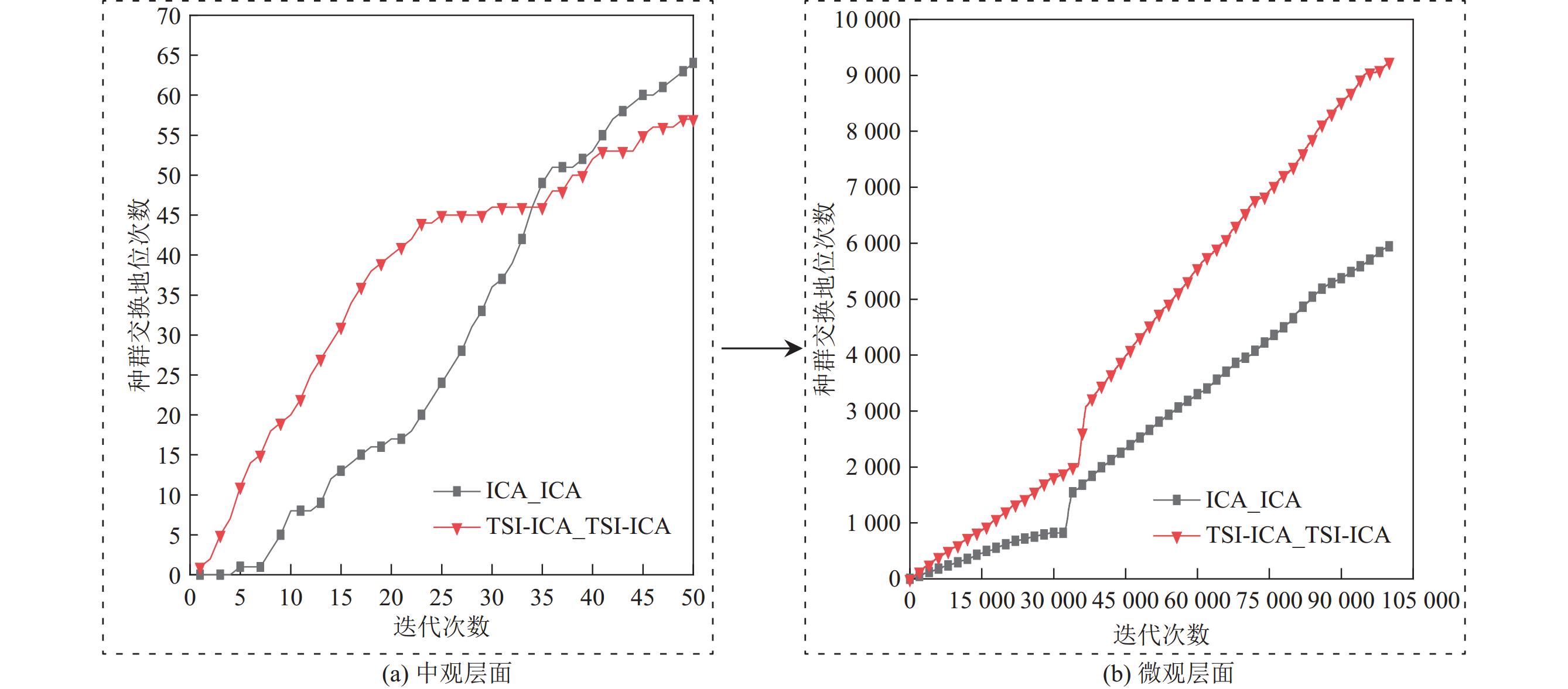
4.4 嵌入式改进ICA演化原理解析

由前述的第3节可知, 面向MCT-TBY-IIS的HNO-TSI-ICA是一种嵌入式层叠计算架构, 通过ICA-CAC-1的每次迭代搜索先确定多码头泊位协同分配计划, 并进一步基于上述计划通过动态滚动决策, 在每个决策周期中调用嵌入的ICA-CAC-2确定各码头堆场作业空间分配计划. 为了形象地展示HNO-TSI-ICA的种群演化过程, 本节收集了“TSI-ICA+TSI-ICA”组合(命名为TSI-ICA_TSI-ICA)和“ICA+ICA”组合(命名为ICA_ICA)求解MCT-TBY-IIS时中观层面的ICA-CAC-1和微观层面的ICA-CAC-2中种群交换地位次数随总迭代次数变化的迭代曲线图, TSI-ICA_TSI-ICA和ICA_ICA在算法构件一和算法构件二的搜索寻优机制均不相同, 这为探讨面向MCT-TBY-IIS问题探索的HNO-TSI-ICA提供了良好的多目标优化计算范式评估.

HNO-TSI-ICA的ICA-CAC-1主要是面向中观战术层面求解MDC-BAP, 内嵌的算法构件二则是应对堆场空间资源分配MPR-YAP, 从图7可以了解到, 战术中观层面种群交换地位次数的一次更新, 微观层面种群交换地位次数就已经更新迭代了较大数量的次数, 换句话说, HNO-TSI-ICA的外层算法构件ICA-CAC-1迭代寻优一次, 内嵌的算法构件二ICA-CAC-2就会被调用一次, 且其会完整地执行一次求解(即迭代寻优多代求得一个阶段性的高质量满意解, 供ICA-CAC-1性能评估). 外层算法构件一对内嵌算法构件二的调用次数与泊位分配计划周期的长度和堆场调度决策周期的长度最为相关. 此外, 从两个算法求解结果来看, TSI-ICA_TSI-ICA在MDC-BAP和MPR-YAP的集成求解以及对单个子问题的求解上均表现得更优, 其结果原因可以部分用图7中中观战术层面和微观执行层面的种群交换地位次数进行解释, 面向MDC-BAP和MPR-YAP对应的ICA类算法构件的种群演化寻优与协同交互共同决定了HNO-TSI-ICA在MCT-TBY-IIS问题空间中的收敛行为与性能表现.

5 结语

本文对当前港航领域中涌现的强非线性、级联性和高耦合度、复杂度的面向进出口集装箱同时装卸作业的MCT-TBY-IIS问题进行了较为深入的探讨, 并面向MCT-TBY-IIS, 融合计算物流与群集智能, 设计了HNO-TSI-ICA的优化计算框架及其相应的ICA类算法构件. 在MCT-TBY-IIS的建模优化探索与求解中, 获得以下初步结论: (1)通过对MCT-TBY-IIS的作业流程与生产运营分析, 基于计算物流利用多重多背包问题对MCT-TBY-IIS进行抽象和建模, 并据此建立MOMI-NLPM, 是一个合理、高效和敏捷的面向问题探索的解决方案. 通过对MOMI-NLPM中目标函数的成分分解与分析, 发现在MCT-TBY-IIS的优化目标之一堆场作业子系统目标成本结构较为稳定, 不受计划周期内港口负荷和计划周期长度的影响; 其中, 出口箱区集装箱水平运输作业成本的贡献度在堆场作业子目标成本的比重最大, 稳定在83%左右. (2)面向MCT-TBY-IIS, 提出了一种嵌入式元启发式算法框架HNO-TSI-ICA, 且在其中DPDO-IICA+BICA的ICA类算法组合表现较好, 结合文献[27]的实验探讨, 可以发现BICA在MPR-YAP的求解上性能较优. (3)分别面向MCT-TBY-IIS的两个重要组成部分: MDC-BAP和MPR-YAP, 利用计算物流和ICA类智能优化算法重点对码头联合作业和独立生产模式进行了对比分析. 大量的计算实验表明, 对多码头作业空间资源进行协同调度与滚动分配能够明显降本增效, 尤其是在码头集群处于繁重作业负荷的情况下. 未来将进一步面向MCT-TBY-IIS和HNO-TSI-ICA, 探讨深度耦合下多码头(三码头及其以上情况)的生产运营与联合作业, 同时对OIC-ODP-POE面向复杂物流系统任务调度与资源分配问题的可行性与可用性进行初步探索.