计算机视觉是人工智能的一个重要领域, 它使计算机能够从数字图像, 视频等一些视觉输入中获取有意义的信息. 其中深度信息是计算机视觉任务中基本的任务之一, 可广泛应用于三维重建、自动驾驶、虚拟现实、工业生产等任务.
传统的深度信息获取方式主要分为主动深度传感和被动测距传感, 主动深度传感主要是通过机械设备来获取场景的深度信息, 常见的设备比如LiDAR、RGB-D相机. 目前由于LiDAR设备本身比较昂贵, 且人力成本较高, 难以推广. RGB-D相机根据近红外光的反射, 通过TOF (time of flight)、结构光等方法获得场景的深度信息. 但是由于深度测距设备本身的测量距离较短, 且对场景环境有一定要求, 因此无法在室外环境广泛应用. 被动测距传感的方法主要分为两类: 单视图和多视图. 多视图的方法主要使用双目图像进行推理, 根据双目测距原理直接计算出场景的深度信息, 这种方法的优点是成本低, 室内外环境都适用, 缺点是基线长度限制了测量范围. 单目深度估计从单幅图像中估计像素深度信息, 成本低, 应用灵活方便. 然而, 由于缺少诸如运动、立体视觉等可靠的深度线索, 并且对于一张RGB图像来说, 其深度信息有无数种可能, 也就是对应无数个可能的深度图, 因此该任务非常具有挑战性.
随着深度学习的兴起与发展, 卷积神经网络在单目视觉中的应用也快速发展. 深度学习在解决目标识别、图像分割等问题中性能优越, 这些方法也大量迁移应用于单目深度估计. 基于RGB图像与深度图像存在某种映射这一基本假设, Eigen等[1]将卷积神经网络应用于单目深度估计任务, 并预测了较准确的深度图. 随后Eigen和他的团队提出可以用于多任务的通用多尺度网络框架. Laina等[2]提出了全卷积残差网络(fully convolutional residual network, FCRN), 提高了输出分辨率, 并提出了更高效的上采样模块, 同时加入berHu损失函数, 进一步提高了网络性能. Hu等[3]提出一种多尺度特征融合的网络结构, 包含编码器、解码器、多尺度特征融合模块和细化模块4个部分, 提升了网络预测结果的精度以及在物体边缘处的预测. Chen等[4]提出一种基于结构感知的残差金字塔网络结构, 并提出了残差细化模块(residual refinement module, RRM) , 用于在解码器优化不同尺度的深度图. 此外, 还提出自适应密集特征融合模块(adaptive dense feature fusion, ADFF)来融合所有尺度的特征, 用于残差预测, 进一步优化解码器的残差深度图.但是以固定比例融合所有尺度的特征并不能更好地利用不同尺度特征图的相同物体的特征信息. Song等[5]、Zhang等[6]都将拉普拉斯金字塔结构用于架构设计中,对不同层次的编码端特征进行残差恢复, 并逐步融合预测结果. Miangoleh等[7]提出一种通过场景内容自适应合并的方法, 该方法通过合并多尺度特征和不同场景物体的深度估计来生成一个高分辨率的深度图. Ranftl等[8]引入vision Transformer代替卷积神经网络作为网络主干, 为深度估计提供了更细粒度和更全局性的预测. 由于深度信息有连续性的特点, 所以也有结合条件随机场(conditional random field, CRF)的深度估计方法, 比如Cao等[9]、Yuan等[10]通过优化全连接CRF并与多尺度网络结合来提高性能. Wu等[11]提出了一种多层次上下文和多模态融合网络(multilevel context and multimodal fusion network, MCMFNet), 用于融合多尺度多层次上下文特征图, 并从深度信息中学习目标边缘, 可以获取具有清晰边界的检测结果. 但是, Hu等[12]已经证明, 不同的通道特征在模型中并不发挥同样重要的作用, 因此, 加强重要通道的特征, 弱化不重要通道的特征有助于提升模型功能性. Yang等[13]提出了深度自适应融合模块(deep adaptive fusion module, DAFM), 对不同尺度的深度图进行估计, 并对这些深度图进行加权求和, 通过减少不同尺度深度图之间的信息差距, 提高融合效果. Xu等[14]提出一种结合坐标注意力和特征融合的预测框架, 包含注意力、多尺度和特征融合模块, 将有用的底层和高层上下文特征集成在一起. Xu等[15]提出一种多层次特征融合模块, 通过水平和垂直结构连接特征图. 并引入一个可学习的权重, 通过该权重实现自适应融合, 以保留最佳特征.
Lee等[16]将空洞空间卷积池化(atrous spatial pyramid pooling, ASPP)模块引入单目深度估计任务, 并提出局部平面引导模块 (local planar guidance, LPG) , 将解码器的特征图与最终输出深度图联系起来, 取得了较好的预测结果. Wu等[17]提出DenseASPP网络模型, 通过融合两种跳层连接来利用不同尺度下的视觉特征, 学习其中的有用特征, 并将残差模块集中到ASPP中, 将残差块中的特征用于增加后向梯度. 廖志伟等[18]提出一种分层压缩激励ASPP的结构, 引入了分层的压缩激励结构块(hierarchical compress excitation, H-CE), 将空间注意纳入网络结构中, 允许网络进行特征重新校准. 但是单目深度估计任务是密集预测任务, 空洞卷积会丢失较多像素点信息, 对小物体的预测有一定的影响. 在这些方法中, 随着卷积神经网络深度的加深, 经过不断的下采样, 特征图中的深度信息会大量丢失, 对深度的预测结果产生较大的影响, 导致边缘模糊等问题的出现. 虽然通过跳层连接以及对特征图的上采样可以保留和恢复一部分深度信息, 但是效果不理想.
本文提出一种自适应多尺度特征融合, 对不同特征图进行统一尺度, 根据训练学习得到的权重进行融合, 并在已经融合的特征图基础上进行下一次融合, 实现自底向上的堆叠融合, 更好保留重要的深度信息, 充分利用相同场景中的物体在不同尺度下的特征信息, 解决物体边缘模糊的问题, 进一步提高深度预测的准确性; 其次在使用ASPP模块对深层特征图进行空洞卷积时, 引入将浅层特征图池化后的特征图, 丰富场景信息, 改善在单目深度估计中使用ASPP模块导致的小物体预测不准确的问题.
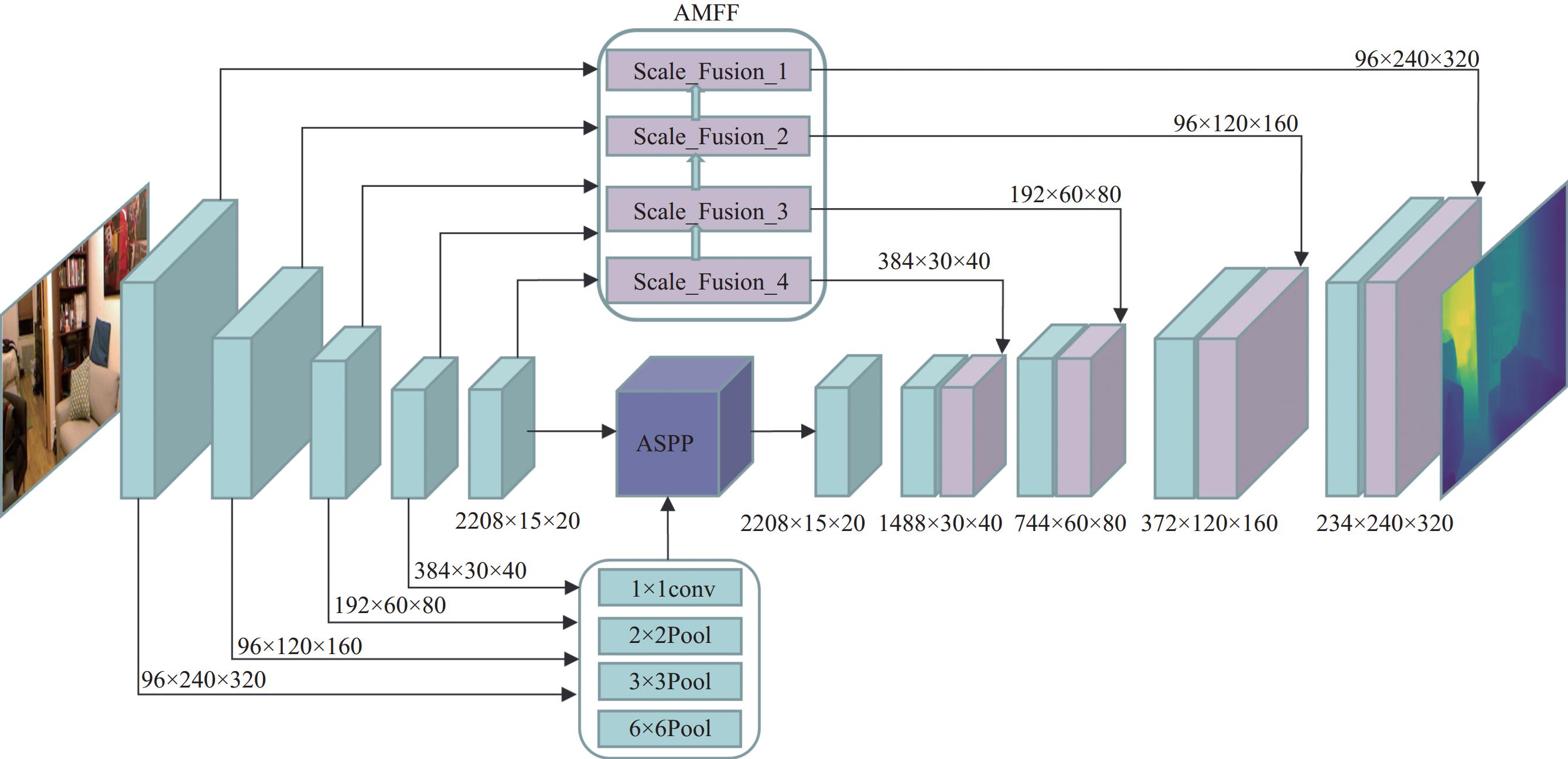
2 网络结构设计本文的网络结构如图1所示, 采用编码-解码网络结构, 并在解码端增加多尺度自适应融合模块(adaptive multi-scale feature fusion, AMFF)和融合浅层特征信息的ASPP模块.
2.1 编码—解码网络结构整体网络采用编码器-解码器的网络结构. 对于编码器, 使用在ImageNet[19]数据集上预训练的DenseNet-161网络, 将输入的640×480大小的RGB图像编码为特征向量并输入到解码器. 在解码器端, 将浅层特征图中的特征信息融合到ASPP模块, 构建特征中的上下文信息, 然后输入到上采样层. 此外, 图像在下采样过程中得到的不同尺度的特征图通过多尺度自适应融合模块进行融合并将大小固定到不同尺度, 然后通过跳层连接与深层特征融合, 最终通过双线性插值进行上采样, 输出320×240大小的深度图. 融合浅层特征信息的ASPP模块、多尺度自适应融合模块(AMFF)、跳层连接以及上采样层共同构成解码器部分.
|
图 1 网络结构 |
2.2 多尺度自适应融合模块(AMFF)
多尺度特征融合是一种常用的特征提取方法, 不同尺度的融合特征能够得到更丰富的语义信息, 更多的空间特征细节信息. 受到Liu等[20]提出的ASFF (adaptively spatial feature fusion)结构启发, 本文引入AMFF模块. 但由于ASFF结构起初是用于目标检测中, 解决不同尺度的特征图中实例的不一致性, 但是对属于密集预测的单目深度估计任务来说, 与目标检测所需的启发式引导特征选择不同, 因为单目深度估计需要在各级特征下预测相同的深度图, 所以与ASFF在解码阶段进行融合不同, 我们对编码阶段的所有特征图进行融合, 减少网络加深造成的特征损失, 并对已融合的特征向后传播, 实现自底向上的堆叠融合, 在这个过程中, 同样采用自适应融合方式, 加强重要通道的特征, 这样融合后的浅层特征更能保留深层特征的信息.
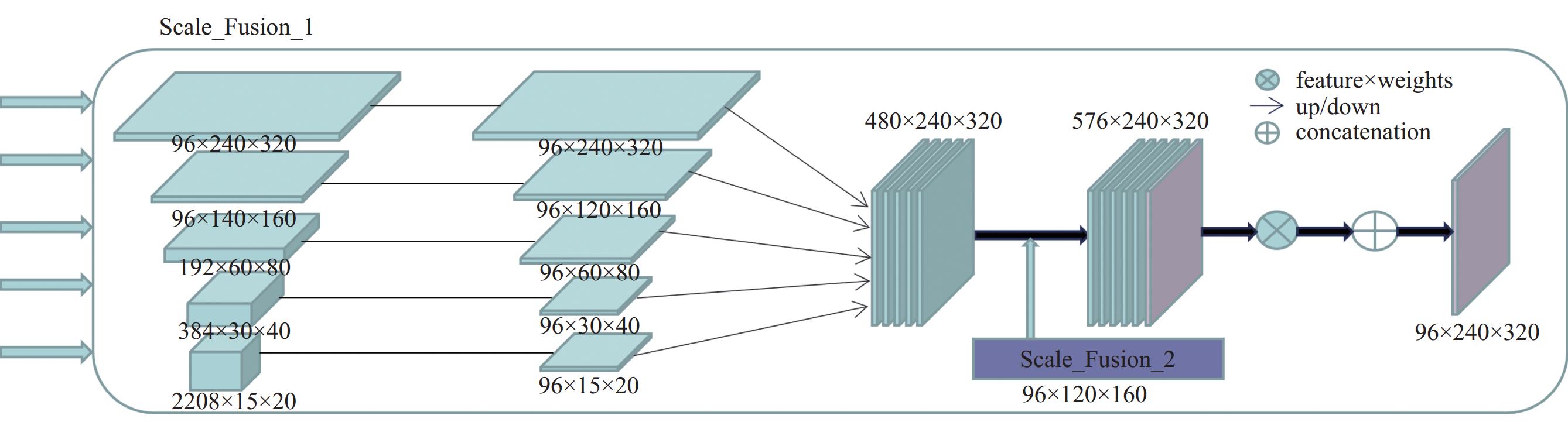
考虑到需要融合的特征图大小与通道数都不一致的问题, 所以设计融合模块对不同特征图进行尺度调整, 以尺度调整到96×240×320为例, 如图2所示, 对通道数分别为96、96、192、384、2208的特征图进行尺度统一, 通过步长为1的1×1卷积实现不同尺度特征图的通道数相同, 得到5个通道数都为96的特征图, 加上前一个融合模块Scale_Fusion_2的输出结果, 对它们进行双线性插值上采样, 得到6个96×240×320的特征图, 然后通过对这些特征图进行1×1卷积得到λ0、λ1、λ2、λ3、λ4、λ5, 经过Softmax函数满足:
| α0=eλ0eλ0+eλ1+eλ2+eλ3+eλ4 | (1) |
得到权重参数
| ylij=α0ijx0ij+α1ijx1ij+α2ijx2ij+α3ijx3ij+α4ijx4ij+α5ijyl−1ij | (2) |
其中,
整体网络结构如图1所示, 其中AMFF模块包括4个融合模块, 选取编码阶段中大小分别为240×320、120×160、60×80、30×40、15×20的特征图以及邻近下一层融合模块的输出作为输入, 4个融合模块分别对其进行尺度调整和融合操作, 输出结果分别为96×240×320、96×120×160、192×60×80、384×30×40的融合特征图, 然后与解码器端的特征图进行融合上采样.
|
图 2 多尺度自适应融合模块 |
2.3 融合浅层特征信息的ASPP模块
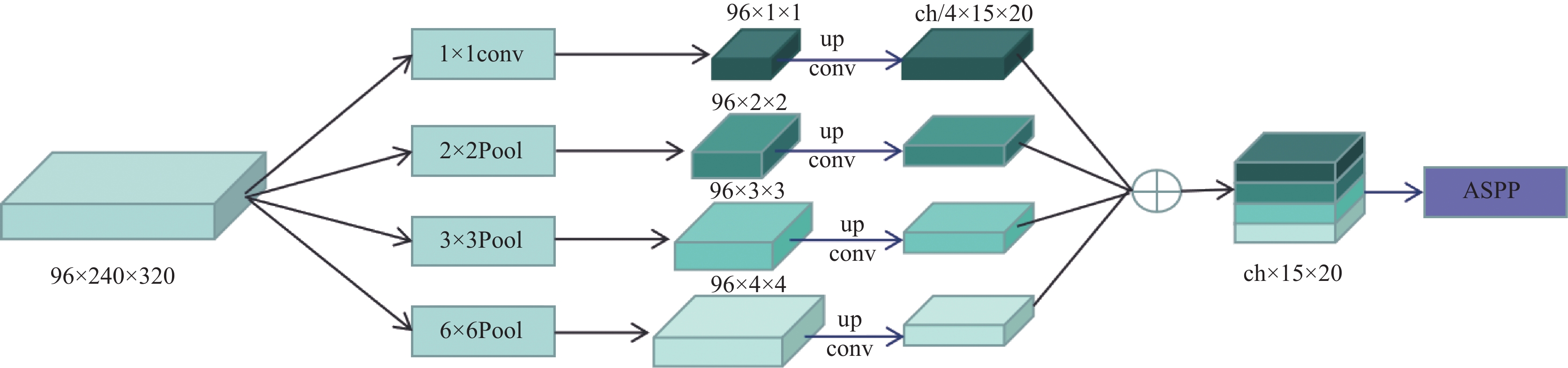
ASPP模块最初是在DeepLabV2[21]模型中提出来, 该模块由4个不同扩张率的空洞卷积并行构成, 目的是获取更大的感受野, 提取更多的上下文信息. 本文采用空洞率分别为6、12、18的空洞卷积, 对于这些大小为3×3的卷积核, 通过提高空洞率, 扩大要提取的像素之间的距离, 实现更大的感受野. ASPP采用多个不同扩张率的空洞卷积对特征图进行提取, 同时对其进行池化以及1×1卷积, 最后进行融合. 空洞卷积在增大感受野的同时, 受卷积核结构的影响, 在卷积过程中会丢失一部分像素信息, 虽然多个并行的空洞卷积可以缓解该问题, 但对于像素级的深度预测任务还是有一定的影响, 并且由于深层特征图经过下采样后会丢失大量信息, 并不能较好的保留小物体的特征信息. 所以我们提出融合浅层特征图中图像信息的方法, 通过池化获取浅层特征图中丰富的场景信息, 对深层特征图Fd经过空洞卷积后丢失的特征信息进行补全, 将编码段4个浅层特征图作为输入, 其中以96×240×320的特征图输入为例, 如图3所示. 分别使用6×6、3×3、2×2池化和1×1卷积提取原图1/2、1/4、1/8、1/16大小的特征图, 经过提取的特征图通过双线性插值的上采样将分辨率调整到与特征图Fd相同的分辨率, 并且通过1×1卷积将特征通道数调整到1/4大小, 将得到的4个特征图进行拼接, 得到与Fd的分辨率和通道数都相同的特征图, 然后与ASPP模块中多分支并行空洞卷积的输出结果通过Concat拼接, 最终通过1×1卷积降维输出结果. 图2中其余输入特征图均做相同的操作.
2.4 损失函数深度估计任务的损失函数是考虑真实深度图y和网络模型的预测深度图ŷ的差异. 我们采用与Alhashim等[22]提出的方法相同的损失函数, 选择图像深度损失、梯度损失以及结构相似性损失的加权和作为损失函数, 如式(3)所示:
| L(y,ˆy)=λLdepth(y,ˆy)+Lgrad(y,ˆy)+LSSIM(y,ˆy) | (3) |
其中, 定义λ为Ldepth的权重参数, 并设置λ=0.1, Ldepth 深度损失, 是像素级深度值的L1损失, 如式(4)所示:
| Ldepth(y,ˆy)=1nn∑p|yp−ˆy| | (4) |
其中, n为样本个数, p为样本, yp为样本的真实深度值,
| Lgrad(y,ˆy)=1nn∑p|gx(yp,ˆy)|+|gy(yp,ˆy)| | (5) |
其中, gx(·)和gy(·)分别计算在x分量和y分量上yp和
| LSSIM(y,ˆy)=1−SSIM(y,ˆy)2 | (6) |
|
图 3 融合浅层特征信息结构 |
3 实验结果与分析 3.1 数据集
本文采用NYU-DepthV2数据集, 该数据集提供在640×480分辨率下的室内场景RGB图像和深度图. 该数据集包含464种不同室内场景共12万张, 249个场景的5万张图片作为训练样本, 其余215个场景的654张图片作为测试样本. 在训练阶段, 我们的网络模型以原始分辨率的图像输入网络, 将数据集中的真实深度图下采样到320×240, 与模型输出最终深度图的大小一致. 在测试阶段, 我们将模型预测深度图进行2倍上采样以匹配数据集中真实深度图的分辨率, 同时对预测深度图的精度进行评估.
3.2 实验环境与参数本文提出的网络模型使用PyTorch深度学习框架. Python环境版本为3.7, Cuda环境版本为10.0.130. 网络在显存为16 GB的Tesla P100上进行训练, 在GTX 960M上进行测试评估. 编码器端主干网络是在ImageNet上训练的DenseNet-161, 解码器权重随机初始化. 优化器采用Adam优化算法, 学习率为0.0001, β1=0.9, β2=0.999. Batch大小为2, 迭代次数epoch为10.
3.3 评估指标本文采用Eigen[1]中提出的评价指标, 从4个方面对模型进行评估, 这4个评估指标分别为: 平均相对误差(AbsRel)、均方根误差(RMSE)、均方根对数误差(RMSElog10)、不同阈值下的准确率(δ1, δ2, δ3), 定义式分别如式(7)–式(10).
| AbsRel=1nn∑p|yp−ˆyp|y | (7) |
| RMSE=√1nn∑p(yp−ˆyp)2 | (8) |
| RMSElog10=1nn∑p|log10yp−log10ˆyp| | (9) |
| δi=max(ypˆyp,ˆypyp)<thr,thr=1.25,1.252,1.253 | (10) |
其中, yp和
通过第2节设计的网络结构, 在NYU-DepthV2数据集上验证模型性能, 并进行不同算法的对比实验, 根据第3.3节提出的评估指标计算, 定量实验结果如表1、表2所示.
从表1的评估指标来看, 本文算法结果均较为理想, 在δ1、RMSE、AbsRel、RMSElog10指标上来看相较一些主流算法取得了更好的效果.
图4给出了本文方法与不同方法的深度图对比, 第1列为原始RGB图像, 第2列为真实深度图, 第3列为Hu等[3]方法结果, 第4列为Alhashim等[22]方法结果, 第5列为Lee等[16]方法结果, 最后一列为本文深度估计结果. 可以看出, 本文的方法在物体边缘的预测效果更好, 对人物的轮廓的预测要比Lee等[16]方法更加细致, 在图4红框中, 玩具熊、桌椅、窗口位置容易出现与周围场景深度一致的问题有所改善.
| 表 1 实验结果对比 |
| 表 2 消融实验结果对比 |

|
图 4 深度图结果对比 |
3.5 消融实验
为验证本文方法中的各个模块在深度估计中的性能, 在NYU-DepthV2数据集上进行了消融实验, 主要分析多尺度特征自适应融合模块、ASPP模块与浅层特征信息融合机制. 设置两个相融方式: 一是模型是否嵌入特征自适应融合模块, 二是模型是否使用ASPP模块并融合浅层特征信息. 由表2可以看出, 在对模型嵌入特征自适应融合模块之后在δ1、RMSE、AbsRel、RMSElog10指标上取得更好的结果, 在图5的第3列、第4列以及第5列对比下, 提升了在场景物体细节方面的预测结果. 具体来看, 红框中, 使用特征自适应融合模块后, 在第1场景下可以预测出灯杆的下半部分, 并且有一个整体的轮廓; 在第2个场景下, 可以预测出椅子把手的细节; 第3个场景下梯子的细节更为清晰; 白框中, 角落处深度更加准确, 并且变化趋势更加明显. 由此我们可以认为对编码器的特征进行自适应融合后通过跳层连接到解码器可以提高深度图的精度、减少误差.

|
图 5 消融实验深度图对比 |
在仅增加ASPP模块的情况下, 由图5可知, 在第1场景下的灯杆的预测结果更加准确, 在第2场景下的左侧红框中的预测结果相比未使用ASPP模块的模型对椅子把手下的空白区域预测更加准确, 但是椅子把手的预测仍存在不连续的问题. 在此基础上, 使用ASPP模块并融合浅层特征信息之后取得最好效果, 由表2可以看出在δ1、RMSE、AbsRel、RMSElog10指标上取得最好的结果, 并且提升了小物体以及细长物体的预测, 比如在第1场景中的灯杆、第2场景中的椅子把手和第3场景的梯子的预测结果中均比之前要清晰, 确保椅子把手的连续性, 并且对第3场景中墙角处的深度预测相比之前更为准确. 由此可以表明使用ASPP模块融合浅层特征信息可以减少空洞卷积下像素信息的丢失, 提升对场景中物体细节的预测精度.
4 结论本文在编码器-解码器结构的网络模型基础上, 提出一种充分利用编码器阶段不同尺度特征的方法, 对不同尺度特征进行自适应融合并连接到解码器端, 实现解码端对编码端的信息合理且高效的利用, 并减少下采样过程中细粒度的深度信息的丢失对密集预测任务的影响. 此外在使用ASPP模块对深层特征进行整体深度信息的提取时, 融合浅层特征信息, 在保证整体深度信息准确的基础上, 优化细节深度信息.未来的研究方向可以建立更轻量级的网络模型, 在精度可以接受范围内提高模型预测速度, 继续推进单目图像深度估计任务的研究.
| [1] |
Eigen D, Puhrsch C, Fergus R. Depth map prediction from a single image using a multi-scale deep network. Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2014. 2366–2374.
|
| [2] |
Laina I, Rupprecht C, Belagiannis V, et al. Deeper depth prediction with fully convolutional residual networks. Proceedings of the 4th International Conference on 3D Vision (3DV). Stanford: IEEE, 2016. 239–248.
|
| [3] |
Hu JJ, Ozay M, Zhang Y, et al. Revisiting single image depth estimation: Toward higher resolution maps with accurate object boundaries. Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV). Waikoloa: IEEE, 2019. 1043–1051.
|
| [4] |
Chen XT, Chen XJ, Zha ZJ. Structure-aware residual pyramid network for monocular depth estimation. Proceedings of the 28th International Joint Conference on Artificial Intelligence. Macao: IJCAI.org, 2019. 694–700.
|
| [5] |
Song M, Lim S, Kim W. Monocular depth estimation using laplacian pyramid-based depth residuals. IEEE Transactions on Circuits and Systems for Video Technology, 2021, 31(11): 4381-4393. DOI:10.1109/TCSVT.2021.3049869 |
| [6] |
Zhang AM, Ma YC, Liu JY, et al. Promoting monocular depth estimation by multi-scale residual Laplacian pyramid fusion. IEEE Signal Processing Letters, 2023, 30: 205-209. DOI:10.1109/LSP.2023.3251921 |
| [7] |
Miangoleh SMH, Dille S, Mai L, et al. Boosting monocular depth estimation models to high-resolution via content-adaptive multi-resolution merging. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Nashville: IEEE, 2021. 9680–9689.
|
| [8] |
Ranftl R, Bochkovskiy A, Koltun V. Vision Transformers for dense prediction. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV). Montreal: IEEE, 2021. 12159–12168.
|
| [9] |
Cao YZH, Wu ZF, Shen CH. Estimating depth from monocular images as classification using deep fully convolutional residual networks. IEEE Transactions on Circuits and Systems for Video Technology, 2018, 28(11): 3174-3182. DOI:10.1109/TCSVT.2017.2740321 |
| [10] |
Yuan WH, Gu XD, Dai ZZ, et al. Neural window fully-connected CRFs for monocular depth estimation. Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). New Orleans: IEEE, 2022. 3906–3915.
|
| [11] |
Wu JW, Zhou WJ, Luo T, et al, Multiscale multilevel context and multimodal fusion for RGB-D salient object detection. Signal Processing, 2021, 178: 107766.
|
| [12] |
Hu J, Shen L, Albanie S, et al. Squeeze-and-excitation networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(8): 2011-2023. DOI:10.1109/TPAMI.2019.2913372 |
| [13] |
Yang X, Chang QL, Liu XL, et al. Monocular depth estimation based on multi-scale depth map fusion. IEEE Access, 2021, 9: 67696-67705. DOI:10.1109/ACCESS.2021.3076346 |
| [14] |
Xu HH, Li F. An efficient monocular depth prediction network using coordinate attention and feature fusion. Journal of Information Processing Systems, 2022, 18(6): 794-802. |
| [15] |
Xu Y, Yu Q. Adaptive weighted multi-level fusion of multi-scale features: A new approach to pedestrian detection. Future Internet, 2021, 13(2): 38. DOI:10.3390/fi13020038 |
| [16] |
Lee JH, Han MK, Ko DW, et al. From big to small: Multi-scale local planar guidance for monocular depth estimation. arXiv:1907.10326, 2021.
|
| [17] |
Wu KW, Zhang SR, Xie Z. Monocular depth prediction with residual DenseASPP network. IEEE Access, 2020, 8: 129899-129910. DOI:10.1109/ACCESS.2020.3006704 |
| [18] |
廖志伟, 金兢, 张超凡, 等. 基于分层压缩激励的ASPP网络单目深度估计. 图学学报, 2022, 43(2): 214-222. |
| [19] |
Deng J, Dong W, Socher R, et al. ImageNet: A large-scale hierarchical image database. Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Miami: IEEE, 2009. 248–255.
|
| [20] |
Liu ST, Huang D, Wang YH. Learning spatial fusion for single-shot object detection. arXiv:1911.09516, 2019.
|
| [21] |
Chen LC, Papandreou G, Kokkinos I, et al. DeepLab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(4): 834-848. DOI:10.1109/TPAMI.2017.2699184 |
| [22] |
Alhashim I, Wonka P. High quality monocular depth estimation via transfer learning. arXiv:1812.11941, 2018.
|
| [23] |
Wang Z, Bovik AC, Sheikh HR, et al. Image quality assessment: From error visibility to structural similarity. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861 |
| [24] |
Hao ZX, Li Y, You SD, et al. Detail preserving depth estimation from a single image using attention guided networks. Proceedings of the 2018 International Conference on 3D Vision (3DV). Verona: IEEE, 2018. 304–313.
|
| [25] |
Fu H, Gong MM, Wang CH, et al. Deep ordinal regression network for monocular depth estimation. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Salt Lake City: IEEE, 2018. 2002–2011.
|
| [26] |
Xu XF, Chen Z, Yin FL. Monocular depth estimation with multi-scale feature fusion. IEEE Signal Processing Letters, 2021, 28: 678-682. DOI:10.1109/LSP.2021.3067498 |
 2024, Vol. 33
2024, Vol. 33



