深度学习技术凭借其卓越的预测性能已在图像识别^[1–3]、自然语言处理^[4–6]等领域得到广泛应用, 取得斐然的成果^[7]. 然而, 神经网络作为代表性技术, 其黑盒特性使它们缺乏解释性和透明度, 无法提供关于预测置信度的信息^[8]. 这一局限性在自动驾驶^[9]和医疗诊断^[10]等安全性要求严苛的应用领域内, 构成了导致灾难性后果的高风险隐患. 正如特斯拉无人驾驶因算法误将白色卡车识别为天空未能进行紧急制动而导致一人死亡的事故, 暴露深度学习算法一个致命问题: 传统模型只能输出特定预测结果, 而不能表明模型本身对决策结果是否自信. 因此, 深度学习不确定性的度量显现出高度重要性, 它本质上评估了模型对自身预测结果的置信程度. 如果模型在维持高性能预测的同时, 提供不确定性度量, 有助于关键时刻及时采取人工干预, 确保决策的可靠性. 这不仅能提升现有系统的安全性^[11], 还能扩展深度学习技术在高风险领域的应用范围. 此外, 深度学习不确定性的研究深化了人类对神经网络内在机制的理解, 还可以在主动学习和强化学习任务中作为策略学习的重要组成部分, 以及在风险评估和环境监控等方面有广阔的应用前景.

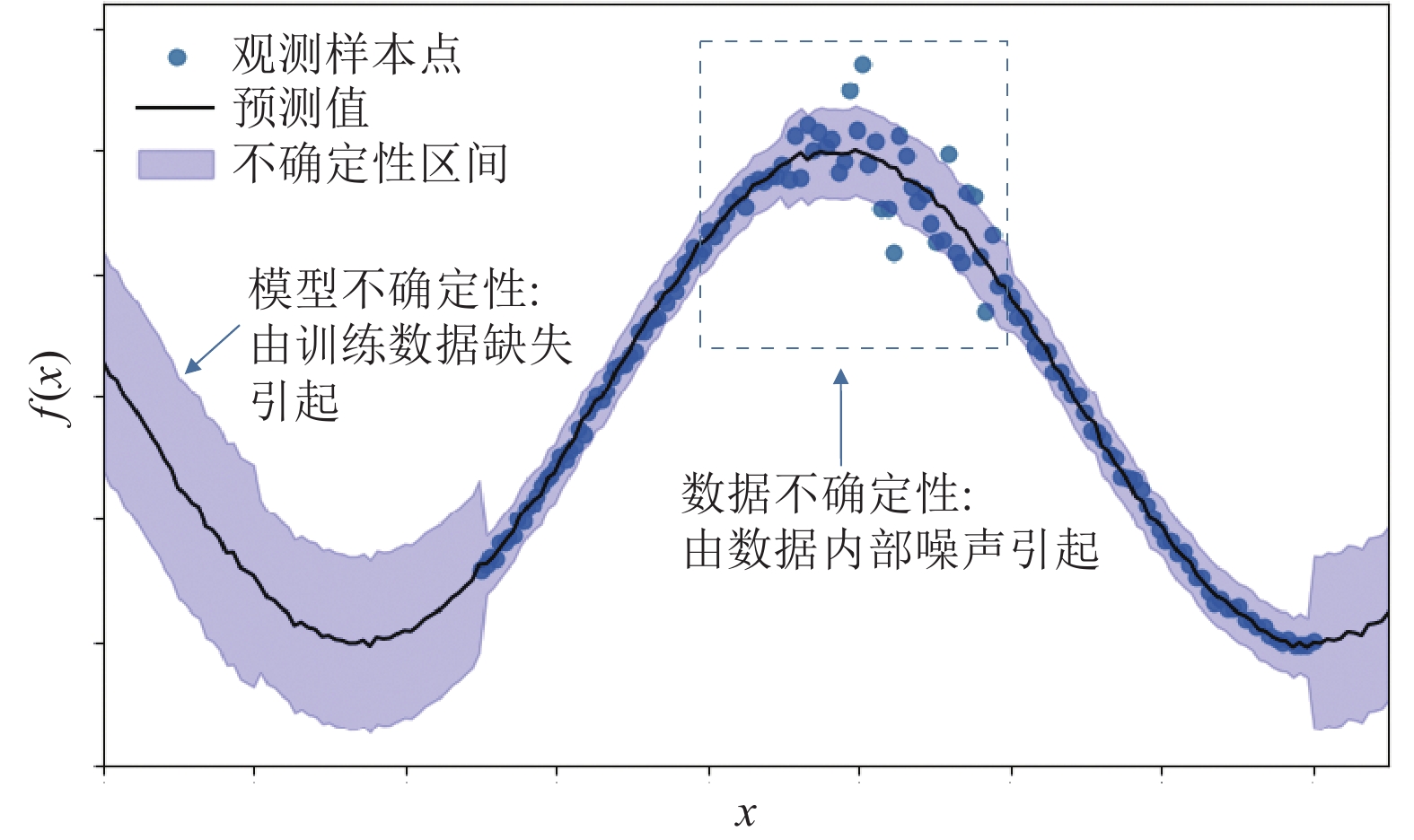
深度学习不确定性根据产生原因通常被分为模型不确定性(model uncertainty)和数据不确定性(data uncertainty). 模型不确定性, 或称认知不确定性(epistemic uncertainty), 源自模型本身的不足, 由训练过程错误、模型结构问题或对未知样本的知识缺乏导致^[12]. 如图1中两端高不确定性区域所示, 模型不确定性在缺乏训练样本的情况下大幅上升, 当未见过的样本加入模型参与训练后, 模型不确定性会降低. 数据不确定性, 亦称偶然不确定性(aleatoric uncertainty), 它描述的是数据中内在噪声, 即由数据本身的随机性造成的不可预测的误差^[13]. 如图1的虚框部分, 数据不确定性在样本模糊或背景繁杂等噪声高的情况下较大, 通常由数据采集过程中的信息损失导致. 例如, 通过特定分辨率的图像像素表示真实世界信息, 或是标注过程中的错误, 这些情况下的信息损失无法通过增加训练样本量减轻. 需要注意的是, 数据不确定性仅在讨论域内样本时有意义, 因为它本质上是量化样本被预测为不同类别的歧义程度^[14]. 本研究聚焦于探究卷积神经网络的模型不确定性, 这有助于发现模型潜在的不足和改进方向, 对于优化模型的训练过程并提高其在面对未知数据时的表现具有重要意义.

在现有不确定性度量方法中, 贝叶斯推断(Bayesian inference)^[15–18]和集成学习(ensemble methods)^[19–21]等传统方法虽然理论基础坚实, 但需要对模型架构或训练过程进行显著修改, 且实施复杂度高. 基于以上, 本文提出一种创新的基于单确定性神经网络(single deterministic methods)的不确定性度量框架AFDU (anomaly factor based deterministic uncertainty). 单确定性神经网络在每次前向传递中提供相同的结果, 符合目前多数深度学习传统任务的模型构建情况. 本文提出方法通过统计建模分析, 充分利用神经网络在单次前向传播过程中的激活值, 无需更改模型结构或训练策略, 既维持原始模型的高准确度, 又实现高效的不确定性度量, 易于融入现有系统. 此外, AFDU通过可视化分析增强模型面对未知或异常情况的可解释性.

本文的基础假设为模型经过良好训练后每个神经元会形成各自的正常工作范围, 超出该范围表明神经元碰到异常状况且不确定度提升. AFDU有两个核心组成部分: 激活分布构建模块与异常因子计算模块. 激活分布构建模块利用改进的核密度估计(kernel density estimation, KDE)技术^[22]精准构建神经元的激活分布以模拟神经元的正常工作范围, 异常因子计算模块引入邻域加权密度估计方法计算异常因子以衡量样本与神经元激活分布的偏离程度. 本文在多个公开数据集和模型进行实验验证, 并对层间特征图进行可视化分析, 直观展示AFDU在区分域内外样本方面的显著效果. 此外, AFDU在域外检测任务上的AUROC指标均超过98%, 在多种实验设置中均超越其他方法, 验证本文提出方法在识别异常样本方面的有效性和通用性, 展现其在实际应用中的巨大潜力.

1 相关工作

在深度学习的不确定性估计领域, 主流方法包括贝叶斯推断^[15,16]、集成算法^[19–21]和测试数据增强(test-time augmentation methods)^[23,24]. 贝叶斯推断通过为模型参数引入概率分布, 提供一种量化不确定性的理论框架. 然而, 由于在实际应用中参数量巨大, 严格根据贝叶斯公式计算不现实. 因此, 研究者通常采用各种形式的变分推理^[17,18]或蒙特卡洛采样^[25]作为近似解, 这些方法虽然有效但需要重新训练模型, 计算资源和时间成本高. 集成算法, 如深度集成学习, 通过结合多个模型的预测结果提高鲁棒性, 同时使用统计度量来表达不确定性. 尽管集成方法已被证明在多个任务中有效, 但这些方法要求保存和处理多个模型或权重版本, 极大地增加了存储和计算负担. 测试数据增强则通过在测试时对输入数据进行多样化处理, 生成多个测试变体以评估不确定性. 这要求对每个测试样本进行多次前向传递, 并且可能需要对整个数据集进行特殊预处理, 导致计算时间增加, 并引入额外的噪声.

相比之下, 基于单确定性网络的不确定性度量方法提供一种更为高效和实用的解决方案. 与贝叶斯和集成方法相比, 这种方法的优势在于其高计算效率, 并能直接利用已训练模型的潜在激活特征. 单确定性神经网络的参数固定, 确保每次前向传播提供一致结果, 这与传统深度学习任务的模型构建相符. 单确定性方法大致分为两种路径, 一种是加入不确定性度量指标对单个网络进行明确建模和重新训练^[26,27], 另一种是基于已训练网络利用额外成分进行不确定性度量^[28], 如引入附加的神经网络用于不确定性估计^[29]. 前者需要在原始模型上进行改动, 后者对不确定性的度量与原始预测任务是分离的, 更易于集成到现有系统中, 适用性更广泛. Hendrycks等人^[30]强调了神经元激活值在评估不确定性方面的作用, 指出激活值能反映模型对特定数据点的信心程度. Lee等人^[31]和 DeVries 等人^[32]的工作通过分析神经网络输出的概率分布来估计不确定性, 但这些方法通常仅依赖于输出层的Softmax分布分析, 无法充分捕捉模型内部的复杂动力机制, 缺乏从整体评估模型的决策过程. 一些研究工作利用特征空间距离^[33,34]和特征空间密度^[35,36]度量不确定性, 在单确定性方法中提供新的视角. 未见数据点在特征空间中相对于训练数据点距离大且密度小, 而加入训练过程后再次计算, 距离降低且密度增大, 符合模型加入未知样本重新训练后模型不确定性降低的定义. DUQ^[33]和SNGP^[34]两种方法分别通过引入径向基函数或高斯过程, 提出距离感知输出层, 并在特征提取的过程中加入归纳偏差以保证特征空间的平滑度和灵敏性, 但它们需要修改网络结构并重新训练模型. DDU^[14]以训练样本在模型最后一个卷积层的输出特征向量为基础, 构建高斯混合模型(Gaussian mixed model, GMM)^[37]作为密度估计器量化模型不确定性. DDU虽然能达到和集成模型相近的效果, 但仅在特征空间经过规范化处理后表现较好, 如有残差结构的模型.

本文提出的基于单确定性神经网络的不确定性度量框架, 无需对原始模型进行改动, 采用基于特征空间密度度量模型不确定性的思想. 利用改进的KDE方法更精确地构建神经元激活分布, 充分挖掘激活值的潜在特征. 通过计算与统计测试样本在各神经元的异常因子, 衡量样本与分布的偏离程度, 从而能更全面地评估模型的不确定性.

2 模型的不确定性度量框架

在本文的基础假设下, 对于经过良好训练的模型, 每个神经元会识别特定的模式, 形成各自的正常工作范围, 超出该范围表明神经元碰到异常状况且不确定度提升. 神经元激活分布及样本异常因子示例如图2所示. 图2中圆形及叉形点由左至右依次表示异常因子(anomaly factor, AF)等于7.85, 1.05, 1.86, 1.00, 1.02, 4.97, 11.68和20.74时的对应情况. 基于训练集样本的激活值, 每个神经元形成的激活分布可以模拟其正常工作范围——正常数据点会落入神经元的工作范围内, 异常因子较低, 从而模型的不确定性较低, 如图2中圆形数据点; 相对地, 异常数据点会偏离神经元的工作分布, 异常因子较高, 导致模型的不确定性较高, 指示模型可能正面对之前未见过的新情况, 如图2中叉形数据点. 此处的正常和异常表现为数据点相对于训练集数据点的域内和域外.

本文研究的问题定义如下: 给定训练样本集$ x = \left\{ {{x_1}, {x_2}, \cdots, {x_n}} \right\} $、预训练模型M和测试样本t, 其中n代表训练集的样本总数. 记$ a_l^N\left( {{x_i}} \right) \in {R^1} $为第i个训练样本x_i在神经网络第l层中第N个神经元的输出激活值, $ a_l^N\left( x \right) = \left\{ {a_l^N\left( {{x_1}} \right), a_l^N\left( {{x_2}} \right), \cdots, a_l^N\left( {{x_n}} \right)} \right\} $为训练样本集在该神经元的激活值集合. 研究目标为充分挖掘并利用神经元激活值的潜在分布特征, 构建神经元正常工作范围, 即激活分布$ f_l^N(x) $. 当测试样本t输入模型时, 在各神经元上的输出值$ a_l^N\left( t \right) $分别计算得到异常因子$ {{WAF}}_l^N(t) $, 用以衡量与激活分布的偏离程度. 最终整合所有神经元的异常因子得到测试样本的不确定性度量u(t).

本文提出的基于神经元统计建模分析的不确定性度量框架AFDU如图3所示. 上方虚线框部分表示卷积神经网络模型的原始分类任务过程, 其训练和测试阶段不会受到不确定性度量过程影响. 下方虚线框部分表示基于已训练模型的不确定性度量过程, 由两个核心组成部分构成: 神经元激活分布构建模块与异常因子计算模块. 神经元激活分布构建阶段, 以训练集样本在模型各神经元上的激活值$ a_l^N\left( x \right) $作为输入, 构建激活分布$ f_l^N(x) $以模拟神经元正常工作范围. 在异常因子计算阶段, 将测试样本在各神经元上的激活值$ a_l^N\left( t \right) $作为输入, 引入邻域加权的密度估计方法, 有效衡量各神经元中测试样本的激活值与激活分布的偏离程度, 得到异常因子$ {{WAF}}_l^N(t) $. 最终使用统计方法综合各神经元的异常因子, 层内取平均, 层间求和, 为每个样本计算得到一个综合的异常统计量, 即最终的不确定性度量u(t). AFDU不仅增强了对模型内部决策过程的理解, 而且提供了一个有效的工具, 有助于在复杂应用中高效监控和评估模型的不确定性. 算法流程总结如算法1.

算法1. 基于神经元统计建模分析的不确定性度量框架

输入: 训练数据x, 预训练模型M, 测试样本t, 其中模型共L层, 每层N_l个神经元.

输出: 测试数据的不确定性度量值u(t).

1) 获得训练数据集在每个神经元上的激活值$\scriptstyle a_l^N\left( x \right) $.

2) 利用改进的核密度估计方法构建神经元的工作分布$\scriptstyle f_l^N(x) $, 见式(3).

3) 计算测试样本在每个神经元上激活值$\scriptstyle a_l^N\left( t \right) $的局部密度$\scriptstyle {KDE} _l^N\left( {a_l^N\left( t \right)} \right) $, 见式(7).

4) 计算测试样本在每个神经元上近邻集的加权邻域密度$\scriptstyle {WDE} _l^N\left( {a_l^N\left( t \right)} \right) $, 见式(8).

5) 计算测试样本在每个神经元上的异常因子$ \scriptstyle {{WAF}}_l^N\left( {a_l^N\left( t \right)} \right) $, 见式(6).

6) 整合各神经元上的异常因子, 层内取平均, 层间求和, 获得一个综合的异常统计量, 即不确定性度量u(t).

$ \scriptstyle u(t) = \sum\limits_{l = 1}^L {\left( {\frac{1}{{{N_l}}}\sum\limits_{N = 1}^{{N_l}} {{{WAF}}_l^N\left( {a_l^N\left( t \right)} \right)} } \right)} $

2.1 神经元激活分布构建模块

在神经网络的训练过程中, 每个神经元都会学习并适应特定的模式或特征, 这些模式和特征在模型内部由神经元的激活值所反映. 为了更精确地评估模型的不确定性, 本文首先定义和构建每个神经元的正常工作范围. 这一范围可以看作是训练样本在神经元上激活值的分布, 记为$ f_l^N \sim F\left( {a_l^N\left( {{x_1}} \right), a_l^N\left( {{x_2}} \right), \cdots, a_l^N\left( {{x_n}} \right)} \right) $, 其中$ a_l^N\left( {{x_i}} \right) \in {R^1} $是第i个训练样本在模型第l层的第N个神经元的激活值, n代表训练数据集中的样本总数.

由于无法获取神经元激活值的先验分布, 传统的概率密度估计方法可能不够准确. 因此, 为了更好地模拟神经元的激活分布, AFDU使用改进的核密度估计方法. KDE作为一种无参数的概率密度估计方法, 能够捕捉数据的微妙结构和模式. 具体而言, KDE会在每个观测数据点周围放置一个核函数, 然后将这些核函数叠加, 从而获得整体的概率密度函数. 通过调整核函数的带宽, 可以控制密度估计的平滑程度, 从而在偏差与方差之间寻找一个平衡点. 公式如下:

$ f_l^N(x) = \frac{1}{{nh}}\sum\limits_{i = 1}^n {{K} \left( {\frac{{x - a_l^N(x)}}{h}} \right)} $

(1)

其中, K(·)是核函数, 此处选择高斯核. 高斯核的形状呈正态分布, 能够为估计提供平滑且连续的结果. 此外, 由于其具有无限支持的特性, 在整个实数轴上都有定义且均不为零, 高斯核可以敏锐地捕获数据的微妙变化. 高斯核的表达式如下:

$ {K} (t) = \frac{1}{{\sqrt {2\text{π}}}}{{\mathrm{e}}^{ - \frac{{{t^2}}}{2}}} $

(2)

式(1)中的$ h $是带宽, 带宽的选择对KDE的结果有着至关重要的影响. 太小的带宽会导致构建分布的过度拟合, 而太大的带宽则会掩盖数据的真实结构. AFDU采用的improved Sheather Jones (ISJ)算法^[38]是一种自适应方法, 能够根据数据的实际分布自动确定一个近似最优的带宽, 从而使得KDE的估计既不过度拟合也不过于平滑. 同时, 在图2中可见, 利用KDE构建的分布(实线)相比于高斯分布的估计(虚线)表现出更高的精准度. KDE方法能够更细致地捕捉数据的复杂结构, 从而生成更符合实际数据分布的曲线, 尤其在处理非标准形状或多峰分布时表现突出, 因此更适用于神经元激活先验分布未知的场景.

为了避免因训练集样本量过大而使后续数据处理变得过于复杂, 本文采取预处理措施. 具体来说, AFDU首先对训练数据集在每个神经元上的激活值输出进行K-means聚类^[39], 将样本空间分解为500个近邻簇, 即原始的激活值空间被简化为500个中心点$ \{ a_l^N( {{c_1}} ), a_l^N( {{c_2}} ), \cdots, a_l^N( {{c_{500}}} ) \} $. 相较于不使用聚类方法时的n个数据点(n一般大于10000), 大幅减少了数据的维度和复杂性. 在构建KDE时, 考虑到每个簇中样本的数量可能不同, 不同的簇对于整体分布的贡献程度也会有所不同. 因此, AFDU根据每个簇的中心点的数值$ a_l^N\left( {{c_i}} \right) $以及相应簇中的样本数量$ {n}_{i} $进行加权计算, 确保在估计整体分布时每个样本簇得到适当的表示. 这种处理方法不仅简化了数据和计算复杂度, 还确保了分布估计的准确性, 兼顾了效率与准确度. 最终的构建分布公式如下:

$ f_l^N(x) = \frac{1}{{\left( {\displaystyle\sum\limits_{i = 1}^C {{\omega _i}} } \right)h}}\displaystyle\sum\limits_{i = 1}^C {{\omega _i}{K} \left( {\frac{{x - a_l^N({c_i})}}{h}} \right)} $

(3)

其中,

$ {\omega _i} = {n_i}/ n $

(4)

$ C = \min (500, n)$

(5)

2.2 异常因子计算模块

在得到神经元激活分布$ {f}_{l}^{N} $后, 需要衡量测试样本点的异常程度. 尽管测试样本输入后在神经元上的激活值可以根据已构建的分布计算得到相应的概率密度函数(probability density function, pdf), 但不同神经元经过KDE构建的分布尺度(scale)不同, 因此无法直接使用这些pdf值来量化异常程度. 本文受Hu等人^[40]异常检测任务的启发, 引入“异常因子”这一指标. 不同的是, 本文关注于将该指标用于统一度量各样本在不同神经元激活分布上的异常程度.

AFDU中的异常因子计算是基于两个主要组件的比值: 局部核密度估计(KDE)和加权邻域密度估计(weighted neighbor density, WDE). 前者表示测试样本自身在该神经元上的激活值在激活分布上对应的pdf值, 后者表示此激活值一定范围内的邻域训练数据点对应的pdf值加权后的统计量. 直观地说, 正常的数据点基本位于训练数据点集的密集区域, 意味着它们局部密度高且与其邻域数据点的pdf值接近. 而异常数据点通常位于训练数据点集的稀疏区域, 即局部密度低且与邻域数据点的pdf值有较大差异. 将数据点$ p = a_l^N\left( t \right) $记为测试样本在模型第l层的第N个神经元的激活值. 则该点的异常因子(weighted anomaly factor, WAF)定义如下:

$ {{WAF}}_l^N(p) = \left( {\frac{{{{WDE}}_l^N(p)}}{{{{KDE}}_l^N(p)}}} \right)$

(6)

其中, $ {{KDE}}_l^N(p) $表示数据点p的局部核密度, 即由第1阶段神经元构建的分布直接计算得出:

$ {{KDE}}_l^N(p) = = \frac{1}{{\left( {\displaystyle\sum\limits_{i = 1}^C {{\omega _i}} } \right)h}}\sum\limits_{i = 1}^C {{\omega _i}{K} \left( {\frac{{p - a_l^N({c_i})}}{h}} \right)} $

(7)

式(6)中$ {{WDE}}_l^N(p) $表示数据点p的加权邻域密度. 计算公式如下:

$ {{WDE}}_{l}^{N}(p)=\frac{{\displaystyle \sum _{q\in {{N}}_{k}(p)}{w}_{q}}\cdot{{KDE}}_{l}^{N}(q)}{{\displaystyle \sum _{q\in {{N}}_{k}(p)}{w}_{q}}} $

(8)

其中, $ {N_k}(p) = \left\{ {a_l^N\left( {{c_j}_1} \right), a_l^N\left( {{c_{j2}}} \right), \cdots, a_l^N\left( {{c_{jk}}} \right)} \right\} $表示该神经元上测试样本激活值$ a_l^N\left( t \right) $的k个近邻集. 近邻集中的元素来源于训练数据集在该神经元的激活值中与$ a_l^N\left( t \right) $最接近的k个数据点. 邻域数据点$ q \in {N_k}(p) $的权重w_q定义如下:

$ {w_q} = \exp\left( { - \frac{{{{\left( {\dfrac{{{{d} _k}(q)}}{{{{min}}_k}} - 1} \right)}^2}}}{{2{\sigma ^2}}}} \right) $

(9)

其中, $ \sigma $为正的缩放因子, $ {{d} _k}(q) $表示数据点q的k距离, 即离q最近的第k个数据点到q的距离. k距离可以描述数据点的局部密度, k距离越大, 意味该数据点所在区域的局部密度越低. $ mi{n_k} $则为属于p的近邻点集$ {N_k}(p) $中最小的k距离, 即:

$ mi{n_k} = \mathop {\min }\limits_{q \in {N_k}\left( q \right)} \left( {{d_k}\left( q \right)} \right) $

(10)

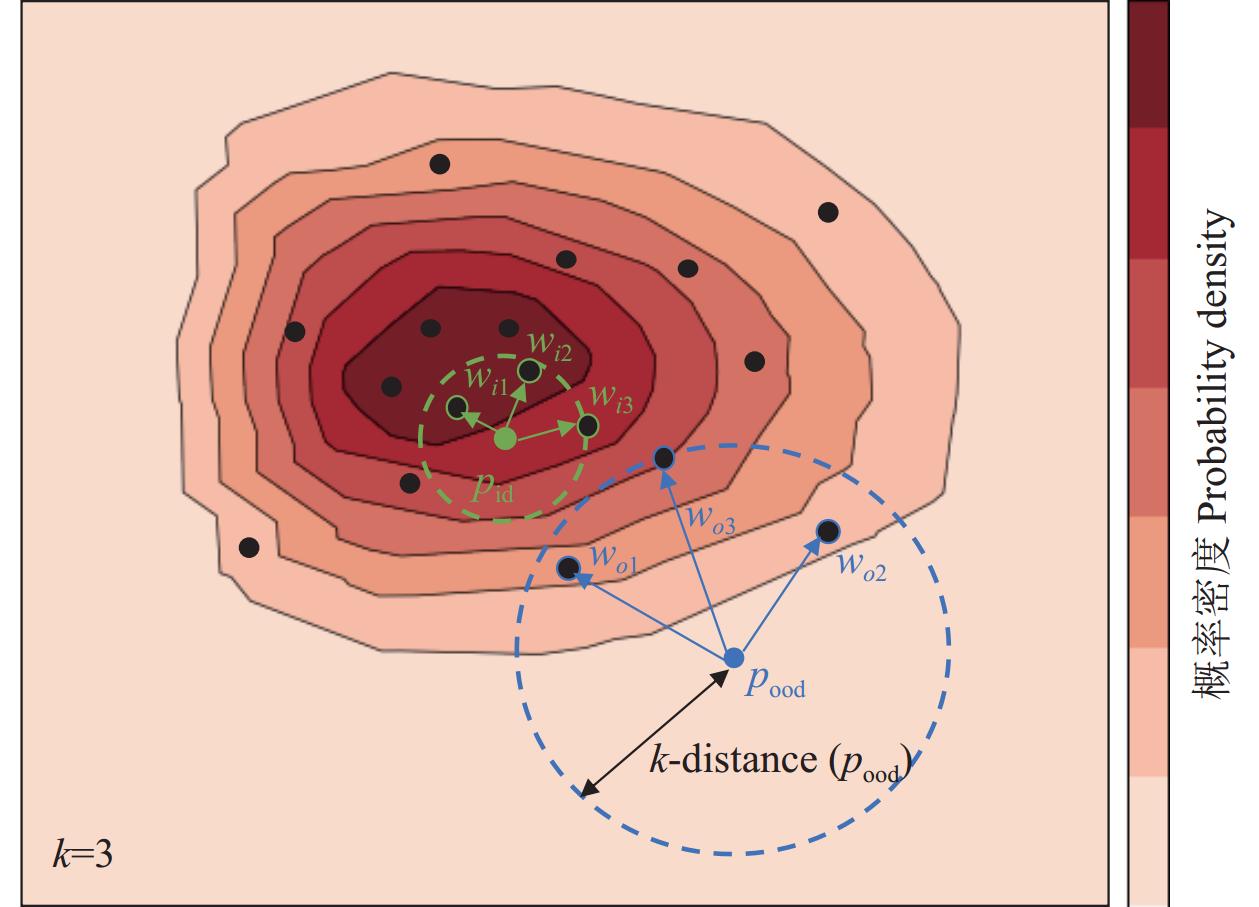
加权邻域密度WDE以每个数据点的k距离为基础, 将邻域数据点的权重设定为其k距离的单调递减函数. 这意味着数据点p的k个近邻点中, 局部密度越大的邻域数据点有更大的权重w, 而局部密度越小的邻域数据点具有更小的权重w. 如图4所示, 阴影部分越深的区域密度越高(pdf值越大, k距离越小), 对于域内测试样本点(p_id)而言, 其k=3的邻域范围内, 邻域数据点越靠近数据密集区, pdf值越大, $ k $距离越小, 其相对于测试点的权重就越大, 即$ {w_{i1}}, {w_{i2}} > {w_{i3}} $. 该权重的设置增大了位于数据密集区域数据点的影响, 即更有效捕捉测试点和整体分布的偏差.

异常因子(WAF)的值反映了测试数据点的局部核密度与其邻域密度之间的关系. 局部核密度较小且邻域密度较大的数据点, 计算得到的异常因子较大. 值得注意的是, 对于大部分与群集明显分离的异常数据点, 它们的局部密度(KDE)与邻域密度(WDE)的差异明显, 即其异常因子(WAF)会远大于1. 相反, 对于大部分正常数据点, 它们的局部密度与邻域密度非常接近, 这使得它们的异常因子围绕1波动. 如图4所示, 域内数据点(p_id)位于数据的密集区域, 其局部密度高且k距离小, 属于其$ k $近邻集的数据点局部密度较高且与域内数据点(p_id)接近, 因此异常因子接近于1; 而域外数据点(p_ood)位于数据的稀疏区域, 其局部密度低且k距离大, 权重高的邻域点局部密度大, 与域外数据点(p_ood)自身局部密度的比值会远大于1. 基于此, 异常因子的计算值能有效反映测试数据点与训练数据点分布的偏差.

3 实验分析

为了验证提出的不确定性度量框架AFDU的有效性, 本文采取了一系列实验措施, 着重从特征图的可视化以及域外样本检测(out-of-domain detection)任务的角度, 评估基于模型不确定性构建的异常因子在区分域内和域外样本方面的性能. 本文选择多组公开数据集与模型进行实验验证, 数据集包括MNIST^[41]、CIFAR-10^[42]、FER2013^[43]、SVHN^[44]、CIFAR-100^[42], 模型架构包括LeNet^[41]、VGG19^[23]、Wide-ResNet-28-10^[45], 以验证提出框架的通用性.

在特征图可视化分析中, 可以观察到域外样本上的异常因子显著高于域内样本, 而且更集中地出现在背景等非关键判别区域及目标主体的轮廓上. 这表明本文方法能够有效识别模型在处理未知数据时的不确定性区域.

在域外样本检测任务中, 本文综合每个样本在各神经元上计算得到的异常因子, 为每个样本生成一个异常统计量. 以该异常统计量作为区分域内外样本的关键指标分数, 实验结果表明本文方法在这一任务上的评价指标结果优于现有的其他不确定性度量方法, 体现该框架的实用性和优越性.

3.1 特征图可视化分析

为了深入理解本文的不确定性度量框架如何识别并展示模型的不确定性, 本文进行了特征图的可视化分析. 这一过程能够揭示域内外样本在不同神经元激活分布上计算得到的异常因子的分布差异.

本文在已训练模型中提取了样本在网络层间的特征图, 这些特征图代表了模型在不同阶段的理解和内部表示. 通过将异常因子映射到这些特征图上, 能够直观地观察到域内样本与域外样本在特征空间中神经元激活值的差异. 图5和图6所展示的例子为模型浅层特征图的示例, 特征图每个像素点的黑白亮度代表样本在相应神经元上激活值的大小, 彩色由紫至红表示异常因子的值由小到大. 在域内样本的特征图中, 异常因子突出的区域较为稀疏, 且异常因子值较低, 表明模型对于这些样本具有较高的置信度和较低的不确定性. 相反, 在域外样本的特征图中, 由于域外样本在多数神经元上的激活值偏离了模型在训练过程中学习到的数据分布, 异常因子突出区域更为集中和显著, 且异常因子值普遍较高, 揭示模型对这些样本的不确定性增加.

图5展示的结果基于的实验设置如下: LeNet模型分别对MNIST数据集和FashionMNIST数据集进行训练, 得到两个高准确率的预训练模型, 并以对方的数据集作为域外样本进行实验. MNIST是手写数字的简单灰度图像, 而FashionMNIST是更复杂的时尚产品图像, 两者明显属于不同的数据领域. 观察结果如下: 图5左半部分为以MNIST作为训练集且分类准确率达到98.37%的LeNet模型, 上半部分为域内测试样本, 下半部分为域外测试样本, 且分别展示了原始图像及浅层特征图. 在MNIST数据集上训练的LeNet模型预期在处理手写数字图像时显示出较低的不确定性, 这在实验中得到了验证. 神经元的激活模式显示, 对于MNIST样本, 异常因子突出的区域较为稀疏, 表明模型对这些样本的预测有较高置信度. 然而, 当同一模型处理FashionMNIST样本时, 特征图展示了显著不同的激活模式. 异常因子突出的区域数量和密集度显著增加, 表明模型在试图对时尚商品的图像进行分类时显示出更高的不确定性, 体现FashionMNIST图像与模型训练时的MNIST手写数字图像在视觉特征上有显著差异. 在交换域内和域外数据集的对比实验中, 当FashionMNIST数据集用于训练LeNet模型时, 相同的图像从域外转为域内样本, 异常因子的值和数量都大幅下降. 当MNIST数据集用作域外测试集时, 特征图中的异常激活区域数量明显增多, 密度也更高. 实验结果强调不同数据集之间的激活差异, 揭示本文提出的不确定性度量框架能够有效地区分域内和域外数据.

为验证所提出框架的通用性, 图6呈现更复杂数据集和模型的实验结果. 在实验中, 本文使用VGG19模型分别对两个不同的数据集进行了训练: CIFAR-10自然图像数据集, 模型分类准确率达到92.86%; FER2013表情图像数据集, 模型分类准确率为73.03%. 此外, 使用SVHN交通标识数据集作为域外测试集. 当模型处理域内数据集的图像时, 异常因子值较低且数量较少, 表现出模型对这类数据有很好的理解和置信度. 然而, 面对SVHN域外数据集的图像时, 异常因子值与数量的增加再次表明模型在处理与训练分布不同的数据时遇到阻碍, 不确定性显著提高. 通过这两种情况的比较, 本文的框架在不同类型的图像数据集上均能有效展示模型的不确定性水平. 由此可见, 尽管数据的特性和模型的训练目标不同, 本文方法仍旧能够捕捉样本在神经元激活模式中的异常, 进一步验证了提出框架在不同数据域的通用性和适应性.

值得注意的是, 样本的异常因子在特征图的背景等非关键判断区域或者边缘区域更加凸显, 比如图6中鸟类头顶区域以及男子衣服的横条区域. 这表明模型对未见过的数据存在较高的不确定性, 以及这些区域的神经元可能对识别新颖或异常的模式更为敏感. 同时, 虽然VGG19 模型框架在FER2013 数据集上训练得到的模型准确度不高, 但异常因子的可视化依然能明显区分域内和域外特征图的差异.

3.2 域外样本检测

域外样本检测任务是评估模型不确定性指标有效性的关键测试场景. 面对模型未曾遇到的域外样本, 预期这些样本会展现出与域内样本截然不同的较高不确定性特征, 在本研究中特指为异常统计量. 测试样本在已训练模型各神经元上计算得到异常因子后, 通过层内取平均、层间求和的方式最终为每个样本整合生成一个异常统计量. 利用该统计量本文能够区分并识别导致模型预测不准确的未知样本, 从而验证本文所提出的不确定性度量框架的有效性.

本项实验的设定包括: (1) LeNet模型架构 + MNIST训练集 + FashionMNIST域外测试集; (2) VGG19模型架构 + CIFAR-10训练集+ SVHN/CIFAR-100域外测试集; (3) WRN-28-10模型架构 + CIFAR训练集 + SVHN/CIFAR-100域外测试集; (4) VGG19模型架构 + FER2013训练集 + SVHN域外测试集. 该实验设定遵循由简至繁验证本文提出方法的通用性. 通过(2)、(3)的比较可以分析相同数据集、不同模型架构的域外检测量化结果差异; 通过(2)、(4)的比较可以分析不同数据集、相同模型架构的域外检测量化结果差异. 评价指标使用AUROC (area under the receiver operating characteristic curve), 表示不同阈值下模型正确区分域内外样本的能力, 取值范围为0–1, 值越高表示模型的识别能力越强.

本文使用模型的Softmax熵作为鉴别模型不确定性的基准方法, 并与以下无需在域外数据上训练或微调的方法进行对比, 方法包括Energy-based^[36]、DDU^[14]、DUQ^[33]、SNGP^[34]、5-Ensemble, 前四者属于单确定性方法, 后者属于目前不确定性评估效果最好的集成方法. Energy-based模型以未经归一化的Softmax密度作为模型不确定性, 即最后一层卷积输出的LogSumExp. DDU利用高斯混合模型在最后一层卷积输出上构建分布, 根据密度度量分辨域内外样本. DUQ和SNGP分别引入径向基函数或高斯过程构建距离感知输出层, DUQ以核估计距离度量模型不确定性, SNGP以预测熵作为度量指标. 5-Ensemble使用5个网络组成的集成模型预测熵作为模型不确定性的度量.

表1为简单数据集MNIST手写图像和简单模型LeNet在域外样本检测任务的定量指标结果, 表2为更复杂且接近真实应用场景的数据集和模型的相关实验结果. 表格中的实验数据展示模型对测试数据集的分类准确度以及在域外数据集上的AUROC分数. 实验结果表明, 本文提出的AFDU在不影响分类准确度的同时, 基于已训练模型, 通过采用异常统计量, 实现对域内外样本的高精度鉴别, AUROC评价指标超越了所有对比方法, 并接近于1. 实验结果验证本文提出框架AFDU的有效性以及在多样化数据集及模型架构中的广泛适用性. 尽管5-Ensemble方法因涉及多个预测模型在分类准确度上均达到最高值, 但单确定性方法仅需基于已训练模型便可获得不确定性度量, 分类准确率同样保持在较高的水平. 同时, 本文提出的AFDU在AUROC评价指标上的表现也超过了5-Ensemble集成方法, 表明本文提出框架在保证原模型分类准确度的同时, 能更高效获得不确定性度量.

表2基于CIFAR-10数据集的实验, 使用不同的模型架构VGG19和WRN-28-10, 观察各个不确定性度量方法的表现差异. 实验结果发现, 本文提出的AFDU不确定性度量框架在AUROC指标的表现上均超过其他方法, 在不同的模型中都能准确识别域内外样本. 尤其在VGG19的模型架构表现上, 在其他方法AUROC的指标只能在90%的情况下, AFDU仍能达到超过96%的水平. 虽然DDU在WRN-28-10的表现上也能达到较高的AUROC值, 但是在VGG19的表现差强人意, 这是由于DDU方法受特征崩塌(feature collapse)的限制, 需要在模型中引入残差连接缓解该问题.

表2基于VGG19模型架构的实验, 比较不同数据集CIFAR-10自然图像和FER2013人脸表情图像的表现. 实验结果展示本文提出的AFDU不确定性度量框架在不同类型的图像数据集上均能有效区分域内样本和域外样本, 且在两个数据集上的AUROC指标都达到了所有方法中的最高值, 进一步验证了提出框架在不同数据域的通用性和适应性.

在深入分析样本的异常统计量时, 注意到域外样本的异常统计量显著高于域内样本, 超出量达到10⁵个数量级. 这一观察验证了以下重要观点: 未受训练的域外样本在模型多数神经元上的激活值会明显偏离它们的激活分布, 导致异常统计量的显著提升. 换言之, 样本的异常统计量揭示了样本与模型激活分布的偏离程度, 反映模型面对未知数据时的不确定性水平. 这一点不仅加强了本文方法的合理性, 也凸显其在识别不确定、异常情境时的有效性.

4 结论与展望

本文针对深度学习模型由于透明度和解释性低导致决策不可信、在安全性要求高领域应用受限的问题, 提出一种新颖的基于神经元统计建模分析的不确定性度量方法. 该方法能够在保证原始预测任务高性能的前提下, 无需修改模型结构或训练过程, 高效且准确评估模型不确定性. 该框架由神经元激活分布构建和异常因子计算两大核心部分构成, 为每个样本构建异常统计量以作为模型不确定性的度量指标. 算法具体利用改进的核密度估计技术, 挖掘训练样本在神经元激活值中的潜在分布特征, 构建激活分布. 引入邻域加权密度估计方法计算异常因子, 精准量化测试点与激活分布偏离程度. 通过可视化实验, 本研究展示异常因子在区分域内外样本方面的显著效果. 在域外检测任务中, 本文提出方法在多种实验设置下性能均超越其他已有方法, 验证本文方法的通用性和有效性. 未来研究计划将进一步探索和改进现有工作在更复杂应用场景的性能和效率, 具体考虑以下几个方向的拓展. (1) 探究神经元间的复杂关联性并构建多元分布: 现有工作基于神经元相互独立的假设, 需改进对单神经元构建激活分布而未考虑神经元间联系的局限性. (2) 实时性提升: 尽管与其他方法相比, 本文提出方法已经降低了存储和计算资源的消耗, 但在实际应用中, 面对巨大的网络和数据规模时, 快速准确度量不确定性依旧复杂而充满挑战. (3) 跨领域应用: 将本文提出的不确定性度量方法应用到更多领域, 如自然语言处理等其他任务, 验证和优化方法在不同任务中的通用性和有效性.