2. 伯明翰大学 计算机科学学院, 伯明翰 B152TT
2. School of Computer Science, University of Birmingham, Birmingham B152TT, UK
推荐系统被广泛应用在电子商务、广告和社交媒体等各种互联网服务中, 其核心是通过算法对特定的数据信息进行分析处理, 分析用户的偏好特征并将处理后的结果推荐给有相关需求的用户[1], 这一方法有效缓解了互联网快速发展导致的信息过载影响[2], 提升用户的体验. 协同过滤[3]通过用户-物品的历史交互信息建立用户-物品矩阵, 分析用户与物品之间的关系和相似性, 预测用户对未接触物品的喜好, 并向其推荐可能感兴趣的内容、产品或服务. 由于协同过滤易于收集数据且具有相对较高的推荐性能, 因此在学术界和工业界都得到了广泛研究和应用[4].
图卷积神经网络(graph convolutional neural network, GCN)是一种用于图数据处理的深度学习模型[5]. 它通过在图结构上进行局部连接和信息传递来捕捉节点之间的关系, 并通过多层的神经网络进行特征提取和表示学习. 近年来, 研究人员开始将图卷积神经网络应用于协同过滤[6]. Berg等人将GCN应用于用户-物品二部图, 提出了GCMC模型[7], 该模型能够提取用户和物品的一阶交互信息, 以链接预测的方式补全交互矩阵. Wang等人根据图结构对消息进行迭代更新, 提出了NGCF模型[8], 该模型可以同时堆叠多个图卷积层来捕获高阶协作信号. 为了进一步提升推荐效果, Chen等人消除GCN中的非线性变换, 提出一种带有残差网络结构的线性传播方法LR-GCCF[9]. He等人提出另一种简化版的GCN模型LightGCN[10], 将图卷积网络中的特征变换和非线性激活部分去除, 只保留最重要的邻域聚合功能, 使推荐更为简单高效.
然而, 现实中用户与项目交互同通常由多种意图主导, 常规的图神经网络训练难以对这些意图进行区分. 例如购物场景中, 用户购买日用品时通常会优先考虑价格因素, 在购买服装鞋饰时会优先考虑外观和舒适度, 在购买电子产品时会优先选择品牌和功能. 为了判断用户的主要意图, 需要对用户-物品历史交互信息进行深入的挖掘. 为了解决这一问题, DGCF[11]将解耦表征学习(disentangled representation learning, DRL)应用到图协同过滤推荐中, 将交互项划分为多个意图, 每一个交互意图独立进行图学习, 最终聚合为完整的嵌入表示. 但是该方法在以下方面仍然存在局限性.
(1)模型解耦仅存在于交互行为层面, 并未关注用户的主要偏好特征, 例如对价格的敏感程度或对品牌的特殊喜好. 通过这种解耦所生成的意图特征并不能充分解释用户的偏好.
(2)模型的学习只考虑邻域信息, 忽视了语义邻居项的特征学习.
(3)模型通过深层迭代进行学习, 遇到大量稀疏数据和流行数据时表现较差.
针对以上问题, 本文将对比学习(contrastive learning, CL)融入图解耦协同过滤中, 提出了一种融合结构邻居和语义邻居的解耦图对比学习推荐模型NFDGCL (neighborhood fusion-based disentangled graph contrastive learning). 该模型在图传播阶段, 依据用户和项目的意图特征挖掘其潜在语义邻居, 这一工作有助于对非连接项目的学习, 改善数据稀疏性; 获取语义邻居后, 模型会根据意图相似性对结构邻居和语义邻居进行解耦表征学习, 生成用户和项目的完整高阶表示. 通过解耦后的特征学习, 能够区分意图的重要程度, 减少噪声数据带来的干扰. 在对比学习阶段, 首先会对节点进行随机扰动并生成对比视图, 在此基础上, 分别构建结构和语义的对比学习任务进行联合优化, 最终对用户和项目交互概率进行预测. 本文主要贡献如下.
(1)将整体图学习进行节点层面的意图解耦, 提供了意图解耦后的语义邻居挖掘方式, 并提出了融合结构邻居和语义邻居的解耦表征学习方法.
(2)建立了基于结构邻居和语义邻居解耦表征的联合对比学习范式, 这一范式能够有效捕捉节点与结构邻居及语义邻居的潜在依赖关系.
(3)基于真实数据集Amazon-Book和Yelp2018, 将本文模型与基线模型NGCF、LightGCN、MacridVAE、DGCN、SGL和NCL进行对比分析, 证明了该模型的有效性.
1 相关工作 1.1 图卷积神经协同过滤算法图卷积神经网络从邻居节点中提取信息, 通过逐层优化节点的嵌入实现高阶表征学习. 假设存在用户-项目二部图
| $ {X}^{l+1}=\sigma ({\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}}{X}^{l}{W}^{l}) $ | (1) |
其中,
| $ \text{ }{X}^{l+1}={\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}}{X}^{l} $ | (2) |
其中,
| $ {Z}_{\rm out}={f}_{\rm GCN}\left({X}_{\rm in}, \hat{A}\right)=\left({\sum }_{l=0}^{L}{\theta }_{l}{\hat{A}}^{l}\right){X}_{\rm in} $ | (3) |
其中,
解耦表征学习可以通过分解嵌入表征来揭示和观察数据的潜在因素, 有助于改善噪声问题和提升可解释性[12]. 基于解耦表征学习的图解耦推荐也是近年来推荐领域的热门话题. Ma等人提出了解耦变分自动编码器MacridVAE[13], 编码器将初始嵌入根据维度进行划分, 使得每个维度表示一种独立的语义. 考虑到物品属性带有丰富的上下文特征信息, 文献[14]提出的DisenHAN模型在异构信息网络中, 将物品属性投影到不同子空间进行内容转换和元关系聚合, 从而得到具有解释性的解耦表示. 为了进一步区分用户偏好的真正意图, 文献[15]提出的DCRS框架将嵌入解耦为类型依赖和独立偏好两部分, 区分了用户偏好的缘由: 项目的类别或项目自身属性. 然而, 现有大多数的解耦推荐系统都建立在完全监督的基础上, 解耦推荐的效果会因为现实场景中标签的稀疏性而受到限制. 为了应对这一挑战, 本文设计了意图解耦对应的图增强方案, 将对比学习纳入解耦推荐中, 为解耦表征学习结合并建立联合对比范式, 通过最大化对比视图一致性, 缓解稀疏性带来的影响, 提升推荐效果.
1.3 对比学习现实中的推荐系统所提供的用户-项目交互标签通常是较为稀疏的, 因此通过图卷积神经网络学习到的表征容易偏向高频用户或项目[16]. 为了解决这一难题, 研究人员提出了用于推荐的自监督学习模型[17]. Wu等人提出自监督模型SGL[18], 该模型通过随机剔除节点或边的方式生成对比视图, 以此建立辅助对比任务来改进用户和物品表征学习. Xia等人将推荐数据拓展到超图上进行建模, 提出了利用超图来提升学习效率的跨视图对比学习框架HCCF[19]. Lin等人考虑到单一图结构可能存在局限性, 提出了潜在邻居挖掘的对比学习算法NCL[20], 通过建立联合对比学习任务来协助表征学习. 现有的对比学习方法在一定程度上改善了数据稀疏性并提升了推荐性能, 但这些方法通常将节点视作独立整体, 很难捕捉用户和项目之间交互的潜在意图. 这种情况下进行图结构随机扩充容易受到用户交互数据噪声的影响, 可能无法很好地保留原始语义关系, 从而导致无法对原始交互结构进行正相关增强, 损害其他性能, 如多样性等[21]. 另外, 一些相关工作[22]已经考虑到图结构在消息传播过程中的不足, 并提出要在对比学习阶段纳入邻域挖掘策略进行优化, 但在图传播阶段忽略了这一策略的相关学习, 这可能使得最终学习的表征效果次优.
2 NFDGCL算法本节对提出的融合结构邻居和语义邻居的解耦图对比学习推荐模型 NFDGCL进行详细介绍, 总体架构如图1所示, 输入为意图解耦后的初始化嵌入, 模型分为3个部分: 图结构学习层、语义邻居学习层、解耦图对比学习层. 图结构学习层基于用户-项目交互图, 学习并输出用户/物品的结构化解耦表示. 语义邻居学习层基于聚类算法, 挖掘带有类似偏好的语义邻居并改进节点表征. 解耦图对比学习层通过所提出的解耦数据增强策略, 为结构和语义学习分别建立对比学习范式, 与图监督任务联合优化预测效果.
2.1 意图解耦表征学习 2.1.1 意图解耦初始化在用户-项目交互二部图
为了捕获不同的选择意图, 本文对用户和项目嵌入分别进行了意图层面的解耦, 将初始化嵌入分割为
| $ u_i^k = {\frac{{\sigma (W_k^{\rm T} \cdot {e_i}) + {b_k}}}{{\left\| {\sigma (W_k^{\rm T} \cdot {e_i}) + {b_k}} \right\|}}_2};v_j^k = {\frac{{\sigma (W_k^{\rm T} \cdot {e_j}) + {b_k}}}{{\left\| {\sigma (W_k^{\rm T} \cdot {e_j}) + {b_k}} \right\|}}_2} $ | (4) |
其中,

|
图 1 NFDGCL模型结构 |
解耦后的用户和项目嵌入分别表示为:
| $ {\mathcal{L}_{\rm dis}} = - \frac{1}{K}{\sum\limits_{k = 1}^K {({e^k})} ^{\mathrm{T}}}\ln {e^k} $ | (5) |
其中,
| $ \int\limits_u {\int\limits_v {P(y, u, v\mid U, V){\mathrm{d}}u{\mathrm{d}}v = \sum\nolimits_{k = 1}^K {P(y, u_i^k, v_j^k\mid U, V)} } } $ | (6) |
其中, 交互得分
在获得解耦后的初始化嵌入后, 本文通过图结构来进行全局性的消息传播, 这种方式能够有效地学习图神经网络的结构化特征, 增强系统鲁棒性.
为了有效获取解耦后的不同意图在消息传播过程中的作用, 本文计算了用户/项目与结构邻居在不同意图上的相似度得分, 计算方式如下:
| $ S(st)_{i \to j}^{k, l} = \frac{{\exp (sim(u_i^{k, l}, v_j^{k, l})/\tau )}}{{\displaystyle\sum\nolimits_{k' = 1}^K {\exp (sim(u_i^{k', l}, v_j^{k, l})/\tau )} }} $ | (7) |
其中,
| $ r(st)_{i \to j}^{k, l} = \frac{{S(st)_{i \to j}^{k, l} \cdot v_j^{k, l}}}{{\sqrt {\left| {\displaystyle\sum\nolimits_{{v_j} \in N(i)} {S(st)_{i \to j}^{k, l}} } \right|} }} $ | (8) |
其中,
虽然现有的深度学习模型已经考虑到解耦后直接对图结构进行学习, 提高了传统协同过滤模型的性能[15], 但相关研究指出, 只考虑用户和项目显式交互的特征不足以产生最优的嵌入, 用户对和项目对之间的相似性也是非常重要的信号[23]. 因此, 本文提出了语义邻居学习策略, 挖掘节点潜在的同质邻居并进行学习. 不同于NCL所提出的语义邻居挖掘机制, 本策略强调意图层面的语义邻居, 能够避免过多相似项目的重复推荐.
上文中
受PGCL[25]启发, 相似的用户/项目的空间距离往往更近, 这些节点可以通过数个聚类簇进行划分. 为了使每个节点获取期望值更高的语义邻居, 本文应用K-means聚类算法来获得用户或项目的原型, 同时使用EM算法对这一过程进行优化, 对用户而言, 优化目标是极大化以下对数似然函数(maximum likelihood estimate, MLE):
| $ \sum\limits_{i = 1}^I {\log p({u_i};\theta )} = \sum\limits_{i = 1}^I {\log \sum\nolimits_{{{\textit{z}}_i} \in \overline {{Z_i}} } {p({u_i}, {{\textit{z}}_i};\theta )} } $ | (9) |
其中,
| $ S(se)_{i \to {{\textit{z}}_i}}^{k, l} = \frac{{\exp (sim(u_i^{k, l}, {\textit{z}}_i^{k, l})/\tau )}}{{\displaystyle\sum\nolimits_{k' = 1}^K {\exp (sim(u_i^{k', l}, {\textit{z}}_i^{k, l})/\tau )} }} $ | (10) |
其中,
| $ r(se)_{i \to {{\textit{z}}_i}}^{k, l} = \frac{{S(se)_{i \to {{\textit{z}}_i}}^{k, l} \cdot {\textit{z}}_i^{k, l}}}{{\sqrt {\left| {\displaystyle\sum\nolimits_{{{\textit{z}}_i} \in N'(i)} {S(se)_{i \to {{\textit{z}}_i}}^{k, l}} } \right|} }} $ | (11) |
其中,
| $ u_i^{k, l} = {W^l}\left[\alpha \sum\nolimits_{{v_j} \in N(i)} {r(st)_{i \to j}^{k, l}} + (1 - \alpha )\sum\nolimits_{{{\textit{z}}_i} \in N'(i)} {r(se)_{i \to {{\textit{z}}_i}}^{k, l}} \right] $ | (12) |
| $ v_j^{k, l} = {W^l}\left[\alpha \sum\nolimits_{{u_i} \in N(j)} {r(st)_{j \to i}^{k, l}} + (1 - \alpha )\sum\nolimits_{{{\textit{z}}_j} \in N'(j)} {r(se)_{j \to {{\textit{z}}_j}}^{k, l}} \right] $ | (13) |
其中, 参数矩阵
| $ u_i^k = \sum\limits_{l = 0}^L {\frac{{u_i^{k, l}}}{{L + 1}}} ; v_j^k = \sum\limits_{l = 0}^L {\frac{{v_j^{k, l}}}{{L + 1}}} $ | (14) |
其中, 当
作为推荐领域内先进的自监督框架, 图对比学习在准确性方面展现了强大的性能, 对数据稀疏问题也有很大改善. 但大多数对比学习方法在一定程度上都破坏了用户-项目交互图的结构信息, 这可能误导表示学习, 并容易受到噪声用户行为的影响[26].
为了应对这一挑战, 本文设计了基于节点扰动的解耦数据增强策略, 能在原有图结构基础上改进交互信息, 自适应的进行解耦对比学习.
2.2.1 解耦数据增强现有的对比学习推荐的数据增强策略一般采用节点丢弃和交互边丢弃方案, 虽然有助于改善数据稀疏性, 但交互信息的减少可能导致弱势项目推荐概率的降低, 对其他性能造成损害, 例如多样性[27]. 本文参考SimGCL[28]提出的节点增强策略, 将解耦后的节点进行扰动, 具体表示如下:
| $ c' = \{ {c_1} + {\Delta _1} \odot {c_1}, \cdots , {c_{I + J}} + {\Delta _{I + J}} \odot {c_{I + J}}\} $ | (15) |
其中,
结构对比损失: 使用上述数据增强并产生对比视图后, 本文在用户和项目的不同视图的嵌入之间进行对比学习. 根据SGL提出的自监督对比方法, 本文将每一层输出的用户嵌入与对比视图中的对应用户嵌入一同组成正样本, 将其他的用户嵌入视为负样本. 基于InfoNCE损失函数[29], 本文提出了最小化两者之间距离的图结构对比学习目标:
| $ \mathcal{L}_{\rm st}^U = \frac{1}{I}\displaystyle\sum\limits_{i = 0}^I {\sum\limits_{l = 0}^L { - \log \frac{{\exp (sim(u_i^l, c_i^{'l})/\tau )}}{{\displaystyle\sum\nolimits_{i' = 0}^I {\exp (sim(u_i^l, c_{i'}^{'l})/\tau )} }}} } $ | (16) |
其中,
| $ \mathcal{L}_{\rm st}^V = \frac{1}{J}\sum\limits_{j = 0}^J {\sum\limits_{l = 0}^L { - \log \frac{{\exp (sim(v_j^l, c_j^{'l})/\tau )}}{{\displaystyle\sum\nolimits_{j' = 0}^J {\exp (sim(v_j^l, c_{j'}^{'l})/\tau )} }}} } $ | (17) |
整体结构对比损失函数可以由上述两种损失加权表示:
| $ \mathcal{L}_{\rm st} = \mathcal{L}_{\rm st}^U + \gamma \mathcal{L}_{\rm st}^V $ | (18) |
其中,
语义对比损失: 由于本文中的语义邻居的选取带有较强的随机性, 故对语义邻居不进行数据增强. 本文用户的语义邻居为同质邻居, 用户与聚类簇中的原型嵌入组成正样本, 其他簇中的语义邻居则被视为负样本, 最小化两者之间距离的语义邻居对比学习目标如下:
| $ \mathcal{L}_{\rm se}^U = \frac{1}{I}\sum\limits_{i = 0}^I {\sum\limits_{l = 0}^L { - \log \frac{{\exp (sim(u_i^l, {\textit{z}}_i^l)/\tau )}}{{\displaystyle\sum\nolimits_{{{\textit{z}}_{i'}} \in {Z_i}}^{} {\exp (sim(u_i^l, {\textit{z}}_{i'}^l)/\tau )} }}} } $ | (19) |
其中,
| $ \mathcal{L}_{\rm se}^V = \frac{1}{J}\sum\limits_{j = 0}^J {\sum\limits_{l = 0}^L { - \log \frac{{\exp (sim(v_j^l, {\textit{z}}_j^l)/\tau )}}{{\displaystyle\sum\nolimits_{{{\textit{z}}_{j'}} \in {Z_j}}^{} {\exp (sim(v_j^l, {\textit{z}}_{j'}^l)/\tau )} }}} } $ | (20) |
整体语义对比损失函数可以由上述两种损失加权表示:
| $ \mathcal{L}_{\rm se}= \mathcal{L}_{\rm se}^U + \gamma \mathcal{L}_{\rm se}^V $ | (21) |
通过这种方式, 可以将用户/项目的结构邻居和语义邻居一同引入对比学习中, 提升推荐性能.
2.3 预测与优化由前文所计算得到的用户/项目最终嵌入后, 可以计算得到预测得分:
| $ {y_{i, j}} = {u_i}^{\rm T}{v_j} $ | (22) |
基于推荐系统通常采用的贝叶斯个性化排名损失[30], 使观测到的交互项预测得分高于未观测到的交互项:
| $ \mathcal{L}_{\rm bpr} = - \frac{1}{{\left| \rho \right|}}\sum\nolimits_{(i, {j^ + }, {j^ - }) \in \rho } {\ln \sigma ({y_{i, {j^ + }}} - {y_{i, {j^-}}})} $ | (23) |
其中,
最终, 本文将推荐损失与自监督损失整合为多任务优化目标, 整体损失函数如下:
| $ \mathcal{L} = {\mathcal{L}_{\rm dis}} + \mathcal{L}_{\rm bpr} + {\lambda _1}\mathcal{L}_{\rm st} + {\lambda _2}\mathcal{L}_{\rm se} + {\lambda _3}{\left\| \Theta \right\|_2} $ | (24) |
其中
本文实验基于Intel(R) Xeon(R) CPU E5-2680 v4 @ 2.40 GHz, RTX 2080 Ti (11 GB)、Ubuntu 20.04系统, 实验环境为Python 3.8、PyTorch 1.10和Cuda 11.3.0.
3.2 数据集和评价指标本文在两个公开数据集Yelp2018和Amazon-Book上进行实验. Yelp2018 是 Yelp 网站 2018 年挑战赛所采用的公开数据集, 内容包括用户查看过的餐厅、酒吧等商户. Amazon-Book数据集为亚马逊评论数据集的子集, 内容为书籍购买记录. 为了保证实验的有效性, 本文根据数据集的大小和稀疏程度进行筛选, 选取交互数大于10的用户和交互项目. 对于每个数据集的任意用户, 随机选择 80%的交互物品作为训练数据, 并在其中随机抽取10%的数据用作验证集, 剩余 20%交互物品将作为测试集进行模型评估. 数据集的统计信息如表1所示.
本实验基于Top-N推荐方法, 采用推荐系统中广泛使用的召回率Recall和归一化折损累计增益NDCG作为评价指标. 按照推荐系统常用设置习惯, 本文中
| $ Recall\text{@}N=\frac{1}{|U|} \sum_{u \in U} \frac{|\hat{R}(u) \cap R(u)|}{|R(u)|} $ | (25) |
| $ NDCG{\text{@}}N=\frac{1}{|U|} \displaystyle\sum_{u \in U}\left(\frac{\displaystyle\sum_{i=1}^N \delta(i \in R(u)) \frac{1}{\log _2(i+1)}}{\displaystyle\sum_{i=1}^{\min (\mid R(u), N)} \frac{1}{\log _2(i+1)}}\right) $ | (26) |
其中,
| 表 1 数据集统计信息 |
3.3 基准算法与参数设置
为了验证模型的有效性, 本文将NFDGCL与以下多种较为先进的基准方法进行对比.
NGCF[8]: 一种基于GCN的协同过滤方法, 基于用户-项目交互图进行消息传播并生成高阶表示.
LightGCN[10]: 简化了GCN中的特征变换和非线性操作, 使得模型更适用于推荐.
DGCF[11]: 一种解耦的图协同过滤方法, 解耦后将在不同的子图中进行学习并合成最终的嵌入.
SGL[18]: 在图监督学习的基础上增加一个辅助的自监督任务, 通过自我识别改进表征学习.
HCCF[19]: 提出了在超图上使用对比学习的图协同过滤模型.
NCL[20]: 提出了一个模型无关的对比学习框架, 在对比任务中挖掘潜在邻居来改进图协同过滤.
本文中列举的对比方法均采用原模型中作者设置的最佳参数. 本文实验中, NFDGCL模型解耦意图数
本文提出的 NFDGCL模型与其他基准方法在两个真实数据集上的实验结果如表2和表3所示, 其中Improv.表示该指标的提升比例.
| 表 2 Yelp2018数据集下的性能比较 |
| 表 3 Amazon-Book数据集下的性能比较 |
根据表2和表3中的实验结果, NFDGCL模型在推荐任务上的性能均显著优于所有基线模型. 其中, LightGCN通过更优的消息传播机制, 相比利用原始图卷积网络结构进行建模的NGCF模型, 大幅提升了性能. DGCF模型展现了比LightGCN更为强大的性能, 原因可能在于明确了意图解耦的真实含义并保持意图独立, 其次根据解耦后的意图引入了新的邻居路由机制, 使原始交互解耦为表现能力更强大的意图交互. 在上述实验中, 基于图自监督的SGL模型和HCCF模型明显优于其他基于监督的模型, 这表明使用对比学习补充推荐任务是十分有效的, 通过生成对比试图并最大化对比视图下的数据一致性, 一方面可以减缓数据稀疏性带来的影响, 另一方面可以改进节点表示的过度光滑问题, 避免过拟合. 另外, HCCF引入了超图概念对图结构进行扩充, NCL在加入了潜在邻居挖掘的对比学习策略, 这两种方式进一步丰富了节点表示, 因此在基线模型中取得了最优的结果.
本文提出的NFDGCL模型对比各基线模型在Recall和NDCG指标上均取得了最好的效果. 更准确地说, 当取Top-20和Top-50进行推荐时, NFDGCL在以下方面的表现优于最佳基线模型NCL: 在数据集Yelp2018上, NFDGCL在Recall指标上提升了7.54%和6.85%, 在NDCG指标上提升了8.57%和7.20%; 在数据集Amazon-Book上, NFDGCL在Recall@20和Recall@50指标上提升了5.65%和4.08%, 在NDCG@20和NDCG@50指标上提升了6.28%和5.06%. 性能提升主要取决于以下几个方面: 首先, NFDGCL采用了和DGCF类似的意图解耦方式, 并引入了用于解耦嵌入的全新邻居路由机制, 邻居的挖掘策略不局限于高阶交互项, 而是将潜在语义邻居一并纳入学习的范畴, 因此具有更丰富的表征学习能力. 其次, NFDGCL联合了结构邻居和语义邻居的解耦对比学习方法, 将自监督学习作为表征学习的辅助任务, 能有效减缓数据稀疏性, 改进图学习过程.
3.4.2 模型性能分析为了体现模型性能变化, 本节将NFDGCL在数据集Yelp2018和Amazon-Book上的训练过程进行分析. 其中, 图2展示了在两个数据集中训练的损失收敛曲线, 图3与图4展示了NDCG指标和Recall在top-20下的精度曲线.

|
图 2 损失收敛曲线 |
根据图2的结果, 模型在训练初期波动较大, 随后逐渐变得平滑, 这是由于本模型涉及的参数较多, 初始训练很难取得理想结果, 需要进行较长时间的优化. 另一方面, 对于Amazon-Book数据集, Yelp2018数据体量更小, 因此收敛速度更快, 训练效果更明显.

|
图 3 Yelp2018精度曲线 |
|
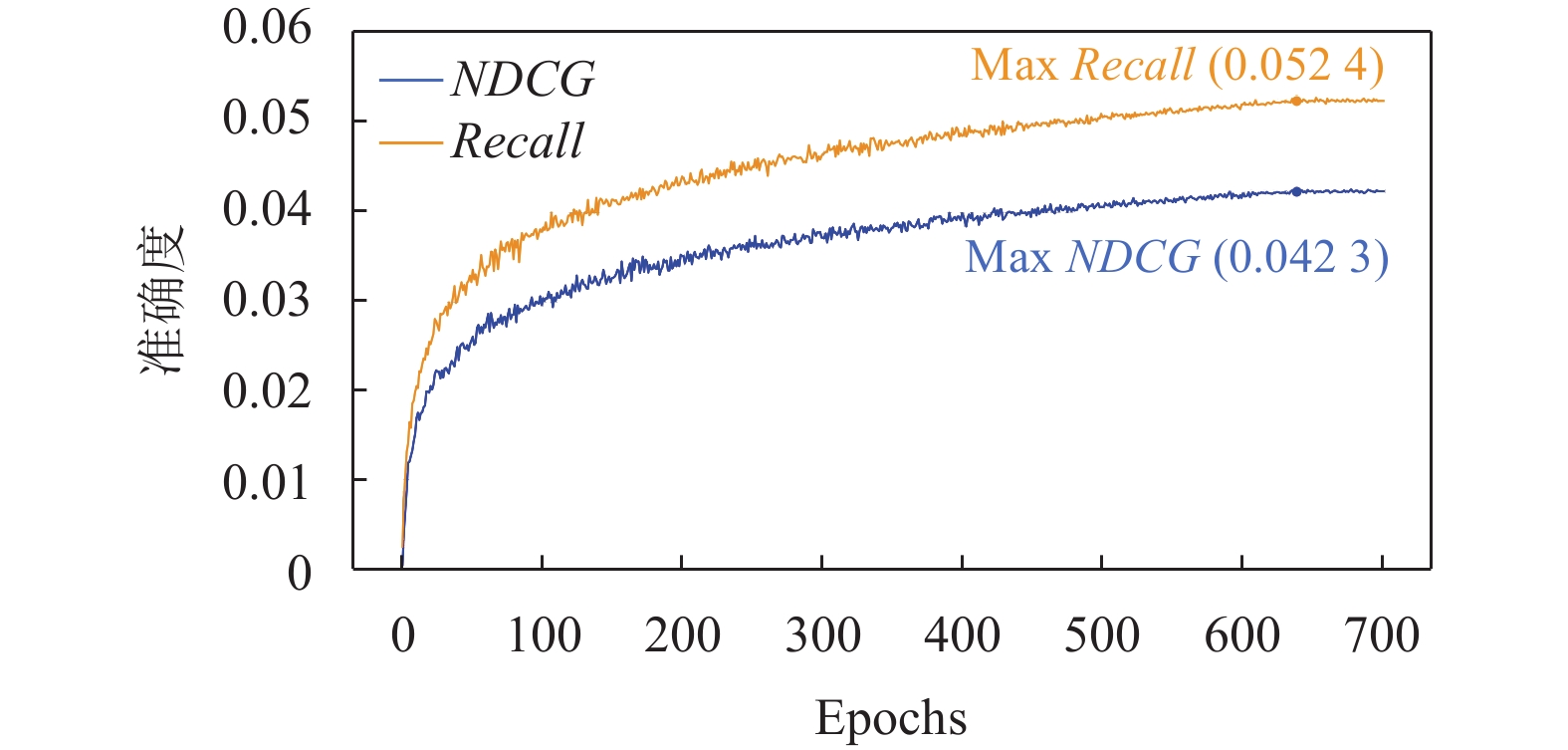
图 4 Amazon-Book精度曲线 |
根据图3与图4的结果, 在不同的数据集中, 模型在top-20项目上的推荐准确度均随着迭代周期的增长而不断提升, 并当迭代周期到达一定数值时, 推荐精度达到最大. 这一趋势与损失收敛曲线基本保持一致. 当迭代周期进一步增大, 整体精度并没有随之提升, 甚至出现了下降趋势, 产生了过拟合问题.
3.5 消融实验 3.5.1 意图解耦的影响为了探究本实验中意图解耦的有效性以及对整体模型的影响, 因此对解耦数
根据图5的结果, 当意图数量为1时, 即移除了模型中的解耦机制后, 得到了最差的实验结果, 相反的, 当开始加入解耦机制时, 会带来大幅度的性能提升. 这说明模型中的意图解耦是有效的, 能够区分节点与异质邻居和同质邻居之间的特征关系, 取得更好的学习效果. 另一方面, 对于Yelp2018和Amazon-Book数据集, 意图数量从4增加至8时, 性能提升幅度有限, 甚至在Yelp2018上出现了下滑. 由此可见, 意图数量过多也会造成性能下滑, 为了进一步解释原因, 本文根据文献[33]提出的方法, 随机抽样经过学习后的嵌入, 并将其从高维距离在二维空间中进行表示, 通过节点之间的欧氏距离来描述意图分布情况. 如图6所示, 在Yelp2018数据集上, 当意图总数为4时, 各意图距离适中, 分布较为均匀; 当意图总数为8时, 各意图之间的距离缩小并出现重合现象, 降低解耦效果, 这表明过多增加意图数量同样会导致意图冗余, 造成性能下降.

|
图 5 交互意图数量对模型的影响 |
3.5.2 语义邻居学习融合的影响
本文中所提到的语义邻居学习的效果是未知的, 因此本节分别在Yelp2018和Amazon-Book数据集上进行实验, 分析语义邻居学习对于模型性能的影响. 对语义邻居的选取数量进行灵敏度分析, 取值范围为[0, 1, 2, 3, 4]. 由于模型默认每个节点选取聚类簇中的原型节点作为语义邻居, 因此在消融实验中, 可将聚类簇中的其他同类节点一并视为语义邻居, 其余参数与对比分析实验保持一致. 图7展示了Yelp2018和Amazon-Book数据集下NFDGCL在Recall@20和NDCG@20的指标变化情况. 为了便于比较, 实验同样选取语义邻居数为1的情况作为基准值, 并以相差值的百分比展示结果.

|
图 6 交互意图分布情况 |
根据图7的结果, 当选取语义邻居的数量为0时, 模型的性能在Recall@20和NDCG@20指标上最低, 当选取语义邻居的数量为1时, 模型的性能得到了大幅提升. 这表明本文提出的语义邻居学习是有效的, 在图学习的过程中适当加入同质节点的特征学习有利于改进节点的表征. 但当语义邻居的数量大于1时, 模型的性能无明显变化, 这是因为聚类获取的语义邻居的相似度是较高的, 重复的学习很难带来大幅的性能提升, 反而会降低训练效率.
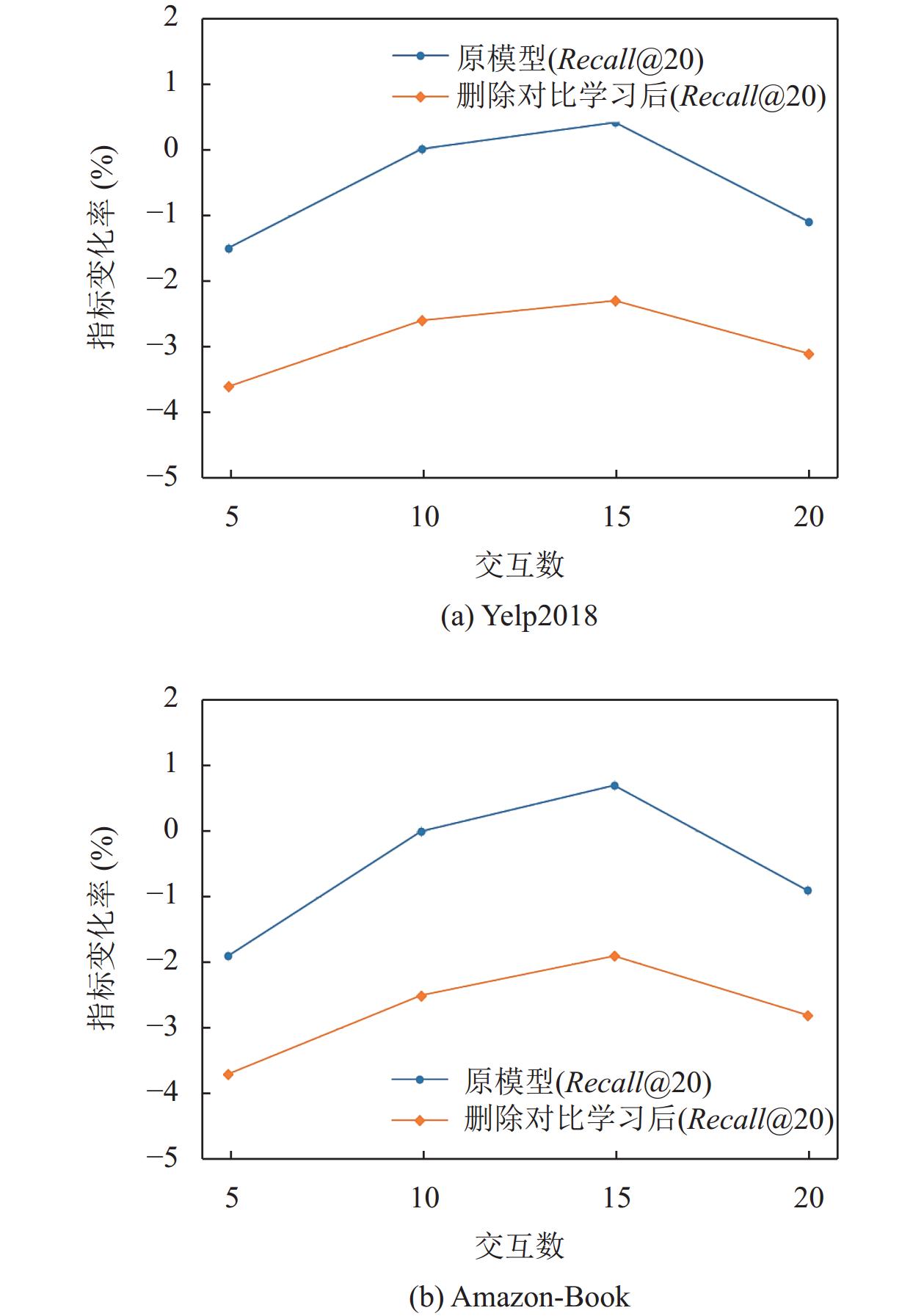
3.5.3 对比学习对模型的影响为了验证本模型中对比学习的有效性, 本节分别在Yelp2018和Amazon-Book数据集上进行实验, 分析对比学习对于模型性能的影响. 在消融实验中, 对交互数进行灵敏度分析, 取值范围为[5,10,15,20], 以此模拟数据集不同的稀疏程度, 将联合对比学习任务进行删除并与原模型进行比较, 其余参数与对比分析实验保持一致. 图8展示了Yelp2018和Amazon-Book数据集下NFDGCL在Recall@20的指标变化情况. 为了便于比较, 实验选取交互数为10的情况作为基准值, 并以相差值的百分比展示结果, 并在统一图表中对两个模型推荐性能进行比较.

|
图 7 语义邻居数量对模型的影响 |
根据图8的结果, 当选取交互数为5时, 模型的性能在Recall@20指标上最低, 当选取交互数为15时, 模型的性能最高, 这表明数据的稀疏程度很大程度会影响模型性能, 合理的稀疏程度会提升推荐性能, 但删除过量的稀疏连接节点也会损害推荐性能. 在删除对比学习后, 模型性能在不同的稀疏情况下都不及原始模型, 并且在数据更稀疏的Amazon-Book数据集中表现更差, 这表明本文提出的对比学习方案是有效的, 在更稀疏的数据集中的提升效果更明显.
4 结束语本文提出了一种融合结构邻居和语义邻居的解耦图对比学习推荐模型NFDGCL. 该模型能够将原始用户/项目嵌入表示进行交互意图解耦, 在图传播阶段通过聚类算法根据意图特征获取节点潜在语义邻居, 然后融合结构和语义邻居进行解耦学习, 改进嵌入高阶表征. 模型中定义的联合对比学习任务框架, 能够在学习的过程中, 挖掘交互的潜在特征, 调节表示分布的均匀性, 减缓稀疏性和减少过拟合. 在两个数据集上的结果表明, NFDGCL比其他基线模型具有更好的表现.
|
图 8 对比学习对模型的影响 |
在未来的工作中, 可以考虑将本文中提到的框架用于其他推荐任务, 如序列推荐、会话推荐等. 另外, 解耦图对比学习和语义邻居在挖掘和捕捉用户偏好展现了巨大的潜力, 可以考虑将模型进行微调并用于下游任务, 如解决流行度偏差、长尾现象等问题.
| [1] |
张玉洁, 董政, 孟祥武. 个性化广告推荐系统及其应用研究. 计算机学报, 2021, 44(3): 531-563. DOI:10.11897/SP.J.1016.2021.00531 |
| [2] |
Liao J, Zhou W, Luo FJ, et al. SocialLGN: Light graph convolution network for social recommendation. Information Sciences, 2022, 589: 595-607. DOI:10.1016/j.ins.2022.01.001 |
| [3] |
Sarwar B, Karypis G, Konstan J, et al. Item-based collaborative filtering recommendation algorithms. Proceedings of the 10th International Conference on World Wide Web. Hong Kong: ACM, 2001. 285–295. [doi: 10.1145/371920.372071]
|
| [4] |
范伟, 周魏, 文俊浩. 基于异构图的双通道交叉自适应对比学习推荐. 电子学报, 2023, 51(7): 1929-1938. |
| [5] |
Kipf TN, Welling M. Semi-supervised classification with graph convolutional networks. Proceedings of the 5th International Conference on Learning Representations. Toulon: OpenReview.net, 2017. 104–118.
|
| [6] |
Gao C, Wang X, He XN, et al. Graph neural networks for recommender system. Proceedings of the 15th ACM International Conference on Web Search and Data Mining. ACM, 2022. 1623–1625. [doi: 10.1145/3488560.3501396]
|
| [7] |
Berg R, Kipf TN, Welling M. Graph convolutional matrix completion. arXiv:1706.02263, 2017.
|
| [8] |
Wang X, He XN, Wang M, et al. Neural graph collaborative filtering. Proceedings of the 42nd international ACM SIGIR conference on Research and development in Information Retrieval. Paris: ACM, 2019. 165–174.
|
| [9] |
Chen L, Wu L, Hong RC, et al. Revisiting graph based collaborative filtering: A linear residual graph Convolutional network approach. Proceedings of the 34th AAAI Conference on Artificial Intelligence. New York: AAAI, 2020. 27–34.
|
| [10] |
He XN, Deng K, Wang X, et al. LightGCN: Simplifying and powering graph convolution network for recommendation. Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval. ACM, 2020. 639–648. [doi: 10.1145/3397271.3401063]
|
| [11] |
Wang X, Jin HY, Zhang A, et al. Disentangled graph collaborative filtering. Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval. ACM, 2020. 1001–1010.
|
| [12] |
Ma JX, Cui P, Kuang K, et al. Disentangled graph convolutional networks. Proceedings of the 36th International Conference on Machine Learning. Long Beach: PMLR, 2019. 4212–4221.
|
| [13] |
Ma JX, Zhou C, Cui P, et al. Learning disentangled representations for recommendation. Proceedings of the 33rd Conference on Neural Information Processing Systems. Vancouver: NeurIPS, 2019. 5712–5723.
|
| [14] |
Wang YF, Tang SY, Lei YT, et al. DisenHAN: Disentangled heterogeneous graph attention network for recommendation. Proceedings of the 29th ACM International Conference on Information & Knowledge Management. ACM, 2020. 1605–1614. [doi: 10.1145/3340531.3411996]
|
| [15] |
Zhang XY, Wang HN, Li H. Disentangled representation for diversified recommendations. Proceedings of the 16th ACM International Conference on Web Search and Data Mining. Singapore: ACM, 2023. 490–498. [doi: 10.1145/3539597.3570389]
|
| [16] |
Yang C, Zou JX, Wu JH, et al. Supervised contrastive learning for recommendation. Knowledge-based Systems, 2022, 258: 109973. DOI:10.1016/j.knosys.2022.109973 |
| [17] |
Xia LH, Huang C, Huang CZ, et al. Automated self-supervised learning for recommendation. Proceedings of ACM Web Conference 2023. Austin: ACM, 2023. 992–1002. [doi: 10.1145/3543507.3583336]
|
| [18] |
Wu JC, Wang X, Feng FL, et al. Self-supervised graph learning for recommendation. Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval. ACM, 2021. 726–735.
|
| [19] |
Xia LH, Huang C, Xu Y, et al. Hypergraph contrastive collaborative filtering. Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval. Madrid: ACM, 2022. 70–79. [doi: 10.1145/3477495.3532058]
|
| [20] |
Lin ZH, Tian CX, Huo YP, et al. Improving graph collaborative filtering with neighborhood-enriched contrastive learning. Proceedings of ACM Web Conference 2022. ACM, 2022. 2320–2329.
|
| [21] |
Cai XH, Huang C, Xia LH, et al. LightGCL: Simple yet effective graph contrastive learning for recommendation. Proceedings of the 11th International Conference on Learning Representations. Kigali: OpenReview.net, 2023. 245–257.
|
| [22] |
Ren XB, Xia LH, Zhao JS, et al. Disentangled contrastive collaborative filtering. Proceedings of the 46th International ACM SIGIR Conference on Research and Development in Information Retrieval. Taipei: ACM, 2023. 1137–1146.
|
| [23] |
Yu JL, Yin HZ, Li JD, et al. Self-supervised multi-channel hypergraph convolutional network for social recommendation. Proceedings of Web Conference 2021. Ljubljana: ACM, 2021. 413–424.
|
| [24] |
Sun JN, Zhang YX, Ma C, et al. Multi-graph convolution collaborative filtering. Proceedings of the 2019 IEEE International Conference on Data Mining. Beijing: IEEE, 2019. 1306–1311.
|
| [25] |
Wu JK, Shi WT, Cao XZ, et al. DisenKGAT: Knowledge graph embedding with disentangled graph attention network. Proceedings of the 30th ACM International Conference on Information & Knowledge Management. New York: ACM, 2021. 2140–2149. [doi: 10.1145/3459637.3482424]
|
| [26] |
Lin S, Liu C, Zhou P, et al. Prototypical graph contrastive learning. IEEE Transactions on Neural Networks and Learning Systems, 2024, 35(2): 2747-2758. DOI:10.1109/TNNLS.2022.3191086 |
| [27] |
Zheng Y, Gao C, Chen L, et al. DGCN: Diversified recommendation with graph convolutional networks. Proceedings of Web Conference 2021. Ljubljana: ACM, 2021. 401–412.
|
| [28] |
Yu JL, Yin HZ, Xia X, et al. Are graph augmentations necessary? Simple graph contrastive learning for recommendation. Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval. Madrid: ACM, 2022. 1294–1303. [doi: 10.1145/3477495.3531937]
|
| [29] |
van den Oord A, Li YZ, Vinyals O. Representation learning with contrastive predictive coding. arXiv:1807.03748, 2019.
|
| [30] |
Rendle S, Freudenthaler C, Gantner Z, et al. BPR: Bayesian personalized ranking from implicit feedback. Proceedings of the 25th Conference on Uncertainty in Artificial Intelligence. Montreal: AUAI Press, 2009. 452–461.
|
| [31] |
Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks. Proceedings of the 13th International Conference on Artificial Intelligence and Statistics. Sardinia: JMLR.org, 2010. 249–256.
|
| [32] |
Kingma DP, Ba J. Adam: A method for stochastic optimization. Proceedings of the 3rd International Conference on Learning Representations. San Diego: ICLR, 2015. 258–273.
|
| [33] |
van der Maaten L, Hinton G. Visualizing data using t-SNE. Journal of Machine Learning Research, 2008, 9(86): 2579-2605. |
 2024, Vol. 33
2024, Vol. 33


