随着世界格局从乌卡(VUCA)时代进入易崩塌(brittle)、焦虑感(anxious)、非线性(nonlinear)、不可知(incomprehensible)的巴尼(BANI)时代[1], 世界的快速发展呈现出错综复杂的反馈关系[2], 任何系统和组织都变得脆弱和不可控. 而产业互联“智造”供需网作为推动智能制造在各个领域实现与推广[3], 连接多产业、多业务的大规模复杂网络系统[4,5], 在巴尼时代下, 面临着生产异常、网络威胁等一系列未知的挑战, 这其中任何问题都可能导致供需网的级联失效, 影响整个网络的稳定性和运行效率. 因此, 在此时代背景下, 研究产业互联“智造”供需网级联失效模型对于预测和应对潜在风险至关重要.
产业互联“智造”供需网的运行依托于新兴技术, 具有大规模、数字化的特点, 是传统供应链的延伸和升级. 而复杂网络理论是研究供需网和传统供应链级联失效的重要方法, 通过构建网络拓扑模型、设计网络级联失效机制等, 该理论能够清楚剖析产业互联“智造”供需网的级联失效问题. 现阶段, 基于复杂网络理论的供需网级联失效研究也大多从这两方面展开.
在供需网的拓扑结构研究方面, 学者们提出了多种网络模型, 例如单层加权网络[6]、双层有向网络[7]、多级有向网络[8], 除此之外, 文献[9]考虑到供应链中节点分级的特性, 构建了包括供应子网和需求子网的哑铃型供需网模型, 文献[10]构建的农业食品供应链网络中划分了5种节点类型, 并考虑了当前没有直接连接但未来可能有直接连接的弱连接节点, 文献[11]认为供应链网络是多个企业通过纵向合作和横向竞合关系连接而成的有机系统, 构建了集群式网络模型. 但是, 产业互联“智造”供需网是多产业互联的复杂网络, 相比于上述研究中非模块化的拓扑结构, 具有社团结构的模块化网络模型更适用于对其进行描述. 社团结构是指网络中内部紧密相连而外部连接较为稀疏的节点群体, 其在许多领域都有重要应用, 比如社交网络分析[12]、生物信息学[13]、金融系统[14]、交通网络[15]等. 在产业互联“智造”供需网中, 每个产业子网可以看作复杂网络中的一个社团, 社团内节点的连接关系代表了产业子网内的合作与协同. 同时, 不同产业子网间也存在一定连接关系, 表示不同产业间的合作与互动, 例如, 传统汽车产业与科技产业连接, 可以实现智能化汽车系统集成. 文献[16]就曾发现产业互联网络中产业间存在的社团结构.
在网络级联失效机制研究方面, 以往研究大多采用过载或欠载失效模型[17]、病毒传播模型[18]等模拟供需网的级联失效过程, 最近几年许多学者在这些模型的基础上进行了改进, 例如, 文献[19]构建了供应链网络上游供应端发生过载失效, 下游需求端发生欠载失效的混合失效模型, 文献[20]将马尔可夫模型与传染病模型相结合, 构建了具有5种节点状态的供应链网络中断风险传播模型, 文献[21]通过建立概率转移树, 利用微观马尔可夫链模型建立了双层部分映射供需网络的风险状态转移方程. 在上述研究中, 网络中的风险始终以确定性的方式传播, 然而, 产业互联“智造”供需网与传统供应链相比, 涉及大量智能设备和自动化系统的实时交互[22], 以及科研院所、金融机构、咨询机构等多种类型节点间错综复杂的合作关系, 其风险传播的复杂性和不确定性均显著强于传统供应链, 导致风险传播的路径变得不可预测, 且更倾向于以概率的形式呈现, 类似的, 由于节点故障后故障原因的多样性和恢复资源的复杂性, 其恢复形式也更倾向于概率恢复. 另外, 当网络中节点故障后, 由于智能系统的紧急控制通常不会使风险立刻传播出去, 而是预留一段恢复时间以修复故障, 导致产生了风险传播与恢复的周期延迟效果. 综上所述, 现有研究尚未详细考虑到产业互联“智造”供需网风险传播与恢复的随机性和延时性特征.
鉴于此, 在现有研究基础上, 本文进一步准确描述产业互联“智造”供需网的级联失效过程和鲁棒性, 针对产业互联“智造”供需网中风险传播与恢复的随机性和延时性, 首先, 构建具有社团结构的复杂网络模型; 接着, 结合考虑不同节点间的相对关联度, 构建考虑相对故障概率的风险传播模型, 并结合节点的相对重要程度, 构建考虑恢复概率和周期的故障恢复模型; 最后, 基于改进引力模型构建网络, 以网络相对连通率R作为鲁棒性评价指标, 对不同故障和恢复场景下的级联失效鲁棒性进行仿真分析.
1 产业互联“智造”供需网模型描述区别于传统供应链网络, 产业互联“智造”供需网是由多种产业协同互联而成, 既包括产业间的跨界融合, 也包括产业内的更深度关联合作, 因此, 其网络结构可以抽象为以产业为边界, 包含多个产业子网的社团结构网络, 且同一产业子网内关联比子网间关联更密切.
将产业互联“智造”供需网模型表述为
采用模块度Q衡量不同产业子网间的稳定性和紧密度, 代表了网络中社团内部连接强度相对于社团之间连接强度的差异程度, 表示为:
| Q=12m∑i,j[Aij−didj2m]δ(i,j) | (1) |
其中, m为所有连边权重之和; 当节点i和节点j在同一社团时, δ(i, j)=1, 否则为0. Q取值最大为1, 越小则表示社团内部的连接强度相对较低, 社团之间的连接较强, 社团结构较为松散.
2 网络故障的传播与恢复由于产业互联“智造”供需网连接多产业、多业务, 相比其他网络结构更复杂、节点类型更多、规模更大, 因此其风险传播的路径和故障恢复形式都更难以预测. 试图通过分析发现其风险传播与故障恢复的特性与规律, 构建基于故障概率的风险传播模型, 和考虑恢复概率与恢复周期的故障恢复模型, 以更确切的模拟真实世界中产业互联“智造”供需网在中断、传播和恢复场景中的情况.
2.1 考虑故障概率的风险传播模型当产业互联“智造”供需网中节点面临风险, 这种风险可能会传播给与其直接或间接关联的其他节点, 并且两节点的关联程度决定了它们之间信息的交流速度和准确性, 进而影响风险传播的可能性. 但需要注意的是, 由于受到业务性质、功能等的影响, 导致两节点间的关联程度可能是相对的, 某些节点可能与少数几个关键节点密切关联, 而另一些节点可能与多个其他节点关联. 因此, 受到节点间相对关联程度的影响, 节点间风险传递的概率也具有相对性.
并且由于社团内部合作更紧密、风险传播路径更短和共享风险管理机制的存在, 风险传播概率更小. 相反的, 由于社团间的节点合作中间环节和信息传递的不确定性, 风险传播概率更高. 因此, 根据风险传播的范围, 将故障概率类型划分为: 产业子网内风险传播和产业子网间风险传播. 采用故障节点i与相邻节点j边权ωij占节点j所有边权之和的比表示两节点的相对关联度, 得到子网内风险传播概率LSij和子网间风险传播概率LDij.
| LSij=ηωij∑p∈Γjωpj | (2) |
| LDij′=(ηωij′∑q∈Γj′ωqj′)α | (3) |
其中, Γj表示节点j所有邻居节点的集合; η为可调参数,
由于节点往往具有对前一次故障和恢复的技术及经验总结, 通常在故障恢复后能够有效降低下一次面临风险时的故障概率. 因此, 本文引入韦伯分布函数, 以表达网络中任意节点的故障概率会随其故障次数的增大而减小.
| LSij(x)=∫[x,∞]f(x)dx | (4) |
| LDij(x)=∫[x,∞]f(x)dx | (5) |
| f(x)=kλ⋅(xλ)k−1⋅e−(x/xλλ)k | (6) |
其中, f(x)表示节点j在第x次故障时的概率密度函数; λ为尺度参数, λ>0, λ越大表示节点故障概率对故障次数的增加下降越快, 取0.1; k为形状参数, 描述分布函数的形状, 取k=1, 表示故障概率随故障次数的增加呈指数下降.
2.2 考虑恢复概率和周期的故障恢复模型当产业互联“智造”供需网发生故障后, 为减少损失和保持业务的连续性, 通常故障节点会第一时间启动相应措施促使节点尽快恢复. 而越重要的节点往往承担着更关键的功能和服务, 其一旦失效对整个网络的影响也更大, 因此, 为了保证其恢复, 通常会投入更多的资源, 使其成功恢复的可能性增大. 但是, 越重要的节点也往往涉及更庞杂的业务架构, 故障后的修复也需要更详细的故障诊断和系统恢复操作, 从而产生一定恢复周期.
节点强度可以有效反映节点在网络中的重要程度, 因此, 将节点的恢复概率设置为:
| Si=∑j∈Γiωij | (7) |
| Qi=(Simax(Si))μ | (8) |
其中, μ为可调参数, 0<μ<1, μ越小的节点的恢复概率越大.
为满足网络中节点越重要则恢复周期越长的规律, 同时避免较大恢复概率与较长恢复周期的绝对相关性, 本文采取对所有节点根据节点强度Si排序并分类的方式设置节点恢复周期RTi={5φ, 4φ, 3φ, 2φ, φ}. 首先, 对所有Si从大到小排序, 接着, 引入恢复周期调节参数φ, 设置前20%的节点恢复周期为5φ, 21%–40%的节点恢复周期为4φ, 41%–60%的节点恢复周期为3φ, 61%–80%的节点恢复周期为2φ, 81%–100%的节点恢复周期为φ.
2.3 级联失效流程及算法根据产业互联“智造”供需网的级联失效模型, 确定级联失效算法如下.
Step 1. 产业互联“智造”供需网初始化. 构建具有社团结构的复杂网络模型, 并计算各个节点的LSij、LDij、Qi、RTi值大小, 构建相应的矩阵.
Step 2. 选择初始故障节点. 从网络中随机选择n个节点, 将其状态设置为故障.
Step 3. 恢复周期RTi判断. 更新网络迭代周期, 并累加故障节点i的故障周期ti, 判断ti是否满足RTi. 如果满足, 则进入Step 3.1以概率Qi确定故障是否恢复; 如果不满足, 则继续累加故障周期ti, 并进入Step 3.2向相邻节点传播故障.
Step 3.1. 如果节点i恢复正常, 则等待迭代结束, 但仍有可能被其他节点传播故障; 如果节点i未恢复正常, 则进入Step 3.2.
Step 3.2. 故障节点i以故障概率LSij和LDij判断其相邻节点j是否发生故障. 如果未故障, 则等待迭代结束; 如果发生故障, 则更新节点状态为故障, 并进入Step 3循环.
Step 4. 迭代结束. 网络循环迭代次数满足设置后, 结束迭代更新. 具体步骤如图1.
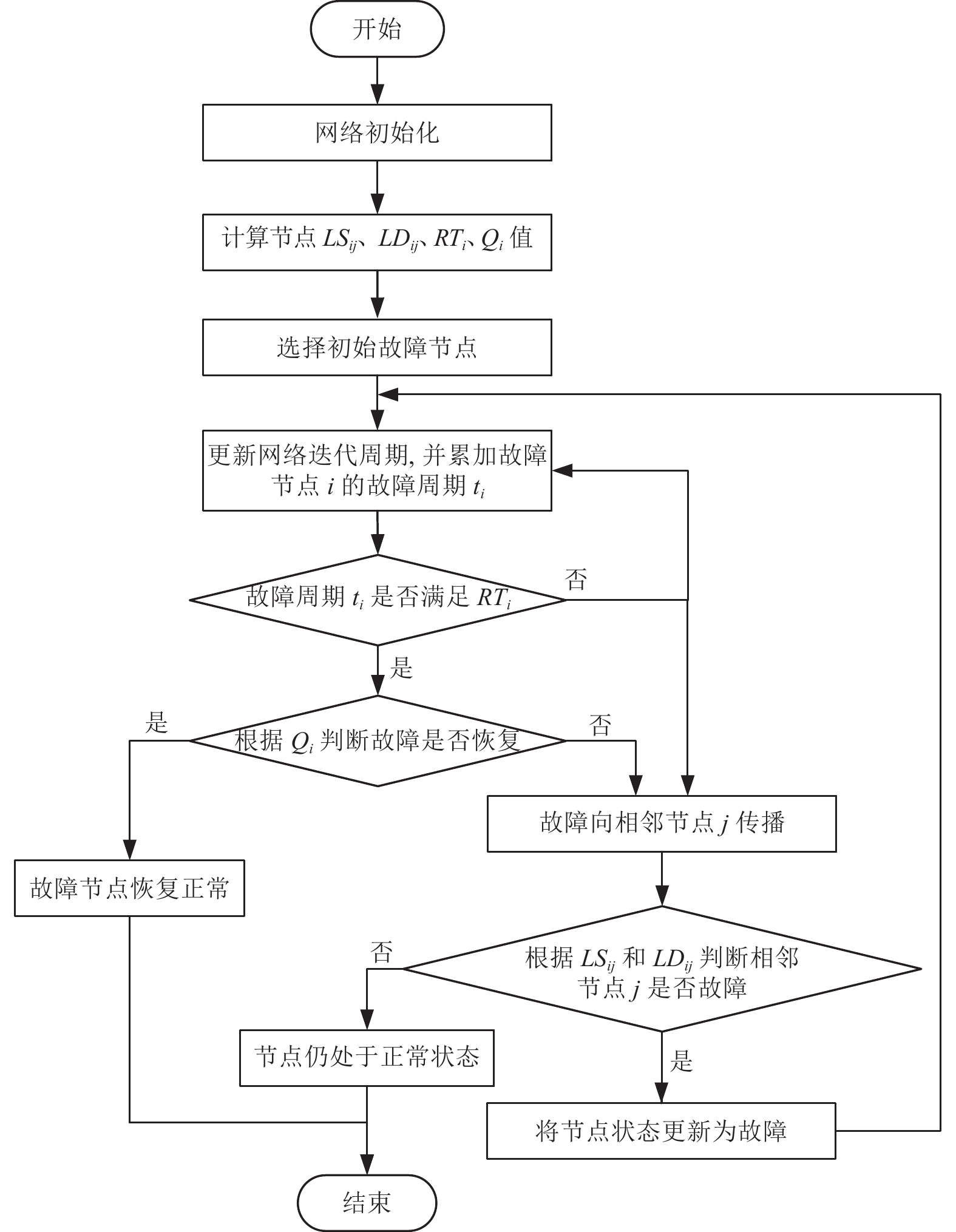
|
图 1 级联失效算法流程图 |
上述过程可以简化为图2所示. (1)开始时网络处于正常运行状态; (2)接着, 节点v1发生故障, 并断开其余相邻节点的连边; (3)故障风险产生级联传播, 相邻节点v2、v3、v4、v5均有可能故障, 但最终节点v3和v5未能成功抵抗此次风险发生级联失效, 同时断开其所有连边; (4)故障节点开始恢复, 经过Pv1个周期后, 节点v1以概率Rv1完成了故障的修复, 并恢复其与所有正常相邻节点的连边(如若未完成恢复, 则可从下一时刻重新开始恢复). 故障节点的风险只在初始故障时刻传播一次, 且其恢复后仍有可能由于级联效应发生再次失效, 经过多轮失效与恢复, 最终网络风险扩散得到终止.
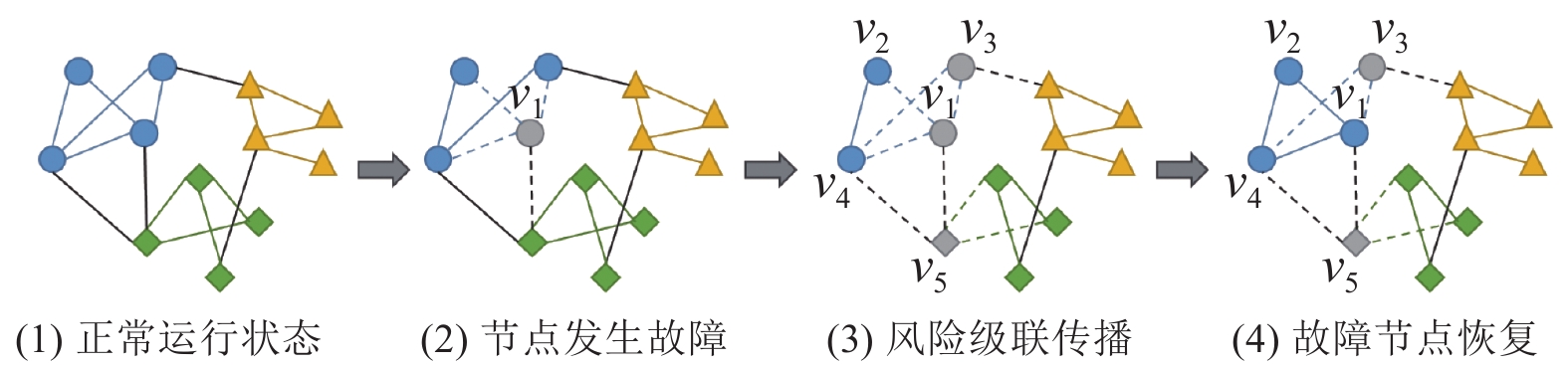
|
图 2 产业互联“智造”供需网级联失效过程 |
2.4 鲁棒性度量指标
网络连通率能够反映企业间信息传递速度和网络面对故障时的风险传播与恢复效率, 网络相对连通率则能衡量网络连通率在级联失效与恢复过程中的变化情况. 采用网络相对连通率R对产业互联“智造”供需网的鲁棒性进行评估, 公式定义为:
| R=2Nt(Nt−1)∑i≠jdtij/2Nt(Nt−1)∑i≠jdtij2N0(N0−1)∑i≠jd0ij2N0(N0−1)∑i≠jd0ij | (9) |
其中, N0和
为尽可能真实模拟现实中产业互联“智造”供需网模型结构, 首先, 以汽车产业智能制造为例, 从Ifind数据库中获取到包含汽车零部件供应商、智能技术供应商等的410个企业节点, 其次, 以各企业注册资本 RC (万元)及2022年的员工人数 NE (人)、营业收入 OR (万元)、研发投入RI (万元)、企业间地理距离 Dij (km)作为基础数据, 基于式(10)–式(12)所示的改进引力模型[23,24]构建智能汽车产业互联“智造”供需网模型, 引力值阈值设置为0.01, 利用Gephi绘图软件中的模块化功能将网络划分为具有317个节点、4个社团且模块度Q为0.468的网络模型, 模型的度分布情况如图3所示, 符合无标度网络的基本特征.
| Wi=4√RCi⋅NEi⋅ORi⋅RIi | (10) |
| SWi=Wi−min(W)max(W)−min(W) | (11) |
| Aij=SWi⋅SWjD2ij | (12) |
其中, Wi为节点企业i标准化前的企业综合实力指数; RCi、NEi、ORi、RIi分别表示企业i在2022年的年度注册资本、员工人数、营业收入、研发投入; SWi为节点企业i标准化后的企业综合实力指数; min(W)表示最小的标准化前企业综合实力指数值; max(W)表示最大的标准化前企业综合实力指数值; Aij代表节点i与节点j之间的引力值. 本文以企业所在城市间距离刻画企业间地理距离Dij.

|
图 3 产业互联“智造”供需网模型节点度分布 |
3.2 参数设置
在网络初始时刻, 随机从网络中选择10个节点, 使其为故障状态并进一步将风险扩散到相邻节点. 为避免实验的偶然性, 每项实验重复进行30次, 取每次实验结果的平均值作为结论进行分析. 为获得更具准确性的实验结果, 在下文实验中, 未特别说明时, 各项参数设置为: η=0.5, α=0.15, μ=0.3, φ=2.
3.3 不同故障场景下供需网鲁棒性变化本节针对产业互联“智造”供需网存在多种故障场景的问题, 通过调节故障概率参数η和跨社团的故障概率放大参数α的值, 模拟不同故障场景, 研究不同参数大小对网络鲁棒性的影响效果.
(1)故障概率参数η
根据式(2)可知, η越大则节点故障的可能性越大. 从图4中可以看出, 随着级联失效迭代次数T的增加, 网络鲁棒性指标R值均逐渐增加, 并恢复至无故障状态. 当R值增大时, 表明网络整体故障概率小于恢复概率; 当R值减小时, 表明网络整体恢复概率小于故障概率, 并且R值在迭代过程中存在振荡现象. 由图4可见, 随着η值增大, 故障传播概率也增大, 初始故障恢复时刻逐渐靠后, 且R值的振荡幅度也逐渐增大, 直到η值达到0.175时, R值将长期处于振荡状态, 供需网难以恢复至R=1的稳定状态, 说明网络失效规模较大, 此时必须加强故障恢复投入才能加快网络恢复速度. 另外, 当η较小时, R值的振荡主要在大于0.95时更加明显, 即在供需网快恢复完成的阶段易出现鲁棒性的小幅度波动; 当η较大时, R值的振荡趋势为先增大后减小, 这是由于网络恢复趋势和较强的故障趋势冲突对抗后又趋于平稳导致的, 并且随着η的增大, R值恢复的速度逐渐减慢, 呈现一定边际递增效应. 因此, 在现实中不同程度的故障类型会使网络鲁棒性表现出不同的恢复趋势, 并且随着故障类型的强度增大, 网络恢复的速度有明显放缓.

|
图 4 不同η值下R变化情况 |
(2)跨社团故障概率放大参数α
根据式(3)可知, α越大则不同社团间节点传播故障的可能性越小. 从图5中可以看出, 随着α值减小, 跨社团故障概率增大, R值的振荡幅度也逐渐增大, 直到α值为0.475时, R值长期处于振荡状态, 且在T=600时仍然未出现较明显的恢复趋势, 说明较大的社团间节点故障传播概率对网络整体鲁棒性具有显著影响. 另外, α为0.475和0.5时R值均在0.9125左右时开始恢复, T=70附近恢复完成, 并且α为0.525和0.55时R值均在0.9左右开始恢复, T=110附近恢复完成, 这说明跨社团故障概率较小时对R值的影响可能存在多次相变, 使α在一定区间内对R值的影响甚微, 超出区间后发生明显变化. 因此, 在实际中可以根据网络故障类型, 对不同程度故障类型的跨社团故障概率进行分类, 有利于对社团间故障传播过程的预测和控制.
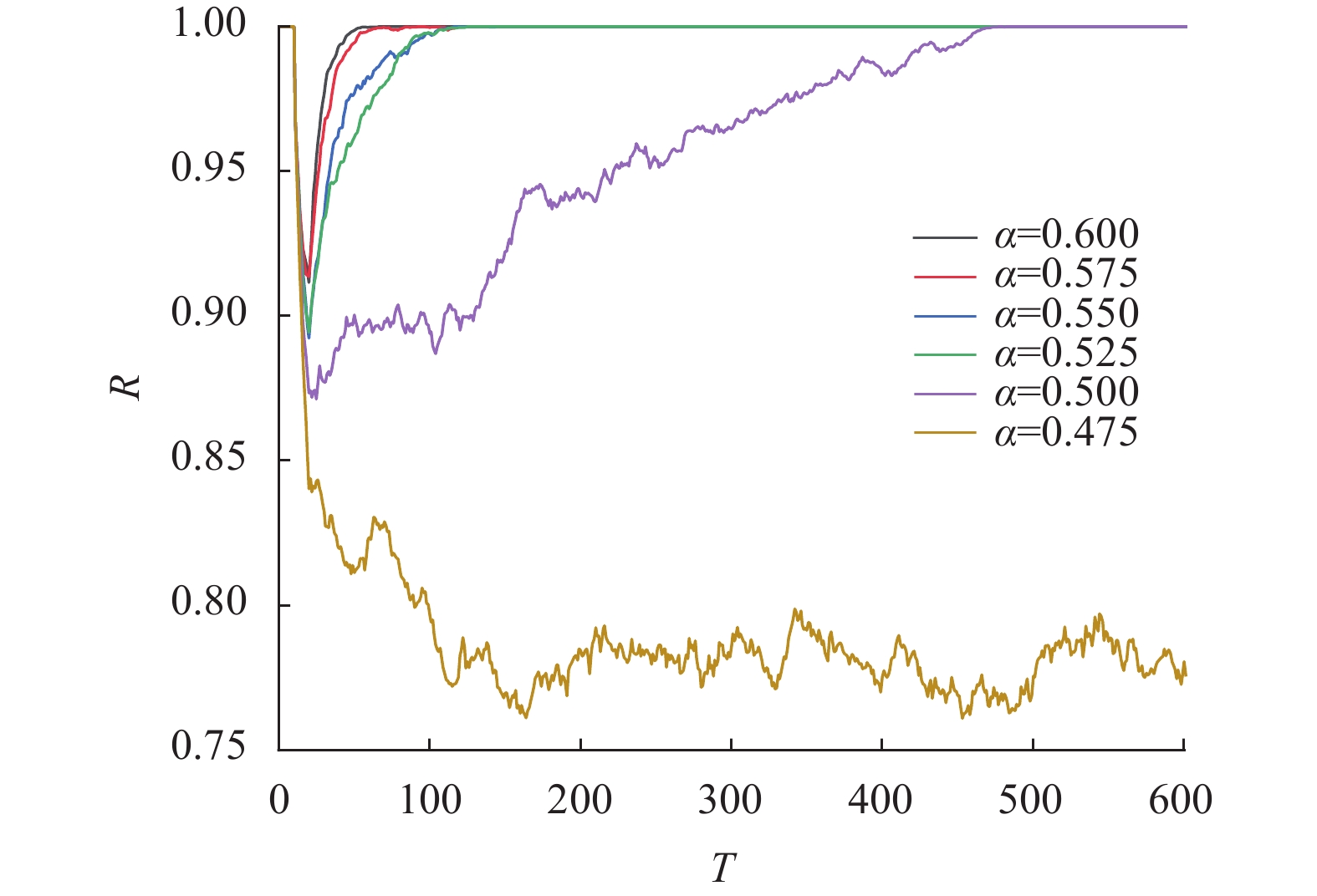
|
图 5 不同α值下R变化情况 |
3.4 不同恢复场景下供需网鲁棒性变化
由于产业互联“智造”供需网故障类型的多样化以及多种应急预案和恢复策略, 促使网络在故障后存在多种恢复场景. 与第3.3节类似, 本节通过调节网络节点恢复概率μ和恢复周期参数φ, 模拟不同恢复场景, 研究不同参数值对网络鲁棒性的影响.
(1)恢复概率参数μ
根据式(8)可知, μ越大则故障节点对应恢复概率越小. 由图6可见, 随着μ值增大, 节点恢复概率逐渐减小, 网络恢复正常的速度也不断变慢, 同时, 曲线的振荡幅度逐渐明显, 代表节点恢复概率与故障概率逐渐接近, 这一现象说明网络R值与恢复概率Q值呈正比, 与恢复概率参数μ值呈反比, 与文献[25]的研究结论相似. 当μ=0.325时, R值从T=500后的增长速度放缓, 且具有长期处于振荡状态的趋势. 另外, 当μ小于0.3时, 随着μ值增大, R值的变化区间也持续增大, 并且R值的增长速度呈现先快后慢趋势, μ大于0.3后R值随μ值的变化更加显著. 这意味着节点恢复概率的增大与网络鲁棒性的增强之间并不是简单的正比例关系, 随着恢复概率的增大, 网络鲁棒性增强的效果会愈发不明显. 这对于实际中的产业互联“智造”供需网抵抗风险具有启示意义, 当网络出现级联故障时, 由于资源投入效益的边际递减效应, 没有必要一味地投入过多资源用于网络的恢复, 如果仅投入适当资源恢复故障, 那么既可以节省成本, 又能够保障网络及时恢复正常.
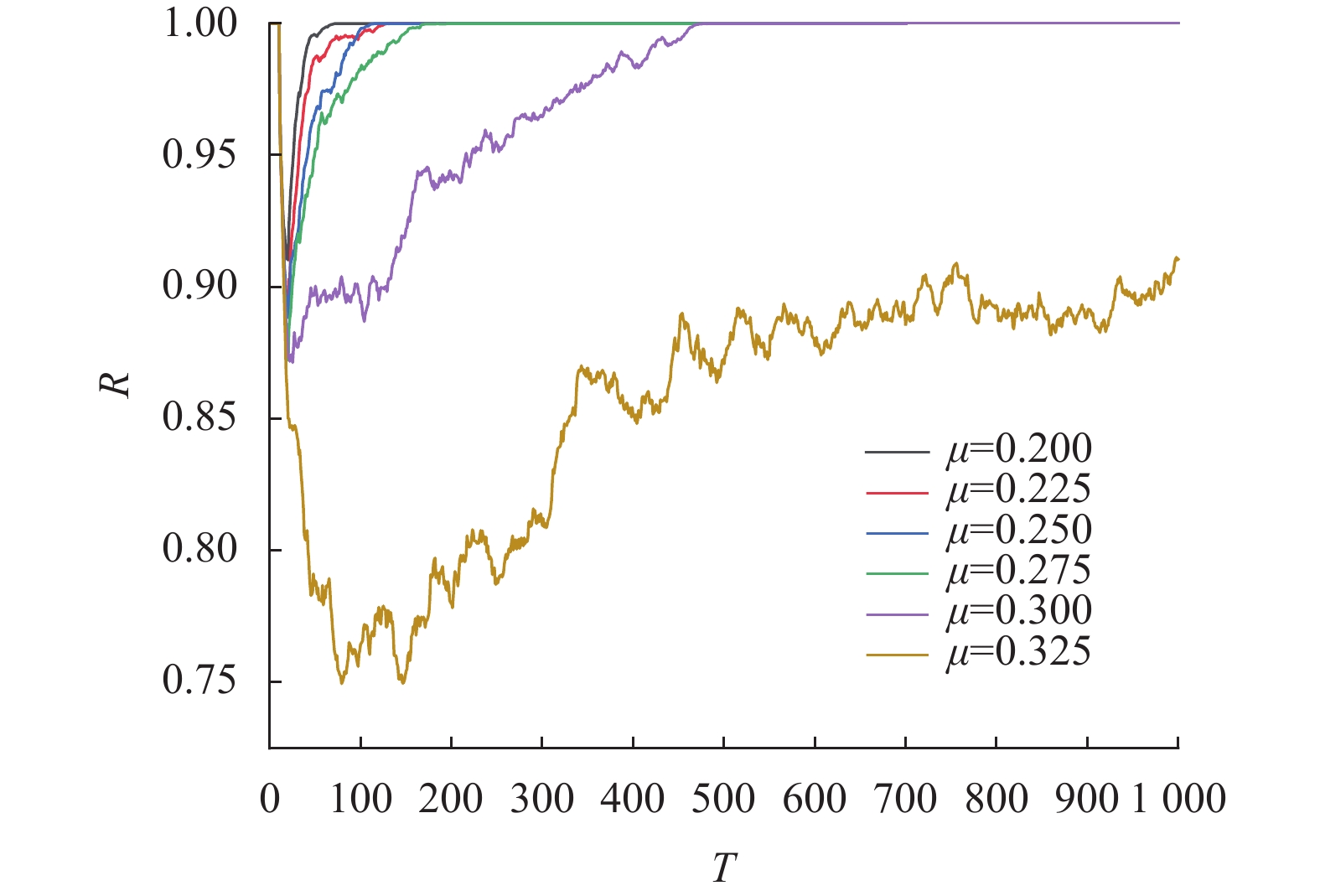
|
图 6 不同μ值下R变化情况 |
(2)恢复周期参数φ
根据第2.2节可知, 越大则故障节点对应恢复周期越大. 由图7可见, 随着φ值增大, 节点恢复周期逐渐增大, 网络恢复正常的速度持续变慢, R值初始恢复时刻不断靠后, 同时, 曲线的振荡幅度逐渐明显, 这与μ对R值的影响规律具有相似性. 当φ=2.5时, R值将长期处于振荡状态, 并且不具有逐渐恢复为1的趋势, 供需网可能将长期处于较大规模失效状. 另外, φ为0、0.5、1时, R值变化速度均为先大后小, 且在大于0.98后出现小幅度振荡, 而当φ为1.5和2时, 均在恢复过程的前半程出现一次突增, 但两次的恢复迭代周期T差异较大. 这说明在产业互联“智造”供需网中, 网络故障规模会随节点恢复周期的增大而增大, 并且网络鲁棒性的突变节点能够反映剩余所需恢复时长, 同时, 当级联失效发生时有必要及时调整恢复策略加快节点恢复周期, 否则网络易长期陷入不稳定状态.

|
图 7 不同φ值下R变化情况 |
4 结束语
为准确描述产业互联“智造”供需网中故障风险的动态传播过程, 建立具有多个产业子网协同运行的网络模型, 并构建考虑故障概率的风险传播模型, 和考虑节点恢复概率及恢复周期的故障恢复模型. 以网络相对连通率R作为鲁棒性评价指标, 通过仿真实验分析不同故障和恢复场景下的网络鲁棒性, 结果表明: (1)在4组不同故障和恢复场景下均存在临界值导致供需网鲁棒性长期处于不稳定状态; (2)故障概率参数η和恢复概率参数μ对网络鲁棒性的影响均具有一定边际效应; (3)当网络故障传播能力一定, 恢复能力越弱则网络鲁棒性振荡越明显, 网络受影响规模越大, 而恢复能力一定, 故障强度越强则网络振荡越明显, 网络受影响规模越大. 以上结果有效反映了产业互联“智造”供需网中节点故障及恢复的现象和特征, 同时也丰富了复杂网络鲁棒性理论. 然而, 考虑实际中不同产业规模及节点类型差异对产业互联“智造”供需网级联失效的影响有待进一步研究; 另外, 如何衡量并优化产业互联“智造”供需网故障后恢复过程中产生的成本也是下一步研究的重点.
| [1] |
国容毓, 陈劲, 李振东. 基于虚拟空间的创新: 空间演进、理论框架与展望. 科学学研究, 2024, 42(2): 383-394. DOI:10.16192/j.cnki.1003-2053.20230414.001 |
| [2] |
Valdez LD, Shekhtman L, La Rocca CE, et al. Cascading failures in complex networks. Journal of Complex Networks, 2020, 8(2): cnaa013. DOI:10.1093/comnet/cnaa013 |
| [3] |
He JJ, Zheng TY. Research on the model of industrial interconnection intelligent manufacturing supply and demand network and its robustness. Discrete Dynamics in Nature and Society, 2022, 2022: 8076551. DOI:10.1155/2022/8076551 |
| [4] |
Yin YC, Yang B, Wang SL, et al. Cloud service composition of collaborative manufacturing in main manufacturer-suppliers mode for aviation equipment. Robotics and Computer-integrated Manufacturing, 2023, 84: 102603. DOI:10.1016/j.rcim.2023.102603 |
| [5] |
张强, 赵爽耀, 蔡正阳. 高端装备智能制造价值链的生产自组织与协同管理: 设计制造一体化协同研发实践. 管理世界, 2023, 39(3): 127-139. DOI:10.19744/j.cnki.11-1235/f.2023.0040 |
| [6] |
赵志刚, 周根贵, 杜辉. 复杂加权供应链网络级联抗毁性研究. 小型微型计算机系统, 2019, 40(12): 2591-2596. DOI:10.3969/j.issn.1000-1220.2019.12.022 |
| [7] |
李帅, 张勇, 郑瑞钊, 等. 基于双层网络级联失效机制的产品设计变更影响分析. 计算机集成制造系统, 2024: 1–20. http://kns.cnki.net/kcms/detail/11.5946.tp.20230602.1424.002.html. (2023-06-05)[2024-03-19].
|
| [8] |
Yang QH, Scoglio CM, Gruenbacher DM. Robustness of supply chain networks against underload cascading failures. Physica A: Statistical Mechanics and Its Applications, 2021, 563: 125466. DOI:10.1016/j.physa.2020.125466 |
| [9] |
Sun JY, Tang JM, Fu WP, et al. Construction of a multi-echelon supply chain complex network evolution model and robustness analysis of cascading failure. Computers & Industrial Engineering, 2020, 144: 106457. DOI:10.1016/j.cie.2020.106457 |
| [10] |
Li ZY, Zhao PX, Han X. Agri-food supply chain network disruption propagation and recovery based on cascading failure. Physica A: Statistical Mechanics and Its Applications, 2022, 589: 126611. DOI:10.1016/j.physa.2021.126611 |
| [11] |
尹航, 侯霁珊, 齐岳. 基于节点蓄意攻击的集群式供应链网络抗毁性研究. 中国管理科学, 2024: 1–13. https://doi.org/10.16381/j.cnki.issn1003-207x.2022.2358. (2023-04-10)[2024-03-19].
|
| [12] |
Li WM, Zhu H, Li SH, et al. Evolutionary community discovery in dynamic social networks via resistance distance. Expert Systems With Applications, 2021, 171: 114536. DOI:10.1016/j.eswa.2020.114536 |
| [13] |
Pio G, Ceci M, Prisciandaro F, et al. Exploiting causality in gene network reconstruction based on graph embedding. Machine Learning, 2020, 109(6): 1231-1279. DOI:10.1007/s10994-019-05861-8 |
| [14] |
Li XR, Xu XY, Liu JQ, et al. Multilayer financial complex networks and their applications. IEEE Transactions on Circuits and Systems I: Regular Papers, 2022, 69(10): 4103-4116. DOI:10.1109/TCSI.2022.3187694 |
| [15] |
Wandelt S, Shi X, Sun XQ. Estimation and improvement of transportation network robustness by exploiting communities. Reliability Engineering & System Safety, 2021, 206: 107307. DOI:10.1016/j.ress.2020.107307 |
| [16] |
McNerney J, Fath BD, Silverberg G. Network structure of inter-industry flows. Physica A: Statistical Mechanics and Its Applications, 2013, 392(24): 6427-6441. DOI:10.1016/j.physa.2013.07.063 |
| [17] |
Liu H, Han YY, Zhu AD. Modeling supply chain viability and adaptation against underload cascading failure during the COVID-19 pandemic. Nonlinear Dynamics, 2022, 110(3): 2931-2947. DOI:10.1007/s11071-022-07741-8 |
| [18] |
肖军弼, 华力. 基于改进SIR模型的网络安全态势分析. 计算机系统应用, 2023, 32(3): 48-57. DOI:10.15888/j.cnki.csa.008955 |
| [19] |
李姝, 杨华, 宋波. 多层供应链网络中欠载失效和过载级联失效的协同演化研究. 计算机科学, 2021, 48(10): 351-358. DOI:10.11896/jsjkx.200900144 |
| [20] |
白世贞, 吴文娅, 鄢章华, 等. 基于马尔可夫与传染病模型的供应链网络中断风险传播研究. 管理工程学报, 2023, 37(4): 206-221. DOI:10.13587/j.cnki.jieem.2023.04.018 |
| [21] |
Yao QY, Fan RG, Chen RK, et al. A model of the enterprise supply chain risk propagation based on partially mapping two-layer complex networks. Physica A: Statistical Mechanics and Its Applications, 2023, 613: 128506. DOI:10.1016/j.physa.2023.128506 |
| [22] |
Modgil S, Singh RK, Hannibal C. Artificial intelligence for supply chain resilience: Learning from COVID-19. The International Journal of Logistics Management, 2022, 33(4): 1246-1268. DOI:10.1108/IJLM-02-2021-0094 |
| [23] |
郑添元, 何建佳. 引力模型下多级供应链网络鲁棒性研究. 科技和产业, 2022, 22(1): 224-230. DOI:10.3969/j.issn.1671-1807.2022.01.034 |
| [24] |
陈雨生. RCEP自贸区内中国农产品出口效应及贸易前景——基于随机模型及细分市场的实证分析. 中国流通经济, 2022, 36(4): 56-66. DOI:10.14089/j.cnki.cn11-3664/f.2022.04.005 |
| [25] |
唐亮, 焦鹏, 李纪康, 等. 带恢复策略的复杂网络级联失效机理及鲁棒性研究. 控制与决策, 2018, 33(10): 1841-1850. DOI:10.13195/j.kzyjc.2017.0728 |
 2024, Vol. 33
2024, Vol. 33



