2. 航天系统部装备部军事代表局驻北京地区第四军事代表室, 北京 100841;
3. 北京机械设备研究所, 北京 100854
2. Fourth Military Representative Office of Military Representative Bureau of Equipment Department of Aerospace System Department in Beijing, Beijing 100841, China;
3. Beijing Institute of Mechanical Equipment, Beijing 100854, China
固体运载火箭水平转运是火箭运输发射的关键环节, 转运过程中, 通过起重设备吊装实现火箭在不同运载车辆间的转载. 通常, 火箭转载以人工操作起重设备为主, 转载操作不仅要求平稳, 更要箭车准确对接. 固体运载火箭重量和尺寸规模大, 对起重设备和人员操作经验提出了较高的要求, 转载过程中需要指挥人员和操作人员协同配合, 不断修正以保证箭车对接精度, 作业时间长. 为降低操作难度, 提升转载效率, 自动化转载应运而生.
自动化转载通过获取起重设备与运载车辆以及火箭的相对位置关系, 利用空间解算、起重设备轨迹规划等步骤完成箭车对准. 自动化转载的核心是箭车接口的自动对准对接, 自动对准对接的成功率取决于自动对准技术和方法的对接实现精度. 高效精准的自动对准方法可有效缩短转载时间, 提升固体运载火箭转载效率.
常用的自动对准技术主要包括基于激光测量的定位对准和基于全局相机的视觉引导对准[1]等.
基于激光测量的定位对准技术广泛应用于工业机器人工件装配[2]、安全距离监测预警[3]、集装箱对箱作业[4]等. 利用激光跟踪仪[5,6]、激光雷达[7]等设备进行数字化测量, 建立空间绝对坐标系, 确定各对接部件的空间位置与姿态, 并由自动对接装配平台根据实时测量的数据自动对部件进行调姿, 使部件能够顺利实现对接及装配. 然而, 该定位对准技术一般需要为对接部件提供可靠的基础平台支撑, 以保证对接基准的稳定性.
基于全局相机的视觉引导对准技术, 将计算机视觉技术与几何量测量原理深度交叉融合, 从而实现运动目标位置与姿态的动态实时测量[8,9], 已广泛应用于工业机器人分拣作业[10–12]、定位[13,14]等场景. 该技术首先需要对运动目标进行光学成像, 进而建立起目标二维图像与三维模型的中心投影几何模型之间的关系, 最终利用所得二维、三维同名特征匹配关系, 解算目标位置与姿态参数, 具有可视化、抗电磁干扰、无累积误差、近场精度高等突出特点.
常见的车载式起重转载设备, 一般采用单级自动转载对准方法, 通过起重设备上安装的测量设备测量起重设备与火箭运载车辆的相对停放位置关系, 并根据起重设备的机构形式以及运载车辆的空间结构尺寸推算转载对准目标点的空间位置, 据此对起重设备的运动路径进行反解并按照该路径执行完成末端对准. 该方法本质上是一种单级的开环控制策略, 测量设备不能对起重设备末端与对接接口的对准情况进行闭环检测; 另外, 转载作业幅度或物体重量不同引起的起重设备变形量差异, 对转载对准精度产生不可控的影响, 导致自动对准动作完成后, 通常需要人工操作辅助修正. 基于激光测量的定位对准等常规方法也难以解决易引起起重设备变形的重载载荷自动转载对接精度问题.
针对上述问题, 本文提出了一种基于两级对准模型的自动转载方法, 一级粗对准为测量运载车辆相对位姿关系, 为起重设备提供初始的转载目标位置; 二级精对准为测量起重设备末端相对于转载目标点的位姿关系, 消除执行机构变形所导致的对准误差, 解决了重载大变形对自动转载对准精度的影响问题. 与传统激光测量定位对准、全局相机视觉引导对准等方法对比, 本文所提出的基于两级对准模型的自动转载方法具有如下特点: 1)对比常规单级的开环控制对准, 采用两级协同的对准, 对起重设备末端对准情况进行闭环检测, 可排除执行机构变形对对准精度的影响; 2)采用粗对准与精对准的两级对准, 在算法时效基本一致的基础上, 可大大提升自动对准精度.
本文首先对对准环节误差影响以及自动转载精度进行分析, 建立了运载火箭自动转载对接的误差模型; 进而提出基于两级对准模型的自动转载方法, 建立了轨迹规划控制与数学求解模型; 最后, 采用蒙特卡洛仿真对所提方法的对接精度进行了验证.
1 运载火箭自动转载对接误差建模本节首先分析了运载火箭自动转载过程对接精度需求, 建立了转载对接误差总量模型; 进而, 分析了转台回转等8项影响该误差模型的因素, 并对误差分布进行建模; 最后, 建立了基于各误差影响因素的对接误差总量数学模型.
1.1 转载对接精度需求箭车能否顺利对接, 主要取决于两者间的相对位置偏差与接口的导向行程, 当偏差小于导向行程时, 可顺利完成对接. 箭车对接时, 应保证箭车相对位置轴向x, 横向y以及轴向夹角θ在对接接口精度要求范围内. 基于此, 对某型起重设备的自动转载对接精度进行分析, 确定影响对接精度的环节及其影响模型.
某型火箭采用回转支耳与运载车辆连接锁对接, 如图1所示. 自动转载时, 转载对接误差[15]总量E满足如下要求即可成功对接:
| $ E=[{E}_{x}\text{, }{E}_{y}\text{, }{E}_{\theta }]\leqslant {E}_{o}=[43, 10.05, 0.2] $ | (1) |
其中, Ex为轴向对接误差总量; Ey为横向对接误差总量; Eθ为轴向夹角对接误差总量; Eo为对接容差量.

|
图 1 对接接口示意图 |
1.2 系统多维误差分析
分析某型起重设备的结构特征, 在自动化对准过程中, 影响最终转载对接定位精度的环节主要包括: 转台回转、变幅、吊具回转、双卷扬调姿的到位执行误差、整车调平误差、吊臂伸缩误差, 测量组合的安装误差和测量组合的测量精度[16].
通过对起重设备机械结构和工作原理的深入分析, 总结出影响最终对接精度的详细误差因素及其影响过程, 如表1所示.
| 表 1 箭车对接多维误差因素及影响 |
上述误差对箭车对接精度的影响各有不同, 因此分别建立对对接精度的影响模型.
1.3 误差影响模型● 转台回转到位误差
转台回转到位误差eα通过几何关系直接引起箭车对接误差 E1(eα). 由几何关系确定eα的影响矩阵E1.
| $ \begin{split} {E}_{1}({e}_{\alpha }) &=[{E}_{x1}, {E}_{y1}, {E}_{\theta 1}]\\ &=[d\sin({e}_{\alpha })\cos({e}_{\alpha }), d\sin({e}_{\alpha })\text{, }180-{e}_{\alpha }] \end{split} $ | (2) |
其中, d为当前作业幅度值.
● 变幅到位误差
作业幅度到位误差eβ通过几何关系直接影响箭车对接误差 E2(eβ). 由几何关系确定eβ的影响矩阵E2.
| $ {E}_{2}({e}_{\beta })=[{E}_{x2}\text{, }{E}_{y2}\text{, }{E}_{\theta 2}]=[0\text{, }{e}_{\beta }\text{, }0] $ | (3) |
● 吊具回转到位误差
吊具回转到位误差eγ通过几何关系直接影响箭车对接误差E3(eγ). 由几何关系确定eγ的影响矩阵E3.
| $ \begin{split} {E}_{3}({e}_{\gamma }) & =[{E}_{x3}\text{, }{E}_{y3}\text{, }{E}_{\theta 3}]\\ &=[L\tan({e}_{\gamma })\text{, }L\tan({e}_{\gamma })\sin({e}_{\gamma })\text{, }({e}_{\gamma })] \end{split} $ | (4) |
其中, L为吊具回转中心至对接支耳的水平距离.
● 双卷扬角度调整误差
双卷扬角度调整误差eτ直接影响火箭调姿角度, 该角度影响质心相对于箭车接口的轴向距离偏差E4(eτ), 由几何关系确定eτ的影响矩阵E4:
| $ {E}_{4}({e}_{\tau })=[{E}_{x4}\text{, }{E}_{y4}\text{, }{E}_{\theta 4}]=[l/2\sin({e}_{\tau })\text{, }0\text{, }0] $ | (5) |
其中, l为双卷扬跨距.
● 整车调平误差
整车调平误差
| $ {E}_{5}({e}_{\kappa })=[{E}_{x5}\text{, }{E}_{y5}\text{, }{E}_{\theta 5}]=[d\mathrm{sin}({e}_{\kappa })\text{, }d\mathrm{cos}({e}_{\kappa })\text{, }0] $ | (6) |
● 吊臂伸缩误差
吊臂伸缩误差
| $ {E}_{6}({e}_{\eta })=[{E}_{x6}\text{, }{E}_{y6}\text{, }{E}_{\theta 6}]=[l/2\sin({e}_{\tau })\text{, }0\text{, }0] $ | (7) |
● 测量组合测量输出误差
测量组合测量输出误差ec(x, y, θ)经位姿结算后, 直接反应至机构的到位误差
| $ \begin{split} {E}_{7}\left({e}_{c}\right)& = [{E}_{x7}\text{, }{E}_{y7}\text{, }{E}_{\theta 7}]\\ &={E}_{1}({f}_{w}{}_{\alpha }\left({e}_{c}\right)) +{E}_{2}({f}_{w}{}_{\beta }\left({e}_{c}\right)) +{E}_{3}({f}_{w}{}_{\gamma }\left({e}_{c}\right))\end{split} $ | (8) |
其中, fwα为位姿解算模型中转台回转角度计算函数; fwβ为位姿解算模型中作业幅度计算函数; fwγ为位姿解算模型中吊具回转角度计算函数.
● 测量标识安装位置误差
根据测量精度对测量标识的敏感度情况, 影响最终识别精度的测量标识安装位置误差eb(x, y, θ)包括横向位置误差、纵向位置误差以及偏航角误差. 3项误差均在测量输出结果中形成等量的测量输出误差
| $ \begin{split} {E}_{8}\left({e}_{b}\right)& =[{E}_{x8}\text{, }{E}_{y8}\text{, }{E}_{\theta 8}]\\ &={E}_{1}({f}_{w}{}_{\alpha }\left({e}_{b}\right)) +{E}_{2}({f}_{w}{}_{\beta }\left({e}_{b}\right)) +{E}_{3}({f}_{w}{}_{\gamma }\left({e}_{b}\right))\end{split} $ | (9) |
将各环节误差对最终对接精度的影响进行叠加, 即得对接总误差E:
| $ E = \sum\limits_{i = 1}^8 {{E_i}} $ | (10) |
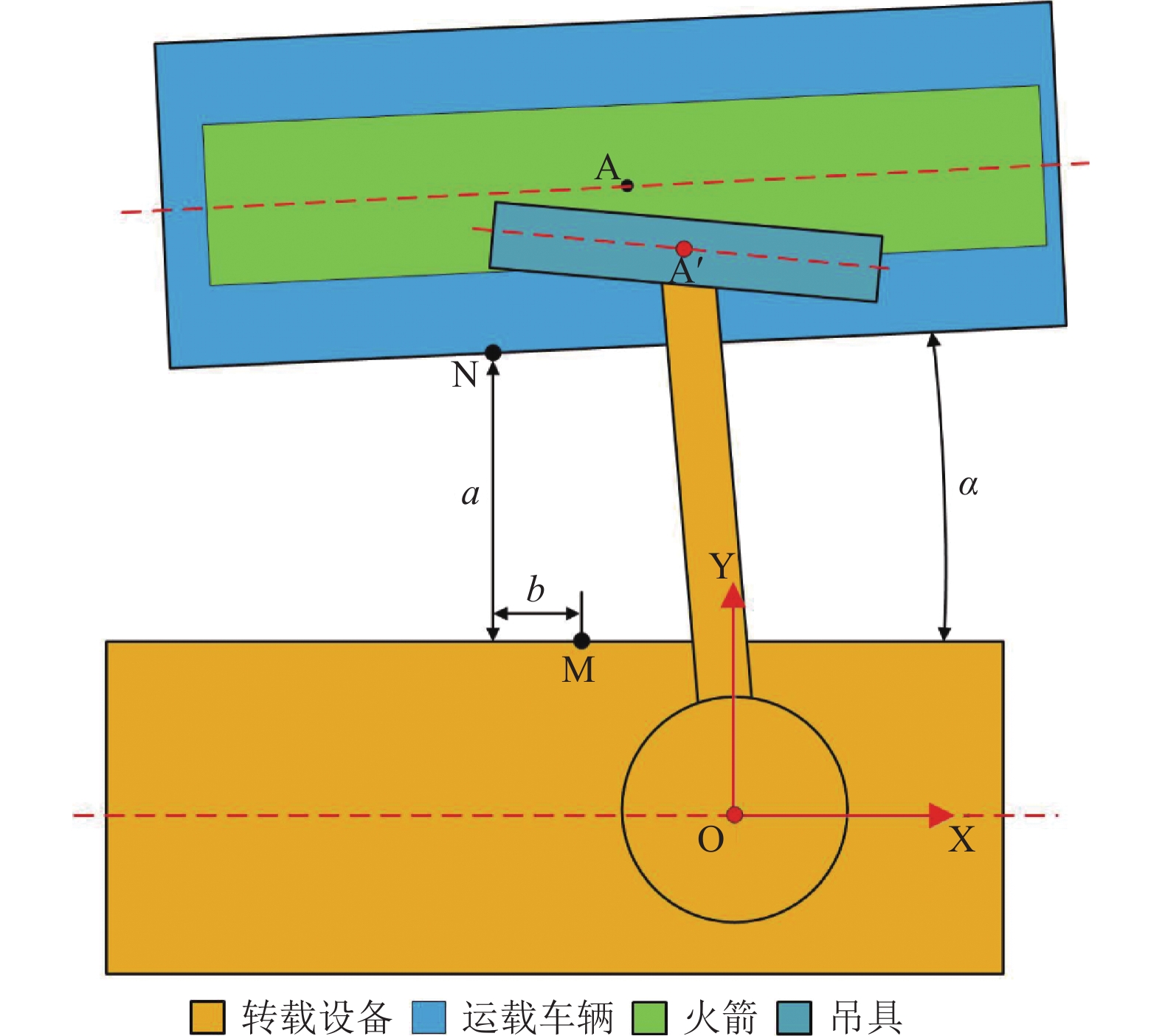
转载对接时, 起重设备吊具与火箭的相对位置固定, 运载火箭可以顺利与运载车辆对接的前提条件为: 吊具中心A′点应与运载车辆的A点(对于同一规格载荷, A点固定)相重合, 且吊具与运载车辆的轴线夹角为0.
2.1 常规自动转载方法 2.1.1 转载轨迹规划控制常规对准模型如图2所示. 由于A点的位置无法直接获取, 因此在起重设备上设置M点作为常规对准测量基准点, 运载车辆上设置N点作为常规对准测量目标点. 通过测量M点和N点在X-Y坐标系的横向偏差b、纵向偏差a, 以及两车轴向夹角θ, 并结合M点和N点分别相对于O点和A的几何距离, 可解算出A点在X-Y坐标系在的坐标. 由此可反算出起重设备运动目标值, 起重设备各执行机构按照该目标值运动, 从而实现A′与A的对准. 常规转载控制流程如图3所示.
|
图 2 常规对准模型 |

|
图 3 常规转载控制流程图 |
2.1.2 转载轨迹规划数学模型
通过位置检测设备与定位解算, 结合起重设备结构参数, 从而确定其转台目标角度、吊臂目标角度、横梁目标角度和目标作业幅度.
首先, 在位置检测设备与定位解算中需确定的过程参数如下:
| $ \left\{ {\begin{array}{*{20}{l}} {x = M \cdot {\text{cos}}\left( {{w_\theta } \cdot {\text π} /{\text{18}}0} \right) + K \cdot {\text{sin}}\left( {{w_\theta } \cdot {\text π} /{\text{18}}0} \right) - {w_x}} \\ {y = K \cdot {\text{cos}}\left( {{w_\theta } \cdot {\text π} /{\text{18}}0} \right) - M \cdot {\text{ sin}}\left( {{w_\theta } \cdot {\text π} /{\text{18}}0} \right) + {w_y} + W} \end{array}} \right. $ | (11) |
其中, x为目标中心在起重设备坐标系的X值, y为目标中心在起重设备坐标系的Y值, wx为位置设备返回的X值, wy为位置设备返回的Y值, wθ为位置设备返回的θ值, 目标中心在位置检测坐标系中的位置为(X=M, Y=K). 位置检测设备相机距离回转中心的距离W.
最终目标参数计算公式如下:
| $ \left\{\begin{array}{l}\alpha \_\text{target}=\text{arctan}\left(x/y\right)\cdot \text{18}0/{\text π} +\text{9}0 \\ \beta \_\text{target}=\text{ arccos}((d\_\text{target}+H)/L)\text{ }\cdot \text{18}0/{\text π} \text{ }+Ap \\ \gamma \_\text{target}= \left\{\begin{array}{l}{w}_{\theta }-\text{arctan}\left(x/y\right)\cdot \text{18}0/{\text π} \text{}\text{}\text{}\text{}\text{}\text{ (}{w}_{\theta } \lt \text{3}0^\circ) \\ {w}_{\theta }-\text{36}0-\text{arctan}\left(x/y\right)\cdot \text{18}0/{\text π} \text{ (}{w}_{\theta } \gt \text{33}0^\circ ) \end{array}\right. \\ d\_\text{target}=\sqrt{{x}^{2}+{y}^{2}} \end{array}\right. $ | (12) |
其中, α_target为转台目标角度, β_target为吊臂目标角度, γ_target为横梁目标角度, d_target为目标作业幅度, L为吊臂回转轴至横梁俯仰轴的长度, H为吊臂俯仰轴至转台中心的距离, Ap为倾角传感器标定值与差值.
2.2 两级对准自动转载方法在自动化转载过程中, 一方面, 受重载吊装物作用, 其所导致的起重设备变形量对于自动转载精度有不可忽略的影响; 另一方面, 长期使用也会导致结构各部件尺寸发生变化, 进一步降低自动转载精度.
针对上述问题, 本文提出了基于两级对准模型的自动转载方法.
2.2.1 转载轨迹规划控制考虑到起重设备执行机构在作业过程中有结构变形, 通过测量的a、b、α值解算的各运动机构位置参数未包含到结构变形对A′的位置影响, 从而在常规对准完成后不能保证火箭与运载车辆精确对准, 故还需要再直接测量吊具与运载车辆的位姿关系: 横向偏差d、纵向偏差c、吊具与运载车辆的轴线夹角β. 据此再计算起重设备各执行机构的运动目标值, 并按此运动, 最终实现A′与A的精确对准且β=0, 两级对准模型如图4所示, 在传统单级位姿识别对准方法基础上, 增加二级位姿检测对准环节, 形成末端位姿闭环检测, 其自动化转载控制流程图如图5所示.

|
图 4 两级对准模型 |
两级对准模型中, 一级粗对准以起重设备为测量基准, 检测运载车辆相对于起重设备的停放位姿(a, b, α), 一级粗对准完成后进入二级精确对准的测量范围; 二级精确对准以末端吊具为基准, 检测运载车辆目标位置相对于吊具的位姿(c, d, β), 可排除起重设备结构变形对对接定位的影响.

|
图 5 两级对准自动化转载控制流程图 |
2.2.2 转载轨迹规划数学模型
起重设备的运动解算主要由两部分组成: 位置检测设备与定位解算和视觉设备与定位解算, 结合其结构参数, 从而确定起重设备的转台目标角度、吊臂目标角度、横梁目标角度和目标作业幅度.
根据位置检测设备的检测值, 获得了起重设备运动所需要的转台、吊臂、横梁角度和作业幅度参数, 控制起重设备运动从而实现多模转载车的粗定位, 为视觉定位测量奠定了良好的视觉范围.
然后, 在视觉设备与定位解算中需确定的过程参数如下:
| $ \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{l}} {xx = {\text{ }} - {\text{cos}}\left( {\alpha \cdot {\text π} /{\text{18}}0} \right) \cdot d} \\ {yy = {\text{sin}}\left( {\alpha \cdot {\text π} /{\text{18}}0} \right) \cdot d} \\ {{r_o} = \alpha + \gamma - {\text{9}}0} \\ {x = sx \cdot {\text{cos}}\left( {{r_o} \cdot {\text π} /{\text{18}}0} \right) + sy \cdot {\text{sin}}\left( {{r_o} \cdot {\text π} /{\text{18}}0} \right) + xx} \end{array}} \\ {y = sy \cdot {\text{cos}}\left( {{r_o} \cdot {\text π} /{\text{18}}0} \right) - sx \cdot {\text{sin}}\left( {{r_o} \cdot {\text π} /{\text{18}}0} \right) + yy} \end{array}} \right. $ | (13) |
其中, xx为横梁坐标系在起重设备坐标系的位置X, yy为横梁坐标系在起重设备坐标系的位置Y, ro为横梁坐标系相对起重设备坐标系的旋转角度, x为目标中心在起重设备坐标系的X值, y为目标中心在起重设备坐标系的Y值, α为转台初始角度, β为吊臂初始角度, γ为横梁初始角度, d为初始作业幅度 (mm), sx为视觉设备返回X值, sy为视觉设备返回Y值, θ为视觉设备返回θ值.
最终目标参数计算公式如下:
| $ \left\{\begin{array}{l}\alpha \_\text{target}=\text{arctan}\left(x/y\right)\cdot \text{18}0/{\text π} +\text{9}0 \\ \beta \_\text{target}=\text{ arccos}((d\_\text{target}+H)/L)\text{ }\cdot \text{18}0/{\text π} \text{ }+Ap \\ \gamma \_\text{target}=\alpha -\alpha \_\text{target}+\gamma +\theta \\ d\_\text{target}=\sqrt{{x}^{2}+{y}^{2}} \end{array}\right. $ | (14) |
基于Matlab平台, 搭建转载对接精度计算模型, 以总误差E计算函数为目标函数, 多维误差因素为变量并按照各自的分布情况进行取样, 采用蒙特卡洛试验方法, 进行10 000次的仿真计算, 获得系统对接误差分布, 并与系统对接需求精度范围包络进行对比. 根据10 000次的计算结果, 统计总误差E输出值在对接精度范围内的次数, 计算对接成功概率[17].
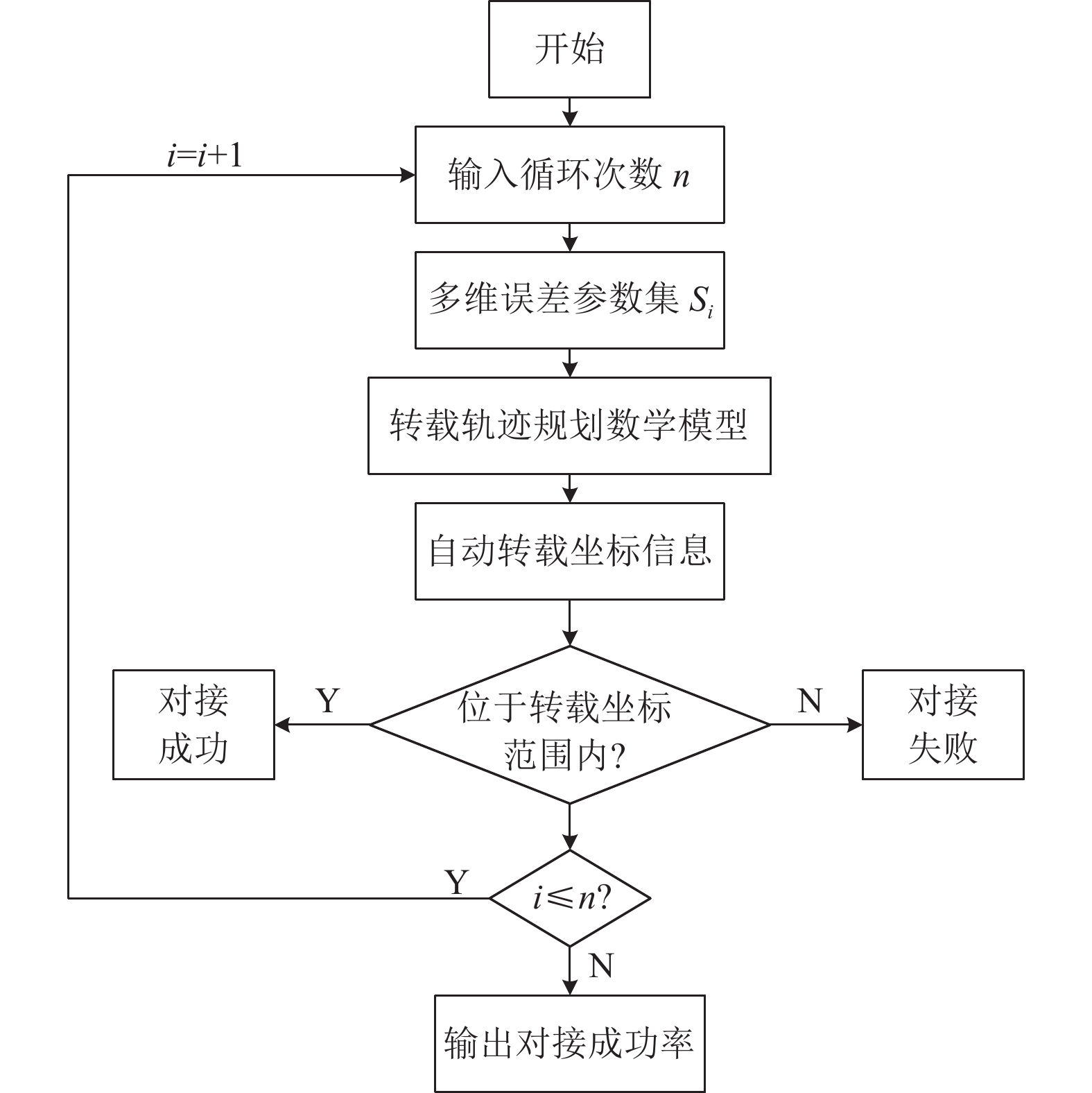
计算模型中预设在起重设备运动坐标系下目标中心坐标为(x0, y0, θ0), 则自动转载所需对接精度范围为([x0–43, x0+43], [y0–10.05, y0+10.05], [θ0–0.2, θ0+0.2]). 根据总误差E计算函数, 输出总误差在该范围内均能实现运载火箭与运载车辆的顺利连接. 模拟仿真计算流程图见图6.
|
图 6 模拟仿真计算流程图 |
3.1 多维误差参数取值
多维误差因素值域范围根据工程实际情况取值, 如表2所示.
| 表 2 箭车对接多维误差取值 |
3.2 仿真计算结果及分析
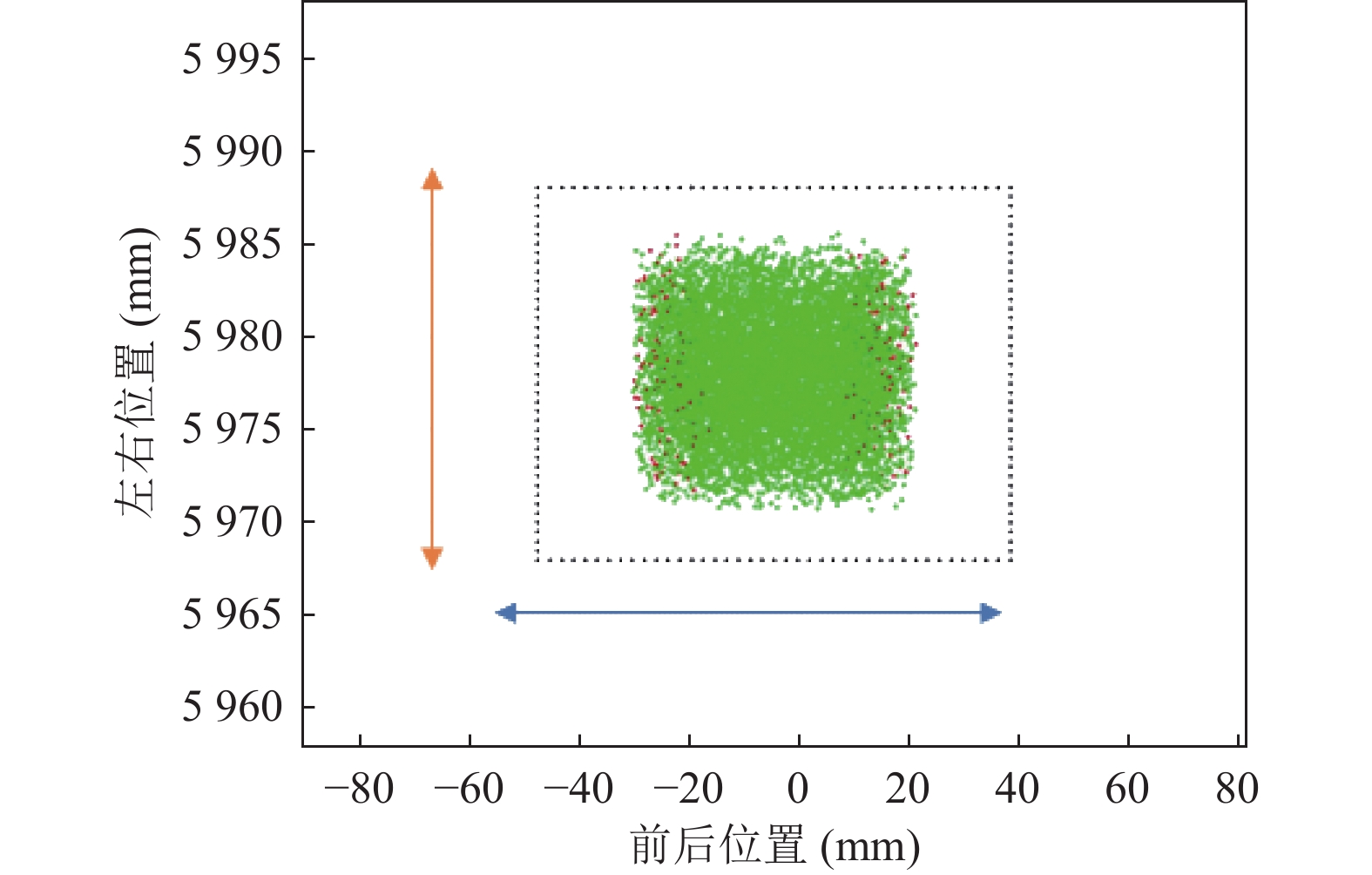
完成10000次仿真计算后, 形成系统总误差分布图. 如图7所示, 虚框表示对接精度需求范围, 当对接点坐标在虚框范围内, 且轴线夹角满足要求, 则判定对接成功.
|
图 7 对接成功标准示意图 |
3.2.1 吊臂变形量对转载精度的影响
针对重载吊装时吊臂变形将会使得吊具偏离其目标中心进而影响其自动化转载精度的问题, 本节讨论了不同吊臂变形量对两种自动化转载方法的影响程度.
受被吊装物载荷的影响, 吊臂将产生向下弯曲变形, 进而影响到起重设备作业幅度. 考虑到不同载重量对吊臂变形的影响程度不同, 结合实际作业环境, 分别采用两种自动转载方法模拟了两车横向偏差d=6500 mm、纵向偏差c=0、吊具与运载车辆的轴线夹角β=0情况下, 由吊臂变形导致的作业幅度缩小量分别为0、5 mm、10 mm、15 mm、20 mm、25 mm和30 mm下的自动化转载精度. 其结果如图8所示.
从图8中可以看出, 在吊臂变形较小的情况下, 两种自动化对准方法均可保证较高的对接成功率, 但是随着被吊装载荷的增加, 吊臂变形量也在不断增加, 由于火箭回转支耳与连接锁间横向对接范围较小, 导致常规对接方法的对接成功率不断下降, 最终无法满足自动对接需求, 需要人工二次干预; 而基于位姿检测的两级对准模型可以精确反馈吊臂变形幅度, 仍能保证较高对接精度, 由图8结果可知, 在吊臂变形导致目标中心偏离值在5–30 mm范围内, 均能达到约96%的对接精度, 减少了人工干预程度, 大大降低了时间成本. 相较于传统的自动转载方法, 本文提出的基于两级对准模型的运载火箭自动转载方法, 考虑了转载作业幅度或物体重量不同引起的起重设备变形量差异, 增加了自动对准反馈调节能力, 消除了执行机构变形所导致的对准误差, 从而保证了较高的对接成功率.

|
图 8 吊臂变形量与对接成功率的关系 |
综上, 通过增加二次对准进行定位修正, 基于两级对准模型的运载火箭自动转载方法可以有效消除执行机构变形所导致的对准误差解决了重载大变形下自动转载对准精度问题.
3.2.2 自动转载精度验证基于两级对准模型, 在转载作业条件下, 分别针对起重设备和运载车辆横向间距(即吊幅)和起重设备和运载车辆轴向夹角(即偏离角度)进行仿真模拟.
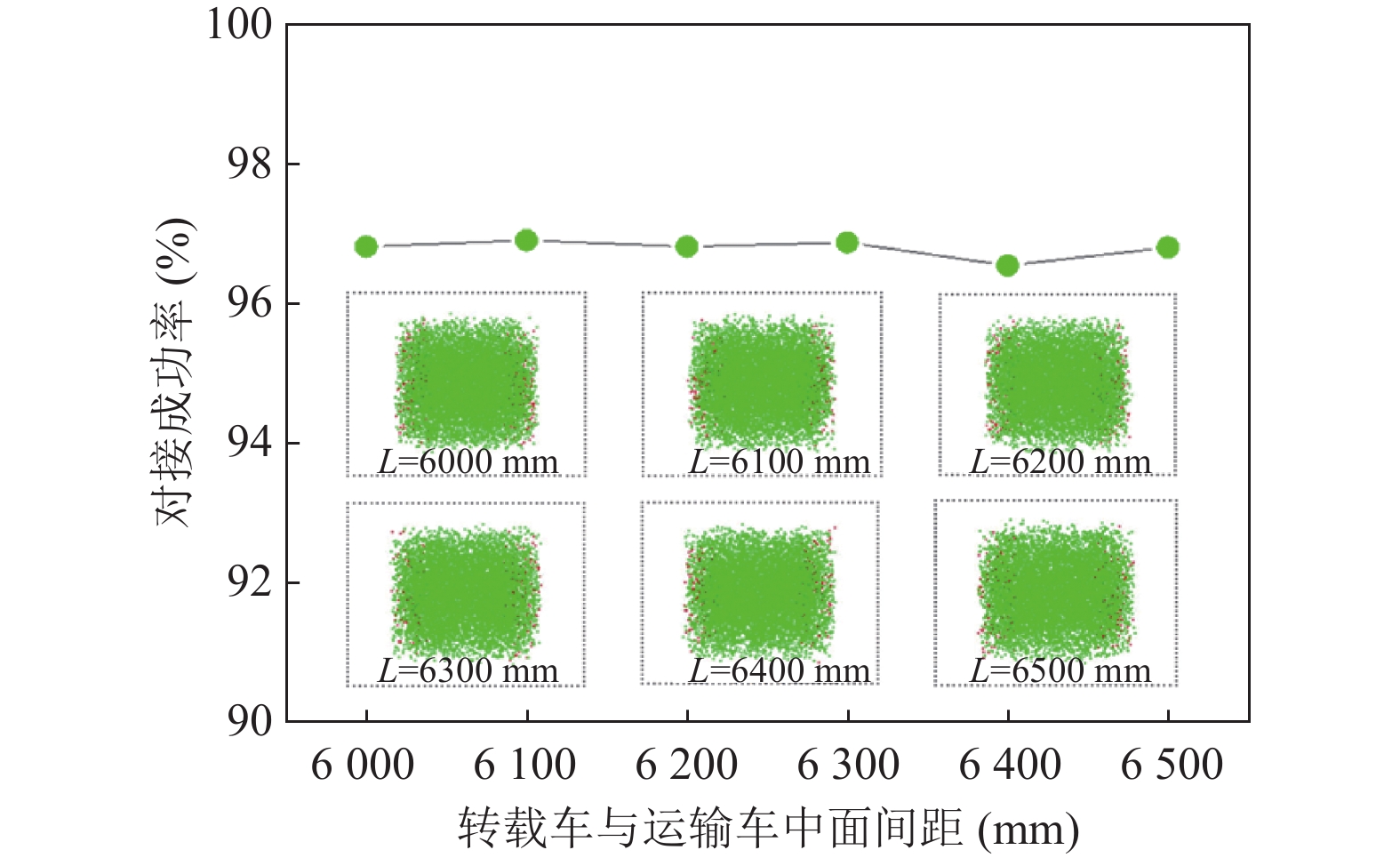
起重设备和运载车辆横向间距通常在6000–6500 mm之间, 为了研究横向间距对起重设备对接成功率的影响, 分别模拟了两车横向间距为6000 mm、6100 mm、6200 mm、6300 mm、6400 mm和6500 mm情况下的对接情况, 其结果如图9所示. 可以看出, 在规定的两车横向间距范围内, 起重设备自动对接成功率约为96%, 转载精度良好, 可以保证运载火箭的精确对接.
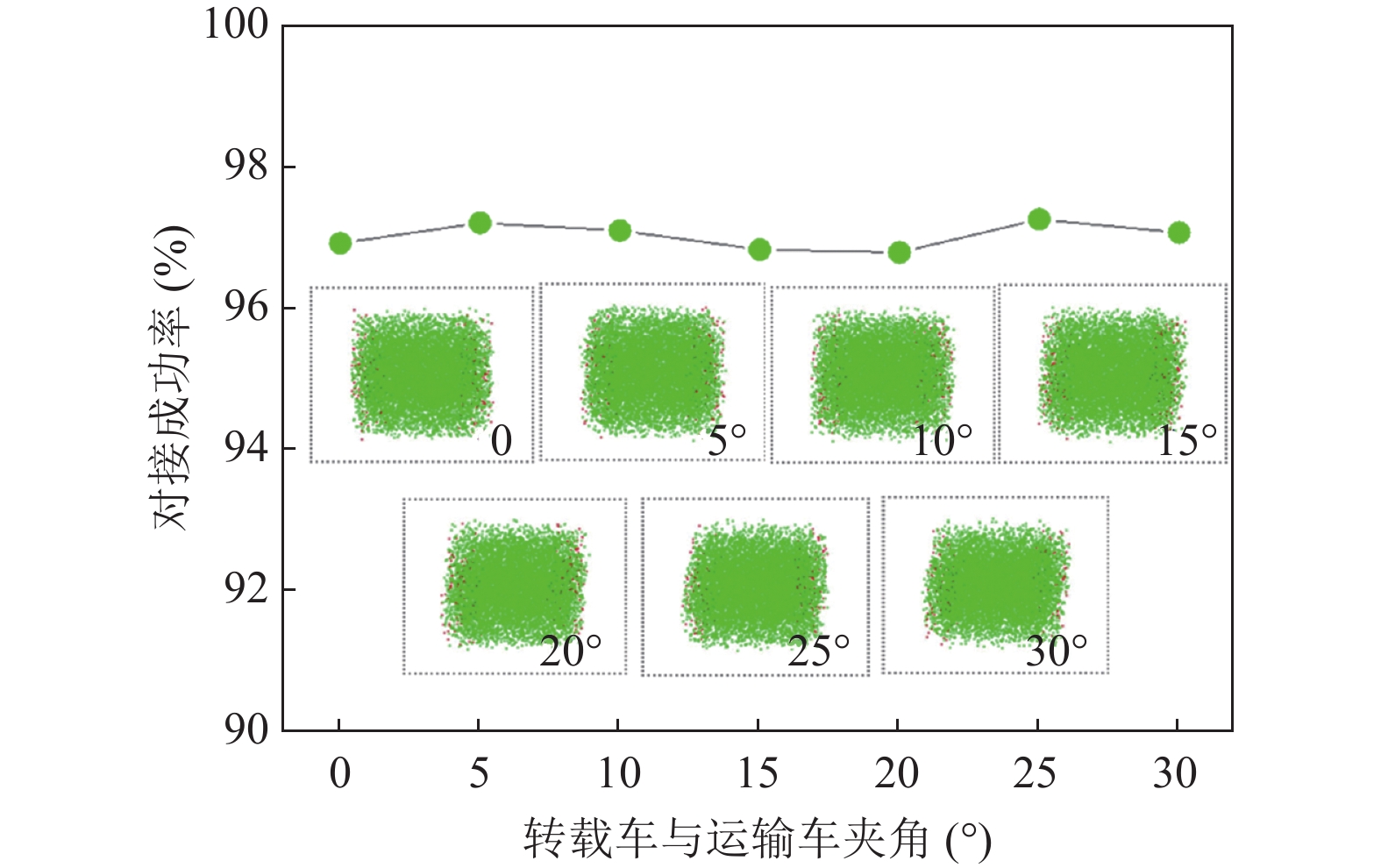
在此基础上, 分析起重设备和运载车辆夹角(0–30°)对其转载精度的影响. 假定两车中间间距6 300 mm, 分别分析两车夹角为0、5°、10°、15°、20°、25°和30°时的装填精度, 如图10所示, 可以看出, 在规定的两车夹角范围内, 自动对接成功率均在96%以上, 可实现可靠对接.
|
图 9 吊幅与对接成功率的关系 |
|
图 10 偏离角度与对接成功率的关系 |
4 结论
针对重载条件下起重设备执行机构变形所导致的运载火箭自动转载对接不准的问题, 本文提出了一种基于两级对准模型的自动转载方法, 有效解决了由于转载作业幅度或物体重量不同引起的起重设备变形量差异对转载精度产生的不可控影响的问题. 通过蒙特卡洛试验对自动转载方法进行仿真验证, 结果表明了所提方法的有效性.
| [1] |
Muelaner J E, Martin O, Maropoulos P. Metrology enhanced tooling for aerospace (META): Strategies for improved accuracy of jig built structures. Proceedings of the 2011 Aerospace Technology Conference and Exposition. SAE, 2011. 187–190.
|
| [2] |
冯志刚, 李泷杲, 熊天辰, 等. 工业机器人视觉定位系统的实现. 航空科学技术, 2018, 29(6): 48-53. |
| [3] |
刘培贤, 丁超, 龚楷. 基于多激光雷达的电力线安全距离监测预警系统. 计算机系统应用, 2021, 30(12): 103-108. DOI:10.15888/j.cnki.csa.008209 |
| [4] |
张冒, 程文明, 覃琴. 基于激光雷达测量技术的集装箱定位系统. 电气传动, 2022, 52(14): 75-80. |
| [5] |
李五朋, 田锡天, 耿俊浩, 等. 飞机大部件装配外形数字化组合测量方法. 航空制造技术, 2018, 61(8): 80-84. |
| [6] |
张春富, 唐文彦, 李慧鹏, 等. 激光跟踪仪在固体火箭发动机推力线测量中的应用. 固体火箭技术, 2007, 30(6): 548-551. DOI:10.3969/j.issn.1006-2793.2007.06.023 |
| [7] |
孙仲旭. 基于激光雷达的AGV定位技术研究 [硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2020.
|
| [8] |
魏振忠, 冯广堃, 周丹雅, 等. 位姿视觉测量方法及应用综述. 激光与光电子学进展, 2023, 60(3): 0312010. |
| [9] |
付芸. 基于CCD光电式两车相对空间位置测量技术研究 [博士学位论文]. 长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2005.
|
| [10] |
邱垚. 基于3D目标识别的工业机器人无序分拣技术研究 [硕士学位论文]. 西安: 西安理工大学, 2019.
|
| [11] |
何泽强. 基于机器视觉的工业机器人分拣系统设计 [硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2016.
|
| [12] |
焦亮, 胡国清, JahangirAlam SM. 基于机器视觉的随机纹理瓷砖的分选系统. 计算机系统应用, 2016, 25(3): 93-100. |
| [13] |
田军委, 闫明涛, 丁良华, 等. 视觉伺服机械臂手机抓取最佳位姿检测. 计算机系统应用, 2021, 30(6): 154-161. DOI:10.15888/j.cnki.csa.007965 |
| [14] |
燕小强, 罗华, 林洪怡, 等. 基于机器视觉的全自动换电机器人定位系统. 计算机系统应用, 2015, 24(9): 234-239. |
| [15] |
Pandey MD, Zhang XF. System reliability analysis of the robotic manipulator with random joint clearances. Mechanism and Machine Theory, 2012, 58: 137-152. DOI:10.1016/j.mechmachtheory.2012.08.009 |
| [16] |
张建新. 天线测试转台的结构设计及对准误差分析 [硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2015.
|
| [17] |
姜健. 基于蒙特卡洛的航空发动机试飞数据模型误差容限分析. 燃气涡轮试验与研究, 2017, 30(3): 1-5. DOI:10.3969/j.issn.1672-2620.2017.03.001 |
 2024, Vol. 33
2024, Vol. 33


