在许多现实生活应用中, 如人脸识别^[1]、图像分类^[2]、文字识别^[3]、生物医学^[4,5]等问题, 将观测对象表示为高维特征向量已成为一种必然趋势. 高维特征向量可以充分描述观测对象, 但也增加了数据可视化和可解释难度^[6]. 在实际应用中, 并不是所有特征都是重要的和有鉴别性的, 高维特征向量中的大多数特征往往相互关联或冗余, 这些特征在聚类中会造成过拟合、处理效率低等问题. 为解决这些问题, 最近的研究关注于从原始特征中选择出具有大量有效信息的特征. 这种方法被称为特征选择^[7].

相比于使用代数方法降低特征维度^[8,9], 特征选择直接从给定的特征集合中选择具有强分类信息且尽可能相互独立的特征组成特征子集, 从而实现更快的降维, 消除冗余. 而且, 由于选择的特征与原始特征有明确的联系, 所以选择出的特征具有更好的解释性, 这有利于可视化和解释任务^[10].

根据算法中标签存在情形, 特征选择可分为有监督^[11]、半监督^[12]、无监督^[13–15]这3类. 前两类算法的执行结果受限于标签信息的使用情况. 在实际应用中, 大量易获取的高维数据通常是无标签的, 而为这些数据添加标签相当耗时且需要额外开销. 因此无监督特征选择方法更为流行和实用.

无监督特征选择方法主要分为3类: 过滤式、包裹式和嵌入式. 过滤式方法通过相关统计量来选择重要特征, 在模型训练过程中先进行特征选择再训练模型^[16,17], 其特征选择和模型训练独立进行, 不能充分考虑特征之间的组合关系. 在包裹式方法中, 特征选择被“包裹”在学习方法中, 并以特征的分类性能作为评价标准^[18], 但其计算开销较大, 不利于大规模数据集求解. 嵌入式方法在模型构建过程中同时进行特征选择^[14], 在实践中具有较好的性能和相当低的计算复杂度.

为实现特征选择, 无监督特征选择通常需要解决两个问题. 首先, 无监督特征选择需要可靠的标签, 但无监督方法并没有真实标签作为参考. 最近的研究方法通常将标签来源与聚类算法^[15]结合, 探索数据特征与伪标签信息的相关性来指导特征选择. 其次, 当数据维度过高时, 运用有效求解方法寻找最优组合选择出有效特征是十分困难的, 因为特征选择本质上属于组合优化问题, 是NP难题^[10]. 在一些方法中, 无监督特征选择方法的目标函数是凸的, 以保证收敛到最优解.

研究表明高维数据并不是均匀线性分布^[19], 其分布通常是稀疏的, 高维数据包含了大量局部信息. 谱图理论在获取数据局部信息方面展现出了良好性能^[20], 因此, 越来越多嵌入式无监督特征选择方法引入谱聚类以获得更好的聚类效果^[21,22]. Cai等^[13]提出MCFS(multi-cluster feature selection)通过谱聚类学习数据局部信息, 然后对特征进行评分以选择有效特征. Li等^[14]提出NDFS (nonnegative discriminative feature selection)引入谱聚类和非负约束, 结合正交约束, 得到更为离散的聚类信息.

在稀疏低秩子空间聚类问题中, 为提高模型性能、避免关联矩阵过于稀疏, 学者们提出了群组效应的概念^[23,24], 即如果样本彼此接近, 则其表示系数也是接近的, 因此群组效应保证了同一子空间内的数据可以分组在一起. Lu等^[23]提出LSR (least squares regression)考虑群组效应, 对关联矩阵应用$F$范数实现了子空间的有效分割. Wang等^[25]提出SRSSC (structural reweight sparse subspace clustering)算法, 利用群组效应和$ {l_{2, 1}} $范数来确保相似的样本归为一类.

在方法学习过程中, 通过对相关系数矩阵施加稀疏性约束^{[13,14,26,27]}、正交约束^[26,28,29]或不相关约束^[30]等方式可以更有效地选择特征. Nie等^[26]提出SOGFS (structured optimal graph feature selection)通过对相关系数矩阵施加$ {l_{2, p}} $范数和正交约束进行稀疏性特征选择. Du等^[27]提出UGFS (unsupervised group feature selection)通过对相关系数矩阵施加${l_{2, 0}}$约束进行组特征选择. Shang等^[28]提出FSDSC (unsupervised feature selection via discrete spectral clustering)引入正交约束学习数据流行结构保留了数据几何信息. 虽然这些研究方法可以有效地进行特征选择, 但其在关注聚类指示矩阵方面存在不足, 无法充分利用聚类指示矩阵的信息.

缺乏对聚类指示矩阵的关注, 可能导致以下问题. 首先, 特征选择方法可能选择与聚类标签不相关但与其他特征高度相关的特征. 这可能导致模型出现过拟合或低解释能力的问题. 其次, 特征选择方法忽略了聚类指示矩阵中的潜在结构和关联性, 导致模型无法捕捉到指示向量之间的复杂关系. 这可能导致聚类结果的不准确和方法泛化能力的下降. 因此, 本文提出对聚类指示矩阵关注不足的解决方法, 即基于$F$范数群组效应和谱聚类的无监督特征选择(unsupervised feature selection based on $F$-norm group effect and spectral clustering, FSGS). 考虑群组效应, 对聚类指示矩阵施加$F$范数约束, 以强化聚类指示矩阵在聚类中的作用, 通过交替迭代法求解优化问题, 最终通过计算相关系数矩阵每行的${l_2}$范数选择出有效特征. 在多个真实数据集上的实验证明了本文方法的有效性.

1 相关基础知识

给定数据矩阵$ {\boldsymbol{X}} = [{{\boldsymbol{x}}_{{1}}}, {{\boldsymbol{x}}_{{2}}}, \cdots , {{\boldsymbol{x}}_{{n}}}] \in {R^{d \times n}}, $其中${{\boldsymbol{x}}_{{i}}} \in {R^{d \times 1}}$表示第$i$个样本, 样本的原始特征数为$d$维, ${{n}}$表示样本数量. 特征选择方法选择的特征数量为${{r}}$, $r \ll {\text{d}}$.

聚类指示矩阵$ {\boldsymbol{G}} = {[{{\boldsymbol{g}}_{{1}}}, {{\boldsymbol{g}}_{2}}, \cdots , {{\boldsymbol{g}}_{{n}}}]^{\mathrm{T}}} \in {R^{n \times c}}, $其中${{\boldsymbol{g}}_{{i}}} \in {R^{c \times 1}}$表示第$i$个样本对应的聚类指示向量, $c$表示数据集的簇类个数.

相关系数矩阵$ {\boldsymbol{W}} = {[{{\boldsymbol{w}}_{{1}}}, {{\boldsymbol{w}}_{{2}}}, \cdots , {{\boldsymbol{w}}_{{d}}}]^{\mathrm{T}}} \in {R^{d \times c}}, $ 其中${{\boldsymbol{w}}_{{i}}} \in {R^{c \times 1}}$表示样本第$i$类特征与各簇类之间的相关系数. 在矩阵${\boldsymbol{G}}$和矩阵${\boldsymbol{W}}$中值越高表示相关性越强.

相似度矩阵使用${\boldsymbol{S}} \in {R^{n \times n}}$表示. ${\boldsymbol{S}}$中的值$ {s_{ij}} $表示样本${{\boldsymbol{x}}_{{i}}}$和样本${{\boldsymbol{x}}_{{j}}}$之间的相似度, 一般采用热核函数^[31]进行计算:

$ {s_{ij}} = {{\text{e}}^{ - \frac{{||{{\boldsymbol{x}}_{{i}}} - {{\boldsymbol{x}}_{{j}}}||}}{{4t}}}} $

(1)

其中, $ {\text{e}} $是欧拉数, $t$是参数.

在实践中, 有全连接法计算所有样本之间的相似度和$k$近邻法, 首先计算样本之间的欧氏距离, 通过给定参数$k$, 选取距离当前样本最近的$k$个样本作为邻居, 然后计算其相似度, 并令其余相似度为0两种方式.

给定矩阵${\boldsymbol{H}} \in {R^{m \times n}}$, ${{\boldsymbol{H}}^{\mathrm{T}}}$表示矩阵的转置, ${\mathrm{tr}}({\boldsymbol{H}})$表示矩阵的迹, ${{\boldsymbol{H}}^{ - 1}}$表示矩阵的逆, 矩阵的$F$范数定义为:

$ ||{\boldsymbol{H}}|{|_F} = \sqrt {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {h_{ij}^2} } } $

(2)

给定向量${{\boldsymbol{h}}_{{i}}} \in {R^{m \times 1}}$, 其${l_2}$范数定义为:

$ ||{{\boldsymbol{h}}_{{i}}}|{|_2} = \sqrt {\sum\limits_{j = 1}^n {h_{ij}^2} } $

(3)

在本文中, 大写字母表示矩阵, 小写字母表示标量、索引或向量.

1.1 谱聚类

聚类指示矩阵需要充分反映出样本的判别信息. 根据谱图理论^[32], 如果两个样本点在数据集的亲和度图中具有高度相关性, 则与它们对应的聚类标签也具有高度相关性. 具体来说, 数据点$ {s_{ij}} $表示的相似度越大, 则指示向量$||{{\boldsymbol{g}}_{{i}}} - {{\boldsymbol{g}}_{{j}}}||$之间的距离越小. 因此, 给定相似度矩阵${\boldsymbol{S}}$, 其学习聚类指示矩阵${\boldsymbol{G}}$的目标函数为:

$ \left\{\begin{split} & \min \frac{1}{2}\sum\limits_{i, j = 1}^n {{s_{ij}}||{{\boldsymbol{g}}_{{i}}} - } {{\boldsymbol{g}}_{{j}}}||_F^2 \\ & {\text{s.t.}}\;\;\;{{\boldsymbol{G}}^{\mathrm{T}}}{\boldsymbol{G}} = {{\boldsymbol{I}}} \end{split} \right.$

(4)

式(4)使${\boldsymbol{S}}$中相邻样本点之间的差异最小. 根据谱理论^[26], 式(4)的最终推导如下:

$ \left\{\begin{split} & \min {\mathrm{tr}}({{\boldsymbol{G}}^{\mathrm{T}}}{\boldsymbol{LsG}}) \\ & {\text{s.t.}}\;\;\;{{\boldsymbol{G}}^{\mathrm{T}}}{\boldsymbol{G}} = {{\boldsymbol{I}}} \end{split} \right.$

(5)

矩阵${\boldsymbol{Ls}}$是关于相似度矩阵${\boldsymbol{S}}$的拉普拉斯矩阵, 其定义为${\boldsymbol{Ls}} = {\boldsymbol{S}} - {\boldsymbol{D}}$, 矩阵${\boldsymbol{D}}$是关于相似度矩阵${\boldsymbol{S}}$的对角矩阵, 其定义为${d_{ii}} = \displaystyle\sum\limits_{j = 1}^n {{s_{ij}}} $.

为了使指示矩阵获得更多的数据信息, 对矩阵${\boldsymbol{G}}$施加正交约束. 正交约束${{\boldsymbol{G}}^{\mathrm{T}}}{\boldsymbol{G}} = {{\boldsymbol{I}}}$促使同一簇类内的指示向量平方和为1. 这避免了在最优化和迭代过程中产生平凡解, 例如, 某个聚类指示向量的值全为0.

1.2 $ F $范数群组效应的无监督特征选择

相关系数矩阵${\boldsymbol{W}}$的作用是选择最有效的样本特征并尽可能准确地将数据矩阵${\boldsymbol{X}}$与聚类指示矩阵${\boldsymbol{G}}$相匹配. 因此, 对于矩阵${\boldsymbol{W}}$的学习经常采用最小化损失函数:

$ \left\{\begin{split} & \min ||{{\boldsymbol{X}}^{\mathrm{T}}}{\boldsymbol{W}} - {\boldsymbol{G}}||_F^2 \\ & {\text{s}}{\text{.t}}{\text{.}}\;\;\;{\boldsymbol{W}}^{\mathrm{T}}{{\boldsymbol{W}}} = {{\boldsymbol{I}}} \end{split}\right. $

(6)

其中, ${{\boldsymbol{X}}^{\rm{T}}}{\boldsymbol{W}}$是一种线性降维的方法, 通过对矩阵${\boldsymbol{W}}$施加正交约束实现原数据集的正交变换. 通过正交变换可以将强相关的空间样本值变换成在新的表示下不相关或者相关性较弱的数据, 去除原高维特征中的冗余特征. 对于给定的低维子空间, 高维数据的正交投影能保留原始数据尽可能多的信息并使原始数据和相应投影之间差异最小化.

在之前的工作中, 主要考虑矩阵${\boldsymbol{W}}$的稀疏性以实现鲁棒性的特征选择. 但这种方法并不能直接描绘出样本与其聚类标签之间的关系. 在以往研究中^[14,26], 具有高度相关性的邻居样本被认为属于同一簇类. 在稀疏低秩子空间聚类问题中, Lu等^[23]和Hu等^[24]进一步证明了数据点之间存在群组效应, 这表明空间中相近的两样本点与其他同类样本点之间具有相似的亲和度.

基于群组效应的考虑, 本文对式(6)添加关于聚类指示矩阵的正则项, 并提出相应定理及证明:

$ \left\{\begin{split} &\mathrm{min}\|{{\boldsymbol{X}}}^{\rm T}{\boldsymbol{W}}-{\boldsymbol{G}}\|_{F}^{2}+\beta \|{\boldsymbol{G}}\|_{F}^{2}\\ &\text{s}\text{.t}\text{.}\;\;{{\boldsymbol{W}}}^{\rm T}{{\boldsymbol{W}}}={{\boldsymbol{I}}} \end{split}\right. $

(7)

其中, $\;\beta $是一个调整$F$范数正则项影响的参数.

定理1. 给定数据集${\boldsymbol{X}} \in {R^{d \times n}}$和与之对应的聚类指示矩阵${\boldsymbol{G}} \in {R^{n \times c}}$, $\forall i \ne j$, 若$||{{\boldsymbol{x}}_{i}} - {{\boldsymbol{x}}_{{j}}}|| \to 0 \Rightarrow ||{{\boldsymbol{g}}_{i}} - {{\boldsymbol{g}}_{j}}|| \to 0$, 则式(7)存在群组效应.

证明: 令${\boldsymbol{x}} \in {R^{d \times 1}}$表示原数据集中的一个样本, ${\boldsymbol{g}} \in {R^{c \times 1}}$表示矩阵${\boldsymbol{G}}$中一个指示向量. 将式(7)写成向量形式:

$ \min ||{{\boldsymbol{W}}^{\mathrm{T}}}{\boldsymbol{x}} - {\boldsymbol{g}}||_F^2 + \beta ||{\boldsymbol{g}}||_F^2 $

(8)

令$ L({\boldsymbol{g}}) = ||{{\boldsymbol{W}}^{\mathrm{T}}}{\boldsymbol{x}} - {\boldsymbol{g}}||_2^2 + \beta ||{\boldsymbol{g}}||_2^2 $, ${{\boldsymbol{g}}^{{*}}}$是式(8)的最优解, 故其最优解满足:

$ \frac{{\partial L({\boldsymbol{g}})}}{{\partial {{\boldsymbol{g}}_{{k}}}}}{|_{{\boldsymbol{g}} = {{\boldsymbol{g}}^{*}}}} = 0 $

(9)

对$L({\boldsymbol{g}})$关于向量${\boldsymbol{g}}$求导:

$ \left(1+\beta \right){\boldsymbol{g}}-{\boldsymbol{W}}^{\rm T}x=0 $

(10)

对于不同的${{\boldsymbol{x}}_{i}}$和${{\boldsymbol{x}}_{j}}$, 有:

$ \left(1+\beta \right){{\boldsymbol{g}}}_{i}-{{\boldsymbol{W}}}^{\rm T}{x}_{i}=0$

(11)

$ \left(1+\beta \right){{\boldsymbol{g}}}_{j}-{{\boldsymbol{W}}}^{\rm T}{x}_{j}=0 $

(12)

由式(11)和式(12)可以得到:

$ {{\boldsymbol{g}}}_{i}-{{\boldsymbol{g}}}_{j}=\frac{1}{1+\beta }{{\boldsymbol{W}}}^{\rm T}({{\boldsymbol{x}}}_{i}-{{\boldsymbol{x}}}_{j})$

(13)

最终推导如下:

$ ||{{\boldsymbol{g}}_{{i}}} - {{\boldsymbol{g}}_{{j}}}|{|_2} = a||{{\boldsymbol{x}}_{{i}}} - {{\boldsymbol{x}}_{{j}}}|{|_2} $

(14)

其中, $a$为正数.

式(14)表明如果样本${{\boldsymbol{x}}_{{i}}}$和${{\boldsymbol{x}}_{{j}}}$属于同一类, 则与之相应的聚类指示向量之间是高度相关的, 它们之间差异几乎为零, 这将提高类内相似性和类间差异性并形成群组以便于聚类.

此外, 在应对噪声时, 聚类指示矩阵上施加$F$范数还可以提升鲁棒性^[23].

2 基于$F$范数群组效应和谱聚类的无监督特征选择 2.1 模型构建

本文提出基于$F$范数群组效应和谱聚类的无监督特征选择(unsupervised feature selection based on $F$-norm group effect and spectral clustering, FSGS), 将聚类标签的学习和特征选择统一到一个联合框架, 同时学习聚类指示矩阵${\boldsymbol{G}}$和相关系数矩阵${\boldsymbol{W}}$. 通过对聚类指示矩阵施加$F$范数约束, 促使簇类形成群组, 结合谱聚类学习数据局部流形信息, 同时, 正交约束避免了平凡解, 最终进行特征选择降低样本维度. 具体目标函数描述如下:

$\left\{ \begin{array}{l}\mathrm{min}\|{{\boldsymbol{X}}}^{\rm T}{\boldsymbol{W}}-{\boldsymbol{G}}\|_{F}^{2}+\alpha {\mathrm{tr}}({{\boldsymbol{G}}}^{\rm T}{\boldsymbol{LsG}})+\beta \|{\boldsymbol{G}}\|_{F}^{2}\\ \text{s.t.}\;\;\;{\boldsymbol{W}}^{\rm T}{\boldsymbol{W}}={{\boldsymbol{I}}}, {{\boldsymbol{G}}}^{\rm T}{\boldsymbol{G}}={{\boldsymbol{I}}}\end{array} \right.$

(15)

其中$\alpha $、$\beta $是正则化参数, 分别用于调整谱聚类和矩阵${\boldsymbol{G}}$对目标函数的影响.

如图1所示, 图1(a)–图1(c)分别表示通过主成分分析方法^[8]对Jaffe数据集的原始所有特征、SOGFS方法选择的有效特征和FSGS方法选择的有效特征分别降至2维时的图示. 两个方法选择的特征维度为140. 通过图示可以明显看到, FSGS方法将原始图像中的绝大部分簇类进行了组别的划分, 形成群组, 而SOGFS方法处理后的簇类则不具备群组效应.

2.2 模型求解

在方法MCFS中, 聚类指示矩阵${\boldsymbol{G}}$首先进行学习, 然后再学习相关系数矩阵${\boldsymbol{W}}$, 这是一个两步走的策略. 与之不同的是, 最近FSDSC、UGFS等方法广泛采用联合学习框架实现更精确的特征选择. 这是因为联合学习在调节损失函数时更具有灵活性. 即使最优化方法的计算复杂度增加, 实验结果依然展现出优越性. 受此启发, 本文提出的FSGS也将采用联合学习框架学习矩阵${\boldsymbol{W}}$和${\boldsymbol{G}}$.

目标函数需要求解矩阵${\boldsymbol{W}}$和${\boldsymbol{G}}$. 由于矩阵${\boldsymbol{W}}$和${\boldsymbol{G}}$都具有正交约束, 因此目标函数是非凸的. 为了最优化目标函数, 本文采用交替迭代法求解目标函数. 在以往的方法中, 矩阵${\boldsymbol{G}}$通常采用特征值分解法求解. 经过实践分析, 在矩阵维度较高时, 特征值分解法求解速度慢且并不容易取得好效果. 因此本文采用代数方法求解矩阵${\boldsymbol{G}}$, 代数方法不仅可以降低方法的计算复杂度而且可以简化相关系数矩阵的计算过程.

首先固定矩阵${\boldsymbol{G}}$, 定义关于矩阵${\boldsymbol{W}}$的函数:

$ {\cal F}({\boldsymbol{G}}, {\boldsymbol{W}})=\left|\right|{{\boldsymbol{X}}}^{\rm T}{\boldsymbol{W}}-{\boldsymbol{G}}|{|}_{F}^{2}+\frac{1}{2}\mu ||{\boldsymbol{W}}^{\rm T}{\boldsymbol{W}}-{{\boldsymbol{I}}}|{|}_{F}^{2}$

(16)

对$ \mathcal{F}({\boldsymbol{G}}, {\boldsymbol{W}}) $关于矩阵${\boldsymbol{W}}$求导并令其为0:

$ \frac{\partial {\cal F}}{\partial {\boldsymbol{W}}}=2{\boldsymbol{XX}}^{\rm T}W-2{\boldsymbol{XG}}+2\mu ({\boldsymbol{W}}{\boldsymbol{W}}^{\rm T}-{{\boldsymbol{I}}})W=0 $

(17)

得到关于矩阵${\boldsymbol{W}}$的更新表达式:

$ {\boldsymbol{W}} = {[{\boldsymbol{X}}{{\boldsymbol{X}}^{\mathrm{T}}} + \mu ({\boldsymbol{W}}{{\boldsymbol{W}}}^{\mathrm{T}} - {{\boldsymbol{I}}})]^{ - 1}}{\boldsymbol{XG}} $

(18)

通过分析可知式(18)的时间复杂度为${\mathrm{O}}(n{d^2} + c{d^2} + cdn + {d^3})$, 对于高维数据其时间复杂度非常之大. 当$d \gg n$时, 采用如下方法, 求解式(15)中的矩阵${\boldsymbol{W}}$等价于求解式(6), 对于任意的矩阵${\boldsymbol{H}}$有运算法则, $||{\boldsymbol{H}}||_F^2 = {\mathrm{tr}}({{\boldsymbol{H}}^{\mathrm{T}}}{\boldsymbol{H}})$, 对式(6)应用该法则可得:

$ \left\{\begin{gathered} \min {\mathrm{tr}}({{\boldsymbol{W}}^{\mathrm{T}}}{{\boldsymbol{A}}^{\mathrm{T}}}{\boldsymbol{W}} - 2{{\boldsymbol{W}}^{\mathrm{T}}}{\boldsymbol{B}}) \\ {\text{s.t.}}\;\;{{\boldsymbol{W}}^{\mathrm{T}}}{\boldsymbol{W}} = {{\boldsymbol{I}}} \\ \end{gathered} \right.$

(19)

其中, ${\boldsymbol{A}}{\text{ = }}{\boldsymbol{X}}{{\boldsymbol{X}}^{\mathrm{T}}}$, ${\boldsymbol{B}}{\text{ = }}{\boldsymbol{XG}}$. 式(19)是一个典型的Stiefel流形上的二次优化问题(quadratic problem of Stiefel manifold, QPSM), 可采用Nie等^[33]提出的GPI(generalized power iteration)方法进行求解, 其时间复杂度为$ {\mathrm{O}}(n{d^2} + c{d^2}) $, 具体过程如算法1所示.

算法1. GPI方法

输入: 矩阵$\scriptstyle {\boldsymbol{A}} \in {R^{d \times {d}}}$, 矩阵$\scriptstyle {\boldsymbol{B}} \in {R^{d \times {c}}}$.

输出: 矩阵$\scriptstyle {\boldsymbol{W}}$.

1)初始化: 初始化矩阵$\scriptstyle {\boldsymbol{W}} \in {[0, 1]^{d \times c}}$, $\scriptstyle {\text{s.t. }}{{\boldsymbol{W}}^{\mathrm{T}}}{\boldsymbol{W}} = {{\boldsymbol{I}}}$; 初始化参数$\scriptstyle v$, 使得$\scriptstyle {\tilde {\boldsymbol A}} = v{{\boldsymbol{I}}} - {\boldsymbol{A}}$是一个正定矩阵.

2)循环:

3) Step 1: 更新矩阵$\scriptstyle {\boldsymbol{R}}:\; {\boldsymbol{R}} \leftarrow {{\tilde A}}{\boldsymbol{W}} + 2{\boldsymbol{B}}$;

4) Step 2: 使用压缩奇异值分解法求解矩阵$\scriptstyle {\boldsymbol{R}}$, 得到$\scriptstyle {\boldsymbol{U\Sigma}}{{\boldsymbol{V}}^{\mathrm{T}}}{{ = }}{\boldsymbol{R}}$;

5) Step 3: 更新矩阵$\scriptstyle {\boldsymbol{W}}:\;{\boldsymbol{W}} \leftarrow {\boldsymbol{U}}{{\boldsymbol{V}}^{\mathrm{T}}}$;

6)收敛或达到最大迭代次数时结束循环.

然后固定矩阵${\boldsymbol{W}}$, 定义关于矩阵${\boldsymbol{G}}$的函数:

$ \begin{split} {\cal L}({\boldsymbol{G}}, {\boldsymbol{W}})=&\left|\right|{{\boldsymbol{X}}}^{\rm T}{\boldsymbol{W}}-{\boldsymbol{G}}|{|}_{F}^{2}+\alpha {\mathrm{tr}}({{\boldsymbol{G}}}^{\rm T}{\boldsymbol{LsG}})\\ & +\beta \left|\right|{\boldsymbol{G}}|{|}_{F}^{2}+\frac{1}{2}\gamma ||{{\boldsymbol{G}}}^{\rm T}{\boldsymbol{G}}-{{\boldsymbol{I}}}|{|}_{F}^{2} \end{split} $

(20)

对$ \mathcal{L}({\boldsymbol{G}}, {\boldsymbol{W}}) $关于矩阵${\boldsymbol{G}}$求导并令其为0:

$ \begin{split} \frac{\partial {\cal L}}{\partial {\boldsymbol{G}}}=&-2({{\boldsymbol{X}}}^{\rm T}{\boldsymbol{W}}-{\boldsymbol{G}})+2\alpha {\boldsymbol{LsG}}\\ & +2\beta {\boldsymbol{G}}+2\gamma ({\boldsymbol{GG}}^{\rm T}-{{\boldsymbol{I}}}){\boldsymbol{G}}=0\end{split} $

(21)

得到关于矩阵${\boldsymbol{G}}$的更新表达式:

$ {\boldsymbol{G}} = {[(1 + \beta - \gamma ){{\boldsymbol{I}}} + \alpha {\boldsymbol{Ls}} + \gamma {\boldsymbol{G}}{{\boldsymbol{G}}^{\mathrm{T}}}]^{ - 1}}{{\boldsymbol{X}}^{\mathrm{T}}}{\boldsymbol{W}} $

(22)

基于以上分析, FSGS步骤如算法2所示.

算法2. FSGS

输入: 数据矩阵$\scriptstyle {\boldsymbol{X}} \in {R^{d \times n}}$, 选择的特征数量$\scriptstyle r$, 正则化参数$\scriptstyle \alpha $、$\scriptstyle \beta $, 聚类数$\scriptstyle c$.

输出: 将所有$\scriptstyle d$维特征根据$\scriptstyle ||{{\boldsymbol{w}}_{i}}|{|_2}\;(i = 1, 2, \cdots, d)$进行降序排列, 选择数据集$\scriptstyle {\boldsymbol{X}} $的前$\scriptstyle r$个有效特征进行聚类.

1)初始化: 初始化矩阵$\scriptstyle {\boldsymbol{W}} \in {[0, 1]^{d \times c}}$, $\scriptstyle {\text{s.t. }}{{\boldsymbol{W}}^{\mathrm{T}}}{\boldsymbol{W}} = {{\boldsymbol{I}}}$; 初始化矩阵$\scriptstyle {\boldsymbol{G}} \in {[0, 1]^{n \times c}}$, $\scriptstyle {\text{s.t. }}{{\boldsymbol{G}}^{\mathrm{T}}}{\boldsymbol{G}} = {{\boldsymbol{I}}}$; 初始化迭代次数$\scriptstyle t = 0$.

2)计算相似度矩阵$\scriptstyle {\boldsymbol{S}}$, 拉普拉斯矩阵$\scriptstyle {\boldsymbol{Ls}}$.

3)循环:

4) Step 1: 更新矩阵$\scriptstyle {\boldsymbol{W}}$: 使用算法1或式(18)更新矩阵$\scriptstyle {\boldsymbol{W}}$;

5) Step 2: 更新矩阵$\scriptstyle {\boldsymbol{G}}$:

$\scriptstyle {{\boldsymbol{G}}^{t + 1}} = {[(1 + \beta - \gamma ){{\boldsymbol{I}}} + \alpha {\boldsymbol{Ls}} + \gamma {{\boldsymbol{G}}^t}{({{\boldsymbol{G}}^t})^{\mathrm{T}}}]^{ - 1}}{{\boldsymbol{X}}^{\mathrm{T}}}{{\boldsymbol{W}}^t} $;

6) Step 3: 更新迭代次数$\scriptstyle t$: $\scriptstyle t = t + 1$;

7)收敛或达到最大迭代次数时结束循环.

2.3 复杂度分析

根据算法2的步骤, 分析每步的时间复杂度.

Step 1中矩阵${\boldsymbol{W}}$采用GPI方法更新的时间复杂度为$ {\mathrm{O}}({d^2}n + {d^2}c) $.

Step 2中${{\boldsymbol{G}}^{\mathrm{T}}}{\boldsymbol{G}}$的时间复杂度为${\mathrm{O}}(c{n^2})$, ${{\boldsymbol{X}}^{\mathrm{T}}}{\boldsymbol{W}}$的时间复杂度为${\mathrm{O}}(cdn)$, 矩阵求逆的时间复杂度为${\mathrm{O}}({n^3})$, 总的时间复杂度为${\mathrm{O}}(c{n^2} + cdn + {n^3})$.

综上所述, 算法2第$t$次迭代时整体时间复杂度为${\mathrm{O}}({n^3} + n{d^2}{{ + c}}{n^2})$. 在算法执行过程中, 设置最大迭代次数为50次.

3 实验及结果分析

实验条件为Windows 10系统, 12 GB内存, Intel(R)Core(TM) i5-7200U @ 2.50 GHz, Python 3.8.

3.1 数据集和对照方法

本文实验在9个真实数据集上进行, 包括人脸数据集(Jaffe^[34], Msra25^[35], Yale^[13], ORL^[13])、物品数据集COIL-20^[36]、生物数据集(Lung^[37], Glioma^[38])、字符数据集(binary alphabet (BA)^[39], USPS^[40]). 表1展示了这些数据集的详细信息.

为了验证本文方法的精度, 对比如下无监督特征选择方法.

1) Baseline: 作为测试结果的基准线, 不进行特征选择, 采用K-means方法对所有样本特征进行聚类.

2) SMR (smooth representation clustering)^[24]: 具有群组效应的子空间聚类算法, 通过应用图拉普拉斯正则化约束学习自表示矩阵, 不进行特征选择.

3) LS^[16]: 通过保留局部流行结构的能力去给每个特征进行评分, 选择分数最高的前$r$个特征作为选择的特征子集.

4) MCFS^[13]: 采用两步走策略, 首先通过归一化割方法获得聚类指示矩阵${\boldsymbol{G}}$, 然后应用${l_1}$范数约束去学习相关系数矩阵${\boldsymbol{W}}$, 最后通过计算每个特征的MCFS分数并降序排列选择出值最高的$r$个特征.

5) NDFS^[14]: 采用联合学习框架, 通过对矩阵${\boldsymbol{W}}$施加${l_{2, 1}}$范数、对矩阵${\boldsymbol{G}}$采用非负约束学习数据结构. 最后通过计算矩阵${\boldsymbol{W}}$每行的${l_2}$范数并进行降序排列选择出值最大的$r$行特征.

6) SOGFS^[26]: 同时进行特征选择和局部结构学习, 可以自适应学习相似度矩阵. 通过对矩阵${\boldsymbol{W}}$施加${l_{2, p}}$范数和正交约束学习数据结构. 最后通过计算矩阵${\boldsymbol{W}}$每行的${l_2}$范数并进行降序排列选择出值最大的$r$行特征.

7) FSDSC^[28]: 通过正交回归模型学习矩阵${\boldsymbol{W}}$, 采用离散化的聚类指示矩阵提供清晰的指示信息, 引入对角特征权重矩阵进行特征评估, 最后将选择最大的$r$个对角元素对应的特征用于聚类.

3.2 评估方法

在应用特征选择方法产生特征标签后, 再使用K-means聚类算法对选择的特征进行聚类. 由于K-means算法的聚类结果与初始化有关, 所以对每个方法采用相同的随机种子进行20次K-means聚类, 然后记录平均结果用于分析.

在所选特征聚类形成簇类标签之后, 将簇类标签使用Kuhn-Munkres算法^[41]与真实标签进行最佳匹配. 对匹配后的标签使用准确率(accuracy, ACC)和归一化互信息(normalized mutual information, NMI)进行评估. 在这两个指标中, 值越高方法越优.

3.3 参数设置

特征选择算法在执行时需要提供选择的特征数量, Jaffe、Msra25、BA和USPS选择50–200个特征, 间隔30; 其他数据集选择50–300个特征, 间隔50. 对于需要调节参数的模型, 参数取值范围设置为{10⁻³, 10⁻², 10⁻¹, 1, 10, 10², 10³}, 其中UDFS和FSGS调节的参数为$\alpha $和$\beta $, SOGFS和FSDSC调节的参数为$\alpha $. 本文分别采用全连接法和$k$近邻法计算相似度矩阵参与方法的特征选择过程, 然后选择最优的结果进行分析, 根据之前的方法^[11,14,15], $k$设置为5.

3.4 实验结果及分析

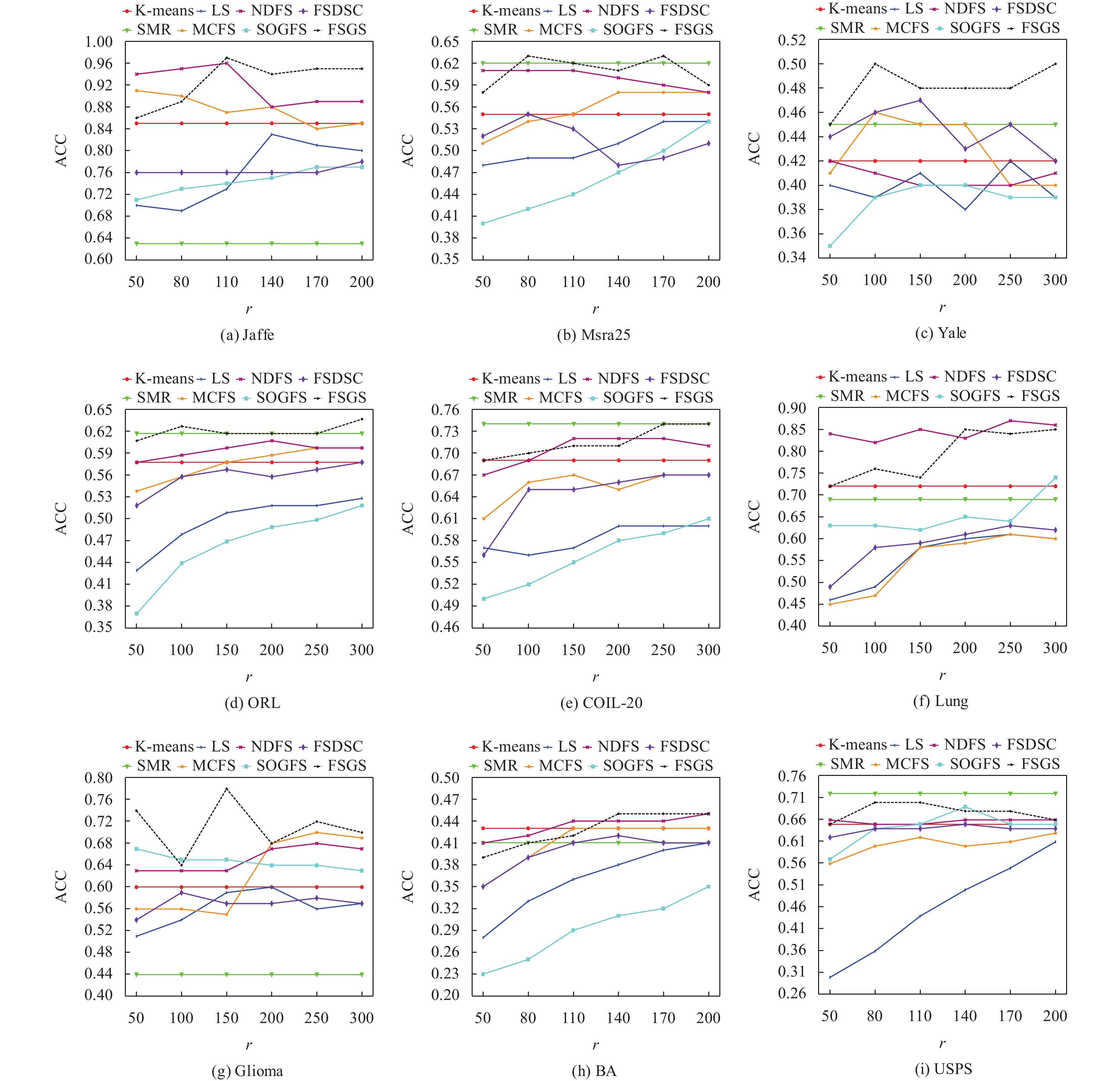
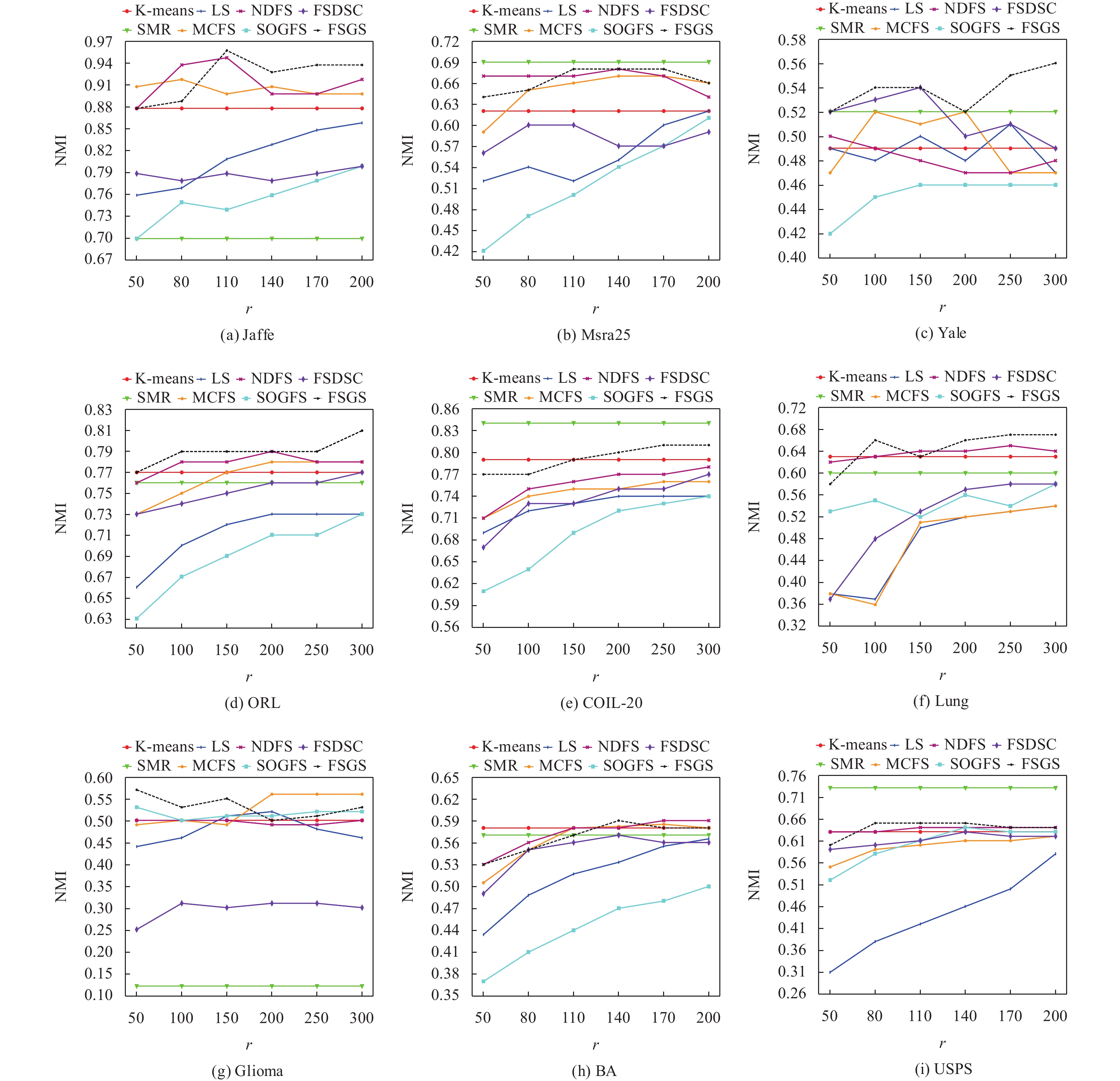
图2和图3分别为8种无监督聚类方法在9个数据集上选择特征个数与ACC和NMI的关系.

实验表明了特征选择的可行性和重要性, 大多数特征选择方法在选择少量特征的情况下可以达到甚至超过K-means方法的结果. 在大多数数据集的ACC和NMI结果中, 本文方法都超过了其他方法的结果.

通过图2和图3可以发现诸如FSGS、UDFS、SOGFS和FSDSC等嵌入式方法的性能要明显优于LS和MCFS等过滤式方法, 这表明嵌入式方法的优越性能. 同时FSGS、UDFS、FSDSC和UGFS等采用的联合学习方法聚类结果要好于MCFS采用的两步走策略.

图2和图3表明具有群组效应的SMR方法在大多数数据集上可以取得较好的效果, 但其似乎受数据集影响较大. 例如, 虽然其在COIL-20和USPS数据集上得到了所有方法中的最好效果, 但其在Glioma和Jaffe数据集上却取得了最差效果. 相反, 本文方法同样考虑了群组效应, 且选择少量特征进行聚类, 但在所有数据集上都具有稳定的表现, 且结果优于或基本等于大多数算法的结果, 这表明了本文考虑群组效应的有效性.

通过图2和图3可以发现考虑聚类指示矩阵的NDFS方法和本文方法在大多数数据集中都取得了最好效果, 这说明了在特征选择方法中充分考虑聚类指示矩阵的必要性. 而NDFS方法对于聚类指示矩阵在迭代过程中全为正时将会失效, 相比之下本文方法的泛化能力更强.

图4和图5分别表示FSGS在每个数据集上选择200个特征时ACC与NMI随不同参数$\alpha $和$\;\beta $变化的结果.

通过图4和图5可以分析参数$\alpha $和$\beta $对聚类效果的影响. 总的来说, 相比于NMI, ACC似乎更易受到参数影响, 在大多数据集中当参数$\alpha $和$\beta $同时取较大值或其中一个取较大值时, 可以获得最佳的聚类效果. 特别是在数据集Glioma的NMI评价中, 在$\beta $取最大值时, 聚类效果明显优于其他参数下的效果. 这表明结合谱聚类和群组效应可以学习到更具判别性的伪标签信息.

表2和表3分别表示各个方法在9个数据集上最高ACC和NMI对比, 其中黑体数字表示最高值, 下划线数字表示次高值.

由表2可以看出, 本文方法在6个数据集上都取得了最优的聚类结果. 在人脸数据集Jaffe、Yale和ORL上, FSGS在聚类准确度上相比于次优结果平均提升4.67%; 在高维数据集Lung和Glioma上FSGS的聚类结果位于首位或次位; 在多类别数据集ORL和BA上FSGS则取得最高的聚类结果. 这表明了FSGS考虑群组效应的鲁棒性.

表4表示各个方法在9个数据集上的平均运行时间对比.

由表4中数据可以看出, 相比于SMR、LS和MCFS等非迭代方法, 其他采用迭代策略的方法运行时间明显上升. 在面临高维数据集Lung和Glioma时, 运行时间达到了最高, 这表明在高维数据集中选择最优组合是具有挑战性的. 其中, 采用的特征值分解法的SOGFS在面临高维数据时会造成极大的时间消耗. 本文方法的运行时间基本与NDFS方法一致且在可以接受的范围内, 并且本文方法也取得了较好的聚类效果.

综上所述, 本文方法可在不同类型的多个数据集上取得较好的效果, 泛化能力强, 运行效率高. 结果表明, 本文方法在人脸识别、生物医学等领域具有一定的应用价值, 而且相较于其他方法, 本文方法在生物医学等高维数据集上具有最短的运行时间, 因此本文方法是合理有效的无监督特征选择方法.

4 结束语

本文提出基于$F$范数群组效应和谱聚类的无监督特征选择(FSGS), 利用群组效应结合谱聚类促使学习更为准确的簇类结构以进行最优的特征子集选择. 为了求解非凸正交约束最优化函数, 将正交约束作为目标函数的一部分并使用矩阵代数方法求解, 通过交替迭代法不断优化变量. 最后通过实验验证本文方法的有效性, 实验表明本文方法在大部分数据集上都取得最佳结果, 相比之前方法得到明显提升. 如何更好地学习聚类指示矩阵指导进行特征选择是今后研究方向之一, 此外, 方法的运行效率也需要考虑使用更好的方法进行优化.