ANN在众多领域表现优异[1,2], 然而其较高的计算开销和能耗需求对硬件部署不利. 随着类脑研究的深入, 具有仿生特性的SNN逐渐受到关注[3]. SNN由离散脉冲时间序列构成的神经元模型, 模拟了实际生物神经网络中的独特机制, 能够通过脉冲序列表达和传递信息, 其更符合生物学上的合理性. 与ANN相比, SNN模拟了生物神经元的工作方式, 只有在需要时才发放脉冲, 因此能够实现更高的能量效率降低网络计算量, 更适合于部署在硬件至上以降低能耗. 且SNN对于处理时间相关的信息具有更好的性能, 其适用于处理时间序列数据、事件驱动的场景、需要低能耗的嵌入式系统等场合. 因此, 采用SNN实现复杂的目标检测任务是一个理想的选择.
然而, 由于SNN的神经元复杂动力学和不可微操作[4], 传统反向传播算法无法直接应用于SNN. 近年来, 有学者提出用近似连续函数替代脉冲函数或其导数, 从而产生基于脉冲的反向传播算法[5,6]. 但此方法局限于浅层SNN和简单任务, 且需要大量计算和存储能力. ANN-SNN转换方法通过建立激活输出和平均发射速率之间的映射关系, 避免了直接训练SNN. 转换方法通常需利用较大时间步长克服转换误差, 但也有许多工作从不同角度优化该方法, 如可训练的阈值[7], 软重置机制[8], 阈值偏移[9]等. 现有研究在较小时间步长下难以消除ANN到SNN的转换误差. Spiking YOLO[10]是深度SNN的首个目标检测模型, 但是该模型需要8000个时间步长才能到达与原始ANN相当的结果. 本文的主要贡献可以总结如下.
1)提出了Spiking YOLOv3模型, 该模型基于YOLOv3-tiny网络模型, 经过优化以适应后续的脉冲神经网络转换. 此外, 本文采用了细粒度通道归一化方法, 使得神经元能够获得适当的放电率, 从而提高了模型的精度.
2)在理论上, 对人工神经网络到脉冲神经网络的转换过程产生的误差进行了分析, 并进一步通过量化激活函数对Spiking YOLOv3模型进行了优化.
3)在PASCAL VOC和MS COCO数据集上对Spiking YOLOv3模型进行测试. 实验发现, 我们所提出的Spiking YOLOv3模型的平均推理时间约为先前工作的1/4, 同时准确率分别提升了约4.65%和9.32%. 经过优化后, Spiking YOLOv3-FC模型在UAV, PASCAL VOC和MS COCO数据集上的平均推理时间约需优化前模型的1/2, 且在PASCAL VOC和UAV数据集上实现了无损转换, 在COCO数据集上的转换误差降低到了0.93%.
1 相关工作对于ANN到SNN的转换研究, 最早由Cao等人[11]发起的, Diehl[12]提出了基于数据和基于模型的归一化方法, 将3层的ANN转换为SNN, Sengupta等人[7]又对阈值进行缩放以减小精度的损失. 为了解决信息的丢失问题, Han等人[8]提出使用“减法重置”神经元. 为了消除ANN-SNN的转换误差, Rueckauer[13]提出使用p-Norm的方法, 用99.9%的激活百分位数作为尺度因子, 避免在激活分布中挑选异常值. Ho等人[14]在ANN的ReLU层后面添加约束, 降低激活值, 从而减小截断误差与量化误差. 此外, Han等人[8]重新调整了SNN阈值, 以避免脉冲神经元的不当激活. Deng等人[9]引入额外的偏差以最小化分层误差, Li等人[15]进一步提出逐层修正误差的校正算法, 通过校准SNN中的参数来匹配转换后的激活, 从而缩小源神经网络与校准后SNN之间的激活分布差距.
Spiking YOLO首次将SNN应用到目标检测上面, 采用通道归一化与IBT平衡神经元的放电率, 在深度SNN中实现快速, 准确的信息传递. 该工作需要8000个时间步长才能达到与原始ANN相当的准确率. 在其后续工作中[16], 使用贝叶斯优化的阈值平衡方法, 找到最优阈值电压, 但仍需5000个时间步长才能达到与ANN相当的准确率.
2 本文方法 2.1 SNN神经元本文在SNN的神经元模型选择上, 采用了IF神经元模型. 为降低信息损失, 采用了文献[8]提出的“减法重置”机制, 神经元放电的瞬间, 超过阈值的部分将被保留. 因此, IF神经元的动力学方程可以表示为:
| $ V_{\rm temp}^l\left( t \right) = {V^l}\left( {t - 1} \right) + {W^l}{x^{l - 1}}\left( t \right) $ | (1) |
| $ {V^l}\left( t \right) = V_{\rm temp}^l\left( t \right) - {s^l}\left( t \right){\theta ^l} $ | (2) |
其中,
| $ {s^l}\left( t \right) = \left\{ \begin{gathered} 1,\quad V_{\rm temp}^l \geqslant {\theta ^l} \\ 0,\quad{\text{else}} \\ \end{gathered} \right. $ | (3) |
对于一个脉冲神经元, 其膜电位超过激发阈值, 则该神经元将发放脉冲, 如果第
| $ {x^l}\left( t \right) = {s^l}\left( t \right){\theta ^l} $ | (4) |
本文中ANN-SNN转换的主要思想是用SNN的脉冲发射率(平均突触后电位)来近似ANN中的激活值. 将式(1)与式(2)结合得:
| $ {V^l}\left( t \right) = {V^l}\left( {t - 1} \right) + {W^l}{x^{l - 1}}\left( t \right) - {s^l}\left( t \right){\theta ^l} $ | (5) |
式(5)对时间步长1–T求和得:
| $ \frac{{{V^l}\left( T \right) - {V^l}\left( 0 \right)}}{T} = {W^l}\frac{{\displaystyle\sum\nolimits_{t = 1}^T {{x^{l - 1}}\left( t \right)} }}{T} - \frac{{\displaystyle\sum\nolimits_{t = 1}^T {{s^l}\left( t \right)} {\theta ^l}}}{T} $ | (6) |
其中,
| $ {\phi ^l}\left( T \right) = \frac{{\displaystyle\sum\nolimits_{t = 1}^T {{s^l}\left( t \right)} {\theta ^l}}}{T} $ | (7) |
| $ {\phi ^l}\left( T \right) = {W^l}{\phi ^{l - 1}}\left( T \right) + \left( { - \frac{{{V^l}\left( T \right) - {V^l}\left( 0 \right)}}{T}} \right) $ | (8) |
式(8)描述了脉冲神经网络中两个相邻层之间神经元的平均突触后电位的关系.
2.3 Spiking YOLOv3模型目标检测是在目标识别的基础上, 确定图像中物体的精确坐标. YOLOv3算法在目标检测领域表现优异, 其借鉴了特征金字塔的思想, 不仅在每个特征图上进行独立的预测, 同时通过上采样小特征图至大特征图尺寸, 再与大特征图拼接以进一步预测. YOLOv3-tiny是YOLOv3的轻量级版本, 其在YOLOv3的基础上减少了一些特征层, 仅保留了两个独立预测分支, 速度更快. 因此, 我们选择YOLOv3-tiny作为基础网络模型.
然而, 将原始的ANN转换成SNN时, 通常会出现不可接受的精度损失. 其主要损失来源包括:
1) ANN中的负输出值在SNN中很难精确的表示, 使用双曲线正切(tanh)或归一化指数函数(Softmax)后, 非线性神经元的输出值可以得正也可以得负, 而脉冲神经元的速率只能是正值. 因此, 负值总被丢弃, 导致转换后的SNN的精度下降.
2) SNN无法直接应用ANN中的批量归一化(batch normalization, BN)层, 用在SNN中, 通常会被舍弃.
3) SNN的信息传递是脉冲形式, 导致最大池化层在转换过程中精度损失, 增加SNN的复杂度.
针对上述问题, 我们对基于YOLOv3-tiny的基础网络模型进行如下改进:
1)使用ReLU激活函数替代Leaky ReLU激活函数.
2)将步长为2的最大池化层替换为步长为2的卷积(convolution, Conv)层, 并移除步长为1的最大池化层.
3)将上采样层替换为反卷积层.
4)将BN层权值折叠进Conv层权值.
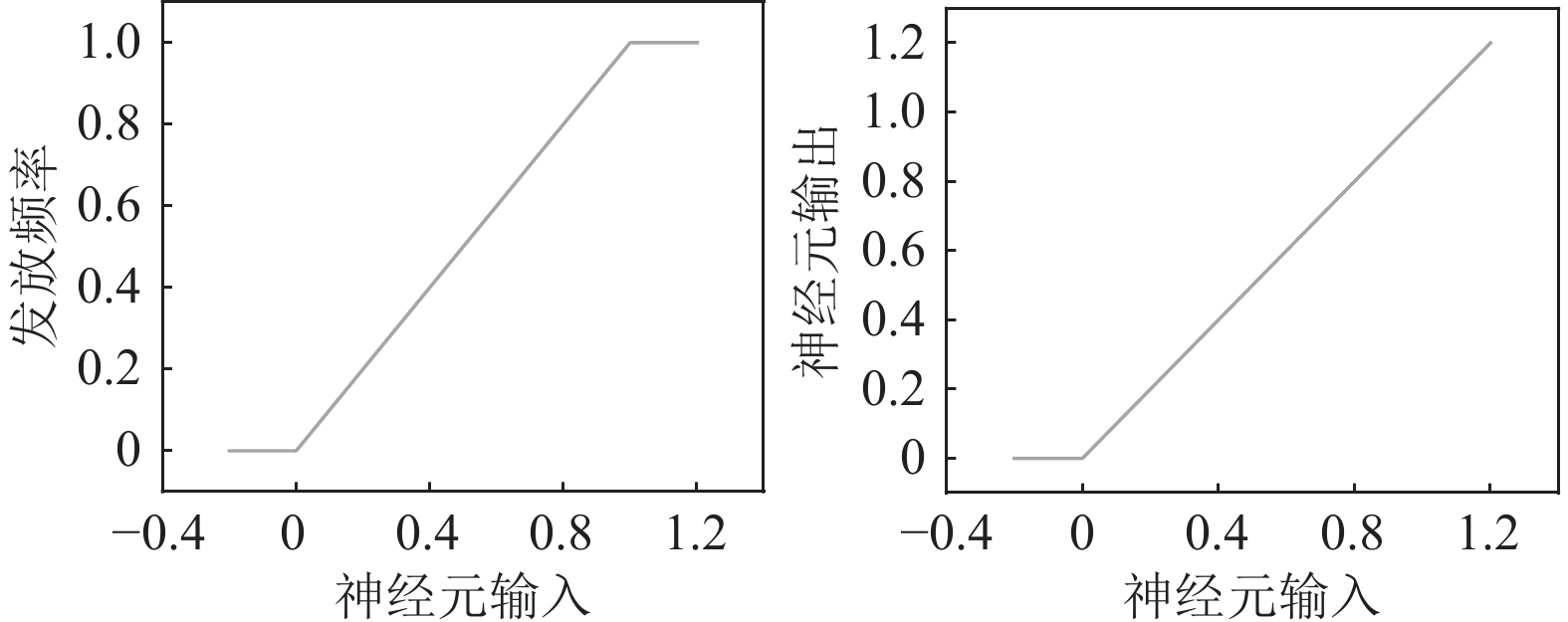
我们采用ReLU激活函数替代YOLOv3-tiny中的Leaky ReLU激活函数的原因在于, ANN中ReLU神经元的非线性激活与SNN中IF神经元的脉冲发放率之间具有较强相关性. 如图1, IF神经元脉冲发放频率与输入的曲线与ReLU曲线几乎一致. 借助这一特性, 我们可以解决负输出问题, 提高转换后的SNN精度.
|
图 1 IF神经元脉冲发放频率和输入 |
我们采取用步长为2的卷积层取代原有步长为2的最大池化层, 同时移除了步长为1的最大池化层. 这一调针对上述提到的精度损失来源第3点. 由于ANN中的最大池化层转化为SNN中的对应层时会导致精度下降, 之前有研究选择用平均池化层来替代, 或直接移除池化层. 然而, Na等人[17]的研究指出用平均层替换最大池化层会对模型的精度和能量效率产生负面影响. 同时, 完全移除池化层会丧失降维和去除冗余信息的功能. 卷积层通过调整步长大小同样可以缩减特征图的尺寸并增大感受野. 因此, 我们选采步长为2的最大池化层来替代步长为2的卷积层, 并移除步长为1的最大池化层.
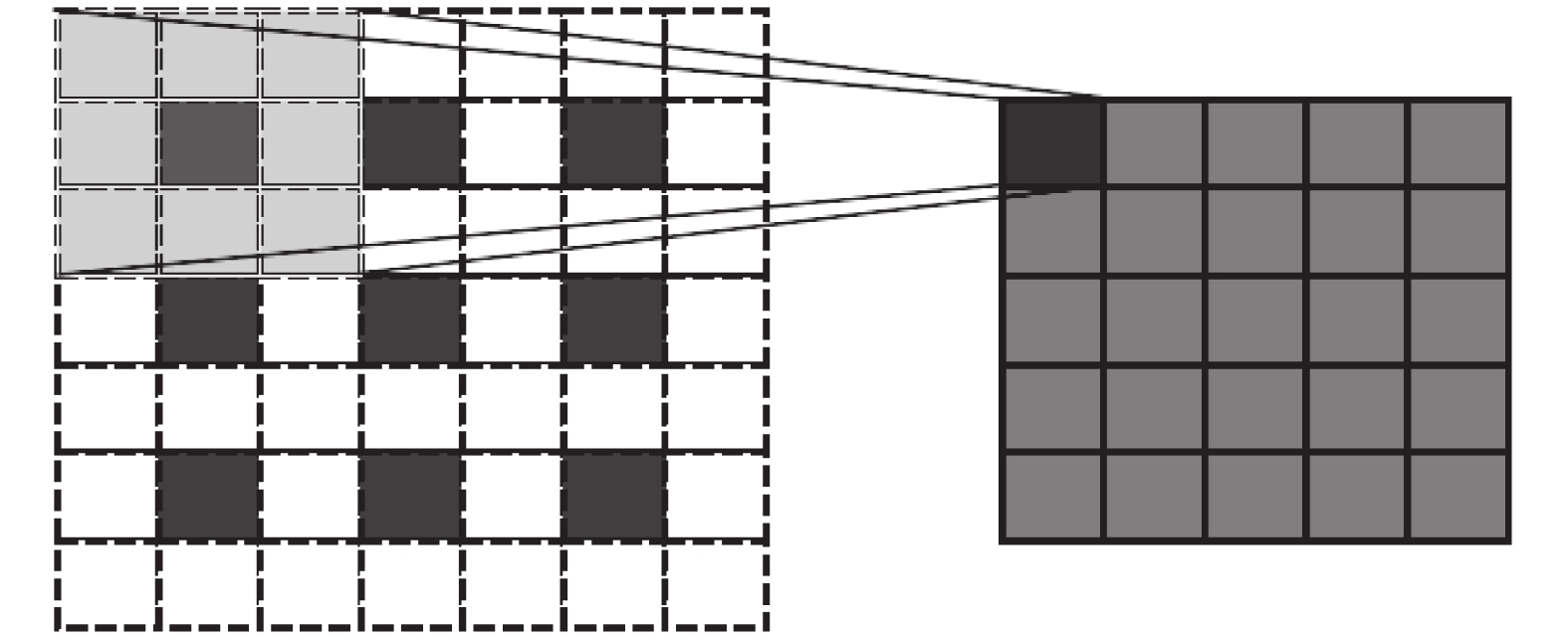
对于YOLOv3-tiny模型中的上采样层, 我们采用反卷积层进行替换. 因上采样层不具备权重, 在转化为SNN结构时存在困难, 而反卷积层与上采样层功能相似, 能够更顺畅地完成这一转换. 反卷积操作如图2所示, 其在四周添加0元素后再进行卷积操作.
|
图 2 反卷积操作图(在输入3×3特征图四周填充0元素, 采用3×3卷积核进行卷积操作, 输出5×5特征图) |
在SNN中, 由于神经元的活动具有脉冲性, BN层的传统应用方式不再适用. BN层在提高模型训练速度的同时, 对模型输出精度有着积极影响, 直接去除BN层可能会导致网络精度的损失. 为解决这一问题, 我们采取将BN层折叠进前一卷积层权值中. 这种融合确保了在SNN中也能保留BN层的优势, 而不会牺牲网络性能. BN层的公式如下:
| $ {\mu _B} = \frac{1}{m}\sum\limits_{i = 1}^m {{x_i}} $ | (9) |
| $ \sigma _B^2 = \frac{i}{m}{\sum\limits_{i = 1}^m {\left( {{x_i} - {\mu _B}} \right)} ^2} $ | (10) |
| $ \hat {{x_i}} = \frac{{{x_i} - {\mu _B}}}{{\sqrt {\sigma _B^2 - \varepsilon } }} $ | (11) |
| $ {y_i} = \gamma \hat {{x_i}} + \beta $ | (12) |
式(9)、式(10)为计算1个批次输入数据的平均值与方差, 式(9)对数据进行标准化, 式(10)为归一化的数据. 其中
| $ \widetilde W_{i, j}^l = \frac{{\gamma _i^l}}{{\sigma _i^l}}W_{i, j}^l $ | (13) |
| $ \widetilde b_i^l = \frac{{\gamma _i^l}}{{\sigma _i^l}}\left( {b_i^l - \mu _i^l} \right) + \beta _i^l $ | (14) |
其中,
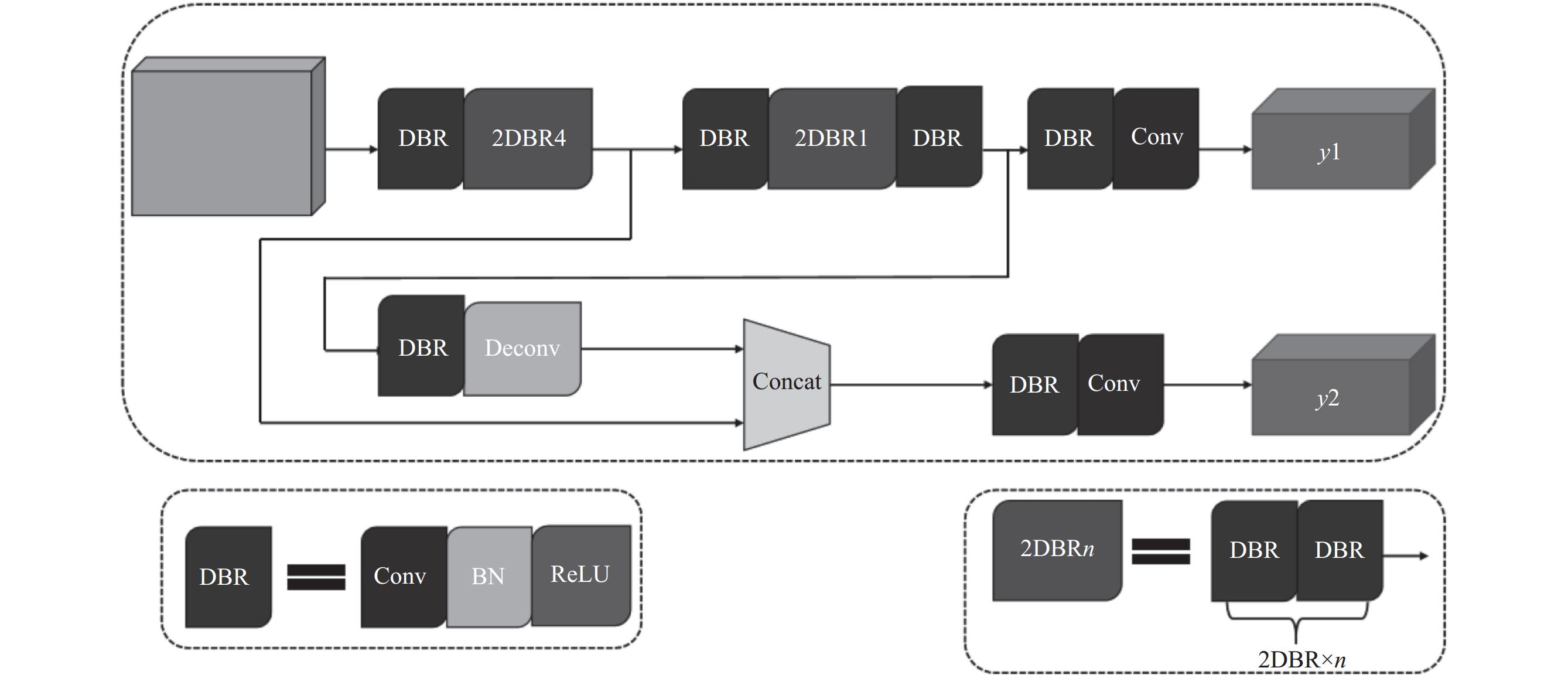
经过上述网络模型调整后, 得Spiking YOLOv3网络模型, 如图3所示.
Spiking YOLOv3网络模型在尽可能地减少精度损失的同时, 还能在较低的时延下实现较高的检测精度. 最终的Spiking YOLOv3网络结构详细参数如表1所示.
|
图 3 Spiking YOLOv3网络模型图 (DBR模块为卷积+批处理归一化+ReLU激活函数组成, 2DBR模块为两个DBR模块) |
| 表 1 Spiking YOLOv3的网络结构表 |
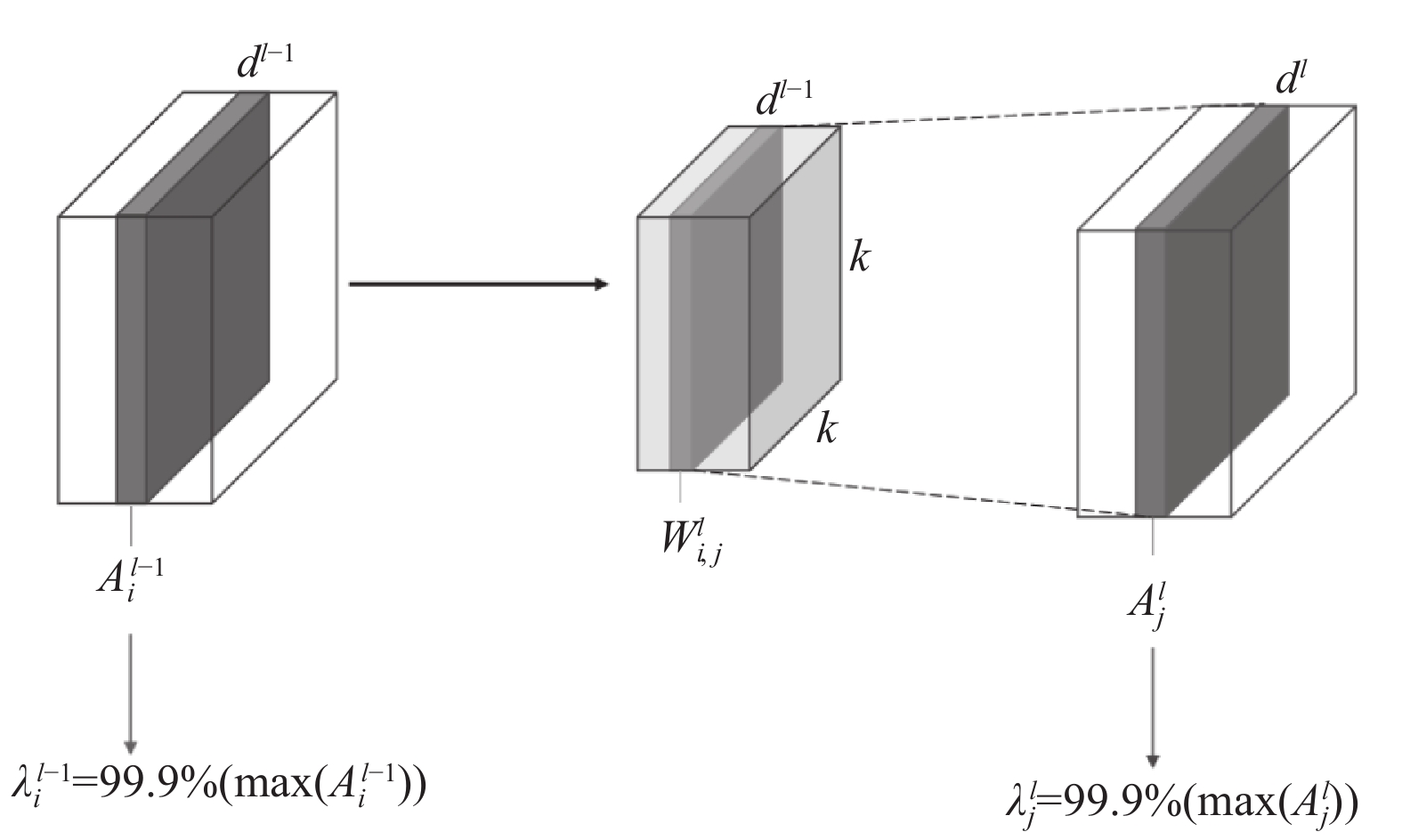
在给定的时间步长下, 当利用SNN进行目标检测时, 神经元的激活不足或过渡激活都可能导致信息的丢失. 为确保神经元的有效性, 我们采用细粒度的归一化方法. 该方法在每层的通道维度上, 使用第99.9个百分位激活值对权值进行归一化, 图4为通道归一化具体操作示意图.
|
图 4 通道归一化 |
通道归一化的具体公式如下:
| $ \widetilde W_{i, j}^l = W_{i, j}^l\frac{{\lambda _i^{l - 1}}}{{\lambda _j^l}}{\text{ and}}\;{\text{ }}\widetilde b_i^l = \frac{{b_j^l}}{{\lambda _j^l}} $ | (15) |
其中,
对于ANN, 前向传播的过程可以描述为一个线性变换过程和一个ReLU激活函数的非线性映射:
| $ {a^l} = f\left( {{W^l}{a^{l - 1}}} \right),{\text{ }}l = 1, 2, 3, \cdots, L $ | (16) |
其中,
假设
| $ {E^l} = {\phi ^l} - {a^l} = {W^l}{\phi ^{l - 1}} - \frac{{{V^l}\left( T \right) - {V^i}\left( 0 \right)}}{T} - f\left( {{W^l}{a^l}} \right) $ | (17) |
因接收相同的输入
| $ {E^l} = {{\textit{z}}^l} - \frac{{{V^l}\left( T \right) - {V^l}\left( 0 \right)}}{T} - {\text{ReLU}}\left( {{{\textit{z}}^l}} \right) $ | (18) |
式(18)可看出转换误差非零, ANN-SNN转换中有3个主要误差, 截断误差, 量化误差, 不均匀误差.
截断误差由ANN与SNN的不同的取值范围造成. 对于ANN, 其
| $ {\phi ^l}\left( T \right) = clip\left( {\frac{{{\theta ^l}}}{T}\left\lfloor {\frac{{{a^l}T}}{{{\lambda ^l}}}} \right\rfloor , 0, {\theta ^l}} \right) $ | (19) |
其中,
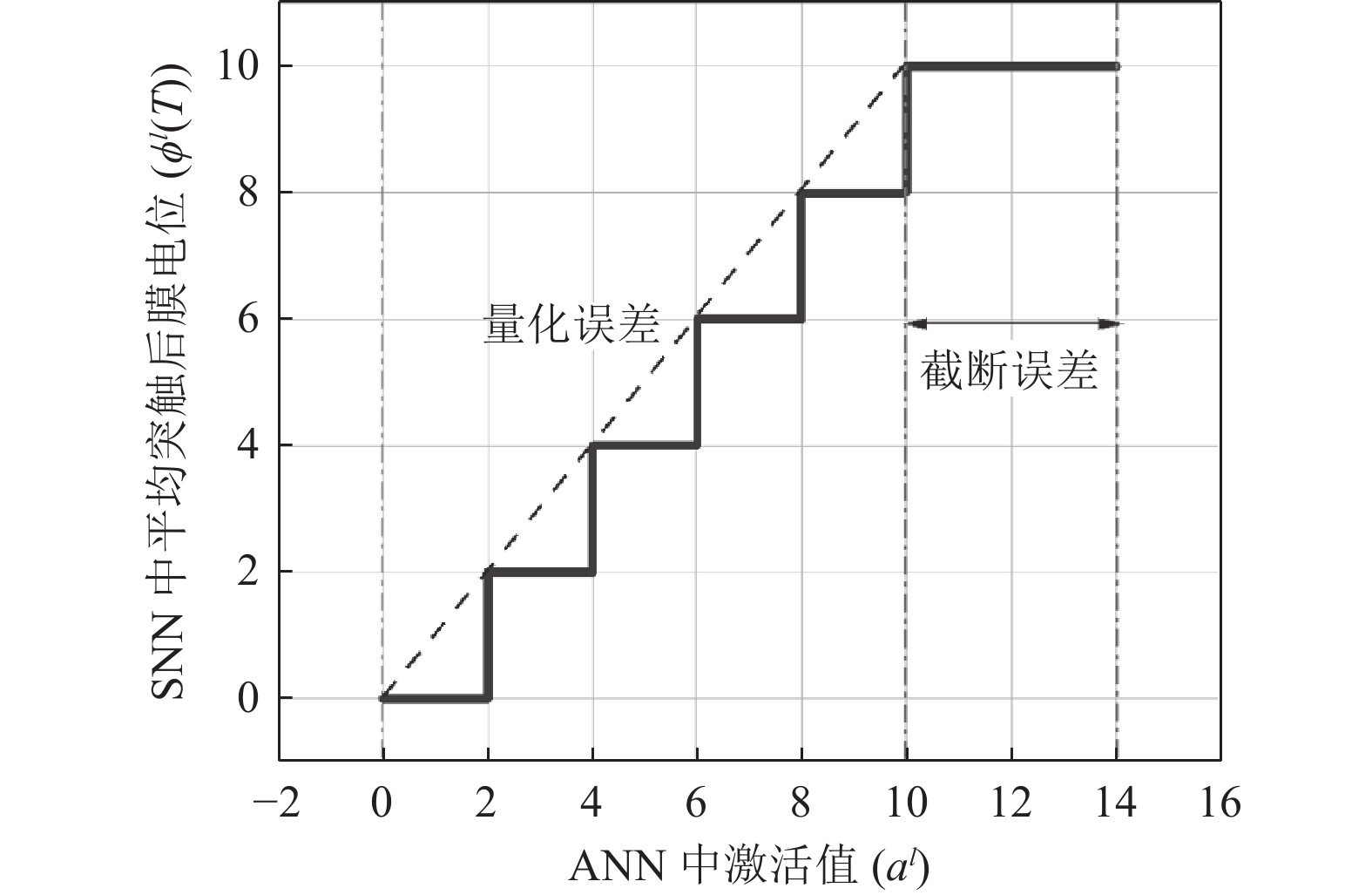
|
图 5 截断误差与量化误差(阈值: 10, 时间步长: 5) |
量化误差是因为在ANN中其激活值
不均匀误差是由于脉冲到达激活层的时间序列不同. 在理想情况下, 期望来自前一层接受脉冲的时间是均匀的. 但在现实情况中, 脉冲传递到深层时间不均匀, 这将会导致比预期产生较多或者较少的脉冲. 设现在有
假设两个脉冲神经元在6个时间步长内都分别发射3个脉冲, 分为以下3种情况.
1)两个突触前神经元分别在t=1, 3, 5和t=2, 4, 6处发出脉冲, 如图6(a)所示, 则
2)两个突触前神经元分别在t=1, 2, 3和t=4, 5, 6处发出脉冲, 如图6(b)所示, 则
3)两个突触前神经元分别在t=4, 5, 6和t=1, 2, 3处发出脉冲, 如图6(c)所示, 则
上述的这3种误差存在着相互依存的关系, 若
| $ {\phi ^l}\left( T \right) \approx {\theta ^l}clip\left( {\frac{1}{T}\left\lfloor {\frac{{{{\textit{z}}^l}T + {V^l}\left( 0 \right)}}{{{\theta ^l}}}} \right\rfloor 0, 1} \right) $ | (20) |

|
图 6 不均匀误差 |
估计的转换误差为:
| $ {\widetilde E^l} = {\theta ^l}clip\left( {\frac{1}{T}\left\lfloor {\frac{{{{\textit{z}}^l}T + {V^l}\left( 0 \right)}}{{{\theta ^l}}}} \right\rfloor , 0, 1} \right) - g\left( {{{\textit{z}}^l}} \right) $ | (21) |
在优化Spiking YOLOv3模型中, 我们采用了量化步长[18]的方法. 优化后的模型为Spiking YOLOv3-FC. 将ANN中的ReLU激活函数替换为带偏移项和量化步长
| $ {a^l} = g\left( {{{\textit{z}}^l}} \right) = {\lambda ^l}clip\left( {\frac{1}{L}\left\lfloor {\frac{{{{\textit{z}}^l}L}}{{{\lambda ^l}}} + \frac{1}{2}} \right\rfloor , 0, 1} \right) $ | (22) |
在式(22)中, 超参数
当ANN中的
对于用量化步长函数的训练过程, 对该函数的导数使用直通估计器[19], 即式(23), 使用式(24)、式(25)的总体推导规则后可以用随机梯度下降算法来训练Spiking YOLOv3-FC模型.
| $ \frac{{{\mathrm{d}}\left\lfloor x \right\rfloor }}{{{\mathrm{d}}x}} = 1 $ | (23) |
| $ \frac{{\partial \hat {{g_i}}\left( {{{\textit{z}}^l}} \right)}}{{\partial {\textit{z}}_i^l}} = \left\{ \begin{gathered} 1,\quad - \frac{{{\lambda ^l}}}{{2L}} < {\textit{z}}_i^l < {\lambda ^l} - \frac{{{\lambda ^l}}}{{2L}} \\ 0,\quad{\text{ else}} \\ \end{gathered} \right.{\text{ }} $ | (24) |
| $ \frac{{\partial \hat {{g_i}}\left( {{{\textit{z}}^l}} \right)}}{{\partial {\lambda ^l}}} = \left\{ \begin{gathered} \frac{1}{{2L}},\qquad\;\;\; - \frac{{{\lambda ^l}}}{{2L}} < {\textit{z}}_i^l < {\lambda ^l} - \frac{{{\lambda ^l}}}{{2L}} \\ - \frac{{{\textit{z}}_i^l}}{{{{\left( {{\lambda ^l}} \right)}^2}}},\quad{\text{ else}} \\ \end{gathered} \right. $ | (25) |
本文使用了3个公开且不同规模的目标检测数据集UAV, PASCAL VOC, MS COCO. 其中, UAV是一个无人机数据集, 总共有1000多张无人机图片, 包含多个场景下的无人机. PASCAL VOC是PASCAL VOC挑战赛的数据集, 是一个中等规模的数据集, 共有20个类别. MS COCO共有330万张图片, 有80个目标类别. 我们将数据集的图像的分辨率统一缩放成416×416, 并对数据集使用了输入图像使用随机剪切框 (cutout)和图片拼接(mosaic)来进行数据增强.
在训练前, 对3个数据集用K-means聚类算法得到6个先验框中心, 3个数据集的先验框中心如表2所示.
| 表 2 3个数据集的先验框中心 |
本文所有的实验均在Python 3.7环境下, 基于PyTorch的深度学习框架上进行编码, 使用NVIDIA GPU进行训练和推理. 本文将所提出的Spiking YOLOv3网络和进一步优化的Spiking YOLOv3-CF网络与Kim提出的Spiking YOLO网络模型分别在PASCAL VOC, MS COCO上作了对比, Spiking YOLOv3网络模型和Spiking YOLOv3-CF网络模型在UAV数据集上做了对比. 训练时UAV, PASCAL VOC, MS COCO数据集的量化步长
本文提出的Spiking YOLOv3模型和Spiking YOLOv3-CF模型与Spiking YOLO分别在PASCAL VOC和MS COCO数据集上进行了对比实验. 表3为PASCAL VOC数据集上的实验结果, 表4为MS COCO数据集上的结果. 表3和表4中Spiking YOLO[10], Spiking YOLOv3, Spiking YOLOv3-CF网络模型分别简写为SY, SY3, SY3-CF.
| 表 3 3类SNN模型在PASCAL VOC数据集上基于不同步长(T)的全类平均精度(mAP)对比 (%) |
| 表 4 3类SNN模型在MS COCO数据集上基于不同步长(T)的全类平均精度(mAP)对比 (%) |
Spiking YOLO, Spiking YOLOv3, Spiking YOLOv3-CF模型的原ANN模型(转换之前的深度学习模型)在PASCAL VOC数据上精度分别为51.83%, 56.50%, 56.70%, 在MS COCO数据集的精度分别为26.24%, 38.70%, 38.78%. 当时间步长为2048时, Spiking YOLOv3-CF模型在VOC数据集上实现原ANN模型的精度, 在COCO数据集上实现的精度有略微的下降.
在精度方面, 在时间步长为2048时, Spiking YOLOv3和Spiking YOLOv3-CF网络模型在PASCAL VOC数据集上可以实现55.48%和56.73%的精度, 两个模型实现精度比Spiking YOLO模型分别提升了5.5%, 6.75%. 在MS COCO数据集上可以实现33.50%和37.85%的精度, 两个模型实现精度比Spiking YOLO模型分别提升了9.4%, 13.75%.
在推理时延方面, 本文所提出的SNN模在短时间步长上具有显著的优势. 尤其是Spiking YOLOv3-FC模型, 在短时间步长内就能达到较高精度. 在PASCAL VOC数据集上, 当Spiking YOLOv3-FC模型实现精度为48.25%时, 所需时间步长为128. 相比之下, Spiking YOLOv3模型实现该精度所需时间步长约为300, Spiking YOLO模型需要约1500个时间步长. 在COCO数据集上, 当Spiking YOLOv3-FC模型实现精度为20.59%时, 所需时间步长为128. 相比之下, Spiking YOLOv3模型实现该精度所需时间步长约为200, Spiking YOLO[10]模型需要约500个时间步长.
在精度转换误差方面, 在PASCAL VOC数据集上, 当时间步长为 1024 时, Spiking YOLOv3-FC模型实现了无损转换. 在COCO数据集上, 当时间步长T为2048, Spiking YOLO, Spiking YOLOv3两个模型的精度转换误差为2.14%, 7.2%, 而Spiking YOLOv3-FC模型的精度转换误差减小至0.93%.
Spiking YOLOv3, Spiking YOLOv3-CF模型在原ANN上该数据集的精度分别为99.10%, 99.12%, 当时间步长为2048时, Spiking YOLOv3-FC模型实现精度比原ANN实现的精度要高.
表5为本文所提出的两个SNN模型在UAV小目标检测数据集上的结果, Spiking YOLOv3-FC模型相比于Spiking YOLOv3模型精度提升了1.05%. 优化后模型在达到相同精度情况下, 约只需优化前1/2的时间步长, 加速了推理过程.
| 表 5 两类SNN模型在UAV数据集上基于不同步长(T)的全类平均精度(mAP)对比 (%) |
图7是不同SNN模型在PASCAL VOC数据集不同时间步长上可视化的对比, 可以看出Spiking YOLOv3-FC模型有在短时间内准确检测多个目标的优势, 而Spiking YOLO在时间步长较小时, 有漏检的情况, 需要比较长的时间步长才能检测多个目标, 这并不利于目标检测的实际应用. 我们所提出的Spiking YOLOv3-FC模型能在低时延情况下实现高效的目标检测, 同时也对部署在神经形态的硬件上友好.

|
图 7 3类SNN模型在PASCAL VOC数据集上基于不同步长的可视化对比 |
我们记录了时间步长为256时, Spiking YOLOv3和Spiking YOLOv3-FC模型在VOC数据集上, 网络的脉冲发射频率的结果, 如图8所示. 可以看出, Spiking YOLOv3和Spiking YOLOv3-FC模型的脉冲发射频率在区间[0.00918, 0.04602]和区间[0.00589, 0.03341]之间变化, 且Spiking YOLOv3-FC模型的脉冲发射频率整体要小于Spiking YOLOv3模型. 这表明本文所提出的两个网络模型的稀疏性, 并且Spiking YOLOv3-FC在提高准确率的基础上, 比Spiking YOLOv3模型具有更少的脉冲数量, 其功耗更低, 所需的时延也更低.
此外, 本文还计算了Spiking YOLOv3-FC模型的能量效率, 在ANN中, 每个运算计算一个点积, 包括一个乘法和一个加法. 然而, 在SNN中, 因其计算是事件驱动的, 在脉冲发射时计算, 在没有脉冲发射的情况下不会发生计算, 每个运算仅包含一次加法, 大大降低了计算开销. 对于32位的浮点运算, 其中乘加运算的消耗为4.6 pJ, 而积分累加运算消耗仅为0.9 pJ. 对于32位的整数运算, 其中乘加运算的消耗为3.2 pJ, 而积分累加运算的消耗仅为0.1 pJ[20]. 根据Rathi等人[21]提出的计算方法, 本文所提出的Spiking YOLOv3-FC检测模型的所需的能耗仅为原ANN的33.50%. 相比于深度学习模型, SNN在实现相同精度的情况下所需的能耗大大减少, 能更好地部署在硬件, 实现嵌入式系统.
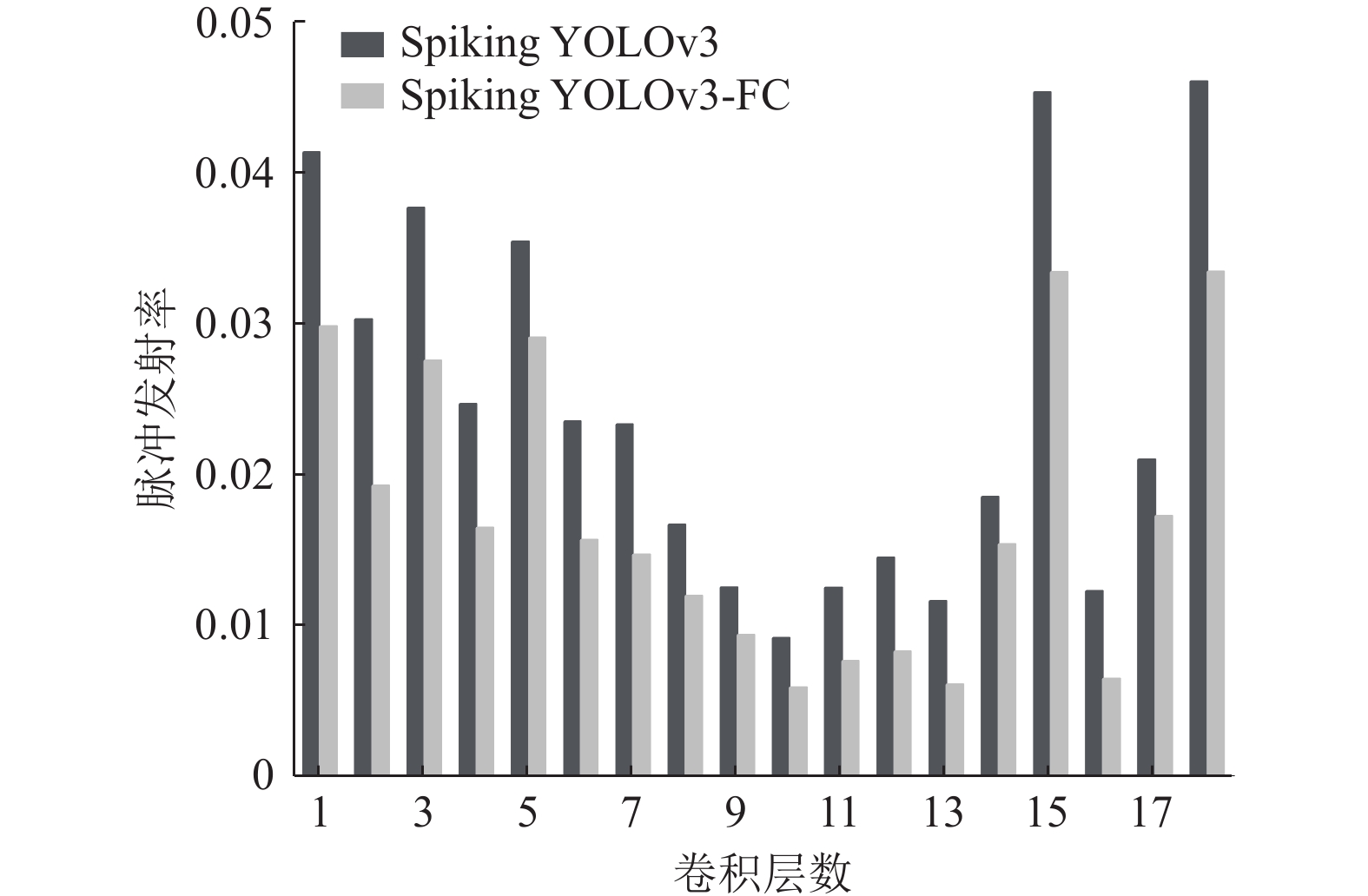
|
图 8 两类SNN模型卷积层脉冲发射率对比 |
4 结论与展望
本文首先提出了一种对ANN-SNN转换友好且完整的转换架构—Spiking YOLOv3网络模型, 并分析了ANN-SNN转换过程中产生的误差, 用量化步长的方法优化Spiking YOLOv3网络模型, 进一步提出了能减少转换误差, 且在低时延情况下实现高精度的Spiking YOLOv3-FC网络模型. 本文实验从精度, 时间步长, 转换误差, 能耗4个方面对比了不同的SNN模型的性能. 实验表明, 本文提出的两个网络模型在精度与推理时延上相较于之前的工作Spiking YOLO模型, 得到提升, 在相同精度下所需的时间步长更少. 特别是Spiking YOLOv3-FC网络模型, 实现了低时延高精度的目标检测任务; 在精度转换误差方面, Spiking YOLOv3-FC检测模型在VOC与UAV两个数据集上实现了无损转换, 在COCO数据集上将精度转换误差降低到0.93%; 在能耗方面, Spiking YOLOv3-FC检测模型相较于深度学习模型, 所需的能耗仅为原来ANN的33.50%, 这对将复杂任务部署在神经形态硬件上具有友好性. 在大型目标检测数据集, 当前模型仍不可能做到完全无损的ANN-SNN转换, 后续工作将着力解决在转化过程中产生的不均匀误差问题, 进一步增强Spiking YOLOv3-FC模型的部署效能.
| [1] |
Xu K, Ba JL, Kiros R, et al. Show, attend and tell: Neural image caption generation with visual attention. Proceedings of the 32nd International Conference on International Conference on Machine Learning. Lille: JMLR.org, 2015. 2048–2057.
|
| [2] |
Hariharan B, Arbeláez P, Girshick R, et al. Simultaneous detection and segmentation. Proceedings of the 13th European Conference on Computer Vision. Zurich: Springer, 2014. 297–312.
|
| [3] |
Maass W. Networks of spiking neurons: The third generation of neural network models. Neural Networks, 1997, 10(9): 1659-1671. DOI:10.1016/S0893-6080(97)00011-7 |
| [4] |
Wu YJ, Deng L, Li GQ, et al. Spatio-temporal backpropagation for training high-performance spiking neural networks. Frontiers in Neuroscience, 2018, 12: 331. DOI:10.3389/fnins.2018.00331 |
| [5] |
Lee JH, Delbruck T, Pfeiffer M. Training deep spiking neural networks using backpropagation. Frontiers in Neuroscience, 2016, 10: 508. |
| [6] |
Jin YYZ, Zhang WR, Li P. Hybrid macro/micro level backpropagation for training deep spiking neural networks. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 7005–7015.
|
| [7] |
Sengupta A, Ye YT, Wang R, et al. Going deeper in spiking neural networks: VGG and residual architectures. Frontiers in Neuroscience, 2019, 13: 95. DOI:10.3389/fnins.2019.00095 |
| [8] |
Han B, Srinivasan G, Roy K. RMP-SNN: Residual membrane potential neuron for enabling deeper high-accuracy and low-latency spiking neural network. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 13555–13564.
|
| [9] |
Deng SK, Gu S. Optimal conversion of conventional artificial neural networks to spiking neural networks. Proceedings of the 9th International Conference on Learning Representations. ICLR, 2021.
|
| [10] |
Kim S, Park S, Na B, et al. Spiking-YOLO: Spiking neural network for energy-efficient object detection. Proceedings of the 34th AAAI Conference on Artificial Intelligence. New York: AAAI, 2020. 11270–11277.
|
| [11] |
Cao YQ, Chen Y, Khosla D. Spiking deep convolutional neural networks for energy-efficient object recognition. International Journal of Computer Vision, 2015, 113(1): 54-66. DOI:10.1007/s11263-014-0788-3 |
| [12] |
Diehl PU, Neil D, Binas J, et al. Fast-classifying, high-accuracy spiking deep networks through weight and threshold balancing. Proceedings of the 2015 International Joint Conference on Neural Networks. Killarney: IEEE, 2015. 1–8.
|
| [13] |
Rueckauer B, Lungu IA, Hu YH, et al. Theory and tools for the conversion of analog to spiking convolutional neural networks. arXiv:1612.04052, 2016.
|
| [14] |
Ho ND, Chang IJ. TCL: An ANN-to-SNN conversion with trainable clipping layers. Proceedings of the 58th ACM/IEEE Design Automation Conference. San Francisco: IEEE, 2021. 793–798.
|
| [15] |
Li YH, Deng SK, Dong X, et al. A free lunch from ANN: Towards efficient, accurate spiking neural networks calibration. Proceedings of the 38th International Conference on Machine Learning. ICML, 2021. 6316–6325.
|
| [16] |
Kim S, Park S, Na B, et al. Towards fast and accurate object detection in bio-inspired spiking neural networks through Bayesian optimization. IEEE Access, 2021, 9: 2633-2643. DOI:10.1109/ACCESS.2020.3047071 |
| [17] |
Na B, Mok J, Park S, et al. AutoSNN: Towards energy-efficient spiking neural networks. Proceedings of the 39th International Conference on Machine Learning. Baltimore: ICML, 2022. 16253–16269.
|
| [18] |
Bu T, Fang W, Ding JH, et al. Optimal ANN-SNN conversion for high-accuracy and ultra-low-latency spiking neural networks. Proceedings of the 10th International Conference on Learning Representations. ICLR, 2022.
|
| [19] |
Bengio Y, Léonard N, Courville A. Estimating or propagating gradients through stochastic neurons for conditional computation. arXiv:1308.3432, 2013.
|
| [20] |
Horowitz M. 1.1 Computing’s energy problem (and what we can do about it). Proceedings of the 2014 IEEE International Solid-State Circuits Conference Digest of Technical Papers. San Francisco: IEEE, 2014. 10–14.
|
| [21] |
Rathi N, Roy K. DIET-SNN: Direct input encoding with leakage and threshold optimization in deep spiking neural networks. arXiv:2008.03658, 2020.
|
 2024, Vol. 33
2024, Vol. 33


