风电的发展对于减少碳排放、改善环境污染、促进可持续发展都具有重要的意义. 风电时间序列指风电机组运行过程相关的气象因素和机组产生的各项参数, 如风速、气压、风电叶片转速、风电输出功率、扇叶角度等. 随着风电装机容量占比的不断提高, 风电并网稳定性问题日益突出, 准确的风电时间序列预测成为保证电力系统稳定调度和安全运行的必要手段^[1]. 时间序列预测(time series forecasting, TSF)是实现准确风电机组相关参数预测的主要手段之一, 它基于历史观测的时间序列数据, 生成未来的预测数据, 可以满足电力系统稳定调度的需求.

时间序列预测模型的研究可分为物理方法^[2]、统计方法^[3]和深度学习方法^[4]. 其中, 物理方法需要大量前置假设, 依赖于风电场周边的气压、气温等环境因素, 并结合数值天气预报结果来预测风速, 需要大量物理量测算成本高昂, 因此难以进行规模化应用和推广, 仅适合冷启动. 机器学习方法和深度学习方法则主要应用于已建设的风电场的功率预测. 常见的机器学习方法有ARIMA^[5]、支持向量回归^[6]、随机森林^[7]等, 这些算法继物理方法后在时间序列预测中被广泛应用, 能够取得良好的预测精度. 近年来, 随着风电场站大规模建设相关数据激增, 为克服处理大规模数据和复杂非线性关系造成的瓶颈, 深度学习方法开始应用在风电场站的相关时间序列预测, 进一步提高了预测精度. 如考虑特征重组与改进Transformer的风电功率短期日前预测方法^[4]等. 这些Transformer方法可以在处理大规模数据时更好地挖掘数据中的非线性关系, 提高预测的准确性和稳定性. 但是由于风速时间序列复杂的非线性演化模式, 以往的Transformer前馈层在将不同通道进行混合时, 由于直接对特征进行通道混合无法捕捉单一通道的特征分布, 忽略了风电时间序列各变量之间的动态耦合关系, 导致模型的预测性能下降, 这种现象被称之为通道漂移^[8]. 而且就风电时间序列本身特性而言, 因为风速的强波动性影响, 风电时间序列可能随着时间推移迅速产生复杂的变化, 直接对序列进行建模会导致模型不能很好地建模这种复杂变化, 进而不能精细化预测结果.

为了改进现有深度学习模型的上述不足, 本文提出一种基于序列分解和注意力机制的风电功率预测方法(progressive decomposition Transformer, PDformer), PDformer不直接对序列进行建模, 而是应用渐进式分解的策略和Transformer捕捉时间序列的全局趋势和周期信息, 并且创新性地设计了多变量融合捕捉模块, 构建了一种新型的Transformer网络, 该模型能更好地捕捉风电时间序列内部各协变量的动态耦合关系. 其主要创新点如下.

1) 针对风电时间序列中错综复杂的序列依赖关系, 设计了多变量融合捕捉模块(multivariate fusion capture, MFC), 深度挖掘时间序列协变量之间的耦合关系, 解决了现有模型受通道漂移影响导致的预测能力下降的问题.

2) 提出了PDformer模型, 针对风电时间序列波动性产生的不稳定序列, 应用渐进式分解架构, 解决了以往模型难以建模强波动序列的问题.

在4个真实数据集上的对比实验结果表明, PDformer具有比基线模型更高的整体预测准确度, 相比于同类模型拥有更高的效率.

1 相关工作 1.1 时间序列分解

风电时间序列由于受风力不稳定和强波动性的影响, 直接对序列建模难以处理其复杂的非线性关系, 变量间依赖关系会被纠缠的时间模式所掩盖. 为了从错综复杂的时间模式中推理出依赖关系, 本研究使用时间序列分解技术分离序列中的元素. 目前, 已涌现出众多与序列分解相关的技术, 如经验模态分解(empirical mode decomposition, EMD)^[9], 王涛等人使用改进的EMD方法将复杂的非线性时间序列分解为一组固有模态函数, 结合支持向量机来预测风电功率, 以提高模型的预测精度和稳定性^[10]. 变分模态分解(variational mode decomposition, VMD)和奇异谱分解(singular spectrum analysis, SSA)也是常用的风电特征提取方法. 这些方法可以将时间序列分解成一系列基函数, 从而提取序列中的重要特征. 例如, Lu等人使用VMD方法对风电序列进行自适应时间尺度特征提取^[11]. Shao等人使用SSA方法提取时间序列的周期性特征, 并结合卷积神经网络(CNN)进行风电功率预测^[12]. 但是以上方法都存在一定缺点, 使用EMD进行序列分解的方法存在过拟合、噪声干扰等问题; VMD和SSA方法需要人工提取时间信息, 增加了模型对数据处理的依赖性. 这些预处理方法受到历史序列简单分解效应的限制, 忽视了时间序列底层模式之间的层次相互作用. Autoformer^[13]将分解作为深度模型的内部块, 在整个预测过程中逐步分解序列. 受Autoformer启发, 本研究使用神经网络中的池化操作, 使用一个平均池化网络, 利用渐进的分解方式去分解时间序列, 将简单的分解操作堆叠达到更好的效果, 针对风电时间序列过于复杂的特点, 将其分解为多个简单的时间序列, 对简单序列进行建模剥离纠缠时间序列内隐含的依赖关系.

1.2 时间序列预测深度学习方法

深度学习模型在风电时间序列预测中的应用已成为当前研究的热点之一. 深度学习模型如LSTM^[14]可以从海量数据中学习到风电时间序列数据的关键特征^[15]. 例如, 基于Bi-LSTM的深度级联残差模型^[16]可以获得可靠的点预测和区间预测结果; 另外, 目前已有多项研究利用注意力机制提高了风电时间序列预测的精度. 例如, 苏向敬等人在LSTM模型的基础上引入了特征空间和时序双重注意力机制, 以提高可解释性和预测性能^[17]. 而Liang等人则构建了基于注意力机制的时序卷积网络(TCN), 用于风电功率的超短期点预测和区间预测^[18]. 此外, 还有文献提出了采用改进自注意力机制的TCN结构并结合1D-CNN取得了较好的预测效果^[19].

针对长时间的时序信息与依赖关系难以捕捉的问题, Qin等人提出了基于两阶段注意力机制的循环神经网络多变量预测算法DA-RNN^[20], 自适应地选择相关的输入特征表示, 有利于捕捉长时间的时序信息与依赖关系. Huang等人提出了一种双重自注意力网络(DSA-Net)^[21], 通过自注意力机制可适用于动态周期或非周期序列的预测. 随着对注意力机制研究的深入Transformer^[22]也被引入时间序列预测领域, 来捕捉时间序列预测中的长期依赖关系. Transformer展示了很有前景的结果, 例如使用稀疏注意力机制的Informer模型^[23]、使用渐进式分解和自动关联机制的Autoformer模型^[13]均取得了较好的结果, 但是Transformer中前馈网络在挖掘风电时间序列中错综复杂的模式时极易受到通道漂移的影响, 模型的效果因此受到影响.

2 数据填充方法与模型构造

本节将介绍风电数据填充方法、PDformer整体结构设计, 频率增强模块和多变量融合捕捉模块的结构.

2.1 风电数据填充方法

风电机组数据在采集过程中不可避免地会出现数据丢失和异常的情况. 缺失值会扰乱预测模型对数据内信息特征的提取, 因此, 需要对原始采集数据中的缺失值进行处理, 以提高数据质量. 本文选择三次样条插值方法^[24]来填充缺失值, 三次样条插值(cubic spline interpolation)简称Spline插值, 该方法假设原始样本点在高维空间内呈一条光滑曲线, 然后在数学上通过求解方程组得出曲线函数填补缺失点. 定义输入时间序列${\mathcal{X}^t} = \{ {\mathbf{x}}_1^t, \cdots , {\mathbf{x}}_{{L_x}}^t|{\mathbf{x}}_i^t \in {\mathbb{R}^{{d_x}}}\} $和输出时间序列${\mathcal{Y}^t} = \{ {\mathbf{y}}_1^t, \cdots , {\mathbf{y}}_{L_y}^t|{\mathbf{y}}_i^t \in {\mathbb{R}^{{d_y}}}\} $, ${\mathcal{X}^t}$和${\mathcal{Y}^t}$之间的函数关系为${\mathcal{Y}^t} = f({\mathcal{X}^t})$. 采样的曲线是区间${\mathbf{x}} \in [{\mathbf{x}}_i^t, {\mathbf{x}}_i^{t + 1}]$中的三次多项式函数, 其三次多项式可以表示为:

$ f_{i}(x)=a_{i}\left(x-x_{i}\right)^{3}+b_{i}\left(x-x_{i}\right)^{2}+c_{i}\left(x-x_{i}\right)+d_{i} $

(1)

风电数据处理前后对比如图1所示, 图1(a)为未经过处理的图, 图1(b)为经过三次样条插值后的图, 由椭圆形圈出的缺失点前后对比, 可看出经过填补后缺失点数据变得连续, 曲线整体过度平稳.

由于风电时间序列各变量数量级不同, 直接输入模型进行训练会出现模型收敛慢, 网络训练不稳定的问题. 为加速模型训练和提升预测效果, 本研究采用z-score标准化对数据进行处理, 控制训练期间不同物理量梯度满足标准正态分布. z-score标准化是一种常用的数据标准化方法, 用于将样本数据转换为服从标准正态分布. 其公式可表示为:

$ \hat{x}_{i}=\frac{x_{i}-\mu}{\sqrt{\sigma^{2}}} $

(2)

$ \mu=\frac{1}{m} \sum_{i=1}^{m} x_{i} $

(3)

$ \sigma^{2}=\frac{1}{m} \sum_{i=1}^{m}\left(x_{i}-\mu\right)^{2} $

(4)

其中, $ {x_i} $为样本的特征, m为数据集大小, $ \mu $为数据集平均值, $ \sigma _{}^2 $为数据集平方差.

2.2 PDformer模型结构

本文PDformer模型整体结构如图2所示. 该模型基于编码器、解码器结构. 编码器和解码器由频率增强模块、分解模块、多变量融合捕捉模块堆叠构成. 模型采用与Informer^[23]相同的一步生成方法.

编码器: 如图2所示, 编码器对时间序列的周期项部分进行建模, 旨在提取长连续输入的远距离依赖性. 输入在经过嵌入表示之后, 第t个序列输入$\mathcal{X}_{_{}}^t$已被嵌入为矩阵$\mathcal{X}_{_{{\mathrm{en}}}}^t \in {\mathbb{R}^{{L_x} \times {d_{{\text{model}}}}}}$. 嵌入表示输入编码器后先经过频率增强, 然后进行周期和趋势项分解, 最后经过一个多变量融合捕捉模块. 编码器可以堆叠N层, 编码器的输出包含过去的周期信息, 编码器输出将会输入到解码器的交叉注意力层来帮助解码器精细化预测结果. 编码器用式(5)表示, 第$ l $个编码器层的公式可总结为:

$ \left\{\begin{aligned} & \mathcal{X}_{{\mathrm{en}}}^l={Encoder}\left(\mathcal{X}_{{\mathrm{en}}}^{l-1}\right) \\ & \mathcal{S}_{{\mathrm{en}}}^{l, 1}, _-={MOEDecomp}\left({\textit{FEB}}\left(\mathcal{X}_{{\mathrm{en}}}^{l-1}\right)+\mathcal{X}_{{\mathrm{en}}}^{l-1}\right) \\ & \mathcal{S}_{{\mathrm{en}}}^{l, 2}, _-={MFC}\left(\mathcal{S}_{{\mathrm{en}}}^{l, 1}\right)+\mathcal{S}_{{\mathrm{en}}}^{l, 1} \end{aligned} \right.$

(5)

其中, MOEDecomp表示分解模块; FEB表示频率增强块; MFC表示多变量融合捕捉模块. “_”为被剔除的趋势部分$ \mathcal{X}_{{\text{en}}}^l = \mathcal{S}_{{\text{en}}}^{l, 2}, l \in \{ 1, \cdots \, , N\} $表示第$ l $个编码器层的输出, $ \mathcal{X}_{{\text{en}}}^0 $是嵌入的$ \mathcal{X}_{{\text{en}}}^{} $分别表示第$ l $层中第i个分解块或多变量融合捕捉模块之后的周期分量. 本文将在第2.3节详细描述多变量融合捕捉模块, 它可以提高模型整体挖掘能力. MOEDecomp是一个池化分解结构, 采用的是平均池化方法, FEB为频率增强块后文有详细介绍.

解码器: 解码器利用频率增强块和编码器-解码器交叉注意力块, 分别捕捉并利用现在和过去的周期信息. 在周期信息的捕捉中交替利用分解模块将原始输入分解. 每个分解模块分解出的潜在趋势与解码器输出进行累加, 使PDformer能逐步细化趋势的预测. 解码器如编码器一般, 也可堆叠若干层. 假设有M个解码器层, 利用来自编码器的潜在变量$\mathcal{X}_{{\text{en}}}^N$和序列的部分输入$\mathcal{X}_{{\text{de}}}^0$, 解码器的公式表示如下:

$ \left\{\begin{split} & {\mathcal{S}_{{\mathrm{de}}}^{l, 1}, \mathcal{T}_{{\mathrm{de}}}^{l, 1} = MOEDecomp\left( {{\textit{FEB}}\left( {\mathcal{X}_{{\mathrm{de}}}^{l - 1}} \right) + \mathcal{X}_{{\mathrm{de}}}^{l - 1}} \right) } \\ & {\mathcal{S}_{{\mathrm{de}}}^{l, 2}, \mathcal{T}_{{\mathrm{de}}}^{l, 2} = MOEDecomp\left( {MA\left( {\mathcal{S}_{{\mathrm{de}}}^{l, 1}, \mathcal{X}_{{\mathrm{en}}}^N} \right) + \mathcal{S}_{{\mathrm{de}}}^{l, 1}} \right) } \\ & {\mathcal{S}_{{\mathrm{de}}}^{l, 3} = MFC\left( {\mathcal{S}_{{\mathrm{de}}}^{l, 2}} \right) + \mathcal{S}_{{\mathrm{de}}}^{l, 2} } \\ & {\mathcal{X}_{{\mathrm{de}}}^l = \mathcal{S}_{{\mathrm{de}}}^{l, 3} } \\ & {\mathcal{T}_{{\mathrm{de}}}^l = \mathcal{T}_{{\mathrm{de}}}^{l - 1} + {\mathcal{W}_{l, 1}} \cdot \mathcal{T}_{{\mathrm{de}}}^{l, 1} + {\mathcal{W}_{l, 2}} \cdot \mathcal{T}_{{\mathrm{de}}}^{l, 2} } \end{split} \right.$

(6)

其中, $\mathcal{X}_{{\text{de}}}^{l - 1}$表示前一个解码器堆栈的输出, 当$l = 0$时, 表示原始编码器初值; MA表示多头注意力计算.

2.3 频率增强模块

如图2所示编码器和解码器均采用了频率增强模块捕捉时间序列中隐藏的周期信息. 图3展示了频率增强块的构造细节, 首先对频率增强块的输入($x \in {\mathbb{R}^{N \times D}}$)应用一个线性层进行投影($w \in {\mathbb{R}^{D \times D}}$)增加其表示能力, 然后对输入应用离散傅里叶变换将输入由时域转换到频域. 下采样操作中, 由于风电时间序列采集过程中受风力不稳和扇叶变相等因素产生了一些噪声, 本文在频域中去除一些高频噪声的同时从其余分量中随机挑选M个分量, 这M个分量为代表性的频域信号. R ($R \in {\mathbb{C}^{D \times D \times M}}$)是一个随机初始化的参数核, 用于增加原始频域空间的表现能力. 将R与下采样的特征图相乘, 然后对运算结果进行零填充, 使尺寸和原大小相同, 之后应用逆傅里叶变换将特征图转换回时域.

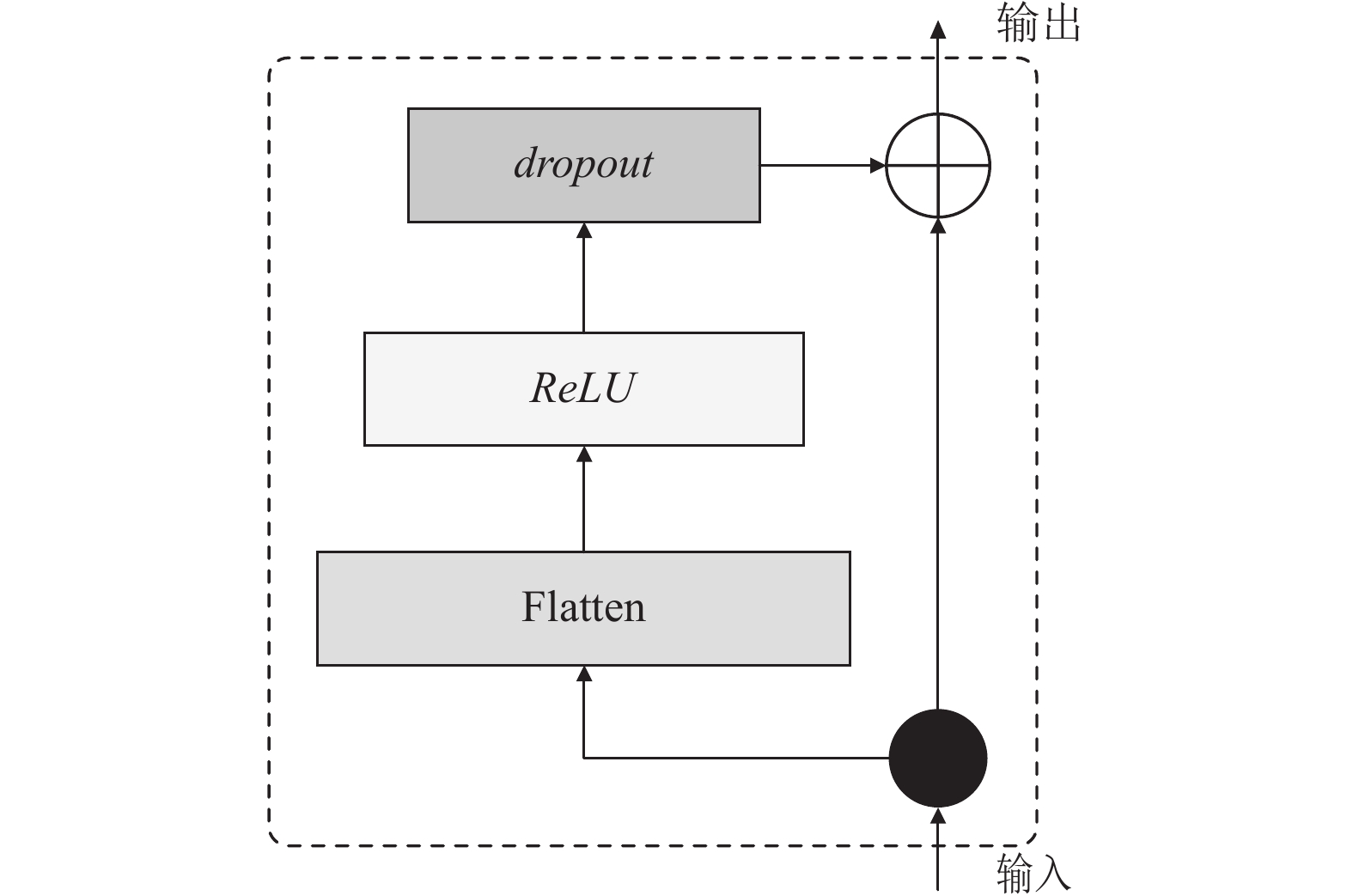
2.4 多变量融合捕捉模块

多变量融合捕捉模块在编码器和解码器中均有使用, 结构如图4所示, 多变量融合捕捉模块的输入$ (x \in {\mathbb{R}^{N \times D}}) $. 首先使用$ {w} \in \mathbb{R}^{H \times N} $进行线性投影, 因此${A^{[1]}} = w \cdot x$, ${A^{[1]}} \in {\mathbb{R}^{H \times D}}$. 然后对$ {A^{[1]}} $应用ReLU激活函数并随机屏蔽一些神经元防止过拟合. 再应用一个线性层$ \psi \in {\mathbb{R}^{N \times H}} $将维度映射回原向量空间内, 以便将网络堆叠多层. 多变量融合捕捉模块可用公式表示如下:

$ \left\{\begin{aligned} & A={ReLU}(w \cdot x) \\ & {MLP}({x})={dropout}[\psi({dropout}({A}))] \end{aligned} \right.$

(7)

其中, dropout表示随机屏蔽操作; $ { ReLU } $表示激活函数.

3 实验 3.1 实验数据集

为评估本文模型PDformer的效果, 在4个真实数据集上开展了实验, 数据集的基本信息如表1所示.

Wind154、Wind112、Wind170数据集收集自于某公司实际风电场站, 记录了3个地区风电场站的实际风电场站数据. 该数据集包含丰富的变量信息如机组功率、天气信息、扇叶转速、扇叶角度等.

Wind公开数据集(https://github.com/PaddlePaddle/PaddleSpatial/tree/main/paddlespatial/datasets/WindPower), 记录了从2020年1月到2021年7月, 以15 min的时间间隔记录风电场的发电量及其协变量数据.

基准算法: 本文主要选取了5个基准算法分别是: Informer、Autoformer、FEDformer、ARIMA、GRU.

● Informer^[23]: 一个基于Transformer的稀疏注意力模型, 它针对多变量时间序列应用了自注意力和交叉机制, 学习历史数据并利用一步生成的策略进行预测.

● ARIMA^[5]: 一种自回归积分滑动平均模型(auto-regressive integrated moving average model), 是一种简单的时间序列预测模型, 通过将非平稳序列转化为平稳序列然后对滞后值和带有随机误差的现值进行建模和回归的模型.

● Autoformer^[13]: 一个基于渐进式分解架构的模型, 它设计了渐进式分解结构和自相关机制, 实现了时间序列复杂的时间模式挖掘.

● FEDformer^[25]: 一个用于长期时间序列预测的频率增强Transformer模型, 设计了频率增强注意力和专家分解机制来控制分布转移.

● GRU^[26]: 一个基于循环神经网络的改进模型, 可以解决循环神经网络不能长期记忆和反向传播中的梯度问题.

评估指标: 本文选取了两种常用的评估指标来衡量模型预测性能, 分别是均方误差(mean squared error, MSE)和平均绝对误差(mean absolute error, MAE), 其计算公式如式(8)和式(9). 这两个指标表示预测值与真实值之间的误差, 因此指标越低代表模型效果越好.

$ {\textit{MSE}}=\frac{1}{n} \sum_{i=1}^n(y-\hat{y})^2 $

(8)

$ { MAE }=\frac{1}{n} \sum_{i=1}^n|y-\hat y| $

(9)

3.2 模型参数

本文实验设置训练和评估的输入长度固定为96, 预测长度分别固定为48、96、192、336, 实验平台为NVIDIA V100 16 GB, CUDA Version 11.6, 系统版本Ubuntu 18.04.6 LTS, GRU和Informer、Autoformer等深度学习模型超参数设置如表2所示. ARIMA模型参数如表3所示.

3.3 实验结果

MAE结果较为保守, MSE为平方误差更能反映风电时间序列预测的波动性. 为了更好地对比模型应对风电波动性的效果, 本文分析更侧重于MSE.

表4给出了Wind154、Wind112、Wind170和Wind数据集下不同算法的MSE和MAE. ARIMA和GRU等传统算法在所有数据集上均表现较差, 随着预测长度变长效果急剧下降, PDformer在4个基线数据集上与ARIMA相比, 336的预测长度下MSE指标平均提升约86%, 这是由于传统模型无法处理非平稳序列和中长期下风电时间序列各项变量间复杂的依赖关系.

PDformer相比Informer、Autoformer、FEDformer提升依旧明显, 在基准数据集上至高可提升60%的MSE指标, 平均提升可达18%. 值得注意的是, 虽然Autoformer、FEDformer也采用了渐进式分解的设计思想, 但是其传统前馈层的设计受到了通道漂移的影响, 混淆了部分变量间的依赖关系, 因此预测的误差高于PDformer. PDformer采用了多变量融合捕捉模块在建模多个变量复杂依赖的同时控制通道混合的次数, 由此获得了最优的性能表现. 以MSE为评价指标, 在全部基准数据集上PDformer在所有预测长度都取得了最好的效果, 这是因为PDformer的多变量融合捕捉模块具有强大的变量间关联挖掘能力. 随着预测长度的延长PDformer的相对优势会更加明显, 这证明了PDformer由于渐进式分解架构的存在, 可以成功对长期风电时间序列进行精准建模, 多变量融合捕捉模块在长距离条件下使得PDformer能更贴合风电时间序列的依赖挖掘需求.

MAE指标下, PDformer同样表现较好, 与所有模型相比PDformer至高可提升64%, 与次优结果相比提升最高可达16%. 这再次验证了PDformer在风电时间序列预测中的有效性, 证明了MFC模块增强了模型的多变量演化挖掘能力.

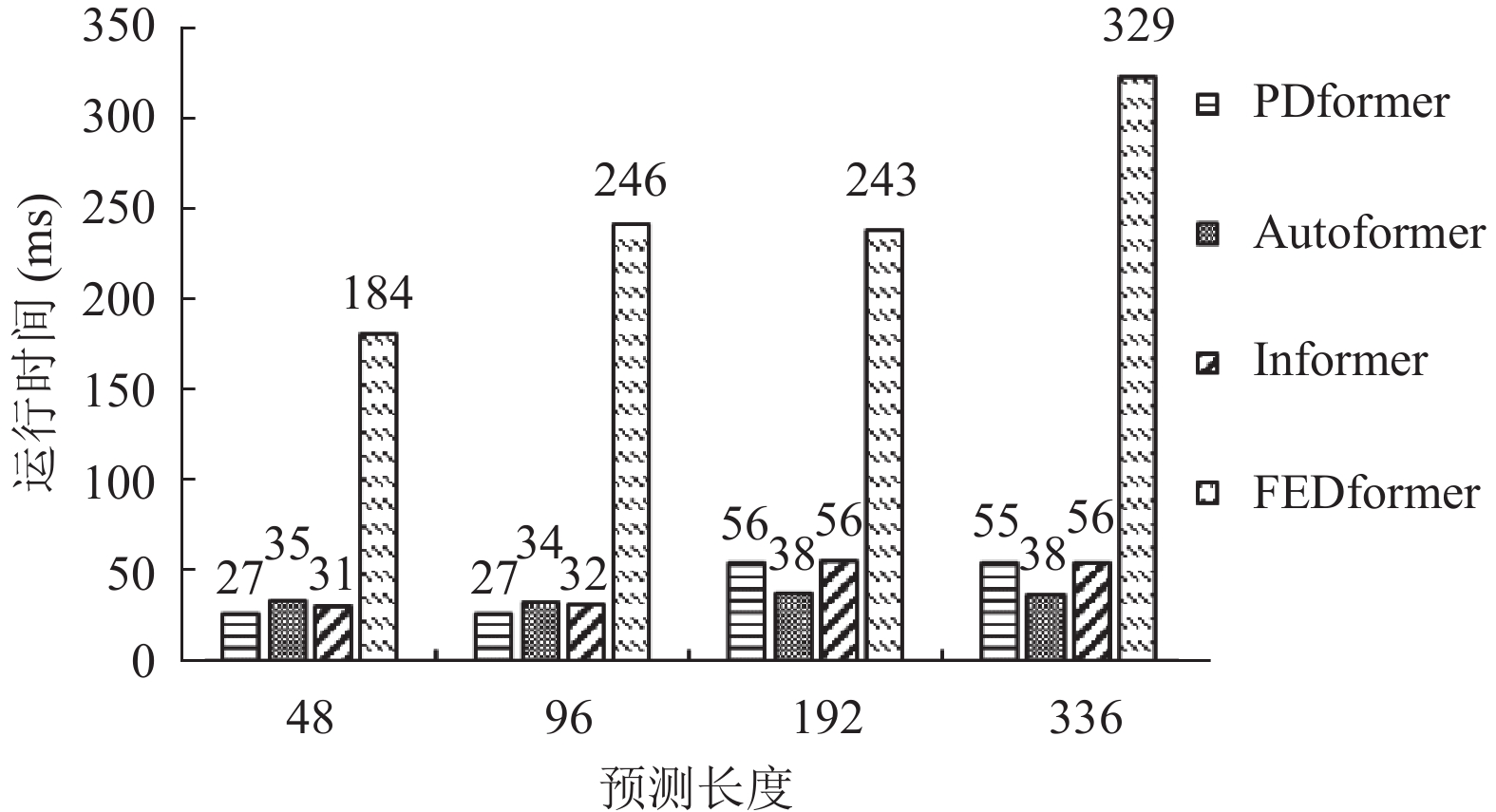
深度学习模型在4个数据集上的平均运行时间如图5所示. PDformer由于减少了堆叠层数和优化了频域采样方法, 与同样应用频域采样技术的FEDformer相比运行速度平均可提升83%, 并且短期预测长度下运行时间低于Autoformer模型. 全部预测长度下优于Informer模型. PDformer在中长期预测长度下, 由于傅里叶变换为平方时间复杂度, 速度会慢于Autoformer, 但是速度的降低换取了平均20%的MSE指标提升.

总体而言, PDformer的改进在不同的预测长度下表现是一致的, 因为MFC模块和渐进式分解架构赋予了模型挖掘复杂依赖的能力, 相对于其他模型没有因为风电的波动性产生预测效果的下降. 实验结果证明了其在风电时间序列预测中可平稳化强波动性的风电时间序列, 在多个预测尺度下均具有稳定的效率和准确率优势.

3.4 消融实验

为了证明MFC模块可以帮助模型更好地学习了当前通道值和历史值的潜在关系, 本节进行了消融实验, 将完整PDformer的结果作为基准和去除MFC模块的PDformer算法进行比较.

从表5可以看出, 在4个基准数据集上引入多变量融合捕捉模块后, 预测结果显著提升, 在Wind170长度为48的预测窗口下, 最高可以提升MSE约77%. 在不同长度的预测窗口下, 带有MFC的模型都达到了最小的MSE, 证明了多变量融合捕捉模块的有效性. 且长预测窗口相对短预测窗口提升更大, 这是因为MFC模块能够对输入数据进行较长跨度的考量和特征提取, 从而捕捉到通道值和历史值之间的复杂关联, 避免了随时间演进产生的通道依赖变化的风险, 进而提高了对风电时间序列数据的建模和预测能力.

4 结论与展望

本研究针对风电时间序列强波动性的特性, 设计了一种新的深度学习模型结构, 改进了现有算法面对风电时间序列多变量演化特性挖掘能力的不足. 本文提出的PDformer模型应用改进型渐进式分解结构, 分离原始序列趋势项和周期项, 使不平稳序列变成平稳序列进而可以更好地学习序列演化规律. 此外, 利用MFC模块替换捕捉到了当前通道值和历史值之间的复杂关联, 以及时间序列值的动态时序特征, 增强了现有模型的预测能力. 在4组风电数据集上进行的详尽实证研究表明, 基于渐进式分解架构的风电时间序列预测模型对于多变量演化特性的挖掘优于现有的时间序列预测算法. 实现了时间序列建模方法对风电时间序列波动性的针对性优化.

虽然在不同预测长度下PDformer均能达到最好效果, 但PDformer在超短期的预测窗口下较之长期相对提升变少, 超短期的预测表现和次优模型相差较小, 因此在超短期预测上仍有提升空间. 在未来的工作中, 会在本算法的基础上研究如何提升超短期预测的效果, 进一步优化风电时间序列的预测精度和模型泛化能力.