传统的网络服务需要专用硬件来提供, 并按特定顺序引导通过硬件的流量. 然而, 这些专用硬件设备不仅带来了高资本支出和运营支出, 而且管理困难^[1,2]. 为了解决以上问题, 研究人员提出了网络功能虚拟化(network function virtualization, NFV)^[1–3]这一新的网络架构概念, 通过将网络功能(例如防火墙, 网络地址转换和入侵检测系统)与专用硬件解耦, 转变为通用设备基于软件实现的虚拟网络功能(virtual network function, VNF)^[4], 从而实现网络服务的灵活和弹性管理. 到达网络的服务请求被转化为服务功能链(service function chain, SFC)^[5–7], 它由一组特定有序的VNF构成. 如图1所示是SFC示例. 利用NFV技术, 将SFC中的VNF部署到底层物理网络的服务器或虚拟机上, 以实现灵活高效的网络服务. VNF放置和链接(VNF placement and chaining, VNFPC)过程是指在NFV网络中的服务器上放置VNF并将它们按序链接起来引导流量, 来提供特定的服务^[4].

一般来说, 合理的VNFPC方案受到一些优化目标的约束, 例如延迟, 资源利用, 能耗, 运营成本和流量. 之前的研究已经在单目标做了大量工作, 推动NFV在学术界和工业界的发展^[6–8], 然而, NFV在多个目标优化进行有效的VNFPC需要考虑几个关键挑战. 特别是, 为了将SFC部署到异构网络功能, 服务提供商需要在不同的目标之间进行权衡, 例如最小化能耗和最大化服务接受率. 这些目标是相互冲突的, 因为在最小化能耗可能会激活更少的服务器, 从而用户服务可能由于资源或者网络延迟约束被拒绝. 同时, 最大化服务接受率可能需要花费更多资源, 优化服务接受率时可能会增加能耗. 为此, 本文重点讨论了如何在NFV网络权衡优化VNFPC问题的能耗和服务接受率.

图1展示了VNFPC场景, 各种网络服务如视频聊天, Web服务等网络请求被NFV编排成SFC, 其流量从入口节点经过不同VNF到达出口节点实现端到端的服务. 具体是将VNF映射到不同的物理节点上进行资源分配和优化, 进行流量引导和控制, 来提供高效的网络服务.

现有的大多数研究人员将VNFPC问题表述为整数线性规划(integer linear programming, ILP)^[9,10]模型进行最优化求解. 文献[9]面对功耗感知和延迟约束的联合VNF放置和路由(PD-VPR)问题提出一种Holu框架可以在线解决PD-VPR问题, 降低能耗同时提高了服务接受率. 在考虑了端到传输延迟和VNF亲和力约束时, 文献[10]是基于VNF链放置问题(VNF-CPP)提供了基于ILP在线解决方案, 并验证所提算法的有效性. 此外, 文献[11]将问题表述为混合整数规划(mixed integer linear programming, MILP)模型, 通过分解模型开发出一种两级算法实现SFC部署, 仿真结果表明该方法实现了接近最优的解决方案. 然而, 由于VNFPC是NP-Hard特性, 因此LP方法仅只能在小规模网络中进行优化, 当网络规模过大时间效率变得很低.

一些研究进一步提出了启发式算法来应对大规模用户服务请求, 并有效指导LP问题在有限的时间内求解. 文献[12]优化VNFPC的资源分配成本, 通过将问题表述为LP模型, 提出了基于背包问题的启发式方法高效解决问题, 并降低了SFC的平均成本. 在文献[13]中, 将部署问题建模为ILP优化, 并扩展到启发式算法用于估计瓶颈资源占用, 来实现接近最优的部署. 虽然启发式方法很高效, 但解的最优性无法保证, 而且容易陷入局部最优解, 甚至偏离全局最优解.

近年来, 深度强化学习(deep reinforcement learning, DRL)也被应用在VNFPC^[14,15]中寻找问题最优解决方案. 该方法不同于传统的方法求解容易陷入局部最优问题, DRL在解决组合优化问题具有前瞻性的解决方案. 文献[14]中考虑边缘网络资源受限且对于服务的延迟容忍性低的问题, 结合强化学习与时延提出一种面向时延优化的SFC的部署方法, 使得时延敏感类业务获得更好体验. 文献[15]的工作中, 为了在服务功能链放置(SFCP)问题中提出了基于DRL的多目标优化服务功能链放置(MOO-SFCP)算法, 具体是将SFCP建模为马尔可夫决策过程(Markov decision process, MDP), 并使用两层策略网络作为智能代理与环境交互进行学习. 上述方案学习模型明显提高求解问题的效率, 但其方案需要严格优化函数进行约束.

综合之前的研究, 在NFV中进行VNFPC面临以下问题. 首先是解决方案如线性规划或启发式算法很难准确高效地找到最优解决策略. 其次, 之前的研究大多是单个优化目标的约束, 很少研究涉及到多目标优化, 特别是, 优化目标之间存在冲突的. 综上所述, 本文提出一种新的算法ACDRL-VNFPC, 具体的贡献点如下.

(1) 首先, 将VNFPC问题化为一个优化问题, 它考虑了能耗, 服务接受率, 延迟和资源需求.

(2) 接着, 通过建立一个目标函数来联合考虑能耗和服务接受率, 旨在最大化服务接受率同时降低能耗.

(3) 然后, 为了获得优化问题的解决方案, 提出了基于Actor-Critic深度强化学习方法(ACDRL-VNFPC), 并在该方法中采用了一种适应性共享策略, 该策略不仅允许多个服务请求之间共享未充分使用的同类型VNF, 通过实例化更少的VNF减少服务器资源消耗; 而且允许服务器中的资源被不同类型的VNF共享, 这样激活了更少的服务器同时降低了能耗.

(4) 最后, 通过构建仿真环境与其他方法进行对比. 实验结果表明, 提出的算法可以获得问题的解, 并且可以权衡优化能耗和服务接受率, 同时执行时间方面也得到了优化.

1 系统模型和问题描述 1.1 物理网络模型

物理网络被建模为无向加权图$ {G_p} = ({N_p}, {E_p}) $, 其中$ {N_p} $和$ {E_p} $分别表示物理节点和物理通信链路的集合. 每个物理节点$ {v_i} $ (包括交换机和服务器), $ {v_i} \in {N_p} $具有有限的物理资源. 计算资源分别用$ R_{{v_i}}^p = (cpu_{{v_i}}^p, mem_{{v_i}}^p, str_{{v_i}}^p) $表示每个节点$ {v_i} $的可用的CPU, 内存和存储的资源. 物理的通信链路用$ {E_p} $来表示, 其中$ {e_{pq}} $表示在物理网络中两个物理节点$ {v_p} $和$ {v_q} $直接相连, 则链$ (p, q) \in {E_p} $ (即$ {e_{pq}} = (p, q) $), 否则$ (p, q) \notin {E_p} $. 对于每个物理链路$ {e_{pq}} \in {E_p} $, 用$ BW_{{e_{pq}}}^p $来表示链路$ {e_{pq}} $的可用带宽容量, 并且$ L_{{e_{pq}}}^p $代表了物理链路的传输时延. 最后用$ \Phi _{{v_i}}^{res} $代表节点资源单位成本, $ \Phi _{{e_{pq}}}^{bw} $来表示链路带宽的单位成本.

1.2 SFC请求模型

假设有$ m $个SFC请求, 每个SFC${\mathit{sfc}_i} $请求被建模为一个加权有向图${\mathit{sfc}_i} = (f_i^1, f_i^2, \cdots, f_i^j, \cdots, f_i^n) $, 其中$ f_i^j $表示在SFC $ \mathit{sfc}_i $中的第$ j $个VNF节点, 用$ E_i^v $表示VNF之间相连的虚拟链路集合. 分别用$ r_{f_i^j}^v = (r_{f_i^j}^{cpu}, r_{f_i^j}^{mem}, r_{f_i^j}^{str}) $表示VNF$ f_i^j $的CPU, 内存和存储的资源需求. 通过$ l_{f_i^j}^d $来表示VNF$ f_i^j $的处理时延. SFC$\mathit{sfc}_i$中的虚拟链路用$ l_i^{uv} $, $ l_i^{uv} \in E_i^v $表示两个VNF$ f_i^u $和$ f_i^v $之间的链路, 链路之间的带宽需求用$ bw_{l_i^{uv}}^v $来表示.

1.3 问题公式化

在NFV中进行VNFPC需要对能耗和服务接受率提出了更严格的要求. 因此, 本文需要权衡优化最小化能耗和最大化服务接受率. 针对VNFPC问题的研究目标是寻找一个最优策略$ {\pi ^*} $来最大化服务接受率和最小化能耗, 目标函数如下:

$ {\pi ^*} = \mathop {\arg }\limits_t \max\left\{ \psi \cdot Ac(t) + (1 - \psi ) \cdot \frac{1}{{{P_{{v_i}}}(t)}}\right\} $

(1)

其中, $ \psi $表示权重因子, 用于实现服务接受率/能耗的权衡优化. 例如$ \psi $越小, 越强调能耗优化, 反之是服务接受率.

服务接受率$ Ac(t) $: 为了满足用户服务质量要求, 服务提供商将成本消耗降至最低, 并尽可能多地部署SFC. 通过接受的SFC请求与所有SFC请求的比率来衡量请求接受率. 在时间$ t \;(0 \leqslant t \leqslant T) $服务接受率$ Ac({{t}}) $表示为:

$ Ac(t) = \frac{{\displaystyle\sum\limits_{t = 0}^T {\mathit{sfc}}_i^{\rm accept}}}{{\displaystyle\sum\limits_{t = 0}^T {\mathit{sfc}}_i^{\rm accept} + \displaystyle\sum\limits_{t = 0}^T {\mathit{sfc}}_i^{\rm refuse}}} $

(2)

其中, $ {\mathit{sfc}}_i^{\rm accept} $表示已经接受并成功部署的SFC请求数量, $ {\mathit{sfc}}_i^{\rm refuse} $表示由于资源或延迟被拒绝的SFC请求的数量.

能耗$ {P_{{v_i}}}(t) $: 能耗主要来源于服务器节点的能耗, 包括空闲状态和工作状态的能耗. 在时间$ t $服务器节点/机器的能耗与服务器的资源利用率相关^[8]. 因此, 在时间$ t $服务器$ {v_i} $的能耗$ {P_{{v_i}}}(t) $表示为:

$ {P_{{v_i}}}(t) = P_{{v_i}}^{\rm idle}(t) + (P_{{v_i}}^M(t) - P_{{v_i}}^{\rm idle}(t)) \times {U_{{v_i}}}(t) $

(3)

其中, $ P_{{v_i}}^{\rm idle}(t) $为服务器$ {v_i} $处于空闲状态时的能耗, $ P_{{v_i}}^M(t) $为当服务器满载时的最大能耗, $ {U_{{v_i}}}(t) \in [0, 1] $表示服务器的资源利用率.

上述目标函数需要遵循以下约束.

式(4)定义了决策变量$ x_{f_j^i}^{{v_i}} $, 当$ x_{f_j^i}^{{v_i}} = 1 $表示VNF$ f_i^j $部署到服务器节点$ {v_i} $, 否则未部署. 决策变量$ x_{f_j^i}^{{v_i}} $表示为:

$ x_{f_j^i}^{{v_i}} = \left\{ {\begin{array}{*{20}{l}} {1, }&{\text{if VNF}\;f_i^j\; \text{is deployed on} \;{v_i}} \\ {0, }&{\text{otherwise}} \end{array}} \right. $

(4)

式(5)约束是为确保每个VNF $ f_i^j $不可分割, 且仅部署一次.

$ \forall i, j\quad \sum\limits_{i = 1}^{|{N_p}|} {\sum\limits_{j = 1}^n {x_{{v_i}}^{f_i^j}} } \leqslant 1, \forall f_j^i \in {\mathit{sfc}_i}, {v_i} \in {N_p} $

(5)

当选择适当的服务器部署VNF时, VNF之间的虚拟链路也需要映射到适当的物理链路. 决策变量$ y_{{e_{pq}}}^{l_i^{uv}} $表示虚拟链路$ l_i^{uv} $与物理链路$ {e_{pq}} $的映射关系. 式(6)的决策变量$ y_{{e_{pq}}}^{l_i^{uv}} $表示为:

$ y_{{e_{pq}}}^{l_{{i}}^{{{uv}}}} = \left\{ {\begin{array}{*{20}{l}} {1, }&{\text{if}\; l_i^{uv}\;\text{is mapped in}\; {e_{pq}}} \\ {0, }&{\text{otherwise}} \end{array}} \right. $

(6)

式(7)为确保每个虚拟链路仅映射到唯一的物理链路上, 且仅映射一次.

$ \forall u, v, p, q\quad \sum\limits_{i = 1}^m {\sum\limits_{u, v}^n {y_{{e_{pq}}}^{l_i^{uv}}} } \leqslant 1, \forall l^{uv}_i \in {\mathit{sfc}_i}, {e_{pq}} \in {E_p} $

(7)

式(8)定义了物理节点计算资源容量的约束. 任何部署成功的VNF, 其所有的资源请求不超过物理节点的可用资源需求.

$\left\{\begin{array}{l} \forall i, j\quad\dfrac{{\displaystyle\sum\limits_{f_i^j \in {\mathit{sfc}_i}} {{\mkern 1mu} {\kern 1pt} } x_{f_i^j}^{{v_i}} \cdot r_{f_i^j}^{\mathit{cpu}}}}{{\mathit{cpu}_{{v_i}}^p}} \leqslant 1\\ \forall i, j\quad\dfrac{{\displaystyle\sum\limits_{f_i^j \in {\mathit{sfc}_i}} {{\mkern 1mu} {\kern 1pt} } x_{f_i^j}^{{v_i}} \cdot r_{f_i^j}^{mem}}}{{mem_{{v_i}}^p}} \leqslant 1\\ \forall i, j\quad\dfrac{{\displaystyle\sum\limits_{f_i^j \in {\mathit{sfc}_i}} {{\mkern 1mu} {\kern 1pt} } x_{f_i^j}^{{v_i}} \cdot r_{f_i^j}^{str}}}{{str_{{v_i}}^p}} \leqslant 1 \end{array} \right.$

(8)

式(9)定义了通信资源的容量约束. 为了确保虚拟链路$ l_i^{uv} $的带宽资源需求不超过物理链路$ {e_{pq}} $的可用剩余带宽资源.

$ \forall i, j, u, v, p, q\quad\frac{{\displaystyle\sum\limits_{f_i^j \in {\mathit{sfc}_i}, l_i^{uv} \in {e_{pq}}} {{\mkern 1mu} {\kern 1pt} } y_{{e_{pq}}}^{l_i^{uv}} \cdot bw_{l_i^{uv}}^v}}{{BW_{{e_{pq}}}^p}} \leqslant 1 $

(9)

式(10)引入了延迟约束, 使用变量$ D_i^t $表示在时间$ t $ SFC $ {\mathit{sfc}_i} $的最大可容忍的服务延迟. 请注意, 这里不仅考虑物理节点之间的通信时延, 也考虑VNF的处理时延.

$ \forall i, j, u, v, p, q\quad\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {x_{f_i^j}^{{v_i}}} } \cdot l_{f_i^j}^d \cdot \alpha + \beta \cdot \sum\limits_{{e_{pq}} \in {E_p}} {y_{{e_{pq}}}^{l_i^{uv}}} \cdot L_{{e_{pq}}}^p \leqslant D_i^t $

(10)

其中, $ \alpha , \beta \in [0, 1] $表示可调参数, 当$ \beta = 0 $表示VNF被部署到同一个物理节点, 仅存在VNF处理时延.

2 算法设计

在DRL中, 智能体学习做决策通过探索未知环境并应用收到的反馈信息, 在每步学习中, 智能体会观察当前状态并基于某个策略采取行动, 然后智能体被反馈一个奖励. 本节首先介绍MDP模型, 然后介绍通过Actor-Critic网络进行训练, 最后介绍ACDRL-VNFPC算法.

2.1 MDP模型

MDP通常提供了一个长期问题中的行动制定的数学框架, 其中输出一般是智能体的随机行为. 此外在MDP模型中设定了假设. 即智能体对环境具有全部的感知能力, 并且当前状态排除了任何不确定性^[16,17]. 接着定义MDP四元组$ (\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}) $. 其中, $ \mathcal{S} $表示状态空间, $ \mathcal{A} $表示动作空间, $ \mathcal{P} $表示状态转移概率, 而$ \mathcal{R} $表示奖励. 在每个时间$ t\;(t = 1, 2, \cdots , T) $, 来描述这几个关键元素.

1) 状态空间: 状态空间$ {\mathcal{S}_t} $包括物理网络节点和链路资源信息和SFC资源请求信息. 具体地定义状态$ {s_t} = (s_t^p, s_t^v) $, 分别表示物理网络状态和SFC请求信息.

2) 动作空间: 动作空间$ {\mathcal{A}_t} $被定义为$ {a_t} \in {\mathcal{A}_t} $则是从可用资源超过VNF $ f_i^j $选择一个节点$ {v_i} $, 否则, $ {a_t} = \bar \zeta $直接到达终止状态.

3) 状态转移概率: 转移概率$ {\mathcal{P}_t} $表示为, 通过$ {s_{t - 1}} $和$ {a_{t - 1}} $转移到下一状态$ {s_t} $的概率.

4) 奖励: 奖励$ {\mathcal{R}_t} $是为了鼓励智能体以最大化长期平均收益为目标来进行放置. 当SFC ${\mathit{sfc}_i} $在时间$ t $被接受时获得的收益.

$ rev({\mathit{sfc}_i}) = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {x_{f_i^j}^{{v_i}}} } \cdot \Phi _{{v_i}}^{res} + \sum\limits_{{e_{pq}} \in {E_p}} {y_{{e_{pq}}}^{l_i^{uv}}} \cdot \Phi _{{e_{pq}}}^{bw} $

(11)

在中间步骤(即$ t < T $), 当满足资源约束时, 智能体获得激励的奖励$ {r_t} = \xi re{v_t}({\mathit{sfc}_i}) $, 否则获得抑制的奖励$ {r_t} = - \xi re{v_t}({\mathit{sfc}_i}) $, $ \xi $为奖励系数.

2.2 Actor-Critic网络训练

Critic网络表示价值网络给采取的动作进行评估. 若$ \omega $表示价值网络的训练参数, 用价值网络$ q(s, a;\omega ) $来近似$ {Q_\pi }(s, a) $. 更新Critic网络为了更好地估计回报值, 这使得Critic判断更加准确. 而在实际训练运用TD (temporal difference)算法来更新$ \omega $ (在价值网络$ q $). 通过计算损失$ L(\omega ) $, 即预测值$ q $与目标TD target $ {{{y}}_t} $差值, 其被表示为如下:

$ L(\omega ) = \frac{1}{2}{[q({s_t}, {a_t};w) - {y_t}]^2} $

(12)

其中, 损失是价值网络参数$ \omega $的函数, 并使用梯度下降更新$ \omega $, 使得$ {y_t} - {q_t} $值更小, Critic判断更准确. 因此, Critic网络参数$ \omega $按照式(13)进行更新:

$ {\omega _{t + 1}} = {\omega _t} - \alpha \cdot \frac{{\partial L(\omega )}}{{\partial \omega }}{|_{\omega = {\omega _t}}} $

(13)

其中, $ \alpha $表示学习率.

Actor网络表示策略网络来生成相应的动作和环境交互. 若$ \pi $和$ \theta $分别表示策略网络和Actor网络的训练参数, 用策略网络$ \pi (a\mid s;\theta ) $来近似$ \pi (a\mid s) $来负责评估Actor的表现, 并指导下一时刻的动作. 因此, 在Actor网络中, 状态价值函数可近似为:

$ V({s_t};\theta , \omega ) = \sum\limits_a \pi (a\mid s) \cdot {Q_\pi }(s, a) \approx \sum\limits_a \pi ({a_t}\mid {s_t};\theta ) \cdot {q_\pi }({s_t}, {a_t};\omega ) $

(14)

更新策略网络$ \pi $为了使得$ V $函数更大, 并运用梯度下降更新$ \theta $(在策略网络$ \pi $). 首先是函数$ V $关于$ \theta $计算梯度, 用$ g(a, \theta ) $表示. 其次对$ \theta $做梯度上升, 更新状态价值函数$ V $值.

$ {\theta _{t + 1}} = {\theta _t} + \beta \cdot g(a, {\theta _t}) $

(15)

其中, $ \beta $表示学习率.

具体的Actor-Critic网络训练过程如算法1所示.

算法1. Actor-Critic网络训练

输入:当前网络状态$\scriptstyle {s_t} $, 最大迭代轮次$\scriptstyle ite{r_{\rm max}} $.

输出: 在线训练的Actor网络参数$\scriptstyle \theta $.

/**训练阶段**/

1) 初始化神经网络参数$\scriptstyle \theta $和$\scriptstyle \omega $;

2) 初始化迭代次数$\scriptstyle iter = 0 $;

3) while $\scriptstyle iter < ite{r_{\rm max}} $ do

4) for $\scriptstyle t = 1, 2, \cdots , T $ do

5) 　观察状态$\scriptstyle {s_t} $, 并随机抽样出动作$\scriptstyle {a_t} $;

6) 　执行动作$ \scriptstyle {a_t} $, 状态$ \scriptstyle {s_t} $更新到$\scriptstyle {s_{t + 1}} $得出$\scriptstyle {{\text{r}}_t} $获得四元组$ \scriptstyle ({s_t}, {a_t}, {r_t}, {s_{t + 1}}) $保存到经验池;

7)　 通过式(13)更新价值网络$\scriptstyle q $参数$\scriptstyle \omega $;

8) 　使用式(15)进行梯度上升更新策略网络$\scriptstyle \pi $参数$\scriptstyle \theta $;

9) end for

10) end while

11) return $\scriptstyle \theta $;

2.3 ACDRL-VNFPC

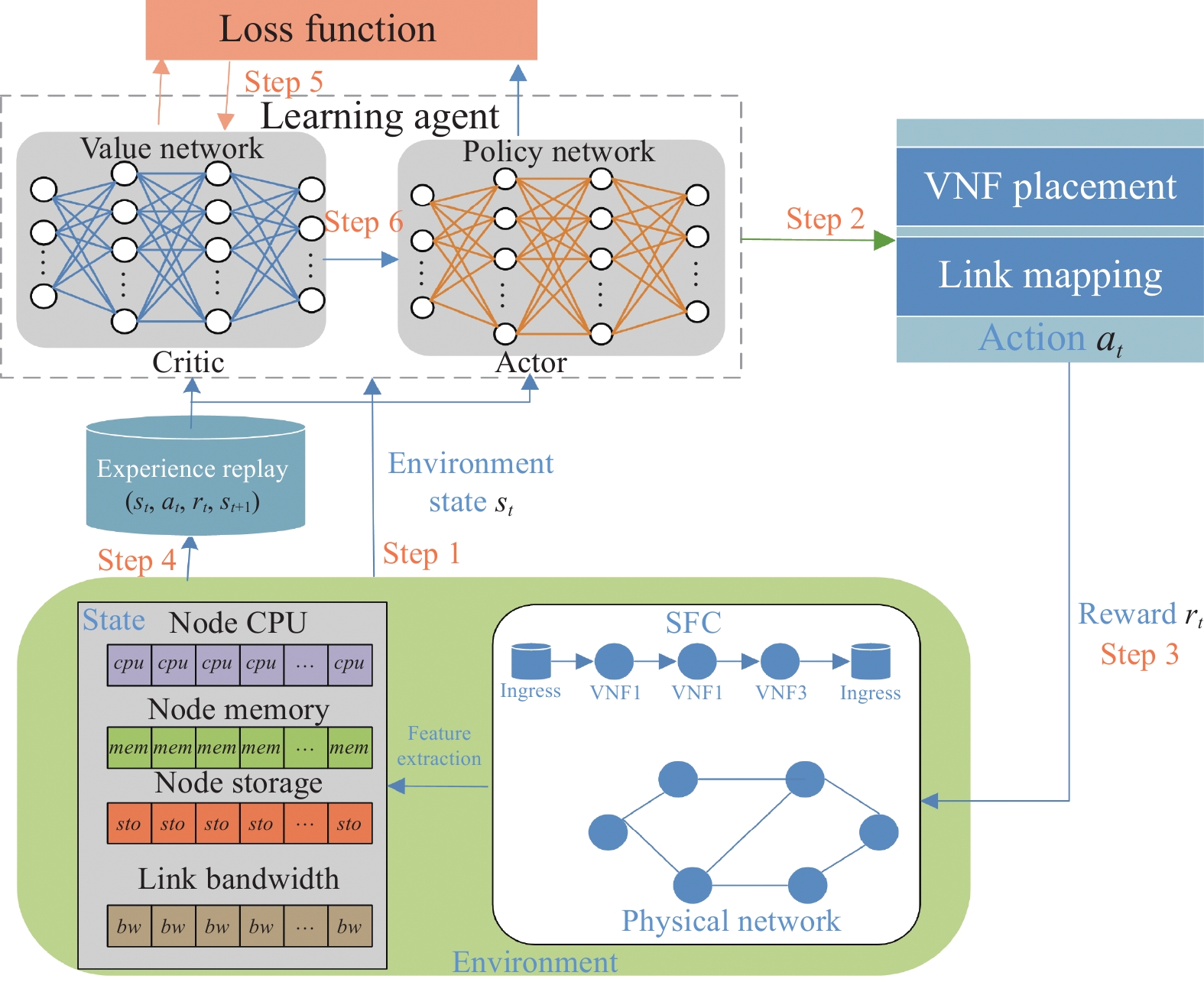
如图2所示, ACDRL-VNFPC整体框架包含6个步骤, 当请求SFC到达时, 我们首先对物理网络进行特征提取, 包括节点和链路的可用资源信息和SFC中的VNF资源请求信息. 在步骤1中将环境中的状态信息传递给学习代理(即算法1训练Actor-Critic网络); 其次在步骤2根据最大状态值获得动作部署SFC请求(即算法2所描述VNF放置和链路映射); 步骤3将采取的动作奖励反馈给环境; 接着, 在步骤4将四元组$ ({s_t}, {a_t}, {r_t}, {s_{t + 1}}) $存储到经验回放池; 在步骤5计算损失函数并更新Critic网络; 最后步骤6通过Critic判断更新Actor网络.

算法2. VNF放置和链路映射

输入: 物理网络$\scriptstyle {G_p} $, SFC请求$\scriptstyle {\mathit{sfc}_i} $.

输出: 在线VNF放置集$\scriptstyle {\mathit{placeSet}_{\rm result}} $, 链路集$\scriptstyle {\mathit{linkSet}_{\rm result}} $.

/**VNF放置**/

1) 初始化Actor网络参数$\scriptstyle \theta $;

2) $\scriptstyle {\mathit{placeSet}_{\rm result}} = \varnothing $, $\scriptstyle {\mathit{linkSet}_{\rm result}} = \varnothing $;

3) for $\scriptstyle t = 1, 2, \cdots , T $ do

4) 　按可用节点资源$\scriptstyle R_{{v_i}}^p $和链路可用带宽资源$\scriptstyle BW_{{e_{pq}}}^p $排序;

5) 　当SFC请求随机到达;

6) 　if $\scriptstyle {a_t} = = \bar \zeta $ then

7) 　　到达终止状态, 拒绝当前$\scriptstyle {\mathit{sfc}_i} $, 撤销之前动作$\scriptstyle {a_t} $;

8) 　　return false;

9)　 else

10) 　　当$\scriptstyle {\mathit{sfc}_i} $和$\scriptstyle {\mathit{sfc}_j} $具有相同类型的$\scriptstyle f_i^j $可共享$\scriptstyle f_i^j $处理能力;

11) 　　执行$\scriptstyle f_i^j $放置到$ \scriptstyle {v_i} $动作$\scriptstyle {a_t} $;

12) 　　更新放置结果集$\scriptstyle plac{e_{\rm result}} $.add($\scriptstyle {a_t} $);

13)　　 continue;

14)　 end if

/**链路映射**/

15) 　从排序的候选链路根据Dijkstra算法在$\scriptstyle {a_t} $ 和$\scriptstyle {a_{t - 1}} $寻找路径最短的链路$\scriptstyle {p_t} $;

16) 　if $\scriptstyle \exists {p_t} $ then

17) 　　将虚拟链路映射到物理链路$\scriptstyle {p_t} $;

18)　　 更新链路集$\scriptstyle {\mathit{linkSet}_{\rm result}} $.add($ \scriptstyle {p_t} $);

19)　　 continue;

20)　 end if

21) end for

22) return $\scriptstyle {\mathit{placeSet}_{\rm result}} $, $\scriptstyle {\mathit{linkSet}_{\rm result}} $;

算法2是VNF放置及链路映射, 输入当前的物理网络和SFC请求, 输出VNF放置结果集合和链路映射结果集合. 首先对于物理节点资源和链路带宽资源按非递减的排序, 倾向于先选择较多资源的节点和链路. 然后对于随即到达的SFC中VNF进行放置, 当没有可供选择的物理节点, 则到达终止状态$ \bar \zeta $, 并且拒绝该SFC, 撤销之前放置动作$ {a_t} $. 在实际放置中利用多服务共享相同类型的VNF, 减少VNF实例数, 节省资源消耗. 从已执行动作$ {a_t} $和$ {a_t} $根据Dijkstra算法寻找最短链路, 如果存在则更新链路结果集.

3 实验与性能分析 3.1 仿真环境设置

本研究的实验全部在仿真环境上进行, 配置如下: 仿真计算机使用的是NVIDIA GTX 3060 GPU, Intel(R) Core(TM) i7-11800H CPU 3.20 GHz, 仿真使用的软件PyCharm 2021.2.2, Python 3.9.

根据Waxman模型^[18]生成物理网络和虚拟网络的拓扑结构. 在每一轮次中, 随机生成5000个SFC请求, 随机确定源节点和目的节点. 具体是每个SFC请求由5–10个不同数量的VNF均匀分布. 此外, 假设每次SFC请求到达率服从泊松分布参数为$ \lambda = 5 $. 具体的仿真参数如表1所示.

为了评估提出的放置算法的有效性和效率, 并将其与增强First-Fit (IFF)启发式算法^[19], 邻近节点蒙特卡洛(NeMC)^[20]树搜索、VNF放置和网络缩放(VPANS)^[21]这3种方法进行对比. 算法的具体描述如表2所示. 请注意, ACDRL-VNFPC与对比算法均使用最短路径算法来选择链路.

3.2 结果分析

在本研究中, 考虑分别用服务请求接受率, 总能耗和执行时间指标来衡量算法性能.

图3(a)和(b)显示了Actor-Critic网络训练过程损失变化, 可以看到损失随着训练数量的增加, 损失呈下降趋势. 当训练次数小于1500次时, 损失值比较高, 这是因为初始模型的参数是随机初始化, 模型是未收敛, 导致损失值比较高. 随着训练次数的增加, 模型不断收敛. 根据奖励和状态值不断学习更新神经网络, 损失值逐渐稳定. 在训练次数大约4000次后, Actor和Critic损失分别收敛到约0.10和0.0025局部最优. 这表明提出的ACDRL-VNFPC算法近似效果很好.

图4展示了5000个SFC请求输入到网络中各算法的表现. 如图4所示, 服务接受率随着SFC请求数量增多, 各算法的接受率呈下降趋势. 这是因为当SFC请求中的VNF被成功放置后, 底层物理资源被消耗逐渐减少. 由于IFF和NeMC优先考虑资源最小化, 但未考虑节点之间负载均衡, 因此算法的整体性能表现相对较差. ACDRL-VNFPC算法由于应用了适应性共享, 在资源方面考虑了共享, 优化了节点部署, 因此ACDRL-VNFPC算法长期来看表现最好. 当SFC请求数量达到1500时, ACDRL-VNFPC算法请求接受率均高于对比算法. 提出的算法ACDRL-VNFPC在服务接受率较IFF算法性能提升了2.39%, 较NeMC算法性能提升了3.02%, 较VPANS算法性能提升了2.57%. 这表明本文提出算法明显提高整体网络性能和服务质量.

图5展示了随着SFC请求数量增加, 4种算法能耗呈上升趋势. 这是因为随着要部署SFC请求数量增多, 节点需要处理更多的数据流量和服务请求, 导致需要启用更多的服务器来放置VNF, 从而消耗更多的能源. 由于ACDRL-VNFPC基于RL方法学习最优部署策略, 通过部署到合理的服务器降低服务器的资源利用率, 从而减少能耗. 此外, ACDRL-VNFPC考虑了适应性共享策略, 使得不同类型的VNF共享同一个服务器, 减少实例服务器的数量的同时降低了能耗成本, 因此, ACDRL-VNFPC算法在能耗方面性能表现最好. ACDRL-VNFPC方法的能耗较IFF, NeMC和VPANS分别降低14.93%, 6.58%. 和9.64%. ACDRL-VNFPC的性能表现是由于神经网络的良好拟合能力和泛化能力.

图6展示了执行时间随着SFC请求数量增多, 4种算法均呈上升趋势, 其中执行时间指的是获得解决方案的时间, 包括模型的训练时间和部署时间, 这个指标反映了问题规模的扩展能力, 即面对在大量SFC请求时, 算法是否可以在合理时间范围内获得解决方案. 从图6可以看出, IFF算法虽然在SFC请求数量较少时, 性能表现较好, 然而面对大量的SFC请求时, IFF算法执行时间增速较大, 因此, IFF整体性能是最差. ACDRL-VNFPC方法随着SFC请求数量的增加, 执行时间仍是以较低时间水平获得解决方案. 提出的算法在执行时间方面较IFF, NeMC和VPANS分别提升了16.16%, 2.42%和8.73%. 这说明该算法面对大量网络请求的求解时间上是可接受的.

4 结束语

本研究是基于深度强化学习方法在NFV网络中VNF放置和链接问题中的应用. 为了满足服务质量前提下, 不降低服务接受率的同时可以权衡优化能耗. 为此, 不仅提取了物理网络信息, 而且考虑了SFC中的VNF特性, 并提出了基于Actor-Critic的深度强化学习的VNFPC (ACDRL-VNFPC)的算法. 算法应用了适应性共享方案, 不仅多服务之间共享相同VNF, 而且多个VNF共享相同的服务器, 使得算法减少资源消耗同时降低能耗. 实验结果表明, ACDRL-VNFPC方法在接受率, 能耗和执行时间方面都有很好的性能. 未来研究方向致力于复杂的云边场景下在线放置和流量路由的解决方案.