图像在采集、处理和传输过程中受外部环境以及成像设备技术等因素影响, 产生信息或亮度随机突变的像素点, 恶化图像质量. 图像去噪旨在利用图像序列的上下文信息去除噪声信号、恢复真实图像, 在视频监控、医学影像以及现实工业场景等领域具有重要应用价值.
传统图像去噪算法主要包括基于滤波的方法和基于变分模型的方法. 基于滤波的方法利用低通滤波器将噪声信号从图像中分离出来, 重构干净图像, 如高斯滤波[1]、双边滤波[2]、非局部均值滤波(non-local means, NLM)[3]、BM3D[4]等. 基于变分模型的方法采用贝叶斯观点将去噪任务转变成最大后验概率(maximum a posteriori, MAP)[5]问题, 然后通过图像先验信息构造正则化最小优化算法, 根据不同的先验约束可分为全变分模型[6]、稀疏模型[7]、自相似性[8]等. 上述方法需要手动调节参数, 且往往只针对特定的图像结构, 难以解决具有复杂分布的真实噪声问题.
基于深度学习的图像去噪算法主要采用卷积神经网络(convolutional neural network, CNN), 依靠CNN强大的学习能力和良好的网络泛化能力, 克服了传统方法依赖于先验信息和人工特征的局限性, 将去噪问题的研究重点转向了难以参数化的真实噪声. Zhang等[9]提出一种端到端的卷积神经网络去噪算法(residual learning of deep CNN for image denoising, DnCNN), 通过残差学习和批量归一化加速去噪网络的训练过程. Zhang等[10]提出处理空间变化噪声的子图像去噪网络(toward a fast and flexible solution for CNN-based image denoising, FFDNet), 以噪声水平估计作为网络输入, 采用正交正则化抑制扩张卷积产生的边界伪影. Guo等[11]提出分阶段盲去噪网络(toward convolutional blind denoising of real photographs, CBDNet), 通过噪声估计子网络调整噪声水平从而实现交互式去噪, 非盲去噪子网络采用残差学习防止网络过拟合. Anwar等[12]提出模块化结构的新型单阶段盲去噪网络(real image denoising with feature attention, RIDNet), 采用特征重标定策略[13]实现通道间的相互依赖关系建模. 但基于CNN的图像去噪算法受卷积核范围的限制, 只能处理空间上局部邻域的构造块, 无法捕获长距离特征之间的上下文联系, 使网络缺乏全局信息感知能力, 难以恢复图像的整体形状和结构.
上述方法所提出的去噪模型缺乏对远程特征相关性的建模能力, 而Transformer[14]能够利用其注意力机制捕获远程像素间的强弱语义关系, 实现上下文信息的全局交互, 弥补了CNN在特征映射能力上的不足. Wang等[15]提出一种基于Transformer的U型图像恢复架构(a general U-shaped Transformer for image restoration, Uformer), 在一定程度上缓解了CNN的局部限制, 但在复杂情况下仍缺乏对高频噪声信号的抑制能力. Liang等[16]在Swin Transformer的基础上, 提出采用滑动窗口机制的强基线模型SwinIR (image restoration using Swin Transformer), 通过限制注意力的作用范围来平衡计算效率, 但这种局部自注意力机制与实现上下文信息的全局交互始终相互矛盾. Zamir等[17]提出针对高分辨率图像的恢复算法(efficient Transformer for high resolution image restoration, Restormer), 采用通道自注意力和双路门控机制, 改进前馈网络的特征筛选方式, 但完全依赖注意力捕获图像特征的方式造成了高额的计算开销.
目前基于CNN和Transformer的图像去噪算法, 面对复杂分布的真实噪声时, 主要通过叠加多层池化和降采样操作以获得高级语义信息, 但在前向传播过程中逐渐丢失像素数较少的细节特征, 无法从局部和全局出发综合考虑特征信息, 导致输出的去噪图像仍存在边缘模糊或过度平滑现象, 难以恢复真实图像的细节纹理信息. 另外, 自注意力机制在捕获像素间的远程依赖关系时, 将不可避免的导致GPU内存不足和计算效率低下.
针对上述问题, 本文提出融合CNN和Transformer的图像去噪网络(hybrid CNN and Transformer image denoising network, HCT-Net). 首先, 提出CNN和Transformer耦合模块(CTB), 构造一种卷积和通道自注意力的并行双分支结构, 利用局部连接和共享权重的特性高效提取浅层特征, 捕获通道维度的关键特征、抑制噪声信号. 其次, 设计自注意力增强卷积模块(SAConv)提升网络对局部特征的关注度, 在实现多频信号感知融合的同时优化网络前馈信息, 保留更多细微特征从而恢复图像的细节和边缘结构. 此外, HCT-Net采用编解码器[18]提取低分辨率和多尺度特征, 利用层级连接融合不同粒度的相邻特征, 最大程度保留原始图像的结构信息, 进一步增强前馈网络的特征表达能力和模型泛化能力. 在高斯噪声数据集和真实噪声数据集上的实验结果均验证了本文算法的去噪性能, 并通过算法效率分析证明了本文网络的合理性.
1 相关工作 1.1 TransformerTransformer是一种完全基于自注意力机制的编解码网络模型, 每个基本模块由多头自注意力机制(multi-head self-attention, MSA)和简单的全连接前馈网络(feed-forward network, FFN)组成.
自注意力机制通过查询和键值的相似性程度来确定值的权重分布, 计算每一个序列对于其他序列的注意力系数, 从而捕捉数据或特征间的内部相关性. 首先, 使用参数矩阵Wq、Wk、Wv对输入矩阵X进行线性变换, 得到输入矩阵X在查询、键值、值上的投影矩阵Q、K、V, 其维度分别为dq、dk、dv. 然后通过Q矩阵和KT矩阵的点积交互进行相似度计算, 得到自注意力权重矩阵QKT, 为了防止内积过大, 将QKT除以
| Attention(Q,K,V)=Softmax(QKT√dk)V | (1) |
多头自注意力机制由多个自注意力层并行组成, 首先将输入矩阵X分别传递到h个不同的自注意力层中, 分别执行式(1)的点积交互操作得到注意力权重矩阵
| MSA(Q,K,V) = Concat(head1,⋯,headh)WO | (2) |
其中,
全连接前馈网络是一种单向多层网络结构, 其中每一层包含若干个神经元, 信号从输入层到输出层单向传播, 整个网络中无反馈信号. 全连接网络具有两层线性层, 第1层的激活函数为ReLU, 第2层不使用激活函数, 通过前馈全连接层后输入和输出的维度不变, 得到输出矩阵X''可表示为:
| FFN(X′)=max(0,X′W1+b1)W2+b2 | (3) |
此后, VIT (vision Transformer)[19–21]将Transformer迁移到计算机视觉领域, 并在此基础上不断提出新的网络结构, 如DeiT[22]、Swin Transformer[23]和Le-VIT[24]等.
1.2 深度可分离卷积如图1, 深度可分离卷积(depthwise separable convolution, DSC)将传统卷积操作拆分成两个独立的步骤, 分别是深度卷积和逐点卷积, 旨在减少神经网络的参数量和计算复杂度, 同时保持模型性能.

|
图 1 深度可分离卷积 |
在传统卷积中, 卷积核是立方体状的, 同时对所有输入通道执行卷积操作, 而在深度卷积中, 每个输入通道都有一个单独的卷积核, 用来在空间上对该通道进行卷积, 使每个通道的卷积核独立地处理输入数据, 产生相应通道的特征图. 由于每个输入通道都有一个独立的卷积核, 大大减少了卷积层的参数数量, 所以深度卷积可以减小模型的复杂度, 降低计算和内存需求. 同时, 深度卷积也可以提高对空间特征的捕捉能力, 因为它在每个通道上分别处理数据, 这样更有助于模型理解输入的局部结构.
逐点卷积采用1×1的卷积核, 将不同通道的特征图汇聚在一起, 通过线性组合融合各通道的特征信息, 从而生成最终的输出特征图. 由于逐点卷积允许在不同通道之间进行线性组合和特征交互, 所以其具有更丰富的网络表达能力. 此外, 逐点卷积还可以用来调整输出通道的数量, 进一步降低计算复杂度.
深度可分离卷积将卷积分为两个步骤, 降低了网络的复杂程度, 并减少参数之间的相关性, 降低过拟合的风险, 并使网络拥有更好的泛化能力.
2 融合CNN和Transformer的图像去噪网络 2.1 网络模型本文提出融合CNN和Transformer的图像去噪网络, 如图2所示. 首先, 将噪声图像

|
图 2 HCT-Net网络结构 |
为了重构下采样阶段造成的信息损失, 将不同层级的特征图进行特征融合, 以确保各层之间的信息流最大化, 避免丢失重要的细节特征. 然后通过1×1卷积实现跨通道的信息交互和线性组合, 降低特征通道维度. 最后, 将3×3卷积层生成的残差图像
CNN和Transformer耦合模块(CNN and Transformer coupling block, CTB)结构如图3所示, 是一种融合卷积和通道自注意力的并行双分支结构, 并提取二者的相同部分作为公共模块, 从而实现利用效率最大化. 在并行分支中, 一方面利用深度可分离卷积实现高效的浅层特征提取, 另一方面, 采用通道自注意力模块提取特征维度的显著纹理信息, 并缓解全局注意力机制所造成的高额计算开销. 最后, 采用非平均混合策略赋予重要特征更高的权值, 抑制无用特征, 使网络在动态关注重要特征信息的同时减少复杂噪声信号的干扰.
CTB模块主要分为两个阶段. 第1阶段基于卷积和自注意力机制之间的内在相关性, 两种方法共同执行3个1×1卷积操作, 强化特征提取, 使每组卷积得到N个中间特征Fi:
| Fi=Conv1×1(LayerNorm(F0)) |
其中,
第2阶段卷积和自注意力模块分别采用不同的聚合操作, 重用上一阶段获得的3×N个中间特征. 在第1分支中, 采用通道维度的全连接操作将通道数从3×N扩张到K2×N, 对应CNN上一阶段的特征维度, 然后将所有输入特征和卷积核分别连接起来, 通过位移操作进一步结合不同方向的特征, 得到移位特征:
| Shift(Fi)=Concat(Fq,Fk,Fv)∗Concat(Kc) |
其中,
| Fconv=N∏h=1Wd(Shift(Fi)) |
其中,
| CA(Fq,Fk,Fv) = Softmax(Wqd(Fq)⋅Wkd(Fk)T√dk)Wvd(Fv) | (4) |
该模块生成具有线性复杂度的转置注意力特征图, 然后将注意力权重特征图与原始图像残差连接, 避免网络出现过拟合的现象, 得到注意力模块的特征输出:
| Fatt = N∏h=1Wp(CA(Fq,Fk,Fv))⊕F0 |
其中,
在训练过程中发现, 不同网络深度的卷积和自注意力模块捕获特征的能力存在差异性. 因此, 设置学习参数α、β, 将两条路径的输出非平均混合, 通过自主学习实现网络对重要特征的动态关注, 并抑制无用特征, 该模块的输出结果为
| Fout=αFconv+βFatt | (5) |
其中,

|
图 3 CNN和Transformer耦合模块结构 |
从计算效率来看, CTB模块采用并行化分支代替传统单分支结构, 在融合CNN时通过整合公共模块, 使网络具有更小的计算开销. 在第1阶段, 两种方法通过执行相同操作完成了模块的主要计算量, 并利用卷积的共享权重特性, 来减少模型的内存占用. 第2阶段, 卷积模块采用轻量级的聚合操作几乎不造成额外的参数负担, 自注意力模块利用跨特征维度的深度可分离卷积避免了计算效率受图像分辨率H、W的影响, 计算成本和训练参数呈通道数的线性相关. 另外, 采用非平均混合策略整合输出特征图, 使网络在关注重要特征的同时降低通道维度, 进一步提升去噪模型的推理速度.
2.3 自注意力增强卷积模块自注意力机制能够提供全局信息使网络实现远程依赖建模, 但也在一定程度上恶化高频信号, 导致基于Transformer的图像去噪算法不能明确的辨别噪声特征, 在复杂背景情况下, 将一些图像细节信息误判为噪声信号, 丢失对局部纹理信息的关注, 导致输出的图像过度平滑甚至模糊了重要细节.
对此, 本文设计了一种即插即用的自注意力增强卷积模块(self-attention enhanced convolution module, SAConv), 利用轻量级的多头自注意力捕获低频信号, 增强后续卷积模块对局部特征的提取. SAConv通过构建邻域像素的相似性程度、放大高频信号, 识别出边缘和轮廓等细微特征. 然后, 在捕获图像多频信号的基础上, 进行局部特征和全局特征融合, 提升网络的特征表达能力, 代替单一的前馈网络, 在关注局部关键特征的基础上筛选显著的特征纹理信息, 从而恢复更多图像细节和边缘信息.
如图4所示, SAConv主要由高效的多头自注意力模块(efficient multi-head self attention module, EMSA)、分组卷积模块(multi-group convolutional block, MGCB)和多层感知器(multilayer perceptron, MLP)串联组成.

|
图 4 SAConv模块结构 |
首先, 采用1×1逐点卷积降低输入特征通道数, 通过批量归一化(BN)聚合空间维度的冗余信息.
| X=BatchNorm(Conv1×1(Fout)) |
将经过上述预处理的图像特征X作为模型输入, 以提升后续EMSA模块的计算效率. EMSA模块通过引入平均池化层聚合特征映射的空间信息, 压缩输入特征图的空间维数, 并逐元素加权合并, 以产生轻量级的通道注意力图. EMSA可表示为:
| SA(X)=Softmax((X⋅Wq)⊗Avgpool(X⋅Wk)T√dk)Avgpool(X⋅Wv) | (6) |
| EMSA(z)=Wp(Concat(SA1(z1),SA2(z2),⋯,SAh(zh))) | (7) |
其中,
输入: 经过预处理的集合X.
输出: 局部和全局特征融合的完整特征图
Step 1:
Step 2:
Step 3:
Step 4:
Step 5:
此外, 通过引入随机收缩因子r降低EMSA和MGCB模块的输入通道数, 使用BN和GELU作为规范化层和非线性激活函数, 利用平均池化、深度可分离卷积等进一步提高模块的训练速率和稳定性.
(1)轻量级的多头自注意力模块(EMSA): EMSA是一种轻量级的高效自注意力模块, 如图5(a)所示. 将输入特征图按特征维度划分为多头自注意力, 跨通道执行查询关键特征交互, 并行地学习不同维度的注意力特征图. 在点积交互计算前采用平均池化层对空间维度进行下采样, 降低多头自注意力机制带来的高额计算消耗, 并通过残差连接弥补下采样造成的特征损失.
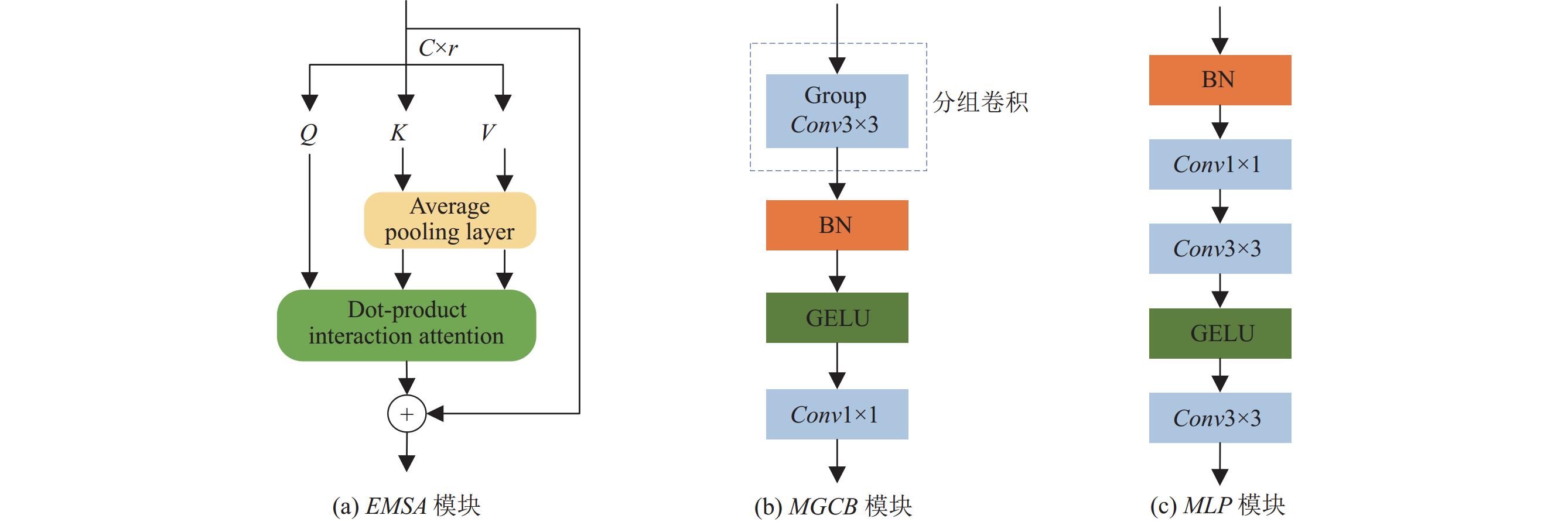
|
图 5 SAConv子模块结构 |
(2)分组卷积模块(MGCB): MGCB主要包括分组卷积和逐点卷积, 如图5(b)所示. 首先, 将输入特征图按通道维度划分为多组卷积的形式, 从多组并行子空间中捕获高频信息. 通过关注不同子空间的不同位置的信息表示, 将空间联系密切的邻域像素高效聚合, 实现有效的局部特征学习, 然后采用逐点卷积促进多组卷积之间的信息交互. 另外, 在训练过程中将所有MGCB模块的通道维度统一设置为32, 以实现快速推理.
SAConv在传统前馈网络的基础上增加聚焦局部特征的功能模块, 采用EMSA和MGCB模块组合的方式增强模型对输入序列中不同特征的理解和提取能力, 降低噪声信号对图像重建的干扰, 利用CNN的平移不变性捕获图像局部特征, 使网络关注局部和全局特征之间的交互, 识别边缘细节信息从而更好地还原真实图像.
2.4 损失函数本文算法采用均方误差损失(mean square error, MSE)进行训练, 损失函数如下:
| minΘ1MM∑i=1‖Xi−fΘ(Yi)‖2F | (8) |
其中, M是训练样本的数量,
本文采用峰值信噪比(peak signal to noise ratio, PSNR)和结构相似性(structural similarity, SSIM)作为算法去噪性能的客观评价指标, 将去噪效果对比图作为主观评价依据. 在计算评价指标时, 高斯噪声数据集以干净图像作为参照图像, 真实噪声数据集以原始图像作为参照图像, 分别计算PSNR、SSIM指标.
PSNR通过计算参照图像与去噪图像
| PSNR=10⋅log10(MAX2MSE) | (9) |
其中, MAX代表参照图像的可能最大像素值, MSE代表大小为H×W的参照图像与去噪图像之间的均方误差, 以均方误差判断图像的失真程度. MSE公式如下:
| MSE=1H×WH−1∑i=0W−1∑j=0[I(i,j),k(i,j)]2 | (10) |
SSIM仿造人类视觉系统, 从亮度、对比度以及结构量化图像的属性, 感知图像在去噪过程中发生的局部结构性改变. SSIM公式如下:
| SSIM(x,y)=(2μxμy+c1)(2σxy+c2)(μ2x+μ2y+c1)(σ2x+σ2y+c2) | (11) |
其中, x、y分别代表参照图像和去噪图像,
本文采用Windows操作系统, 在GeForce GTX 1080 Ti处理器的Python环境下, 搭建PyTorch深度学习框架进行HCT-Net的训练和测试.
在6个基准数据集下验证本文算法的有效性. 灰度图像合成噪声实验采用BSD400为训练集, Set12和BSD68为测试集. BSD400数据集包括400张灰度图像, Set12数据集包括12张不同尺寸的灰度图像, BSD68数据集包括68张不同尺寸的灰度图像. 彩色图像合成噪声实验采用CBSD400为训练集, Kodak24和CBSD68为测试集. CBSD400数据集包括400张彩色图像, Kodak24数据集包括24张500×500的彩色图像, CBSD68数据集包括68张不同尺寸的彩色图像. 真实图像去噪实验采用SIDD为训练集, SIDD、DND为测试集. SIDD、DND数据集分别由320对、50对噪声图像和相应的真实图像组成.
3.3 实验结果与分析为验证融合CNN和Transformer的图像去噪算法去噪性能的有效性和运行效率的可行性, 本文分别选取近年来各类主流图像去噪方法进行对比, 包括基于图像先验的传统去噪算法、基于卷积神经网络的图像去噪算法和基于Transformer的图像去噪算法, 并通过设置不同噪声类型和噪声等级验证本文算法的普适性.
实验测试包括高斯合成噪声的图像去噪实验和真实噪声的图像去噪实验. 其中, 高斯合成噪声分为灰度图像合成噪声和彩色图像合成噪声. 在合成噪声图像实验时, 通过对原始图像添加不同等级的高斯噪声(
表1列出了在高斯灰度图像测试集上不同算法的平均PSNR和SSIM指标. 实验结果表明, 在Set12数据集上, 除噪声等级为75时本文算法的平均PSNR指标略低于FFDNet, 在其他噪声等级下均取得了最好的PSNR和SSIM指标. 在BSD68数据集上, 在噪声等级为75时, 本文算法的SSIM指标略低于FFDNet算法, 但PSNR指标的结果是最好的. 此外, 在其他噪声等级下均取得了最好的PSNR和SSIM指标值.
| 表 1 在Set12和BSD68数据集上不同方法的平均PSNR和SSIM结果 |
图6给出了在Set12数据集中部分灰度图像的去噪结果(
图7给出了在BSD68数据集中部分灰度图像的去噪结果(

|
图 6 Set12中的部分图像去噪结果( |

|
图 7 BSD68中的部分图像去噪结果( |
3.3.2 彩色图像合成噪声的实验结果
表2列出了各种算法在高斯彩色图像测试集上的平均PSNR和SSIM指标. 通过表2可以看出, 本文算法在Kodak24数据集的不同噪声等级下, 均取得了较好的去噪性能. 在CBSD68数据集上, 除了噪声水平为50时, 本文算法的PSNR指标略低于CDnCNN, 其他情况下的各项性能指标均表现为最优, 验证了本文算法对于彩色高斯噪声的有效性.
图8给出了在Kodak24数据集上的部分图像去噪结果(σ=25), 与灰度合成噪声实验结果相似, 本文算法在彩色图像去噪任务中仍获得了较好的视觉效果. 在图8的第1组图像中, CBM3D的去噪结果中仍存在噪点, CDnCNN和FFDNet在云朵区域丢失了一些细节信息. 在第2组和第3组图像中, 对比其他方法的细节部分处理, 本文算法恢复出更多的帆面纹理信息, 使图像更具真实性.
图9给出了CBSD68数据集上的部分图像去噪结果(σ=50), 通过对比可以发现, 在第1组图像的背景山脉部分、第2组图像的大象皮肤部分以及第3组图像的花瓣区域, IRCNN和Restormer等方法均存在局部失真和背景过度平滑现象, 而本文算法通过抑制高频噪声保留了更丰富的图像细节信息, 使得纹路层次更加清晰准确. 另外, 本文算法得到的恢复图像不存在色调偏移和饱和度失衡现象, 在图像色彩和对比度等方面更接近于干净图像.
| 表 2 在Kodak24和CBSD68数据集上不同方法的平均PSNR和SSIM结果 |

|
图 8 Kodak24中的部分图像去噪结果( |

|
图 9 CBSD68中的部分图像去噪结果( |
3.3.3 真实噪声图像的实验结果
为了评估本文算法在真实噪声情况下的去噪性能, 本文测试了SIDD和DND两个真实噪声数据集, 所有算法仅使用SIDD数据集上160张噪声图像作为训练集, 然后将剩余图像和DND数据集作为测试集.
表3给出了在SIDD和DND数据集上不同方法的平均PSNR和SSIM指标, 结果表明, 在SIDD数据集上本文算法的平均PSNR和SSIM指标均处于最高, 相比之前去噪性能最优的卷积神经网络去噪算法APD-Nets-C224和基于Transformer的图像去噪算法Restormer, PSNR指标分别提升了2.1 dB和1.8 dB. 另外, 在DND数据集上的结果显示, 本文算法依旧取得了最优的去噪性能.
图10和图11分别给出了在SIDD和DND数据集上部分真实图像的去噪效果. 通过对比图10中第1组和第3组图像的字母边界部分、图11的3组建筑图像的图案花纹部分, 观察到本文算法相比于Uformer和Restormer等算法, 更关注图像的局部特征, 善于捕捉图像细节和边缘等关键信息, 从而在不影响精细纹理的情况下生成更为清晰的图像, 避免出现高频噪声恶化细节纹理信息和模糊边界的情况.
3.4 算法效率分析图像去噪作为图像预处理中的重要步骤, 在现实场景中具有广泛的应用价值, 而网络的复杂程度和运行速率作为能否实施部署的关键影响因素, 决定了图像去噪网络的真实性能.
| 表 3 在SIDD和DND数据集上不同方法的平均PSNR和SSIM结果 |

|
图 10 SIDD中部分真实图像去噪结果 |

|
图 11 DND中部分真实图像去噪结果 |
表4给出了在SIDD真实数据集上部分网络框架的运行效率对比, 分别比较不同去噪方法的参数量(param)和每秒10亿次的浮点运算数(GFLOPs). 实验结果表明, 本文提出的去噪算法所需的参数量相较于目前基于Transformer的图像去噪算法最少, 运行速率仅次于CBDNet, 而CycleISP、MIRNet和APD-Nets-C224等算法依赖于强大的硬件能力, 在处理高分辨率图像时将造成高额的计算开销. 综合分析, 本文算法在复杂的现实场景中依然能保证良好的计算效率, 实现了图像去噪的最优性能.
| 表 4 不同算法的计算效率对比 |
3.5 消融实验
HCT-Net是由CTB模块和SAConv模块串联组成的网络结构, 为验证各个模块的有效性, 本文在SIDD数据集上, 保持编解码网络深度不变, 进行消融实验, 模块间的组合方式如图12所示.

|
图 12 模块的组合情况 |
实验结果如表5所示, 表中黑色加粗字体为最优值, 验证了HCT-Net中各个模块对图像去噪算法的有效性. 对比不同模块对网络去噪性能的影响可以看出, CTB模块能够抑制噪声信号, 增强网络对整体结构和高级语义信息的理解, 提升重建图像的质量和相似度, SAConv模块则更擅于关注局部特征, 减少边界伪影和细节误判, 恢复更多纹理细节信息. 本文网络在CTB模块和SAConv模块串联组合时图像去噪效果最优.
此外, CTB模块构造了融合卷积和通道自注意力的双分支结构, 并采用非平均混合策略进行特征融合. 为验证并行分支和混合策略对图像去噪性能的影响不同, 对CTB模块进行不同分支间的消融实验.
结果如表6所示, 对比第1组、第2组、第3组, 在单分支情况下, 两种特征提取方式的去噪指标均明显下降, 而双分支结构能够抑制噪声信号、捕捉关键特征, 从而恢复更多图像特征. 对比第3组、第4组, 并行融合机制通过非平均混合策略不断优化深层迭代, 提升了重建图像质量, 验证了动态注意力分配机制的有效性.
| 表 5 各模块之间的消融实验 |
| 表 6 CTB模块不同分支的消融实验 |
4 结论与展望
本文提出了融合CNN和Transformer的图像去噪网络(HCT-Net), 采用CNN和Transformer耦合模块(CTB)抑制噪声信号、捕捉关键特征, 并缓解全局注意力机制导致计算效率低下的问题, 达到准确性和计算效率的平衡. 通过自注意力增强卷积模块(SAConv)提升网络对局部特征的关注度, 捕获多频信号从而实现局部和全局信息融合, 使网络既能关注局部特征又能捕获远程依赖关系. HCT-Net与目前先进的深度学习去噪算法相比, 具有较好的去噪效果和一定的性能优势. 在未来的工作中, 将进一步减少网络参数, 优化算法的网络结构.
| [1] |
Pronina V, Kokkinos F, Dylov DV, et al. Microscopy image restoration with deep Wiener-Kolmogorov filters. Proceedings of the 16th European Conference on Computer Vision. Glasgow: Springer, 2020. 185–201.
|
| [2] |
Gavaskar RG, Chaudhury KN. Fast adaptive bilateral filtering. IEEE Transactions on Image Processing, 2019, 28(2): 779-790. DOI:10.1109/TIP.2018.2871597 |
| [3] |
Buades A, Coll B, Morel JM. A non-local algorithm for image denoising. Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego: IEEE, 2005. 60–65.
|
| [4] |
Dabov K, Foi A, Katkovnik V, et al. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Transactions on Image Processing, 2007, 16(8): 2080-2095. DOI:10.1109/TIP.2007.901238 |
| [5] |
Gauvain JL, Lee CH. Maximum a posteriori estimation for multivariate Gaussian mixture observations of Markov chains. IEEE Transactions on Speech and Audio Processing, 1994, 2(2): 291-298. DOI:10.1109/89.279278 |
| [6] |
Chan TF, Shen JH, Zhou HM. Total variation wavelet inpainting. Journal of Mathematical Imaging and Vision, 2006, 25(1): 107-125. DOI:10.1007/s10851-006-5257-3 |
| [7] |
Elad M, Aharon M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Transactions on Image Processing, 2006, 15(12): 3736-3745. DOI:10.1109/TIP.2006.881969 |
| [8] |
Hou YK, Xu J, Liu MX, et al. NLH: A blind pixel-level non-local method for real-world image denoising. IEEE Transactions on Image Processing, 2020, 29: 5121-5135. DOI:10.1109/TIP.2020.2980116 |
| [9] |
Zhang K, Zuo WM, Chen YJ, et al. Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising. IEEE Transactions on Image Processing, 2017, 26(7): 3142-3155. DOI:10.1109/TIP.2017.2662206 |
| [10] |
Zhang K, Zuo WM, Zhang L. FFDNet: Toward a fast and flexible solution for CNN-based image denoising. IEEE Transactions on Image Processing, 2018, 27(9): 4608-4622. DOI:10.1109/TIP.2018.2839891 |
| [11] |
Guo S, Yan ZF, Zhang K, et al. Toward convolutional blind denoising of real photographs. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 1712–1722.
|
| [12] |
Anwar S, Barnes N. Real image denoising with feature attention. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 3155–3164.
|
| [13] |
Hu J, Shen L, Sun G. Squeeze-and-excitation networks. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 7132–7141.
|
| [14] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 6000–6010.
|
| [15] |
Wang ZD, Cun XD, Bao JM, et al. Uformer: A general U-shaped Transformer for image restoration. Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022. 17662–17672.
|
| [16] |
Liang JY, Cao JZ, Sun GL, et al. SwinIR: Image restoration using Swin Transformer. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision Workshops. Montreal: IEEE, 2021. 1833–1844.
|
| [17] |
Zamir SW, Arora A, Khan S, et al. Restormer: Efficient Transformer for high-resolution image restoration. Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022. 5718–5729.
|
| [18] |
Ronneberger O, Fischer P, Brox T. U-Net: Convolutional networks for biomedical image segmentation. Proceedings of the 18th International Conference on Medical Image Computing and Computer-assisted Intervention. Munich: Springer, 2015. 234–241.
|
| [19] |
Pan XR, Ge CJ, Lu R, et al. On the integration of self-attention and convolution. Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022. 805–815.
|
| [20] |
Park N, Kim S. How do vision Transformers work? Proceedings of the 10th International Conference on Learning Representations. OpenReview.net, 2022.
|
| [21] |
Dosovitskiy A, Beyer L, Kolesnikov A, et al. An image is worth 16x16 words: Transformers for image recognition at scale. Proceedings of the 9th International Conference on Learning Representations. OpenReview.net, 2021.
|
| [22] |
Touvron H, Cord M, Douze M, et al. Training data-efficient image Transformers & distillation through attention. Proceedings of the 38th International Conference on Machine Learning. PMLR, 2021. 10347–10357.
|
| [23] |
Liu Z, Lin YT, Cao Y, et al. Swin Transformer: Hierarchical vision Transformer using shifted windows. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021. 9992–10002.
|
| [24] |
Graham B, El-Nouby A, Touvron H, et al. LeViT: A vision Transformer in ConvNet’s clothing for faster inference. Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021. 12239–12249.
|
 2024, Vol. 33
2024, Vol. 33



