聚类分析是一种常用的数据分析方法, 它可以将具有相似特征的数据对象划分为同一类别, 为数据挖掘和机器学习提供了有力的工具^[1]. 随着计算机技术的发展和数据规模的增大, 传统的聚类算法, 如K-means算法, 难以解决高维数据中的聚类问题. 因此研究者对聚类算法进行了广泛的研究, 提出了许多新的算法和技术, 主要有: (1)基于子空间, 旨在将不同子空间的高维数据用低维子空间进行线性表示^[2]. (2)基于图学习, 旨在利用节点之间的依赖关系, 发现数据未知的潜在结构^[3]. (3)基于深度学习, 旨在利用深度神经网络的多层非线性表示来发现高维数据中的深度潜在表示^[4]. 上述类型聚类算法的提出能够处理高维数据和大规模数据集, 所以被广泛应用于图像识别^[5]、目标检测^[6]、推荐系统^[7]和医疗诊断^[8]等领域.

由于单一视图的数据往往很难完整的描述数据本身, 而多个视图可以提供更加全面和准确的数据信息, 因此研究人员提出了多视图聚类(multi-view clustering, MVC)^[9]. 多视图聚类算法旨在从不同视图的多样性信息中学习到更加全面和准确的一致性共识表示, 来提高模型的聚类性能. Mi等人^[10]提出采用投影的方法学习各视图潜在空间的多样性. Wang等人^[11]提出在多图自编码器中引入多图注意力对多视图数据的互补信息进行编码. 李顺勇等人^[12]提出采用信息熵加权来保证各视图之间的差异性. Liu等人^[13]提出了一种自适应加权的多视图核矩阵分解方法学习不同视图的权重. Gu等人^[14]提出将视图分解为一致因子和不一致因子, 再利用希尔伯特-施密特独立性准则(HSIC)作为多样性惩罚项, 诱导一致因子比初始图干净, 并将其以自加权方式融合到一致图中. Tang等人^[15]提出利用潜在表示构造权重矩阵, 即通过各视图潜在表示学习各视图的多样性. Cai等人^[16]提出了使用增强视图的自动加权的多视图聚类算法. Liu等人^[17]提出一种基于GCN的多视图聚类算法, 在编码器部分采用基于注意力加权机制对多视图融合层中的视图权重进行建模, 在解码器部分采用重建损失的自适应加权机制来衡量不同视图对反向传播损失贡献.

上述办法中, 无论是从潜在表示、图结构或原始数据角度衡量各视图之间的多样性信息, 都是从全局角度出发, 忽略了局部样本之间的多样性信息. 这使得最终得到的多样性信息不够全面, 从而影响聚类性能. 针对上述问题, 因此本文提出了多样性引导的深度多视图聚类算法(diversity guided deep multi-view clustering, D2MVC), 算法中引入图自编码器学习各视图节点属性信息和结构信息, 从而最大化各视图多样性信息. 主要工作如下.

(1)提出了融合多头自注意力机制的软聚类模块, 利用多头自注意力机制学习全局多样性信息, 模糊C均值算法学习局部多样性信息, 通过最小化软聚类损失来更新分配权重.

(2)在基于图自编码器的多视图聚类算法中引入软聚类模块, 挖掘各视图全局和局部多样性信息以提高聚类性能.

(3) 在3个数据集上进行对比实验和消融实验, 实验证明本文提出的D2MVC算法是有效的, 所提出的多样性信息学习模块能有效提高聚类性能.

1 相关工作 1.1 多头自注意力机制

自注意力机制的基本思想是, 序列数据中的每个元素都与序列中其他元素有着关联关系, 通过计算元素之间的相对重要性来捕捉元素之间的长期以来关系. 具体而言, 自注意力机制计算序列中的每个元素和其他元素之间的相似度, 并将相似度归一化为注意力权重, 然后将每个元素与对应的权重进行加权求和即得到自注意力机制的输出. 自注意力机制计算如式(1):

$ Attention(Q, K, V) = {\mathit{Softmax}}\left(\frac{{Q{K^{\mathrm{T}}}}}{{\sqrt {{{{d}}_k}} }}\right)V $

(1)

其中, Q, K, V表示输入序列经过线性变换生成的查询向量、键向量和值向量. $\sqrt {{{{d}}_{{k}}}} $表示对$Q{K^{\mathrm{T}}}$进行d维缩放.

自注意力机制同时关注序列中的所有元素, 通过并行计算捕捉序列中每个元素之间的全局依赖关系^[18], 从而实现全局性的关注和表征.

多头自注意力机制通过将注意力机制扩展为多个head, 然后分别计算每个head的Attention, 最后将结果进行拼接, 通过全连接层输出得到结果. 多头自注意力机制计算如式(2):

$ MultiHead(Q, K, V) = Concat(hea{d_1}, \cdots, hea{d_h}){W^o} $

(2)

其中, $hea{d_{{i}}} = Attention(Q{W_i^Q}, K{W_i^K}, V{W_i^V})$, ${W_{{i}}^{\text{*}}}$表示与第i个head对应的向量的训练权重参数, ${W^{{o}}}$是输出变换矩阵. 多头自注意力机制能够从不同角度对输入序列进行关注, 从而获得更为丰富的表示.

1.2 软聚类算法

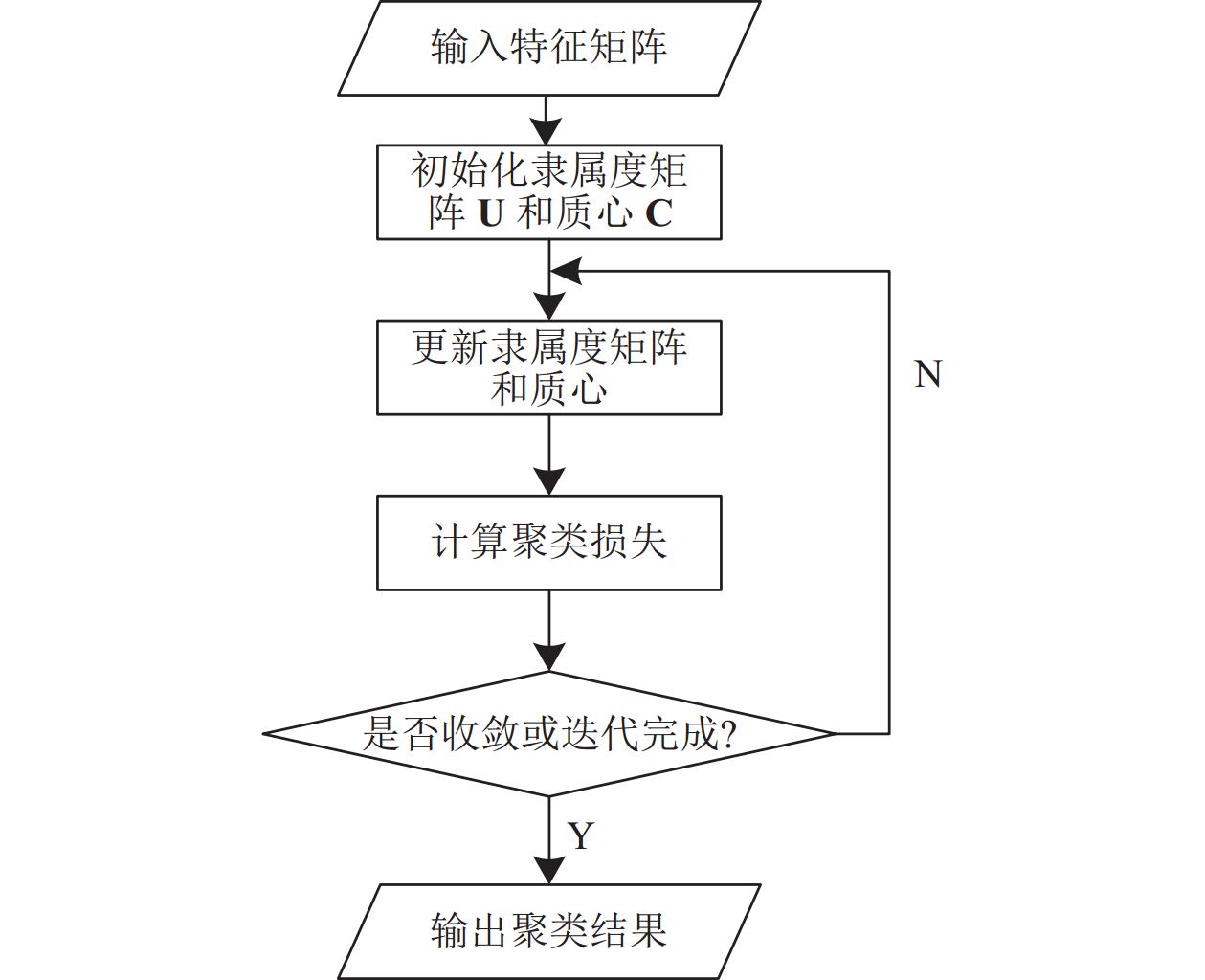
在多视图聚类中, 每个视图都包含着数据的不同方面的信息, 这些信息被视为不同的特征. 软聚类是一种聚类方法(如模糊C均值聚类), 它将每个数据点分配到每个聚类的概率, 而不是将其硬性分配到一个聚类中^[19]. 软聚类算法是根据样本点之间的相似度进行聚类, 从而使得类内相似度最大, 类间相似度最小. 模糊C均值聚类是通过优化目标函数得到每个样本对质心的隶属度, 从而决定样本点的类属以达到自动对样本数据进行分类的目的^[20]. 模糊C均值聚类算法流程图如图1所示.

模糊C均值聚类算法优化目标损失函数如式(3):

$ {{{L}}_{\text{cluster}}} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{{({u_{ij}})}^\rho }} } ||{{\mathbf{x}}_i} - {{\mathbf{c}}_j}{||^2} $

(3)

其中, n表示样本总数, m表示聚类数, $ \rho $表示样本是否属于某一类的重要程度, $ {u_{ij}} $表示样本$ {{\mathbf{x}}_i} $属于j类的隶属度值, $ {{\mathbf{x}}_i} $表示样本X中的数据点, $ {{\mathbf{c}}_j} $表示质心, $ || \cdot{ ||^2} $表示计算样本到质心的距离.

隶属度的计算如式(4):

$ {{u}}_{ij}=\frac{1}{{\displaystyle \sum _{\alpha=1}^{m}{\left(\frac{{d}_{ij}}{{d}_{i\alpha}}\right)}^{\frac{2}{m-1}}}}\text{, }其中{{d}}_{ij}=\left|\right|{{\bf{x}}}_{i}-{{\bf{c}}}_{j}|{|}^{2} $

(4)

聚类中心(质心)的更新如式(5):

$ {\bf{c}}_{j}=\frac{1}{{m}_{i}}{\displaystyle \sum _{j=1}^{m}{({u}_{ij})}^{\rho }}{{\bf{x}}}_{i}\text{, }其中{{m}}_{j}={\displaystyle \sum _{j=1}^{m}{({u}_{ij})}^{\rho }} $

(5)

1.3 基于图自编码器的深度聚类算法

基于图学习的聚类算法, 其主要思想是对不同视图中的节点进行匹配, 然后通过匹配结果来获得节点之间的相似度, 最终将节点聚类到不同的簇中. 考虑到浅层图聚类算法, 难以将图的拓扑结构和节点内容用于聚类中, 研究人员提出了基于深度学习的图聚类算法^[21]. 主要包括图卷积神经网络嵌入表示学习的方法^[22]、结合图神经网络GNN与自编器融合的图自编码器GAE^[23]和变分图自编码器VGAE^[24]嵌入表示学习方法. 图自编码器(graph auto-encoder, GAE)使用GCN作为编码器, 通过将节点属性信息和结构信息输入编码器来得到节点潜在表示, 然后使用特定激活函数作为解码器将潜在表示进行重构. 由于GAE在一般聚类任务中难以构建数据的图结构, Li等人^[23]提出了基于自适应图自编码器(AdaGAE)聚类算法, 根据图的生成视角自适应地构建图. 构建邻接矩阵时, 自适应方法可以解决k值难以确定的问题.

AdaGAE算法在编码器中采用两层GCN网络来对数据节点属性信息和结构信息进行学习, 然后得到潜在表示. 算法提出用条件概率$ p(x\mid {x_i}) $来代表节点之间的连通分布(即结构信息), 其中$\displaystyle\sum\limits_{j = 1}^{{n}} {p({x_j}\mid {x_i})} = 1$, 且$p({x_j}\mid{x_i}) \ne p({x_i}\mid{x_j})$. 然后计算编码器训练得到的潜在表示$ {\bf Z} $之间的距离${{{\hat d}}_{ij}} = ||{{\textit{z}}_i} - {{\textit{z}}_j}||_2^2$, 并在解码器中采用归一化方法来重构连通分布:

$ {{{q}}_{ij}} = \frac{{\exp ( - {{\hat d}_{ij}})}}{{\displaystyle\sum\limits_{i = 1}^{{n}} {\exp ( - {{\hat d}_{ij}})} }} $

(6)

并采用KL散度衡量两个分布之间的差异(即重构损失), AdaGAE算法的目标损失函数为:

$ \mathop {{\text{min}}}\limits_{q, {\bf{Z}}}\left\{ \sum\limits_{i, j = 1}^n {p({x_j}\mid{x_i})} \lg \frac{1}{{q({x_j}\mid{x_i})}} + \lambda {\rm{tr}}({{{\bf Z}\tilde {\bf L}}}{{\bf{Z}}^{\mathrm{T}}})\right\} $

(7)

其中, $ {\bf{L}} $表示拉普拉斯矩阵. 公式第1项表示重构损失, 第2项表示图约束. 公式的具体推导过程可参考文献[23].

2 多样性引导的深度多视图聚类算法

为了学习各视图节点属性信息和结构信息的多样性, 本文在AdaGAE算法基础上将其扩展为多视图聚类模型, 提出了多样性引导的深度多视图聚类(D2MVC)算法. 设计了融合多头自注意力机制的软聚类模块从全局和局部角度学习各视图多样性, 并选择以视图权重来体现多样性.

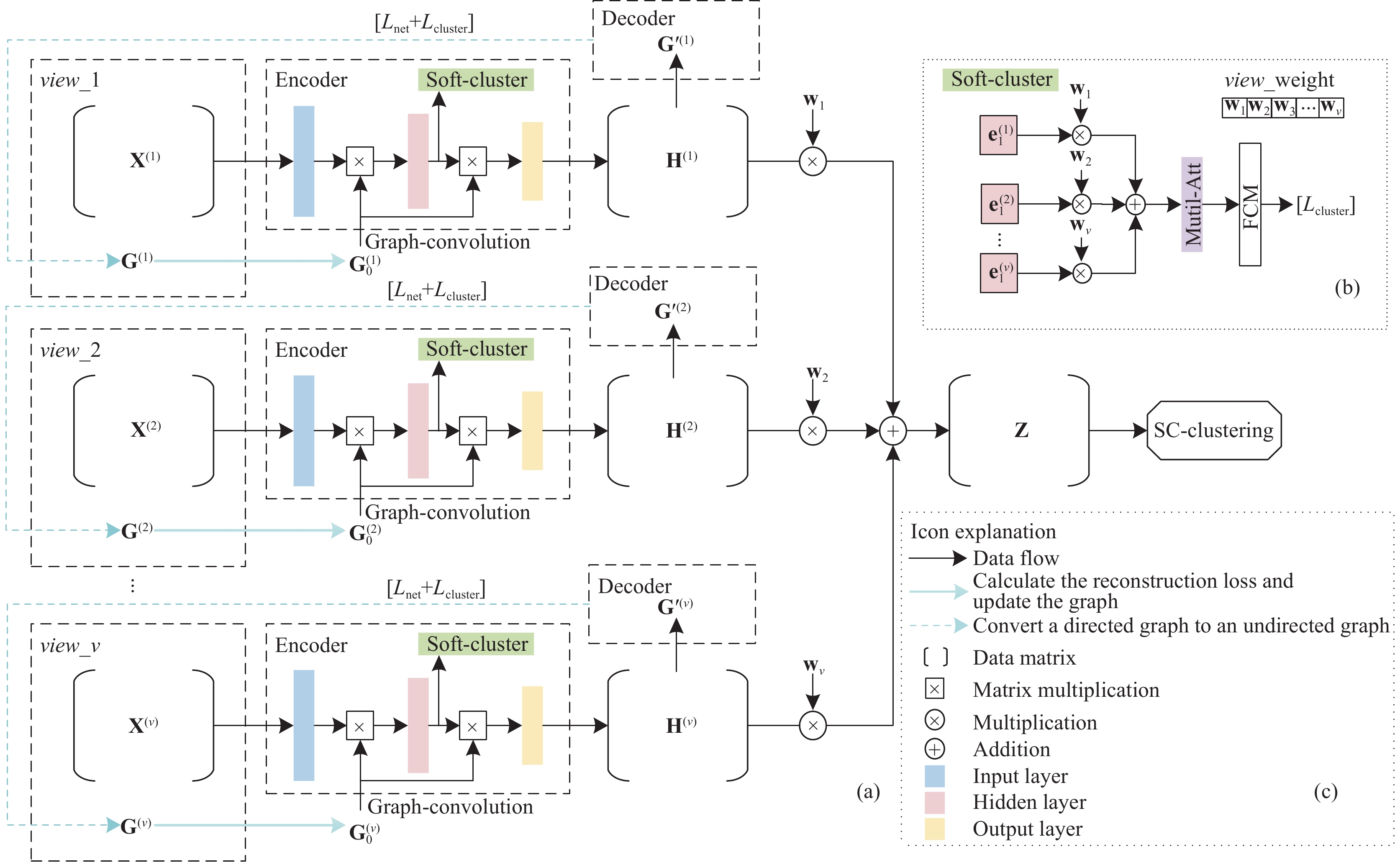
D2MVC的网络结构由编码器、解码器和软聚类模块组成, 如图2所示. 其中(a)为模型整体网络结构, (b)为学习多样性信息的软聚类模块, (c)为网络结构图中出现的线条及符号解释面板. 其中面板(a)中view_i表示第i个视图, Encoder表示图编码器, Decoder表示使用特定函数的解码器, soft-cluster表示学习各视图多样性信息的软聚类模块, L_net表示网络训练损失, L_cluster表示软聚类模块聚类损失. 面板(b)中view_weights表示各视图权重, Mutil-Att表示多头自注意力机制, FCM表示模糊C均值聚类算法. 图2中涉及符号定义如表1所示.

2.1 融合多头自注意力机制的软聚类模块

本文将不同视图多样性信息以聚类损失的形式反馈给编码器网络, 提出了学习视图多样性信息的软聚类模块. 首先通过图卷积操作将节点属性信息和结构信息进行融合得到信息矩阵$ {\bf{e}}_1^{(s)} $(即编码器隐藏层输出), $ {\bf{e}}_1^{(s)} $为软聚类模块的输入. 然后采用均匀分布初始化质心, 采用概率分布初始化权重:

$ {\mathbf{C}} = [{{\mathbf{c}}_1}, {{\mathbf{c}}_2}, \cdots, {{\mathbf{c}}_m}] $

(8)

$ {{\bf{w}}_1} = {{\bf{w}}_2} = \cdots = {{\bf{w}}_v} = \frac{1}{v} $

(9)

再通过加权融合得到特征矩阵$ F $, 其中$ F = \displaystyle\sum\limits_{s = 1}^v {{\bf{w}}_s} {\mathbf{e}}_1^{(s)} $. 然后输入多头自注意力机制中学习特征矩阵的全局多样性.

$ \left\{ \begin{array}{l} F{'}=MultiHead(Q, K, V)=Concat(hea{d}_{1}, \cdots, hea{d}_{h}){W}^{o}\\ 其中{{head}}_{h}=Attention(Q{W}^{Q}, K{W}^{K}, V{W}^{V}), \\ Q=K=V=F\end{array} \right.$

(10)

$ F' $为多头自注意力机制的输出, 再将$ F' $输入模糊C均值聚类算法中学习特征矩阵的局部多样性, 因此聚类目标损失函数由式(3)更改为:

$ {{{L}}_{\rm{cluster}}} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{{({u_{ij}})}^\rho }} } ||F{'_i} - {{\mathbf{c}}_j}|{|^2} $

(11)

其中, $ F{'_i} $表示第i个样本的特征向量, $ {{\mathbf{c}}_j} $表示第j个质心向量. 隶属度矩阵和质心更新如式(12)和式(13)所示:

$ {{u}}_{ij}=\frac{1}{{\displaystyle \sum _{c=1}^{m}{\left(\frac{{d}_{ij}}{{d}_{cj}}\right)}^{\frac{2}{m-1}}}}{, }\;其中{{d}}_{ij}=\left|\right|F'_{i}-{\bf{c}}_{j}||^{2} $

(12)

$ {{\bf{c}}}_{j}=\frac{1}{{m}_{i}}{\displaystyle \sum _{j=1}^{m}{({u}_{ij})}^{\rho }}{{F}}'_{i}{, }\;其中{{m}}_{j}={\displaystyle \sum _{j=1}^{m}{({u}_{ij})}^{\rho }, \rho =1} $

(13)

软聚类模块算法流程简单描述如算法1.

算法1. 软聚类模块算法流程

输入: 各视图隐藏层输出$\scriptstyle {\bf{e}}_1^{(v)} $, head;

输出: 软聚类损失$\scriptstyle {L_{\rm{cluster}}} $, 视图权重$\scriptstyle view\_w $.

1) 根据式(8)、式(9)初始化质心和权重;

2) 将隐藏层输出进行加权融合$\scriptstyle F $, 根据式(10)得到$\scriptstyle F' $;

3) 将$\scriptstyle F' $输入到式(11)中得到聚类损失$\scriptstyle {L_{\rm{cluster}}} $;

4) 根据式(12)更新质心, 通过聚类损失的反向传播来实现对权重的正修剪或负修剪的更新;

5) 检测迭代是否完成, 若未完成则返回2), 重复执行2)–5). 若迭代完成, 则输出$ \scriptstyle {L_{\rm{cluster}}} $和$\scriptstyle view\_w $.

2.2 网络结构

D2MVC的网络结构包括编码器、解码器、软聚类模块. 编码器由两层GCN网络组成, 负责将数据节点属性信息和结构信息进行联合学习, 得到低维潜在表示; 解码器则通过特定函数对低维潜在表示进行重构. 软聚类模块则通过多头自注意力机制和模糊C均值聚类算法学习视图多样性信息.

在式(7)的基础上, 将其扩展到多视图的网络损失如下:

$ {L_{\rm net}} = \left\{ \begin{gathered} {\rm{min}}\sum\limits_{{{s}} = {{1}}}^{{v}}\Bigg\{ {\sum\limits_{i = 1, j = 1}^{{n}} {{p^{(s)}}({x_j}\mid{x_i})\lg \frac{1}{{{q^{(s)}}({x_j}\mid{x_i})}}} }\Bigg. \\ \quad \;\;\Bigg.+\lambda {\mathrm{tr}}({{\bf{H}}^{(s)}}{{\tilde {\bf{L}}}^{(s)}}{{\bf{H}}^{(s){\mathrm{T}}}})\Bigg\} \\ {\text{s.t. }}{{\tilde {\bf{L}}}^{(s)}} = {{\tilde {\bf{D}}}^{(s)}} - {{\tilde {\bf{A}}}^{(s)}}, {{\tilde {\bf{D}}}^{(s)}} = {{\bf{D}}^{(s)}} + {\bf{I}}, \\ \quad\;\;{{\tilde {\bf{A}}}^{(s)}} = {{\bf{A}}^{(s)}} + {\bf{I}} \\ \end{gathered} \right. $

(14)

其中, 第1项为KL散度计算重构损失, 第2项为图的自动约束性. $ \lambda $为图约束惩罚项. $ {{v}} $表示视图总数, $ {{n}} $表示样本总数, $ {x_i} $表示第i个样本点, $ \tilde {\bf{D}} $表示度矩阵, $ {\bf{D}} $表示对角线为0的度矩阵. $ {\tilde {\bf{A}}_{{{ij}}}} = {\mathbf{A}} + {\mathbf{I}} $, $ \tilde {\bf{L}} $表示拉普拉斯矩阵, $ \tilde {\bf{A}} $表示邻接矩阵, $ {\bf{A}} $表示对角线为0的邻接矩阵, $ {\bf{I}} $表示对角线为1的单位矩阵.

本文提出算法目标函数主要包括网络损失和软聚类模块损失, 如式(15)所示:

$ {L_{\rm loss}} = {L_{\rm net}} + \beta {L_{\rm cluster}} $

(15)

其中, $\; \beta $为软聚类损失惩罚项.

最后将网络训练得到每个视图对应潜在表示$ {\bf{H}}^{(s)} $和视图权重$ {{\bf{w}}_s} $进行加权融合得到共识表示矩阵$ {\bf{Z}} $:

$ {\bf{Z}} = \sum\limits_{s = 1}^v {{{\bf{w}}_s}{{\bf{H}}^{(s)}}} $

(16)

D2MVC算法的目标是为了得到共识表示, 并通过谱聚类得到最终的聚类结果. 算法的输入包括各视图对应节点属性矩阵和结构信息矩阵(即k-邻接矩阵), k值是算法中设定的邻接样本数目, 输出为谱聚类算法得到的聚类标签向量. 算法流程为: 首先将数据节点属性信息和结构信息一同输入到图编码器中, 将得到的编码器中隐藏层输出$ {\bf{e}}_1^{(s)} $作为软聚类模块的输入, 编码器输出潜在表示$ {\bf{H}}^{({s})} $; 再将潜在表示使用特定函数重构为邻接矩阵$ {{\bf{G}}'^{(s)}} $, 同时通过式(14)计算网络损失L_net, 在软聚类模块中通过式(11)计算软聚类损失L_cluster, 并通过式(15)计算总体损失loss, 训练网络时使用Adam优化算法最小化loss, 以求得各视图的最佳潜在表示; 当迭代结束或k值达到设定最大值时, 将潜在表示和软聚类模块更新输出的权重代入式(16)计算得到共识表示, 最后采用谱聚类算法输出得到一组标签向量. 具体算法流程描述如算法2.

算法2. D2MVC算法流程

输入: 多视图数据集$\scriptstyle \left\{ {X_{{i}}^{(s)}} \right\}_V^{n} $, head, $\scriptstyle \lambda $, $\scriptstyle \beta $, $\scriptstyle \gamma $, k₀, k_m, $\scriptstyle T$;

输出: 聚类结果标签向量$\scriptstyle Y$.

1) 初始化各视图权重$\scriptstyle view\_w $, 计算各视图k邻接图$\scriptstyle {\bf{G}}$$\scriptstyle ({{k}} = {{{k}}_{{0}}}) $, $\scriptstyle iter = 0 \scriptstyle (iter \leqslant T)$;

2) 将数据特征信息和结构信息输入编码器, 得隐藏层输出$ \scriptstyle {\bf{e}}_1^{(s)} $、低维潜在表示$\scriptstyle {\bf{H}}^{(s)} $;

3) 将隐藏层输出$\scriptstyle [{\bf{e}}_1^1, {\bf{e}}_1^2, \cdots, {\bf{e}}_1^{(v)}] $、head输入软聚类模块, 得到聚类损失$\scriptstyle {L_{{\text{cluster}}}} $和视图权重$\scriptstyle view\_w $;

4) 重构低维潜在表示邻接图$ \scriptstyle {{\bf{G}}'^{(s)}} $, 计算网络重构损失$\scriptstyle {L_{{\text{net}}}}$;

5)将$\scriptstyle {L_{{\text{cluster}}}}$和$\scriptstyle {L_{{\text{net}}}}$代入式(15)得到总体loss, 然后采用Adam优化算法最小化loss;

6) 如果$\scriptstyle {{iter}} \leqslant {{T}}$或$ \scriptstyle {{k}} \leqslant k_m$, k+1, iter+1, 计算各视图k+1邻接图, 重复执行步骤2)–5);

7) 若$\scriptstyle {iter}> {T} $或$\scriptstyle {k}> k_m$: 根据式(16)得到共识表示矩阵$ \scriptstyle {\bf{Z}} $;

8) 将共识表示矩阵采用谱聚类得到聚类标签向量$ \scriptstyle Y $, 并输出$ \scriptstyle Y $.

算法2中head为多头自注意力机制的参数, $ \gamma $表示学习率, k₀、k_m分别表示初始邻居值和终止值, ${{T}}$表示迭代次数.

3 实验分析 3.1 数据集

为了评估D2MVC的性能, 在数据集Yale、UCI-digit和3Sources上, 与3个单视图聚类算法、7个多视图聚类算法分别进行了对比实验. 并采用4种常用的性能评价指标对聚类效果进行评估, 主要包括准确率(ACC)、归一化互信息(NMI)、F1 (F-measure)、AR. 具体数据集描述如表2所示.

Yale数据集: 包含15个人分别在不同情况下形成的11张图像, 共有165张图像. 实验中主要采用intensity(4096维)、LBP (3304维)以及Gabor (6750维)这3种类型特征构造三视图数据.

UCI-digit数据集: 包含手写体数字0–9共10类样本图片, 共有2000张图像. 实验中主要采用轮廓相关性特征(216维)、傅里叶系数矩阵(76维)以及Karhunen-Love系数矩阵(64维)这3种类型特征构造三视图数据.

3Sources数据集: 包含6类416篇新闻数据, 其中169篇文章来自3家不同媒体(BBC、Guardian和Reuters). 实验使用来自3家媒体的数据来构造三视图数据.

3.2 对比算法

为了验证本文算法的有效性, 本文与多种聚类算法进行了对比.

(1)单视图聚类算法

SC^[25]: 使用谱聚类算法在每个视图上进行聚类, 然后取最好的单视图聚类结果.

GAE^[26]: 使用图自编码器获得低维潜在表示用于聚类的单视图聚类算法.

AdaGAE^[23]: 采用自适应k近邻构建邻接图, 将图结构信息输入图自编码器以获得低维潜在表示的单视图聚类算法.

(2)多视图聚类算法

DiMSC^[27]: 利用希尔伯特-施密特独立性准则(HSIC)作为多样性正则化方法, 从全局探索多视图之间的互补性信息.

AMGL^[28]: 通过对谱聚类模型进行修改以实现自适应权值的分配, 可用于多视图聚类和半监督任务.

LMSC^[29]: 从全局角度利用多视图数据的互补信息, 并同时寻找潜在的共同表示, 使用更全面的信息来提高聚类的有效性.

ECMSC^[30]: 提出在模型中引入位置感知排他项来利用不同视图自表示矩阵之间的差异性, 排他性项强制两个矩阵相同位置为零, 即鼓励两个矩阵尽可能地多样化, 是从局部考虑不同视图之间的多样性.

CSMSC^[31]: 提出一致性和多样性学习分为两个步骤, 将一致性公共自表示矩阵与每个视图的特异性自表示矩阵结合起来, 特异性用来从全局捕获每个视图的固有差异.

GMC^[32]: 提出一种新的融合技术, 从全局角度学习权重信息, 并对各个视图图矩阵进行自动加权, 从而得到统一的图矩阵用于聚类.

MCLES^[33]: 利用一种潜在的嵌入表示来利用不同视图的全局互补信息, 再根据嵌入表示学习全局结构, 进一步利用全局结构得到聚类指标矩阵.

3.3 实验结果与分析

表3–表5给出不同聚类算法在3个数据集上的实验结果, 表中加粗字表示最优结果. 对比实验中, D2MVC在各项指标上基本取得最优结果. 与单视图聚类算法相比, 在3个数据集上所提算法的聚类性能最好, 证明了多视图聚类算法比单视图聚类算法具有优越性. 与多视图聚类算法相比, 在Yale数据集上, 所提算法在ACC和NMI方面分别提高了3.46%和0.36%, 但在F1和AR方面低于次优算法DiMSC, 这是因为DiMSC算法使用HSIC考虑了自表示矩阵之间的相关性, 本文算法未考虑相关性, 因此得到的聚类结果与真实分类之间的差异性较大(F1、AR值较低); 在UCI-digit数据集上, 所提算法在ACC、NMI、F1、AR方面分别提高了3.82%、1.26%、6.39%和2.79%; 在3Sources数据集上, 所提算法在ACC、NMI、F1、AR方面分别提高了4.93%、0.26%、2.95%和2.41%. 实验结果表明: 本文提出的加入软聚类模块从全局和局部学习各视图多样性信息的D2MVC算法优于其他只考虑全局多样性或局部多样性的聚类算法, 因此可以得出同时考虑全局多样性和局部多样性信息可以提高模型的聚类性能.

为了验证软聚类模块中多头自注意力机制对全局多样性信息学习和模糊C均值算法对局部多样性信息学习对提高多视图聚类算法性能的有效性, 进行了消融实验. 消融实验为不同学习策略下的对比实验, 主要包括无多样性信息学习的简单融合实验(add)、有局部多样性信息学习的简单融合实验(fcm-add)、局部和全局多样性信息学习的融合实验(fcm-sa-add)、采用加权融合的实验(fcm-sa-add_w). 从表6中可以看到, 加入融合多头自注意力机制的软聚类模块在3个数据集上相对于其他学习策略均取得最优结果. 实验结果证明融合了多头自注意力机制的软聚类模块能提高算法聚类性能.

3.4 参数分析

D2MVC中参数$T$, k₀, k_m, head是根据经验来给定的, 学习率$\gamma $、图约束惩罚项$\lambda $和软聚类损失惩罚项$ \;\beta $则是通过网格搜索法来确定. 因为Yale数据集和3Sources数据集均为小样本, 故[k₀, k_m]=[5, n/c], UCI-digit数据集中[k₀, k_m]=[20,30]. 实验证明, 当$T = 20$时, 在Yale和UCI-digit数据集上模型聚类性能最优; $T = 10$时, 在3Sources数据集上模型聚类性能取得最优; $\gamma $为0.001时, 所提算法在3个数据集上聚类性能最优.

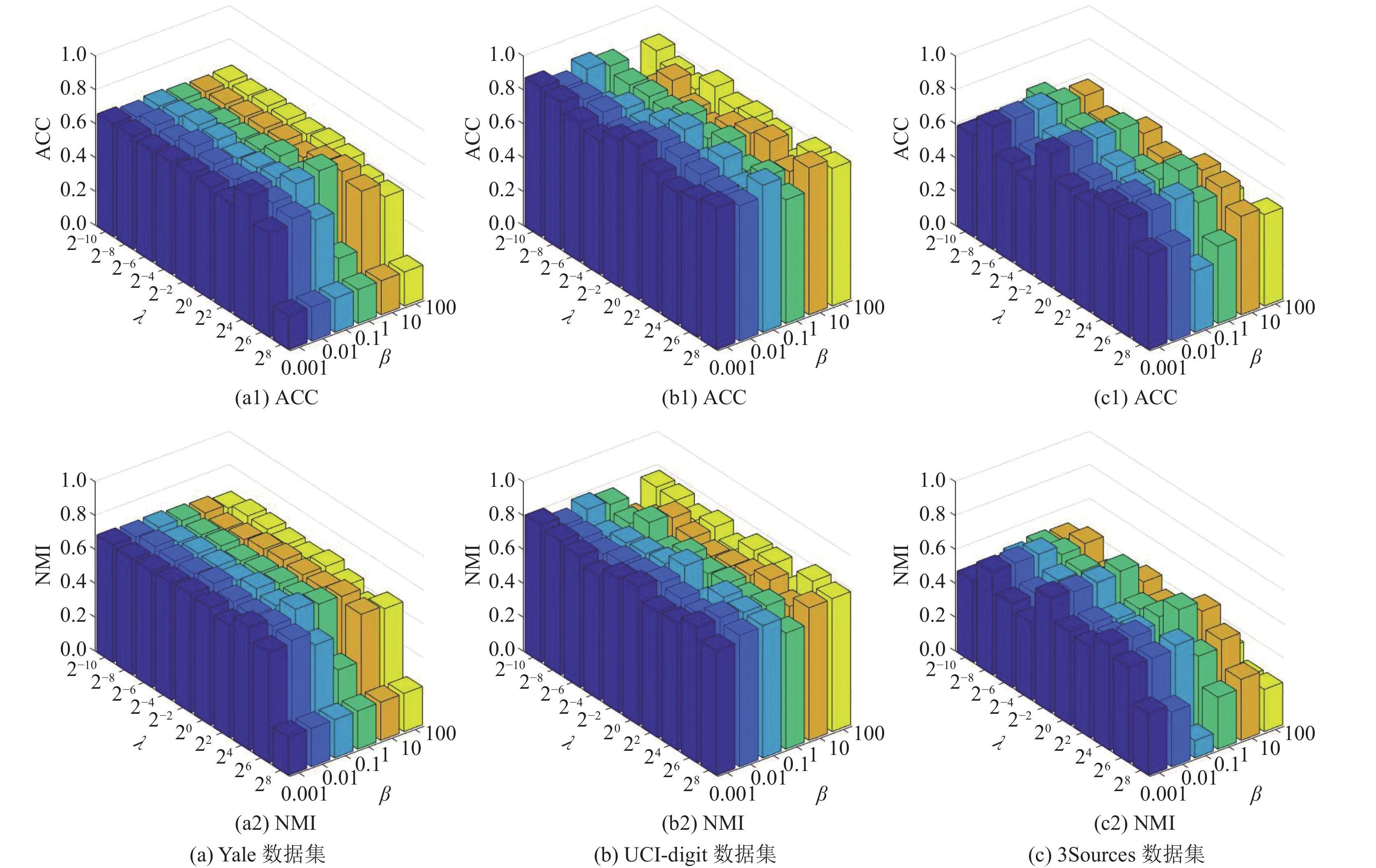
模型对参数的敏感度如图3所示, 其中$\lambda \in [2^{-10}, 2^8]$, $\;\beta \in [0.001, 100.0]$. 由图可知, 在Yale数据集上, 参数$\lambda $在[2⁻¹⁰, 2⁴]时, 算法稳定性较好, 且在$\lambda=2^4 $, $\;\beta=1.0 $, head=2时取得最优值; 在UCI-digit数据集上, 参数$\lambda $和参数$\;\beta $在所给范围内, 算法基本保持稳定, 且在$\lambda =1.0$, $\;\beta=0.001$, head=2时取得最优值. 在3Sources数据集上, 算法稳定性略有下降, 这是因为算法对于稀疏特征矩阵学习具有一定的敏感性, 导致ACC和NMI在区间内波动较大, 在$\lambda =2^{-2}$, $\;\beta =1.0$, head=4时取得最优值.

观察Yale数据集和3Sources数据集在$\lambda $参数过大时, 算法的聚类效果不太理想, 通过实验发现在Yale数据集上, 算法使用较大的$\lambda $参数会出现欠拟合的情况. 由于以上两个数据集均为小样本, 因此可以得出在小样本数据集上, $\lambda $参数不宜过大.

4 结束语

本文针对多视图聚类中各视图的多样性信息学习, 提出了融合多头自注意力机制的软聚类模块, 从全局和局部角度全面学习各视图多样性信息. 在深度图自编码器网络中引入软聚类模块, 提出了多样性引导的深度多视图聚类(D2MVC)算法. 算法将各视图的节点属性信息和结构信息输入到软聚类模块中, 然后联合优化模块得到的聚类损失和网络损失, 以实现多样性信息引导潜在表示生成的目的. 实验结果证明, 提出的融合多头自注意力机制的软聚类模块可以提高算法聚类性能. 虽然算法在Yale数据集和UCI-digit数据集上表现稳定, 然而在3Sources数据集上稳定性略有下降. 因此, 下一步研究工作将致力于改进算法以适应稀疏特征矩阵聚类.