1 引言

随着移动设备广泛使用和私有数据急剧增长, 依托大数据的机器学习技术实现了在云端的集中式训练. 但由于本地终端设备数据涉及敏感的个人信息, 集中式训练易引发隐私泄露风险, 使用户不愿上传数据至云端^[1,2]. 为解决集中式训练存在的数据安全问题, 谷歌提出了一种新型的分布式机器学习-联邦学习(federated learning, FL)^[3]. FL通过去中心化方式, 实现了数据在各终端设备上的本地存储和模型参数更新, 从而实现模型的协同训练. 然而, 在FL中, 为确保模型训练达到既定精度, 大量模型参数需跨复杂网络多轮传输, 导致网络拥塞和通信故障等问题^[4]. 针对上述题, 分层联邦学习应运而生^[5]. 终端设备将本地更新的模型参数上传到边缘服务器用于中间聚合, 并上传至SP下的云服务器实现全局聚合.

在HFL中, 参与学习任务的终端设备需耗费计算、通信等资源. 如果没有足够的补偿, 终端设备无偿地贡献其资源是不切实际的^[6], 同时, HFL架构中存在梯度反演、搭便车攻击、成员推理攻击等安全隐患, 这些威胁可能导致终端设备数据部分泄露, 从而削弱终端设备的参与动机. 因此有必要设计一种有效的激励机制来激励终端设备参与并上传训练后的模型参数. 同时, 目前基于HFL的激励机制多采用博弈论的思想对参与方与联邦的关系进行建模, 来求解满足系统收益最大化的最优解. 然而, 通过整理相关研究可以发现, 现有工作假设终端设备、边缘服务器以及云服务器的博弈过程是信息对称的. 这种假设与FL保护终端设备隐私信息的初衷是相违背的^[7].

针对上述问题, 在本文中提出了一种隐私保护的学习博弈HFL激励机制. 在边端层, 边缘服务器采用多维度契约论设计不同类型的多维合约鼓励终端设备在不泄露参与成本的前提下传输模型参数. 在云边层, 使用Stackelberg博弈建模边缘服务器与云服务器关于模型参数大小和其单位价格之间的交互关系, 并证明了存在唯一的斯塔克伯格均衡. 此外, 本文采用多智能体深度强化学习方法, 在保障边缘服务器和云服务器隐私的前提下逐步逼近SE. 通过实验分析, 首先验证了提出的分层激励机制的有效性. 然后与其他基线方法比较, 提出的分层激励机制使云服务器的收益提升了接近11%, 单位成本获取增益提升接近18倍.

2 相关工作

基于HFL激励机制设计^[8,9]工作中, 文献[8]提出了ODAM-DS算法. 该算法基于在线双边拍卖机制, 优化边缘服务器在限定时间内选择移动设备, 以降低能耗. 针对实际场景中终端设备存在自私性的问题, 文献[9]提出一种基于博弈论的激励机制. 在激励预算有限的条件下, 得到了终端设备和边缘服务器之间的均衡解和最小的边缘模型训练时延. 然而上述文献聚焦于边缘服务器和终端设备之间关于激励策略的交互设计, 忽略了云服务中心和边缘服务器之间的策略交互设计.

在基于演化博弈激励机制设计^[4,10]的现有工作中, 文献[10]提出了一个层次化博弈框架, 该框架利用演化博弈来模拟FL工作者与边缘服务器的动态关联, 并使用Stackelberg博弈来建模边缘服务器和模型所有者的最优带宽分配和奖励分配策略. 同时文献[4]针对HFL研发出资源分配及激励机制框架, 并应用演化博弈理论解决集群选择问题, 同时引入基于深度学习的拍卖机制评估集群头节点服务, 并通过性能评估证明了改方案的稳定性和效益.

在基于 Stackelberg博弈激励机制设计^[11–15]的现有工作中, 文献[11]将移动设备之间的交互构建为演化博弈, 同时将多边缘服务器之间的竞争构建为非合作博弈, 提出了基于多领导者 Stackelberg 博弈的激励机制, 该机制通过调整移动设备和边缘服务器的策略, 解决了收益的最优化问题. 文献[12]将端-边-云系统中的分层训练过程映射为通过实用函数相互连接的子博弈, 其中这些函数描述了每一层的实际价格情况, 并采用逆Stackelberg博弈理论方法来分析博弈过程, 进而指导参与者有效地获取所需的数据资源和利润. 文献[13]在边缘服务器和终端设备间使用联盟博弈进行边缘关联和带宽分配, 云中心和边缘服务器间采用Stackelberg博弈来优化边缘聚合次数和云服务器的奖励, 文献[14]提出了三阶段Stackelberg博弈, 旨在模型所有者、集群头和无人机工作者之间建立一个层次化的互动模型, 以优化资源分配和学习效率. 文献[15]进一步基于HFL将单轮的激励机制优化为多轮的激励机制, 其中结合了基于拍卖的算法和组合多臂老虎机方法, 解决了客户端选择的挑战, 也最小化了HFL的训练延迟. 然而上述研究聚焦于对称信息下的激励机制设计, 其中对称信息的假设与HFL保护隐私的意图相违背. 因此, 在保护终端、边缘服务器和云服务器隐私的前提下, 本文提出了一种基于学习博弈和契约论的分层联邦学习激励机制.

3 系统模型

本节涉及的核心变量如表1所示.

3.1 系统模型

如图1所示, HFL架构由一个云服务器, $M$个边缘设备, $N$个终端设备组成, 其中${N_{{m}}}$表示第$m$个边缘服务器内的终端集合, ${n_m}$表示第$m$个边缘服务器下第$n$个终端设备, 考虑完全同步的FL, 此架构完成一次全局训练过程如下.

(1)终端设备: 终端设备${n_m}$从边缘服务器接收全局模型${w^{\textit{z}}}$, 并利用本地数据$ {x_{m, n}}{D_{}} $进行模型训练. 其中${\textit{z}}$代表第${\textit{z}}$次全局聚合, $ D $表示终端设备${n_m}$可收集的最大数据量, ${x_{m, n}}$表示终端设备${n_m}$收集数据的比例, 通过最小化损失函数训练完成后^[5], 终端设备${n_m}$将更新后的本地模型参数$w_{m, n}^{{\textit{z}}, \sigma }$上传至边缘服务器$m$, 并获得来自边缘服务器$m$的奖励, 其中$\sigma $表示终端设备${n_m}$本地迭代次数. 终端设备${n_m}$在参与上述训练过程中会有一定成本, 即数据采集成本, 模型训练成本以及模型传输成本. 参考文献[16], 由于终端设备${n_m}$需收集数据参与训练, 其数据采集成本定义如下:

$ C_{m, n}^{{\text{col}}} = \lambda _{m, n}^{{\text{col}}}{x_{m, n}}D $

(1)

其中, $ \lambda _{m, n}^{{\text{col}}} $表示终端设备${n_m}$数据采集的单位成本.

参考文献[16], 终端设备${n_m}$本地模型训练成本定义如下:

$ C_{m, n}^{{\text{com}}} = \lambda _{m, n}^{{\text{com}}}D\sigma {x_{m, n}}s\eta {\kappa _{m, n}}f_{m, n}^2 $

(2)

其中, $\lambda _{m, n}^{{\text{com}}}$表示终端设备${n_m}$本地模型训练的能量消耗的单位成本, $s$表示单位数据量的比特数, $ \eta $表示终端设备${n_m}$处理单位比特数的数据需要的算力, ${\kappa _{m, n}}$表示有效电容开关, $f_{m, n}^{}$表示终端设备${n_m}$提供的算力.

此外, 终端设备${n_m}$会因与边缘服务器$m$通信产生一定的传输成本, 则模型传输成本定义如下:

$ C_{m, n}^{{\text{upl}}} = \lambda _{m, n}^{{\text{upl}}}{d_{m, n}}\left( {{t_{\max }} - \frac{{D{x_{m, n}}\eta s}}{{{f_{m, n}}}}} \right) $

(3)

其中, $\lambda _{m, n}^{{\text{upl}}}$表示终端设备${n_m}$传输更新的本地模型参数的能量消耗的单位成本, ${d_{m, n}}$表示传输功率, ${t_{\max }}$表示本地模型训练以及更新后的模型参数上传至边缘服务器$m$的总时间.

(2)边缘服务器: 边缘服务器$m$对汇集的模型参数进行整合, 并将聚合后的参数$ w_m^{{\textit{z}}, \tau \sigma } = \displaystyle\sum\nolimits_{n \in {N_m}} {{{({x_{m, n}}w_{m, n}^{{\textit{z}}, \tau \sigma }} / {}}} $$\displaystyle\sum\nolimits_{n \in {N_m}} {{x_{m, n}})} $上传至云服务器, 其中$\tau $表示边缘服务器$m$的迭代次数, 作为回报, 边缘服务器$m$将从云服务器获得相应的奖励. 同时边缘服务器$m$利用契约论为终端设备${n_m}$设计最优多维合约, 终端设备${n_m}$选择使其收益最大化的多维合约.

(3)云服务器: 在云端, 服务器对模型参数进行全局聚合, 得到新的全局模型为:

$ {w^{{\textit{z}} + 1}} = \sum\limits_{m \in M} {\frac{{\displaystyle\sum\limits_{n \in {N_m}} {{x_{m, n}}} }}{{\displaystyle\sum\limits_{m \in M} {\displaystyle\sum\limits_{n \in {N_m}} {{x_{m, n}}} } }}} w_m^{{\textit{z}}, \tau \sigma } $

(4)

一旦更新完成, 新的全局模型随即被发送至边缘服务器$m$, 边缘服务器进一步将其下发给终端设备${n_m}$. 同时在确保模型性能满足的前提下, 云服务器会下发使其和边缘服务器$m$收益最大化的最优单位数据奖励. 由于终端设备${n_m}$所提供的数据越多, 模型精度就越准确, 同时随着数据量的增加, 训练的全局模型的准确性会以较慢的速度提升, 参考文献[7,17], 本文将模型训练的准确性定义为:

$ {A^{{\text{sp}}}} = \ln \left( {1 + \sum\limits_{m \in M} {\sum\limits_{n \in {N_m}} D } {x_{m, n}}} \right) $

(5)

上述3个步骤将循环迭代, 直至全局模型收敛.

3.1.1 终端设备收益

边缘设备经过$\tau $轮本地模型参数聚合后, 终端设备${n_m}$会收到来自第$m$个边缘服务器的奖励$ {r_{m, n}} $, 则终端设备${n_m}$的收益定义如下:

$ \begin{split} u_{m, n}^{ed} =& {r_{m, n}} - \lambda _{m, n}^{{\text{col}}}D{x_{m, n}} - \lambda _{m, n}^{{\text{com}}}\tau \sigma D{x_{m, n}}s\eta {\kappa _{m, n}}f_{m, n}^2 \\ & - \lambda _{m, n}^{{\text{upl}}}\tau {d_{m, n}}\left( {{t_{\max }} - \frac{{D{x_{m, n}}\eta s}}{{{f_{m, n}}}}} \right) \end{split} $

(6)

式(6)经过简化, 可重新定义如下:

$ u_{m, n}^{ed} = {r_{m, n}} - {\gamma _{m, n}}D{x_{m, n}} - {v_{m, n}}D{x_{m, n}} + {\varphi _{m, n}}D{x_{m, n}} - {\delta _{m, n}} $

(7)

其中, ${\gamma _{m, n}} = \lambda _{m, n}^{{\mathrm{col}}}$, ${{{v}}_{m, n}} = \lambda _{m, n}^{{\mathrm{com}}}\tau \sigma \eta s{\kappa _{m, n}}f_{m, n}^2$, ${\varphi _{m, n}} = {{\lambda _{m, n}^{{\mathrm{upl}}}\tau {d_{m, n}}\eta s} / {}}$${f_{m, n}}$, ${\delta _{m, n}} = \tau \lambda _{m, n}^3{t_{\max }}{d_{m, n}}$, 为了简化分析, 参考文献[16], $\delta $的值针对所有终端设备保持一致.

本文聚焦信息不对称场景. 边缘设备对于终端设备在参与FL任务的过程当中所产生的数据采集成本, 模型训练成本以及模型传输成本一概不知, 然而, 边缘设备可以通过历史记录获取到终端设备各个成本的分布情况, 因此边缘服务器$m$下某个终端设备可根据成本类型划分为3种, 分别定义为: $ {Y _m} = \{ {\gamma _{m, i}}:1 \leqslant i \leqslant {I_m}\} $, $ {\Lambda _m} = \{ {v_{m, j}}:1 \leqslant j \leqslant {J_m}\} $, ${\Psi _m} = \{ {\varphi _{m, k}}:1 \leqslant k \leqslant {K_m}\} $, 故第$m$个边缘服务器通信范围内共存在${I_m}{J_m}{K_m}$类型的终端设备. 边缘服务器$m$下某个终端设备属于类型$ {\gamma _{m, i}} $,$ {v_{m, j}} $, ${\varphi _{m, k}}$的概率定义为${q_{m, i, j, k}}({\gamma _{m, i}}, {v_{m, j}}, {\varphi _{m, k}})$, 可得出$ \displaystyle\sum\nolimits_{i \in I} {\displaystyle\sum\nolimits_{j \in J} {\displaystyle\sum\nolimits_{k \in K} {{N_m}} {q_{m, i, j, k}} = {N_m}} } $. 因此边缘服务器$m$下某个终端设备的成本类型可重新定义为$0 < {\gamma _{m, 1}} \leqslant {\gamma _{m, 2}} \leqslant \cdots $$ \leqslant {\gamma _{m, I}}$, $ 0 < {v_{m, 1}} \leqslant {v_{m, 2}} \leqslant \cdots \leqslant {v_{m, J}} $, $0 < {\varphi _{m, 1}} \leqslant {\varphi _{m, 2}} \leqslant \cdots \leqslant {\varphi _{m, K}}$, 边缘服务器$m$内上述3种成本类型的终端设备可定义为类型$ - (m, i, j, k)$. 类型$ - (m, i, j, k)$终端设备收益可重新定义如下:

$ \begin{split} u_{m, i, j, k}^{ed} = &{r_{m, i, j, k}} - {\gamma _{m, i}}D{x_{m, i, j, k}} \\ & - {v_{m, j}}D{x_{m, i, j, k}} + {\varphi _{m, k}}D{x_{m, i, j, k}} - \delta \end{split} $

(8)

其中, $ {r_{m, i, j, k}} $表示为类型$ - (m, i, j, k)$终端设备收到的来自第$m$个边缘服务器的奖励, $ {x_{m, i, j, k}} $表示为类型$ - (m, i, j, k)$终端设备收集数据的比例.

3.1.2 边缘服务器收益

在HFL架构中, 云服务器给予边缘服务器的奖励越高, 边缘服务器的满意度也相应越高, 但随着奖励逐渐递增, 满意度的边际效用会逐渐下降. 因此边缘服务器$m$的满意度定义为$ \displaystyle\sum\nolimits_{i \in I} {\displaystyle\sum\nolimits_{j \in J} {\displaystyle\sum\nolimits_{k \in K} {{N_m}} } } {q_{m, i, j, k}} \ln (1 + pD{x_{m, i, j, k}}) $, 其中$p$表示单位数据奖励, 同时边缘服务器会下发奖励以此激励终端设备参与到FL任务中, 则边缘服务器的激励支出可定义为$\displaystyle\sum\nolimits_{i \in I} \displaystyle\sum\nolimits_{j \in J} \displaystyle\sum\nolimits_{k \in K} {{N_m}{q_{m, i, j, k}}{r_{m, i, j, k}}} $ , 最终边缘服务器$m$的收益定义如下:

$ \begin{split} u_m^{es} = &\sum\limits_{i \in I} {\sum\limits_{j \in J} {\sum\limits_{k \in K} {{N_m}} } } {q_{m, i, j, k}}{\xi _m}\ln \left( {1 + pD{x_{m, i, j, k}}} \right) \\ & - \sum\limits_{i \in I} {\sum\limits_{j \in J} {\sum\limits_{k \in K} {{N_m}} } } {q_{m, i, j, k}}{r_{m, i, j, k}} \end{split} $

(9)

其中, ${\xi _m}$表示单位满意度所获得的利润.

3.1.3 云服务器收益

参考文献[7], 本文在${A^{{\text{sp}}}}$的基础上, 将$N$个终端设备的平均增益定义为$ \psi \ln (1 + \displaystyle\sum\nolimits_{m \in M} \displaystyle\sum\nolimits_{i \in I} \displaystyle\sum\nolimits_{j \in J} \displaystyle\sum\nolimits_{k \in K} {{N_m}{q_{m, i, j, k}}} D $$ {x_{m, i, j, k}}) $, 其中$\psi $表示单位精度获得的利润. 云服务器负责分配激励给每个边缘服务器, 其激励成本定义为$ \displaystyle\sum\nolimits_{m \in M} {\displaystyle\sum\nolimits_{i \in I} {\displaystyle\sum\nolimits_{j \in J} {\displaystyle\sum\nolimits_{k \in K} {p{N_m}} } } } {q_{m, i, j, k}}D{x_{m, i, j, k}} $, 因此, 云服务器的收益定义如下:

$ \begin{split} {u^{{\mathrm{sp}}}} = &\psi \ln \left( {1 + \sum\limits_{m \in M} {\sum\limits_{i \in I} {\sum\limits_{j \in J} {\sum\limits_{k \in K} {{N_m}} } } } {q_{m, i, j, k}}D{x_{m, i, j, k}}} \right) \\ & - \sum\limits_{m \in M} {\sum\limits_{i \in I} {\sum\limits_{j \in J} {\sum\limits_{k \in K} p } } } {N_m}{q_{m, i, j, k}}D{x_{m, i, j, k}} \end{split} $

(10)

4 信息不对称下的激励机制

在HFL框架中, 终端设备面临着信息不完整的问题. 由于缺乏来自终端设备的先验信息, 云服务器无法准确判断哪些设备愿意参与模型训练, 其次边缘服务器对终端设备参与训练所产生的数据采集成本, 模型训练成本以及模型传输成本一概不知, 同时云服务器无法掌握终端设备本地模型训练的可用数据量, 因此无法给出给予边缘服务器最优的单位奖励. 最终以上问题会导致对终端设备提供激励时的过度支出.

为了解决上述问题, 本文基于HFL架构, 设计出一种分层激励机制. 在上层云服务器和边缘服务器间引入基于MADRL的Stackelberg博弈, 在下层边缘服务器和终端设备间引入契约论. 通过上述机制, 云服务器, 边缘服务器, 终端设备能够在各自信息不对称的前提下, 保证自身收益的最大化以及隐私的同时设计出最优的单位价格激励.

4.1 边端层契约论问题定义与求解 4.1.1 契约论问题定义

本文将HFL架构中下层终端设备与边缘服务器间的交互定义为契约论问题. 每个边缘服务器$m$为其交互范围内的所有终端设备根据其自身成本类型设计多维合约, 同时保证了自身收益的最大化. 其中合约包括边缘服务器提供给参与FL的终端设备的激励奖励$r$以及终端设备应当为模型训练提供的数据量$x$, 故将多维合约定义为$ B(Y, A, \Psi ) = \{ {\pi _{m, i, j, k}} = \{ {r_{m, i, j, k}}, {x_{m, i, j, k}}\} $$ , 1 \leqslant i \leqslant I, 1 \leqslant j \leqslant J, 1 \leqslant k \leqslant K\} $.

为了保证合约的有效性与可行性, 即终端设备需确保选择符合自身成本类型的合约, 保证自身收益的最大化, 本文引入激励兼容条件(incentive compatibility, IC), 同时终端设备需保证获取到自身期望的最低收益, 本文引入个体合理性条件(individual rationality, IR)^[18]. 对于类型$ - (m, i, j, k)$的终端设备, 其IR定义如下:

$ u_{m, i, j, k}^{ed}\left( {{\pi _{m, i, j, k}}} \right) \geqslant 0, \;1 \leqslant i \leqslant I, 1 \leqslant j \leqslant J, 1 \leqslant k \leqslant K $

(11)

IC定义如下:

$ \left\{\begin{array}{*{20}{l}} {u_{m, i, j, k}^{ed}\left( {{\pi _{m, i, j, k}}} \right) \geqslant u_{m, i, j, k}^{ed}\left( {{\pi _{m, {i^\prime }, {j^\prime }, {k^\prime }}}} \right)} \\ {1 \leqslant i \leqslant I, 1 \leqslant j \leqslant J, 1 \leqslant k \leqslant K} \\ {1 \leqslant {i^\prime } \leqslant I, 1 \leqslant {j^\prime } \leqslant J, 1 \leqslant {k^\prime } \leqslant K} \end{array}\right. $

(12)

在单位数据奖励固定的前提下, 每个边缘服务器作为合约的制定方需要在满足IC和IR条件的前提下最大化自己的收益, 故优化问题P1定义如下:

$ \left\{\begin{array}{*{20}{l}} {{{\max }_{{r_{m, i, j, k}}, {x_{m, i, j, k}}}}u_m^{es},\; \forall m \in M} \\ {\text{s}}{\text{.t.}}\left\{\begin{array}{l} {\text{C1:\;式(11), 式(12) }} \\ {{\text{C2: }}0 \leqslant {r_{m, i, j, k}} \leqslant 1, 1 \leqslant i \leqslant I, 1 \leqslant j \leqslant J, 1 \leqslant k \leqslant K} \\ {{\text{C3: }}0 \leqslant {x_{m, i, j, k}} \leqslant 1, 1 \leqslant i \leqslant I, 1 \leqslant j \leqslant J, 1 \leqslant k \leqslant K} \\ {1 \leqslant {i^\prime } \leqslant I, 1 \leqslant {j^\prime } \leqslant J, 1 \leqslant {k^\prime } \leqslant K} \end{array}\right. \end{array} \right.$

(13)

4.1.2 契约论问题求解

优化问题P1涉及$IJK$个非凸IR约束和$ IJK(IJK - 1) $个非凸IC约束, 当涉及多个非凸条件时, 优化问题P1很难直接求解. 因此, 为了求解可行的多维合约, 需将多维合约先转化为单维合约. 基于式(8), 类型为$ - (m, i, j, k)$的终端设备的成本定义为$ {C_{m, i, j, k}}({x_{m, i, j, k}}) = {\gamma _{m, i}}D{x_{m, i, j, k}} + {v_{m, j}}D{x_{m, i, j, k}} - {\varphi _{m, k}}D{x_{m, i, j, k}} + \delta $, 进而推导出类型为$ - (m, i, j, k)$的终端设备关于数据量的边际参与成本$\alpha $定义如下:

$ \begin{split} \alpha \left( {{\gamma _{m, i}}, {v_{m, j}}, {\varphi _{m, k}}} \right)& = \frac{{\partial {C_{m, i, j, k}}\left( {{x_{m, i, j, k}}} \right)}}{{\partial {x_{m, i, j, k}}}} \\ & = D{\gamma _{m, i}} + D{v_{m, j}} - D{\varphi _{m, k}} \end{split} $

(14)

其中, 当$\alpha \left( {{\gamma _{m, i}}, {v_{m, j}}, {\varphi _{m, k}}} \right)$非负且数值越大时, 表明具有较高边际参与成本的终端设备并不愿意参与到HFL任务当中.

为便于后续合约求解, 本文对${I_m}{J_m}{K_m}$个类型按照边际参与成本非递减顺序进行重新排序如下:

$ {\Phi _{m, 1}}(x), {\Phi _{m, 2}}(x), \cdots , {\Phi _{m, h}}(x), \cdots , {\Phi _{m, IJK}}(x) $

(15)

其中, ${\Phi _{m, h}}(x)$表示某些类型$ - (m, i, j, k)$终端设备属于$ - (m, h)$类型的终端设备.

终端设备边际参与成本按照升序重新排列为:

$ \alpha \left( {{\Phi _{m, 1}}, x} \right) \leqslant \cdots \leqslant \alpha \left( {{\Phi _{m, h}}, x} \right) \leqslant \cdots \leqslant \alpha \left( {{\Phi _{m, IJK}}, x} \right) $

(16)

为便于后续引理及定理的证明, 本文将类型为${\Phi _{m, h}}(x)$的终端设备所对应的合约定义为${\pi _{m, h}} = \left( {{x_{m, h}}, {r_{m, h}}} \right)$, 终端设备边际参与成本的排序重新定义为$ C\left( {{\Phi _{m, h}}, {x_{m, h}}} \right) $.

下面将使用终端设备的边际参与成本类型来分析满足IR和IC条件的可行合约的充要条件.

本文参考文献[16], 得到如下的引理1–引理4.

引理1. 对于任何可行的合约, 当且仅当$ {r_{m, i}} < {r_{m, j}} $时, ${x_{m, i}} < {x_{m, j}}, i, j \in [1, IJK]$.

引理1表明当合约可行时, 当终端设备贡献的数据量越多时所需要的奖励越多.

引理2. 对于可行的合约$B(Y , \Lambda , \Psi )$, 如果对于任意$x$, $\alpha \left( {{\Phi _{m, i}}, x} \right) > \alpha \left( {{\Phi _{m, j}}, x} \right)$成立, 那么$ {x_{m, i}} \leqslant {x_{m, j}} $.

引理2表明合约的单调性, 即当终端设备的边际参与成本越大时, 其越不愿意贡献数据.

由引理1和引理2可知, 可行合约的必要条件为:

$ \left\{ {\begin{array}{*{20}{c}} {{x_{m, 1}} \geqslant {x_{m, 2}} \geqslant \cdots \geqslant {x_{m, i}} \geqslant \cdots \geqslant {x_{m, IJK}}} \\ {{r_{m, 1}} \geqslant {r_{m, 2}} \geqslant \cdots \geqslant {r_{m, i}} \geqslant \cdots \geqslant {r_{m, IJK}}} \end{array}} \right. $

(17)

引理3. 对于可行的合约, 如果类型为${\Phi _{m, IJK}}$的终端设备的IR约束成立, 其余类型终端设备的IR约束随之成立.

引理4. 对于可行的合约, 如果${\pi _{m, i - 1}}\mathop \Leftrightarrow \limits^{{\mathrm{PIC}}} {\pi _{m, i}}$并且${\pi _{m, i}}\mathop \Leftrightarrow \limits^{{\mathrm{PIC}}} {\pi _{m, i + 1}}$, 那么${\pi _{m, i - 1}}\mathop \Leftrightarrow \limits^{{\mathrm{PIC}}} {\pi _{m, i + 1}}$.

通过引理4可将${{IJK(IJK - 1)} \mathord{\left/ {\vphantom {{IJK(IJK - 1)} 2}} \right. } 2}$个PIC约束简化为$IJK - 1$个PIC约束. 同时由引理4的证明可得合约可行的充分条件为:

$ \left\{\begin{array}{*{20}{l}} {{r_{m, IJK}} - C\left( {{\Phi _{m, IJK}}, {x_{m, IJK}}} \right) \geqslant 0} \\ {{r_{m, h + 1}} - C\left( {{\Phi _{m, h + 1}}, {x_{m, h + 1}}} \right) + C\left( {{\Phi _{m, h + 1}}, {x_{m, h}}} \right) \geqslant } \\ {{r_{m, h}} \geqslant {r_{m, h + 1}} - C\left( {{\Phi _{m, h}}, {x_{m, h + 1}}} \right) + C\left( {{\Phi _{m, h}}, {x_{m, h}}} \right)} \end{array}\right. $

(18)

综上所述, 可得合约可行的充要条件如下.

定理1. 在信息不对称场景下, 一个可行的合约必须满足如下3个条件.

$ \left\{ {\begin{array}{*{20}{l}} {(1)\;\alpha \left( {{\Phi _{m, 1}}, x} \right) \leqslant \cdots \leqslant \alpha \left( {{\Phi _{m, h}}, x} \right) \leqslant \cdots \leqslant \alpha \left( {{\Phi _{m, IJK}}, x} \right), } \\ \quad\; {{r_{m, IJK}} \leqslant \cdots \leqslant {r_1} \leqslant 0, {x_{m, IJK}} \leqslant \cdots \leqslant {x_1} \leqslant 0} \\ {(2)\;{r_{m, IJK}} - C\left( {{\Phi _{m, IJK}}, {x_{m, IJK}}} \right) \geqslant 0} \\ {(3)\;{r_{m, h + 1}} - C\left( {{\Phi _{m, h + 1}}, {x_{m, h + 1}}} \right) + C} \left( {{\Phi _{m, h + 1}}, {x_{m, h}}} \right) \\ \quad\; \geqslant {r_{m, h}} \geqslant {r_{m, h + 1}} - C\left( {{\Phi _{m, h}}, {x_{m, h + 1}}} \right) { + C\left( {{\Phi _{m, h}}, {x_{m, h}}} \right)} \end{array}} \right. $

(19)

证明: 基于引理1和2可得式(19)中的条件(1), 引理3的数学表示形式即式(19)中的条件(2), 基于引理4可得到式(19)中的条件(3).

定理2. 对于任意终端设备所提供用于训练的数据量, 可通过式(20)得到其最优奖励.

$ r_{m, h}^* = \left\{ \begin{gathered} C\left( {{\Phi _{m, h}}, {x_{m, h}}} \right),\; h = IJK \\ {r_{m, h + 1}} - C\left( {{\Phi _{m, h}}, {x_{m, h + 1}}} \right) + C\left( {{\Phi _{m, h}}, {x_{m, h}}} \right), \\ \qquad\qquad\qquad h = 1, \cdots, IJK - 1 \\ \end{gathered} \right. $

(20)

为便于求解合约, 参考文献[19,20], 定理1中的条件(1)和条件(3)需转化如下:

$ \left\{ \begin{gathered} {\text{(1) }}{r_{m, IJK}} - C\left( {{\Phi _{m, IJK}}, {x_{m, IJK}}} \right) = 0 \\ (2)\;{r_{m, h + 1}} - C\left( {{\Phi _{m, h}}, {x_{m, h + 1}}} \right) = {r_{m, h}} - C\left( {{\Phi _{m, h}}, {x_{m, h}}} \right), \\ \qquad\qquad\quad\;\; h \in \{ 1, \cdots , IJK - 1\} \\ \end{gathered} \right. $

(21)

令$ {\Delta _h} = {r_{m, h + 1}} - {r_{m, h}} = {\text{ }}C({\varphi _{m, h}}, {x_{m, h + 1}}){\text{ }} - {\text{ }}C({\varphi _{m, h}}, {x_{m, h}}) $, $h = 1, \cdots , IJK - 1$以及${\Delta _{IJK}} = 0$. 则根据转化后的式(21), 可将$r_{m, h}^*$改写为以下形式:

$ r_{m, {{h}}}^* = \left\{ {\begin{array}{*{20}{l}} {C\left( {{\phi _{m, IJK}}, {x_{m, IJK}}} \right),\;\;\qquad\quad h = IJK} \\ {C\left( {{\phi _{m, IJK}}, {x_{m, IJK}}} \right) - \displaystyle\sum\limits_{k = h}^{IJK} {{\Delta _k}} ,\; h = 1, \cdots , IJK - 1} \end{array}} \right. $

(22)

为了得到终端设备用于模型训练的最优数据量, 需将式(22)代入优化问题P1, 将其改写为新的优化问题P2:

$ \left\{\begin{array}{*{20}{l}} {{{\max }_{{x_{m, h}}}}u_m^{es}} \\ {{\text{s}}{\text{.t}}{\text{.\;C1: }}0 \leqslant {x_{m, IJK}} \leqslant \cdots \leqslant {x_{m, h}} \leqslant \cdots \leqslant {x_{m, 1}} \leqslant 1} \end{array}\right. $

(23)

其中, $ u_m^{es} = \displaystyle\sum\nolimits_{h = 1}^{l/K} {N_m}{q_{m, h}}{\zeta _m}\ln ( 1 + pD{x_{m, h}} ) - \displaystyle\sum\nolimits_{h = 1}^{l/K} D{x_{m, h}} {b_{m, h}} $, 且当$h = 1$时, ${b_{m, h}} = {\text{ }}{N_m}{q_{m, 1}}\alpha \left( {{\phi _{m, 1}}, {x_{m, 1}}} \right)$, 当$h = 2, \cdots , IJK$时, $ {b_{m, h}} = \alpha \left( {{\phi _{m, h}}, {x_{m, h}}} \right)\displaystyle\sum\nolimits_{j = 1}^h {{N_m}{q_{m, j}}} - {\text{ }}\alpha ( {\phi _{m, h - 1}}, {x_{m, h}} ) \displaystyle\sum\nolimits_{j = 1}^{h - 1} {{N_m}{q_{m, j}}} $. 因此优化问题P2可视为凸优化问题, 并可根据优化问题P2中函数${u_m}$对于${x_{m, h}}$的一阶导数等于零求得最优数据量的解为:

$ x_{m, h}^* = \frac{{{N_m}{q_{m, h}}{\zeta _m}}}{{D{b_{m, h}}}} - \frac{1}{{Dp}} $

(24)

最终将式(24)代入式(22)得到最优合约为$(r_{m, h}^*, x_{m, h}^*)$.

4.2 云边层基于学习的Stackelberg博弈问题定义与求解 4.2.1 基于学习的Stackelberg博弈问题定义

本文首先将HFL架构中上层云服务器与边缘服务器间的交互定义为Stackelberg博弈问题. 该问题中, 云服务器担任领导者, 且拥有一个最优单位价格激励. 边缘服务器作为追随者, 其根据云服务器所提供的最优单位价格激励, 决定终端设备参与模型训练所需要贡献的数据量^[21,22]. 在信息对称的前提下, 二者不断调整策略, 以达到双方收益的最大化, 并证得存在唯一的SE, 然而信息对称的假设与HFL架构保护隐私的初衷相违背, 故本文将Stackelberg博弈问题转化为马尔可夫决策过程(Markov decision process, MDP), 并采用一种分布式且保护隐私的MADRL方法在信息不对称的情况下逐步逼近SE.

定义1. 对于任意一个边缘服务器$m \in M$和云服务器之间, 当且仅当满足以下条件时, 存在一组特定的最优解$({X^*}, {p^*})$, 使得边缘服务器和云服务器之间存在唯一SE.

$ \left\{ {\begin{array}{*{20}{l}} {{u^{cs}}\left( {{x^*}, {p^*}} \right) \geqslant {u^{cs}}\left( {{x^*}, p} \right) } \\ {u_m^{es}\left( {x_m^*, r_m^*, {p^*}} \right) \geqslant u_m^{es}\left( {{x_m}, r_m^*, {p^*}} \right),\; \forall m \in M } \end{array}} \right. $

(25)

其中, ${{{X}}^*} = [{{x}}_1^*, \cdots , {{x}}_m^*, \cdots , {{x}}_M^*]$, ${{x}}_m^* = [x_{m, 1}^*, \cdots , x_{m, h}^*, \cdots , x_{m, IIK}^*]$, ${{r}}_m^* = [r_{m, 1}^*, \cdots , r_{m, h}^*, \cdots , r_{m, IJK}^*]$.

为保证信息对称下唯一的SE, 即云服务器能够选择最大化其收益的最优单位价格激励, 优化问题P3定义如下:

$ \left\{\begin{array}{*{20}{l}} {{{\max }_p}{u^{cs}}} \\ {{\text{s}}{\text{.t}}{\text{. }}{{\max }_{{r_{m, i, j, k}}, {x_{m, i, j, k}}}}u_m^{es}} \\ {\forall m \in M, \forall i \in I, \forall j \in J, \forall k \in K} \end{array}\right. $

(26)

4.2.2 基于学习的Stackelberg博弈问题求解

针对优化问题P3, 可得定理3.

定理3. 当$ 2p(D{\text{ }} + {\text{ }}\displaystyle\sum\nolimits_{m \in M} \displaystyle\sum\nolimits_{h \in IJK} {({N_{m, h}}q_{m, h}^2{\xi _m}{\text{ }}} / {{\text{ }}{b_{m, h}}} )) > \displaystyle\sum\nolimits_{m \in M} {} $$ \displaystyle\sum\nolimits_{h \in IJK} {{N_{m, h}}{q_{m, h}}} $时, SE的解析解如下所示:

$ {p^*} = \frac{{{B_2} + \sqrt {B_2^2 + 4{B_1}{B_3}} }}{{2{B_1}}} $

(27)

$ x_{m, h}^* = \frac{{{N_m}{q_{m, h}}{\zeta _m}}}{{D{b_{m, h}}}} - \frac{1}{{Dp}},\; h = 1, \cdots , IJK $

(28)

$ r_{m, h}^* = \left\{ {\begin{array}{*{20}{l}} {C\left( {{\Phi _{m, h}}, x_{m, h}^*} \right),\; h = IJK } \\ \begin{gathered} r_{m, h + 1}^* - C\left( {{\Phi _{m, h}}, x_{m, h + 1}^*} \right) + C\left( {{\Phi _{m, h}}, x_{m, h}^*} \right), \\ \qquad\qquad\qquad h = 1, \cdots , IJK - 1 \\ \end{gathered} \end{array}} \right. $

(29)

其中, ${B_1} = D + \displaystyle\sum\nolimits_{m \in M} {\displaystyle\sum\nolimits_{h \in IJK} {{{({N_{m, h}}q_{m, h}^2{\xi _m}} / {{b_{m, h}}}}} } )$, ${B_2} = \displaystyle\sum\nolimits_{m \in M} {\displaystyle\sum\nolimits_{h \in IJK} {} } $${N_{m, h}}{q_{m, h}}$, $ {B_3} = \psi \displaystyle\sum\nolimits_{m \in M} \displaystyle\sum\nolimits_{h \in IJK} {N_{m, h}} {q_{m, h}} / {\displaystyle\sum\nolimits_{m \in M} {\displaystyle\sum\nolimits_{h \in IJK} {({{{N_{m, h}}q_{m, h}^2{\xi _m}} / D}} } } $$ {b_{m, h}}) $.

证明: 见附录A.

4.2.2.1 信息非对称下基于学习的智能决策方法

在本节中, 将探讨如何在信息不对称下逐渐逼近SE. 由定理3可知, 在信息对称的下云服务器和边缘服务器之间存在唯一的SE, 然而该分析是基于集中决策的, 即需要收集所有边缘服务器的隐私信息来确定SE的存在, 这与HFL框架保护隐私的初衷相违背. 为了解决上述问题, 参考文献[23–26], 本文将Stackelberg博弈问题转化为MDP, 并采用MADRL方法在信息不对称的情况下逐步逼近SE.

为了在隐私保护的情况下逼近SE, 云服务器与$M$个边缘服务器都会成为MADRL中的一个智能体, 每个智能体需要基于不完全信息做出决策. 这些智能体组成的集合为$M = [0, 1, 2, \cdots , M]$, 其中智能体$m = 0$代表云服务器, 其他智能体对应不同的边缘服务器. 一个智能体的训练过程被划分为$T$次迭代, 在每次迭代$t$中, 云服务器以博弈的领导者身份与环境交互, 通过获取的状态${{S}}_0^t$, 确定动作${{a}}_0^t$, 而边缘服务器$m$以博弈从方身份通过与环境交互获取状态${{S}}_m^t$, 确定动作${{a}}_m^t$, 并通过收集所有参与方的策略分别计算它们的奖励$G_0^t$和$G_m^t$, 之后根据收集的策略来创建下一时刻的状态. 同时, 智能体会将所有操作的历史数据保存到一个大小为$L$的缓冲队列中, $d$个时隙之后, 将缓冲队列中的经验回放计算奖励, 以更新网络参数. 由于在每次迭代训练中, 智能体的状态是根据动作决策生成的, 并没有获取任何隐私信息, 这样就可以在没有隐私泄露的情况下逼近SE.

4.2.2.2 马尔可夫决策过程

状态空间: 在Stackelberg博弈中, 每个智能体的状态是参考其他智能体的历史策略来确定的. 在第$t$次训练步骤中, 每个边缘服务器$m$ (即智能体$m > 0$)与环境互动, 以获得历史信息并了解当前状态, 此状态定义为${{S}}_m^t = \{ {{x}}_{ - m}^{t - L}, {p^{t - L}}, {{x}}_{ - m}^{t - L + 1}, {p^{t - L + 1}}, \cdots , {{x}}_{ - m}^{t - 1}, {p^{t - 1}}\} $, 其中$ {{{x}}_{ - m}} = [{{{x}}_1}, \cdots, $$ {{{x}}_{m - 1}}, {{{x}}_{m + 1}}, \cdots , {{{x}}_M}] $、$L$代表历史记录的长度、${{{x}}_m} = [{x_{m, 1}}, \cdots , {x_{m, h}}, \cdots , {x_{m, IJK}}]$, 对于云服务器, 其状态包括所有边缘服务器在过去$L$次历史动作, 故可将此状态定义为${{S}}_0^t = \{ {{{x}}^{t - L}}, {{{x}}^{t - L + 1}}, \cdots , {{{x}}^{t - 1}}\} $.

动作空间: 由于智能体的行动由决策变量所定义, 故在第$t$次训练步骤中, 云服务器的行动直接与决策变量相关, 可表示为$a_0^t = p$. 为加速智能体的学习过程, 需为行动设置一个上限${p^{\max }}$, 其中${p^t} \in [0, {p^{\max }}]$. 对于每个边缘服务器, 其动作空间可表示为${{a}}_m^t = [x_{m, 1}^t, x_{m, h}^t, \cdots , $$x_{m, IIK}^t]$. 由于每个智能体的行动空间是连续的, 可将每个行动除以其最大值, 使云服务器和边缘服务器所对应的两个行动空间统一映射到区间$[0, 1]$.

奖励函数: 当所有策略执行完毕后, 每个智能体通过观察其他玩家的行为, 并根据收益函数来决定自身的即时奖励, 此奖励定义如下:

$ G_n^t = \left\{ {\begin{array}{*{20}{l}} {{u^{cs, t}},\; m = 0} \\ {u_m^{es, t},\; m \geqslant 1} \end{array}} \right. $

(30)

其中, 在第$t$次训练步骤中, $u_m^{es, t}$代表优化问题P3中每个边缘服务器的收益. 此时环境会更新每个代理的新状态, 并进入下一次训练$t + 1$.

4.2.2.3 actor-critic网络与策略优化

本文在每个智能体上设计了一个actor网络${\pi _\theta }$和critic网络${v_\sigma }$, 通过学习${\pi _\theta }$来近似策略函数, 学习${v_\sigma }$来近似值函数, 其中$\theta $和$\sigma $是actor网络和critic网络的参数. 更进一步, 对于智能体$m$使用$V(S_m^t;{\pi _{{\theta _m}}})$表示状态价值函数, 使用$Q(S_m^t, a_m^t;{\pi _{{\theta _m}}})$表示动作价值函数, 将智能体$m$的学习目标记为${\mathcal{L}_m}$, 那么可以将它的学习目标表述为:

$ \begin{split} \theta _0^* &= {\rm{argmax} _{{\theta _0}}}{\mathcal{L}_0}\left( {{\pi _{{\theta _0}}}} \right) = {\rm{argmax} _{{\theta _0}}}\mathbb{E}\left[ {V\left( {{{s}}_0^t;{\pi _{{\theta _0}}}} \right)} \right] \\ & = {\rm{argmax} _{{\theta _0}}}\mathbb{E}\left[ {Q\left( {{{s}}_0^t, a_0^t;{\pi _{{\theta _0}}}} \right)} \right] \end{split} $

(31)

本文中采用文献[23]中的近端策略优化裁剪算法来执行训练过程. 具体来说策略梯度被定义为:

$ \begin{split} \theta _m^* &= {\rm{argmax} _{{\theta _m}}}{\mathcal{L}_m}\left( {{\pi _{{\theta _m}}}} \right) \\ & = {\rm{argmax} _{{\theta _m}}}\mathbb{E}\left[ {V\left( {{{S}}_m^t;{\pi _{{\theta _m}}}} \right)} \right] \\ & = {\rm{argmax} _{{\theta _m}}}\mathbb{E}\left[ {Q\left( {{{S}}_m^t, a_m^t;{\pi _{{\theta _m}}}} \right)} \right] \end{split} $

(32)

$ \begin{split} & C_{{\pi _\theta }}^m\left( {{S_m}, {a_m}} \right) = \min [{P^m}A_{{\pi _\theta }}^m\left( {{S_m}, {a_m}} \right), \mathcal{F}\left( {{P^m}} \right)A_{{\pi _\theta }}^m\left( {{S_m}, {a_m}} \right)] \end{split} $

(33)

$ {P^m} = \frac{{\pi _\theta ^m\left( {{{{S}}_{{m}}}\mid {{{a}}_{{m}}}} \right)}}{{\hat \pi _\theta ^m\left( {{{{S}}_{{m}}}\mid {{{a}}_{{m}}}} \right)}} $

(34)

$ A_{{\pi _\theta }}^m\left( {{{{S}}_{{m}}}, {{{a}}_{{m}}}} \right) = Q_{{\pi _\theta }}^m\left( {{{{S}}_{{m}}}\mid {{{a}}_{{m}}}} \right) - V_{{\pi _\theta }}^m\left( {{{{S}}_{{m}}}} \right) $

(35)

$ \mathcal{F}\left( {{P^m}} \right) = \left\{ {\begin{array}{*{20}{l}} {1 + \varepsilon },&{{P^m} > 1 + \varepsilon } \\ {{P^m}},&{1 - \varepsilon < {P^m} < 1 + \varepsilon } \\ {1 - \varepsilon },&{{P^m} < 1 - \varepsilon } \end{array}} \right. $

(36)

$\varepsilon $是可调参数, 之后分别使用随机梯度上升和梯度下降更新actor-critic网络模型, 随着训练过程的继续, 智能体逐渐学习到最优策略. 当训练过程收敛时, 智能体根据行动者网络的输出来确定策略.

5 仿真实验

为评估本文提出的激励机制, 实验设计1个云服务器和3个边缘服务器, 每个边缘服务器连接8个终端设备. 终端设备的每种类型的取值范围是[1, 5], 同时每种类型的数量设置为$I = J = K = 2$. 每种类型的概率分布服从均匀分布, 即$q = 1/8$. 参考文献[27–30], 详细的配置参数见表2.

5.1 激励机制有效性验证

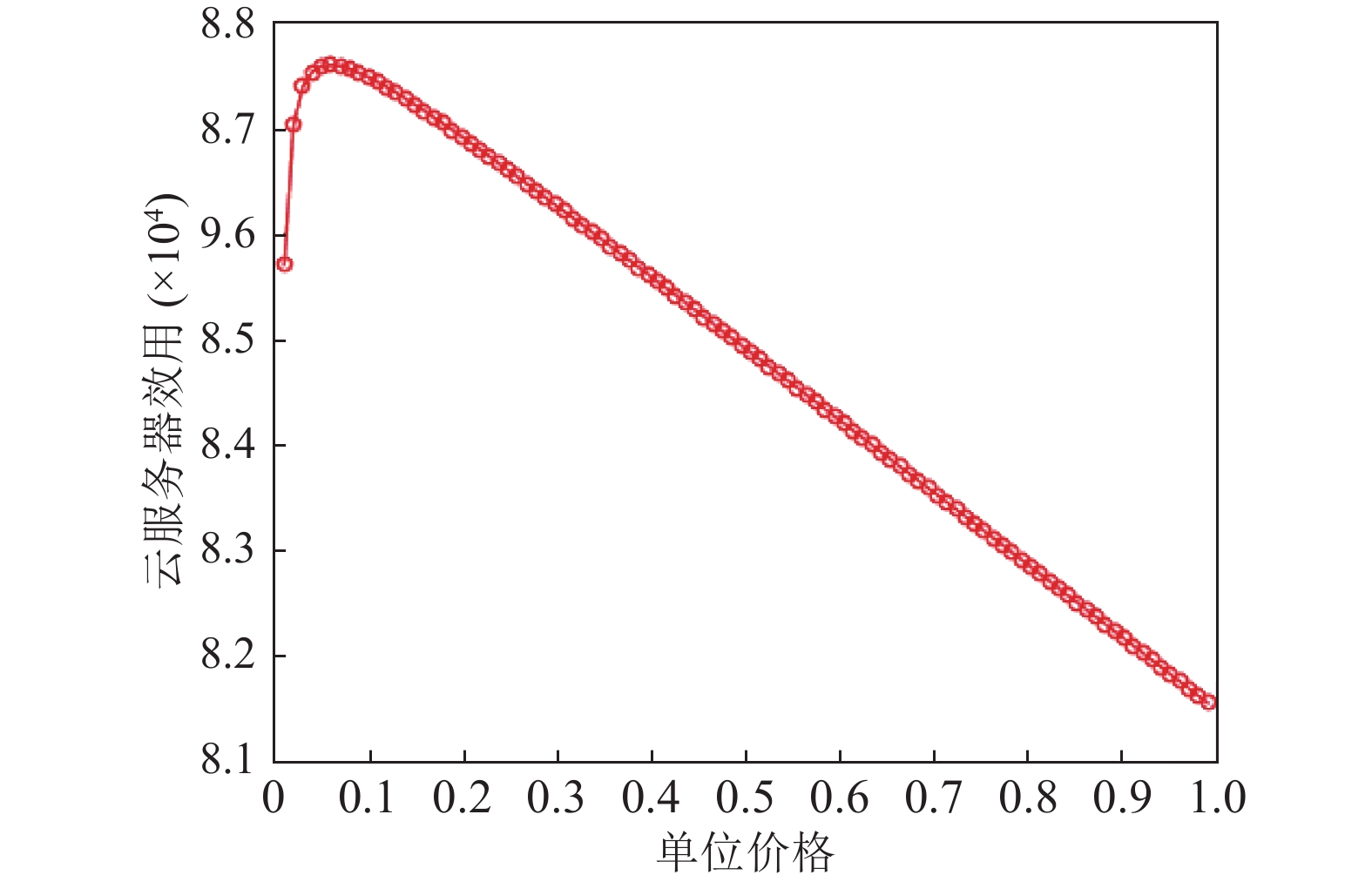
图2展示了不同单位利润下单位价格和云服务器收益之间的关系. 当单位利润固定时, 随着单位价格的增加, 云服务器收益先增加后减少. 即云服务器的收益关于单位价格是严格凹函数的, 存在最大值. 间接验证了定理3的有效性, 因为当云服务器和边缘服务器逐渐逼近SE时, 云服务器的收益也会逐渐达到最大值, 同时验证了激励机制的有效性.

图3–图5展示了云服务器, 边缘服务器1, 边缘服务器2的策略收敛情况. 其中云服务器的策略是单位价格, 而边缘服务器1和2的策略则基于终端设备提供的数据量. 随着迭代次数的增加, 云服务器、边缘服务器和终端设备的策略不断演化, 直至收敛. 结果显示, 所有参与者的策略最终收敛于理论SE值, 且这一收敛状态在约600次训练集后达成. 这一结果表明, MADRL方法极大地促进了参与者在合理时间内学习并找到近似最优策略.

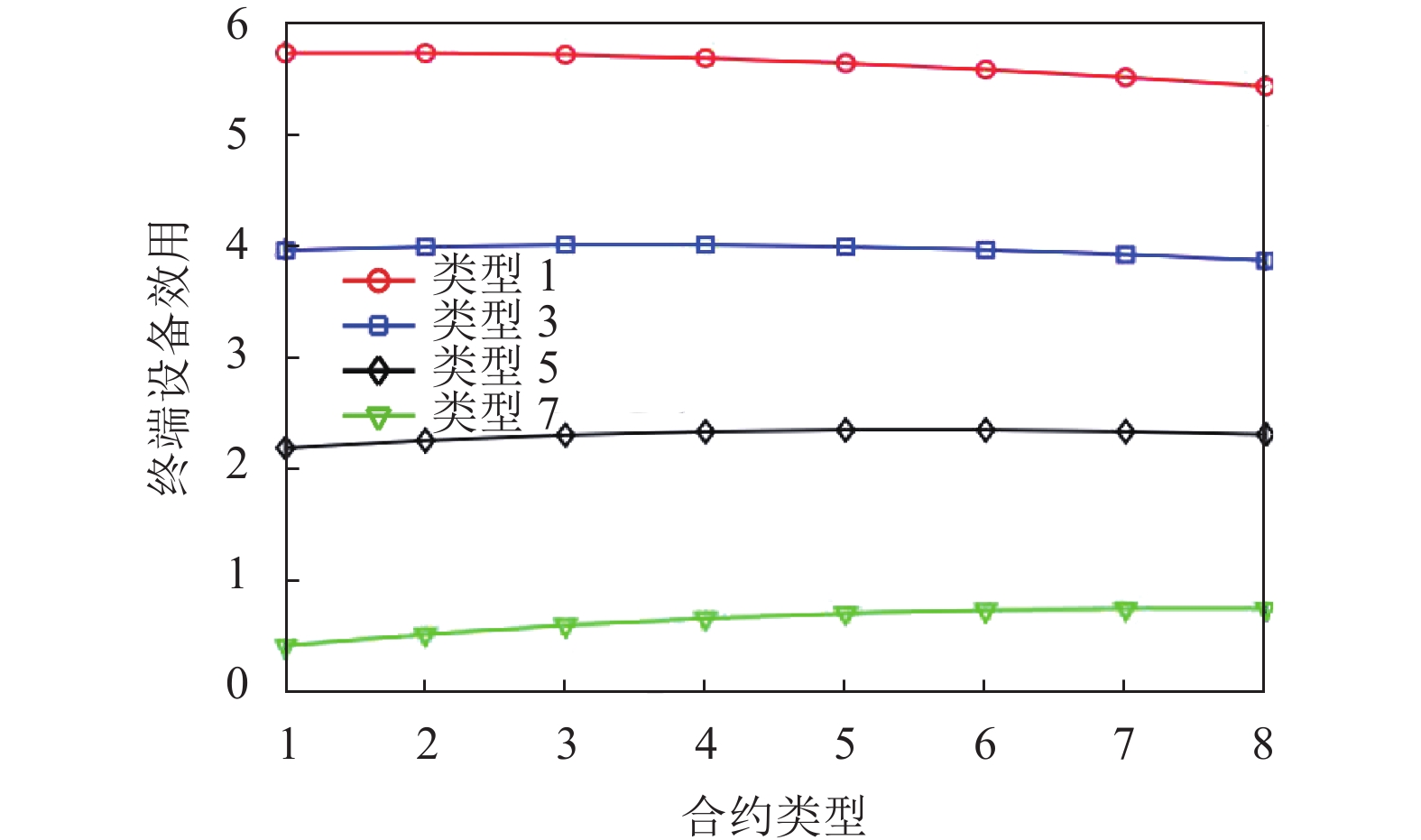
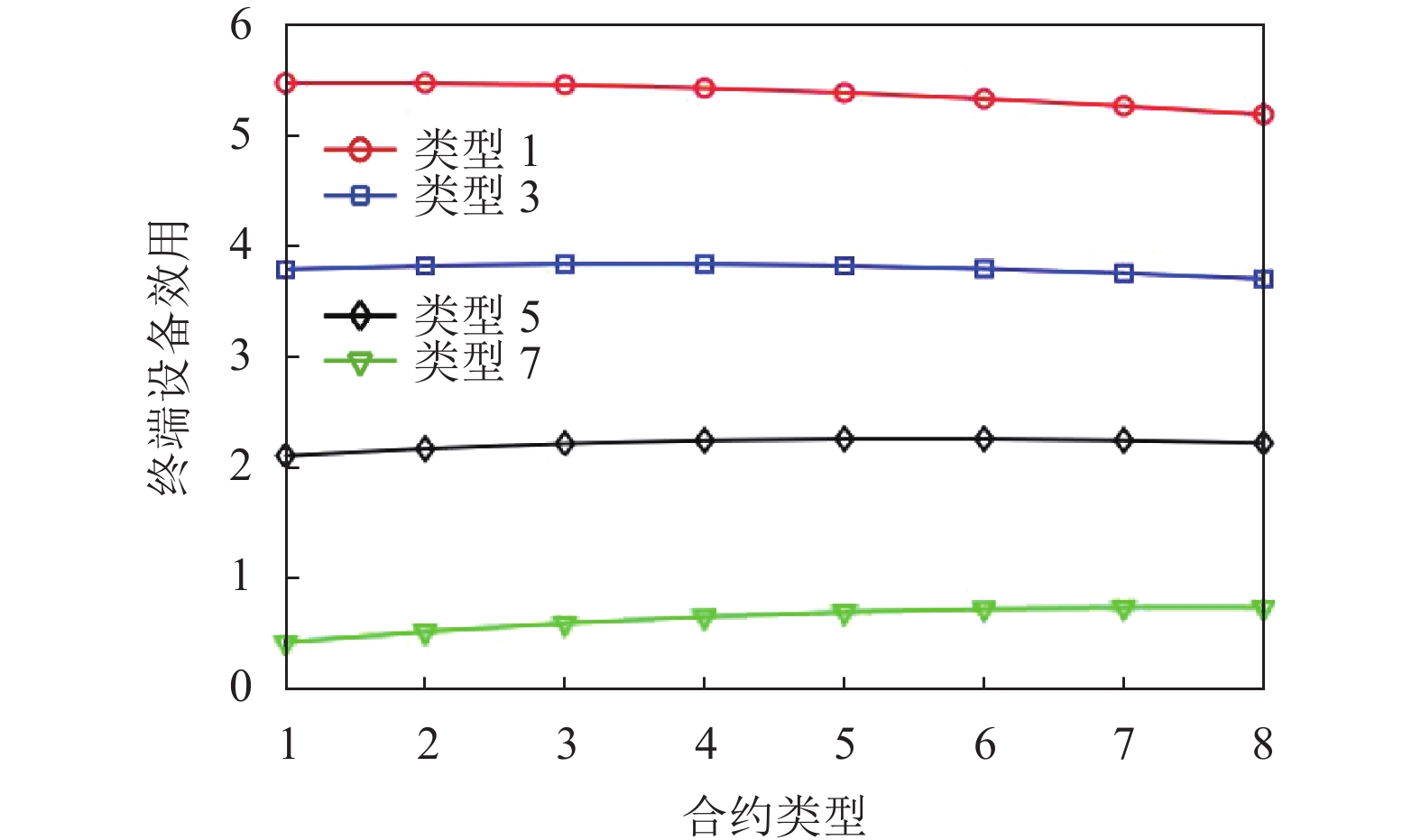
图6–图7展示了在信息不对称(IR和IC)的情况下, 本文所设计的多维合约针对成本类型为1、3、5、7的终端设备的激励有效性的验证. 即当终端设备选择适合其类型的合约时, 自身的收益都会达到最大, 例如当类型3的终端设备选择专为其设计的合约条款(x₃, r₃)时, 其收益最高, 如果选择其他合约条款, 其收益会降低, 这表明满足IC约束. 同时每个终端设备都能保证获取到自身期望最低收益, 即收益非负, 这表明满足IR约束.

5.2 激励机制对比

现有的工作设计了基于双层斯坦克尔伯格博弈(Stackelberg-Stackelberg, SS)激励机制^[7], 其中终端设备收益定义如下:

$ \begin{split} u_{m, i, j, k}^{ed, SG} =& \frac{{Dx_{m, i, j, k}^{SG}R_m^{SG}}}{{\displaystyle\sum\limits_{i \in I} {\sum\limits_{j \in J} {\displaystyle\sum\limits_{k \in K} D } } x_{m, i, j, k}^{SG}}} - {\gamma _{m, l}}Dx_{m, i, j, k}^{SG} \\ & - {v_{m, j}}Dx_{m, l, j, k}^{SG} + {\varphi _{m, k}}Dx_{m, i, j, k}^{SG} \end{split} $

(37)

边缘服务器收益定义如下:

$ \begin{gathered} u_m^{es, SG} = \sum\limits_{i \in I} {\sum\limits_{j \in J} {\sum\limits_{k \in K} {{N_m}} } } {q_{m, i, j, k}}{\xi _m}\ln \left( {1 + {p^{SG}}Dx_{m, i, j, k}^{SG}} \right) - {\text{R}}_m^{SG} \end{gathered} $

(38)

云服务器的收益定义如下:

$ \begin{split} {u^{cs, SG}} =& \psi \ln \left( {1 + \sum\limits_{m \in M} {\sum\limits_{i \in I} {\sum\limits_{j \in J} {\sum\limits_{k \in K} {{N_m}} } } } {q_{m, i, j, k}}Dx_{m, i, j, k}^{SG}} \right) \\ & - \sum\limits_{m \in M} {\sum\limits_{i \in I} {\sum\limits_{j \in J} {\sum\limits_{k \in K} {{p^{SG}}} } } } {N_m}{q_{m, i, j, k}}Dx_{m, i, j, k}^{SG} \end{split} $

(39)

本文将提出的基于学习博弈-契约(learning-based Stackelberg-contract, LSC)激励机制与SS激励机制进行比较.

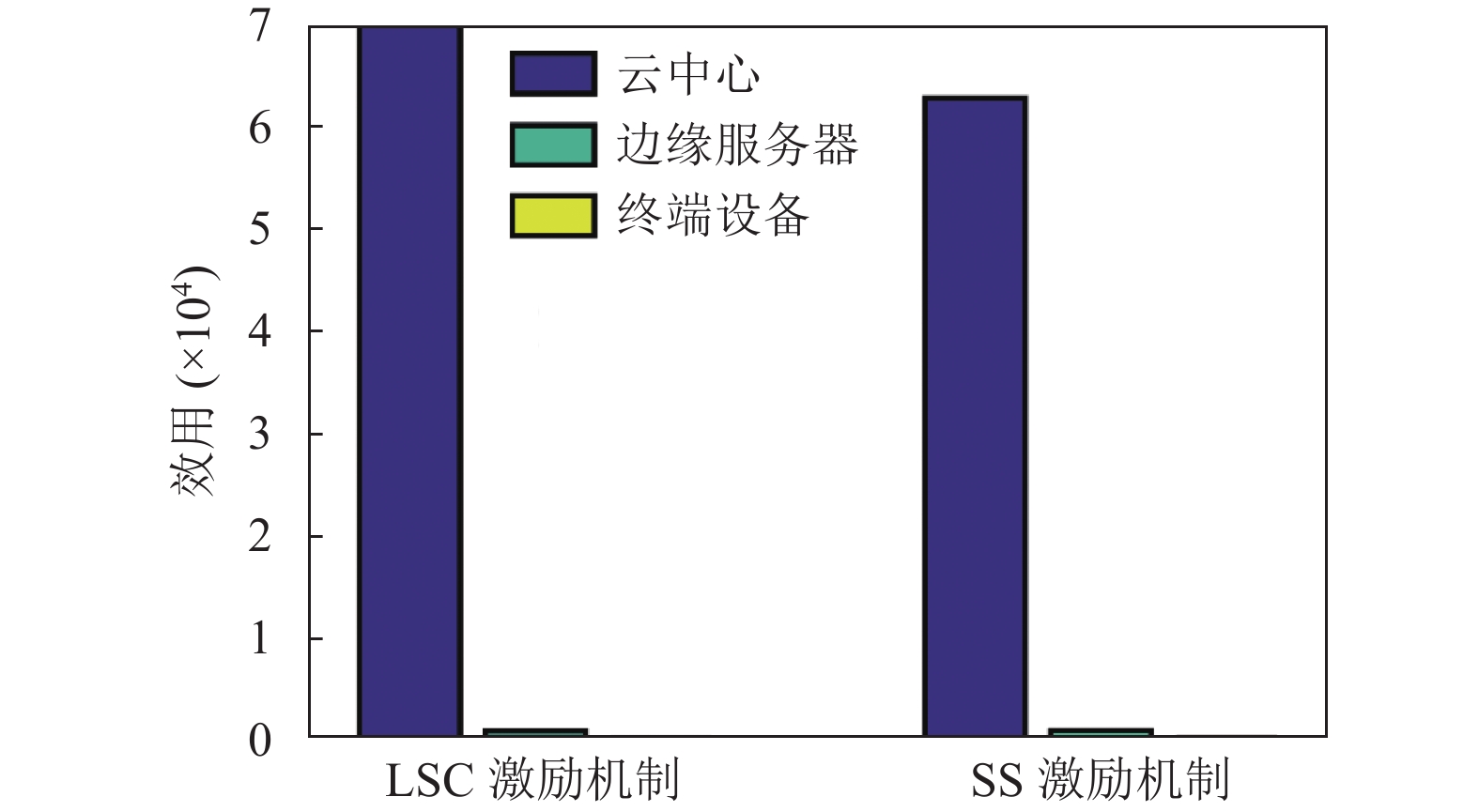
从图8可以看出, 与现有的SS激励机制方案, 本文提出的LSC激励机制方案能够使云服务器从边缘服务器和终端设备获得更多的收益, 收益提升了接近11%. 同时边缘服务器和终端设备获得的收益是较低的, 原因在于SS激励机制方案考虑了边缘服务器与终端设备收益的最大化, 因而降低了云服务器的收益. 参考文献[7], 其实验结果显示云中心获取的收益与分层联邦学习的模型精度成正相关. 因此本文提出的LSC激励机制方案更有助于提升HFL模型精度.

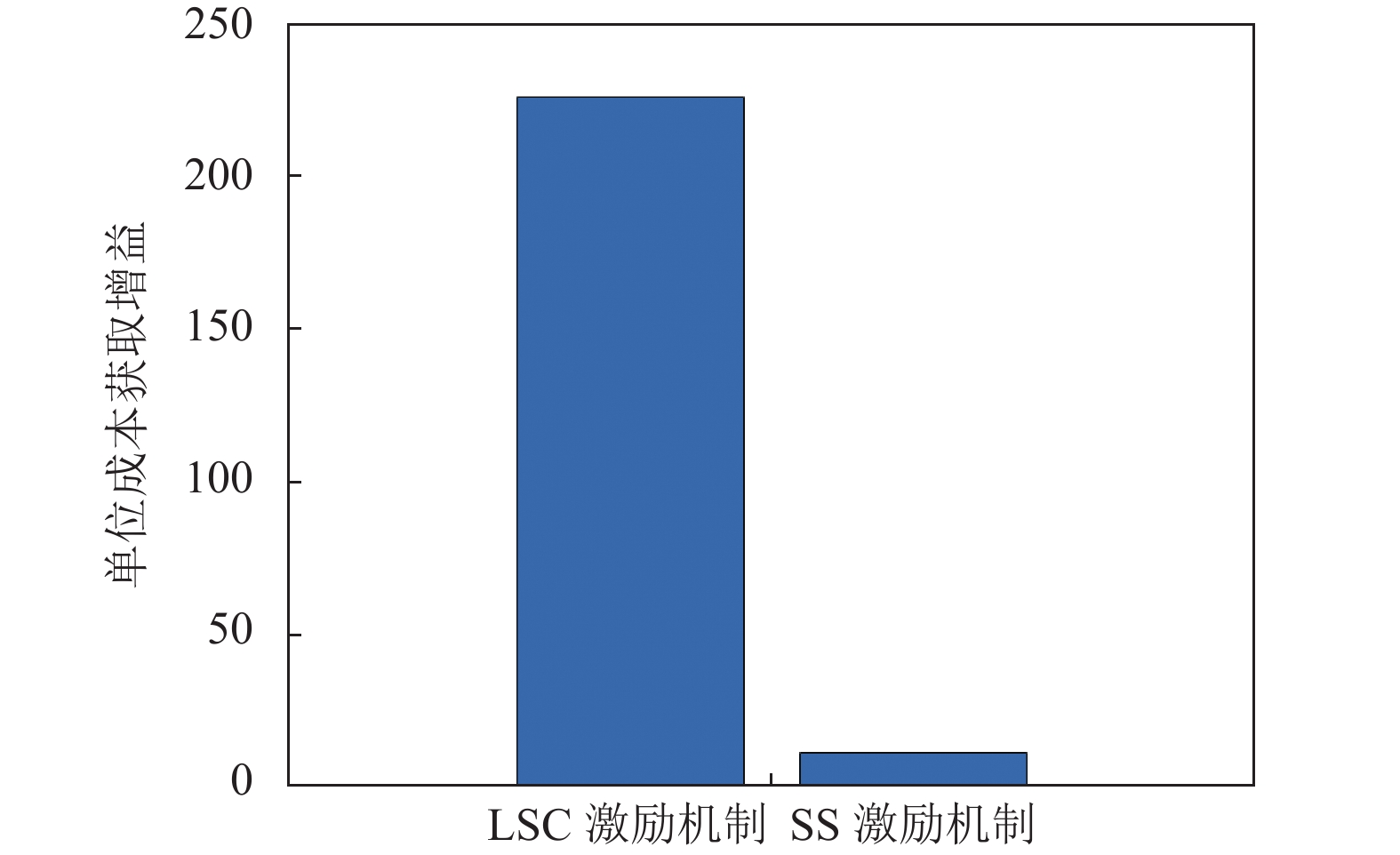
由于本文LSC激励机制方案与已有SS激励机制方案增益和总成本支出各不相同, 故为了进一步展示本文LSC激励机制方案的优越性, 本文在相同成本支出的情况下, 进一步比较两种方案获取的增益, 并将试验指标定义为增益除以总成本. 图9展示出本文提出的LSC激励机制方案能够使云服务器从边缘服务器和终端设备获得更多的单位成本获取增益, 提升接近18倍. 同时由式(10)可知, 增益和数据量成正比, 因此LSC激励机制方案在相同成本支出情况下, 能使云服务器获取更多的数据量, 从而分层联邦学习中云服务器的模型精度能够提升更高.

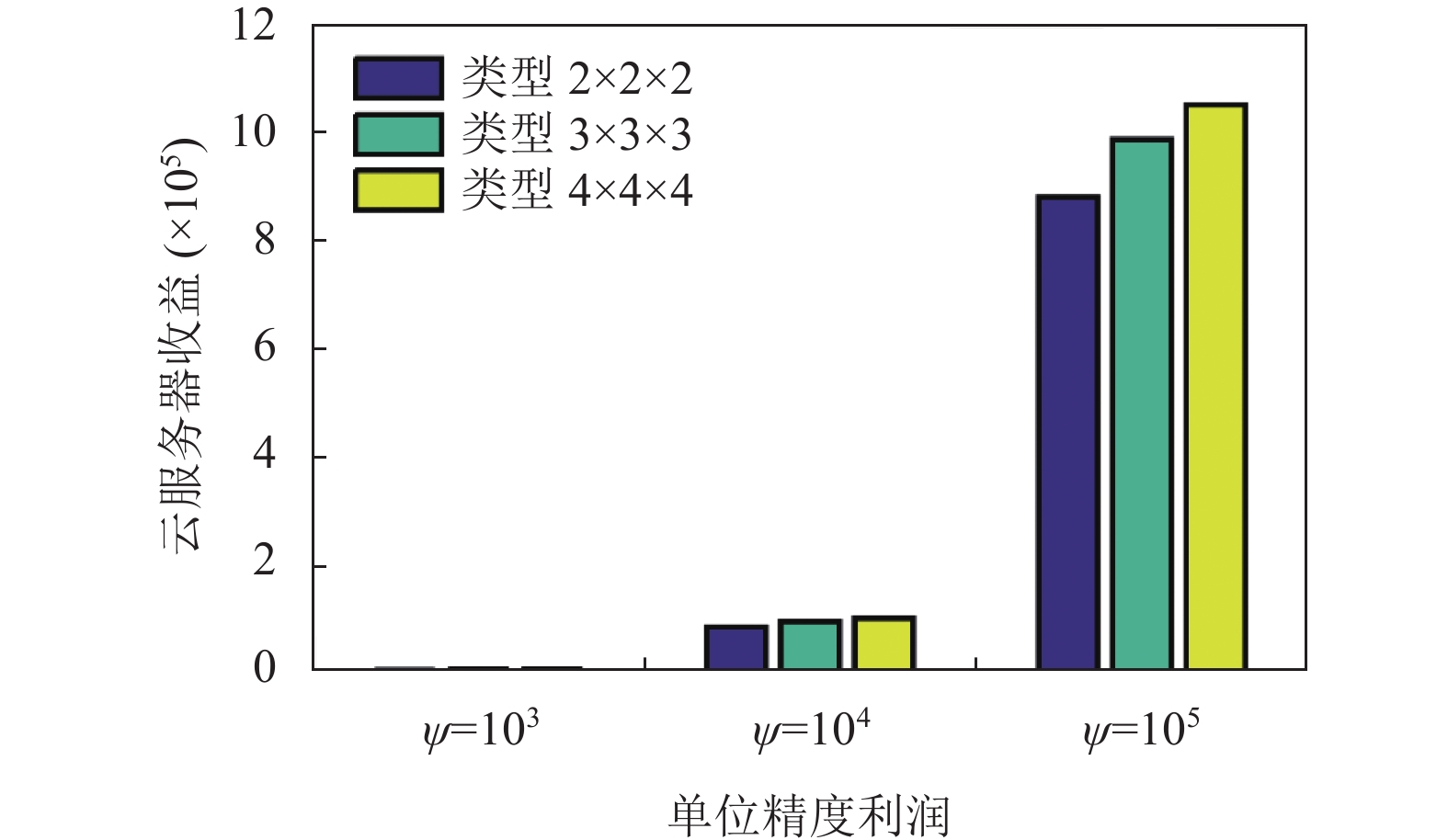
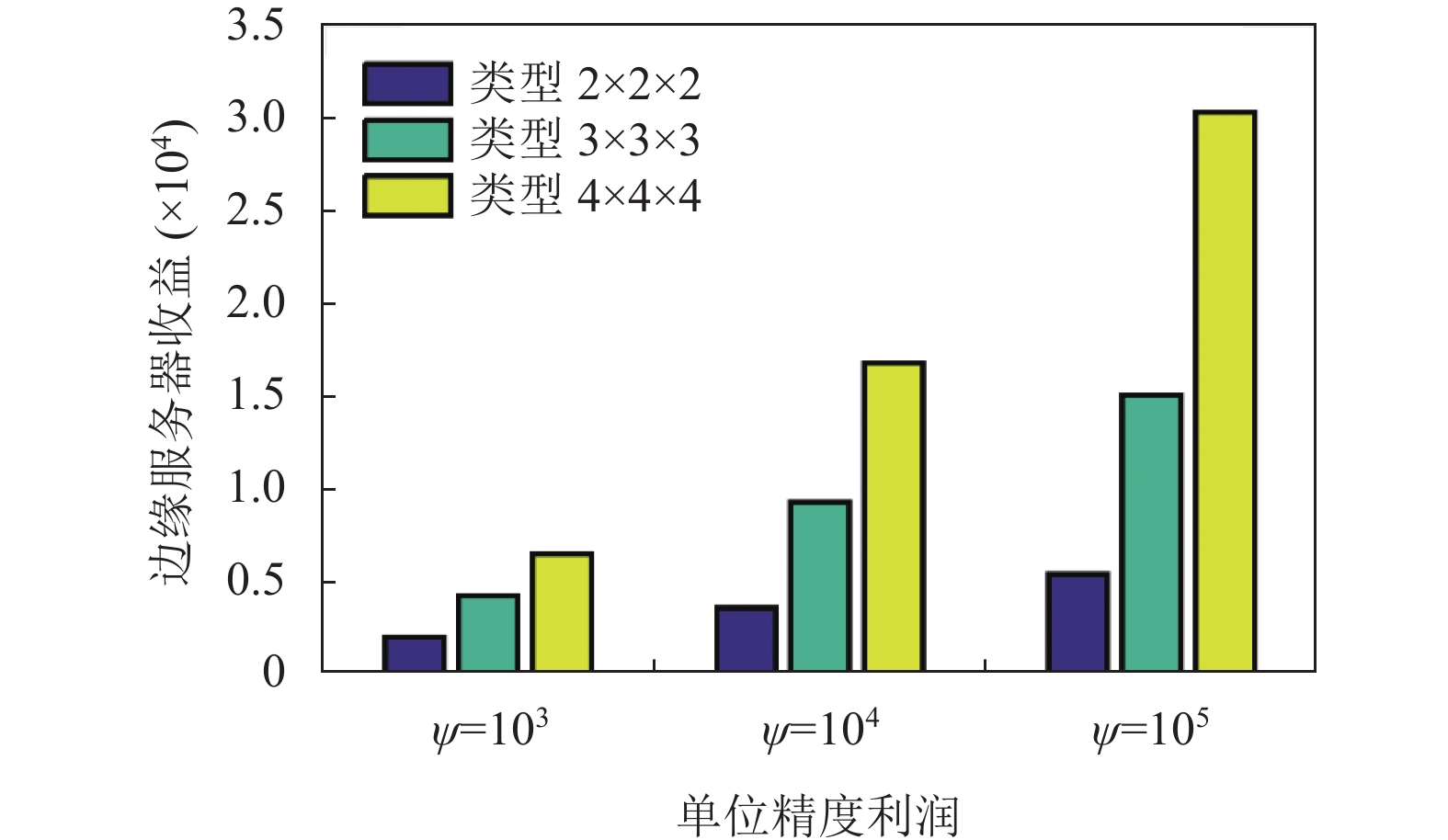
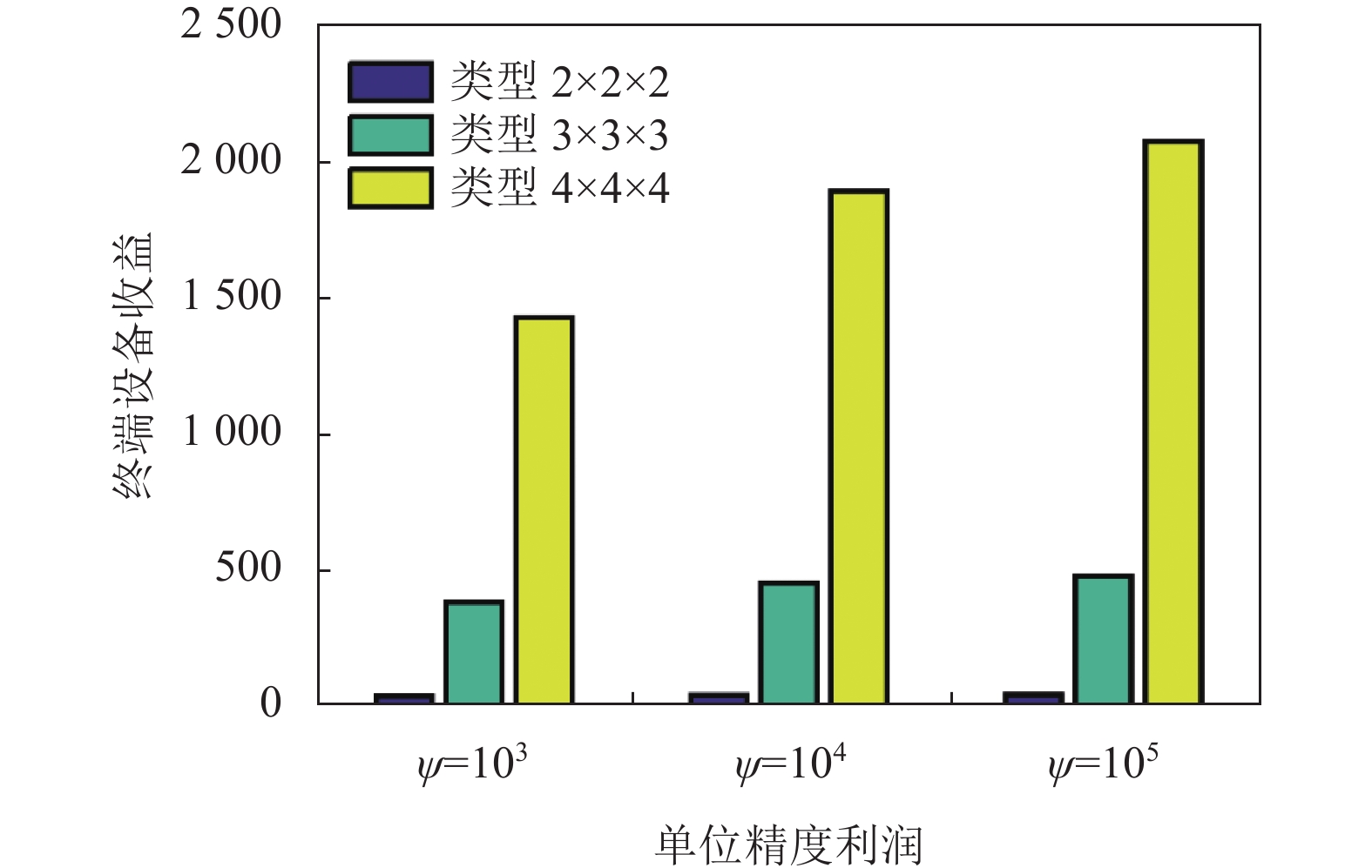
5.3 参数对性能的影响

图10–图12探讨了单元利润和用户类型的变化对系统性能的影响. 结果显示, 提升单元利润显著增加了云服务器及边缘服务器与终端设备的整体收益. 同时, 用户类型的增加也相应提高了云服务器及边缘设备的整体收益.

6 结论与展望

针对隐私保护下的HFL资源分配问题, 本文设计了一种保护参与者隐私的分层激励机制. 在边缘-设备层, 边缘服务器作为中间商利用多维契约论设计不同的合约激励不同类型的终端设备参与到HFL任务当中. 在服务提供商-边缘层中, 本文使用Stackelberg博弈来说明服务提供商下云服务器和边缘服务器之间的交互, 证明在信息对称的情况下, 边缘服务器和云服务器之间存在唯一SE. 此外, 本文采用分布式MADRL方法, 在信息不对称的情况下, 迭代收敛到SE. 实验表明本文所提出的激励机制可以取得比其他基准方案更好的性能, 使云服务器的收益提升接近11%, 单位成本获取增益提升接近18倍. 本文探究了单任务下的HFL激励机制. 在未来的工作中会尝试从多任务的角度出发, 使用多维双层契约理论方法设计HFL激励机制以达到提高其效率的目的.