中国煤炭开采历史悠久, 但发生在井下的微震事故仍然备受关注. 矿井内部的微震信号是井下岩石破裂和围岩垮塌最重要的前兆信息, 实时捕捉井下的微震信号并及时处理是保障下井人员安全的重要手段. 由于井下环境存在着各种人为的噪声导致微震的波形信号要比普通地震信号复杂的多[1]. 常规降噪方法用于信噪比较低的微震信号时, 往往存在鲁棒性低, 阈值难以统一, 信号失真严重等问题导致降噪不能有良好的效果.
小波降噪方法在应对微震信号表现良好, 但是定义其在降噪时的阈值是决定降噪效果的重要因素[2,3]. 为此本文提出了基于复小波变换卷积自编码微震波形降噪方法, 通过全监督的方法训练一个深度神经网络模型来学习图像中的噪声和信号表示. 此模型的降噪过程是将含噪信号首先通过复小波变换生成不同尺度的小波系数并构建时频图, 这些系数通常具有
本文的主要贡献包括:
(1)提出了基于复小波变换全监督学习的微震波形降噪与相位拾取方法, 从半真实地震数据中学习更丰富的特征, 在时频域中分离信号和噪声.
(2)设计了基于CNN的1-D卷积神经网络完成降噪信号的P波、S波相位拾取, 验证了拾取效果的提升降噪对拾取效果的提升.
(3)构建了Earthquake2023地震信号数据集并训练了降噪模型和拾取模型的深度神经网络.
2 相关工作 2.1 微震信号降噪在常规的微震信号处理中, 经常采用谱滤波[8](通常基于傅里叶变换)来抑制噪声, 但当噪声和微震信号有着相同的频率范围时, 这种方法就会将有用的微震事件信号给滤掉, 从而给后续的微震事件信号分析带来较大的损失和难度. 此外, 用于滤波的最佳参数也是不直观的, 它随时间的变化而变化, 有时甚至会改变波形的形状, 使得最后结果与原始数据有着较大的误差. 由于滤波的种种限制, 专家学者开始研究更有效的降噪方法应用, 最广泛的就是基于时频降噪的方法如小波变换[9]、短时傅里叶变换[10]、S变换[11]等, 即使用时间-频率变换. 其中小波变换降噪方法能衰减与噪声相关联的时频系数并找到信号系数的估计值[12], 衰减后的系数又会被逆变换回时域, 从而重构降噪信号. 通过将微震波形变换到其他域来使它变得稀疏, 其中的可用信号则可以用稀疏特征集来表示, 使得信号和噪声可以更容易地分离[13]. 他的优点是即使在噪声与信号是相同的频率范围时也可以抑制噪声[14]. 但是选择合适的阈值函数来将噪声数据衰减到最优降噪信号是这个方法的难点也是弊端所在, 阈值的选择将直接影响降噪的效果. 由于微震信号信噪比相对较低, 所以经典的小波函数降噪在处理微震信号时存在些许不足. 本文则针对这些不足设计了基于复小波变换全监督学习的微震波形降噪方法, 该方法受DeepDenoiser[15]降噪方法的启发利用神经网络处理含噪信号, 实现信号在时频域的噪声分离. 此方法能更好地保留信号特征, 适用于不同的含噪信号.
2.2 微震信号的震相拾取震相拾取是微震信号研究的另一关键方面. 在早期, 震相拾取主要依赖于经验丰富的研究人员手动处理, 然而这种方法效率低且不够理性. 因此, 人们开始探索用机器代替人力的想法, 其中包括基于振幅和能量的算法(例如STA/LTA或波形相似性的模板匹配算法)以及机器学习方法, 如使用指纹和相似性阈值[16]. 这些方法原理简单, 适应性较强, 但在处理信噪比较低的微震信号时, 往往容易产生拾取误差.
从2017年开始, 学者们开始考虑使用深度学习来完成震相拾取任务. 目前, 基于卷积神经网络(CNN)和循环神经网络(RNN)的方法较为流行[17]. 波形到时拾取是计算震源参数的关键因素之一, 容易受到噪声的干扰. 因此, 噪声的彻底去除对拾取效果产生重要影响.
本文设计了基于CNN的1-D卷积神经网络来完成降噪信号的P波和S波相位拾取. 由于篇幅有限, 本文侧重介绍了降噪过程, 因此在后文中将对这一震相拾取方法进行简略介绍. 这一方法的实现对于微震信号的震相准确拾取具有重要意义, 为后续的震源参数计算提供了可靠的基础.
3 本文方法在本节中主要介绍基于复小波变换全监督学习的微震波形降噪方法包括多维度复小波分解与重构和基于全监督学习的深度神经网络降噪方法. 另外介绍基于CNN的1-D卷积神经网络的微震信号震相拾取的方法.
3.1 多尺度复小波变换地震信号降噪方法主要有基于时频分析的降噪方法和基于频域分析的降噪方法. 其中小波分解则是基于此的一种局部分析方法, 他可以对信号的不同时间段和频率进行分析, 从而能提供更好的时频局部特征, 相较于傅里叶变换它更适合非平稳信号如信噪比较低的微震信号[17]. 所以本文采用小波分解作为信号时频分析的工具. 首先是数据的取样, 由Nyquist[18]采样定理可知取样率至少是细节频率的两倍才能保证细节频率不会失真. 基于取样率和分解层数确定原始信号

|
图 1 分解过程 |
图1中
| ψ(t)=A⋅ei2πft⋅e−t22σ2 | (1) |
其中,
传统的小波分解加上一定的滤波可以在噪声和微震信号占据相同的频率范围时抑制噪声, 但如何选择一个合适的阈值函数从而将噪声数据映射到最优降噪信号是降噪效果好坏的关键. 为了提高降噪性能, 本文考虑利用神经网络来改进样本特征集的稀疏性和映射函数, 此神经网络的创新点在于: 基于卷积自编码(convolutional auto-encoder, CAE)实现一个Encoder和一个Decoder过程, Encoder通过对时频图进行一系列的卷积操作学习数据在时频域的稀疏表示, Decoder将稀疏表示映射到两个Mask (MN、MS)将Mask与时频图做哈达玛积实现信号和噪声的分解, 解决了手工设计特征值与阈值难以兼顾各种噪声同时缺乏泛化性的问题.
微震检测系统所记录的含噪信号
| M(t,f)=S(t,f)+N(t,f) | (2) |
其中,
| Error=1nn∑i=1(S(t,f)i−¯S(t,f)i)2 | (3) |
其中,
| Sm(t,f)=11+|N(t,f)||S(t,f)| | (4) |
| Nm(t,f)=|N(t,f)||S(t,f)|1+|N(t,f)||S(t,f)| | (5) |
该神经网络结构主要包含3个关键部分: 编码器、解码器以及它们的表示形式(见图2). 编码器通过一系列卷积层对输入数据进行处理, 逐步提取特征, 将输入数据映射到低维向量H所在的潜在空间. 解码器则通过一系列逆卷积层逐步生成输出数据. 本文采用一系列大小递减然后递增的完全卷积层来组成降噪网络(见图3).

|
图 2 编码-解码表示图 |

|
图 3 本文降噪神经网络构成图 |
在网络的前半段, 即编码阶段, 本文方法选取数据的时频系数的虚部和实部作为网络的输入. 通过0边缘填充法将数据尺寸从(29×199×2)重塑为(31×201×2), 以避免在卷积过程中丢失图像的边缘信息. 随后, 对输入时频系数进行一系列卷积层的处理和变换, 实现特征提取. 每个卷积层都附加有ReLU激活函数和批量标准化(BZ), 卷积核的大小设置为(3×3), 保持不变. 为了逐步缩小特征空间, 提高训练效率, 逐渐减小卷积层的stride (移动步长), 同时为防止精度下降, 增加卷积层的深度. 由于数据尺寸较小, 无需进行池化操作.
网络在瓶颈层实现输入数据的非常稀疏表示, 并完成编码到解码的转换. 在解码阶段, 网络使用反卷积层(卷积层的转置)生成稀疏表示到输出掩码的高维非线性映射. 在网络的最后一层使用Softmax指数函数生成两个掩码, 即用于信号与噪声分离的最终输出. 网络通过优化交叉熵损失函数, 学习数据的稀疏表示和最佳掩码, 以实现信号与噪声的有效分离.
为了提高训练和预测性能的收敛性, 该网络引入了跳过连接. 这些连接使得信息能够直接在不同层之间流动, 有助于减轻梯度消失问题, 提高训练的稳定性. 这一设计架构的整体流程通过编码器、解码器和稀疏表示的互动, 使得神经网络能够更有效地从时频域中学习到丰富的特征, 并在降噪任务中展现出卓越的性能.
图4展示了本文降噪的整体流程, 首先通过复小波变换将微震信号映射到时频域, 并生成相应的时频系数. 由于时频系数呈现复数形式, 因此将其实部和虚部作为神经网络的输入数据. 神经网络通过一系列卷积操作对输入数据进行处理, 输出两个掩码Sm和Nm. 这些掩码与时频图进行哈达玛积运算, 从而实现对噪声或信号信息的遮蔽, 估计得到信号和噪声的时率系数. 最后, 通过逆复小波变换, 得到降噪后的图像.
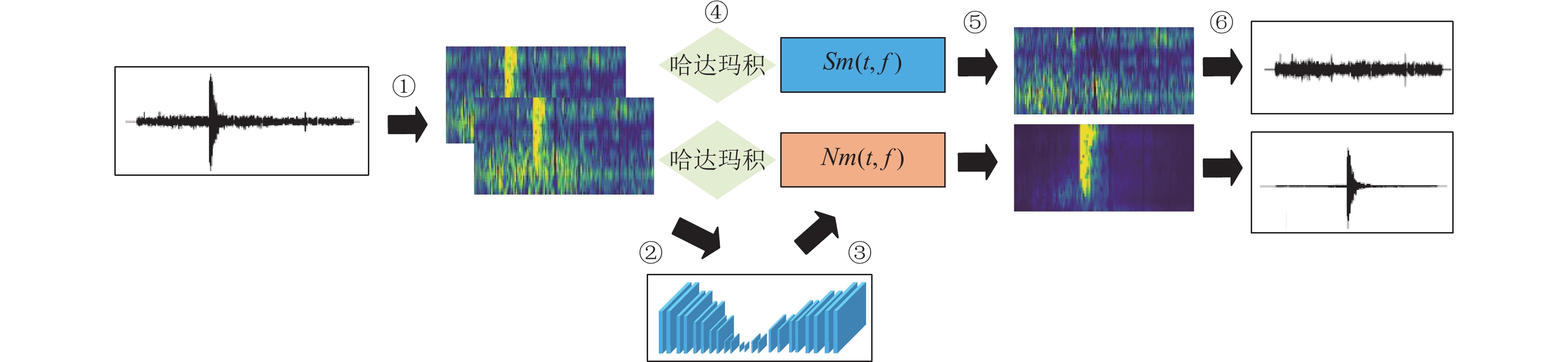
|
图 4 降噪的整体流程 |
这个网络模型的显著优势之一在于其无需手动定义不同的特征和阈值来区分信号和噪声. 相反, 它通过对人为合成的地震数据进行学习, 从中提取丰富的时频域特征, 使其能够有效地区分信号和噪声. 通过经过充分的训练, 该网络模型在微震信号降噪方面具有巨大的潜力. 其自动学习能力使得模型能够适应不同的信号特征, 无需手动调整参数, 从而提高了在真实场景中的应用鲁棒性.
本文通过整合复小波变换和神经网络技术, 本方法不仅能够更好地捕捉微震信号的时频特性, 还能够实现对噪声的准确识别和抑制. 这一综合性的降噪框架为微震监测和地震事件分析提供了一种创新的解决方案, 有望在相关领域推动技术的发展.
3.3 基于CNN的1-D卷积神经网络的微震信号震相拾取的方法由于微震信号降噪的目标是为了更好地进行信号分析和后续处理, 其中震相拾取是至关重要的一环. 为了在信号经过降噪处理后准确地进行震相拾取, 本文引入了一种基于深度学习的方法, 即对经过降噪处理的信号进行准确的P波和S波到达时间标注. 这一步骤对于后续对震源位置和震动时间的准确研究至关重要.
在降噪完成后, 信号被恢复成了时域表示, 因此变为了一维数据, 即数据按时间顺序记录, 每个数据点与特定时间点相关联, 数据大小为(1×6000). 由于降噪后数据的有用信息基本居中, 因此无需对数据进行边缘填充. 对于这种1-D时间序列数据, 使用卷积神经网络(CNN)通常能够取得显著的效果.
基于这一背景, 本文设计了一个基于CNN的1-D卷积神经网络模型(见图5). 该网络的输入数据为微震波形的时间序列表示, 并从中选取P波、S波作为训练的标签数据. 网络输出是P波、S波的概率分布. 输入数据通过4个下采样阶段和4个上采样阶段, 每个下采样阶段包含一个1-D卷积层和一个ReLU激活函数, 卷积核大小为7, 步幅设置为6. 下采样旨在从原始地震数据中提取有用信息并降低维度. 上采样通过反卷积将信息扩展, 并在最后一层使用Softmax指数函数转化为每个时间点的P波、S波的概率分布. 在训练过程中, 采用跳过连接来提高训练和预测性能的收敛性. 使用真实概率分布和预测分布之间的交叉熵来定义损失函数, 以评估模型的训练结果. 最终, 利用概率分布生成一串可视化数据, 其中0代表无到达, 1代表已到达. 通过这一步骤, 本文为微震信号的震相准确拾取提供了可靠的工具和方法.

|
图 5 本文相位拾取神经网络结构 |
4 实验
本节首先在第4.1节中使用 Earthquake2023数据集进行降噪神经网络模型的训练测试并初步得到降噪结果, 证明了本文方法的有效性. 降噪结束后对降噪数据进一步优化和训练得到了本文的波形拾取模型, 通过可视化结果验证了拾取的精度. 接着在第4.2节中通过模拟信号和真实的微震信号进行降噪实验对比验证了本文方法较其他方法的优越性. 最后在第4.3节中通过多种参数和方法的对比验证了本文拾取方法的有效性.
4.1 训练和测试结果分析本文采用的训练数据集是Earthquake2023. 该数据集由5634个信噪比较高的地震波形作为信号样本和7923个与各种非地震波形相关联的地震记录作为噪声样本. 信号数据被随机地分成4517个样本的信号训练集, 557个样本的信号验证集、566个样本的信号测试集, 噪声数据被随机地分成4755个样本的噪声训练集, 2376个样本的噪声验证集和792个样本的噪声测试集. 在训练降噪网络时为了构建合成地震图用于训练神经网络, 本文从噪声训练集中随机选择噪声样本, 并将其叠加到信号样本上, 以生成不同信噪比水平的训练数据. 通过信号和噪声样本之间的这种组合建立了超过数万个样本的最终训练数据集. 其中验证集用于调整深度神经网络的超参数, 从而防止数据的过拟合. 使用Adam梯度下降优化算法训练深度神经网络, 学习速率为0.001, 最小批量为200. 训练轮次为200轮, 批量处理大小为64. 图6显示了训练集和验证集的损失(Loss)变化情况, 损失值越小训练效果也好, 验证集的曲线越接近于训练集说明拟合效果越好.
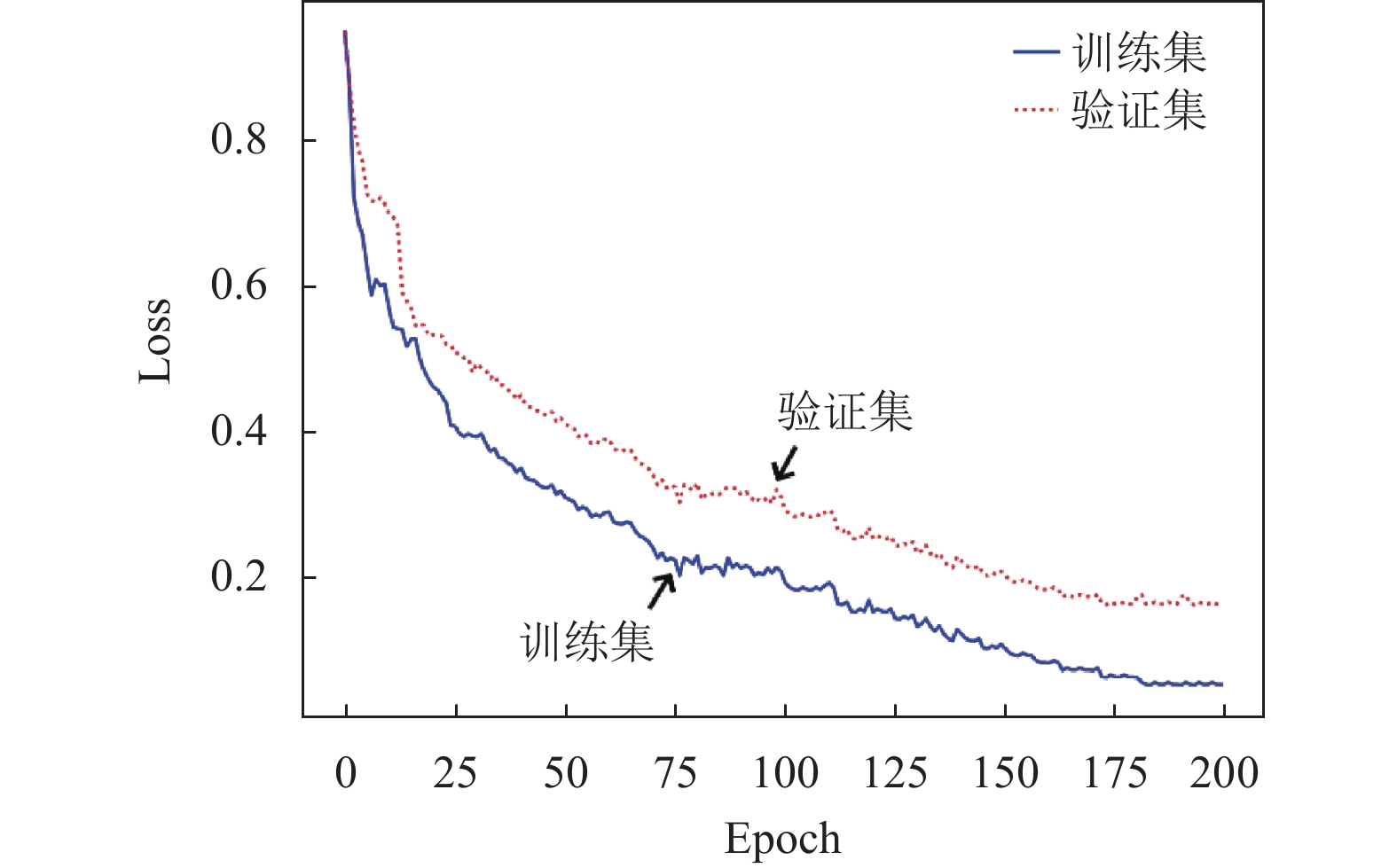
|
图 6 降噪网络Loss值变化情况 |
通过对模型完成200轮的训练可以发现在最后50轮epoch中, Loss值没有进一步降低, 表明模型训练结果达到了预期水平, 最终训练集和验证集的Loss分别为0.05和0.15. 可以看出此网络模型在训练过程中表现良好. 降噪网络训练结束后, 本文选取了2000个较为典型的微震信号进行降噪并将降噪结果进行人工表波即在P波和S波到达处进行人工标注(图7). 由于P波要早于S波到达, 所以图7中左侧箭头指向P波到达时间, 右侧箭头为S波到达时间, 标注数据也作为神经网络的标签数据.

|
图 7 人工标注结果 |
本文将2000个数据分为1300个训练集, 600个验证集和100个测试集. 由于数据有限, 为防止过拟合, 本文经验证集的多次测试发现在0.001学习率的情况下, 100个epoch时Loss达到了最佳拟合状态(图8), 所以本文最后设置学习速率为0.001, 最小批量为100. 训练轮次为100轮, 批量处理大小为16. 最终训练集和验证集的Loss分别为0.0285和0.283. 可以看出此网络模型在训练过程中表现良好.
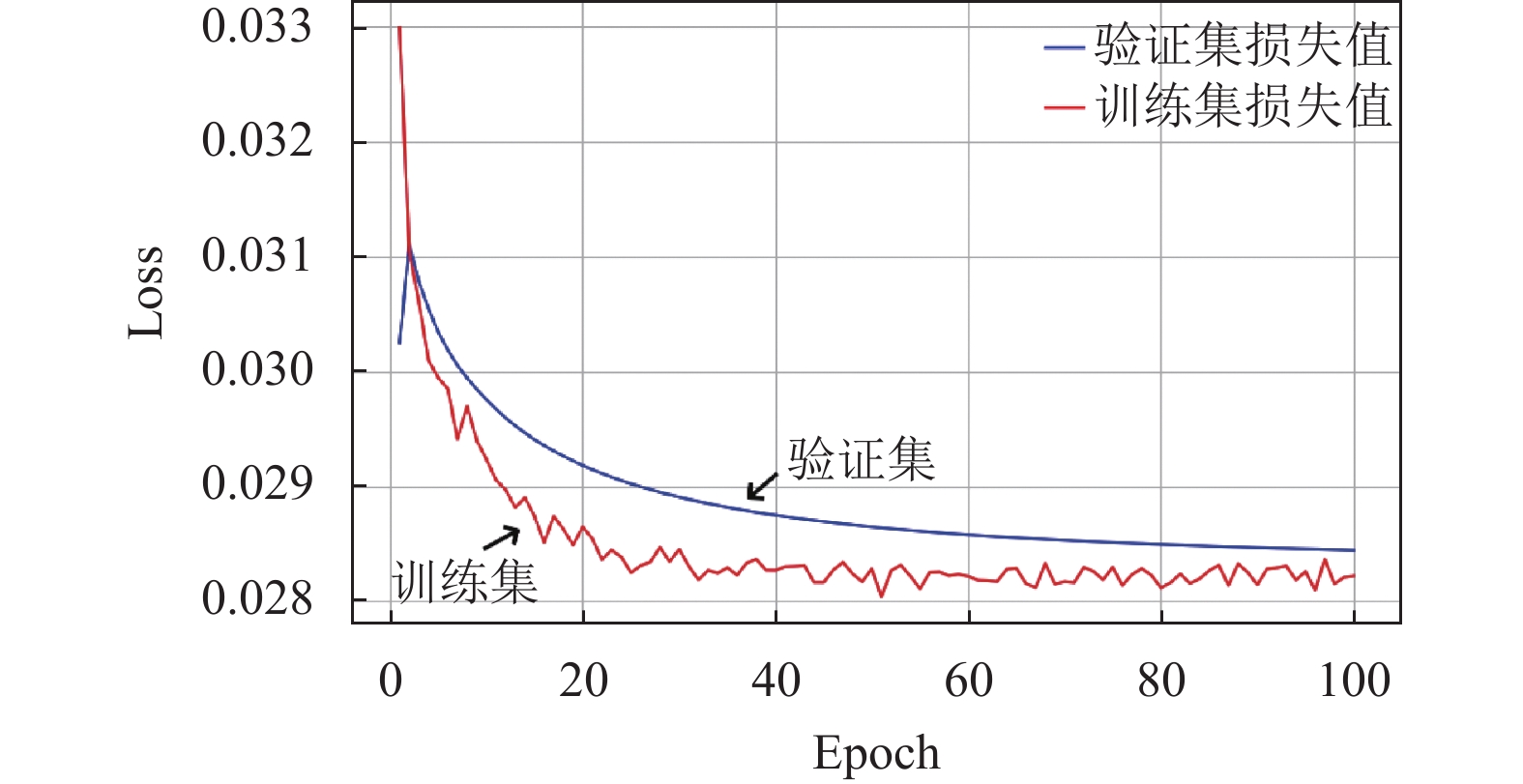
|
图 8 相位拾取模型Loss值 |
为验证降噪模型的降噪效果, 利用Earthquake2023数据集1400个样本构造了1000个测试数据, 其中包含了各类噪声集. 本文则选取了4种典型的含噪信号包括: 低频、高频、循环和纯噪声, 并同过可视化来验证降噪结果, 可视化图分别为图9(a)–图9(d).

|
图 9 测试集4种典型的噪声降噪结果 |
图9每幅图有3个波形, 分别为含噪波形, 降噪后波形和预估的噪声. 可视化结果表明本文方法可以成功将具有不同特性的噪声信号分离, 并且在噪声信号与干净信号重叠时也能有效降低信号损失, 极大还原了原始信号. 更多地, 本文还将此降噪算法应用到2000个真实噪声样本进行测试. 图10显示了本文降噪算法在不同噪声上的降噪效果, 包括各种循环噪声和其他未知噪声. 结果显示本文提出的降噪网络对于真实的噪声信号具有一定的鲁棒性, 即当没有有用信号被预测时, 预估的噪声几乎等于原始输入的噪声样本.

|
图 10 本文方法对不同真实噪声的降噪性能 |
图11显示了实际噪声样本与预估噪声之间的最大振幅差的分布, 结果表明60%以上噪声样本的最大振幅差<0.005, 95.59%以上噪声样本的最大振幅差<0.02, 这意味着本文提出的方法能较好地分离含噪信号中的噪声, 仅会对原始信号造成轻微的波形失真.
微震信号降噪的最终目的是帮助科研人员对信号进行更好的后续处理, 所以降噪算是微震数据预处理中最重要的一个环节, 降噪完毕后对信号后续的处理包括信号的相位拾取和震源定位等, 同时信号到时拾取的准确性也能从一方面反映出降噪效果的好坏.

|
图 11 实际噪声与预估噪声的最大振幅差 |
本文则是在降噪方法的基础上设计了一个震相拾取的方法来实现对数据预处理之后的效果验证, 本文也选取了3个信噪比不同的真实微震信号来实现降噪-拾取的完整步骤(图12(a)–图12(c)). 并通过初步观察拾取的精确度来检验此过程结果的准确性.
从图12中可以看出经过本文设计的震相拾取方法在P波、S波的初至到时拾取上有更多的尝试, 且精度较高.

|
图 12 不同信噪比的信号降噪-拾取结果 |
4.2 降噪方法对比实验
由于微震信号比模拟信号要复杂的多, 所以本文也通过实验获取了约2000个信噪比较低的真实微震信号如图13, 此信号由高精度微震监测系统(seismological observation system, SOS)获取, 系统由信号采集站、记录仪系统、检波测量探头等组成. 图14展示了实验设备和现场图片, 振动由人工激发并通过检波测量探头传递到信号采集站.
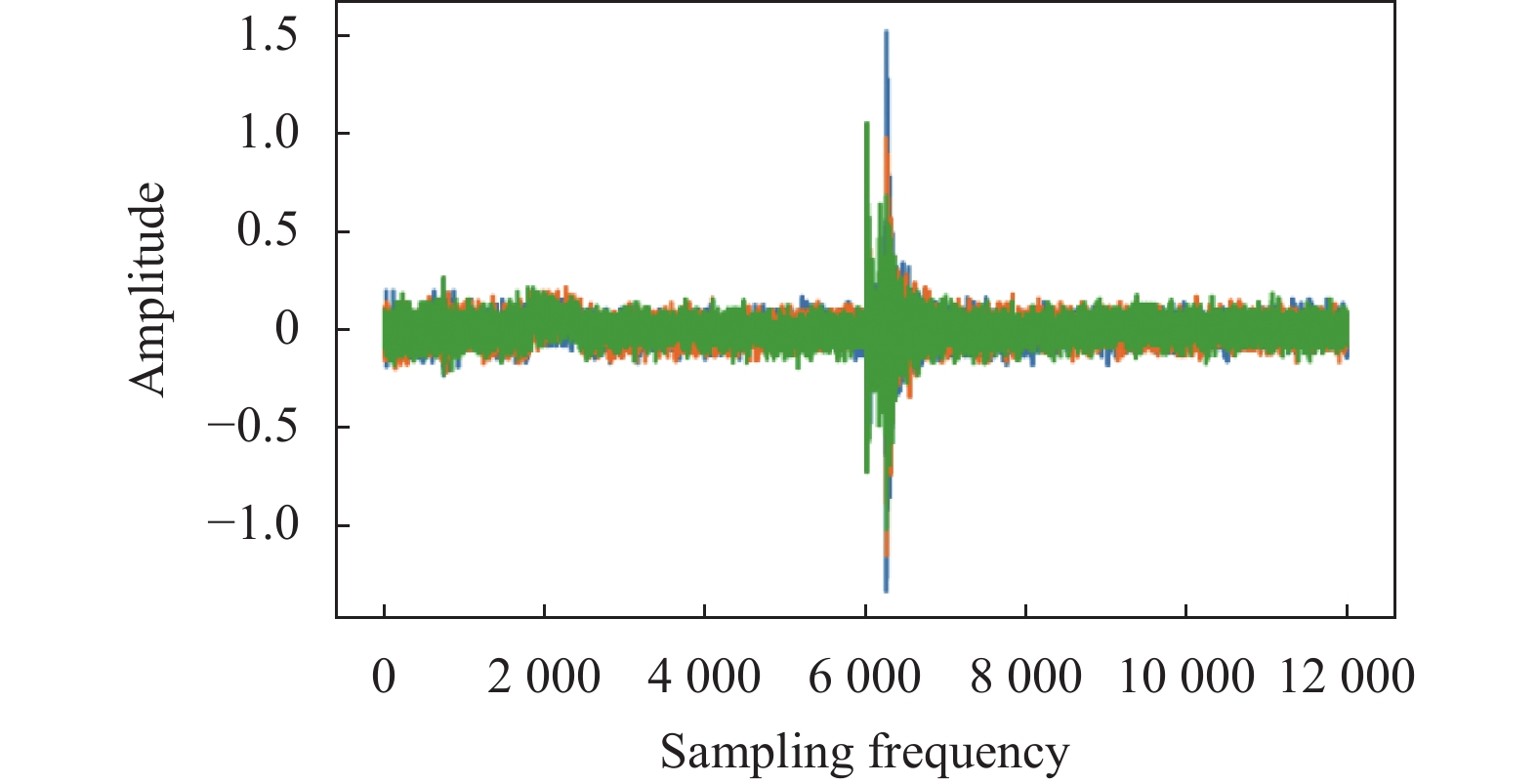
|
图 13 真实微震信号 |

|
图 14 实验设备以及现场图 |
为了进一步证明该方法的优越性, 本文基于干净的微破裂信号和噪声的频率分布设计了高通滤波器, 以实现最佳的降噪性能. 同时选取小波降噪方法并将上述两种降噪方法与本文方法进行对比. 为了更直观地分析降噪结果, 本文采用了信噪比(SNR)和均方根误差(RMSE)[20]进行数值分析.
SNR是有用信号的强度与接收到的干扰信号(噪声和干扰)的强度的比值, 能够量化的评估降噪的效果. 较高的SNR值通常表示有用信号较多, 即降噪效果较好. RMSE是一种用来衡量预测值与真实值之间偏差的度量标准. 较小的RMSE值表示降噪后信号与原始信号的拟合较好, 误差较小.
通过SNR和RMSE的综合分析, 能够全面评价不同降噪方法在保留信号特征的同时抑制噪声的效果.
式(6)为信噪比SNR公式, 其中
| SNR=10×log10((2n−1)2n∑i=1(h(xi)−yi)2)s | (6) |
式(7)为均方根误差RMSE公式, 其中
| RMSE(X,h)=√1mm∑i=1(g(xi)−fi)2 | (7) |
| 表 1 3种方法降噪结果 |
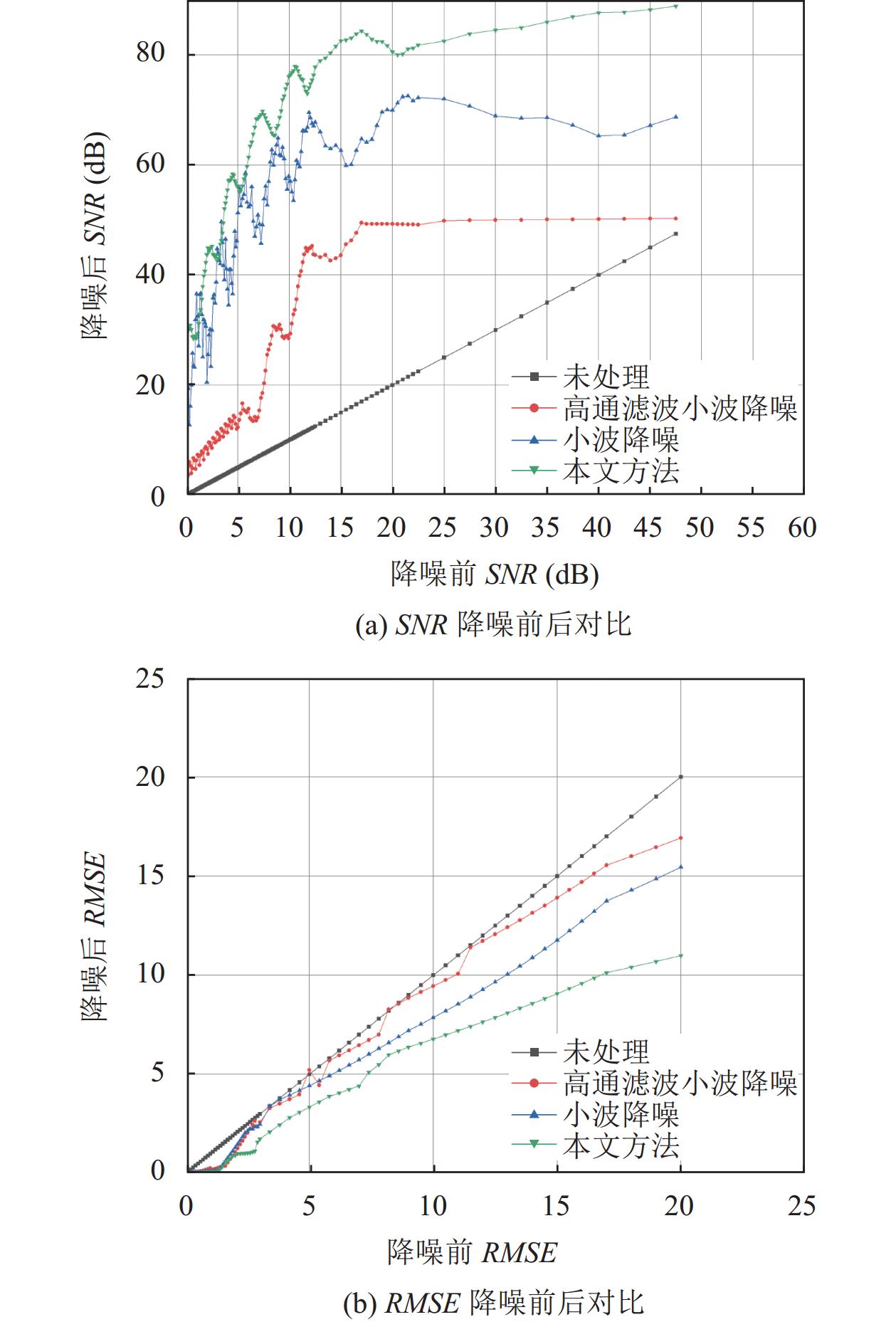
如图15(a)、图15(b)是含噪信号经过高通滤波器、小波降噪和本文方法处理后的信噪比、均方根误差变化的比较. 结果表明本文方法与高通滤波器相比提高的相对明显信噪比平均提高了39.251 dB、RMSE平均减小了9.943 (表1), 表明本文方法能较好地分离含噪信号中的噪声信号和保留其中的有用信号, 相比之下高通滤波器在降噪过程中则有着较高的失真. 同时图像表明当信号的信噪比逐渐升高即信号中噪声含量变低时, 3种方法对信号质量都有着较为平缓的提高趋势, 而当信噪比较低时, 本文方法对信号质量的提高明显优于其余两种方法. 综上所述信号经过本文方法降噪后可以实现噪声和有用信号的分离, 且在信号处于较低的信噪比水平时也能够很好地避免波形信息的流失.
4.3 相位拾取对比实验为了更加直观地展示本文拾取效果的准确性, 本文将上述2000个真实的微震信号进行了手动拾取并将计算了与本文方法拾取的到时误差:
|
图 15 3种方法性能比较 |
|
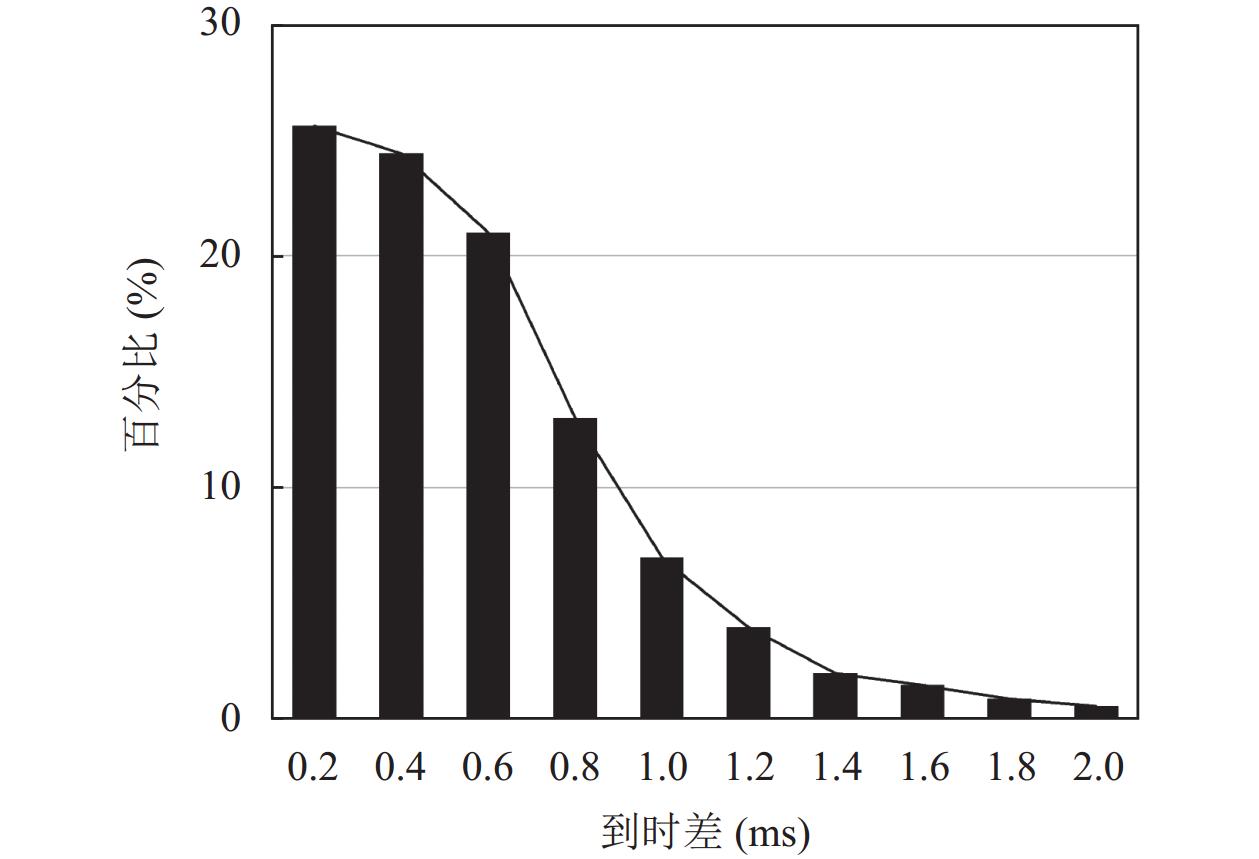
图 16 人工与本文方法到时拾取误差 |
由图16中2000个真实含噪信号的到时拾取误差分布可知, 平均误差是0.577, 其中81%的含噪信号误差<0.6 ms, 91%的含噪信号误差<1 ms. 结果表明和人工相比本文方法能较好地接近人工水平实现相位到时拾取.
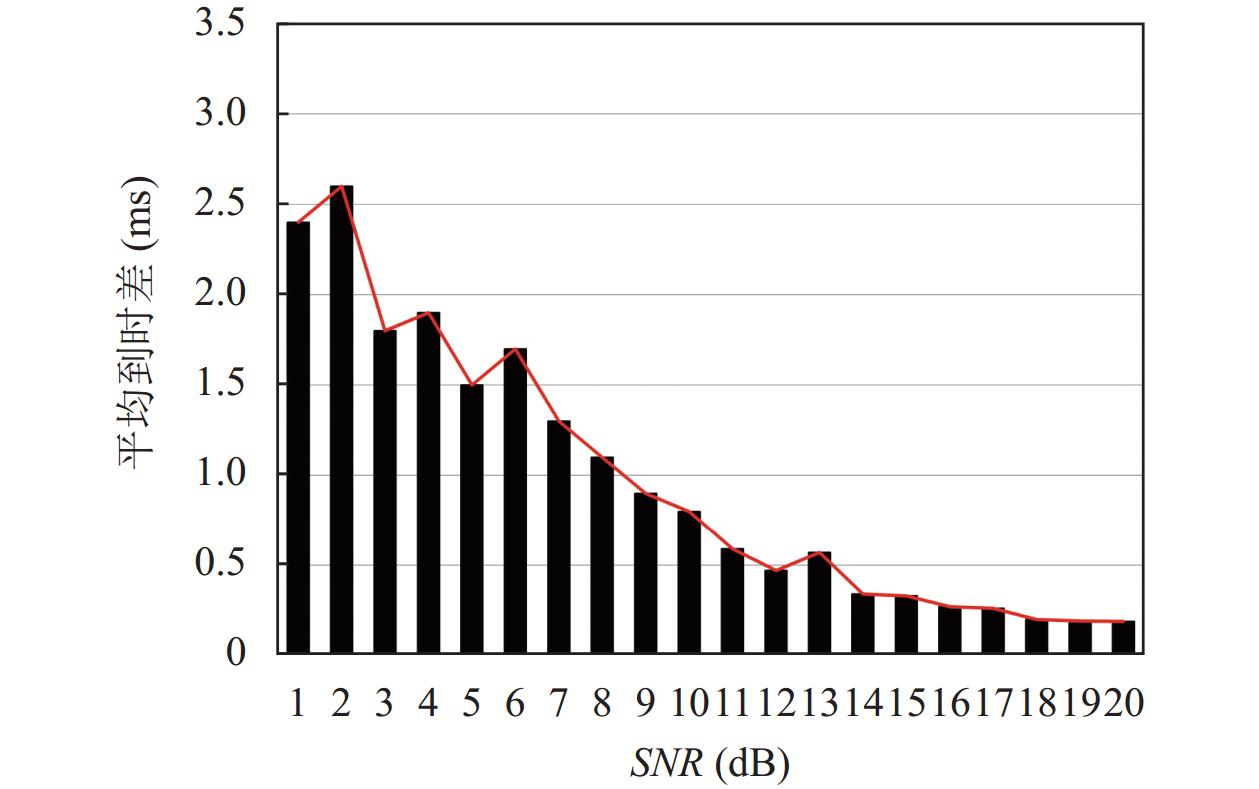
同时本文还对比了不同信噪比信号的拾取结果如图17所示, 结果表明信噪比<10的含噪信号平均拾取误差为1.67, 信噪比>10的含噪信号平均拾取误差为0.39. 说明本文拾取方法更适用于降噪后含噪信号, 但对于降噪前的信号也有一定的拾取精度.
|
图 17 不同信噪比的拾取误差 |
为了更直观地验证效果, 本文利用上述2000组数据进行测试并对比了STA/LTA和EqTransformer拾取方法并引入准确率(accuracy)和召回率(recall)两个评价指标. 其中准确率指的是模型正确预测为正类别(相位存在)的样本数量占所有预测为正类别的样本数量的比例, 即准确率衡量的是模型在预测正类别时的精确程度. 准确率越高, 表示模型预测的正类别更加可靠. 召回率指的是模型正确预测为正类别的样本数量占所有真正的正类别样本数量的比例, 召回率衡量的是模型找到了多少真正的正类别样本, 是一个关于模型查全率的指标. 召回率越高, 表示模型能够找到更多真正的正类别样本, 具体如图18所示.
本节内容说明了本文方法拾取精度上相对于STA/LTA有着较大的提升, 到时误差为0.577 ms相比提高了0.473 ms、准确率平均值78.14%相比提高了7.59%、召回率平均值为72.48相比提高了7.13% (表2). 但相较于较为先进的EqTransformer算法还是略微有些不足, 后续将继续改进震相拾取算法, 以保证在降噪效果较高的前提下达到更高的拾取精度.
5 总结本文提出了基于复小波变换全监督学习的微震波形降噪方法, 此方法在复小波分解的基础上加上神经网络, 训练出一个无需手动定义不同的特征和阈值来去除噪声, 相较于传统的小波阈值函数降噪, 本文提供的方法能够在信噪比较低的微震信号中拥有较好的降噪效果, 同时根据降噪结果设计了基于CNN神经网络的震相拾取方法, 为优化其他降噪算法提供了思路.

|
图 18 3种方法到时拾取误差对比 |
| 表 2 平均到时误差结果 |
未来的工作包括3个方面. 一是继续改进提高信号的领域的稀疏性, 从而进一步提高算法降噪的准确性. 二是进一步提高训练精度, 提高方法的普适性. 三是加大训练样本, 让模型有更高的鲁棒性
| [1] |
魏国武, 万小军, 微震事件波形分析与信号处理研究. 能源与环保, 2023, 45(1): 154–161, 174.
|
| [2] |
戴庆, 卢杨, 栗磊, 基于多小波自适应阈值的地震图像去噪方法. 科学技术与工程, 2009, 9(24): 7533–7536.
|
| [3] |
马杭, 陆文总, 耿世宇, 等. 基于改进阈值函数的小波降噪方法研究. 激光杂志, 2023, 44(10): 19-24. |
| [4] |
Woollam J, Münchmeyer J, Tilmann F, et al. SeisBench—A toolbox for machine learning in seismology. Seismological Research Letters, 2022, 93(3): 1695-1709. DOI:10.1785/0220210324 |
| [5] |
Sara U, Akter M, Uddin MS. Image quality assessment through FSIM, SSIM, MSE and PSNR—A comparative study. Journal of Computer and Communications, 2019, 7(3): 8-18. DOI:10.4236/jcc.2019.73002 |
| [6] |
王俊, 杨驰, 詹小艳, 等. P波初至到时自动拾取技术研究. 地震研究, 2018, 41(1): 38-45. DOI:10.3969/j.issn.1000-0666.2018.01.005 |
| [7] |
Yu ZY, Chu RS, Sheng MH. Pick onset time of P and S phase by deep neural network. Chinese Journal of Geophysics, 2018, 61(12): 4873-4886. |
| [8] |
Zhu WQ, Beroza GC. PhaseNet: A deep-neural-network-based seismic arrival-time picking method. Geophysical Journal International, 2019, 216(1): 261-273. |
| [9] |
Bentley PM, Mcdonnell JTE. Wavelet transforms: An introduction. Electronics & Communication Engineering Journal, 1994, 6(4): 175-186. |
| [10] |
Griffin D, Lim J. Signal estimation from modified short-time Fourier transform. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1984, 32(2): 236-243. DOI:10.1109/TASSP.1984.1164317 |
| [11] |
Gu JH, Liu Q. A basis for efficient representation of the S transform. Journal of Henan Normal University (Natural Science Edition), 2009, 37(2): 60-63. DOI:10.3969/j.issn.1000-2367.2009.02.019 |
| [12] |
Sifuzzaman M, Islam MR, Ali MZ. Application of wavelet transform and its advantages compared to Fourier transform. Journal of Physical Sciences, 2009, 13: 121-134. |
| [13] |
Mousavi SM, Zhu WQ, Sheng YX, et al. CRED: A deep residual network of convolutional and recurrent units for earthquake signal detection. Scientific Reports, 2019, 9(1): 10267. DOI:10.1038/s41598-019-45748-1 |
| [14] |
Gilles J. Empirical wavelet transform. IEEE Transactions on Signal Processing, 2013, 61(16): 3999-4010. DOI:10.1109/TSP.2013.2265222 |
| [15] |
Zhang YS, Lin HB, Li Y, et al. A patch based denoising method using deep convolutional neural network for seismic image. IEEE Access, 2019, 7: 156883-156894. DOI:10.1109/ACCESS.2019.2949774 |
| [16] |
谢杰成, 张大力, 徐文立. 小波图象去噪综述. 中国图象图形学报, 2002, 7(3): 209-217. DOI:10.3969/j.issn.1006-8961.2002.03.001 |
| [17] |
杨梅, 张振文, 孙宏强, 等. 小波分析与傅里叶分析的比较及其在故障诊断中的应用. 中国测试技术, 2005, 31(2): 58-59, 61. |
| [18] |
Landau HJ. Sampling, data transmission, and the Nyquist rate. Proceedings of the IEEE, 1967, 55(10): 1701-1706. DOI:10.1109/PROC.1967.5962 |
| [19] |
张华, 陈小宏, 杨海燕. 地震信号去噪的最优小波基选取方法. 石油地球物理勘探, 2011, 46(1): 70-75. |
| [20] |
Mousavi SM, Ellsworth WL, Zhu WQ, et al. Earthquake Transformer—An attentive deep-learning model for simultaneous earthquake detection and phase picking. Nature Communications, 2020, 11(1): 3952. DOI:10.1038/s41467-020-17591-w |
 2024, Vol. 33
2024, Vol. 33



