1 引言

在零件制造行业中, 智能制造已成为行业关注的热潮. 智能制造, 是新一代先进信息技术与先进制造技术融合的产物^[1], 目标是用计算机辅助技术模拟工艺设计人员在零件生产过程中的分析、推理、决策等应用人类智能的活动. 近些年, 随着智能制造技术的应用, 产生了大量的工艺数据(如三维CAD模型、CAM模型). 这些数据凝聚了工艺设计人员进行零件制造时各环节运用的制造经验和工艺知识, 其已成为获取工艺知识的最得力工具^[2]. 如何有效传递工艺数据中隐式的工艺知识, 使之成为制造业的有效驱动力, 已在制造业中变得越来越关键^[3–6].

通常对工艺数据的挖掘主要应用衍生法. 衍生法的中心思想是通过相似性评价, 建立相似度评价模型并计算待制零件与已制零件相似度, 若存在相似结构则采取相同或改进的工艺方案. 但往往该方法在构建相似性评价模型时只关注于某个特定的层面并对其进行表述, 这导致工艺知识通常孤立地存在^[7,8]. Bai等^[9]提出了一种创新的零件设计模式提取技术, Huang等^[10,11]通过对已制的单一零件使用相似性评估方法来实现其重用. 王体春等^[12]采用相似性评价原理, 结合层次分析法与最近相邻策略实现了汽轮机叶片零件加工工艺设计过程的自主决策. 然而, 上述方法未能挖掘工艺数据中的隐藏工艺知识, 所以采用相似性评价原理的数控工艺设计方法只能完成一些特定零件的个性化复用, 很难大规模推广.

此外, 当前的工艺知识总是隐式地存在于各种加工特征中, 工艺设计人员参考和选择已有的工艺知识时, 总是无法全面地考虑到所有潜在的风险和问题. 因此, 工艺设计过程中, 会存在经验丰富的设计人员生产的零件优于其他设计人员的情况. 出现该情况的原因, 正是经验丰富的设计人员掌握更丰富、全面的隐式工艺知识, 且其经验难以通过知识表示模型向下传递^[13]. 综上所述, 工艺知识并未得到充分地学习, 因此如何学习和挖掘工艺数据中隐藏的隐式和显式工艺知识变得尤为重要.

针对以上问题, 本文提出一种数据与知识双驱动的零件特征工艺决策方法. 首先, 通过建立数控加工工艺模型, 有效表征零件三维CAD模型与加工工艺的关联. 接着, 利用基于注意力机制的深度学习MLP模型, 从这些结构化的工艺数据中学习零件特征及其对应的工艺标签之间的映射关系, 并计算其对应工艺标签的概率分布. 该方法不仅减少了工艺决策中的人工干预, 也为制定出合乎逻辑且语义精确的数控加工方案提供了必要的准备.

2 基本方法与概述 2.1 基本概念

定义1. 加工特征. 加工特征定义为在固定装夹下, 零件满足某些特定制造属性(如刀具轴向、精度约束、合适加工工艺等)的一组相邻表面集合, 可以表示为:

$ \begin{split} & \lt F \gt :: = [{T_D}] \lt {\mathit{TAD}} \gt \lt {G_s} \gt \\ & {G_s} = B \cup {\mathit{FFS}} \cup C \cup S \end{split} $

(1)

其中, T_D表征与加工特征关联的技术数据, 如材料, 公差, 表面粗糙度等; TAD用于描述加工特征的方位; G_s表征满足拓扑约束的几何形状, 它由底面B, 底角面集合FFS, 转角面集合C, 轮廓面集合S所构成. 实质上, 本文所描述的加工特征是对零件进行有效划分, 将其划分为符合零件加工数据、几何拓扑约束的一个个零件子集, 有意义地表示零件的三维CAD模型^[14].

定义2. 特征工艺. 特征工艺定义为工步集合, 其包含零件加工过程中涉及的关键工步, 涵盖从毛坯到零件成品的整个加工序列. 其由多个工步WS_j (如粗铣内孔、精铣筋、补铣外形等)组成, 并且每个工步都能在最终加工方案中找到对应. 同时每个特征工艺P_i与一个标签向量l_i相关联, 可以表示为:

$ {P_i} = \bigcup\limits_{j = 1}^n {W{S_j}} \leftrightarrow {{l}_i} $

(2)

其中, n为P_i的工步数量, l_i为一位有效编码, 即有且只有1个元素为1, 其余元素都为0的向量. 特征工艺的种类数量决定着one-hot向量的维度. 因此, 在零件制造过程中, 每一个加工特征都有对应的特征工艺.

2.2 方法概述

通常, 工艺数据中蕴含着工艺设计人员的丰富知识与经验. 经验丰富的设计人员通过与其交互标记, 能够深入挖掘数据中的工艺逻辑, 从而提炼出关键工艺知识, 采用多层次结构化数控加工工艺模型可以有效地将加工特征与加工操作有效关联. 同时, 由于零件的加工特征与特征工艺之间存在隐式映射关系, 深度学习方法可以有效地学习这种映射关系. 因此, 本文在工艺数据结构化表达的基础上, 通过深度学习方法挖掘零件的每个加工特征与工艺标签的映射关系, 从而减少工艺决策过程中的人工干预, 为后续生成符合逻辑、语义准确的数控加工工艺方案奠定基础.

图1给出了本文方法的总体流程, 包含两部分, 具体如下.

(1)工艺数据的结构化表征

该部分主要将工艺数据中的三维CAD模型与三维CAM模型进行有效交互, 以加工特征与加工操作作为多层次结构化工艺模型的关联性桥梁, 生成有效的加工操作工艺设计意图.

(2)数据与知识融合的零件特征工艺决策

该部分使用基于注意力机制的MLP深度学习算法, 从结构化工艺数据中挖掘工艺知识, 从中得到零件特征与特征工艺标签的映射信息, 用于训练神经网络模型, 为后续待制零件的数控加工工艺方案制定提供关键的决策支持.

3 工艺数据的结构化表征

为了准确地挖掘和表达加工特征与加工操作之间的关联关系, 本方法设计的多层次、结构化的数控加工工艺模型主要是由结构化的CAD模型和结构化的CAM模型组成. 而CAD模型和CAM模型均采用了分层的设计思路.

(1) CAD模型的结构化设计自上而下有以下3层: ① 零件层: 主要对零件的客观组成要素进行阐述, 包括材料、毛坯; ② 方位层: 在零件加工进程中为确保加工精度, 加工零件时, 要先使零件拥有一个正确的方位. 该层能够为零件加工提供明确的方向指引; ③ 加工特征层: 主要深入阐述了特征的制造含义及其几何拓扑结构.

(2) CAM模型的结构化设计自上而下有以下3层结构: ① 加工序列层: 其目的在于需要清晰地表达零件整个加工流程的顶层设计思路, 由工位、工步和特征工艺3部分组成; ② 加工操作层: 需要表达每一个工步的细节信息, 即对程序中加工操作以及工步对应的特征进行解释; ③ 工艺参数层: 主要表达了进行加工操作时, 机器实际的参数配置, 例如转速、进给速度等信息.

如图2所示, 给出了零件I的工艺数据实例. 如图2(a), 其为零件I的P.P.R特征树(部分), P.P.R特征树构成了零件的数控加工工艺(包含工艺过程、工艺模型以及工艺资源). 图2(b)为零件三维CAD模型, 由图2可知, 该零件一共有2个方位A与B, 加工特征F₁, F₃, F₄为型腔, 加工特征F₅, F₆, F₉, F₁₀为筋, 加工特征F₂为外形, 加工特征F₇, F₈为内孔. 以上的工艺数据都是工艺设计人员在数控加工工艺设计阶段时, 根据零件的加工要求来命名的, 如工步和加工操作的名称. 但是, 其中缺乏工艺设计人员在进行设计时的意图表示. 比如, 设计人员命名G023C0101时, 期望对零件采取粗铣内形操作; 命名加工操作“Profile Countouring.50”时，设计人员期望对零件的加工特征F₂采取粗铣外形操作, 即关联加工操作粗铣外形与加工特征F₂. 所以, 挖掘加工操作与加工特征之间的映射关系, 就可以获得工艺设计人员在进行数控加工工艺设计时的设计意图, 由此可以自底向上获得每个加工特征工艺的工步构成.

4 数据驱动的零件特征工艺决策

零件特征工艺决策是指在零件的加工阶段, 根据具有不同属性的加工特征选择合适的特征工艺的过程. 为更好地进行决策, 需要探索一种更加综合的特征工艺决策方法. 目前流行的特征工艺决策方法往往忽视了加工特征相关属性与工艺方案各组成部分之间的映射关系. 这导致1个加工特征往往只能对应1个特定的特征工艺选择. 但在实际生产中, 设计人员总是需要考虑加工特征之间的相互影响问题, 才能设计出最终的工艺方案. 本文通过对结构化工艺数据进行二次加工, 提取出了零件的加工特征与特征工艺间的映射关联关系. 接下来, 对这一特征工艺决策模型进行探讨.

4.1 特征属性定义

为高效地学习零件加工特征的工艺知识, 需要构建一个能够描述零件多层次信息的特征描述子, 该描述子应覆盖从高层级制造语义信息到底层级几何信息的全过程. 表1给出了本文特征描述子的组成要素.

● 制造语义层

制造语义层主要描述了加工特征的本质内涵, 主要涵盖了特征类型, 公差/表面粗糙度, 几何开敞性等. 第一, 特征类型的种类不同可能导致特征工艺在工步组成上的差异, 本文的特征类型主要包括型腔、外形、筋、内孔等; 第二, 加工特征的公差和表面粗糙度密切影响着零件所采用的加工方法. 如两个几何拓扑结构相似的加工特征, 若公差或表面粗糙度存在数值差异, 其最终采用的加工方法可能完全不同; 第三, 几何开敞性决定了加工特征所适用的刀具直径范围, 进而对特征工艺的构成工步产生影响. 因此对于型腔类特征, 还需要计算直径相关的特征属性, 而本文参考文献[15]中的方法计算其最大宽度D_max与最小宽度D_min.

● 几何层

几何层主要描述加工特征的形状和大小的信息, 由以下3种要素组成: 第一, 转角、底角、高, 主要描述了其形状信息. 形状的不同也就对应了刀具几何参数的不同, 进而工步的构成也会受到影响. 本文统一计算了每个加工特征的这3个指标的最大值与最小值作为其客观描述; 第二, 开/闭角, 由于是否存在开/闭角轮廓面对应着是否需要采取补加工措施, 该指标仅需使用0或1用于标识即可; 第三, 厚度主要包括底厚与壁厚, 对于某一特定零件, 若其多个加工特征呈现为薄底或薄壁特征, 为有效预防加工过程中的零件变形, 通常需要增设半精加工步骤. 鉴于此, 本文计算每个加工特征在厚度方面(含底与壁)的最小数值.

4.2 MLP学习算法

给定X, 零件的每个加工特征的特征工艺学习的目标是查找一个最优的零件的特征工艺标签矩阵Y^*, 使其具有最大的后验概率, 记作:

$ {\boldsymbol{Y}}^* = {\arg\max}_{\boldsymbol{Y}} p({\boldsymbol{Y}}\mid {\boldsymbol{X}}) $

(3)

但是, 直接计算式(3)的最优特征工艺标签矩阵Y^*相当复杂. 因此, 使用一组训练数据{(X, Y)}来构建一个神经网络模型f_θ, 以实现X与Y之间的非线性映射, 记作: $ \boldsymbol{Y} = {f_\theta }{{(}}\boldsymbol{X}{\text{)}} $. 通过这种方式, 将式(3)的计算问题转化为神经网络模型参数θ的学习问题.

在零件的特征工艺决策环节, 零件中的各个加工特征总是会相互影响. 而设计人员除了需要考虑每个加工特征独立的加工操作外, 还需要考虑上述问题, 才能设计出真正符合实际生产条件的工艺方案. 因此, 一个加工特征的工艺方案的正确表达, 理应是有其自身和其余特征的参与, 如式(4)所示.

$ p({{\boldsymbol{Y}}}\mid{{\boldsymbol{X}}}) = \prod\limits^{n}_{i=1} {{p}({\boldsymbol{y}_i}\mid{\boldsymbol{x}_i}, {\boldsymbol{X}})} $

(4)

因此, 本文将零件特征工艺的学习问题转换为以自身特征及零件中的其他特征为影响因子的分类问题. 本文构造了基于全连接网络的深度学习模型对加工特征进行计算, 最终输出其对应的$ {p_\theta }({{{\boldsymbol{y}}}_i}\mid{{{\boldsymbol{x}}}_i}, \boldsymbol{X}) $概率分布, 即:

$ {p_\theta }({{{\boldsymbol{y}}}_i}\mid{{{\boldsymbol{x}}}_i}, \boldsymbol{X}) = {f_{\rm FCN}}({\boldsymbol{x}_i}, \boldsymbol{X}) $

(5)

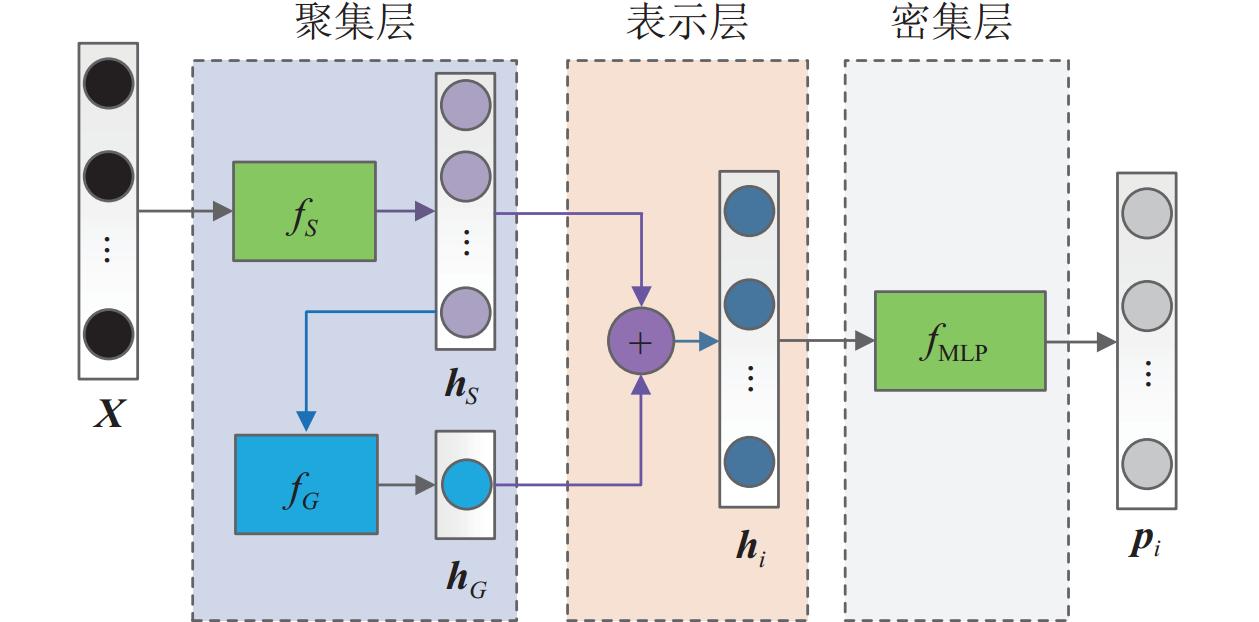
图3描述了特征工艺决策模型f_FCN的网络结构. 该模型用公式可以表达为:

$ {f_{\rm FCN}}({\boldsymbol{x}_i}, \boldsymbol{X}) = {f_{\rm MLP}}({f_G}(\boldsymbol{X}) \oplus {f_S}({\boldsymbol{x}_i})) $

(6)

整体结构可以分为以下3层.

(1)聚集层分为两部分, f_S的目标是学习零件的每个加工特征, 并转换为自身表达进行输出, 而f_G则是学习零件的整体特征. 相关变量的定义为, 加工特征x_i, 加工特征的学习结果输出h_S, 零件X, 零件整体特征的学习结果输出h_G. (2)表示层的唯一目标则是将聚集层输出的h_G与h_S进行整合, 获得零件加工特征的统一表达, 最终将输出定义为h_i. (3)密集层f_MLP实质是基于多层感知器(multi-layer perception, MLP)学习算法. MLP神经网络学习算法属于前馈神经网络的一种, 在训练过程中需要通过反向传播算法计算梯度, 将误差从输出层反向传播回输入层, 用于更新网络参数. 因此, f_MLP基于h_i计算每个加工特征的特征工艺标签的概率分布p_i, 最后将所有加工特征的结果进行整合得到特征工艺标签置信度矩阵P_m=[p_i]_m.

考虑到零件的每个加工特征在特征工艺决策过程中的重要性差异, 本文引入了注意力机制来学习零件的整体表示h_G. 假设每个加工特征的注意力系数为α_i, 则h_G可以表示为:

$ {{{\boldsymbol{h}}}_G} = \sum\limits_{i = 1}^m {{\alpha _i} \times {f_S}({\boldsymbol{x}_i})} $

(7)

4.3 损失函数

为了获得模型的一个最优参数θ^*, 使得零件的特征工艺标签矩阵具有最大的后验概率, 损失函数L定义为零件的特征工艺标签置信度矩阵P_m=[p_i]_m与零件的目标特征工艺标签矩阵Y_m= [y_i]_m之间的交叉熵, 主要反映了f_FCN预测结果与目标特征工艺标签矩阵之间的差异性, 记作:

$ L=-\sum_{i=1}^{m} {\boldsymbol{y}}_{i} \log {\boldsymbol{p}}_{i} $

(8)

5 算法验证与讨论 5.1 模型训练

在实验中, 训练数据来自合作的航空制造企业以及实验室. 总数为500个样本. 为了有效地评估和优化模型性能, 本文将数据集划分为3个子集. 其中, 训练集占比65%, 在训练集上进行训练; 测试集占比15%, 使用测试集对模型进行测试并观察其指标, 根据其效果调整参数; 验证集占比20%, 用于考察模型真实能力.

在训练f_FCN模型时, 考虑到实际的工艺数据中, 不同零件的加工特征不一定相同, 导致特征向量矩阵X的维度不同. 为了提升矩阵降维计算的速度, 本方法将批次大小设定为1. 此外, 在模型f_S中, 对于X中的每个加工特征的属性向量v, 首先运用1个线性层, 即将输入数据v和权重矩阵进行矩阵乘法, 再加上偏置, 得到线性变换的结果h_S, 其表征256维的特征向量; 接着, 计算每个加工特征的注意力系数α_i, 使用这些系数更新h_S, 即得到X的整体表示h_G; 最后, 通过拼接策略将h_S与h_G拼接起来, 由此得到加工特征F的最终向量表达h_i, 其维度为512.

此外, 过拟合问题是深度学习模型训练时必然需要面对的问题. 为了解决该问题, 本方法使用了以下两种优化方式: (1)提前终止法: 当模型在连续的指定轮数训练后, 其表现并未超过此前的最佳表现, 则提前终止迭代训练. 在本方法中将连续迭代数限制设置为40; (2) dropout: 在模型结构中加入dropout层, 即通过忽略某些特征检测器, 减少它们之间的相互作用, 避免模型过于依赖某些局部特征并提高模型泛化表现. 经过多个测试集的验证, 模型f_FCN的部分超参数如表2所示.

5.2 结果

图4给出了模型的训练曲线, 包括图4 (a)准确率收敛曲线以及图4 (b)损失收敛曲线. 从图可知, 在训练过程中经过40次迭代以后, 模型的表现已不再具有显著提升, 最终在验证集上的准确率为96.87%. 由图4 (b)可以看出随着模型迭代次数的增加, 训练集损失函数不断下降, 验证集的损失函数也随之下降.

为了评估训练的f_FCN模型的性能, 引入F1_score指标进行评估, 其是分类问题的一个衡量指标, 定义为模型的准确率和召回率的调和平均数. 为了计算F1_score, 首先获得每个分类的准确率Precision_i和召回率Recall_i, 可以表示为:

$ Precisio{n_i} = \frac{{N_{\rm right}^i}}{{N_{\rm right}^i + N_{\rm wrong}^{i + }}} $

(9)

$ Recal{l_i} = \frac{{N_{\rm right}^i}}{{N_{\rm right}^i + N_{\rm wrong}^{i - }}} $

(10)

其中, $ {N}_{\rm{right}}^{i} $是第i类的正确预测的数量, $ {N}_{\rm{wrong}}^{i+} $是被分类到第i类中的其他类的样本的数量, $ {N}_{\rm{wrong}}^{i-} $是被分类到其他类中的第i类样本的数量. 因此, 第i类的F1_score可以表示为:

$ {\left( {{{F}}1\_{{score}}} \right)_i} = 2\frac{{Precisio{n_i} \times Recal{l_i}}}{{Precisio{n_i} + Recal{l_i}}} $

(11)

由此可得模型的F1_score可以通过将所有分类的F1_score平均, 记作:

$ {{F}}1\_{{score}} = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{{F}}1\_{{score}}} \right)}_i}} $

(12)

其中, n为预测分类数.

最后使用测试集对完成训练的模型进行测试实验, 其准确率为95.26%, F1_score为94.78%, 当前模型的表现已能够满足实际生产的需求.

5.3 实例分析

如图5所示一个零件II实例. 该零件是典型飞机结构零件, 其制造采用铝合金. 铝合金具有高强度、轻质、耐腐蚀的优点. 其中加工特征F₁–F₁₇为型腔、F₁₈为外形, F₁₉–F₂₀为内孔, F₂₁–F₃₆为筋. 表3列举了该零件部分加工特征属性及其对应值. 图5(c)展示了模型f_FCN对预测的置信度矩阵. 表4给出了采用本文方法生成的加工特征与特征工艺的映射关系.

根据表4, 零件的工艺方案包含2个工位: 工位A包含6个工步(粗铣内形—半精铣腹板—精铣筋—精铣腹板—精铣内形—补铣内形), 而工位B包含3个工步(粗铣外形—精铣外形—精铣内孔). 特征工艺则涵盖6种类型, 具体包括P₁: 工位A—粗铣内形—精铣腹板—精铣内形, P₃: 工位A—粗铣内形—精铣腹板—精铣内形—补铣内形, P₄: 工位A—粗铣内形—半精铣腹板—精铣腹板—精铣内形—补铣内形, P₁₃: 工位B—粗铣外形—精铣外形, P₁₇: 工位A—粗铣内形—精铣筋, P₁₈: 工位B—精铣内孔.

考虑到加工特征F₉, F₁₁存在闭角轮廓面, 因此对这些特征的底角补加工是必要的. 另外, 当加工特征的底面存在下陷时, 也需要进行补加工, 如加工特征F₆, F₈, F₁₀, F₁₂. 特别的, 在进行粗加工操作时, 对于一些最小宽度比较小的加工特征(F₈, F₁₀), 粗加工往往无法完善加工这些部位, 会导致与零件终态之间存在偏差, 因此需要采取半精加工操作. 同时, 加工特征F₁₈在两个工位上有着不同的形态, 其在工位B不存在闭角轮廓面, 所以将加工特征F₁₈在工位B进行加工, 避免在工位A无法使用普通铣刀进行切削操作的情况. 另外, 加工特征的孔直径大时(F₁₉, F₂₀), 为增强零件的强度, 这些加工特征会在最后一个工步进行加工. 因此, 本文方法的表现已能够满足实际生产的需求, 能够生成完善工艺方案.

6 结论与展望

本文提出了一种数据与知识双驱动的零件特征工艺决策方法. 本文的主要创新之处在于利用深度学习方法, 对已经过实际加工验证的工艺数据进行结构化表征, 从而实现了工艺数据中隐式与显式知识的有效学习, 挖掘零件特征与特征工艺标签之间的映射关系. 最终为零件加工方案的决策提供了数据基础和决策支持. 综合飞机结构件的实例说明和测试实验的结果, 本方法能够准确预测零件各加工特征的特征工艺, 其置信度已经能够满足实际地生产需求. 通过本方法预测的特征工艺概率分布, 设计人员能够设计出高精度、高可解释性的加工方案. 在下一步工作中, 本方法的能力也将覆盖更多类型的零件.