物联网、5G、工业互联网等新一代信息通信技术的发展, 加快了传统行业转型升级的步伐. 例如在智能制造中, 实时控制、边缘计算、数字孪生等应用场景对网络低延时、低抖动和高可靠性的要求愈发严格. 传统以太网已经不能满足越来越多的数据和广泛分布的网络需求, 时间敏感网络(TSN)技术应运而生. 时间敏感网络以传统以太网为基础, 通过时钟同步、数据调度、网络配置等机制, 提供确定性数据传输能力.
TSN是IEEE 802.1任务组开发的一套数据链路层协议, 用于构建更可靠、低延迟、低抖动的以太网. TSN技术标准起源于音视频行业, 用于满足广播、直播等网络应用需求. 并且应用到了汽车和工业领域. 在汽车领域中, 主要应用在高级驾驶辅助系统方面. 在工业领域, 则主要应用在智能制造、工业互联网领域[1].
本文主要针对工业4.0中的工业自动化领域. 该领域主要研究静态调度和动态调度两种调度方式. 静态调度[2–4]常用在智能工厂中, 集中式网络配置CNC[5]拥有全局视角, 能够获得将要调度的业务流的全局信息. 计算流的路径后, 使用Cplex求解器得到流的传输开始时间(SST), 以最大化可成功调度的流数量, 但是计算时间通常为小时级甚至天级. 动态调度则无法事先知道要调度业务流的全局信息, 每当到来一条流时, 以增量的形式计算这条流的路径和传输开始时间, 该计算过程通常为秒级[6].
本文研究的是动态调度场景. 动态调度存在一些不足: 1) 动态调度场景中流的到达顺序是随机的, 无法更改调度顺序, 因此计算产生的是次优解. 相比于产生最优解的静态调度, 动态调度计算的网络吞吐率低、可调度成功的流数量少; 2) 动态调度的求解目标要求每个流的传输开始时间尽可能小, 这会导致大量的流聚集在超周期的第1个时间段进行传输, 其余时间段有着大量的空余时隙.
相关研究提出了在动态调度后进行全局流重新配置的方法[7], 每当动态调度完若干条流后, 就将网络中所有业务流进行重新规划, 来优化链路和时间资源的分配, 为之后到来的流预留调度空间. 然而, 全局流重配置算法的运行时间随流数量的增多而急剧增长, 导致后续到来的流可能无法及时被规划. 因此, 该算法仅适用于几十条或者几百条流的小型网络, 对于典型工业场景, 网络中可能会存在上千条业务流[8], 全局流重配置算法无法在这种大型网络中使用.
本文提出了时间敏感网络业务流动态调度场景中的批量重配置算法(下文简称为批量重配置算法), 该算法遵循无等待调度机制, 使用整数线性规划(ILP)对问题进行建模, 并通过Cplex求解器来对问题进行求解. 本文的贡献如下.
(1) 提出了一种批量重配置算法, 在动态调度场景中, 每处理若干条流后, 选择一部分已调度的流进行重新规划, 来优化网络资源的配置.
(2) 提出了新的评价指标——网络吞吐率, 该指标综合考虑了流数量、流周期和流大小带来的影响.
(3) 给出了负载最高流和相关流的选取标准, 从而选出重配置的流集合.
(4) 优化路径选择标准和传输开始时间计算, 为网络中后续到来的流预留出更多可用资源.
(5) 通过实验, 我们验证了本算法可以在数千条流的大型网络中运行, 相比于动态调度, 本算法在网络吞吐率和调度成功的流数量指标上有16.5%和5.5%的提升, 且算法运行时间满足秒级要求.
(6) 与全局重配置方案相比, 本算法在各项指标上表现良好, 与分组全局重配置方案[9]对比, 本算法拥有短暂且稳定的计算时间, 在网络吞吐率和调度成功的流数量指标上仅减少1%–2%左右.
本文的结构如下. 第2节介绍相关工作. 第3节介绍背景和现存问题. 第4节给出批量重配置算法. 第5节展示该算法的实验结果. 第6节则是总结与展望.
2 相关工作TSN业务流调度方面, 目前已有不少专家和学者对其进行了工业应用研究和学术研究. Huang等人[6]提出了一种基于TAS的在线路由和调度机制. 使用可变时隙并最小化每个流的传输开始时间. 设计了一种新的增量式路由调度算法(IRAS)来实现流量部署, 并采用预路由算法减少运行时间. Nayak等人[10]提出了时间敏感软件定义网络(TSSDN), 为系统中时间触发流的传输提供实时保证. 文献[10]提出了各种ILP公式, 解决了时间触发流的路由和调度组合问题. 随后, Nayak等人[11]又提出了在TSSDN中增量添加时间触发流的算法. 该算法可以在亚秒级内计算时间触发流的增量调度, 平均相对最优性为68%. Dürr等人[4]引入无等待分组调度机制来模拟时间敏感网络中的业务流调度问题, 并将其映射为运筹学领域中的无等待车间作业调度问题. 文献[4]提出了一种用于高效计算调度的Tabu搜索算法和一种用于减少调度中保护带数目的调度压缩技术.
对于重新配置方面而言, Bülbül等人[7]提出并评估了支持SDN (software defined network, 软件定义网络)的时间敏感网络动态路径配置策略, 提出了TSOR-P, TSOR-T, TSOR-U这3种机制. 该策略根据当前网络环境中的资源利用率, 对流路径和时间进行重新配置, 来最大化可接受流的数量. Li等人[12]指出SDN为网络更新提供了更加高效的方法—将控制平面与数据平面分离, 数据平面只需转发数据即可, 所有的调度和计算都交给控制平面来进行. 控制平面配置新的流规则, 通过两阶段更新机制来更新网络中流的转发行为. Raagaard等人[13]提出了一种在运行时进行流动态重新配置的方案. 如果网络不能容纳新到来的流, 则重新调度所有业务流, 来尝试容纳新流.
本文在现有的动态调度算法和全局重配置算法的基础上, 综合考虑了重配置的流数量和运行时间, 提出一种改进的批量重配置算法. 该算法每次仅选出网络中的部分业务流进行重新配置, 能减少算法运行时间, 同时为后续到来的流预留出更多资源.
3 背景和现存问题 3.1 背景2018年发布的IEEE 802.1Qcc中定义了TSN的3种网络配置模型, 分别是全分布式模型、集中式网络/分布式用户模型和全集中模型[1]. 本文对应的是全集中模型, 该模型借鉴了SDN的思想, 将网络的控制逻辑与底层的硬件进行分离, 可以更好地对网络进行管理[5]. 在全集中模型中, 底层的网络设备(终端、交换机等)负责数据的转发, 并将网络和设备自身的状态信息上传至集中网络配置CNC, 并且接收CNC下发的指令, 根据指令来调整设备相关状态, 以适应网络的变化. CNC向上层的集中用户配置CUC提供开放的网络资源和能力, 并向下层的网络设备下发指令, 来实现设备控制、流量调度、网络监控等功能. CUC则根据需要向用户提供自适应服务, 来实现全网拓扑发现、网络状态监测和业务连接与调度等功能[14]. 全集中模型为业务流的动态调度和重新配置提供了基础.
TSN业务流调度的核心在于计算出业务流的全局调度时间表以及合成门控队列GCL, 从而让业务流在整个网络范围内同步地、周期性地进行传输. 动态调度适用于需要一定灵活性的网络, 例如在工业自动化场景中, 操作者需要往生产线中添加“即插即用”设备, 此类业务流的到来是不可预知的, 网络需要在秒级时间内计算出该设备是否可以部署的结果[15,16], 并更新TSN交换机的配置[10]. 相关研究[6]提出了增量路由与调度算法(IRAS)来应对TSN业务流动态调度的场景, 该算法已知网络的超周期, 并使用了无等待调度机制, 给出了3个约束: 传输开始时间约束、无冲突时隙约束和相邻边约束, 并以最小化每个流的传输开始时间作为计算目标.
业务流动态调度会引起资源浪费的问题, 不时地对网络进行重新配置可以改善现有业务流的资源分配, 并提高网络所能容纳的最大业务流数量[7]. 业务流的重新配置包括被动重新配置和主动重新配置, 被动重新配置是如果网络不能容纳该业务流, 则重新调度网络中的所有业务流, 来尝试容纳新业务流[13]. 主动重新配置则是定期进行全局重新配置, 每新增若干条流, 就对网络中的所有业务流进行重新配置[7].
3.2 现存问题传统动态调度和全局重新配置均存在一定不足.
(1) 评价指标过于片面. 当前的动态调度算法的主要目标是提升网络中调度成功的流数量[6]. 该评价指标未考虑流周期和流大小带来的影响, 难以对业务流的负载大小进行区分, 也无法根据该指标来比较网络的拥塞程度. 因此, 批量重配置算法提出了新的评价指标——网络吞吐率, 来综合比较业务流的数量、大小和周期.
(2) 不可更改的调度顺序. 当前的动态调度算法只能按照业务流的到达顺序进行调度, 容易产生时隙碎片, 如图1所示. 动态调度算法先调度f3, 后调度f4, 会产生2 μs的时隙浪费. 批量重配置算法则可以自由地对部分流的调度顺序进行排列组合, 先调度f4, 后调度f3, 可以更充分地利用时隙资源, 减少时隙碎片.

|
图 1 不同调度顺序引起的时隙浪费 |
(3) 路径选择标准只考虑流数量. 当前的动态调度路径选择标准仅考虑了流路径上已存在的业务流数量[6], 但是如前所述, 只考虑业务流数量而不考虑流周期和流大小是片面的, 无法很好起到负载均衡的效果. 因此, 批量重配置算法将网络链路利用率方差纳入路径选择标准, 可以更客观地反映网络链路的负载情况.
(4) 动态调度的求解目标导致时隙资源浪费. 当前的动态调度算法的求解目标是最小化业务流的传输开始时间[6]. 这会使得业务流的调度集中在第1个基周期[11]所在的传输时间范围中, 而其余传输时间范围中的流数量较少, 从而导致业务流的调度时间不均匀, 造成时隙资源的浪费. 如图2所示, 该图展示了在超周期为4 ms的网络中, 某个交换机端口的传输时隙分布. 业务流f1和f3的周期为4 ms, f2和f4的周期为2 ms, f5的周期为1 ms, 所有流的传输时间均为10 μs, 且流的到来顺序为f1, f2, f3, f4, f5. 若采用动态调度算法, 且求解目标为最小化业务流的传输开始时间, 会产生图中动态调度所示的调度结果. 由于低频流f1和f3各占据了第1个传输时间范围中的一段传输时隙, 会导致网络中周期为1 ms和2 ms的高频流大大减少, 空余的时隙资源也很难被充分使用, 造成大量时隙资源浪费. 若增加批量重配置算法, 则可以分散业务流的传输时间, 避免业务流产生聚集. 如图2中批量重配置方法所示的调度结果, 业务流经过调整之后, f1和f3可以分配到不同传输时间范围的相同时隙段进行传输, f2和f4同理, f5的传输开始时间提前了20 μs, 可以为后续到来的流节省时隙资源.

|
图 2 不同求解目标产生的传输时间分布 |
(5) 全局重配置计算时间过长. 全局重配置需要对网络中的所有业务流进行重新规划, 其时间复杂度最坏情况下为
为了更好地衡量算法在TSN业务流动态调度场景下的性能, 本节给出4个关键的性能指标: 网络吞吐率、调度成功的流数量、一轮重配置平均计算时间和传输时间范围方差. 其中网络吞吐率为主要指标, 其余3个为辅助指标. 本文涉及的符号如表1所示.
(1) 网络吞吐率. 如前所述, 现有评价标准, 即网络中调度成功的流数量[6], 无法客观和准确地反映业务流的负载情况. 因此, 本文提出了新的评价指标网络吞吐率. 网络吞吐率综合考虑了流大小和流周期带来的影响, 其含义是单位时间内网络成功传输的字节数量. 网络吞吐率的定义如式(1)所示:
| 网络吞吐率=(n∑i=1fi.size×(sp/fi.p))/sp | (1) |
(2) 调度成功的流数量. 本文保留了原始动态调度的评价指标, 只是不再将其作为主要指标, 而是作为辅助指标进行参考. 将其与主要指标网络吞吐率共同进行研究, 可以更客观、更合理地分析网络当前的负载情况. 在大部分情况下, 调度成功的流数量和网络吞吐率是正相关的.
(3) 一轮重配置平均计算时间. 该指标的含义是运行一次重配置算法所要花费的平均计算时间, 动态调度场景要求该时间为秒级. 网络吞吐率和一轮重配置平均计算时间呈负相关, 极致地追求网络吞吐率将导致不可容忍的计算时间, 会对后续到来的业务流产生影响.
(4) 传输时间范围方差. 超周期可以划分为若干个时间范围(基周期), 传输时间范围方差指的是在这些传输时间范围中整个网络被占用的传输时隙数量的方差. 其定义如式(2)所示:
| 传输时间范围方差=1nn∑i=1(time_slot_numi−time_slot_num_avg)2 | (2) |
其中, n为超周期和基周期的比值, 变量
| time_slot_numi=∑i×bpt=(i−1)×bp∑flow_numk=1FT[fk][t] | (3) |
传输时间范围方差可以用来衡量流的调度时间在不同时间范围中的分散程度. 该指标越低, 说明流的调度时间越均匀, 网络吞吐率提升的可能性就越大.
| 表 1 本文涉及的符号 |
4.2 指标平衡
批量重配置算法的3个辅助指标与主要指标之间存在着相辅相成、相互制约的关系, 因此需要对4个关键指标进行平衡. 结合第3.2节中存在的问题, 以及第4.1节中各关键指标之间的关系, 批量重配置算法通过以下改进来平衡各关键指标.
(1) 对业务流进行重新配置. 不可更改的业务流调度顺序决定了时隙浪费是动态调度不可避免的问题, 如果要减少时隙浪费, 那么就必须更新网络资源的配置, 优化其中不合理的地方. 反映在关键指标上, 重配置可以提升网络吞吐率和调度成功的流数量, 但同时会引入额外的计算时间.
(2) 优化路径选择标准. 相比于流数量, 链路利用率方差可以更合理、更客观地体现网络链路负载的均衡情况, 更适合作为路径选择的标准. 选取路径时应优先考虑那些能使得网络链路利用率方差最低的路径, 有利于平衡网络中各链路的利用率, 从而减少瓶颈链路的出现. 反映在关键指标上, 优化路径选择标准可以提高网络吞吐率和调度成功的流数量.
(3) 优化业务流的传输时间计算. 动态调度的求解目标会产生传输时间集中的问题. 批量重配置算法可以通过增加约束条件和优化求解目标来避免流的聚集. 反映在关键指标上, 优化传输时间计算可以降低传输时间范围方差以及降低一轮重配置平均计算时间.
(4) 缩减重配置的业务流规模. 由第3.2节中给出的时间复杂度可知, 问题规模直接决定了重配置算法的计算时间. 要想满足动态调度场景的秒级时间要求, 就需要对问题规模进行缩减, 因此需要进行“批量重配置”.
4.3 算法流程批量重配置算法在业务流动态调度之后, 添加了一个尾处理过程, 因此本算法的系统模型及使用的符号和变量与IRAS类似[6]. 批量重配置算法综合考虑了动态调度和全局重配置机制的优点, 可以定期优化网络配置. 该算法的流程如算法1所示, 其中涉及的具体细节在算法后给出.
算法1. 批量重配置算法
输入: 拓扑G, u[f][e], t[f][e], 流集合 list, 重配置周期 K, 重配置流集合大小M, 闭集close.
输出: 调度结果Result, u[f][e], t[f][e].
1. if 调度的流数量不为K的倍数 then
2. Result =“不进行重配置”;
3. 返回Result, u[f][e], t[f][e];
4. end if
5. 计算出网络中负载最高的流
6. 计算出与负载最高流
7. 释放流集合FL中所有流占据的链路和时间资源;
8. 根据新的路径选择标准, 为流集合FL中的每个流重新计算路径R;
9. 通过求解器计算FL中所有流的传输开始时间集合list_sst;
10. if list_sst不为空 then
11. 得到每个流的SST, 将新的路径和时间记录在u[f][e]和t[f][e]中;
12. Result = “重配置成功”;
13. else
14. 恢复流集合FL中每个流的最初路径和传输时间, 恢复u[f][e]和t[f][e];
15. Result = “重配置失败”;
16. end if
17. 将流集合FL中的每个流加入闭集close;
18. 返回Result , u[f][e], t[f][e];
批量重配置算法在动态调度算法之后运行, 先判断流数量是否为K的倍数, 如果不是算法终止. 如果是, 则先计算出网络中负载最高的流, 然后计算出M–1个相关流, 组成流集合FL. 随后释放FL中每个流的链路和时间资源. 根据新的路径选择标准WT_Variance, 为每个业务流重新计算路径R. 根据路径和流集合FL, 利用Cplex求解器计算出FL中每个流的传输开始时间. 如果计算成功, 则更新流的传输开始时间SST、u[f][e]和t[f][e], 标记重配置成功. 如果计算失败, 则恢复流的路径和传输开始时间, 标记重配置失败. 将FL中的流加入闭集close, 下次重配置时不会再选取到这些流, 随后返回重配置结果.
(1) 计算重配置流集合. 本文提出了资源占用指数ROI来衡量网络中某个流占据链路和时间资源的多少. ROI的定义如式(4)所示, 其中, Length为流路径跳数, Transmission为流在交换机端口的一跳传输时间, Period为流周期.
| ROI=Length×TransmissionPeriod | (4) |
本文定义了关联度Relevancy来选取与负载最高流相关的其他流, 如式(5)所示. 其中, OL和OT为流与负载最高流重叠的路径跳数和传输时间长度.
| Relevancy=OL×OT | (5) |
(2) 优化路径选择标准. 批量重配置算法改进了动态调度路径选择标准WT[6], 引入了当前网络中链路利用率的方差, 提出了新的路径选择标准WT_Variance, 如式(6)所示. 其中, new_variance是流f的路径加入网络之后, 网络的链路利用率方差. max_variance是网络中出现过的最大链路利用率方差.
| WT_Variance=HC2(1+|ε|)+new_variance(1+max_variance) | (6) |
(3) 优化业务流的传输时间计算. 除了无等待调度机制的基本约束[6]之外, 还需要额外添加两个约束: FL无冲突时隙约束和分散SST约束.
FL无冲突时隙约束如式(7)所示. 其规定了对于FL中任意两个不相同的流
| {∀fn∈FL,∀fc∈FL,fn≠fc,e∈ε:∀x∈X,∀y∈Y:if (u[fn][e]+u[fc][e]⩾2) then(t[fn][e]+x⋅fn.p⩾t[fc][e]+y⋅fc.p+fc.t ort[fc][e]+y⋅fc.p⩾t[fn][e]+x⋅fn.p+fn.t) withX={x∈N:0⩽x⩽sp/fn.p}Y={y∈N:0⩽y⩽sp/fc.p} | (7) |
分散SST约束如式(8)所示. 其目的是把流的传输开始时间SST分散到各个传输时间范围中. 一方面可以避免不同的流在某一时间段产生聚集, 另一方面缩小SST的计算范围可以加快求解器的计算速度.
| {∀fn∈FL,x=[0,0,⋯,0],x.length=sp/bp:x[f.p]⋅bp⩽f.SST⩽(x[f.p]+1)⋅bp withx[f.p]=x[f.p]+1, x[f.p]=x[f.p] mod (sp/f.p) | (8) |
其次, 不同于动态调度[6], 批量重配置算法定义了新的求解目标, 如式(9)所示:
| ∀f∈FL,min(sum((sp/f.p)×f.t×(f.SSTmodbp))) | (9) |
新的求解目标综合考虑了流的周期和传输时间, 不同周期和传输时间的流被赋予不同的权重, 使得那些周期较小、传输时间较长的流的传输开始时间SST尽可能小. 新的求解目标让流的调度更加紧密, 有效减少了时隙碎片的产生.
5 仿真实验本节对批量重配置算法进行仿真实验, 首先给出实验设置, 然后给出实验结果与分析.
5.1 实验设置本文进行了4组实验. 实验①: 设计了基于传统动态调度算法(IRAS)和批量重配置算法(BR)的对比实验. 目的是比较动态调度和不同K和M下批量重配置算法的运行结果. 实验②: 设计了IRAS和BR在不同流周期和流大小组合下的对比实验, 并对每种组合下IRAS、BR-TIME (只优化时间计算)、BR-PATH (只优化路径选择)和BR (同时优化时间计算和路径选择)这4种调度算法进行了消融实验. 目的是验证BR算法在不同流周期和流大小组合下的运行情况及可靠性, 以及探寻不同的优化指标对于算法提升效果的影响. 实验③: 设计了基于全局重配置方案(GR)和批量重配置方案的对比实验. 目的是探寻全局重配置方案和批量重配置方案在4个评价指标上的差异. 实验④: 设计了分组全局重配置方案(GRBG)[9]和批量重配置方案的对比实验. 目的是在实验③未能充分展现出的网络吞吐率和流数量指标上进行扩展实验. 其中, BR的K和M均为10, GR和GRBG的K为10, GRBG的分组大小为10, 15和20. 每个实验均进行了5次重复实验, 取其平均值作为结果进行展示. 实验条件如下.
(1) 网络拓扑. 对于实验①和实验②, 使用添加链路的OCEV拓扑[6], 该拓扑共有44个节点, 53条边. 对于实验③和实验④, 使用工业中常见的雪花拓扑[17], 该拓扑共有37个节点, 36条边.
(2) 流量特征. 对于实验①, 使用周期为{1 ms, 2 ms, 4 ms, 8 ms}, 大小为50–1500字节的业务流. 对于实验②, 使用如表2所示的不同周期和大小的流组合. 对于实验③和实验④, 使用周期为{0.5 ms, 1 ms, 2 ms, 4 ms}, 大小为1500字节的业务流. 所有业务流都是在IEC/IEEE 60802标准[18]的指导下生成的.
(3) 机器配置. 本文所有仿真实验都是在服务器上运行的. 该服务器的CPU为Intel(R) Xeon(R) CPU E5-2660, RAM为125 GB, Linux版本为4.15.0.
5.2 实验结果与分析实验①的结果如图3所示, 1) 增加了BR算法之后, 网络吞吐率和调度成功的流数量均优于原始的动态调度算法. 2) 在不同K和M的组合下, BR算法在网络吞吐率方面提升4.8%–16.7%, 在调度成功的流数量方面提升1.59%–5.58%. 3) 在大多数组合下, 一轮重配置平均计算时间可以满足动态调度的秒级时间要求. 4) 在传输时间范围方差方面, BR算法可以不同程度地改善该指标, 避免流的调度时间过于集中. 5) 当K不变时, 随着M的增大, BR算法的吞吐率和调度成功的流数量随之提升, 传输时间范围方差逐渐降低, 但与此同时, 一轮重配置的平均计算时间也在提升. 6) 当M不变时, 随着K的减小, BR算法的吞吐率和调度成功的流数量逐渐增大, 传输时间范围方差逐渐降低, 一轮重配置平均计算时间则没有明显变化.
| 表 2 实验②使用的流周期和流大小组合 |
实验②的结果如图4所示. 1)网络吞吐率方面, 在9种不同的流组合下, BR算法在网络吞吐率方面均有一定的提升, 提升范围为1.2%–16.4%; 随着流大小和流周期范围的增大, 网络吞吐率的提升效果也在增强. 2)调度成功的流数量方面, 在组合6、组合7、组合8和组合9下, BR算法在调度成功的流数量方面有一定的提升, 提升范围在1.5%–5.5%; 而在其余的流组合情况下, 由于BR方案节省出的链路和时间资源被调度频繁、字节数更大的流所占据, 因此在流数量方面有一定下降, 通过分析网络吞吐率和流数量的关系可以得出这一结论. 且随着流大小和流周期范围的增大, 调度成功的流数量的提升效果也在增强. 3)一轮重配置的平均计算时间方面, BR-TIME和BR因为限定了流的传输时间范围, 加快了求解速度, 因此在所有9种流组合下, 一轮重配置的平均计算时间均在10 s以内, 满足动态调度的秒级时间要求; 而BR-PATH没有优化时间分配, 所以在流周期和流大小组合范围较大时, 计算复杂度会增加, 因此重配置的计算时间也会较长, 在组合7、组合8和组合9的情况下无法满足动态调度的秒级时间要求. 但随着流周期和流大小的组合范围逐渐缩小, BR-PATH的计算时间也在减小, 因此在其他流组合的情况下, BR-PATH逐渐能够满足秒级计算时间的要求. 4)在传输时间范围方差方面, 由于BR-TIME和BR将流的传输开始时间均匀分布到各个时间范围中, 因此BR-TIME和BR显著降低了传输时间范围方差, 使得流的分布更加均匀. BR-PATH并未优化时间计算, 因此该指标与IRAS处于同一个数量级. 5) 在大部分组合下, BR算法在网络吞吐率和调度成功的流数量上的提升效果超过了BR-TIME和BR-PATH, 对二者的提升效果进行了叠加, 获得了更高的提升率.

|
图 3 实验①结果 |

|
图 4 实验②结果 |
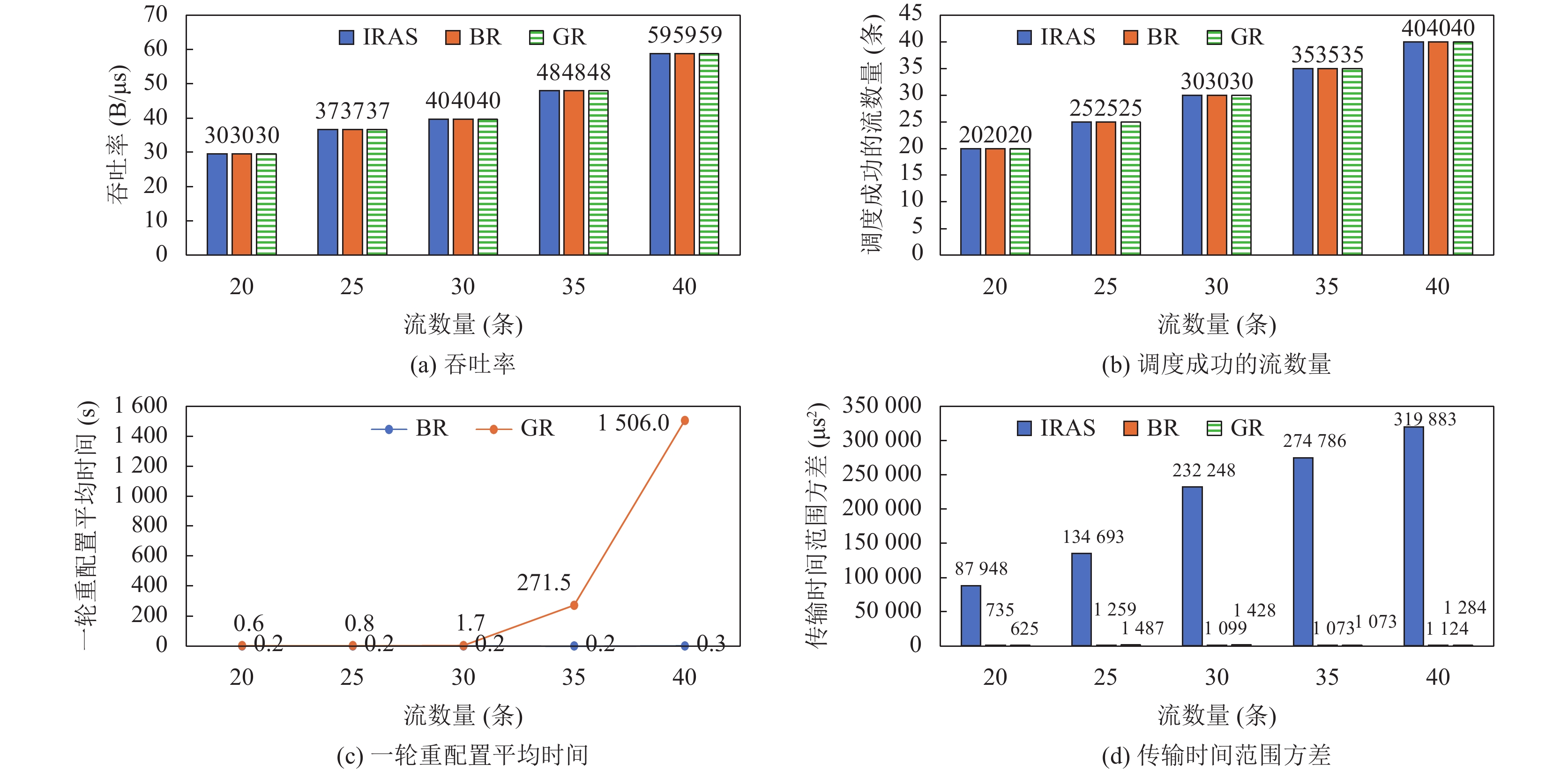
实验③的结果如图5所示, 1) 在20–40条流的情况下, BR和GR在网络吞吐率和调度成功的流数量上均相同. 2) 在一轮重配置平均计算时间方面, BR稳定在0.2 s左右, 而GR的一轮重配置平均计算时间随着流数量的提升而急剧增长, 无法满足秒级时间要求. 在45条流时, GR算法在24 h之后没有返回计算结果, 因此无法将GR扩展到流数量较多的大型网络中. 3) 在传输时间范围方差方面, BR和GR均可有效减小该指标, 使得流的调度时间均匀到各个传输时间范围中.
实验④的结果如图6所示, 1) 将流数量扩展到500时, 相比于IRAS算法, BR在吞吐率方面大约有20.3%的提升, 在流数量方面提升了8.3%. 相比于GRBG, BR在吞吐率上低1%–2%, 在流数量上低0.5%–1%. 2) BR的计算时间在1 s左右, GRBG的计算时间则随着分组数量的增大而急剧增长. 在分组数量为20时, 一轮重配置平均计算时间达到了268 s, 无法满足动态调度的秒级时间要求. 3) BR和GRBG有效降低了传输时间范围方差, 使流的调度时间更加均匀.
|
图 5 实验③结果 |

|
图 6 实验④结果 |
6 总结与展望
本文设计了时间敏感网络业务流动态调度场景中的批量重配置算法, 该算法在动态调度的基础上, 能够定期对部分业务流进行重新配置, 优化网络资源的分配. 实验结果表明, 该算法能够适用于上千条流的大型网络, 在吞吐率方面提高16.5%, 在调度成功流数量方面提升5.5%, 并且计算时间满足秒级要求. 与分组全局重配置算法相比, 该算法在计算时间上拥有巨大优势, 且在吞吐率和流数量上仅减少2%和1%左右.
在工业场景中, 可能会存在不同传输速率的异构交换机, 并且各交换机之间的线路长短也可能不一样. 因此探讨该算法在复杂网络场景下的适用情况, 是未来需要关注的一个问题.
| [1] |
中国电子技术标准化研究院. 时间敏感网络白皮书. 北京: 中国电子技术标准化研究院, 2020.
|
| [2] |
Craciunas SS, Oliver RS, Chmelík M, et al. Scheduling real-time communication in IEEE 802.1 Qbv time sensitive networks. Proceedings of the 24th International Conference on Real-time Networks and Systems. Brest: ACM, 2016. 183–192. [doi: 10.1145/2997465.2997470]
|
| [3] |
Pozo F, Steiner W, Rodriguez-Navas G, et al. A decomposition approach for SMT-based schedule synthesis for time-triggered networks. Proceedings of the 20th Conference on Emerging Technologies & Factory Automation. Luxembourg: IEEE, 2015. 1–8. [doi: 10.1109/ETFA.2015.7301436]
|
| [4] |
Dürr F, Nayak NG. No-wait packet scheduling for IEEE time-sensitive networks (TSN). Proceedings of the 24th International Conference on Real-time Networks and Systems. Brest: ACM, 2016. 203–212. [doi: 10.1145/2997465.2997494]
|
| [5] |
IEEE. 802.1Q-2022 IEEE standard for local and metropolitan area networks-bridges and bridged networks. https://1.ieee802.org/maintenance/802-1q-2022-rev/. (2018-05-07).
|
| [6] |
Huang YD, Wang S, Huang T, et al. Online routing and scheduling for time-sensitive networks. Proceedings of the 41st International Conference on Distributed Computing Systems. Washington: IEEE, 2021. 272–281. [doi: 10.1109/ICDCS51616.2021.00034]
|
| [7] |
Bülbül NS, Ergenç D, Fischer M. Towards SDN-based dynamic path reconfiguration for time sensitive networking. Proceedings of the 2022 IEEE/IFIP Network Operations and Management Symposium. Budapest: IEEE, 2022. 1–9. [doi: 10.1109/NOMS54207.2022.9789890]
|
| [8] |
Jin X, Xia CQ, Guan N, et al. Real-time scheduling of massive data in time sensitive networks with a limited number of schedule entries. IEEE Access, 2020, 8: 6751-6767. DOI:10.1109/ACCESS.2020.2964690 |
| [9] |
Mahfouzi R, Aminifar A, Samii S, et al. Stability-aware integrated routing and scheduling for control applications in Ethernet networks. Proceedings of the 2018 Design, Automation & Test in Europe Conference & Exhibition. Dresden: IEEE, 2018. 682–687. [doi: 10.23919/DATE.2018.8342096]
|
| [10] |
Nayak NG, Dürr F, Rothermel K. Time-sensitive software-defined network (TSSDN) for real-time applications. Proceedings of the 24th International Conference on Real-time Networks and Systems. Brest: ACM, 2016. 193–202. [doi: 10.1145/2997465.2997487]
|
| [11] |
Nayak NG, Dürr F, Rothermel K. Incremental flow scheduling and routing in time-sensitive software-defined networks. IEEE Transactions on Industrial Informatics, 2018, 14(5): 2066-2075. DOI:10.1109/TII.2017.2782235 |
| [12] |
Li D, Wang ST, Zhu KL, et al. A survey of network update in SDN. Frontiers of Computer Science, 2017, 11(1): 4-12. DOI:10.1007/s11704-016-6125-y |
| [13] |
Raagaard ML, Pop P, Gutiérrez M, et al. Runtime reconfiguration of time-sensitive networking (TSN) schedules for fog computing. Proceedings of the 2017 IEEE Fog World Congress. Santa Clara: IEEE, 2017. 1–6. [doi: 10.1109/FWC.2017.8368523]
|
| [14] |
赵奕, 王海涛. 时间敏感网络研究现状与关键技术探析. 邮电设计技术, 2022(10): 65-70. DOI:10.12045/j.issn.1007-3043.2022.10.0013 |
| [15] |
Said SBH, Truong QH, Boc M. SDN-based configuration solution for IEEE 802.1 time sensitive networking (TSN). ACM SIGBED Review, 2019, 16(1): 27-32. DOI:10.1145/3314206.3314210 |
| [16] |
Gutiérrez M, Ademaj A, Steiner W, et al. Self-configuration of IEEE 802.1 TSN networks. Proceedings of the 22nd IEEE International Conference on Emerging Technologies and Factory Automation. Limassol: IEEE, 2017. 1–8. [doi: 10.1109/ETFA.2017.8247597]
|
| [17] |
Li Q, Li D, Jin X, et al. A simple and efficient time-sensitive networking traffic scheduling method for industrial scenarios. Electronics, 2020, 9(12): 2131. DOI:10.3390/electronics9122131 |
| [18] |
Yan JL, Quan W, Jiang XY, et al. Injection time planning: Making CQF practical in time-sensitive networking. Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications. Toronto: IEEE, 2020. 616–625. [doi: 10.1109/INFOCOM41043.2020.9155434]
|
 2024, Vol. 33
2024, Vol. 33



