随着我国的城市化进程不断加快, 汽车保有量不断增加, 现有的交通系统已经不足以调配庞大的机动车数量, 交通拥堵成为制约我国城市经济发展的主要瓶颈, 改善交通拥堵成为政府和城市建设决策者面临的重大问题. 早期交通拥堵问题的解决方式主要是增加交通基础设施建设. 与修建更复杂的道路相比, 更经济的解决方式是优化交通信号的控制策略^[1], 合理的交通信号控制策略将相互冲突的交通流从空间和时间维度中分离, 有效提高了交通流的吞吐量和交叉路口的通行效率.

1 交叉口信号控制方法

现有的交通信号控制优化方法主要分为定时控制和自适应交通信号控制(adaptive traffic signal control, ATSC)^[2]. 自适应交通信号控制因其更出色的控制性能而被广泛应用, 如早期的分时循环偏移优化技术(split cycle offset optimization technique, SCOOT)^[3], 但由于缺乏实时适应性和灵活性, 该方法在处理紧急交通状况时效率低下. 实时分层优化分布式系统以实时的方式解决了交通信号的动态优化问题^[4], 但会遇到系统架构和算法设计过于复杂的困扰. 此外还有各种交叉技术, 如模糊逻辑控制算法^[5]、遗传算法^[6]等, 这些方法虽然增强了交叉口信号控制系统的性能和适应性, 但是现实中的交通流会随着时间的变化而随机波动, 难以建立精确的数学模型, 导致此类最优控制方法无法被大规模应用.

近年来, 更多先进的控制理论和方法应用在交叉口信号控制领域中, 包括粒子群优化算法^[7]、强化学习(reinforcement learning, RL)^[8]等. 与基于模型的方法相比, 强化学习在马尔可夫决策过程(Markov decision process, MDP)框架下提供了一种有效解决交叉口信号控制的方式, 通过学习适应性的信号控制策略以应对实时变化的交通条件. 2003年, Abdulhai等首次将强化学习Q-learning算法应用于单路口信号控制问题^[9]. Alegre等采用Q-learning算法并将交通状态表示为向量形式, 以降低模型对环境状态可观测性的影响^[10]. 随着交通环境复杂性的增加, 从Q值表中搜索某一状态非常耗时, 还会造成计算机存储空间不足等问题. 深度强化学习(deep reinforcement learning, DRL)利用神经网络强大的表征能力拟合Q值表或直接拟合策略^[11], 克服了强化学习算法难以处理高维度状态空间的问题. Li等应用一种堆叠式自动编码器, 该编码器将交叉口各个方向的队列长度作为输入来估计深度Q网络(deep Q-network, DQN)的值函数^[12]. Li等通过离散交通状态编码(discrete traffic state code, DTSE)技术将各个道路按照一定的距离网格化, 综合提取网格内的车辆和速度信息作为DQN模型的输入^[13]. 刘智敏等在DQN模型基础上构建基于相邻采样时间步实时车辆数变化量的奖励函数^[14], 缩短了单路口排队车辆的等待时间. 孙浩等提出一种分布式双重Q网络(double deep Q network, DDQN)的交叉口信号控制方法^[15], 将单路口的高维实时交通信息离散化建模, 实现对交叉口信号的自适应控制. Liang等提出的双决斗深度Q网络(double dueling deep Q network, 3DQN)交叉口信号控制方法^[16], 通过从车辆网络中提取信息来控制一个周期内的红绿灯持续时间, 从而提高交叉口通行效率. 但此类基于价值函数的方法在处理长时间信号控制相位连续选择问题时, 由于状态空间和信号相位组合随时间呈指数式增长, 难以准确估计信号策略的价值, 导致模型计算出的动作值出现过度估计, 以及模型收敛不稳定等问题.

策略梯度算法(policy gradient, PG)^[17]解决了价值函数方法过度估计的问题, 且具有较好的收敛特性, 但PG算法在策略更新时变量的方差波动较大, 进而影响模型训练的稳定性. 近端策略优化算法(proximal policy optimization, PPO)的提出解决了PG算法中学习率难以确定的问题. Ma等应用PPO算法动态的调整交通信号的时序, 提高了单路口车辆的通行效率^[18]. Huang等在PPO算法的Actor网络中引入长短期记忆网络(long short-term memory, LSTM)提取交通状态的时序特征^[19]. 但是传统PPO算法使用剪切函数使得样本数据的采集不够完善, 从而影响最优动作的选择, 为此本文提出一种基于样本优化的PPO算法的单路口信号控制模型, 通过对PPO算法中代理目标函数进行最大化提取, 提高动作样本的选择质量, 增加模型控制动作的灵敏度, 避免了模型训练过程中低质量样本对交通环境的不利影响. 同时采用一种新的交通状态向量作为模型的输入, 有效提取出交通流数据的状态特征, 提高了模型对交叉口信号的控制效率.

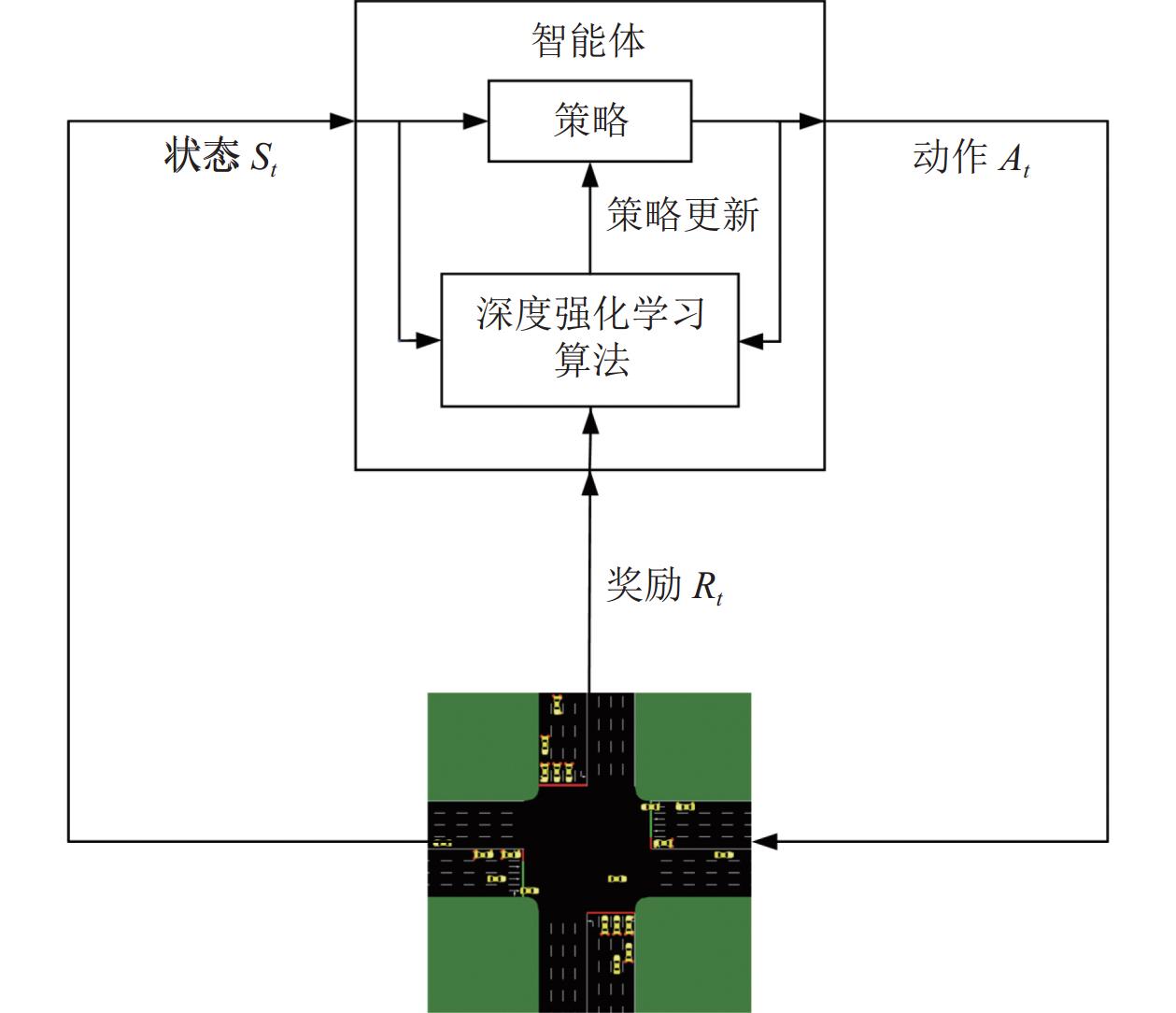
2 基于强化学习的单路口信号控制概述

在单路口信号控制的强化学习场景中, 智能体通过与交通环境的交互进行学习. 交通环境包括交通状况和红绿灯阶段, 状态则是当前交通环境的提取特征表示, 智能体将交通环境信息提取成状态作为输入, 根据状态学习选择动作的策略. 策略被定义为交通状态到动作的映射, 用来描述智能体在某一状态下执行各个动作的概率分布. 智能体在给定的状态$ {S_t} $下学习并选择一个可行的动作$ {A_t} $, 动作被执行后智能体从环境中接收反馈$ {R_t} $, 包括正反馈和负反馈, 其中正反馈是对正确动作的奖励, 负反馈是对错误动作的惩罚. 智能体在当前状态$ {S_t} $下选择的动作$ {A_t} $影响环境使得环境发生改变, 通过与复杂交通环境的交互学习最佳的控制策略, 这种训练循环实体之间的交互被公式化为马尔可夫决策过程, 其交叉口信号控制框架如图1所示.

强化学习的目标是使智能体最大限度地获得长期奖励, 从而学习到最优的决策序列. 不同于维持一个价值函数模型的价值学习方法, 策略学习方法不依赖模型, 通过求解策略函数直接搜索出最优决策序列. 策略函数由一组可调参数定义, 通过调整这些参数观察结果奖励的差异, 并向产生更高奖励的方向更新. 由于策略$ \pi $具有随机性, 其参数$ \theta $决定了动作的采样概率, 进而影响数据轨迹$ \tau = \{ {s_1}, {a_1}, {r_1}, {s_2}, {a_2}, {r_2}, \cdots, {s_t}, {a_t}, {r_t}\} $的概率, 由此定义基于策略梯度的强化学习算法的目标函数:

$ J(\theta ) = {E_{\tau \sim {\pi _\theta }}}R(\tau ) = \sum\nolimits_\tau {P(\tau ;\theta )R(\tau )} $

(1)

其中, $ R(\tau ) $表示轨迹$ \tau $的累积奖励, $ P(\tau ;\theta ) $表示轨迹$ \tau $出现的概率. 策略函数的参数更新方向与期望奖励的梯度方向一致, 以使累积期望奖励最大化, 并通过梯度上升的方法更新策略函数的参数直至收敛:

$ \theta \leftarrow \theta + \alpha {\nabla _\theta }J(\theta ) $

(2)

3 单路口信号控制MPPO算法模型 3.1 状态空间

对于交通信号的状态信息, 大多数的研究采用离散交通状态编码将车辆位置信息、速度信息以及交叉口当前绿灯的相位作为状态输入, 虽然DTSE方法相较于图像输入能有效减少输入信息量, 但是由于该方法的状态输入维数单一, 且获得位置和速度矩阵需要部署许多的物理传感器, 导致DTSE方法难以直接捕获交叉口俯视图并进行相应的编码. 为了能够充分提取交通环境状态并降低状态空间的复杂度, 本文采用一种新的交通状态表示法, 为了避免频繁切换相位所导致各方向上连续到达的交通流强行中断, 需将当前绿灯时间是否经过最小绿灯时间作为模型的输入状态之一. 另一方面, 由于信号相位将直接影响交叉口各方向的交通流顺序, 需将当前绿灯相位$ \rho $作为输入状态, 采集信号相位采用One-Hot编码的形式对相位进行编码, 具体如表1所示.

本文将4种交通特征元素组合成一个多维状态向量作为输入, 智能体观察到的交叉口状态表示为:

$ {S_t} = [\rho , \delta , {\Delta _{|d|}}, {q_L}] $

(3)

其中, $ \;\rho \in P $是一个One-Hot编码向量, 表示当前绿灯相位; $ \delta $是一个二进制变量, 表示当前相位阶段是否经过了最小绿灯时间; 车辆密度$ {\Delta _{|d|}} \in [0, 1] $定义为进入车道$ l \in L $的车辆数除以该车道的总容量; 队列长度$ {q_L} \in [0, 1] $定义为进入车道$ l \in L $的排队车辆数除以该车道的总容量, 如果车辆的速度低于0.1 m/s, 表示该车辆在队列中处于排队状态.

3.2 动作空间

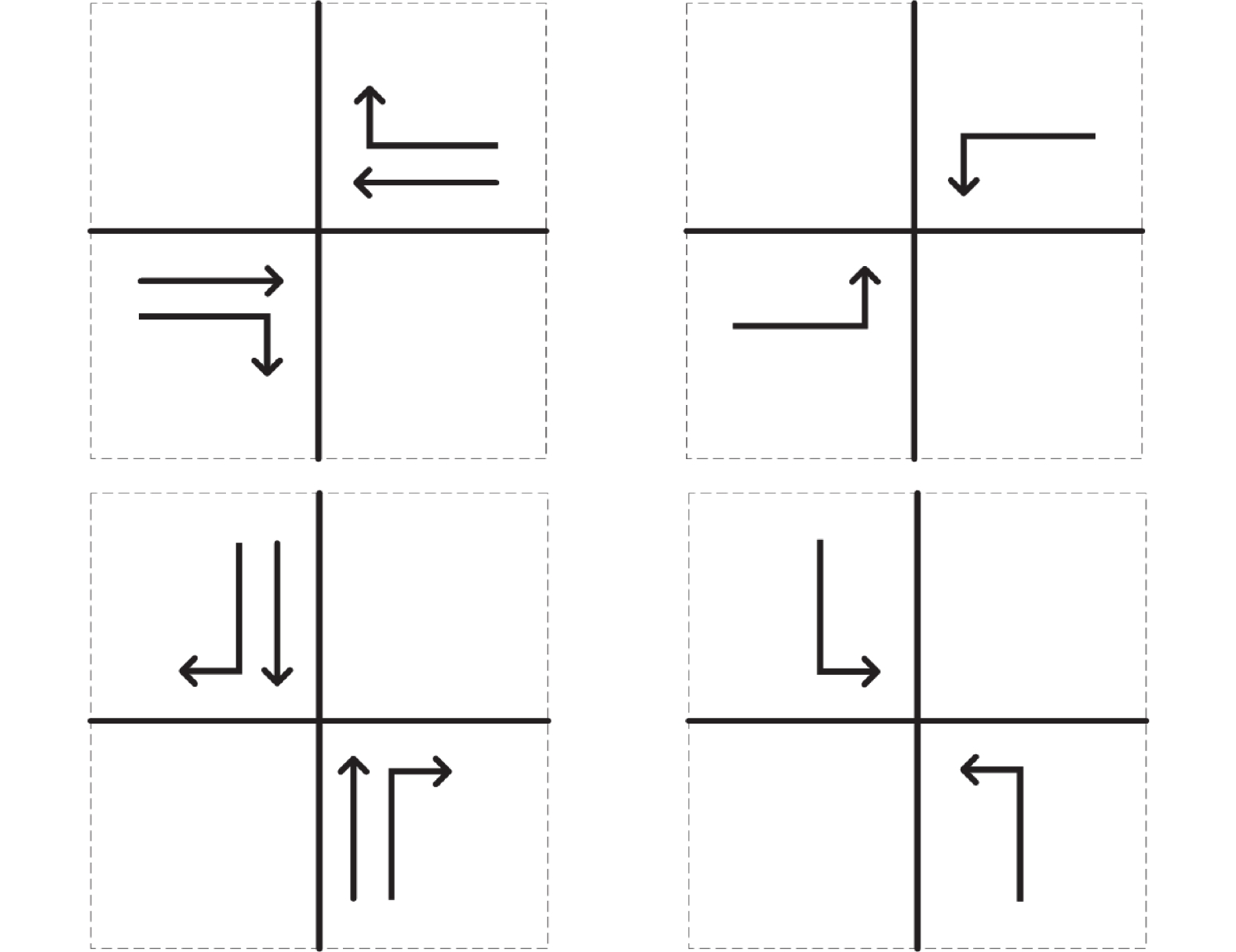
交通信号控制问题中的动作定义为根据当前交通灯状态, 是否转换到下一个相位. 本文以四路交叉口为背景, 设置4个绿灯相位. 由于实际交叉口右转不影响其他方向车辆的通行, 因此右转方向的信号设置为常绿状态, 其他方向的绿灯相位设置为: 东西直行和右转(EW)、东西左转(EWL)、南北直行和右转(NS)、南北左转(NSL), 如图2所示. 智能体在每个时间步只能选择执行4个绿灯相位中的1个, 不允许同时执行多个相位.

4个绿灯相位的固定相序构成动作空间集A={NSG, NSLG, EWG, EWLG}. 在每次的决策中, 从动作集中选择动作作为输出值以控制信号量改变, 每个相位信号的颜色状态如表2所示. 由于相位时长不会因当前相位车流量较大而持续增加. 因此, 需要设置每个相位的最大绿灯时间50 s和最小绿灯时间5 s. 当前阶段的绿灯持续时间超过50 s或小于5 s时, 延长当前阶段的绿灯时间或强制切换到下一阶段, 并给予当前动作负奖励.

3.3 奖励函数

为了减少车辆停留在交叉路口的时间, 缓解交通拥挤程度, 智能体需向交叉口信号控制模型提供先前动作表现的反馈. 本文将奖励函数定义为连续动作之间车辆累计等待时间的变化:

$ {r_t} = {W_t} - {W_{t + 1}} $

(4)

其中, $ {W_t} $和$ {W_{t + 1}} $表示在执行动作之前和之后在交叉口处车辆的累计等待时间, 计算公式如下:

$ {W_t} = \sum\nolimits_{v \in {V_t}} {{w_{v, t}}} $

(5)

其中, $ {V_t} $表示在时间步长$ t $到达交叉口的车辆集合, $ {w_{v, t}} $是车辆$ v $从进入其中一条道路到达交叉口到时间步$ t $的总等待时间. 该奖励函数以一段时间内所有车辆通过交叉口的总等待时间来评估模型的控制性能. 通过最大化奖励函数, 最小化车辆的等待时间训练模型, 从而优化交叉口信号的控制效率.

3.4 MPPO交叉口信号控制模型

PPO算法^[20]由OpenAI于2017年提出, 是一种基于AC架构^[21]的深度强化学习算法, 旨在解决信任区域策略优化算法(trust region policy optimization, TRPO)的计算复杂性问题. 在策略梯度方法中, 小幅度的策略更新通常更有利于收敛到最优决策序列, 但是传统的PG算法对更新步长极为敏感且难以选择合适的步长. 若步长太小会导致训练过程太慢且无法解决大规模问题, 步长过大可能会得到一个非常糟糕的策略, 导致算法效率低下甚至训练失败. 而PPO算法通过引入一个裁剪策略更新幅度的机制, 使得策略参数的更新在一定的范围内, 以确保稳定性和收敛性. 该裁剪操作有助于避免过大的策略参数更新, 从而更稳定地优化策略. 传统的PPO算法使用CLIP代理目标函数, 以限制策略更新的范围:

$ {L^{\mathit{CLIP}}}(\theta ) = \hat E[\min ({r_t}(\theta ){A_t}, {\mathit{CLIP}}({r_t}(\theta ), 1 - \varepsilon , 1 + \varepsilon ){A_t})] $

其中,

$ {A_t}({s_t}, {a_t}) = {r_t} + \gamma {V_\omega }({s_{t + 1}}) - {V_\omega }({s_t}) $

(6)

$ {r_t}(\theta ) = \frac{{{\pi _\theta }({a_t}\mid{s_t})}}{{{\pi _{{\theta _{\rm old}}}}({a_t}\mid{s_t})}} $

优势函数$ {A_t} $的作用是降低方差, 提高模型更新的鲁棒性, $ {r_t}(\theta ) $用来衡量当前策略与上一步策略相比的变化幅度, 目的是修正前后策略分布的差异, 从而更加稳定地进行策略优化, 第2项CLIP函数将这个比率裁剪到$ (1 - \varepsilon , 1 + \varepsilon ) $的范围内, 消除了当前策略偏离旧策略太远的可能性, 最后取裁剪目标和未裁剪目标的最小值. 虽然这种保守的策略迭代有效地改善了DQN、TRPO等算法在模型鲁棒性、计算复杂度方面的问题, 但传统的PPO算法在目标函数中进行最小化操作会忽略对模型更新有很大影响的样本, 同时保留了大量对模型更新有不良影响的样本. 在交通环境中低质量的样本信息对模型更新的影响极为不利, 为此将PPO算法中的CLIP代理目标函数修改为:

$ {L^{\mathit{MAXCLIP}}}(\theta ) = \max [\min ({r_t}(\theta ){A_t}, \mathit{CLIP}({r_t}(\theta ), 1 - \varepsilon , 1 + \varepsilon ){A_t})] $

其中,

$ {A_t}({s_t}, {a_t}) = {r_t} + \gamma {r_t}(\theta ){V_\omega }({s_{t + 1}}) - {V_\omega }({s_t}) $

(7)

$ {r_t}(\theta ) = \frac{{{\pi _\theta }({a_t}\mid{s_t})}}{{{\pi _{{\theta _{\rm old}}}}({a_t}\mid{s_t})}} $

MPPO算法对已经通过最小化和裁剪过滤的样本进行另一次最大化提取, 选择对模型改进最显著的经验样本进行更新, 可以防止模型受到质量较差样本的影响, 同时减少了对交通环境不必要的改变. 由于MPPO算法可以在一次迭代中被多次更新, 因此两个相邻的状态可能来自不同的策略分布, 这将导致目标函数不再是无偏的. 为此, 在优势函数中引入重要性采样系数, 以确保算法的无偏性. Critic网络的目标函数由式(8)给出:

$ {L_{\rm critic}}(\omega ) = {({r_t} + \gamma {r_t}(\theta ){V_\omega }({s_{t + 1}}) - {V_\omega }({s_t}))^2} $

(8)

基于样本优化的PPO算法中Actor网络的目标函数为:

$ {L^{\mathrm{MPPO}}}(\theta ) = {L^{\mathit{MAXCLIP}}}(\theta ) - \beta KL({\pi _{{\theta _{\rm old}}}}, {\pi _\theta }) $

(9)

其中, $ \beta $是KL惩罚因子, 用于保持KL值在一定范围内. 引入KL惩罚项的目的是确保旧策略和新策略分布足够接近, 以在多次更新时实现稳定的策略改进. 改进后的PPO算法筛选出质量较高的策略进行优化, 使用多个样本进行更新, 并在每个样本上执行多个优化步骤, 提高了采样效率和训练速度, 减少了算法的复杂性. MPPO算法的伪代码见算法1.

算法1. MPPO算法

1.初始化经验缓存M、Actor参数$\scriptstyle \theta $、Critic参数$ \scriptstyle \omega $, 设置超参数: 批处理大小B、学习率γ

2. for epoch = 1, 2, 3, …, N do

3. 　重置环境并初始化状态$\scriptstyle s $

4.　 for episode = 1, 2, 3, …, T do

5. 　　通过Actor网络的输出分布选择动作$\scriptstyle a $

6. 　　收集$\scriptstyle (s, a, r, s') $到经验缓存M

7.　　梯度上升小批量更新Actor网络B次

$\scriptstyle \theta \leftarrow \theta + \alpha {\nabla _\theta }{L^{\rm MPPO}}(\theta ) $

8. 　　梯度下降小批量更新Critic网络B次

$\scriptstyle \omega \leftarrow \omega - \delta {\nabla _\omega }{L_{\rm critic}}(\omega ) $

9. 　 end for

10.　清除经验缓存M

11. end for

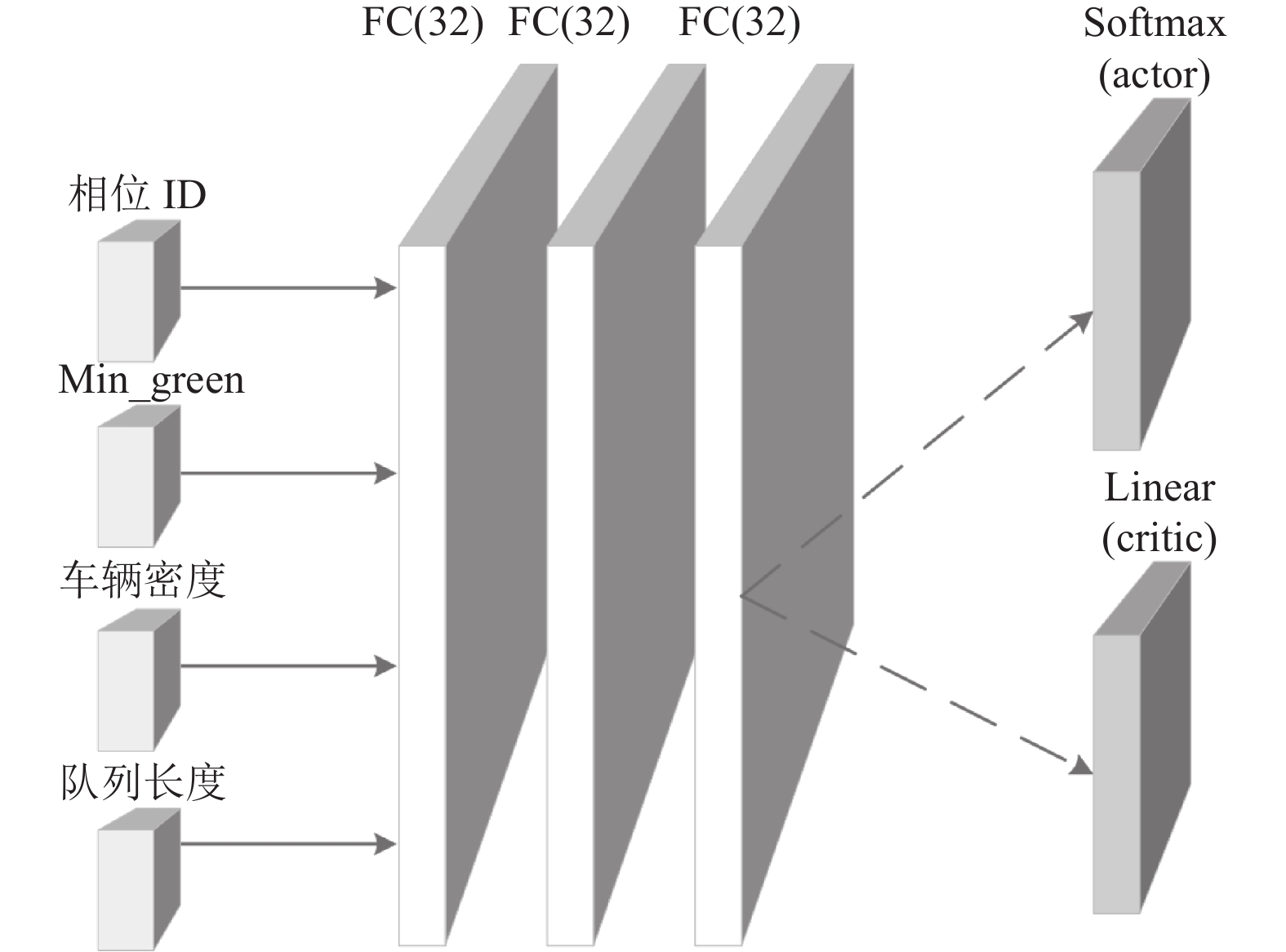
MPPO算法用两个结构完全相同的深度全连接神经网络表示Actor网络和Critic网络, 如图3所示. Actor通过Critic提供的奖励信号来更新策略, 以改善动作, 而Critic通过监督Actor的动作来不断提高自身的价值估计, 两者相互协作以达到更好的性能. 输入是由相位ID、最小绿灯时间、车辆密度、队列长度组成的状态特征向量, 通过3个含有32个神经元的全连接隐藏层, 隐藏层之间通过ReLU函数激活. Actor网络的输出是一个动作空间大小的Softmax层, 该层输出表示每个动作的概率分布, Critic网络的输出是状态价值函数的单个标量值, 作为状态价值的估计.

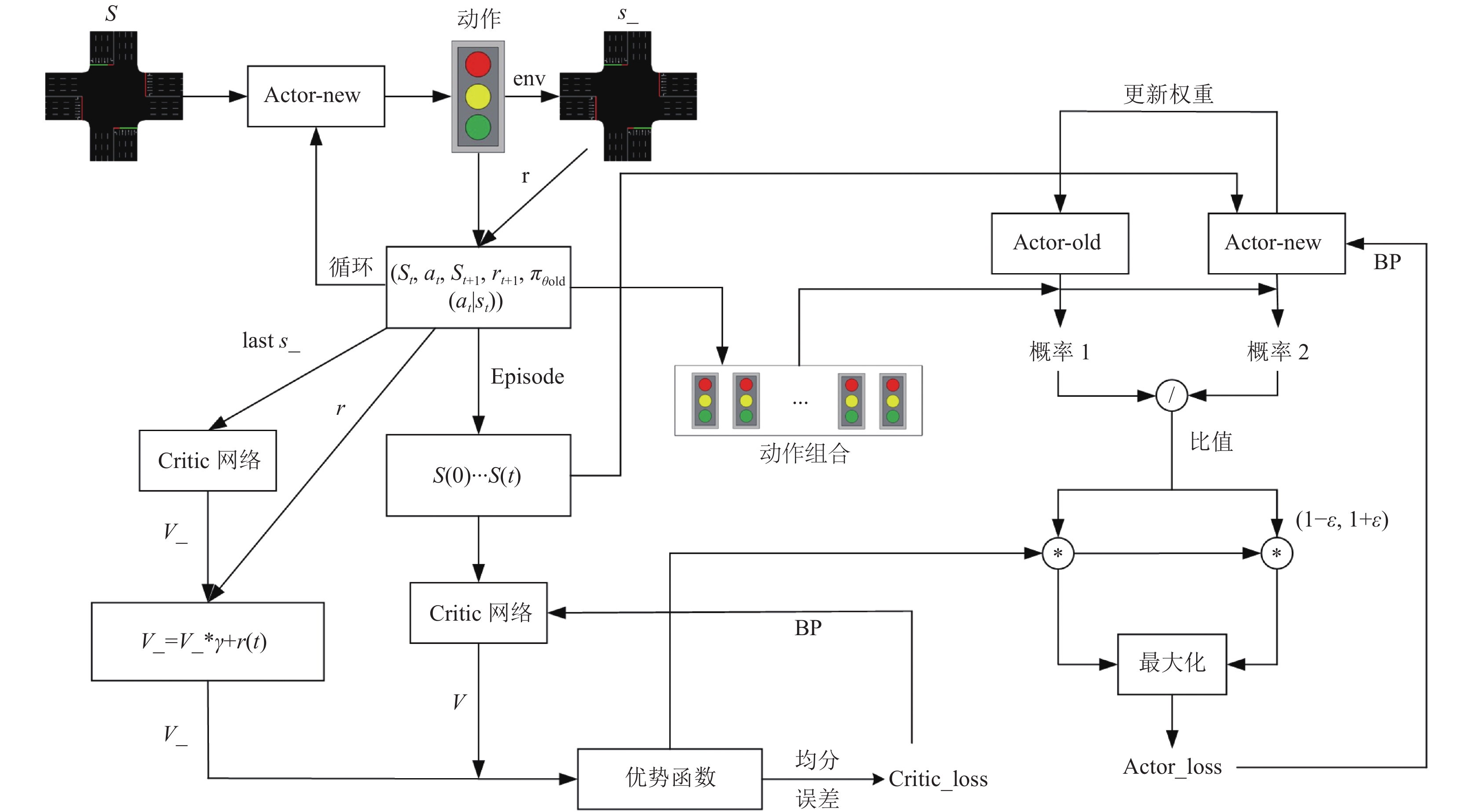
MPPO控制模型通过Actor-new网络与交通环境交互得到的数据训练Actor-old网络, 使一次收集到的数据可以重复利用多次. 在更新步骤中, Critic网络预测当前状态估计值和下一状态估计值, 根据值函数预测计算出优势值作为奖励的估计值, 通过保守的策略迭代提升算法训练的鲁棒性. 如图4所示为基于MPPO算法的交叉口信号控制框架.

4 实验结果与分析 4.1 仿真环境与参数设置

为验证MPPO算法模型的有效性, 本文在城市交通微观模拟软件(SUMO)上进行仿真实验. 与Aimsun、Vissim等仿真软件相比, SUMO的执行速度更快, 它不仅可以进行大规模的交通流量管理, 还可以与机器学习库TensorFlow等应用链接. 而且SUMO自带的API接口TraCI (交通控制接口)可以调用一系列库函数, 实现仿真数据信息的获取和仿真对象的状态修改, 以实现算法模型与交通环境的交互过程.

实验基于Python 3.7的集成开发环境, 采用深度学习库TensorFlow 2.0作为后端, Adam求解器求解内层优化问题. 为了尽可能逼真地模拟真实的交通流, 本文将交通流近似为威布尔分布, 即车辆随机产生并分布在整个路网中, 以确定车辆是转弯还是继续直行, 并且在相同的时间间隔引入. 表3总结了详细的交通模拟参数设置.

实验采用车辆累计等待时间、车辆平均等待时间和车辆平均队列长度评估MPPO算法的训练情况, 其中模型的训练参数设置如表4所示.

4.2 仿真结果分析

实验通过200轮迭代仿真验证了基于样本优化的PPO算法在单路口信号控制的自适应能力. 在模型的训练过程中, 监测车辆的累计等待时间、车辆的平均队列长度、不同交通流模式下车辆的平均等待时间, 并综合对比了基于价值函数的Q-learning控制模型、Double DQN控制模型的控制效率.

表5所示的是3种深度强化学习控制方法的1500辆车的平均队列长度. 从表中可以得到MPPO控制模型的平均队列长度最短, 且明显优于其他两种基于值函数的控制模型.

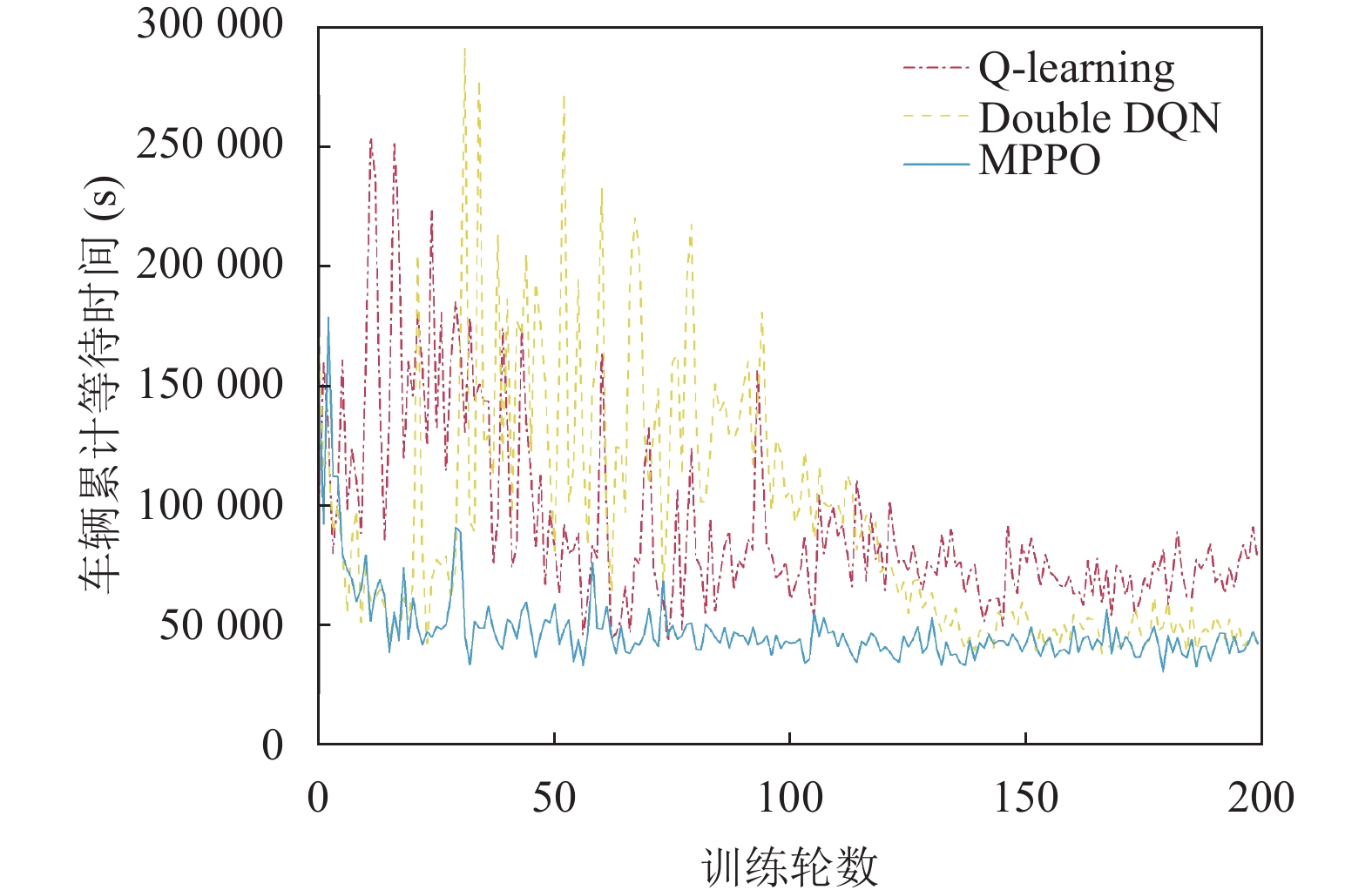
如图5所示的是3种自适应控制方法的1500辆车的累计等待时间迭代仿真对比. 从图中可以看出, 训练到第30轮左右时, MPPO控制模型的车辆累计等待时间迅速收敛并趋于稳定, 而Q-learning控制模型和Double DQN控制模型在训练到100轮左右时才逐渐收敛, 且收敛过程不稳定. 从迭代曲线走势来看, 本文模型在车辆累计等待时间和模型收敛速度方面都有显著的提升.

为了进一步验证MPPO控制模型的有效性和可行性, 实验还进行了在低交通流(500辆车)、中交通流(1000辆车)、高交通流(1500辆车)这3种模式下的车辆平均等待时间的对比实验. 其中图6(a)展示了3种方法在低交通流模式下的车辆平均等待时间迭代仿真曲线, 与Q-learning控制模型相比, MPPO控制模型的平均等待时间约降低63%; 与Double DQN控制模型相比, MPPO控制模型的平均等待时间约降低50%. 此外, 本文所提方法从训练稳定性方面也明显优于Q-learning控制模型和Double DQN控制模型.

图6(b)和图6(c)分别为中交通流模式(1000辆车)和高交通流模式(1500辆车)的车辆平均等待时间迭代仿真曲线. 随着交通环境中车流量的增加, Q-learning控制模型从庞大的Q值表中搜索最优动作非常耗时, 且过多的状态数据导致Q-learning控制出现“维数爆炸”的情况; 而Double DQN控制模型随着车流量的增加出现收敛不稳定和过度估计的问题. 从图6(b)、图6(c)可以看出, 在中交通流和高交通流模式下本文所提方法的车辆平均等待时间明显优于Q-learning控制模型和Double DQN控制模型, 可以有效缓解车流量高峰期的交通拥堵问题, 验证了本文所提方法的有效性.

5 结束语

针对单交叉口的交通拥堵问题, 本文提出了一种基于样本优化的PPO算法的交通信号控制方案, 通过对传统PPO算法中的剪切函数进行最大化提取, 使模型更容易选择到最优的样本信息. 将多维交通状态向量作为状态输入, 有效降低了智能体对环境状态的可观测性的影响. 实验结果表明, MPPO信号控制模型在车辆的累计等待时间、平均等待时间和平均队列长度方面均优于值函数强化学习控制模型, 验证了本文所提方法具有更好的鲁棒性和泛化能力. 对于单交叉口的信号控制问题, 模型只需感知交叉口交通流状态的变化, 而在多交叉口信号控制问题中, 需要构建一个多智能体信号控制系统. 为了有效协调各交叉口的信号相位, 需要进一步完善交通状态空间的表达, 实现对交通流特性的多尺度感知. 因此下一步研究的重点是多交叉路口协同控制的交通信号问题, 以实现整体交通网络的优化.