由于知识图谱具有语义表示和推理等功能, 因此近年来相关技术快速发展, 出现了大量知识图谱^[1]. 不同图谱通常会包含许多互补信息, 将这些图谱进行融合有助于提高对知识的利用率. 然而不同来源的知识图谱之间存在着异构性和数据冗余等问题. 需要利用知识融合技术, 对图谱中冗余信息进行对齐、合并, 形成全局统一的知识表示和关联^[2]. 实体对齐(entity alignment, EA)是知识融合过程中关键技术, 旨在关联不同来源知识图谱中指向真实世界同一对象的等价/匹配实体^[3], 实现知识图谱间信息共享, 从而提供一个信息较为完备的知识库.

早期, 研究人员使用字符串的各种特征进行实体对齐. 近年来随着知识表示学习技术的快速发展, 研究人员提出许多基于表示学习的实体对齐方法, 利用机器学习技术将图谱数据表示为低维稠密的向量, 通过向量之间的距离来反映对象之间的语义关系^[4].

1 相关工作

早期的知识图谱实体对齐技术主要采用相似度计算^[5], 人工特征提取^[6]等方法, 但是这些方法难以有效地匹配异构知识图谱, 限制其应用范围. 目前, 随着表示学习的兴起, 根据知识图谱建模方式的不同, 可以分为: (1) 基于三元组表征模型的翻译模型; (2) 基于图结构特征的图神经网络模型.

1.1 翻译模型

以TransE^[7]为代表的翻译模型, 对于每个三元组$(h, r, t), $将关系看作头尾实体的连接, 并且关系存在方向, 来学习实体的向量表示, 该方法孤立学习每个三元组, 无法感知更多的全局信息. MTransE^[8]模型创造性地将TransE这一经典的翻译模型运用于知识图谱实体对齐任务; BootEA^[9]模型针对缺乏足够的训练数据, 迭代地将可能对齐的数据作为训练数据来增强模型效果, 实现实体对齐; SEA^[10]中指出图谱实体的度差异会对具有不同度数的实体造成不同的匹配难度, 因此通过结合翻译模型和对抗训练方法提升对齐效果. 翻译模型存在依赖三元组的局部语义信息, 缺乏对知识图谱全局信息的有效捕获的问题, 因此研究人员将研究重点转移到基于图神经网络的实体对齐方法上.

1.2 图神经网络模型

基于图神经网络的方法主要利用图卷积网络(graph convolutional network, GCN)^[11]和图注意网络(graph attention network, GAT)^[12]对节点邻居信息进行聚合, 获得对齐实体之间的邻居相似度从而实现实体对齐, 但是此类方式并未考虑真实世界中不同关系的影响, 不能满足异构图的需要. HGCN^[13]通过获取基于头尾实体的关系谓语嵌入来进行辅助对齐; RDGCN^[14]通过探索原始图谱和对偶关系图之间丰富的关系特征进行实体对齐; HyperKA^[15]通过引入基于层次结构的双曲关系图神经网络(hyperbolic relational GNN), 使得能够以更低维的实体嵌入向量实现卓越的匹配效果; HMAN^[16]在利用GCN嵌入结构信息的同时加入了实体标签、拓扑信息、关系类型和文本描述等信息综合进行实体嵌入; AttrGNN^[17]按照属性和结构信息进行通道划分, 分别进行嵌入学习, 其取得的效果要优于一些联合使用实体属性和结构信息进行对齐的模型, 但是该模型在实体对齐过程中忽略了对关系信息和多阶邻居信息的考虑. 因此本文在AttrGNN模型的基础上提出了FSAAM模型, 本文的主要贡献如下.

(1) 利用双通道模块实现对实体属性和结构信息的联合学习.

(2) 考虑了在实体对齐任务中不同类型的关系信息对实体的重要度并不相同的影响.

(3) 利用图注意力机制与Transformer编码器共同编码的方式实现了多阶邻居信息聚合从而获得更佳的实体嵌入表示用于实体对齐任务.

因此本文具有的实际应用价值主要在于实现了对图谱中结构、关系、属性等多种信息的学习, 从而在真实公开数据集上取得较好的效果.

2 问题定义

定义1. 知识图谱可以被形式化定义为一个六元组$ G = (E, R, A, V, {T^r}, {T^a}) $, 其中E、R、A、V分别表示图谱中的实体(entities)、关系(relations)、属性(attributes)、属性值(values)的集合; ${T^r} = \{ (h, r, t)\mid h, t \in E, r \in R\} $表示关系三元组的集合; ${T^a} = \{ (e, a, v)\mid e \in E, a \in A, v \in V\} $表示属性三元组的集合^[17].

定义2. 实体对齐就是找到源知识图谱(Gs)和目标知识图谱(Gt)之间的映射, 即为$\psi = \{ (e, {e{'}})\mid e \in E, {e{'}} \in {E{'}}\} $, 其中的e与e'为两个图谱中等价的实体. 等价实体的种子集${\psi ^s}$被用作训练数据^[17].

3 融合结构与属性注意力机制的实体对齐模型

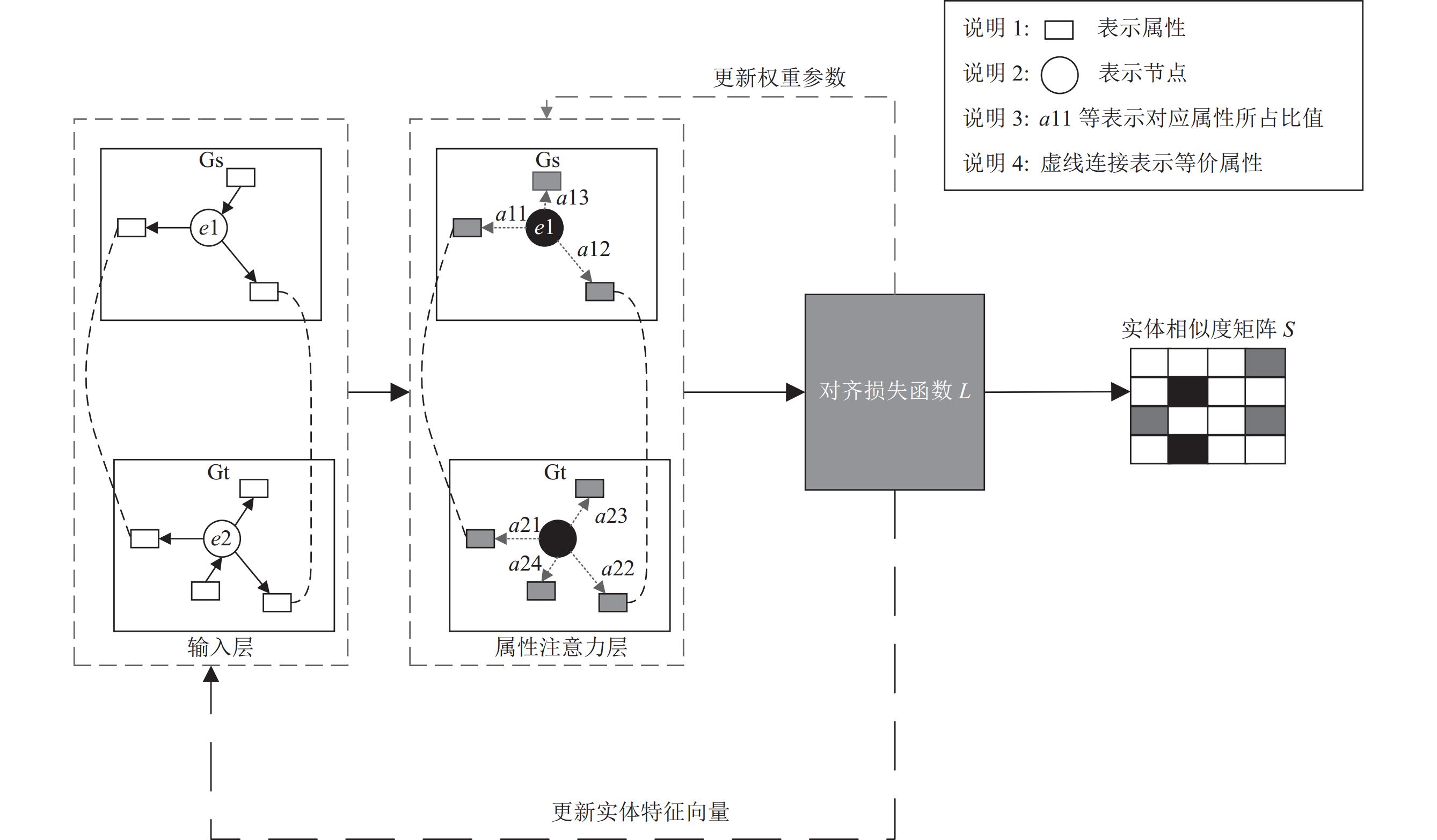
FSAAM模型框架如图1所示, 它主要由3个模块组成: (1)属性通道模块: 通过属性注意力机制实现对图谱中属性信息的利用, 从而得到属性通道相似度矩阵; (2)结构通道模块: 通过GraphSAGE-RelationAware聚合层实现对图谱中邻居和关系信息的利用, 再通过GAT-Transformer多阶邻居聚合层实现对图谱中多阶邻居信息的利用, 从而得到结构通道相似度矩阵; (3)双通道特征融合模块: 是为了同时利用上述两个通道模块学习到的有用信息, 为两个相似度矩阵分配不同的比重, 从而得到集成相似度矩阵实现实体对齐.

3.1 结构通道模块

结构通道实现流程步骤如图2所示.

输入层: 实体名称对于实体对齐是非常重要的信息, 使用预训练的词嵌入模型对实体的语义信息进行编码, 使得初始特征不再是随机初始化, 减少模型训练成本. BERT^[18]在大规模的多语言数据集上进行训练, 已经捕捉了大规模文本数据中的语言特征, 能够得到较好的初始实体嵌入表示, 故本文利用BERT实现对实体名称进行编码获得初始实体特征表示$ h_e^{(0)} $ (表示第0层的实体表示).

GraphSAGE-RelationAware聚合层: 该层搭建的主要目的就是为了学习知识图谱中的邻居以及关系信息.

为了利用邻居的特征来生成实体特征表示, 依据Alinet^[19]中所得结论, 一阶邻居有着更小的异构性, 因此采用均值聚合器(graph sample and aggregate, GraphSAGE)^[20]方式实现对信息聚合. 其计算公式如下:

$ h_e^l = {Re} LU({W^l}MEAN(\{ h_e^{l - 1}\} \cup \{ h_j^{l - 1}, \forall j \in N(e)\} )) $

(1)

其中, $ {W^l} $表示可学习的权重矩阵; $ MEAN( \cdot ) $表示对输入向量求平均值; $ h_e^l $表示顶点为e的第$l$层的嵌入表示.

$ N(e) = \{ j\mid \forall (j, r, e) \in {T^r}\;{\mathrm{or}} \;\forall (e, r, j) \in {T^r}, \forall r \in R\} $表示e的邻居实体.

在实体对齐任务中, 关系反映了实体间特殊的作用关系, 不同类型的关系对于同一实体而言其贡献度不同, 因此在实体的表示学习过程中增加对实体间关联关系的学习. 受RAGA^[21]启发, 模型首先使用实体注意力机制计算关系在头实体作用下的关系表示$ r_k^h $以及在尾实体作用下的关系表示$ r_k^t $ (二者计算过程类似), 通过将$ r_k^h $和$ r_k^t $相加得到关系的向量表示$ {r_k} $. 其计算公式如下:

$ {a_{ijk}} = \frac{{\exp (LeakyReLU({\beta _1^{\mathrm{T}}}[{h_i}{W^{h1}};{h_j}{W^{t1}}]))}}{{\displaystyle\sum\limits_{{e_{{i'}}} \in H} {\displaystyle\sum\limits_{{e_{{j'}}} \in T} {\exp (LeakyReLU({\beta _1^{\mathrm{T}}}[{h_{{i'}}}{W^{h1}};{h_{{j'}}}{W^{t1}}]))} } }} $

(2)

$ r_k^h = {Re} LU\left(\sum\limits_{{e_i} \in H} {\sum\limits_{{e_j} \in T} {{a_{ijk}}{h_i}{W^{h1}}} } \right) $

(3)

$ {r_k} = r_k^h + r_k^t $

(4)

其中, $ {a_{ijk}} $表示基于头实体$ {e_i} $和尾实体$ {e_j} $作用下从头实体$ {e_i} $到关系$ {r_k} $的注意力系数; H表示关系$ {r_k} $连接的头实体的集合, T表示头实体$ {e_i} $和关系$ {r_k} $对应的尾实体的集合; $ \;{\beta _1} $表示用于降维的向量; $ {W^{h1}} $表示头实体作用下关系的权重矩阵, $ {W^{t1}} $表示尾实体作用下关系的权重矩阵.

在获得关系的向量表示$ {r_k} $后需要将关系信息重新聚合到实体表示中, 因此利用关系注意力机制分别计算实体节点作为关系的头节点和作为关系的尾节点的嵌入表示. 计算公式如下所示:

$ {a_{ik}} = \frac{{\exp (LeakyReLU(\beta _2^{\mathrm{T}}[{h_i};{r_k}]))}}{{\displaystyle\sum\limits_{{e_j} \in T{e_i}} {\displaystyle\sum\limits_{{r'_k} \in {R_{{e_i}{e_j}}}} {\exp (LeakyReLU(\beta _2^{\mathrm{T}}[{h_i};{r_{{k'}}}]))} } }} $

(5)

$ h_i^{\rm in} = {Re} LU\left(\sum\limits_{{e_j} \in {T_{{e_i}}}} {\sum\limits_{{r_k} \in {R_{{e_i}{e_j}}}} {{a_{ik}}{r_k}} } \right) $

(6)

其中, $ {a_{ik}} $表示从关系$ {r_k} $到实体$ {e_i} $的注意力系数; $ {T_{{e_i}}} $表示头实体$ {e_i} $对应的尾实体集合, $ {R_{{e_i}{e_j}}} $表示头实体$ {e_i} $和尾实体$ {e_j} $之间的关系集合; $ {\beta _2} $表示用于降维的向量; $ h_i^{\rm in} $表示实体$ {e_i} $作为关系的头节点的嵌入表示(说明: 实体$ {e_i} $作为关系的尾节点的嵌入表示$ h_i^{\rm out} $的计算过程类似).

在计算不同方向关系作用下的实体表示后, 将输入层得到的初始实体特征表示$ h_e^{(0)} $、$ {h^{\rm in}} $、$ {h^{\rm out}} $、$ {h_e} $ (表示经过均值聚合器得到的输出)进行拼接得到新的实体表示, 公式如下所示:

$ {h_{r\_e}} = [h_e^{(0)};{h^{\rm in}};{h^{\rm out}};{h_e}] $

(7)

Highway层: 为了控制GraphSAGE-RelationAware聚合层中可能学习到的噪声信息传播的影响, 受RDGCN启发, 使用Highway网络^[22]来控制初始实体特征表示$ h_e^{(0)} $与前阶段学习到的特征表示$ {h_{r\_e}} $之间的信息平衡. 计算公式如下所示:

$ {h}_{\rm highway1}=G({h}_{e}^{(0)})\cdot{h}_{r\_e}+(1-G({h}_{e}^{(0)}))\cdot{h}_{e}^{(0)} $

(8)

$ G(h_e^{(0)}) = \mathit{Sigmoid}(h_e^{(0)}{W_{h1}} + {b_{h1}}) $

(9)

其中, $ {h_{\rm highway1}} $表示第1次通过Highway网络的输出, $ {W_{h1}} $表示Highway网络所需权重矩阵, $ {b_{h1}} $表示偏置向量.

GAT-Transformer多阶邻居聚合层: 为进一步增强实体的特征信息, 需要实现对多阶邻居信息的考虑.

因此首先使用图注意力机制寻找到对于对齐实体有积极作用的邻居. 计算公式如下:

$ {a_{ij}} = \frac{{\exp (LeakyReLU(\beta _3^{\mathrm{T}}[W{h_i};W{h_j}]))}}{{\displaystyle\sum\limits_{{j'} \in {N_i}} {\exp (LeakyReLU(\beta _3^{\mathrm{T}}[W{h_i};W{h_{{j'}}}]))} }} $

(10)

$ {h_{ne{r_i}}} = \left[{h_{{\rm highway1}_i}};ReLU\left(\sum\limits_{j \in {N_i}} {{a_{ij}}\beta _3^{\mathrm{T}}{h_j}} \right)\right] $

(11)

其中, $ {a_{ij}} $表示从实体$ {e_j} $到实体$ {e_i} $的注意力系数; $ {\beta _3} $表示用于降维的向量; $ {W} $表示图注意机制所需权重矩阵; $ {h_{ne{r_i}}} $表示实体$ {e_j} $经过图注意力机制与经过Highway层输出的拼接的特征向量.

针对图注意力机制过度关注局部信息, 无法充分利用图的整体拓扑结构的缺点, 在图注意力机制网络后添加Transformer编码器对图中信息再次进行编码. 计算公式如下所示:

$ \begin{split} {h_{te}} =& LayerNorm({h_{ner}} + A({h_{ner}}{W_q}, {h_{ner}}{W_k}, {h_{ner}}{W_v})+\\ & {\mathit FFN}({h_{ner}})) \end{split} $

(12)

$ \begin{split} A({h}_{ner}{W}_{q}, & {h}_{ner}{W}_{k}, {h}_{ner}{W}_{v})=\\ &{\mathit{Softmax}}\left(\frac{{h}_{ner}{W}_{q}\cdot{({h}_{ner}{W}_{k})}^{\rm T}}{\sqrt{{d}_{k}}}\right)\cdot({h}_{ner}{W}_{v})\end{split} $

(13)

$ {\mathit{FFN}}({h_{ner}}) = \max (0, {h_{ner}}{W_{f1}} + {b_{f1}}){W_{f2}} + {b_{f2}} $

(14)

其中, $ LayerNorm $表示Layer Normalization对输入进行归一化处理; ${W_{{k}}}$, ${W_v}$, ${W_q}$表示自注意力机制所需权重矩阵; ${d_k}$表示注意力头中的特征维度(解释: 是通过经图注意力机制处理得到的$ {h_{ner}} $维度处处以注意力的数量计算得到的); ${W_{f1}}$, ${W_{f2}}$表示前馈神经网络所需权重矩阵, ${b_{f1}}$, ${b_{f2}}$是对应偏置.

Highway层: 同前一个阶段Highway层作用一样是为了减少学习到的噪声数据, 计算得到$ {h_{\rm highway2}} $.

对齐损失函数: 根据预对齐的实体种子集训练损失函数, 将结构通道的两个子图中的实体嵌入到同一向量空间, 并在训练过程中更新GraphSAGE-RelationAware聚合层、GAT-Transformer多阶邻居聚合层以及Highway层中的模型参数, 获取更新后的实体特征向量, 基于更新的实体特征向量得到结构通道相似度矩阵$ {s^1} $. 计算公式如下所示:

$ \begin{split} L = &\sum\limits_{(e, {e{'}}) \in {\psi ^s}} \sum\limits_{({e_{\rm negative}}, {e{'}_{\rm negative}}) \in {\psi ^{{s{'}}}}} \max (dis(e, {e{'}})- \\ & dis({e_{\rm negative}}, {e'_{\rm negative}}) + \lambda , 0) \end{split} $

(15)

$ dis(e, {e{'}}) = \sum\limits_{i = 1}^n {|x'_e- x'_{{e{'}}}|} = ||x'_e - x'_{{e{'}}}|{|_1} $

(16)

其中, $\left( {e, {e{'}}} \right)$表示预对齐的种子实体对; ${\psi ^s}$表示实体预对齐的种子对集合; $\left( {{e_{\rm negative}}, e'_{\rm negative}} \right)$表示负采样的负例种子对; ${\psi ^{{s{'}}}}$表示通过负采样得到的实体对的集合; $dis(e, {e{'}})$表示曼哈顿距离(又称作L1范数), 是用来求向量中元素的绝对值之和; $x'_e$和$x'_{{e{'}}}$表示结构通道中两个子图中实体的最终向量表示; $\lambda $为超参数.

3.2 属性通道模块

属性通道实现流程步骤如图3所示.

输入层: 同结构通道一样, 给定属性三元组$\{ (e, {a_1}, {v_1}), \cdots, (e, {a_n}, {v_n})\} $作为某个实体e的输入, 利用BERT对实体名称、属性序列以及属性值序列进行初始学习, 从而分别得到实体的初始特征表示$ h_e^{(0)} $, 该实体对应的属性特征序列为{attr₁,$\cdots $, attr_n}和属性值特征序列为{value₁,$\cdots $, value_n}.

属性注意力层: 为了学习到对于实体特征表示更加有意义的属性信息, 通过将$\{ {a_1}, \cdots, {a_n}\} $作为边, $\{ {v_1}, \cdots, {v_n}\} $作为节点, 连接$\{ {v_1}, \cdots, {v_n}\} $和e, 那么就可以将实体的注意力计算应用到属性信息的计算, 使用注意力分数来计算不同属性和属性值的加权平均值. 计算公式如下所示:

$ h_e^1 = ELU\left(h_e^{(0)} + \sum\limits_{j = 1}^n {{a_j}{W_1}} [att{r_j};valu{e_j}]\right) $

(17)

其中, $ h_e^1 $表示经属性注意力层输出的特征表示, ${W_1} \in {R^{{D_{h1}} \times ({D_a} + {D_v})}}$是可学习的参数矩阵, $ {D}_{h1}、{D}_{a}、{D}_{v} $分别表示$ {h}_{e}^{1}、{a}_{i}、{v}_{i} $ 的向量维度, $ {a_j} $表示公式如下:

$ {a_j} = \frac{{\exp (LeakyReLU({\beta ^{\mathrm{T}}}[h_e^{(0)};att{r_j}]))}}{{\displaystyle\sum\limits_{k = 1}^n {\exp (LeakyReLU({\beta^{\mathrm{T}}}[h_e^{(0)};att{r_k}]))} }} $

(18)

其中, n表示与实体相关的属性数量, $ \beta \in {R^{({D_e} + {D_a}) \times 1}} $是可学习的参数矩阵, ${D_e}$表示$h_e^0$的向量维度.

然后在获得实体属性特征表示$ h_e^1 $后利用式(15)中的损失函数计算损失更新网络, 得到属性通道实体相似度矩阵$ {s^2} $.

3.3 双通道特征融合模块

分别从结构通道和属性通道获取各自对应的实体相似度矩阵${S^k}\;(k \in \{ 1, 2\} )$后, 为同时利用前文学习到的结构和属性信息, 受AttrGNN模型启发搭建LS-SVM网络得到集成的相似度矩阵${S^*} = {w_1}{S^{^1}} + {w_2}{S^2}$, 其中$w = [{w_1}, {w_2}]$通过如下公式学习得到:

$ \begin{split} {L_{\rm svm}} =& C\sum\limits_{l = 1}^m [{y_l} \cdot \max (0, 1 - {w^{\mathrm{T}}}{x_l}) + \\ & (1 - {y_l}) \cdot \max (0, 1 + {w^{\mathrm{T}}}{x_l})] + \frac{1}{2}{w^{\mathrm{T}}}w \end{split} $

(19)

其中, C是正则化参数, 用于控制拟合误差和模型复杂性之间的平衡, ${x_l} = [S_{e, {e{'}}}^1, S_{e, {e{'}}}^2]$是相似度分数组成的向量, 如果$(e, {e{'}}) \in {\phi _s}$即为Gs和Gt中等价的实体对时${y_l}$取1, 否则取0.

具体实现是通过调用Scikit-learn库中SVC函数, 采用线性核, 视为二分类问题(解释: 将Gt和Gs中等价的实体对标签设置为1, 随机生成固定数量的不等价的实体标签设置为0)来搭建LS-SVM网络进行训练, 优化式(19)中目标函数$ {L_{\rm svm}} $, 从而求出结构通道和属性通道各自相似度矩阵所占比重信息.

4 实验结果及分析 4.1 数据集

本文采用跨语言数据集DBP15K^[23]作为实验数据集, 该数据集是大规模知识图谱DBPedia^[24]的子集. 其中包含ZH-EN (中-英)、JA-EN (日-英), FR-EN (法-英), 每个数据集在两个不同语言的知识图谱中包含15000个对齐实体对, 作为本文实验的训练、验证和测试集. DBP15K中每个数据集的具体统计信息如表1所示.

4.2 基线模型

为了评估提出的模型有效性, 本文选择一些具有竞争性的实体对齐模型进行比较.

BootEA^[9]: 2018年发表于IJCAI国际会议, 针对训练集有限导致的嵌入表示不够准确的问题, 该模型使用一种迭代的策略标记训练数据, 从而提高实体嵌入的准确性.

HGCN^[13]: 2019年发表于EMNLP国际会议, 该模型根据实体表示得出关系的表示, 在实体表示中融入关系的信息, 利用关系的信息促进实体对齐.

RDGCN^[14]: 2019年发表于IJCAI国际会议, 探索通过对原始图和对偶关系图之间的交互进行建模, 利用Highway门控GCN层捕获邻居结构, 以学习更好的实体表示.

AttrGNN^[17]: 2020年发表于EMNLP国际会议, 基于图神经网络方法联合学习实体结构和属性嵌入, 来实现实体对齐.

RNM^[25]: 2021年发表于AAAI国际会议上, 利用邻居匹配和从连接关系中探索有用的信息实现实体对齐.

DATTI^[26]: 2022年发表于ACL会议上, 提出了一种基于三阶张量同构(DATTI)的高效实体对齐解码算法, 有效地利用了知识图谱中的邻接和自身现象来增强实体对齐的解码过程.

NAMN^[27]: 2022年发表于计算机工程, 提出依据每跳邻居对中心实体重要性不同的特点, 采用分层的思想区别处理每跳邻居信息, 通过门控机制进行聚会以学习图结构的表征.

STEA^[28]: 2023年发表于ACM, 提出利用实体之间的依赖关系, 来进行自我训练实现实体对齐.

4.3 评价指标

本文采用实体对齐模型中常用的评价指标: Hits@N以及平均倒数排名(MRR)作为评价指标. Hits@N是通过排名在前N个的正确对齐实体的比例来进行计算, MRR是指所有正确实体的平均倒数排名. 这两个指标越高, 表明实体对齐模型效果越好. 其公式分别计算如下:

$ {Hits}{\text{@}}{N}=\frac{{\displaystyle \sum _{e\in {\mathit{Seed}}}\left(ran{k}_{e}\leqslant N?1:0\right)}}{\mathit{Seed}} $

(20)

$ {{MRR}} = \frac{1}{{\left| N \right|}}\sum\limits_{i = 1}^{|N|} {\frac{1}{{ran{k_e}}}} $

(21)

其中, Seed表示测试实体对; $ran{k_e}$表示与实体e对齐的实体预测排名; $N$为对齐实体对.

4.4 实验设置与环境 4.4.1 实验设置

为利用实体名称信息, 首先使用谷歌翻译将数据集中的中文、法语以及日文的实体信息都翻译成英文, 再实现节点特征预嵌入.

模型训练过程中使用30%的种子实体对作为训练集, 其余70%实体对作为测试集. 使用BERT构建初始实体嵌入从而使得结构通道和属性通道得到的嵌入维度为768的向量. 采用Adagrad优化器, 通过网格搜索寻找结构和属性通道实体对齐的最佳参数配置. 具体参数设置如表2所示.

4.4.2 实验环境

实验环境基于Windows 10专业版, 采用的语言为Python, 具体环境如表3所示.

说明1: 在torch-geometric库中封装了包括图注意力机制在内的各种图神经网络算法;

说明2: 利用Scikit-learn搭建LS-SVM网络.

4.5 实验结果 4.5.1 参数设置与影响

本文在结构通道和属性通道模块的实验通过网格搜索方式最佳的L2正则化和学习率参数的值对评价指标Hits@1的影响. 图4–图6展示了结构通道模块中DBP15K的3个子集Hits@1的变化情况.

取3个子集对应的Hits@1效果最佳时的学习率和L2正则化参数, 其结构通道模块中DBP15K的3个子集损失收敛曲线对应如图7所示.

图8–图10展示了属性通道模块中DBP15K的3个子集Hits@1的变化情况.

取3个子集对应的Hits@1效果最佳时的学习率和L2正则化参数, 其属性通道模块中DBP15K的3个子集损失收敛曲线对应如图11所示.

对上述实验现象进行分析: 对于结构通道其Hits@1最佳的学习率为0.001和正则化参数L2为0时, 且3个子集数据在训练过程中损失函数的值都较为平滑的下降并最终保持稳定; 而对于属性通道而言学习率为0.004, 正则化参数L2为0时对应的Hits@1最佳, 并3个子集数据在训练过程的中间阶段其损失函数都有较大的波动情况, 在训练轮数达到175次后趋于稳定. 因此后续第4.5.2节以及第4.5.3节均采用最佳学习率及正则化参数进行实验.

4.5.2 对比实验

本文所提模型和各个基线模型对比结果如表4所示, 其中BootEA、RDGCN、HGCN均来自RNM论文中实验结果, AttrGNN通过实验验证得到, DATTI、NAMN以及STEA分别来自其各自对应论文中实验结果, 并将各个基线模型中效果最好的进行加粗标注.

BootEA利用迭代的策略标记训练数据进行实体对齐, 但是并未考虑不同图谱间存在多对一, 多对多以及一对多实体的情况; RDGCN通过与对偶关系图之间的交互实现对关系的考虑, HGCN利用实体名称嵌入表示作为实体初始嵌入并融入关系, 但是二者都未能考虑多阶邻居信息以及属性信息的影响; AttrGNN通过通道划分实现了对结构信息和属性信息的考虑, 但是未能引入关系信息和多阶邻居信息; RNM通过使用关系感知邻居匹配和实体感知匹配模块进行关系和实体对齐, 但未能考虑属性信息对于异构图谱的影响; DATTI专注于改进实体对齐解码过程, 没有对现有实体编码过程进行改进; NAMN通过对一阶邻居和多阶邻居信息的考虑并采用邻居匹配的方式进行实体对齐, 但未能考虑关系信息和属性信息的作用; STEA利用实体之间的依赖关系进行实体对齐, 这种半监督学习方式其准确率往往不佳. 本文针对上述模型中存在的问题进行优化, 实验结果表明, 本文所提模型其Hits@1分别在3个数据集上相较于表格中基线模型加粗标注的结果分别提升2.7%, 4.3%, 1.7%, 且Hits@10和MRR也均有一定提升. 证明本文所提模型实现了对图谱中属性、邻居和关系等多信息的综合学习, 利用双通道学习图谱中不同信息, 从而有助于从潜在的实体集合中找出正确的实体, 提高实体对齐的命中率.

4.5.3 消融实验

为了证明本文搭建的结构通道实现了对邻居信息和关系信息的有效利用, 以及将图谱信息进行通道划分的有效性, 本文通过消融实验进行对比分析.

(1)结构通道消融实验

为了验证本文搭建的结构通道对实体对齐结果的影响, 本文使用不同的策略来设计FSAAM的变体. FSAAM-0表示结构通道模块保持第3.1节中所有网络层的情况; FSAAM-1表示在引入图注意力机制后不添加Transformer编码器; FSAAM-2表示在一阶邻居信息和关系信息拼接后不添加Highway网络; FSAAM-3表示在经过Transformer编码器学习后不添加Highway网络; FSAAM-4表示不引入图注意力机制; FSAAM-5表示不考虑关系信息. 上述变体在进行实验时, 均保持其他实验条件不改变, 其实验结果对比如表5、表6所示, 其中表5为结构通道消融实验结果对比, 表6为双通道特征融合消融实验结果对比.

FSAAM-1在表5中的3个数据集的Hits@1平均下降3.4%, 在表6中的3个数据集的Hits@1平均下降1.1%, 证明了本文在利用图注意力机制实现引入图注意力机制后添加Transformer编码器实现对全局特征的考虑对于实体对齐结果的有效性; FSAAM-2在表5中的3个数据集的Hits@1平均下降0.97%, 在表6中的3个数据集的Hits@1平均下降0.83%, FSAAM-3在表5中的3个数据集的Hits@1平均下降32%, 在表6中的3个数据集的Hits@1平均下降19%, 证明为了避免误差累积引入Highway网络能够很好平衡实体初始特征和学习了关系邻居信息的特征信息, 并通过FSAAM-2与FSAAM-3实验结果对比, 搭建的网络模型深度越深误差累积可能会越多, 引入Highway网络效果越明显; FSAAM-4在表5中的3个数据集的Hits@1平均下降7.4%, 在表6中的3个数据集的Hits@1平均下降0.83%, 证明为缓解结构异质性从而利用注意力机制实现对更有益于实体对齐任务邻居信息考虑的有效性; FSAAM-5在表5中的3个数据集的Hits@1平均下降3.6%, 在表6中的3个数据集的Hits@1平均下降3.1%, 证明在实体对齐任务中增加对关系信息的考虑对于最终实体对齐效果的提升.

(2)通道划分消融实验

为证明采用通道划分的方式相较于直接将实体结构和属性信息拼接利用的作用, 提出相应变体. FSAAM-6表示只考虑结构通道信息进行实体对齐, FSAAM-7表示只考虑属性通道信息进行实体对齐, FSAAM-8表示不通过双通道特征融合模块, 直接将结构通道获取的结构实体表示和属性通道获取的属性实体表示进行向量拼接, 得到增强实体表示进行实体对齐. 上述变体在进行实验时, 均保持其他实验条件不改变, 其实验结果对比如表7所示.

通过表7可知FSAAM-8直接将属性和结构信息进行拼接得到的实体对齐效果相比与FSAAM-6只考虑结构通道信息在3个数据集上的Hits@1平均下降6.37%, 证明直接将不同类型的信息拼接进行实体对齐的效果并不理想, 相反不恰当的使用信息会带来噪声干扰导致实体对齐效果下降; 同时FSAAM-6在表7中的3个数据集相较于FSAAM的Hits@1平均下降4.97%, FSAAM-7在表7中的3个数据集相较于FSAAM的Hits@1平均下降39.7%, 证明单独考虑图谱中的属性或结构信息获得的实体对齐的结果并不佳, 需要充分考虑图谱中的属性、结构和关系等多种信息从而获取更佳的实体表示用于实体对齐任务.

5 结束语

针对现有实体对齐模型并未很好地处理结构和属性之间的交互关系, 同时忽略对关系信息及多阶邻居信的利用的问题, 本文提出一种融合结构与属性注意力机制的实体对齐方法. 该方法通过对属性和结构信息的划分实现了对图谱中属性、邻居和关系信息等多方面信息的利用. 本文模型的Hits@1, Hits@10以及MRR指标均优于上述基线模型, 证明了本文所提模型的有效性. 但由于现有实体对齐效果依赖于已对齐的实体种子集, 而在实际生产中已有的实体种子集数量较少, 使得现有实体对齐模型效果下降, 因此在下一步研究中将采用一些无监督或者半监督方式来实现实体对齐任务.