图像分割指的是在像素层面上理解一幅图像, 根据图像的纹理、亮度、色彩、形状等方面特征分割成均匀的且互不重叠的区域. 由于图像的复杂性, 设计一个高效且鲁棒的分割方法仍是一个相对困难的工作. 目前图像分割的相关技术主要有阈值分割^[1]、边缘检测^[2]、聚类^[3–6]、区域生长^[7]等. 本文是在基于聚类的方法下进行图像分割工作.

模糊C-均值(fuzzy C-means, FCM) 聚类算法最早由Dunn^[8]引入, 后来又经过Bezdek^[9]发展成熟. 尽管FCM在无噪声图像上有着良好的性能, 但由于在对图像进行处理时完全忽视了空间信息, 导致其对噪声非常敏感, 并且分割精度和运行时间都需要进一步优化.

为了解决FCM忽视空间信息的问题, 一些学者将局部空间信息与标准FCM算法的目标函数相结合进行改进. Ahmed等人^[10]提出了基于领域项的模糊C-均值(fuzzy C-means with spatial constraints, FCM_S)算法, 该算法允许中心像素受到领域像素的影响, 增强了中心像素的抗噪性. 然而处理图像时每次都需要计算中心到领域的距离, 这非常耗时. 为了解决FCM_S时间复杂度高的问题, Chen等人^[11]提出了两种FCM_S的变体FCM_S1和FCM_S2, 分别使用均值滤波和中值滤波代替了FCM_S中的邻域信息, 这两种滤波是在分割前计算的, 减少了算法的整体计算量. Szilagyi等人^[12]进一步加快图像分割的过程, 提出速度更加快的增强型模糊C-均值(enhanced fuzzy C-means, EnFCM)聚类算法, 将像素邻域的平均灰度与原始图像组成新的线性加权图像, 基于此图像的直方图信息进行图像的聚类, 一般来说图像的灰度级远比像素数量要少, 因此分割速度更快. Cai等人^[13]设计了类似的快速广义C-均值(fast generalized fuzzy C-means, FGFCM)算法, 该算法结合了相似性度量与灰度信息, 同样的使用直方图进行聚类. 因此, FGFCM与EnFCM在时间开销方面相似, 这些算法都需要参数α或λ在鲁棒性和图像细节之间进行平衡, 参数的选择需要大量的实验和不断试错才能完成. 为了解决这个问题, Krinidis等人^[14]提出了一种鲁棒的模糊局部信息C-均值(fuzzy local information C-means, FLICM)算法, 该算法在FCM目标函数上加入了一个局部模糊因子来代替上述参数自动平衡图像. 然而, FLICM的模糊因子虽然能平衡边界内存在噪声的像素区域, 但在对边界上存在噪声的像素点作用时会受到噪声影响而导致边界出现误分现象.

图像边界的不确定性同样严重影响着分割精度, 因此许多学者把关注点放在常用来处理边界问题的模糊集理论上. 近年来学者们使用直觉模糊集^[15]、二类模糊集^[16]、区间值模糊集^[17–19]和模糊多集^[20]等来处理这种不确定性. Pelekis等人^[21]提出了直觉模糊方式处理数据的方法, Xu等人^[22]在此基础上提出了直觉模糊C-均值(intuitionistic fuzzy C-means , IFCM)算法并应用于图像分割. Torra^[23]引入了犹豫模糊集(hesitant fuzzy set, HFS), 相比于直觉模糊集, HFS允许隶属度存在多个值来客观反映出人对于数据的“犹豫”性, 因此HFS比直觉模糊集包含更多的信息. Zeng等人^[24]基于HFS提出了犹豫模糊C-均值算法(hesitant fuzzy C-means algorithm, HFCM), 该算法改善了像素边界的不确定性以提高分割精度, 但是由于目标函数中并没有包含任何局部空间信息, 导致该算法对原图像的要求较高. 然而图像存在噪声是较难避免的, 因此HFCM在对含噪声的图像进行分割时效果并不理想.

针对HFCM对噪声敏感的问题, 本文结合局部信息提出了改进的犹豫模糊C-均值聚类算法(IHFCM). 首先, 基于HFS的相关理论提出了犹豫模糊元之间的相似性度量, 其次, 该算法引入一个新的模糊因子, 称为犹豫模糊因子, 它以犹豫模糊的方式将局部空间信息和灰度信息融入HFCM的标准函数中, 并且它不受任何参数影响. 新犹豫模糊因子的构建主要基于以下几个方面: 1) 新的模糊因子需要包含局部灰度信息和空间信息. 2) 在像素聚类的过程中, 自动维持图像与噪声之间的平衡. 3) 不需要对图片进行预处理. 最后, 使用合成图像、BSDS500数据集图像^[25] 、自然图像将本文所提出方法与FCM、FCM_S、FCM_S1、FCM_S2、FLICM、HFCM和IFCM进行比较, 以验证提出方法的有效性.

1 前言理论 1.1 犹豫模糊集

定义1^[23]. 给定$X = \{ {x_1}, {x_2}, \cdots, {x_n}\} $为一个参考集, 犹豫模糊集(HFS)为X上的一个映射函数, 当HFS作用于X时返回[0, 1]上的一个子集. 数学符号表示如下:

$ {{E = }}\left\{ {x, {h_E}(x)\mid x \in X} \right\} $

(1)

其中, ${h_E}(x)$是在[0, 1]范围内由有限个值组成的集合, 表示对象x隶属于E的多个隶属度取值. 称$h(x) = {h_E}(x)$为犹豫模糊元, 简写为HFE.

定义2^[26]. 对于一个给定的犹豫模糊元$h(x)$, 其得分函数定义如下:

$ s(h(x)) = \frac{1}{{l(h(x))}}\mathop \sum \nolimits_{\gamma \in h(x)} \gamma $

(2)

其中, $\gamma $代表$h(x)$中所有可能的取值, $l(h(x))$为$h(x)$中犹豫模糊元的个数.

1.2 HFS之间的距离和相似性度量

定义3^[27]. 设A和B为两个$X = \{ {x_1}, {x_2}, \cdots, {x_n}\} $上的HFSs, d(A, B)为A, B之间的距离度量, 满足以下3个性质.

1) 0 ≤ d(A, B) ≤ 1;

2) d(A, B) = 0 当且仅当 A = B;

3) d(A, B) = d(B, A).

定义4^[27]. 设A和B为两个$X = \{ {x_1}, {x_2}, \cdots, {x_n}\} $上的HFSs, d(A, B)为A, B之间的距离度量. A, B之间的欧氏距离度量定义如下.

欧氏距离:

$ d(A, B)=\frac{1}{n} \sum_{i=1}^n\left[\frac{1}{l_{x_i}} \sum_{j=1}^{l_{x_i}}\left|h_A^{\sigma(j)}\left(x_i\right)-h_B^{\sigma(j)}\left(x_i\right)\right|^2\right]^{1 / 2} $

(3)

其中, $h_A^{\sigma (j)}({x_i})$和$h_{{B}}^{\sigma (j)}({x_i})$分别代表${h_A}({x_i})$和${h_{{B}}}({x_i})$中第j个最大值. ${l_{{x_i}}}$指${h_A}({x_i})$和${h_{{B}}}({x_i})$两者中最大的长度.

定义5^[27]. 设A和B为两个$X = \{ {x_1}, {x_2}, \cdots, {x_n}\} $上的HFSs, S(A, B)为A, B之间的相似性度量, 其满足以下3个性质.

(1) 0 ≤ S(A, B) ≤ 1;

(2) S(A, B) = 0 当且仅当 A = B;

(3) S(A, B) = S(B, A).

文献[27]通过研究定义3与定义5的性质, 提出了HFSs之间的相似性度量表示为:

$ S(A, B) = 1 - d(A, B) $

(4)

1.3 图像模糊化和解模糊

例1. 设A为一个有N=P×Q个像素的图像, P为图像的高度, Q为图像的宽度, ${{{x}}_i}$为像素的灰度值范围在0–255. 图像模糊化的定义为:

$ {\mu _A}({x_i}) = \frac{{{x_i} - {{({x_i})}_{\min}}}}{{{{({x_i})}_{\max}} - {{({x_i})}_{\min}}}},\; i = 1, 2, \cdots , N $

(5)

解模糊是模糊化的逆过程. 当使用HFEs去描述一幅图像的时候, 需要使用HFE的得分函数将它转化成像素的隶属度. 对于给定的一个犹豫模糊元${{h}}({x_i})$, 根据定义2中的式(2)计算得分函数${{s}}(h({x_i}))$. 最后将隶属度转化成像素完成解模糊的过程, 公式如下:

$ \begin{gathered} {x_i} = (s(h({x_i})) \times ({({x_i})_{\max}} - {({x_i})_{\min}})) + {({x_i})_{\min}},\; i = 1, 2, \cdots , N \\ \end{gathered} $

(6)

当图像开始分割时需要模糊化图像以便后续构造犹豫模糊元, 分割完成时需要解模糊来还原出清晰的图像.

2 相关工作 2.1 鲁棒模糊局部信息C-均值聚类算法(FLICM)

文献[14]提出了模糊局部信息C-均值算法(FLICM), FLICM的目标函数中模糊因子${{{G}}_{{{ji}}}}$的作用是维持图像细节和噪声之间的平衡, 它并不需要任何参数. 假设一幅图像有N个像素点, 每个像素点的灰度值为${x_i}$ (i=1, 2,…, N), 目标函数如下所示:

$ \left\{\begin{split} &{J}_{m}=\displaystyle\sum _{i=1}^{N}\displaystyle\sum _{j=1}^{c}\left[{u}_{ji}^{m}\left|\right|{x}_{i}-{v}_{j}|{|}^{2}+{G}_{ji}\right]\\ & {\mathrm{s.}}{\mathrm{t.}}\sum _{j=1}^{c}{u}_{ji}=1,\;\;1\leqslant i\leqslant N\end{split} \right.$

(7)

其中, m为模糊指数, 通常m=2, c为聚类个数, $ {u}_{ki} $表示第j个簇中$ {{x}}_{{i}} $的隶属度, ${{{v}}_{{j}}}$为第j类的聚类中心, ${{{G}}_{{{ji}}}}$为模糊因子, 被定义为:

$ \left\{\begin{split} &{G}_{ji}=\sum _{\begin{array}{c}k\in {N}_{{i}}\\ \end{array}}\frac{1}{{d}_{ik}+1}{(1-{u}_{jk})}^{m}\left|\right|{x}_{k}-{v}_{j}|{|}^{2}\\ & 1\leqslant j\leqslant c, 1\leqslant i\leqslant N \end{split}\right. $

(8)

其中, 像素i为局部窗口的中心像素, 像素k为中心像素i的邻接像素, ${{{N}}_{{i}}}$是第i个中心像素位于局部窗口内邻近像素的数目, ${{{d}}_{i{{k}}}}$表示像素i和k之间的空间欧氏距离, ${{{u}}_{{{jk}}}}$表示像素${{{x}}_{{k}}}$在簇j中的隶属度. 通过拉格朗日乘数法对目标函数${{{J}}_{{m}}}$进行优化, 得到隶属度矩阵和类心迭代公式如下:

$ u_{j i}=\dfrac{1}{\displaystyle\sum_{k=1}^c\left(\frac{\left\|x_i-v_j\right\|^2+G_{j i}}{\left\|x_i-v_k\right\|^2+G_{j i}}\right)^{\frac{1}{m-1}}} $

(9)

$ v_j=\frac{\displaystyle\sum_{i=1}^N u_{j i}^m x_i}{\displaystyle\sum_{i=1}^N u_{j i}^m} $

(10)

FLICM的具体算法流程如算法1所示.

算法1. FLICM

1) 确定聚类数目c, 迭代的终止条件$\scriptstyle \varepsilon $和模糊常数m.

2) 随机初始化隶属度矩阵U.

3) 设置循环计数b=0.

4) 用式(10)计算类中心$\scriptstyle {v_{{j}}}$.

5) 用式(9)更新隶属度矩阵$\scriptstyle {{{U}}^{{{b + 1}}}}$.

6) 若$\scriptstyle {U^{(b)}} - {U^{(b + 1)}} < \varepsilon $则停止迭代, 否则b=b+1, 转回步骤4).

2.2 犹豫模糊C-均值聚类算法(HFCM)

文献[24]将犹豫模糊集与FCM算法相融合提出了犹豫模糊C-均值聚类算法(HFCM), 该算法利用犹豫模糊集处理不同灰度块之间的不确定性, 提出了一种新的犹豫模糊元之间的距离度量并应用于HFCM, 目标函数如下所示:

$ \left\{\begin{split} & J_m=\sum_{i=1}^N \sum_{j=1}^c u_{j i}^m d^2\left(x_i^{{\mathrm{HFS}}}, v_j^{{\mathrm{HFS}}}\right) \\ & \text { s.t.} \sum_{j=1}^c u_{j i}=1, \quad 1 \leqslant i \leqslant N \end{split}\right. $

(11)

其中, ${X^{{\mathrm{HFS}}}} = {\{ x_1^{{\mathrm{HFS}}}, x_2^{{\mathrm{HFS}}}, \cdots , x_N^{{\mathrm{HFS}}}\} }$表示N个犹豫模糊元, m为模糊指数, c为聚类数目, ${u_{ji}}$表示隶属度, $U = {({u_{ji}})_{c \times N}}$为隶属度矩阵, ${d^2}\left( {x_i^{{\mathrm{HFS}}}, \nu _j^{{\mathrm{HFS}}}} \right)$为像素${{{x}}_i}$与类心之间的欧氏距离, 隶属度矩阵和类心迭代公式如下所示:

$ u_{j i}=\frac{1}{\displaystyle\sum_{n=1}^c\left(\dfrac{d^2\left(x_i^{{\mathrm{H F S}}}, v_j^{{\mathrm{H F S}}}\right)}{d^2\left(x_i^{{\mathrm{H F S}}}, v_n^{{\mathrm{H F S}}}\right)}\right)^{\frac{1}{m-1}}}, \quad 1 \leqslant j \leqslant c, 1 \leqslant i \leqslant N $

(12)

$ h\left(v_i\right)^l=\frac{\displaystyle\sum_{i=1}^N u_{j i} h\left(x_i\right)^l}{\displaystyle\sum_{i=1}^N u_{j i}}, \quad 1 \leqslant i \leqslant c, 1 \leqslant l \leqslant l_{x_i} $

(13)

HFCM的具体算法流程如算法2所示.

算法2. HFCM

1) 确定聚类数目c, 迭代的终止条件$\scriptstyle \varepsilon $和模糊常数m.

2) 对图像进行模糊化之后生成每个像素对应的HFE.

3) 初始化隶属度矩阵, 设置循环计数b=0.

4) 用式(12)和式(13)分别更新隶属度矩阵$\scriptstyle {U}^{b+1} $和类心$\scriptstyle {v^{{\mathrm{HFS}}}}.$

5) 若$\scriptstyle {U^{(b)}} - {U^{(b + 1)}} < \varepsilon $则停止迭代, 否则b=b+1, 转回步骤4).

3 所提出的方法

HFCM算法从式(11)中可以看出目标函数上不包含任何空间信息, 犹豫模糊元之间没有任何联系. 通常情况下, 在图像采集过程中会出现噪声, 噪声会改变像素的灰度值, 因此含噪声的像素会被错误分类. 从式(12)中可以看出HFCM的隶属度是犹豫模糊元的灰度值与类中心距离的函数, 当距离越近, 此时的隶属度就越大, 距离越远, 隶属度随之就小. 因此, 当噪声存在时, 隶属度就会变得非常敏感. 对于其他分割算法, 例如FCM_S1、FCM_S2、EnFCM、FGFCM等, 它们在一定程度上处理了噪声, 得到了颇为有效的分割结果. 然而它们都需要参数, 分割效果的好坏取决于参数的调优情况, FLICM算法不需要参数调优, 也提高了分割性能, 但无法处理不确定性.

为了克服上述研究工作中的问题, 本文将HFCM算法与局部信息结合, 提出基于改进犹豫模糊C-均值(IHFCM)的图像分割方法, 提出利用包含犹豫模糊元之间相似性的犹豫模糊因子解决HFCM算法分割过程中的噪声敏感问题. 在第3.1节中给出了构造犹豫模糊元的方法, 并在后续章节中对犹豫模糊因子进行阐述.

3.1 构造犹豫模糊元

在大多数情况下, 不同HFEs之间的元素数量并不相等, 也就是说对于两个犹豫模糊集A和B, $l({h_A}({x_i})) \ne l({h_B}({x_i}))$. 因此, 当对两个HFEs进行比较的时候, 文献[27]制定了如下的比较规则: 当需要对HFEs进行比较时, 需要扩展长度较短的HFEs直到它们的长度相同. 事实上, 决策者可以根据自身的风险偏好在较短的HFEs中添加任何相同的值直到和较长的HFE长度相等.

例2. 设存在一个包含9个像素的图像A:

$ A = \left( {\begin{array}{*{20}{c}} {0.62}&{0.69}&{0.57} \\ {0.59}&{0.66}&{0.64} \\ {0.55}&{0.63}&{0.64} \end{array}} \right) $

位于A(0, 0)位置上的像素的隶属度为0.62, 本文将坐标像素与周围的相邻像素共同构成一个HFE. 因此A(0, 0)所构成的HFE为{0.69, 0.66, 0.62, 0.59}, 而位于A(1, 1)上的隶属度为0.66, 它所构成的HFE为{0.69, 0.66, 0.64, 0.64, 0.63, 0.63, 0.59, 0.57, 0.55}, 可以发现他们的HFE长度并不相同, 为了方便, 本文选择向较短的HFE中添加最小值来达到相同的长度. 经过上述过程, 每个像素都有了自己的HFE, 并且它们的长度相同.

通过添加相同的值去补足较短的HFEs可能对后续的计算产生影响, 因为每个人对风险偏好(通过添加最大值的乐观决策和添加最小值的悲观决策)会有所不同, 对结果就有不同的期待, 在一些文献中^[28,29]也谈及到了这一情况. 在本文中, 本文进行处理时都统一使用悲观决策.

3.2 HFEs之间的相似性度量

为了进一步研究IHFCM算法, 同时由于基于聚类的图像分割是在像素级别上进行的, 文献[24]中提出的HFEs中的欧氏犹豫模糊距离将模糊集之间的距离引申到犹豫模糊元之间, 同时也满足定义3, 表示如下:

$ d\left(h_1, h_2\right)=\frac{1}{n} \sum_{i=1}^n\left[\left.\frac{1}{l_{x_i}} \sum_{j=1}^{l_{x_i}} \right\rvert\, h_1^j\left(x_i\right)-h_2^j\left(x_i\right)\right]^{\frac{1}{2}} $

(14)

其中, ${{{d}}^2}$表示两个犹豫模糊元${h_1}, {h_2}$之间的距离, ${l_{{x_i}}}$为HFE的长度(相当于进行决策的专家人数), $h_A^j({x_i})$为HFE的每一个维度的值.

本文基于HFSs的相似性度量定义(定义5)提出了HFEs之间的相似性度量, 设存在两个犹豫模糊元$ {h}_{1}和{h}_{2} $, $ {h}_{1}和{h}_{2} $间的相似性度量定义为:

$ S\left( {{h_1}, {h_2}} \right) = 1 - d({h_1}, {h_2}) $

(15)

式(4)满足定义5所具有的性质, 由于犹豫模糊集由多个犹豫模糊元构成, 因此对于犹豫模糊元之间来说提出的式(15)所满足的性质如下所示:

1) $0 \leqslant S({h_1}, {h_2}) \leqslant 1$;

2) $S\left( {{h_1}, {h_2}} \right) = 0$当且仅当${h_1} = {h_2}$;

3) $S({h_1}, {h_2})$=$S({h_2}, {h_1})$.

3.3 犹豫模糊因子

为了融合进局部空间信息, IHFCM算法引入了犹豫模糊因子, 并具有以下特点.

1)不需要设置任何参数.

2)对噪声不敏感.

3)分割过程中考虑了相似性度量.

4)保留更多图像细节.

在数学上, 犹豫模糊因子${{{P}}_{{{ji}}}}$定义为:

$ \left\{\begin{split} & P_{{ji}}=\frac{1}{N_i} \sum_{k \in N_i} \frac{1}{d_{{ik}}+1}\left[\left(1-u_{{jk}}\right)^m+\left({S}_{{jk}}^{\mathrm{HFEs}}\right)^m\right] \\ & 1 \leqslant j \leqslant c, 1 \leqslant i \leqslant N \end{split} \right.$

(16)

其中, k像素是处于中心位置i像素周围的邻接像素, ${{{N}}_{{i}}}$表示中心像素${{{x}}_i}$相邻的像素数目, ${{{u}}_{{{jk}}}}$表示第k个像素与第j个聚类中心的隶属度, m为模糊化常数, ${{{S}}_{{{jk}}}}$为第k个像素形成的HFE与第j个聚类中心的HFE之间的相似度度量并在式(15)中给出定义, ${{{d}}_{ik}}$是分别对应第i个和第k个像素的空间坐标(${{{p}}_i}$, ${{{q}}_i}$)和(${{{p}}_{{k}}}$, ${{{q}}_{{k}}}$)之间的空间距离.

犹豫模糊因子${{{P}}_{{{ji}}}}$通过图像中每个像素包括其周围像素组成一个固定的窗口所确定的, 它通过犹豫模糊元之间的相似性度量和隶属度的变化来体现局部灰度信息的改变. 实际上, ${{{P}}_{{{ji}}}}$是为了找出固定窗口中的最大相似性度量和隶属度. 通过结合犹豫模糊集理论, 犹豫模糊因子能够包含更多隶属度信息, 它根据相似性度量与距离实现灵活变化. 此外, 从式(16)可以看出它不需要任何参数就可以实现图像细节与噪声之间的平衡.

如图1所示, 以背景灰度为100的3×3像素灰度值窗口为例来说明${{{P}}_{{{ji}}}}$通过平衡隶属度实现对噪声的抵抗过程. 可以清楚地看到, 左上角和中心像素均被破坏(加粗部分为噪声像素). 由于${{{P}}_{{{ji}}}}$不仅包含距离信息, 从式(16)可以看出也包含了中心像素与非中心像素HFEs之间的相似性, 这使得在存在噪声的情况下, ${{{P}}_{{{ji}}}}$通过计算区域内的相似性度量使用非噪声的邻接像素代替中心像素. 通过图1(b)–(d)可以看出无论噪声是在中心像素产生还是非中心像素产生, 在数次迭代之后, 隶属度在${{{P}}_{{{ji}}}}$的影响下快速收敛到相近的值. ${{{P}}_{{{ji}}}}$通过每次迭代自适应的变化不断平衡噪声像素的隶属度值, 使非噪声像素和噪声像素在经历若干次迭代之后使隶属度快速收敛到一个相近的值.

3.4 改进的犹豫模糊C-均值的图像分割方法(IHFCM)

在本节中, 本文引入了新的犹豫模糊因子, 提出了一种新的图像分割方法: 改进的犹豫模糊C-均值(IHFCM)的图像分割方法. 通过犹豫模糊因子${{{P}}_{{{ji}}}}$将局部灰度以及空间信息结合起来, 空间信息中灵活多变的距离可以获得更多分割信息. 需要指出的是引入的${{{P}}_{{{ji}}}}$和FLICM算法中的模糊因子相比并不是简单的扩展而是包含更多信息的一种新模糊因子, 旨在处理噪声问题. IHFCM的目标函数优化问题为:

$ \left\{\begin{array}{l} J_m=\displaystyle\sum_{{j}=1}^{{c}} \displaystyle\sum_{i=1}^N\left(u_{j i}\right)^m d^2\left({x}_i^{\mathrm{HFS} }, {v}_{{j}}^{\mathrm{HFS} }\right) P_{j i} \\ \text {s.t.} \displaystyle\sum_{j=1}^{{c}} u_{j i}=1, \quad 1 \leqslant i \leqslant N \end{array}\right. $

(17)

其中, ${X^{{\mathrm{HFS}}}} = {\{ x_1^{{\mathrm{HFS}}}, x_2^{{\mathrm{HFS}}}, \cdots , x_N^{{\mathrm{HFS}}}\} }$为N个像素对应的犹豫模糊元HFEs, m为模糊常数通常取2, c为聚类个数, ${u_{ji}}$为隶属度, $U = {({u_{ji}})_{c \times N}}$为隶属度矩阵, ${{{P}}_{{{ji}}}}$为犹豫模糊因子在式(16)中定义, ${V^{{\mathrm{HFS}}}} = \{ {h_1}({x_i}), {h_2}({x_i}), \cdots \, , {h_k}({x_i}) \}\:$, ${{{d}}^2}\left( {x_i^{{\mathrm{HFS}}}, v _j^{{\mathrm{HFS}}}} \right)$表示像素${{{x}}_i}$与类心${{{v}}_{{j}}}$分别对应的犹豫模糊元HFEs之间的欧氏距离, 其定义在式(14). 用拉格朗日乘数法最小化目标函数表示如下:

$ J_m=\sum_{i=1}^N \sum_{j=1}^c u_{j i}^m d^2\left(x_i^{{\mathrm{HFS}}}, v_j^{{\mathrm{HFS}}}\right) {P}_{j i}-\sum_{i=1}^N k_i\left(\sum_{j=1}^c u_{j i}-1\right) $

(18)

其中, ${{{k}}_i}$为拉格朗日常数, 计算${{{J}}_{{m}}}$对${u_{ji}}$和${{{k}}_i}$的偏导数, 令偏导数为0:

$ \frac{{\partial J_m^{}}}{{\partial {u_{ji}}}} = 0,\; \forall 1 \leqslant i \leqslant N, 1 \leqslant j \leqslant c $

并且:

$ \frac{{\partial J_m^{}}}{{\partial {k_i}}} = 0,\; \forall i $

由此可以得到隶属的矩阵的迭代公式:

$ \left\{\begin{split} & u_{j i}=\frac{1}{\displaystyle\sum_{r=1}^c\left(\frac{d^2\left(x_i^{{\mathrm{H F S}}}, v_j^{{\mathrm{H F S}}}\right) P_{j i}}{d^2\left(x_i^{{\mathrm{H F S}}}, v_r^{{\mathrm{H F S}}}\right) P_{j i}}\right)^{\frac{1}{m-1}}} \\ & 1 \leqslant j \leqslant c, 1 \leqslant i \leqslant N \end{split}\right. $

(19)

和类心迭代公式:

$ h\left(v_i\right)^l=\frac{\displaystyle\sum_{i=1}^N u_{j i} h_1\left(x_i\right)}{\displaystyle\sum_{i=1}^N u_{j i}},\; 1 \leqslant i \leqslant c, 1 \leqslant l \leqslant l_{x_i} $

(20)

到此, 得到了类心与隶属度的迭代公式, IHFCM的算法流程如算法3所示.

算法3. IHFCM

1) 确定聚类数目c, 迭代的终止条件$\scriptstyle \varepsilon $和模糊常数m.

2) 使用式(5)模糊化图像.

3) 对于每个像素以它为中心创建N×N的窗口生成犹豫模糊元HFEs.

4) 初始化隶属度矩阵$\scriptstyle {{{U}}^0}$, 设置循环计数器b=0.

5) 使用式(20)更新类心$\scriptstyle \nu _j^{{\mathrm{HFS}}}$.

6) 使用式(15)计算HFEs之间的相似性度量$\scriptstyle {{{S}}_{{{kj}}}}$.

7) 使用式(16)计算犹豫模糊因子$\scriptstyle {{{P}}_{{{ji}}}}$.

8) 使用式(19)更新隶属度矩阵$\scriptstyle {{{U}}^{{{b}} + 1}}$.

9) 若$\scriptstyle {U^{(b)}} - {U^{(b + 1)}} < \varepsilon $则停止迭代, 否则b=b+1, 转回步骤5).

10) 使用式(6)解模糊并输出图像.

4 实验

在本节中, 本文分别在合成图像、BSDS500数据集中的图像和自然图像上来测试所提算法的实验结果. 此外, 本文将IHFCM算法与其他7种模糊聚类算法比较FCM、FCM_S、FCM_S1、FCM_S2、FLICM、HFCM和IFCM来验证所提出方法的有效性.

将上述8种算法使用目前最流行的图像分割评价指标最优分割精度(SA)来评价分割性能. SA为被算法正确分类的像素之和除以总像素数目^[30]:

$ {\textit{SA}}=\sum_{i=1}^c \frac{A_i \cap C_i}{\displaystyle\sum_{j=1}^c C_j} $

(21)

其中, c为聚类个数, ${{{A}}_{{i}}}$为算法找到的像素数目集合, ${{{C}}_{{j}}}$为参考簇中第j类像素的集合.

在实验中统一采用的是3×3的窗口. 实验参数设值如下: 终止阈值$ \mathrm{\varepsilon }=0.00001 $, 模糊指数m=2, 窗口NR=9, 迭代次数上限为10000, FCM_S、FCM_S1和 FCM_S2中的参数$ \mathrm{\alpha } $=0.3在区间[0.2, 8]中寻优得到.

4.1 合成图像

首先在人工合成的图像上使用上述算法进行测试. 图像大小为128×128像素, 包含两个类, 两个类的灰度值分别为20和120. 在这个原始图像上分别添加高斯噪声和椒盐噪声, 其中破坏图像的噪声强度为10%–20%, 步长为5%. 一共生成了300张合成图片.

图2展示了128×128尺寸的人工合成图像上被20%强度高斯噪声破坏后, 使用上述算法处理的聚类结果. 其中, 图2(a)子图为原始图像, 图2(b)子图为加入20%强度的高斯噪声图片, 图2(c)–(j)为8种算法的聚类结果. 从视觉上看, FCM (图2(c))算法对噪声相当敏感, FCM_S (图2(d)) 、FCM_S1 (图2(e)) 和FCM_S2 (图2(f))去除了部分噪声, 但结果仍然不令人满意, 缺乏对噪声足够的鲁棒性. FLICM (图2(g))由于有模糊因子的存在去除了大部分噪声, 但仍然也受到噪声的影响. HFCM (图2(h))和IFCM (图2(i))由于目标函数并没有局部信息所以不适合处理存在噪声的情况. 另一方面, IHFCM (图2(j))几乎去除了所有高斯噪声, 结果表明犹豫模糊因子比起FLICM中的模糊因子起到了更令人满意的作用, 表1分割精度(SA)表中也验证了这点.

表1给出了8种算法在被不同程度的高斯和椒盐噪声破坏的图像中分割精度的数值结果. 从结果可以清晰地看出IHFCM的结果无论在何种类型与强度的噪声破坏下, 均高于另外7种算法. 尤其对于高斯噪声, IHFCM具有优秀的鲁棒性, 在20%强度的噪声下数值结果高达99.976%. 结果表明, IHFCM比另外7种算法具有更好的去噪性能.

4.2 BSDS数据集图像

本节将8种算法应用在伯克利分割数据集(BSDS500)的真实图像^[25]上来测试算法的性能, 此数据集包含200张训练图像, 200张测试图像和100张具有ground truth的验证图像. 原始图像为481×321像素, 该图像由老虎和背景组成, 原始图像如图3(a)所示, 它的ground truth如图3(b)所示. 可以明显看到此图像细节非常丰富, 背景的杂乱程度较高, 因此对聚类性能要求也较高. 本文将所提出的方法和上述7种算法进行比较, 分割的结果分别如图3(c)–图3(j). 由图3可以看到, FCM、FCM_S、FCM_S1、FCM_S2 (图3(c)–(f))、HFCM (图3(h))和IFCM (图3(i))的聚类效果明显不如FLICM (图3(g))和本文提出的算法(图3(j)). 图3(g)与图3(j)相比, 图3(g)中老虎的背部和前肢更加清晰, 图3(j)中有更多相似像素聚在一起, 背景更加整洁. 由于目视判别存在一定的主观性, 本文给出了8种算法的定量评价结果, 如表2所示. 从表2可以看出, 本文算法的分割精度是最高的.

4.3 自然图像

本节将上述算法应用到自然图像上进行测试, 图像为摄影师所拍的真实图像, 像素为179×240. 图像用不同程度的高斯和椒盐噪声进行破坏(10%–20%, 步长为5%), 测试算法在真实图像中的对噪声的鲁棒性. 此外, 由于自然图像不同于处理过或者合成的图像, 更加具有真实性, 本文引入了另外一个指标: 量化分数(R)来比较算法之间的性能. 定义如下^[31]:

$ {R}=\sum_{i=1}^c \frac{A_i \cap C_i}{A_i \cup C_i} $

(22)

其中, c为聚类个数, ${{{A}}_{{i}}}$表示由算法找到的第i类像素的集合, ${{{C}}_{{i}}}$表示真值图像中第i类像素的集合. 指标R实际上是一个模糊相似度度量, 表示${{{A}}_{{i}}}$和${{{C}}_{{i}}}$之间的相等程度, R越大表示聚类性能越好.

图4表示8种算法在同一张自然图像(花朵)的分割结果, 其中, 图4(a)子图为原始图像, 图4(b)子图为加入15%椒盐噪声破坏后的图像. 图4(c)–(i)分别为上述7种比较算法的分割结果, 图4(j)为本文所提出的方法的分割结果.

从图4中可以清晰地看到, IHFCM聚类结果轮廓更加清晰, 细节更加丰富, 这是因为犹豫模糊因子保持了对噪声和异常值的不敏感. 然而, FCM、FCM_S、FCM_S1和FCM_S2对于自然图像的噪声抵抗性非常不理想, HFCM和IFCM的抗噪和分割精度也不够理想, 这是因为它们并没有融合局部信息, FLICM虽然能抵抗大部分噪声, 但是会出现边界模糊的现象. 此外, 表3和表4分别为8种算法在自然图像上的分割精度(SA)和量化分数(R), 由表3和表4可知, IHFCM能够应对大部分情况下的噪声, 实验表明IHFCM的综合表现明显优于其他7种算法.

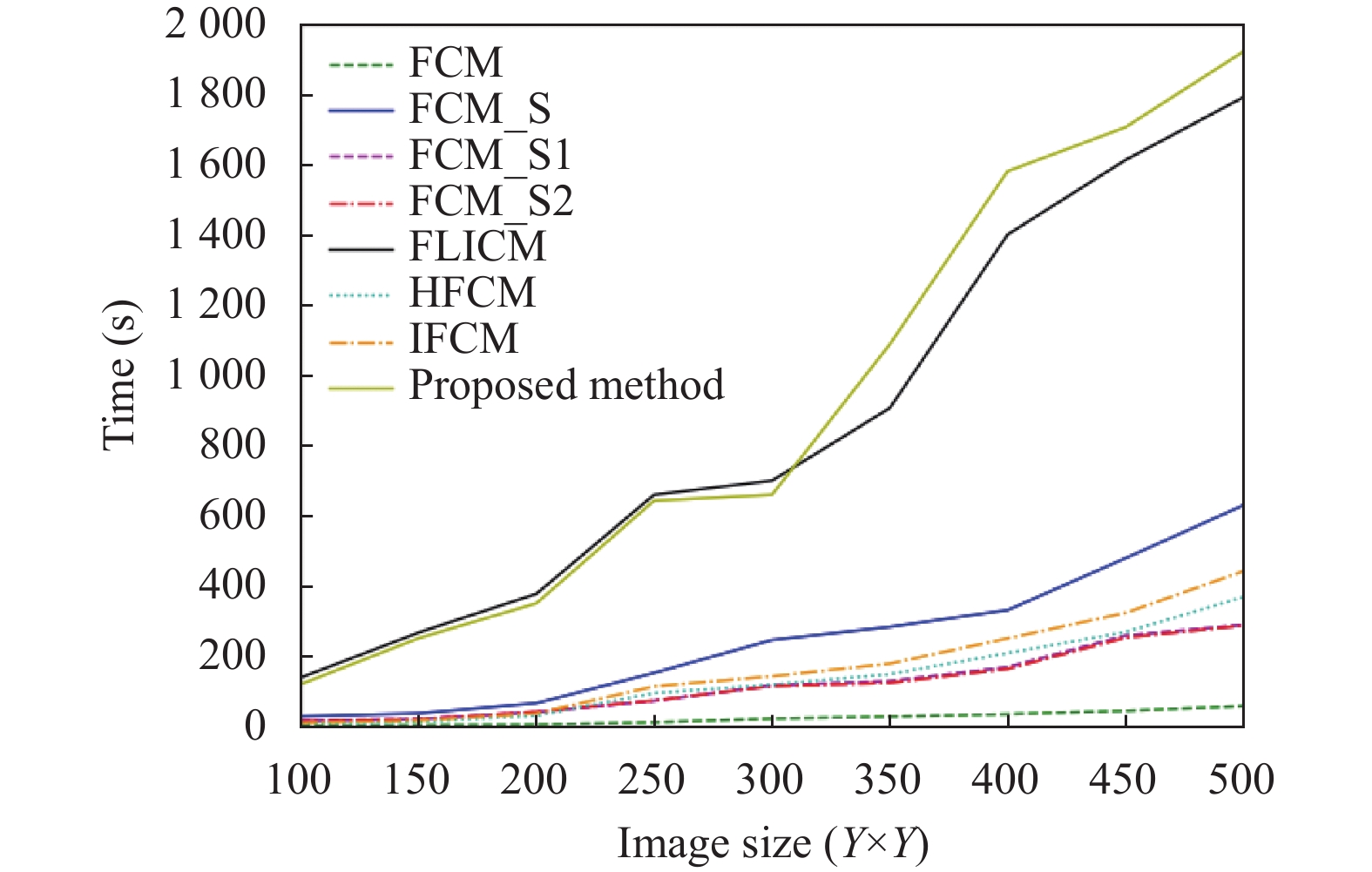
4.4 时间复杂度分析

图5给出了8种算法在不同尺寸图像上的平均运行时间, 其中每个尺寸图像运行10次取平均值.

从图5中可以看到, 运行最快的是FCM, 因为它不包含任何空间信息. 除FLICM和本文所提出的算法外, 其余算法的运行时间都较快. 本文所提出的算法运行较FLICM在大尺寸图像上时间成本更高一些, 相比于FLICM的模糊因子G, IHFCM需要额外计算新的模糊因子P中相似性度量, 然而通过与这7种算法在不同类型图像上的实验结果比较, IHFCM展现了明显优于它们的分割效果, 弥补了时间上较慢的缺点. 本文所有实验均在Python 3.9上进行, 相关条件为Windows 10, 2.50 GHz, 8 GB RAM.

5 结论

本文提出了一种新的图像分割方法称为改进的犹豫模糊C均值(IHFCM)算法. IHFCM算法克服了现有FCM算法及其变体由于噪声或边界不确定性引起分割精度不良的缺点, 这是由于其引入了结合局部空间信息与灰度信息的新模糊因子实现的, 此外, 模糊因子也不需要任何参数调优. 在实验中, 本文使用分割精度和聚类得分两种评价指标, 在对合成图像、BSDS500图像以及自然图像数据集上对IHFCM方法进行了测试, 其中合成图像与自然图像都被不同程度的高斯和椒盐噪声污染, 实验结果表明该算法的聚类性能在一定程度上均优于其他7种算法, 且对于噪声有良好的鲁棒性.