石油集输是指把分布在油田的各潜油电泵井所开采的石油及其混合物集中起来, 经过初步分离加工, 通过长距离输油管线输送到陆地原油库的全部过程. 管网产量即各电泵井汇总后输出总产量, 油田对管网产量进行计算主要分为两种: 正算法和倒算法[1]. 正算法是从生产的角度出发, 计算管网中各潜油电泵井的产量后再计算石油产量; 倒算法是从销售与使用的角度, 根据周期销售量、使用量等, 经过盘库后进行推算. 正算法中, 对于集输管网中各油井汇入管道的产量计算主要通过机理模型或模拟仿真软件实现. 机理模型指结合油井液体密度流速公式、井口压力流速公式、管道压降等物理知识形成的计算方法. 油田的滚动开发过程中, 随着潜油电泵井和输油管道投入运营的数量不断增加, 集输管网结构复杂度急剧升高, 产量模拟计算需要考虑更多的约束条件. 受电泵井启停操作、井口非线性回压、管道温降、可变摩阻等因素影响, 基于传统机理模型的正向产量计算方法与实际数据偏差大, 倒算法人工成本高、统计周期长、盘库存在计量与统计误差, 亟需一种准确、快速的原油集输管网产量模拟计算方法.
国内外针对石油产量从各方向进行研究, 在基于专家系统分析法中, Almedallah等人[2]结合使用线性逼近约束优化(COBYLA)和混合整数线性规划 (MILP)来集成实际钻井路径、平台位置和井分配的优化, 根据上述因素分析产量. 李传亮等人[3]分析油井压裂情况, 将地层中的复杂流分为径向流和线性流, 根据水电相似原理, 求得产量计算公式. 张鑫等人[4]通过结合抽油井泵效公式、压强公式和能耗, 得到了压力、耗电量与产量的关系, 量化分析了集输系统中回压对产能的影响; 基于统计学方法中, AlRassas等人[5]使用Aquila优化器改进神经模糊推理系统(ANFIS), 开发AO-ANFIS模型, 计算分析了也门两个油田生产过程中的产量变动情况. Zhao等人[6]开发了井间数值模拟模型(INSIM)和带前沿跟踪的INSIM (INSIM-FT), 用于注水储层的历史匹配、预测、特征描述和优化, 通过精确的井间连通性计算、动态流路跟踪和注水预测来分析变动后产量; 基于深度学习的方法中, Fan等人[7]融合自回归综合移动平均模型ARIMA和LSTM模型, 提取时间和空间相关特征, 提高了流体计算的准确性; Abdullayeva等人 [8]提出一种卷积神经网络(CNN)和长短期记忆网络(LSTM)的混合网络模型, 通过卷积操作解决时间窗口之间的连续性问题, 初步实现产量计算. Chahar等人[9]提出一种结合人工神经网络(ANN)、随机森林回归器(RF)和梯度提升回归器(GB)的方法, 利用可用的生产参数来预测每日石油产量. 张战敏等人[10]开发了一种由双层GRU网络和3层全连接网络组成的深度学习模型, 提高了电参量油模型的准确性和泛化性, 提升了产量预测的精度. Gong等人[11]提出一种机理知识与数据双驱动建模方法, 将各井口的实时生产数据输入到模型中, 通过 Beggs-Bril 和 Leapienzon 方程计算管道各处的压力和温度, 然后将测量值和计算值输入到储运机制约束的基于Transformer模型中, 对方程的计算结果进行误差修正, 以达到准确的目的, 实现管网各处运行参数的综合预测.
但上述方法存在人工参与程度高、计算繁琐、误差较大、普适性差的问题, 对管网拓扑图结构信息和时序信息关注度不足, 导致计算偏差大、周期长, 结果不准确. 因此本文主要工作如下.
(1)提出一种三维矩阵化电泵井数据表示学习方法, 便于挖掘数据之间潜在的关系, 方便模型对时空数据进行分析处理, 提高模型的性能和效率.
(2)从时空角度出发, 设计一种基于时空图卷积神经网络(AST-GCN)的产量计算模型, 提取电泵井生产数据中的时间和空间特征, 根据管网运行状况, 准确模拟计算集输管网产量.
1 集输管网的表示学习考虑到集输管网内各井的生产参数会直接影响其余相邻井的产量, 充分利用该井和相邻井的生产参数有利于提高产量模拟计算的准确度和可靠性, 因此我们提出一种集输管网表示学习方法, 为时空图卷积神经网络模型的训练及优化打下基础.
1.1 电泵井时空特征矩阵构建结合电泵井空间位置、生产参数和时间序列, 构造电泵井的三维时序特征矩阵. 如图1所示, 将三维矩阵图1(a)沿时间轴切片, 得到“空间-特征”二维平面数据图1(b), 其数据表示如图1(d)所示,
| WFT=(WF,TF)={e(w,f,t),w,f,t∈N} | (1) |
其中, WFT表示“电泵井-特征-时间”的3D矩阵; WF和TF分别表示“空间-特征”“时间-特征”的二维平面数据集;
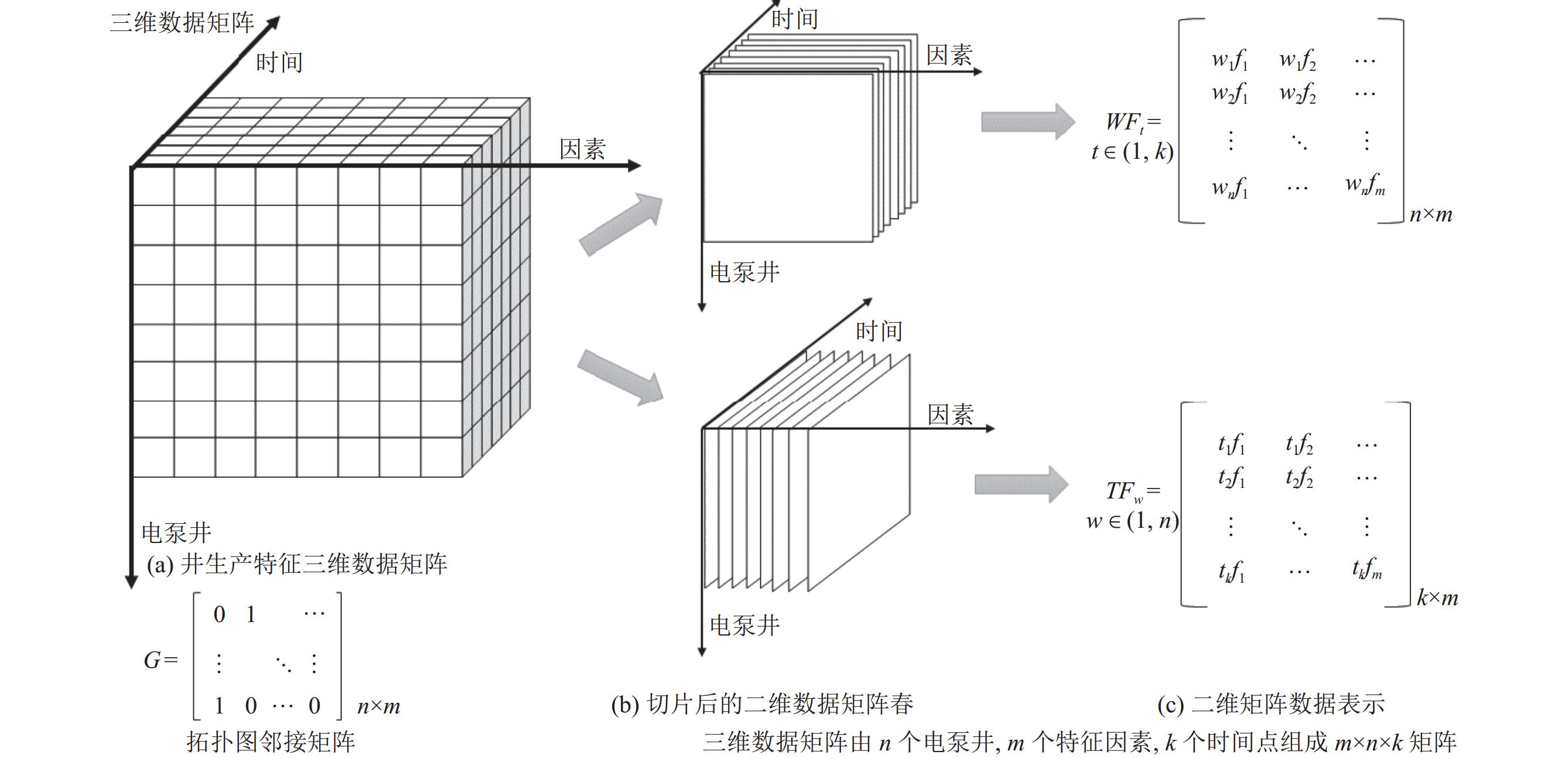
|
图 1 集输管网学习表示与切片操作流程图 |
1.2 管网时空图构建
集输管网由电泵井和输油管道组成, 其拓扑结构错综复杂, 可以抽象定义为非欧图数据. 我们定义一个连续时刻序列, 其中在t时刻及其相邻时刻中连续观察到多个时刻的图结构数据没有发生任何变化, 将此时间序列下的集输管网进行图论化, 和特征矩阵一起合并为一个管网数据快照(data snapshots), 用式(2)表示:
| Gt={Vt,Et,WFT} | (2) |
其中,
在电泵井实际生产过程中, 时常根据生产计划调整油井生产时间, 调整某口井会对整体管网系统产生一定影响, 时空图卷积神经网络模型可对停开井前的集输管网时间快照进行分析, 预测产量数据集合
各潜油电泵井和输油管道组成的管网图数据为非欧几里德结构数据, 建立在欧氏数据上的卷积神经网络(CNN)并不能发挥有效作用, 提取空间结构信息. 为有效利用管网数据的空间结构信息和时间序列信息, 本文基于图卷积神经网络 (GCN)[12]、时间卷积神经网络(TCN)[13]和长短期记忆网络(LSTM)[14]搭建了一种3层时空交替的网络模型AST-GCN如图2所示.
图2中自下而上, 时空特征矩阵和邻接矩阵作为输入; 第1层为空间特征提取层, 由adaptive module组成, 内部使用LSTM-GCN提取管网拓扑图的空间信息, GCN使各节点聚合一阶邻域的信息, 同时LSTM对GCN处理拓扑不同的图带来的权重变化进行长短期记忆并更新, 最后形成各节点带有空间信息的高质量嵌入向量输出到下一层; 第2层为时间特征提取层, 使用因果扩张卷积的TCN对时间序列数据进行扩张因果卷积, 使每个节点获取自身历史信息; 第3层为时空信息融合层, 此时传入的节点向量, 分别包含当前时刻自身和一阶邻域节点信息, 历史时刻自身信息, 本模块使用GCN进行一次一阶邻域图卷积, 使每个节点包含当前时刻自身、相邻节点的信息, 历史时刻自身、相邻节点的信息, 形成蕴含丰富时空信息的向量, 最后通过全连接输出为管网产量数据. 模型通过3个模块的时空交替学习, 能够深度利用时间和空间信息, 进行准确的管网产量模拟计算, 得到管网系统中各电泵井和总输出产量情况.

|
图 2 时空图卷积神经网络模型架构图 |
2.2 自适应图卷积空间特征提取
图论化的集输管网拓扑图具有非欧氏的空间结构, 节点之间存在复杂的空间依赖关系, 图中的每个结点均受到相邻节点影响, 直到最终平衡. 同时, 受生产计划影响, 管网拓扑图会随时间产生变化, 节点和边会被添加或删除.
本文采用GCN提取图中的节点特征, 将特征表示为向量; LSTM学习演化GCN中的参数, 加强GCN对不同图的适应性. 两者结合完成自适应空间特征提取任务, 过程如图3(a)所示. 图3(a)为GCN-LSTM更新流程图, 其中
| Hl+1i=σ(1ci∑j∈NiHljWl) | (3) |
其中,
| ft=σg(Wfxt+Ufht−1+bf) | (4) |
| it=σg(Wixt+Uiht−1+bi) | (5) |
| ot=σg(Woxt+Uoht−1+bo) | (6) |
| ct=ft∘ct−1+it∘σc(Wcxt+Ucht−1+bc) | (7) |
其中, Wf, Wi, Wo, Wc是LSTM的权重参数; bf, bi, bo, bc是LSTM状态更新的偏置; ft, it, ot分别代表遗忘门、输入门和输出门, ct是单元状态, 3个门控和单元状态形成对GCN权重矩阵的长短期记忆.

|
图 3 GCN-LSTM自适应更新机制流程图 |
对于集输管网3D特征矩阵WFT, 按照时间轴切片操作后, 每一个
| Hl+1=σ(D−12ˆAD−12HlWl) | (8) |
| ht=LSTM(ht−1,Wh,Wx) | (9) |
| ht=σ(∑u∈N(v)Whhu+Wxxv) | (10) |
当图结构发生变化时, 需要重新计算节点之间的特征关系, 调整GCN的权重参数, 以适应新的拓扑图结构[15]. 在表示学习中, 拓扑图的变化直接体现在不同快照之间邻接矩阵A的变化和3D数据矩阵WFt的变化. 使用LSTM在时间维度上向后传递了两份信息: (1)包含GCN权重变动长期信息的单元状态Ct; (2)包含序列短期信息的状态ht. LSTM接收自身的权重矩阵Wh、GCN的权重Wx, 和其先前的状态向量ht–1, 计算出新的状态向量ht, 如式(9)所示. 经过引入LSTM模型, GCN参数传递更新机制如式(10)所示. 其中,
原油集输管网的生产参数有时间依赖性, 因此我们使用TCN提取时序特征. 通过因果卷积确保对时间序列进行建模时, 只依赖0~t–1时刻的值来预测第t时刻的特征值; 采用扩张卷积以保持计算效率的同时扩大卷积核视野, 捕捉序列中长依赖关系. TCN结构的扩张因果卷积如图4所示.
| F(s)=∑k−1i=0f(i)⋅xs−d⋅i | (11) |
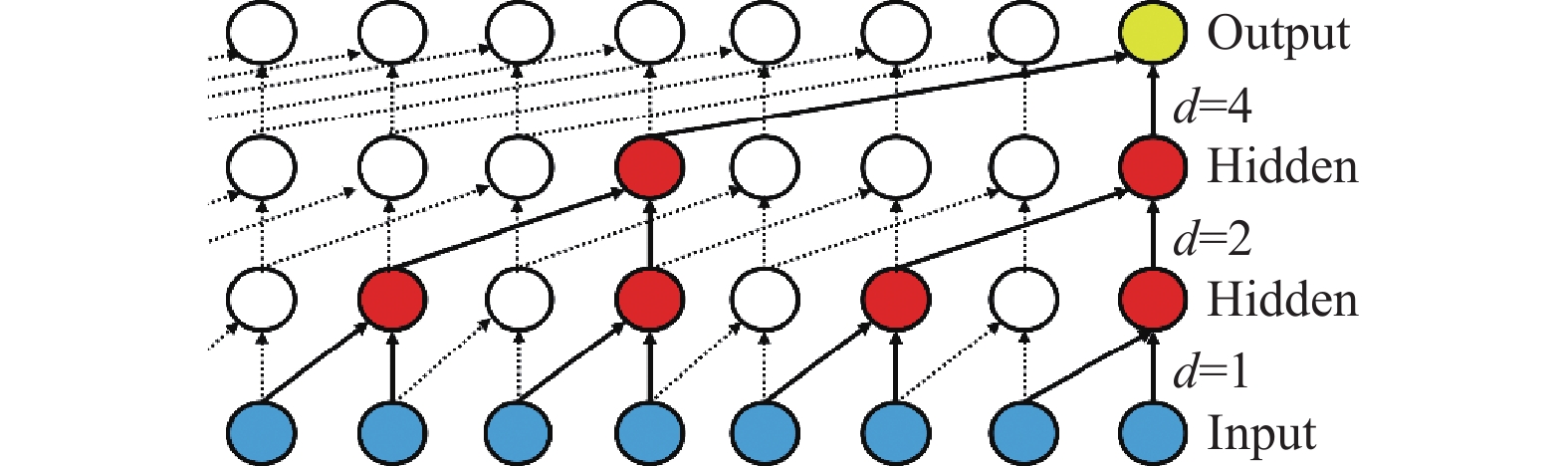
|
图 4 TCN扩张因果卷积 |
对于当前的时间步s, 在时间步s处的输出值F(s)根据输入序列x和权重系数f进行计算得到, 如式(11)所示. 式中k为卷积核大小, i表示权重系数的索引, f(i)代表在卷积核中的第i个位置上的权重值.
t时刻自适应图卷积层聚合相邻点特征信息后, 使节点

|
图 5 时空特征提取全流程 |
全局特征融合的目标是使每个节点拥有当前时间自身和邻居节点信息, 历史时间自身和邻居节点信息, 共4部分时空信息,
为验证提出方法在原油集输管网进行产量模拟计算的有效性和先进性, 我们在某油田区域的集输管网系统上进行了实验. 结果显示, 本文方法的产量计算获得了更准确的结果, 证明了该方法的有效性和先进性.
3.1 数据集选取某油田2018年1月1日–2022年12月31日共计5年的生产数据, 构建数据集. 原始数据如表1所示. 每行数据包含井号、日期和9种传感器记录数据和最终人工统计的真实结果, 分别为: 油压(YY)、回套(HY)、套压(TY)、井口温度(WD)、耗电量(HDL)、电压(DY)、电流(DL)、油嘴(YZ)、日产油量(RU), 日产油量是我们模拟计算的目标. 涉及保密数据, 表1中为脱密后的样例. 将其命名为SLYTHR数据集.
| 表 1 数据集样本 |
将管网的每个数据快照作为一个训练数据单元, 所有训练单元组合成为实验所需数据集. 最终数据集共有1 823天的电泵井生产记录, 有325次电泵井停开造成拓扑变化, 产生325个时空特征3D数据矩阵, 每个数据矩阵中时间序列数为1–71不等, 将其按照80%、20%的比例划分训练集、测试集.
3.2 对比实验设计目前尚未有对集输管网产量计算方法, 对比方法选取现有采取不同核心技术且能够处理时空图数据的深度学习方法, 形成对比实验, 通过计算平均误差等评价指标来进行评价, 如表2所示.
| 表 2 对比实验方法 |
(1) Geom-GCN[16]: 模型通过利用连续空间来构建结构邻域, 克服传统消息传递类神经网络在处理图结构数据时的部分局限性.
(2) SSA-TCN[17]: 基于时间卷积神经网络的产量计算方法. 其使用麻雀搜索算法快速筛选出神经网络的最优超参数, 对网络进行优化.
(3) TCN-GCN[18]: 模型首先使用基于扩张因果卷积算法的TCN, 从时序数据提取特征信息; 其次再构建拓扑结构图, 使用GCN从拓扑结构图中获得的信息来进行预测. GCN的邻接矩阵中的元素被Pearson相关系数替代, 以提高预测的准确性.
(4) PP-STNN[19]: 使用图卷积网络(GCN)捕获管网的空间相关性, 门控循环单元(GRU)用于捕获时间相关性, 结合二者计算结果.
3.3 实验环境与模型设置本文方法所用模型运行在配有Xeon E5-2686 v4处理器和两块GeForce RTX 3080 Ti的Torch环境, 部分采用了图学习的扩展库PyTorch-geometric[20]. 训练中, Adam优化器设置为0.001, 迭代次数为500次. 本文所提模型参数设置为: 自适应图卷积模块所需过滤器数量in_channels设置为8; 时间卷积层中输入的时间序列数据的输入、输出通道数input_channels、output_channels设置为8, 每个层级的通道数合为一个数组num_channels设置为[32, 64, 128, 8], 卷积核大小kernel_size设置为2, dropout设置为0.2; 全局特征融合图卷积层节点维度特征features设置为8, 隐藏层数hidden设置为16.
评估体系采用平均绝对误差MAE、平均绝对百分比误差MAPE、均方差MSE、均方根RMSE作为评价指标.
3.4 实验结果与分析表3显示了AST-GCN模型与对比模型的计算结果. 从表3中可以看出, 本文提出的方法模型在SLYTHR数据的所有仿真中都达到了最好的计算能力. 图6和图7展示了各个方法的计算结果与真实值的对比.
| 表 3 不同方法在 SLYTHR 数据集上的实验结果 |

|
图 6 计算结果对比曲线图 |

|
图 7 计算结果对比曲线图 |
GCN 的计算结果如图中深绿色曲线所示, 由于只考虑了空间结构, 因此计算结果差异较大; TCN 的计算结果如草绿色曲线所示, 它只考虑了数据之间的时间相关性, 忽略了图结构; GCN+GRU 被用作对比模型, 其计算结果如青色曲线所示, 其计算结果不如 GCN+TCN 精确; GCN+TCN 的计算结果如蓝色曲线所示, 模型考虑了时空因素, 计算结果较准确, 但在数据变动较大的时间点, 不能很好地计算结果. 本文所提出的方法结果标注为黄色曲线, 和真实值(红色曲线)差距最小.
此外, 通过观察图7中1700–1800时刻内的曲线可以看出, 本文提出的AST-GCN模型能够应对电泵井变化导致的产量数据瞬变的情况, 这主要得益于自适应图卷积模块中的LSTM所具备的长短期记忆能力, 而LSTM在GCN参数的演化过程中起到了重要的作用.
4 结论与展望本文提出了一种通过自适应时空图卷积神经网络进行原油集输管网产量模拟计算方法. 从集输管网数据的时空特征出发, 进行特征提取和融合计算; 通过时空反复结合, 彻底捕捉管网数据的时空特征, 准确进行集输管网产量模拟计算, 能够为油田集输过程提供参考.
下一步工作应考虑如何使用更少的数据样本进行小样本训练, 保持结果准确性的同时减少资源消耗.
| [1] |
刘丽. 浅析原油盘库统计中的误差因素. 中国石油和化工标准与质量, 2012, 32(1): 243. DOI:10.3969/j.issn.1673-4076.2012.01.213 |
| [2] |
Almedallah MK, Branch G, Walsh SDC. Combined well path, submarine pipeline network, route and flow rate optimization for shallow-water offshore fields. Applied Ocean Research, 2020, 105: 102396. DOI:10.1016/j.apor.2020.102396 |
| [3] |
李传亮, 庞彦明, 周永炳, 等. 压裂直井产量公式. 新疆石油地质, 2023, 44(6): 683-689. |
| [4] |
张鑫, 高星星, 王繁荣. 油井集输回压对产能影响及控制策略. 化学工程与装备, 2023(7): 80-81, 114. DOI:10.19566/j.cnki.cn35-1285/tq.2023.07.074 |
| [5] |
AlRassas AM, Al-Qaness MAA, Ewees AA, et al. Optimized ANFIS model using Aquila Optimizer for oil production forecasting. Processes, 2021, 9(7): 1194. DOI:10.3390/pr9071194 |
| [6] |
Zhao H, Xu LF, Guo ZY, et al. Flow-path tracking strategy in a data-driven interwell numerical simulation model for waterflooding history matching and performance prediction with infill wells. SPE Journal, 2020, 25(2): 1007-1025. DOI:10.2118/199361-PA |
| [7] |
Fan DY, Sun H, Yao J, et al. Well production forecasting based on ARIMA-LSTM model considering manual operations. Energy, 2021, 220: 119708. DOI:10.1016/j.energy.2020.119708 |
| [8] |
Abdullayeva F, Imamverdiyev Y. Development of oil production forecasting method based on deep learning. Statistics, Optimization & Information Computing, 2019, 7(4): 826–839. [doi: 10.19139/soic-2310-5070-651]
|
| [9] |
Chahar J, Verma J, Vyas D, et al. Data-driven approach for hydrocarbon production forecasting using machine learning techniques. Journal of Petroleum Science and Engineering, 2022, 217: 110757. DOI:10.1016/j.petrol.2022.110757 |
| [10] |
张战敏, 朱丹丹, 刘重伯, 等. 抽油机井原油产量计量新方法. 钻采工艺, 2023, 46(2): 71-76. DOI:10.3969/J.ISSN.1006-768X.2023.02.12 |
| [11] |
Gong FM, Du CZ, Ji XF, et al. Mechanistic and data-driven modelling of operational parameters prediction on oil and gas transportation pipeline network. Proceedings of the 2023 International Conference on New Trends in Computational Intelligence (NTCI). Qingdao: IEEE, 2023. 329–335. [doi: 10.1109/NTCI60157.2023.10403749]
|
| [12] |
Kipf TN, Welling M. Semi-supervised classification with graph convolutional networks. Proceedings of the 5th International Conference on Learning Representations. Toulon: OpenReview.net, 2017.
|
| [13] |
Bai SJ, Kolter JZ, Koltun V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv:1803.01271, 2018.
|
| [14] |
Sagheer A, Kotb M. Time series forecasting of petroleum production using deep LSTM recurrent networks. Neurocomputing, 2019, 323: 203-213. DOI:10.1016/j.neucom.2018.09.082 |
| [15] |
Manessi F, Rozza A, Manzo M. Dynamic graph convolutional networks. Pattern Recognition, 2020, 97: 107000. DOI:10.1016/j.patcog.2019.107000 |
| [16] |
Pei HB, Wei BZ, Chang KCC, et al. Geom-GCN: Geometric graph convolutional networks. Proceedings of the 8th International Conference on Learning Representations. Addis Ababa: OpenReview.net, 2020.
|
| [17] |
Zhang L, Dou H, Wang TZ, et al. A production prediction method of single well in water flooding oilfield based on integrated temporal convolutional network model. Petroleum Exploration and Development, 2022, 49(5): 1150-1160. DOI:10.1016/S1876-3804(22)60339-2 |
| [18] |
Luo DS, Fang J, He HY, et al. Prediction for dissolved gas in power transformer oil based on TCN and GCN. IEEE Transactions on Industry Applications, 2022, 58(6): 7818-7826. DOI:10.1109/TIA.2022.3197565 |
| [19] |
Liao ZY, Liu MH, Du BW, et al. A temporal and spatial prediction method for urban pipeline network based on deep learning. Physica A: Statistical Mechanics and Its Applications, 2022, 608: 128299. DOI:10.1016/j.physa.2022.128299 |
| [20] |
Fey M, Lenssen JE. Fast graph representation learning with PyTorch geometric. arXiv:1903.02428v3, 2019.
|
 2024, Vol. 33
2024, Vol. 33



