2. 昆明文理学院, 昆明 650221;
3. 昆明市公安局 情报指挥中心, 昆明 650217
2. The College of Arts and Sciences·Kunming, Kunming 650221, China;
3. Intelligence and Command Center, Kunming Public Security Bureau, Kunming 650217, China
视频结构化、移动互联、位置服务、物联网等技术的发展, 产生了大量的时空轨迹数据, 仅一个地(市)级公安部门一年所采集的这类数据其规模就可能达到PB级别, 形成了大量可用于数据挖掘和关系计算的“算料”. 如何高效挖掘和利用这类数据是当前研究的热点和难点[1,2]. 由于受限于资金规模, 市、县级公安部门“算力”有限, 以本单位为例, 全局数十名数据治理和分析师可使用的计算服务器仅30多台. 在这种条件下, 不可能将全部“算力”都投入到时空轨迹数据的计算中, 使用常见的计算方法难以“全量”计算分析这些大规模的轨迹数据. 因此, 通过高效“算法”弥补“算力”的“不足”, 研究一种适合市、县级公安机关的, 用于低集群资源环境下的高效时空关系查询和计算方法, 有着十分重要的现实意义和实践价值. 通过挖掘这些巨量轨迹数据内蕴含的特定时空关系, 例如通过挖掘人与人之间同时空关系, 可用于判断人员间一定时间段内的轨迹伴随关系, 以及一定时间内的关系圈、朋友圈等, 在各类行政、刑事案件的扩线, 违法犯罪的延伸打击等方面都有很大的业务价值, 在赋能公共安全、国家安全等领域有十分重要的意义和实践价值.
各级公安机关收集的轨迹数据常被存储于Hive或其他类似的分布式数据仓库里. 以Hive为例: 其是一款基于Hadoop生态(包括HDFS、Yarn、MapReduce、TEZ、Spark等组件和引擎)的分布式数据仓库, 其自2.2版起增加了对复杂表达式连接查询的支持, 可通过复杂表达式连接查询得到时空轨迹间的时空关系. 这对大量的时空轨迹类数据的挖掘提供了又一选项, 但直接使用Hive复杂表达式连接查询, 由于需实时计算连接条件后并根据计算结果才能完成连接, 存在Map阶段的排序结果在关联过程中得不到利用, TEZ等计算引擎的内置优化失效等问题, 导致连接查询过程中出现集群资源得不到有效利用, 连接查询需要耗费大量的时间等问题. 因此, 完成n·n对象的同时空关系连接查询工作, 其时间复杂度往往是O(n2)[3], 效率低下. 例如: 完成4千万条左右轨迹数据“全量”同时空关系的连接查询任务, 时间消耗一般都在1 h以上.
若不采取可行优化策略, 在没有大规模服务器集群资源的低集群计算资源(算力)场景下, 通常难以在可接受的时间范围内完成所需的时空关系的计算. 本文的实战场景仅30多台服务器(每台划分为2个节点), 可用于连接查询的只有70多个节点. 这种条件下, 若按照Hive提供的复杂表达式进行连接查询, 完成对一天上亿条轨迹数据之间时空关系的连接查询, 实测当数据规模在3千万–4千万时, 时间消耗基本都超过1 h, 而当数据超过某个阈值时(6千万条), 还存在得不到计算结果的情况. 因此, 提升时空轨迹类数据的连接查询效率, 采用更高效的方法优化或替代复杂表达式连接查询, 对提升时空轨迹类数据时空关系挖掘效率和提升计算稳定性有重要意义.
本文对轨迹数据的采集时间进行分段交叉编码, 并按照“时空”二级分区存储等预处理. 基于预处理结果, 通过用“等值”连接查询替代复杂表达式实时计算连接查询的方式, 避免关联条件的实时计算, 减少连接条件的比对次数, 解决计算引擎的内置优化失效等问题. 所提出的融合“时空二级分区+时间段交叉编码”的快速连接查询方法, 其做法: 首先把连续的时空数据通过时空编码进行离散化, 相当于提前计算好连接查询的关联条件, 把原本需要在连接查询过程中进行n·n次实时连接查询条件计算, 优化为了在数据预处理阶段提前进行n次计算; 其次, 利用时间段编码以“等值”连接查询替代复杂表达式连接查询的方式, 避免了计算引擎的内置优化失效问题; 第三, 通过交叉的时间段编码进行“斜向”交叉“等值”连接, 解决因时间段“等值”连接出现的连续的时间段编码间的间隙问题. 通过这些步骤, 可实现不同对象间同时空关系的快速连接查询且能保证不丢失时空关系. 采用文献所提出的方法进行优化后, 完成一天轨迹数据同时空关系的连接查询任务, 时间消耗从原来的1 h以上, 减少到了3–5 min, 而且也更加的稳定.
以该方法计算的不同对象间(例如人员、车辆、电子设备等)“同时空”关系为基础, 可将复杂的同行伴随关系、对象间亲疏远近关系的判定等算法转化为简单的聚合统计查询就可以实现的问题. 例如: 通过该方法计算出的存在同时空关系的m辆电动自行车, 当其在一定时间内同时空点位大于某个数字, 且时空顺序相同, 基本就可作轨迹伴随的候选集. 又比如取半年内, 人脸白天同时空或晚上同时空天数大于某个数字的人, 就能够快速地筛选出相关人员的同事、家人等关系人员. 算法的计算结果, 可广泛服务于维护国家安全、维护社会治安、预防和打击电信网络诈骗犯罪、统筹城乡规划等领域的情报线索挖掘.
本文第1节介绍国内外类似研究的相关工作. 第2节介绍使用的样本数据、集群环境以及对数据进行的加工和转换工作, 包括数据分区、空间网格化、空间网格区域分区计算、时间交叉编码等. 第3节给出基于时空二级分区融合时间段交叉编码的时空关系快速连接查询优化策略及算法的主要步骤, 并与两种当前普遍采用的算法进行对比, 验证文章所提出方法的必要性和可行性. 第4节对3种不同算法进行实验, 验证了该方法对连接查询的加速效果. 第5节对实验结果数据进行分析, 并对DPCP-CROSSS-JOIN等算法时间复杂度进行简要分析. 第6节总结展望.
1 相关工作目前经有大量对时空大数据的研究, 甚至出现了量子计算用于挖掘时空的关系等方面的研究[1], 相关研究数量非常多, 各种解决方案也相继被提出. 主要包括通过优化Hadoop生态各组件性能提升效率, 利用双向连接等方法提升查询效率, 采用分区或分桶等建立时空索引提升效率以及结合业务特征针对性的治理数据和优化提升效率等几类.
1.1 优化Hadoop相关配置、算法及执行策略赵彦荣等人[4]通过设计多副本一致性哈希算法以及通过Hash Map Join并行连接查询提升Hive连接查询效率. 王华进等人[5]基于ORC元数据的key频率分布估计方法和相应的负载均衡key划分方法提升Hive连接查询效率. 马东等人[6]通过Hive中大小表关联的优化方法, 利用其中大表的索引特性, 降低传输和分析的数据量, 进而提升大小表关联分析的效率, 解决大表存在索引的时效率低下的问题. 吴锦坤等人[7] 、Kulkarni等人[8]通过优化Hadoop各组件和计算引擎配置参数, 防止数据倾斜等方法提升Hadoop集群计算效率. 郑灵逸等人[9]通过增加任务并行度和建立中间表组合等方法优化查询. Margoor等人[10]针对连接查询数据快速膨胀问题, 提出一种贪婪的连接重新排序算法, 在没有统计数据的情况下提升连接查询效率.
1.2 利用分区、分桶和索引提升查询效率齐恒等人[11]使用时间分区的排序数组和空间分区四叉树数据结构, 局部三维R树索引, 实现了数据的时空局部性和负载平衡, 达到时空伴随轨迹的快速查询. Sahal等人[12] 提出一种基于索引的查询优化方法. Costa等人[13]通过分区、分桶等方法组织数据, 并验证了这些方法在查询性能提升方面的效果. Arpitha等人[14]分析优化器、查询等价规则、索引、成本估计和SQL表达式隐含依赖关系, 在查询优化中的重要性和作用, 构建查询优化器, 能够以最短的执行时间或响应时间生成评估计划. Xia等人[15]提出了基于MapReduce的并行频繁模式增长(MR-PFP)算法, 在Hadoop平台上使用大规模出租车轨迹和海量小文件并行处理策略来分析出租车运营的时空特征. 房俊等人[16]针对HBase无法直接建立时空索引问题, 基于HBase行键创建时空索引, 并通过Geohash编码对数据进行降维处理, 实现区域时空数据查询性能的提升. Zhao等人[17]通过轨迹数据库网格索引和分区两种技术解决top-k类似性搜索问题. Jin等人[18]通过降维策略与WR树索引以加快搜索速度, 提出优化方法来提高链接的准确性和鲁棒性. Qin等人[19]利用时空K-近邻(KNN)算法和贝叶斯方法, 提出一种基于不完全和完整轨迹的链路TTD估计框架. 通过KNN算法来估计不完整轨迹的虚拟链路旅行时间, 改进粒子滤波器和吉布斯采样等方法, 提高KNN查找的准确性. 王晨旭等人[20]采用时空二级分桶、多级索引、时间槽索引以及通过建立起“全局索引+动态网格范围计数索引+三维R树索引”多级索引等方法实现相似时空轨迹数据的查找, 解决了指定的常数条轨迹的相似轨迹快速查询问题, 适用于k·n的大规模数据查找或其他较小数据规模场景.
1.3 利用双向连接等方法提升查询效率Dwivedi等人[21]采用双向连接技术提升查询效率, 使用TPC-H基准数据集进行了测试, 数据查询效率得到一定程度的提升. Kadari等人[22]通过多路空间连接的二进制分割方法和条分割技术, 实现了更好的总体周转时间.
1.4 根据业务特征治理数据提升查询效率何文婷等人[23]公开了一种根据外表关联列的取值集进行分区优化, 通过重复利用各分区的中间结果的方式提升查询效率. 陈喜洲[24]提供了一种提升时序数据快速查询的方法, 通过时间戳偏移, 新增原始记录的时间偏移记录, 实现通过“等值”连接查询解决“非等值”连接查询需求. 该方法在面对需增加偏移数据较多时, 会导致数据的快速膨胀(例如假设业务发生的前后1 min都认为是时间相关的, 使用该算法将导致原始数据120倍的膨胀), 增加连接查询的比对次数, 从而影响SQL连接查询效率, 业务应用场景比较有限.
1.5 现有研究的重点和不足以及改进方法这些研究几乎都是围绕着提升时空关系数据的查询或查找的效率问题进行的研究. 如前文所述, 目前主要的几类研究.
第1类: 赵彦荣等人[4]、王华进等人[5] 、马东等人[6] 、吴锦坤等人[7] 、Kulkarni等人[8]、郑灵逸等人[9]以及Margoor等人[10]主要是针对Hadoop各组件特性进行优化, 例如使用Map Join提高效率, 防止数据倾斜等方法提升Hadoop集群计算效率.
第2类: 齐恒等人[11]、Sahal等人[12]、Costa等人[13]、Arpitha等人[14]、Xia等人[15] 、房俊等人[16]、Zhao等人[17] 、Jin等人[18]、Qin等人[19]、王晨旭等人[20]的研究聚焦通过建立各种形式的索引, 提升与给定轨迹相似轨迹的查找效率, 对于解决类似K-近邻查找有很好的借鉴作用.
第3类: Dwivedi等人[21]、Kadari等人[22]采用双向连接、多路空间连接这些方法来提升Hive连接查询的效率.
第4类: 何文婷等人[23]、陈喜洲[24]实现通过“等值”连接查询解决“非等值”连接查询需求.
当前已有的这些研究, 第1类主要存在优化完全依赖于大数据组件, 可优化空间有限的问题; 第2类主要解决k·n (k为常数)的快速查询问题; 第3类仅是一些一般性的优化方法; 第4类受制于特定业务场景, 而且会存在连接时数据的快速膨胀的问题, 以及没有解决“间隙”问题. 已有的这些研究对于本文要需要解决的n·n对象间“全量”时空关系不能很好适用, 尤其是不能直接利用Hive SQL实现轨迹数据的空间关系快速连接查询.
鉴于此, 本文在第1类优化的基础上, 参考第2、4类优化方法, 着眼于解决时空轨迹类数据连接查询过程中集群资源利用率低, 连接查询过程中数据膨胀过快和查询时间消耗过多等几个方面问题, 以期实现时空轨迹关系的快速连接查询和挖掘. 主要做法包括: 融合“时空二级分区 + 时间段交叉编码”, 把连续的时空数据进行离散化, 通过用“等值”连接查询替代复杂表达式连接查询, 通过交叉编码避免时空数据进行离散化后连接查询产生的“间隙”等. 使用本方法, 可实现n·n对象间的时空关系, 例如同时空关系的快速计算, 可将n·n对象间同时空关系连接查询时间复杂度从O(n2)降为O(nlogn).
2 数据结构与数据预处理为实现低“算力”条件下同时空关系的快速连接查询, 对时空轨迹数据进行时间段交叉编码和二级分区存储等预处理. 用于对比实验的数据是X市各类传感器2022年6月–2023年5月采集的约63亿条, 约230 GB的时空轨迹数据t_ost_dp, 数据格式及主要字段见表1.
| 表 1 时空数据原始数据 (t_ost_dp) |
提取采集时间中的日期部分, 并按照日期(天) dp进行分区存储. 其余字段主要包括对象编号(oid), 经度(lon), 维度(lat), 采集时间(t)等字段, 数据总规模230 GB, 记录总数达63亿条. 实验过程中详细记录连接查询过程中的任务划分、执行查询的任务数、集群资源占用以及连接查询时间消耗等过程数据.
为绕开Hive SQL复杂表达式的n·n关联条件的实时计算, 首先对数据作系列的预处理, 包括对数据格式化, 提取采集时间中的日期, 对空间位置网格化编码, 计算空间网格区域分区值, 计算时间编码以及其交叉编码等预处理; 其次将预处理的数据以“日期”和“空间网格区域编码”进行二级分区存储, 供后续用, 主要步骤如下.
步骤1. 将当前日期分区前一天最后一个
步骤2. 根据网格编码计算网格区域编码, 作为二级分区字段.
步骤3. 对每条记录的采集时间进行编码, 生成3个时间编码字段和3个扩展时间编码字段.
步骤4. 将时间编码后的数据按照时间以日期(天)分区, 空间按网格区域分区, 进行二重分区进行存储, 表名: t_ost_cc.
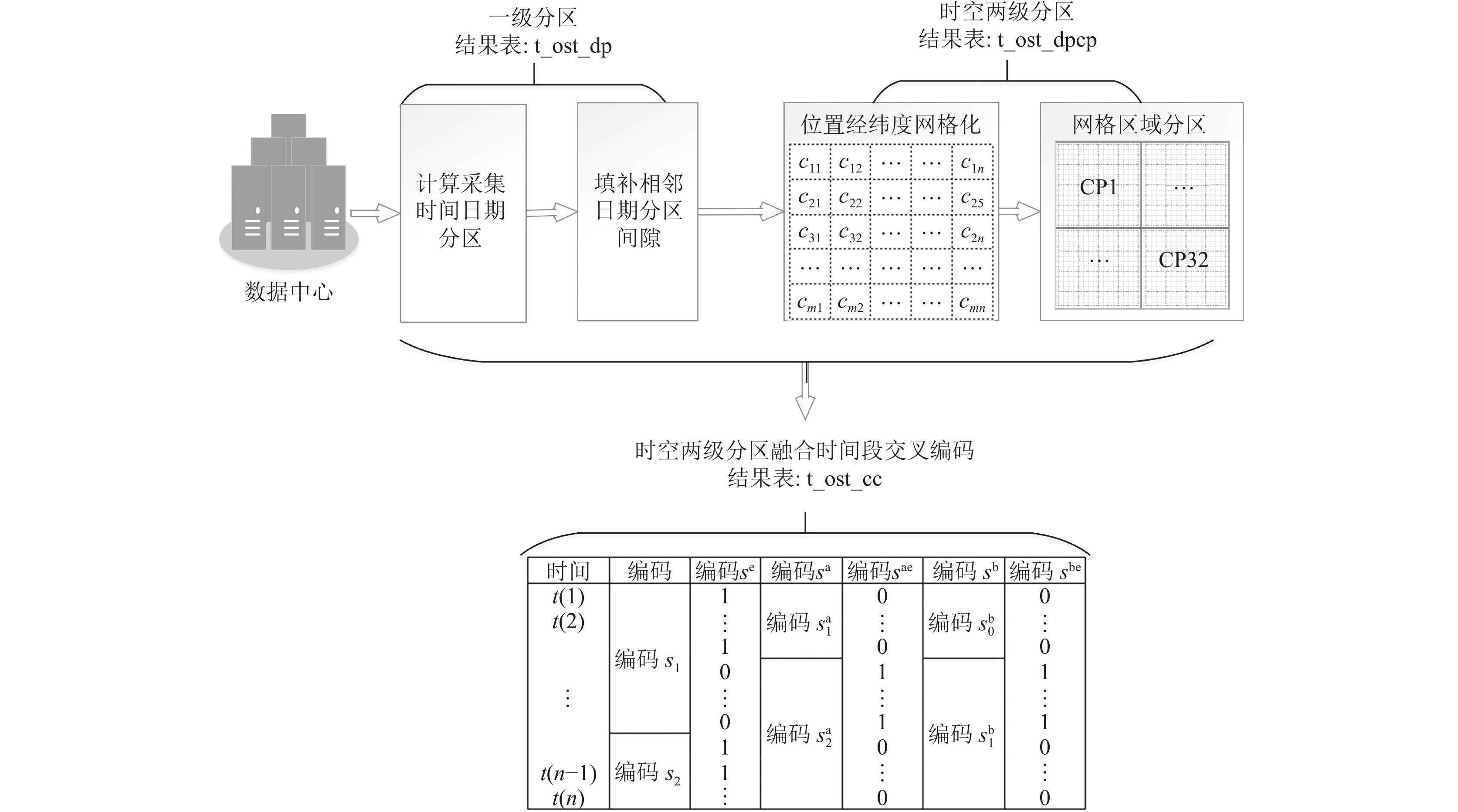
数据的预处理流程包括提取采集日期, 进行日期分区间隙填充, 计算空间位置网格编码, 计算空间位置网格区域编码, 进行时间段交叉编码以及根据预处理的结果按时空两级分区对数据进行存储等过程, 如图1所示.
|
图 1 时空数据预处理主要流程 |
2.1 数据空间位置编码
空间网格: 采用Geohash对所有位置经纬度进行编码, 该编码是Gustavo Niemeyer于2008年发明的公共领域地理编码系统方法, 是国际上较为通用的一种空间位置网格化方法. 本文计算精度保留前7位, 每个编码对应网格覆盖约153 m×152 m范围, 将位置纬度对应Geohash二进制数据并进行Base32编码, 使用的编码字符与十进制数据对应关系见表2, 得到该经纬度对应的网格编码串, 例如经纬度位置(25.06, 102.71)编码后为: wk3n91u, 标记为c, Geohash计算公式见式(1), 目前该算法已有Java、Python等不同语言版本实现.
| $ c(lon, lat) = GH(lon, lat, {\mathrm{Base32}}) $ | (1) |
| 表 2 Geohash Base32编码字符与十进制数据对应关系 |
2.2 对象间同时空关系定义
此研究的对象间同时空关系, 特指两对象(人员、车辆、电子设备等)间, 当对象a在t时刻出现在某空间网格c内, 另一对象b在其前、后一定时间
| $ F(a, b) = E(a, t, c)\Lambda E(b, t', c) $ | (2) |
其中,
因时空轨迹类数据规模巨大, 在进行时空数据连接查询时, 使用循环选取每个日期分区数据并进行关联的方式进行. 这种方式存在正在进行连接的当前日期分区数据与前一日期分区及后一日期分区时间连续, 但被割裂的问题. 因此将前一日期分区最后一个
算法1. DP_SP_FILL
输入: t_ost_dp.
输出: t_ost_dp # 更新的t_ost_dp.
1. D←Query t_ost_dp’s partitions names
2. Foreach d in D do
3.
4. Store tab1 to t_ost_dp(d) #将tab1插入Hive仓库t_ost_dp的dp=d分区中
5.
6. Store tab2 to t_ost_dp(d) #将tab2插入Hive仓库t_ost_dp的dp=d分区中
7. End
算法1中, σ、ρ、∧等符号系关为运算里面的选择、重命名以及条件合取; FT(d)表示取时间d对应当天的最后时刻对应的时间, 精确到秒, 例如当d取20230502时, 无论t取2023年05月02日什么时刻, FT(d)都取2023年05月02日00时00分00秒, FT(d+1)都取2023年05月03日00时00分00秒; abs(value)表示对value取绝对值.
2.4 位置信息网格化及分区空间网格区域码: 把网格编号c转换为十进制, 再进行mod 32运算, 目的是把一个日期分区的数据再相对均匀的划分为常数个(本研究划分为32个, 可视集群算力设置合理数值)不同的空间网格区域, 记cp, 式(3), 即把同一日期分区数据再约等分为32个空间网格区域, 区域码主要作为分区字段存储.
| $ cp(c) = \left(\sum\nolimits_{i = 1}^L {(D({c_i}} ){(32)^{i - 1}})\right){\text{%}} 32 $ | (3) |
其中, L表示使用的Geohash编码的长度, D(ci)表示把Geohash编码从右到左第i个字符转换为对应的十进制数, 例如wk3n91u的第7位字符“w”对应的十进制数是28, 第6位字符“k”对应的是18, 以此类推. 采用长度为7的Geohash编码时, 计算“wk3n91u”的cp编码可对照表2 (Geohash Base32编码字符与十进制数据对应关系表)查找到w、k、3、n、9、1、u各自对应的十进制数字28、18、3、20、9、1和26, 通过式(3), 即: cp(wk3n91u) = (28×326+18×325+3×324+20×323+9×322+1×32+26) % 32 = 26 , 计算出具体的网格区域分区cp值. 根据计算规则可知, 一个网格编码对应若干经纬度, 一个空间网格区域包含若干空间网格, 空间网格化及按网格区域存储的过程见算法2.
算法2. DPCP_ETL
输入: t_ost_dp.
输出: t_ost_dpcp # 将t_ost_dp按时空二级分区存入t_ost_dpcp.
1. Begin
2.
3. Store tab1 to t_ost_dpcp(dp, cp) #将tab1存入Hive仓库t_ost_dpcp表的dp, cp二级分区中
4. End
算法2中, c按照经纬度网格化式(1)计算得出; cp按照网格区域码式(3)计算得出.
2.5 时间段交叉编码将采集时间t, 转换为对应的Unix时间戳(从1970年1月1日00时00分00秒所经过的秒数, 每过1 s, 数值加1), 记为: u = UT(t). 为能通过等值连接解决复杂表达式连接, 需用长度为
| $ s = \left\lceil { (u+1 +p)/ 2\Delta t} \right\rceil $ | (4) |
使用式(4), p值取0, 计算出时间戳u对应的时间段编码s, 其中“
| $ s^{\mathrm{e}} = (\left\lceil {(ut+1+p)/ \Delta t} \right\rceil ){\text{%}}2 $ | (5) |
再按照式(5), p值取0, 计算出s的扩展码se, 其目的是把同一个时间段编码对应的采集时间落在第1个
类似地, 通过式(4), p值取
同样通过式(4), p值取
算法3. DP_SP_TSEC
输入: t_ost_dpcp.
输出: t_ost_cc # 将计算结果按时空二级分区存入t_ost_cc.
1. Begin
2.
3. Store tab1 to t_ost_cc(dp, cp) # 将tab1存入Hive仓库t_ost_cc的dp, cp二级分区中
4. End
2.6 时空分区及网格化数据按照前述方法计算t_ost_dpcp中每条轨迹中采集时间对应的时间段编码s、sa、sb以及对应的扩展编码se、sae、sbe, 计算经纬度位置的Geohash网格编码c, 网格区域分区值cp, 计算结果存入t_ost_cc, 见算法3.
3 优化策略及相关算法如第2节所述, 存在复杂表达式的Hive SQL连接查询, 全部数据连接完成至少需要n·n次连接条件的实时计算, 需要的计算次数多、耗时长, 连接条件计算成为整个连接查询过程的瓶颈, 难以在低集群计算资源(算力)环境下实现高效时空关系连接查询. 为实现低“算力”环境下时空关系的高效连接查询, 需要一是避免连接条件的实时计算, 减少关联条件计算次数; 二是针对存在复杂表达式的连接查询导致的Hadoop相关组件优化失效的问题进行优化. 利用数据预处理过程对采集时间的分段编码, 以时间的分段编码而不是时间范围计算作为连接条件可避免连接查询关联条件的实时计算, 同时 “等值”关联代替复杂表达式计算关联又能够避免引擎失效等问题. 为便于标识, 文中所提融合时空二级分区存储和时间段交叉编码的连接查询算法简称DPCP-CROSS-JOIN. 算法以第2节的数据预处理结果t_ost_cc为基础, 连接查询主要骤如下.
步骤1. 通过Java等编程语言开发工具, 生成SQL, 循环提交每个日期分区对应的数据进行连接查询.
步骤2. 每次只进行一个日期分区数据的连接查询, 待连接表分别标记为tab1、tab2, 每次连接查询首先判断空间网格区域分区是否相等, 再比较空间网格是否相等, 然后比较tab1与tab2时间段编码s是否相等, 选取相等的进行连接.
步骤3. 依然对选定的日期分区数据连接查询, 前几个比对条件同步骤2, 但是连接查询关联的最后一个条件由比较tab1、tab2的s字段是否相等变为分别比较tab1的s与tab2的sa、sb以及tab1的扩展编码se与tab2的sae、sbe是否相等, 选取相等的分别进行连接.
步骤4. 对tab1与tab2的连接结果进行过滤, 以编码s、sa、sb以及se、sae、sbe等值连接的结果, 连接结果中存在部分关联上的对象时间差大于
步骤5. 按照日期和网格区域分区进行二级分区存储连接查询结果.
主要步骤说明: 步骤2–步骤5以循环和并行方式提交运行, 其中使用步骤1提供的工具的目的是为了提高任务的并行度, 步骤2通过使用时间段编码实现等值连接查询避免每次连接时实时计算连接条件, 同时避免了MapReduce、TEZ等引擎优化失效问题, 从而达到提升连接查询效率的目的, 对应算法见DPCP-CROSS-JOIN算法(第3.1节).
步骤3通过比较tab1的s与tab2的sa、sb以及tab1的扩展编码se与tab2的sae、sbe是否相等, 选取相等的分别进行连接, 主要解决时间离散化后“等值”关联带来的间隙问题, 例如假设在任意一个对象前后5 s出现在同一空间网格c为存在同时空关系, 按照数据预处理的方法第0–9 s将被编码为1, 记s(1), 第10–19 s编码为2, 记s(2), o1在第9 s出现即时间分段编码s(1)与o2在11 s即时间分段编码s(2)出现, 明明符合同时空关系, 但因为使用编码s作为等值关联条件, 漏算该同时空关系. 通过tab1.s = tab2.sb且tab1.se = tab2.sbe (斜向连接)作为关联条件进行再次连接查询, 可解决上述漏算问题. 类似地, 通过tab1.s = tab2.sa且tab1.se = tab2.sae(交叉连接)解决o2与o1的时空关系漏算问题.
为对比算法的优化效果, 验证过程中也对当前主流的以时空进行二级分区的DPCP-JOIN算法和仅以日期进行分区的连接算法DP-JOIN也进行了实现(第3.2节).
3.1 时间编码等值连接查询算法该算法简称DPCP-CROSS-JOIN, 通过循环日期分区集合D, 取出每个分区d对应的数据, 分别存放于tab1, tab2临时表中. 对tab1, tab2进行连接查询, 连接条件为:
(1) tab1, tab2对应记录的空间网格区域分区相同;
(2) tab1, tab2对应记录的空间网格编号相同;
(3) tab1, tab2对应记录的时间段编码相同.
连接完成后, 对连接结果进行过滤, 条件: (ts←
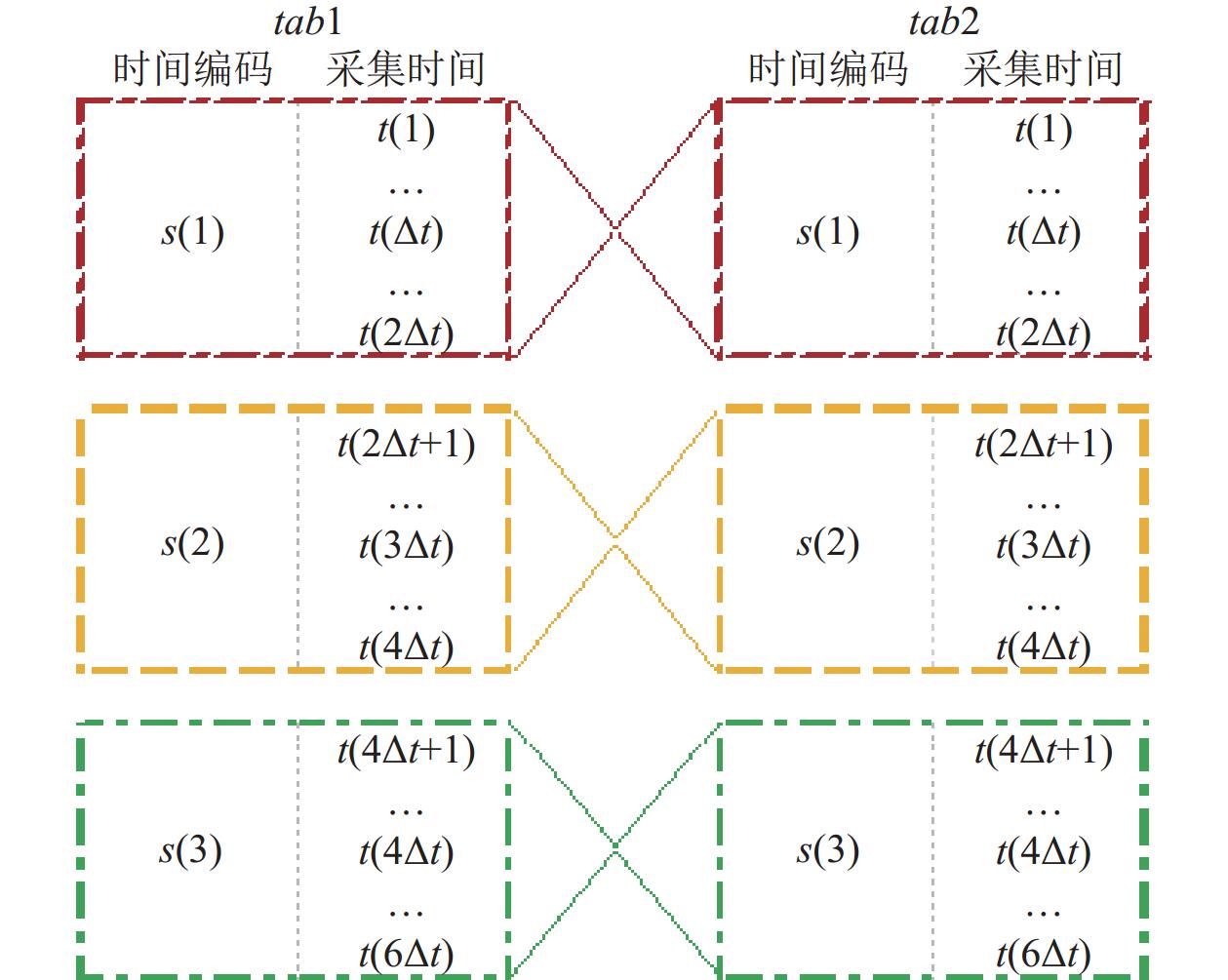
通过这些步骤得到tab1, tab2表中每条记录对应其时间段编码的同时空关系, 见图2, 结果记: γ1.
|
图 2 数据时空分区及时间段连接查询过程 |
按此方法, 存在:
(1) tab1表时间编码s(1)的后半段即后一个
(2) tab2表时间编码s(2)的前半段即前一个
通过tab1表时间编码s(1)的后半段即后一个
连接查询条件: 使用
算法4. DPCP-CROSS-JOIN
输入: t_ost_cc.
输出:
1. D←Query t_ost_cc’s partitions names
2.
3.
4. Foreach d in D do
5. # 并发提交
6. Begin Concurrency execute(part 1, part 2, part 3) part 1:
7.
8. Store γ1 #将连接查询结果γ1存入Hive数据仓库
9. End Concurrency part 1
10. Begin Concurrency execute(part 1, part 2, part 3) part 2:
11.
12. Store γ2 #将连接查询结果γ2存入Hive数据仓库
13. End Concurrency part 2
14. Begin Concurrency execute(part 1, part 2, part 3) part 3:
15.
16. Store γ3 #将连接查询结果γ3存入Hive数据仓库
17. End Concurrency part 3
18. End
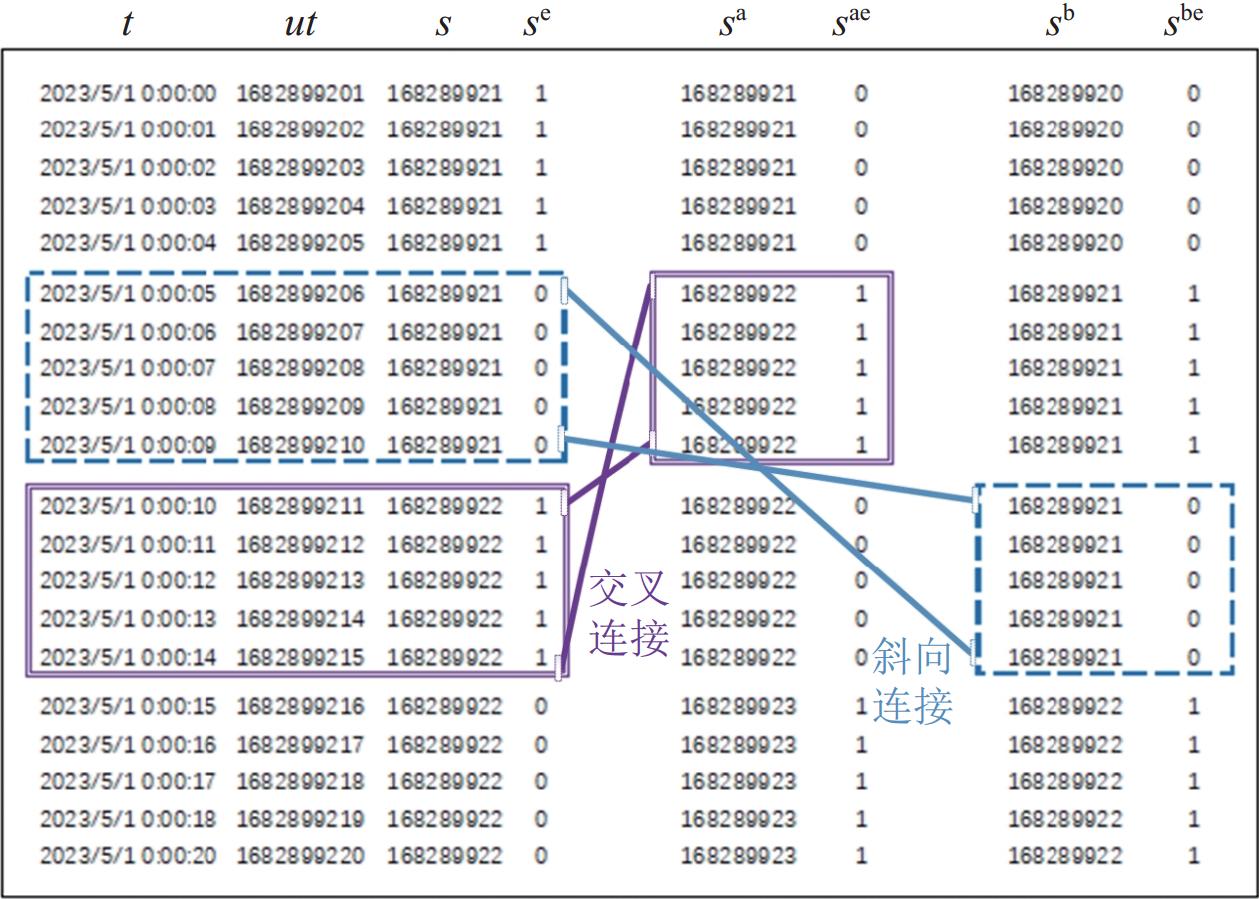
|
图 3 数据时空分区及时间段交叉连接查询过程 |
3.2 常规两级索引优化连接查询算法
常规两级索引查询优化算法(简称DPCP-JOIN), 通过循环日期分区集合D, 取出每个日期分区d对应的数据, 分别存放于tab1, tab2临时表中. 对tab1, tab2进行连接查询, tab1, tab2表字段命名规则同算法4, 连接条件如下:
(1) 空间网格区域分区cp与cp2相同;
(2) 空间网格编号c与c2相同;
(3) tab1, tab2每条记录的采集时间u与u2差的绝对值ts小于等于
为了便于后续比较, 连接查询结果标记为β.
仅按日期分析的查询优化算法(简称DP-JOIN), 通过循环计算数据表日期分区集合D, 取每个日期分区d对应的数据, 分别存放于tab1, tab2临时表中, 使用该算法对tab1, tab2进行连接查询, 连接条件如下:
(1) 空间网格编号c与c2相同;
(2) tab1待关联记录与 tab2每条记录的采集时间u与u2差的绝对值ts小于等于
连接后tab1对应的oid, c, t等字段名称保持不变, tab2(oid, c, t)字段分别重命名为(oid2, c2, tab2), 为了便于后续比较, 连接查询结果标记为α.
4 实验及数据为比较DPCP-CROSS-JOIN算法的在低“算力”条件下的性能优势, 使用2023年5月中31天的轨迹数据在腾讯“私有云”上分别对3个算法进行了SQL实现和实验, 并记录了主要的过程数据. 为简化实验过程, 连接查询采用同一轨迹数据表的自连接, 故tab1和tab2的记录集相同, 记录数为n.
DPCP-CROSS-JOIN算法的主要过程包括, 首先通过Java编写的并行批处理程序循环提交每个日期分区“一天”的轨迹数据连接查询任务, 任务依算法4实现, 计算出γ1、γ2和γ3. 因为γ1、γ2和γ3逻辑上可分, 计算结果可合并, 故其计算通过并行方式提交至服务集群. 然后, 将γ1、γ2和γ3按照日期和网格区域分区进行二级分区并写入连接结果表.
DPCP-JOIN算法和DP-JOIN比较简单, 直接通过工具循环提交每一天的轨迹数据, 并分别按照第3.2节所述的关联方式完成连接查询, 并把结果β、α存入对应的表中.
为便于比对优化效果, 在查询过程中, 详细记录了每个日期分区对应的轨迹数据连接查询过程中的任务划分、执行查询的任务数、集群资源占用、时间消耗等数据. 实验环境、工具和数据预处理, 实验过程及记录详见第4.1–4.6节.
4.1 实验软硬件环境此实验环境包含75个节点, 每个节点含24个VCores和40 GB内存. 分配的实验租户内存1.8 TB, HDFS存储容量200 TB. 在进行本实验前, 已对Hadoop后台各类参数进行了反复优化和调整. Hive采用的版本是3.1.2, 相关大数据组件及版本见表3.
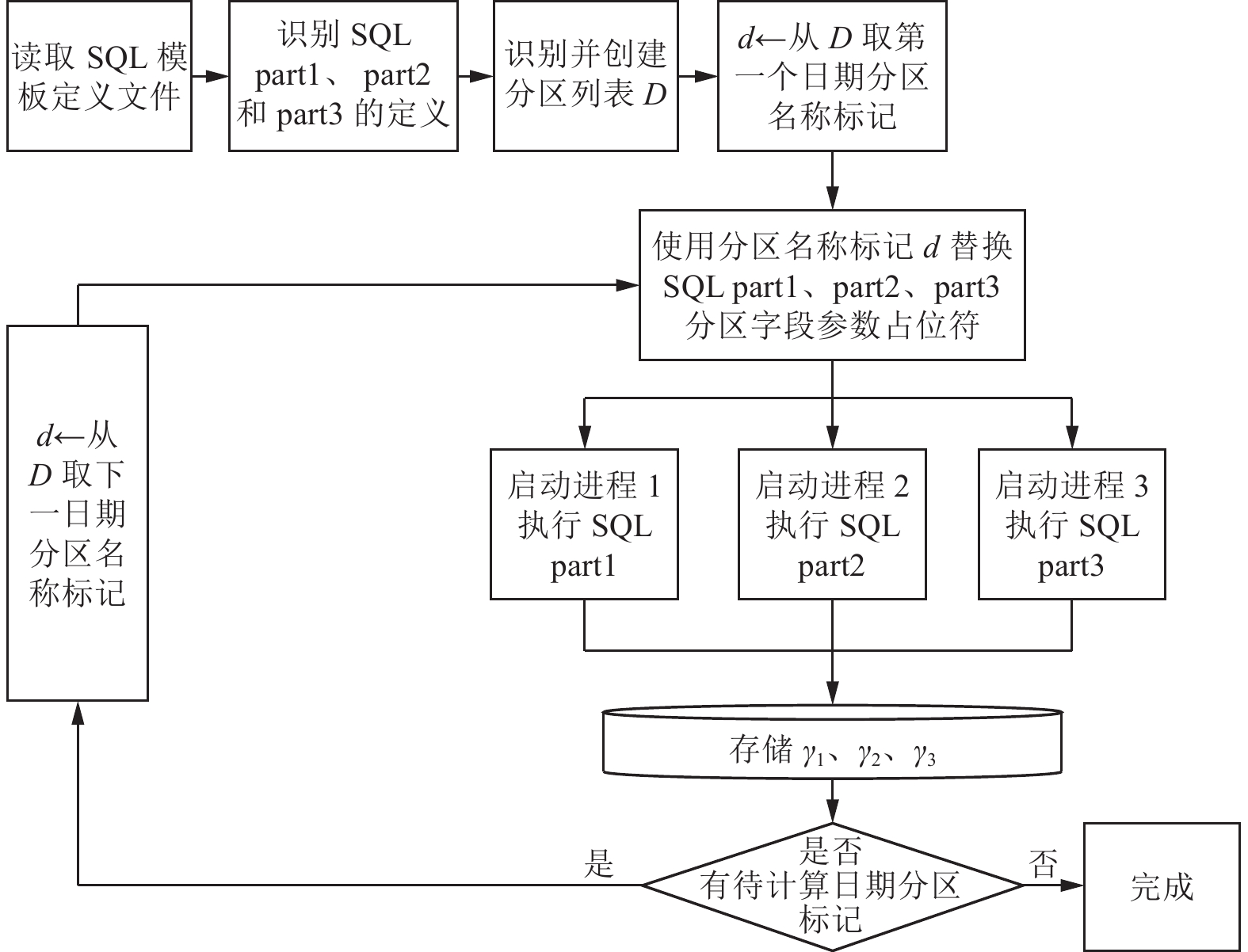
4.2 并行提交工具为实现自动及并行按日期分区提交连接查询SQL语句, 使用Java语言开发程序, JDK版本17.0.1. 工具的主要处理流程见图4. 本文的用到连接查询语句, 都使用模板进行定义, 涉及需要循环执行的日期分区信息通过占位符进行表达, 执行过程中依次取出每个日期分区参数列表中的内容替换占位符内容, 然后启动进程将连接查询语句提交至HiveServer2端执行.
| 表 3 大数据组件及编程环境 |
|
图 4 工具并行处理流程 |
4.3 仅按日期分区存储连接查询
DP-JOIN算法的第7个步骤对应的主要连接查询语句见SQL 01.
SQL 01
SELECT t1.c, t1.oid, t1.t, t2.oid AS oid2, t2.t AS t2, t1.u – t2.u AS ts, t1.dp FROM (SELECT * FROM t_ost_dp WHERE dp = [:d]) AS t1 JOIN (SELECT * FROM t_ost_dp WHERE dp = [:d]) AS t2 ON t1.c = t2.c AND abs(t1.u – t2.u) <= 5
SQL 01提交到Hive服务后, 连接查询共创建Map1和Map5这2类Map, 平均预分配任务数大约都是2.9个; 创建Reducer 2 、Reducer 3和Reducer 4这4类Reducer, 平均预分配任务分别为55.1、1009和4.7个.
通过实验: 20230501–20230531每个日期分区连接查询时间消耗分别是: 4507 s, 4721 s, 3920 s, 4877 s, 4237 s, 3929 s, 6559 s, 4607 s, 9182 s, 5230 s, 4222 s, 4348 s, 3868 s, 3429 s, 2960 s, 4596 s, 4038 s, 3816 s, 5221 s, 5406 s, 3907 s, 6718 s, 4701 s, 10457 s, 6303 s, 6664 s, 4935 s, 4036 s, 4862 s, 10138 s, 4733 s. 累计耗时161127 s (约44.76 h), 平均每天数据的连接查询消耗5197.65 s (约1.44 h).
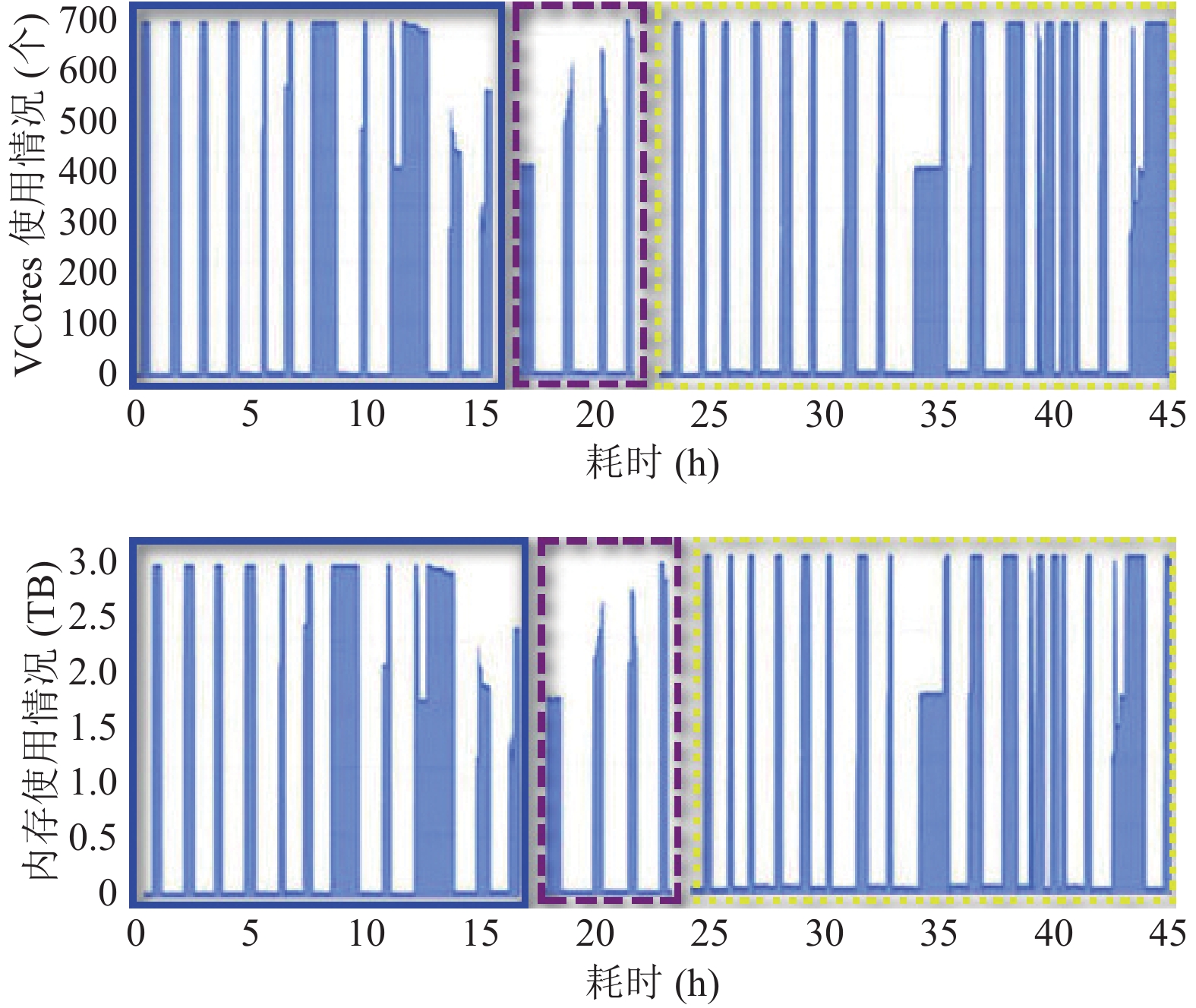
使用DP-JOIN算法执行连接查询, 由于耗时过多, 因未在一次实验完成31个日期分区数据的连接查询, 故实验依日期分区先后顺序进行了3次(对应集群资源消耗用蓝色实线、紫色线段、黄色点线框定), 任务执行期间集群CPU和内存使用及消耗是紧密正相关的, 具体资源消耗情况见图5.
|
图 5 DP-JOIN连接查询集群资源消耗 |
4.4 两级分区存储连接查询
DPCP-JOIN算法的第7个步骤对应的主要连接查询语句见SQL 02.
SQL 02
SELECT t1.c, t1.oid, t1.t, t2.oid AS oid2, t2.t AS t2, t1.u – t2.u AS ts, t1.dp FROM (SELECT * FROM t_ost_dpcp WHERE dp = [:d]) AS t1 JOIN (SELECT * FROM t_ost_dpcp WHERE dp = [:d]) AS t2 ON cp = t2.cp AND t1.c = t2.c AND abs(t1.u – t2.u) <= 5
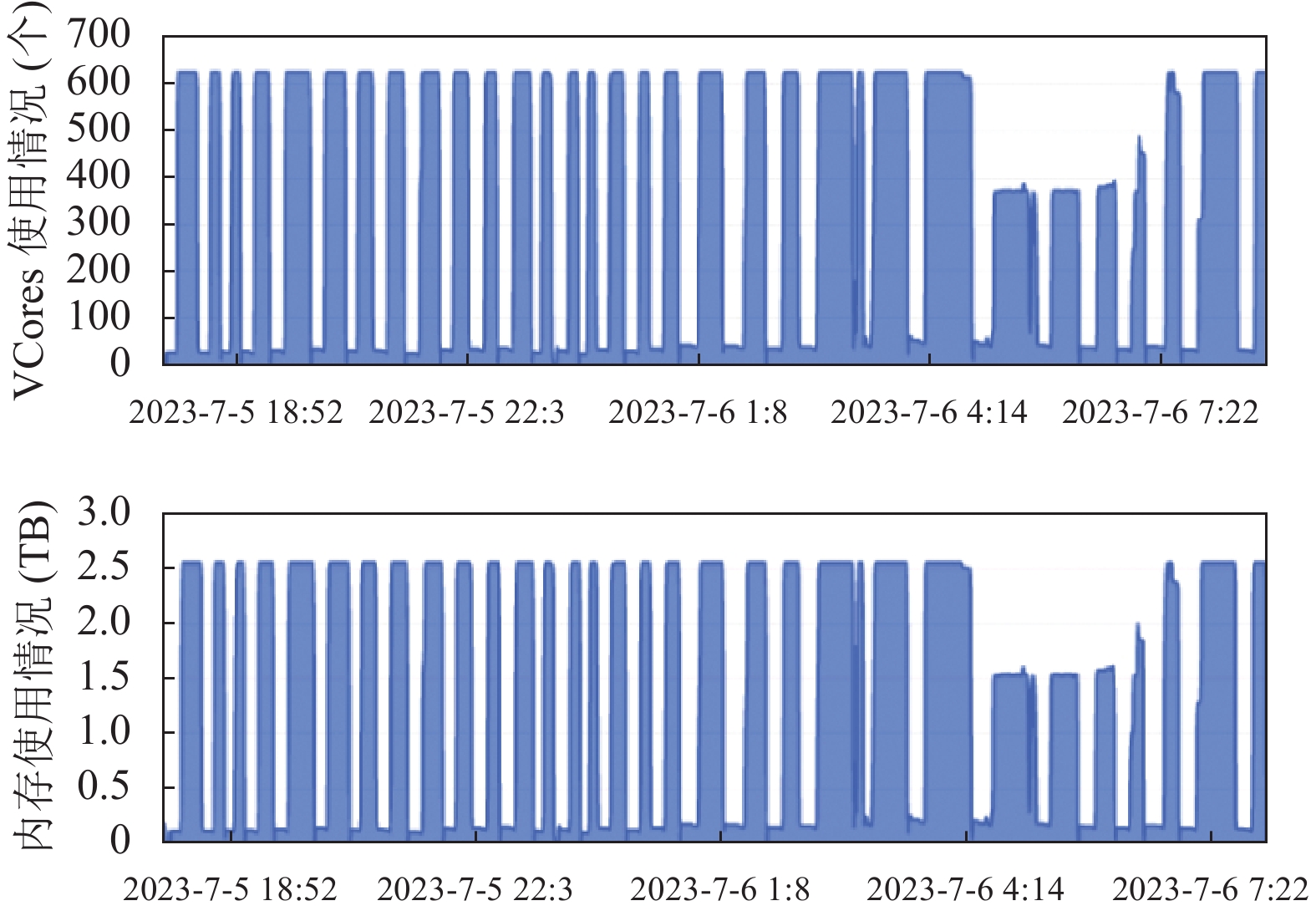
SQL 02提交到Hive及Hadoop后, 连接查询共创建Map1和Map5这2类Map, 平均预分配任务数都是32个; 创建Reducer 2 、Reducer 3、Reducer 4这4类Reducer, 平均预分配任务分别为216.2个、1009个和145.7个. 20230501–20230531每个日期分区数据连接查询时间消耗分别是: 1570 s, 1144 s, 1100 s, 1504 s, 1999 s, 1786 s, 1224 s, 1568 s, 1742 s, 1482 s, 1364 s, 1674 s, 1148 s, 1161 s, 838 s, 1370 s, 1140 s, 1404 s, 2308 s, 2002 s, 1548 s, 2735 s, 2635 s, 3230 s, 2677 s, 2472 s, 1896 s, 1414 s, 1814 s, 2958 s, 1490 s. 累计耗时54397 s (约15.11 h), 平均执行一天数据的连接查询消耗1754.74 s (约0.49 h). 使用DPCP-JOIN算法执行连接查询期间集群CPU和内存使用及消耗同样是紧密正相关的, 具体资源消耗情况见图6.
|
图 6 DPCP-JOIN连接查询集群资源消耗 |
4.5 三级索引四级加速连接查询
DPCP-CROSS-JOIN算法对应的交叉连接查询SQL语句共分3个部分, 对应的连接查询语句包括SQL 03 part1、SQL 03 part2和SQL 03 part3, 即DPCP-CROSS-JOIN算法中的第9、13、17这3行, 以并发方式提交执行. 实验期间集群资源相对充裕, part1、part2和part3并发执行SQL实现了并行执行.
SQL 03 part1
SELECT t1.c, t1.oid, t1.t, t2.oid AS oid2, t2.t AS t2, t1.u – t2.u AS ts, t1.dp FROM (SELECT * FROM ots_dpcp_cc WHERE dp = [:d]) AS t1 JOIN (SELECT * FROM ots_dpcp_cc WHERE dp = [:d]) AS t2 ON cp = t2.cp AND t1.c = t2.c AND t1.s = t2.s WHERE abs(t1.u – t2.u) <= 5
SQL 03 part2
SELECT t1.c, t1.oid, t1.t, t2.oid AS oid2, t2.t AS t2, t1.u – t2.u AS ts, t1.dp FROM (SELECT * FROM ots_dpcp_cc WHERE dp = [:d]) AS t1 JOIN (SELECT * FROM ots_dpcp_cc WHERE dp = [:d]) AS t2 ON cp = t2.cp AND t1.c = t2.c AND t1.s = t2.sa AND t1.se = t2.sae WHERE abs(t1.u – t2.u) <= 5
SQL 03 part3
SELECT t1.c, t1.oid, t1.t, t2.oid AS oid2, t2.t AS t2, t1.u – t2.u AS ts, t1.dp FROM (SELECT * FROM ots_dpcp_cc WHERE dp = [:d]) AS t1 JOIN (SELECT * FROM ots_dpcp_cc WHERE dp = [:d]) AS t2 ON cp = t2.cp AND t1.c = t2.c AND t1.s = t2.sb AND t1.se = t2.sbe WHERE abs(t1.u – t2.u) <= 5
SQL 03的3个部分的连接查询语句以并行方式提交到Hive服务, 每个日期分区连接查询平均集群资源分配Map和Reducer数量见表4.
| 表 4 Hadoop集群平均资源分配 (DPCP-CROSS-JOIN) |
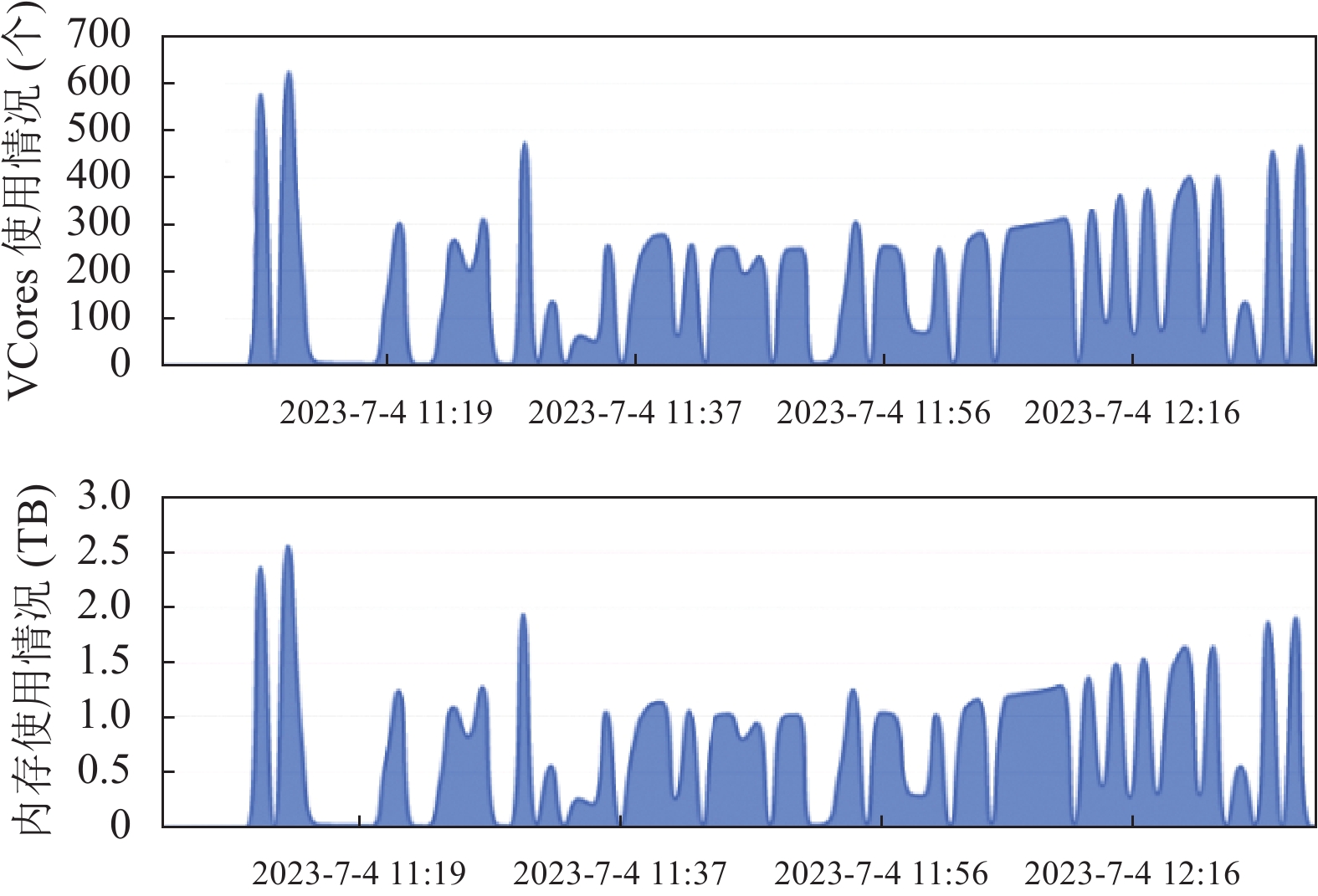
使用DPCP-CROSS-JOIN算法执行连接查询耗时秒数见表5, 期间集群CPU和内存使用及消耗见图7. 并发执行完SQL 03的每个日期分区d的3个部分part1、part2和part3连接查询共耗时间5255 s (约1.46 h), 仅为表5所示的每个日期分区3个部分耗时合计14809 s的37.3%, 系并行加速带来的优势, 平均执行一天数据的连接查询消耗169.53 s (约0.05 h).
| 表 5 DPCP_ CROSS-JOIN连接查询耗时(s) |
4.6 更大规模数据连接查询扩展实验
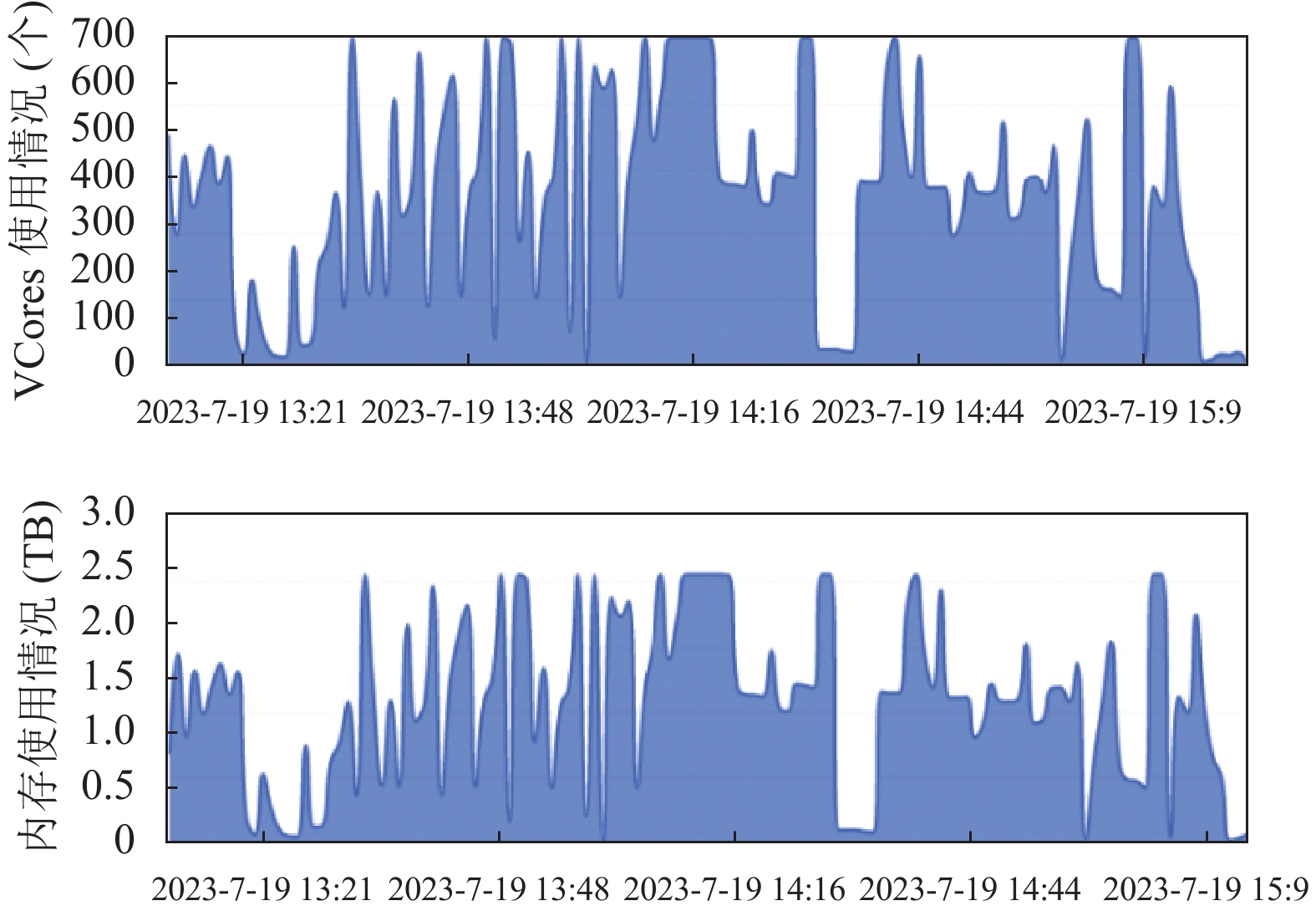
使用DPCP-CROSS-JOIN算法, 实验数据扩大10倍, 同样选取31个日期分区数据共计(485 GB, 59.6亿条)数据进行连接查询. DP-JOIN算法和DPCP-JOIN算法面对更大规模数据时, 仅执行1个日期分区数据的同时空连接查询时间消耗都超过6 h, 难以满足业务需求, 故未进行进一步的实验. 使用DPCP-CROSS-JOIN算法完成31个日期分区数据的同时空连接查询共耗时6960 s, 计算10倍于第4.5节实验的数据仅多消耗1705 s, 多耗时32.45%. 连接查询期间集群资源消耗图8所示.
|
图 7 DPCP-CROSS-JOIN连接查询集群资源消耗 |
|
图 8 DPCP-CROSS-JOIN更大规模连接查询资源消耗 |
5 实验数据分析
本节主要对DPCP-CROSS-JOIN、DPCP-JOIN和DP-JOIN实验过程中集群资源利用情况, 执行任务的Map、Reduce数量, 各算法执行相同任务的时间消耗情况进行对比分析. 实验结果表明: DPCP-CROSS-JOIN算法相比DP-JOIN算法, 连接查询性能提升了30.66倍, 总体性能提升21.38倍, 相比DPCP-JOIN算法也有明显提升, 能更好适用于低“算力”条件下时空轨迹类数据的快速连接查询. 第4.6节的扩展实验数据每个日期分区数据规模平均达1.92亿条, 在使用DPCP-JOIN和DP-JOIN在本文的实验环境下执行6 h以上都未计算出结果的情况下, DPCP-CROSS-JOIN算法每个日期分区对应数据的连接查询仍然能在5 min以内完成, 进一步说明的算法的连接查询性能提升明显, 而且非常稳定.
5.1 通过分区索引优化的连接查询效率提升有限显然通过连常规接查询计算
相比较于DP-JOIN算法, DPCP-JOIN算法通过日期分区(dp)+空间位置网格区域分区(cp)二级分区, 降减少每次连接查询的加载的数据规模, 增加了并行的Map和Reducer数, 一定程度上减少每次连接查询比对和时间差的计算次数, 但是由于连接条件存在复杂表达式, 每次进行连接都要计算和所有记录的时间差, 导致Hadoop的TEZ等引擎无法利用Map阶段的排序结果, 故连接查询性能提升有限, 耗时仍然多. 通过分析DPCP-JOIN算法可知, 同一日期分区的tab1和tab2记录进行连接查询时, tab1的每一条记录首先判定tab2表记录的空间网格区域分区相同是否相等, 然后再计算日期分区内对应的所有记录采集时间差后判断, 计算次数为n2/Size(cp), 查询效率有了一定提升, 但还是存在TEZ等引擎无法利用Map阶段的排序结果, 导致引擎优化失效的问题, 因此该算法的时间复杂度仍是O(n2).
因为此次实验将空间网格进一步划分为了32个区域作为分区, 故Size(cp) = 32, 故时间差的计算次数仅是DP-JOIN算法的1/32. 实验结果表明, DPCP-JOIN算法所采取的时空二重分区索引方法的时间消耗为DP-JOIN算法的33.76%.
5.2 DPCP-CROSS-JOIN连接查询效率高DPCP-CROSS-JOIN算法在DPCP-JOIN算法的基础上, 结合交叉编码, 在极大地减少每次连接查询的加载的数据规模的基础上, 通过时间编码进行“等值”连接, 可充分利用集群计算引擎(如MapReduce、TEZ)的优化能力, 实现类似“日期分区+空间分区+交叉编码索引”三级加速的效果.
通过分析DPCP-CROSS-JOIN算法可知, 同一日期分区的tab1和tab2记录连接关联计算次数主要如下.
(1)首先判断 tab1记录与tab2表记录的空间网格区域分区相同是否相等, 按照等值连接可利用Map阶段排序结果的优势, 完成一条记录的连接需log(Size(cp))次判断.
(2)再在同一个空间网格区域内, 查找是有满足关联条件的网格, 平均判断次数为log(n/Size(cp)) .
(3)然后再判断时间编码是否相等, 由于已经将复杂表达式连接优化为了等值连接, 可以充分利用Map阶段的排序结果, 在有序表中查找条件可能符合的记录比对判断(logn) 次. 因此完成一条记录γ1、γ2和γ3共计需要比对3logn次, 比对完成n条需(3nlogn)次判断.
(4)最后连接结果根据u1与u2的时间差过滤, 共需比较2kn次, 包含γ1的kn次计算及过滤, γ2、γ3各kn/2次计算及过滤(kn为连接后的结果表记录数, 其中k远小于n).
(5)综合上述4项, 其主要比较次数为nlog(Size(cp)) + nlog(n/Size(cp)) + 3nlogn + 2n.
通过上述步骤分析可知该算法总的时间复杂度为O(nlogn). 在相同集群及相同租户资源分配环境下, DPCP-CROSS-JOIN算法把DPCP-JOIN算法中需要通过复杂表达式计算才能进行的连接转换为交叉编码法的“等值”连接实现, 避免了连接条件之一的时间差绝对值的实时和反复计算. 计算γ1、γ2和γ3的3个子算法相互独立, 故可通过并行提交相应SQL, 进一步提高了资源利用率.
从表6可以看出, 集群为DPCP-CROSS-JOIN算法分配的Map 1、Map 5、Reducer 2和Reducer 3对应的任务要远多于DP-JOIN算法和DPCP-JOIN算法, 资源利用率得到了提高. 从图8可以看出, 任务执行期间, DPCP-CROSS-JOIN算法所占用的集群资源相对较均衡, VCores和内存占用都明显少于DP-JOIN算法和DPCP-JOIN算法.
| 表 6 3种算法对应连接查询集群资源分配对比表 |
DP-JOIN、DPCP-JOIN和DPCP-CROSS-JOIN算法业务目标相同, 执行耗时比较见统计表7.
| 表 7 3种算法对应连接查询时间消耗对比表 |
由表7数据可得到以下结论.
(1) DPCP-JOIN相比DP-JOIN, 其性能有所提升. 实验结果数据表明其连接查询性能提升了2.96倍, 总体性能提升2.94倍.
(2) DPCP-CROSS-JOIN相比DP-JOIN, 其性能提升明显. 实验结果数据表明其连接查询性能提升了30.66倍, 总体性能提升21.38倍.
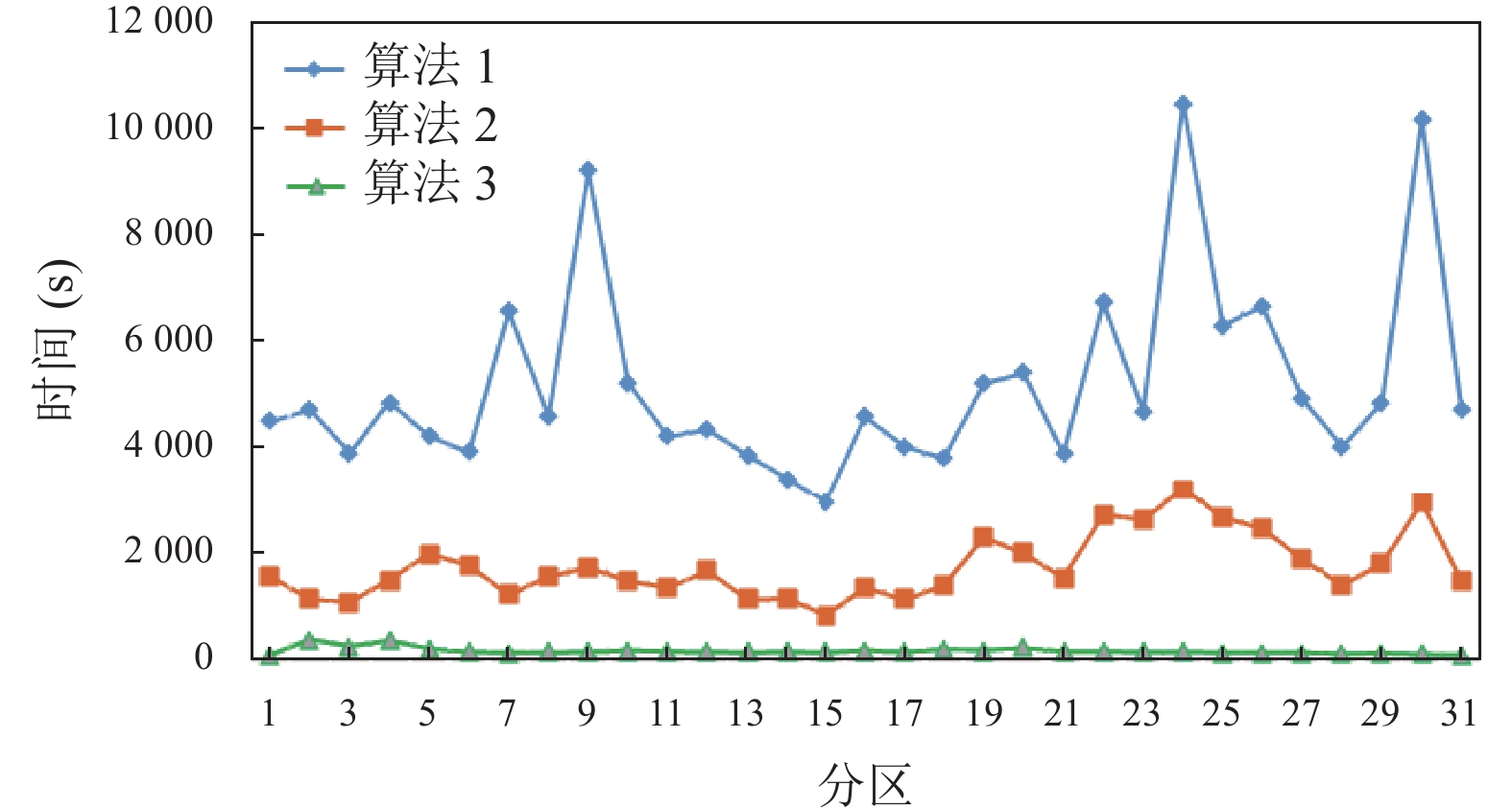
从图9可以看出, 一是处理相同规模数据连接查询时, DPCP-CROSS-JOIN算法时间消耗最小; 二是DPCP-CROSS-JOIN算法在每个日期分区, 即每天数据的连接查询时间消耗波动幅度不大, 整体运行稳定.
|
图 9 3种算法各日期分区连接查询时间消耗对比 |
5.3 存在的问题
采用DPCP-CROSS-JOIN算法优化连接查询, 性能提升显著而且更稳定, 但也存在如下问题.
(1) 进行DPCP-CROSS-JOIN算法连接查询之前先要对数据进行交叉编码, 需消耗一定时间.
(2) 交叉编码后每条记录增加了6个编码相关字段, 会额外占用存储. 本次选择的实验数据21.6 GB, 通过交叉编码后47.4 GB, 存储空间增加了1.19倍.
(3) 该算法适用于Hive等行式存储的关系或者类似的其他关系数据库环境, 在图数库等非关系数据以及HBase等列式存储的数据库环境下适用性有待进一步验证.
6 结语通过DPCP-CROSS-JOIN算法, 可实现低集群计算资源即: 低“算力”环境下大规模时空轨迹类数据同时空关系的高效连接查询, 可通过提高算法效率弥补市、县级公安机关当前存在的“算力”不足问题, 又能解决完成“全量”对象间同时空关系计算的现实需求. 通过该算法对时空类关系数据连接查询的优化, 可将n·n对象间同时空关系查询的时间复杂度从O(n2)降为O(nlogn). 在进行大规模数据的连接查询时, 性能稳定, 并能将连接查询效率最高提升至普通日期分区表优化查询的30.66倍. 在该算法实现连接查询过程中, 虽然需要增加一些额外的存储空间, 但总体性能最高提升至了21.38倍, 瑕不掩瑜. 这种方法可作为时空轨迹伴随查找, 不同对象间关系亲密度判定等算法的原子算法. 可广泛应用于维护国家安全、预防和打击犯罪等领域, 也可用于人员流量分析, 人员群落稳定性分析, 辅助区域城乡规划等领域. 当然本次研究主要针对的是Hadoop生态, Hive数仓内的连接查询优化, 在其他数据库或者数据仓库环境里的必要性和适应性, 还需要更多学者进行更深入的研究和实践.
| [1] |
高强, 张凤荔, 王瑞锦, 等. 轨迹大数据: 数据处理关键技术研究综述. 软件学报, 2017, 28(4): 959-992. DOI:10.13328/j.cnki.jos.005143 |
| [2] |
王家耀, 武芳, 郭建忠, 等. 时空大数据面临的挑战与机遇. 测绘科学, 2017, 42(7): 1-7. DOI:10.16251/j.cnki.1009-2307.2017.07.001 |
| [3] |
陈叶旺, 曹海露, 陈谊, 等. 面向大规模数据的DBSCAN加速算法综述. 计算机研究与发展, 2023, 60(9): 2028-2047. |
| [4] |
赵彦荣, 王伟平, 孟丹, 等. 基于Hadoop的高效连接查询处理算法CHMJ. 软件学报, 2012, 23(8): 2032-2041. DOI:10.3724/SP.J.1001.2012.04124 |
| [5] |
王华进, 黎建辉, 沈志宏, 等. 基于ORC元数据的Hive Join查询Reducer负载均衡方法. 计算机科学, 2018, 45(3): 160-166. DOI:10.11896/j.issn.1002-137X.2018.03.025 |
| [6] |
马东, 周帅锋, 郑伟, 等. 一种Hive中大小表关联的优化方法: 中国, 201710032231.4. 2021-10-19.
|
| [7] |
吴锦坤, 张金波, 张睿智, 等. 一种用于Hive-SQL执行效率的提升方法及系统: 中国, 202111611070. 2022-05-13.
|
| [8] |
Kulkarni A, Dharmadhikari S, Emmanuel M. Enhancing HiveQL engine using Map-Join-Reduce. Data Mining & Knowledge Engineering, 2013, 5(1): 9–12.
|
| [9] |
郑灵逸, 李擎. 一种基于HiveSQL的增加任务并行度与建立中间表组合的优化查询方法. 现代计算机, 2021, 27(36): 55-59. DOI:10.3969/j.issn.1007-1423.2021.36.010 |
| [10] |
Margoor A, Bhosale M. Improving join reordering for large scale distributed computing. Proceedings of the 2020 IEEE International Conference on Big Data (Big Data). Atlanta: IEEE, 2020. 2812–2819. [doi: 10.1109/BigData50022.2020.9378281]
|
| [11] |
齐恒, 张志齐, 文瑞, 等. 大规模轨迹数据时空伴随者查询方法和系统: 中国, 202211362098.6. 2023-07-14.
|
| [12] |
Sahal R, Nihad M, Khafagy MH, et al. iHOME: Index-based join query optimization for limited big data storage. Journal of Grid Computing, 2018, 16(2): 345-380. DOI:10.1007/s10723-018-9431-9 |
| [13] |
Costa E, Costa C, Santos MY. Evaluating partitioning and bucketing strategies for Hive-based big data warehousing systems. Journal of Big Data, 2019, 6: 34. DOI:10.1186/S40537-019-0196-1 |
| [14] |
Arpitha P, Kumar PV. Efficient query optimization in data warehouse using indexing & partitioning techniques by limit clause. International Journal of Engineering Science and Computing, 2019, 9(1): 19561–19566.
|
| [15] |
Xia DW, Lu XN, Li HQ, et al. A MapReduce-based parallel frequent pattern growth algorithm for spatiotemporal association analysis of mobile trajectory big data. Complexity, 2018, 2018: Paper ID 2818251. DOI:10.1155/2018/2818251 |
| [16] |
房俊, 李冬, 郭会云, 等. 面向海量交通数据的HBase时空索引. 计算机应用, 2017, 37(2): 311-315. DOI:10.11772/j.issn.1001-9081.2017.02.0311 |
| [17] |
Zhao P, Rao WX, Zhang CX, et al. SST: Synchronized spatial-temporal trajectory similarity search. Geoinformatica, 2020, 24(4): 777-800. DOI:10.1007/s10707-020-00405-y |
| [18] |
Jin FM, Hua W, Zhou T, et al. Trajectory-based spatiotemporal entity linking. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(9): 4499-4513. DOI:10.1109/TKDE.2020.3036633 |
| [19] |
Qin WW, Zhang MF, Li W, et al. Spatiotemporal K-nearest neighbors algorithm and Bayesian approach for estimating urban link travel time distribution from sparse GPS trajectories. IEEE Intelligent Transportation Systems Magazine, 2023, 15(6): 152-176. DOI:10.1109/MITS.2023.3296331 |
| [20] |
王晨旭, 汪谨权, 杨鑫. 基于二级时空分桶的伴随轨迹查询. 计算机学报, 2024, 47(1): 131-147. |
| [21] |
Dwivedi M, Agrawal D. Performance optimization of Hive by two-way join. International Journal of Modern Engineering and Research Technology, 2017, 4(4): 14-20. |
| [22] |
Kadari P, Potluri A, Sristy NB, et al. Skew aware partitioning techniques for multi-way spatial join. Proceedings of the 7th International Conference on Mining Intelligence and Knowledge Exploration. Goa: Springer, 2019. 52–61.
|
| [23] |
何文婷, 程学旗, 郑天祺, 等. 一种非等值关联子查询的优化方法和系统: 中国, 201810097136.7. 2020-12-25.
|
| [24] |
陈喜洲. 一种基于业务特征优化Hive中两个大表不等值关联的方法. 广东通信技术, 2017, 37(11): 52-55. DOI:10.3969/j.issn.1006-6403.2017.11.011 |
 2024, Vol. 33
2024, Vol. 33

