随着物联网设备数量的爆炸式增加, 到达网络的服务请求正变得密集和多样化, 传统的网络设备为硬件专用, 其功能由硬件和软件紧密耦合实现, 难以灵活适应网络请求. NFV是一种很有应用前景的技术, 为物联网中5G设备实现超低时延、高带宽等不同的性能需求奠定了基础^[1], 其通过将传统网络中专用的硬件中间件(例如防火墙、入侵检测系统、网络地址转换器)转变为通用设备上基于软件的虚拟网络功能(virtual network function, VNF)实例, 使底层异构的网络资源成为服务共享的公共基础设施, 提升了服务的灵活性和弹性, 从而可以满足用户指数级增长的服务需求, 同时能够控制资本支出和运营成本.

到达网络的用户服务请求由NFV实例化为服务功能链(service function chain, SFC), 它由一组有序虚拟网络功能构成, 如图1中的SFC示例所示. 利用NFV技术, SFC可以在底层网络之间进行服务和资源编排, 以实现更灵活和高效的资源分配^[2]. SFC编排过程是指服务提供商在NFV网络中按序对组成SFC的VNF进行资源分配和优化, 进行流量引导和控制, 在满足资源约束的同时优化不同网络服务的编排需求, 实现端到端的服务的过程^[3]. 先前的研究对单域SFC的编排做出了贡献^[4–7], 推动了NFV学术研究和工业应用的发展, 然而这些工作大多没有考虑多域场景(即SFC需要部署在不同的域上), 随着边缘计算和物联网的兴起, 服务提供商正在将服务从集中式云转移到边缘网络, 而由于边缘网络缺乏资源、严格的延迟或服务质量需求, 单个边缘网络难以覆盖各类服务功能, 因此多个基础设施提供商(infrastructure provider, InP)会达成合作协议, 组成多个InP管理的多域网络, 实现资源共享, 从而提升整体服务收益.

图1展示了多域SFC编排场景, 物联网中如虚拟现实、视频聊天等网络请求被实例化为SFC通过接入网络发送到多个InP管理的边缘网络在不同InP管理的域中进行编排, 其流量依次通过被部署在3个域的VNF, 从起点(src)到达终点(dst)实现端到端的服务, 如果需要进一步分析则发送到核心网络进行处理.

现有的多域SFC编排算法分为集中式和分布式^[8]. Guo等人^[9]提出基于强化学习的编排算法优化编排成本. Sarrigiannis等人^[10]建立了基于本地域和外部域的架构, 并提出了一种基于跳数的启发式算法来降低SFC编排的成本. Zhang等人^[11]利用Dijkstra算法提出启发式服务编排算法, 对服务成本进行了优化. 然而, 与单域SFC编排不同, 由于多域网络安全和业务竞争问题, InP不愿意共享其拓扑和内部策略信息, 因此这些方法不适合信息公开有限的场景. 为了维护InP的隔离性和隐私性, Sun等人^[12]基于边界网关协议^[13]对多域网络进行了抽象, 然后对时延和负载均衡进行了优化. Joshi等人^[14]提出pSMART算法通过匹配域中的VNF类型来确定候选路径, 然后根据单个域中部署的VNF类型的历史成功率来选择编排域. Toumi等人^[15]提出了一种集中式跨域SFC编排框架, 设置多域编排器和单域编排器, 从应用层面实现了多域SFC编排过程. 上述研究中, 没有有效的解决域间负载均衡的问题, 使得网络域的服务接受率表现欠佳. Liu等人^[8]和Dalgkitsis等人^[16]提出了分布式编排方法, 但未给出域内的编排算法. Chen等人^[17]提出了一种分布式框架, 其中入口编排器确定最短成本路径, 然后沿路径的候选域的编排器确定SFC编排方案. 上述分布式方法避免了信息泄露问题, 但其划分方案需要域间频繁通信才能达成共识, 增加了通信成本和响应延迟.

综合上述研究, 多域SFC的编排面临以下问题, 首先各网络域不愿意披露域内敏感信息来进行SFC编排决策, 导致多域SFC编排时缺少关键信息, 使编排方案效果不佳; 其次先前的研究在进行SFC编排时只考虑了服务的性能, 忽略了域间负载的平衡, 使得各个域负载不均导致服务接受率的降低. 本文针对上述挑战, 首先, 考虑到多域网络由不同的InP管理, 各个InP出于安全、业务竞争等原因, 因此不愿意公开域内的网络拓扑和详细资源信息, 本文基于物理网络设置域级图来隐藏敏感信息, 进一步协调多域资源以实现经济有效且资源高效的网络服务. 其次, 针对域间负载平衡问题, 设计了域负载权重的计算方法, 该计算方法弥补先前研究中使用整个域资源计算权重导致VNF部署失败的缺点, 将该权重的计算细化到域内节点的资源负载, 提高服务接受率. 此外, 物联网中如视频通话等服务, 对服务提供商而言, 针对只有降低成本和提高网络服务性能才能带来有利可图的商业模式^[18], 需要设计算法降低编排成本及服务响应时间.

1 系统模型及问题定义 1.1 物理网络建模

物理网络被建模为无向图$G = (N, L)$, 其中N和L分别是物理服务器节点和节点之间的物理链路的集合. 在多域场景中, 网络由域间链路连接的M个管理域组成. 第i个域可以表示为${G_i} = ({N_i}, {L_i})$. ${{{L}}_{{\rm{inter}}}}$表示域间物理链路的集合. 物理节点${n_i} \in {N_i}$的总计算资源容量和剩余资源分别记为$n_i^{\rm cpu}$和$n_i^{\rm resd}$. 此外, 用${\phi _{{n_i}}}$来表示${n_i}$的邻居节点, $l_i^{n, m} \in {L_i}\;(n \in {N_i}, m \in {\phi _{{n_i}}})$表示节点n和m之间的连接链路. 同一域内节点n和m之间的链路带宽容量和通信延迟分别表示为${b^{l_i^{n, m}}}$和${d^{l_i^{n, m}}}$, 同时域间链路的带宽和时延分别表示为${{{b}}^{{{l}}_{{\rm{inter}}}^{{{n, m}}}}}$和${{{d}}^{{{l}}_{{\rm{inter}}}^{{{n, m}}}}},$其中${{l}}_{{\rm{inter}}}^{{{n, m}}} \in {{{L}}_{{\rm{inter}}}}.$

1.2 SFC建模

SFC被建模为有向图, 每个SFC请求$r \in R$表示为$r = ({N^r}, {L^r}, {\eta ^r}, src, dst, dl{y^r})$, 其中${N^r}$和${E^r}$分别表示SFC请求的虚拟功能节点和虚拟链路集合. 对于请求节点$n_j^r \in {N^r}(1 \leqslant j \leqslant \left| {{N^r}} \right|)$, $de{m^{n_j^r}}$表示节点$n_j^r$的计算资源需求. 然后, $l_k^r \in {L^r}\;(1 \leqslant k \leqslant \left| {{N^r}} \right| - 1)$是连接两个相邻虚拟节点$n_k^r$和$n_{k + 1}^r$的虚拟链路. ${\eta ^r}$为SFC请求的带宽需求, $src$和$dst$为每个SFC请求流量的入口和出口, $dl{y^r}$为完成请求的最大容忍延迟.

1.3 域级图建模

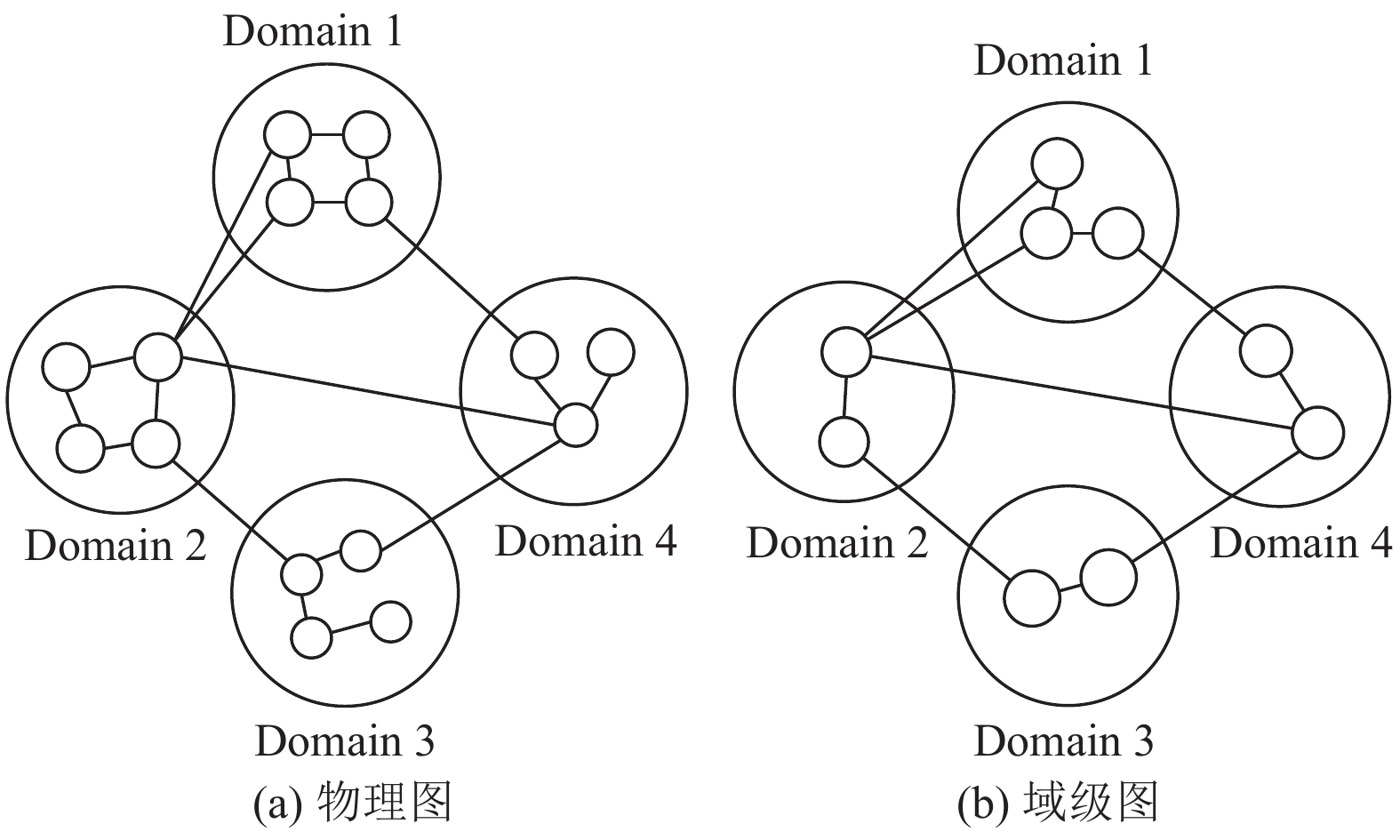
为保证域内资源信息的隐私性, 将图2(a)的物理拓扑进行抽象, 构建了域级图如图2(b), 保留了域间链路及其端点. 域级图被建模为${G_D} = (W, I)$, 其中W为每个域的权重参数集合, I是域间链路资源信息集合, 该集合包含了域间链路时延、带宽容量和单价. 域i的权重${W_i} \in W$为域中节点的平均可用资源, 旨在加强域内可用资源丰富且域内负载节点较少的域的服务部署, 实现域间负载均衡, 并提高请求接受率. ${W_i}$由式(1)表示.

$ {W_i} =\dfrac{{\dfrac{1}{{|{N_i}|}} \cdot \displaystyle\sum\limits_{{n_i} \in {N_i}} {\dfrac{{n_i^{\rm resd}}}{{n_i^{\rm cpu}}}} }}{{\displaystyle\sum\limits_{i = 1}^M {\left(\dfrac{1}{{|{N_i}|}} \cdot \sum\limits_{{n_i} \in {N_i}} {\dfrac{{n_i^{\rm resd}}}{{n_i^{\rm cpu}}}} \right)} }} $

(1)

1.4 编排成本优化

多域SFC编排需要跨域进行服务部署对成本和响应时间提出了更严格的要求, 因此本文提出资源感知的编排算法旨在实现编排成本最小化. 针对每个InP基于商业因素并没有公开域内资源信息的现实情况, 因此编排成本分为域间成本${{{C}}_{{\rm{inter}}}}$和域内成本${{{C}}_{{\rm{intra}}}}$两部分, 目标函数如下:

$ \min {{C}} = \min ({{{C}}_{{\rm{inter}}}} + {{{C}}_{{\rm{intra}}}}) $

(2)

● 域间成本最小化: 将域级图与SFC的src和dst结合起来, 最小化域间链路成本, 从而确定多域编排的候选路径. 域间链路成本的目标函数${C_{\rm{inter}}}$如下:

$ {{{C}}_{{\rm{inter}}}} = \sum\limits_{e_k^r \in {E^r}} {\sum\limits_{e_{\rm inter}^{n, m} \in {E_{\rm inter}}} {\beta _{\rm inter}^{n, m}} } \cdot {\eta ^r} \cdot {y^{l_k^r, l_{\rm inter}^{n, m}}} $

(3)

其中, $\beta _{\rm inter}^{n, m}$为域间链路带宽单价, ${y^{l_k^r, l_{\rm inter}^{n, m}}}$为决策变量, 该值为1时表示虚拟链路$l_k^r$被部署在物理链路${{l}}_{{\rm {inter}}}^{{{n, m}}}$上, 否则为未部署.

● 域内成本最小化: 单位时间SFC的域内编排成本由节点单位计算成本${C_{\rm comp}}$和单位带宽成本${C_{\rm band}}$组成, 域内编排成本${{{C}}_{{\rm{intra}}}}$可表示为:

$ \begin{split} {{{C}}_{{\rm{intra}}}} = &{C_{\rm comp}} + {C_{\rm band}} \\ = & \sum\limits_{{n_i} \in {N_i}} {\sum\limits_{n_j^r \in {N_r}} {{\alpha _d}} } \cdot de{m_{n_j^r}} \cdot {x^{n_j^r, {n_i}}} + \sum\limits_{n \in {N_i}, m \in {\phi _n}} {\sum\limits_{e_k^r \in {E_r}} {{\beta _d}} } \cdot {\eta ^r} \cdot {y^{l_k^r, l_i^{n, m}}} \end{split} $

(4)

其中, ${\alpha _d}$和${\beta _d}$为域d计算资源和带宽的单价, $ {x^{n_j^r, {n_i}}} $和$ {y^{l_k^r, l_i^{n, m}}} $为决策变量, 当其值为1时, 表示虚拟节点、链路成功部署在物理网络上, 否则部署失败.

上述目标函数必须遵循以下约束.

式(5)约束请求中每个VNF只能被分配一次:

$\sum_{i=1}^{M} \sum\limits_{{n_i} \in {N_i}} {{x^{n_j^r, {n_i}}}} \leqslant 1,\; \forall r \in R , \forall n_j^r \in N^r$

(5)

式(6)为物理节点计算资源容量限制.

$\sum\limits_{n_j^r \in {N^r}} {{x^{n_j^r, {n_i}}}} \cdot de{m^{n_j^r}} \leqslant {{n_i^{\rm resd}}},\; \forall i \in [1,M], \forall {n_i} \in {N_i} $

(6)

式(7)和式(8)分别为域内和域间物理带链路带宽限制.

$\sum\limits_{k = 1}^{|{N^r}| - 1} {{y^{l_k^r, l_{\rm inter}^{n, m}}}} \cdot {\eta ^r} \leqslant {b^{l_i^{n, m}}},\; \forall i \in [1,M], \forall l_i^{m, n} \in {L_i} $

(7)

$ \sum\limits_{k = 1}^{|{N^r}| - 1} {{y^{l_k^r, {{l}}_{{\rm{inter}}}^{{{n, m}}}}}} \cdot {\eta ^r} \leqslant {b^{{{l}}_{{\rm{inter}}}^{{{n, m}}}}},\; \forall {{l}}_{{\rm{inter}}}^{{{m, n}}} \in {{{L}}_{{\rm{inter}}}} $

(8)

式(9)引入延迟约束, 式(10)表示SFC请求的端到端延迟T必须满足最大容忍延迟的约束.

$ \begin{split} T = & {T_{\rm proc}} + {T_{\rm prop}} + {T_{\rm inter}}\\ = & \sum\limits_{{n_i} \in {N_i}} {\sum\limits_{n_j^r \in {N_r}} {{x^{n_j^r, {n_i}}}} } \cdot {t^{n_j^r}} + \sum\limits_{l_i^{n, m} \in {L_i}} {\sum\limits_{l_k^r \in {L_r}} {{y^{l_k^r, l_i^{n, m}}}} } \cdot {d^{l_i^{n, m}}} \\ & + \sum\limits_{l_{\rm inter}^{n, m} \in {{{L}}_{{\rm{inter}}}}} {\sum\limits_{l_k^r \in {L_r}} {{y^{l_k^r, {{l}}_{{\rm{inter}}}^{{{n, m}}}}}} } \cdot {d^{{{l}}_{{\rm{inter}}}^{{{n, m}}}}} \end{split} $

(9)

其中, ${t^{n_j^r}}$为VNF的处理时延.

$ T \leqslant dl{y^r} $

(10)

2 多域服务功能链编排算法 2.1 集中式多域SFC编排算法实现

多域SFC编排方法首先根据优化目标确定一组最优候选域, 然后在每个域中进行SFC编排, 最后将SFC部署到物理网络上. 现有网络中的服务对成本、接受率及响应时间提出了更高的需求. 多域SFC编排被认定为NP难问题^[17], 因此, 本文提出一种集中式多域SFC编排方法(MDSCO), 以在可行的时间内获得接近最优的编排, 主要包括3个部分: 候选域的获取、SFC分块以及域内成本优化编排. 首先在多域编排器处确定候选域, 然后基于候选域的权重进行SFC分块, 分块获得的子SFC被多域编排器发送至各候选域内在域编排器管理下进行编排, 各域编排结束后, 将域内确定的编排方案返回多域编排器, 若失败则返回编排失败结果.

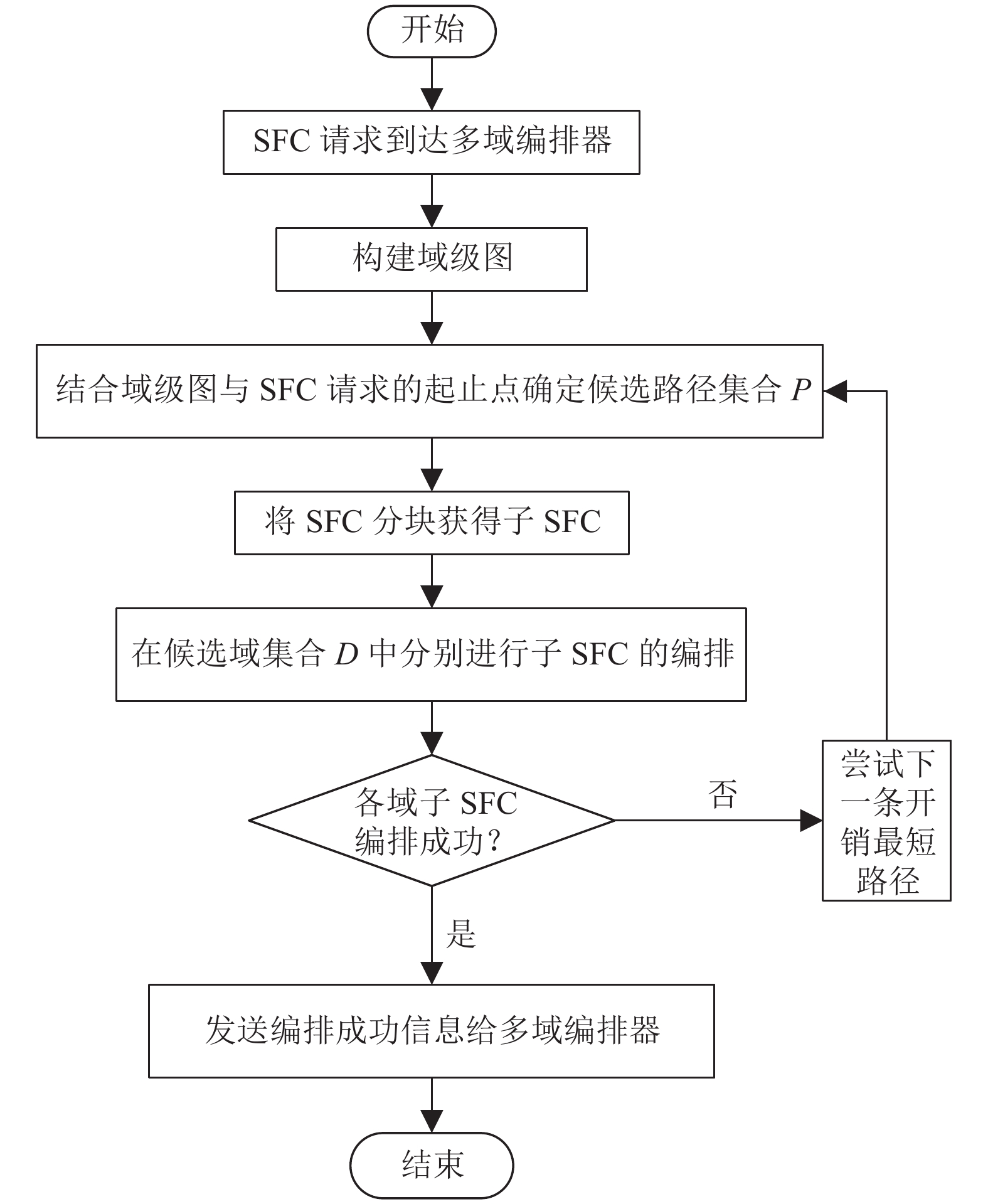
MDSCO的算法流程如图3所示, SFC请求到达多域编排器后, 各网络的InP基于商业因素不公开域内详细资源信息, 因此本文提出了域级图的构建方法隐藏InP的网络拓扑和资源信息; 然后算法将域级图和SFC请求的入口和出口节点相结合, 使用最小化域间成本k最短路算法^[19]确定候选编排路径集合P, 其中候选路径经过的域集为候选编排域集D; 然后算法基于式(1)确定的各域权重进行SFC分块; SFC的分块方案由多域编排器发送至各域的域内编排器, 然后各候选域分别对分配到的子SFC进行编排, 如果某个候选域的子SFC编排失败, 算法将尝试下一条成本最低的候选路径; 反之, 所有候选域都编排成功则向多域编排器返回编排成功的方案.

算法1. 多域SFC编排算法(MDSCO)

输入: SFC请求集合R, 物理网络G.

输出: SFC在多域物理网络的编排方案.

1. 将物理网络抽象为域级图;

2. 将SFC的src和dst与域级图结合确定SFC编排的候选路径集合P, 并根据式(3)计算P的通信成本对候选路径排序;

3. while $\scriptstyle {P^g} \in P \ne \varnothing $ do

4. 　if $\scriptstyle {P^g}$中链路的带宽需求大于物理带宽容量, 则重新选择下一条候选路径进行编排;

5. 　 end if

6. 　根据候选路径$\scriptstyle {P^g}$经过的路径确定候选域集合D;

7. 　 for $\scriptstyle d \in D$ do

8. 　　 调用算法2对子SFC进行域内部署;

9. 　　 if 算法2部署失败, 则选择下个候选域部署;

10.　　end if

11.　end for

12.　if 请求r部署成功并满足时延等约束

13. 　　return 多域SFC编排方案;

14.　end if

15. end while

16. return 请求r编排失败.

多域SFC算法的伪代码见算法1, 算法包含的3部分的具体实现如下.

(1) 候选域的获取: 为了降低多域复杂网络拓扑的编排成本和计算复杂度, 构建候选路径集来过滤管理域从而获取编排候选域, 候选路径的构造方法如下.

将SFC流的入口和出口与算法1第1行抽象获得的域级图相结合, 基于域级图公开的单位域间链路传输成本构建候选路径集P. 第g条最小候选路径$ {P^g} \in P $的单位域间传输成本计算如下:

$ {{{C}}^{{P^g}}} = \sum\nolimits_{p \in {P^{{g}}}} {{{\beta }}_{{\rm{inter}}}^{{p}}} $

(11)

其中, p为物理网络中任意一条域间链路, 将最短路径$ {P^g} $经过的域视为候选域集合D.

(2) SFC分块: 为充分利用各域资源, 避免因各域资源利用不均导致网络拥塞, 违反服务的最大时延容忍约束造成编排失败. 本算法考虑基于各域可用资源的权重进行SFC分块, 实现域间负载均衡, 提高域内子SFC编排的成功率, 从而提高服务接受率, 算法使用域级图中披露的权重集合W对SFC进行分块, 第i个域中子SFC的长度如式(12).

$ le{n_i} = \left\lfloor {\frac{{{W_i}}}{{\displaystyle\sum\limits_{i = 1}^D {{W_i}} }} \cdot len} \right\rfloor $

(12)

$ le{n_{\max}} = le{n_{\max}} + \left(len - \sum\limits_{i = 1}^D l e{n_i}\right) $

(13)

其中, $len$为SFC的长度, $le{n_{\max }}$为权重最大的域中的SFC的长度.

(3) 域内子SFC编排: 通过候选域获取、SFC分块操作多域编排器将SFC划分为多个子SFC, 并将其发送给各域的域内编排器, 各域内的子SFC基于成本最小化的编排的伪代码见算法2. 首先基于算法1选择的路径${P^g}$确定每个子SFC流量的入口和出口, 然后根据式(4)域内成本最小化函数使用k最短路算法确定域内候选编排路径集合${P^d}$; 算法2的第3–9行首先根据候选路径的带宽容量排除不满足带宽容量的候选路径, 然后进行VNF的部署, 淘汰不满足计算资源需求的物理节点, 选择候选路径上的下一个物理节点; 最后将部署结果返回到算法1的多域编排器. 各域编排器将各子SFC的编排结果发送给多域编排器进行确认, 确定最终多域SFC的编排方案.

算法2. 域内子SFC编排

输入: 子SFC请求$\scriptstyle {r_d},$候选路径$\scriptstyle {P^g}.$

输出: $\scriptstyle {r_d}$在域d上的编排方案.

1. 结合$\scriptstyle {P^g}$和域级图信息集合确定域d的src和dst;

2. 使用式(4)求src和dst之间成本最小的路径集合$\scriptstyle {P^d}$;

3. while $\scriptstyle p \in {P^d} \ne \varnothing $ do

4.　 if $\scriptstyle {{p}}$中链路的带宽需求大于物理带宽容量, 选择$\scriptstyle {P^d}$中下一条路径;

5.　 end if

6. 　for $\scriptstyle n_j^r \in {r_d}$ do

7. 　　if 物理节点$\scriptstyle {n_i}$计算资源不能满足$\scriptstyle n_j^r$的需求, 则进入p的下一个物理节点;

8. 　　end if

9. 　end for

10. end while

11. if $\scriptstyle {r_d}$部署成功 return $\scriptstyle {r_d}$部署方案;

12. return $\scriptstyle {r_d}$部署失败.

2.2 MDSCO重新分块算法实现

在域内编排过程中, 由于多域网络未披露域内详细资源信息, 初始分块方案中子SFC可能无法全部编排成功, 为提升算法服务接受率, 本文在MDSCO的基础上提出了SFC的重新分块算法MDSCO-RP. 该算法的思想是当某域内子SFC k条候选路径均编排失败后, 算法不是从整个SFC的起点重新分块, 而是保存SFC编排成功的最长长度(即部署成功的VNF个数最多)的候选路径, 并将该候选路径返回, 然后从下一个候选域开始, 对剩余SFC基于剩余候选域的权重重新分块, 调用算法2对重新分块后的子SFC进行编排.

2.3 时间复杂度分析

MDSCO和MDSCO-RP时间复杂度主要分为两部分: 域间候选域的获取时的时间复杂度${\rm{O}}(k\left| D \right| {{(}}\left| {{L_{\rm inter}}} \right| {{ + }} \left| D \right|\log \left| D \right|{{))}}$ 与算法2在域内编排时的时间复杂度${\rm{O}}{{(k}}\displaystyle\sum\limits_{{{i}} = 1}^{\left| D \right|} {(k\left| {{N_i}} \right|(\left| {{L_i}} \right| + \left| {{N_i}} \right|\log \left| {{N_i}} \right|))} {\text{)}}$之和, 其中k为k最短路候选路径的值, $ \left| D \right| $和$\left| {{L_{\rm inter}}} \right|$为候选域的数量和域间链路的数量, $\left| {{{{N}}_i}} \right|$和$\left| {{{{L}}_i}} \right|$分别为域i中服务节点和链路的数量.

3 实验分析 3.1 实验设置

在本节中, 设置了实验来验证本文提出的算法性能, 仿真实验采用Python语言实现, 实验在CPU Intel(R) Core(TM) i5-7300H的计算机进行. 网络拓扑使用来自Internet Topology Zoo^[20]中的4个拓扑, 其节点和链路设置如表1所示.

(1) 网络拓扑设置: 实验网络设置4个域, 分别使用表1中的4种拓扑, 任意两个域都至少有一条路径连接, 为保证多域信息的隐私性, 域间链路的信息只包含相邻域的链路信息, 根据先前研究^[8,12]设置模拟实验参数, 资源和成本的指标均为虚拟单位. 域中的节点的计算资源和链路的带宽容量分别服从均匀分布400–600个单位和800–1200个单位, 域内节点的单位计算资源价格和带宽价格均服从U(0.1, 0.8). 对于域间链路, 带宽容量服从均匀分布2500–4000个单位, 其单位带宽价格服从均匀分布U(1, 4). 此外, 域内和域间链路时延分别服从均匀分布U(1, 6) 和U(10, 20).

(2) SFC请求设置: SFC由5–10个VNF组成, 其src和dst均匀分布在物理网络中. SFC中VNF的计算资源和带宽需求分别服从均匀分布U(5, 10)和U(10, 20), VNF处理延迟${t^{n_j^r}}$和服务最大容忍时延分别服从均匀分布U(0, 2)和U(10, 100). SFC请求的到达服从平均值为5的泊松分布, SFC的生命周期服从平均单位为1200的指数分布.

(3) 算法对比: 比较了多域SFC编排的3种算法以及本文提出的重新分块算法, 实验设置环境均与本文一致.

1) DFSC^[17]. 该算法为分布式编排算法, 利用SFC源与目的地之间的路径确定候选域, 并从资源单价最低的域开始编排, 最小化目标成本.

2) Heuristic^[11]. 该算法为集中启发式算法, 其未对多域信息进行隐私性操作, 首先基于Dijkstra算法最小化SFC流的源节点和目的节点的带宽成本, 然后减少参与编排的候选域, 将VNF放置在资源利用率少的服务器节点, 提升资源利用率.

3) WGT_LB^[12]. 该算法为集中式算法, 根据域可用资源进行SFC分区, 然后使用贪心算法在域内进行最小化成本编排.

4) MDSCO-RP. 本文第2.2节提出了MDSCO的重新分块算法, 该算法为提升SFC编排成功率, 对MDSCO进行改进.

(4) 指标对比: 算法对比以下指标, 其中实验结果为同一环境设置下重复10次实验的平均数据.

1) 接受率${{AR}}$, 指成功部署编排解决方案的SFC数量与到达的SFC总数的比率, 定义如下:

$ {{AR}} = \frac{{sum(\mathit{successSFC})}}{{sum(\mathit{arrivedSFC})}} $

(14)

其中, ${{sum}}(\mathit{successSFC})$和${{sum}}({\mathit{arrivedSFC}})$分别为成功编排和到达网络的SFC的数量.

2) 平均服务成本${{{C}}^{\rm avg}}$, 指根据编排方案成功部署SFC的平均成本, 定义如下:

$ {C^{\rm avg}} = \frac{{\displaystyle\sum\limits_{r \in {\mathit{successSFC}}} {{C^r}} }}{\mathit{sum(successSFC)}}$

(15)

其中, $ {{{C}}^{{r}}} $为使用式(2)计算的第r个编排成功的请求的服务成本.

3) 平均响应时间${{T}}_{\rm response}^{{\rm{avg}}}$, 指到达SFC的决策时间之和与到达SFC总数的比值, 定义如下:

$ {{T}}_{\rm response}^{\rm avg} = \frac{{\displaystyle\sum\limits_{r \in {\mathit{ArrivedSFC}}} {T_{\rm end}^r - T_{\rm start}^r} }}{{sum({\mathit{arrivedSFC}})}} $

(16)

其中, ${{T}}_{\rm end}^r$和${{T}}_{{\rm{start}}}^r$分别为第r个请求的开始和结束时间.

3.2 实验结果与分析

(1) 不同SFC数量下编排算法对比

图4展示了200–2000个SFC分别输入网络后各算法的表现, 从图4(a)可以看出随着网络中请求数量的增加, 各算法的接受率呈现下降趋势, 其中MDSCO和MDSCO-RP的接受率分别比WGT_LB约低4%和2%, 但如图4(b)所示, 当输入2000个SFC时, WGT_LB的平均服务成本比MDSCO和MDSCO-RP分别高约13%, 这是由于WGT_LB使用贪心算法对网络进行遍历实现部署, 因此服务接受率高于MDSCO和MDSCO-RP, 但贪心算法为提升服务接受率造成的路径折返使其成本优化性能削弱, 而MDSCO和MDSCO-RP权衡了平均服务成本和接受率, 在接受率较高的前提下, 降低了编排成本. 由于DFSC和Heuristic优先考虑编排成本最小化, 均未考虑域间负载平衡, 其中DFSC优先在资源单价较低的域进行编排, 随着请求数量的增加造成该域的资源不足; Heuristic减少参与编排的域, 算法考虑了节点的资源利用率阈值但未考虑节点间链路带宽容量, 同样会导致域内资源不足, DFSC和Heuristic多域资源利用率较低, 其接受率下降趋势最明显. 此外, Heuristic的服务接受率高于DFSC, 这是由于DFSC总是从单价最低的域开始编排, 其多域资源利用率更差. 图4(b)中DFSC的平均服务成本随着请求数量的增多逐渐高于MDSCO, 后比MDSCO低, 这是由于DFSC在请求数量较少时, 其成本优化性能较好, 但随着请求的增加SFC部署到资源单价更高的域中, 其成本优化性能下降; 当SFC的数量高于1000时, 接受率的降低使其服务成本低于MDSCO. 同样的, Heuristic的平均服务成本随着请求数量的增多逐渐高于MDSCO, 后比MDSCO低, 这是由于基于Dijkstra的带宽成本最小化随着域内资源的消耗, 候选路径的成本优化性能下降, 当SFC的数量高于1600时, 接受率的降低使其服务成本低于MDSCO. 从图4(a)和图4(b)中显然可以得出, MDSCO-RP有效提升了服务接受率, 其平均服务成本也逐渐优于MDSCO, 这是由于MDSCO-RP在SFC编排失败后, 不需要从SFC的起点重新进行编排, 降低了编排成本.

如图4(c)随着SFC数量的增加, 3种算法平均响应时间呈上升趋势, WGT_LB的平均响应时间比MDSCO和DFSC高约40 ms, 这是同样是贪心算法较k最短路算法需要遍历更多的节点, 导致其响应时间大大增加; DFSC的接受率逐渐低于MDSCO, 表明其服务拒绝率较高, 其平均响应时间逐渐低于MDSCO. Heuristic的平均响应时间与MDSCO相近. MDSCO-RP的平均响应时间略高于MDSCO, 这是由于MDSCO编排失败直接拒绝, 而MDSCO-RP进行了重新分块.

(2) 不同SFC长度下编排算法对比

图5展示了将2000个SFC输入网络, 随着SFC长度的增加, 服务接受率呈下降趋势, 其中如图5(a)所示MDSCO和MDSCO-RP的接受率分别比WGT_LB低约5%和3%, DFSC接受率远低于MDSCO和WGT_LB, 同前文分析一致, DFSC忽略域间负载平衡使其接受率表现较差, WGT_LB通过遍历网络节点使其接受率高于MDSCO. 随着SFC长度的增加, Heuristic的接受率与MDSCO的差距逐渐增大, 同前文分析一致, Heuristic将SFC编排到尽可能少的域中, 该算法只考虑了节点的阈值, 使得域内链路带宽容量不足, 导致以此域为流量起点或终点的SFC编排失败. SFC长度下平均服务成本如图5(b)所示, WGT_LB遍历网络节点进行SFC部署时, 虽然接受率表现较好, 但如前文所分析的使用贪心算法会导致路径折返, 提升了服务成本, 因此WGT_LB的平均服务成本比MDSCO高约10%; DFSC和Heuristic的平均服务成本逐渐高于MDSCO, 后逐渐低于MDSCO, 这是由于随着SFC长度的增加, 网络负载逐渐增大, 而DFSC和Heuristic域间负载失衡更为明显, 导致其接受率大大降低, 服务成本逐渐低于MDSCO. 基于前文阐述MDSCO-RP在SFC编排失败后, 不需要从SFC的起点重新进行编排, 降低了编排成本, 因此MDSCO-RP在2000个SFC输入网络(即资源短缺)的平均服务成本优于MDSCO.

图5(c)展示平均响应时间随SFC长度的增加呈上升趋势, 其中WGT_LB的响应时间比MDSCO和DFSC高约45 ms, 原因为当请求数量较大时, 贪心算法比k最短路时间复杂度更高; 随着SFC长度的增长, DFSC接受率远低于MDSCO, 因此其响应时间逐渐低于MDSCO. 与前文一致, Heuristic的响应时间与MDSCO相近. MDSCO-RP的响应时间略高于MDSCO, 这是由于随着域内资源的减少MDSCO的 编排失败率高于MDSCO-RP. 因此我们提出的算法MDSCO相较于DFSC和Heuristic能够权衡服务成本和接受率, 在保证服务接受率性能可接受的前提下, 优化了服务成本, 重新分块算法MDSCO-RP的服务成本和服务接受率均得到了提升. 此外MDSCO和MDSCO-RP的平均响应时间随着网络负载的增大性能比较稳定.

4 结论与展望

本文提出了基于资源感知的多域SFC编排成本优化算法MDSCO和MDSCO-RP, 对域级图进行建模保护域内资源信息的机密性; 结合域级图披露的网络资源负载设计了一种域权重的计算方法实现域间负载的平衡, 提升了服务接受率; 并基于目标函数设计算法实现了服务成本和响应时间的优化. 接下来的研究工作是当一个或多个VNF发生故障或失效时, 考虑SFC的可用性和运营成本等因素设计SFC编排算法.