随着数据规模的急剧增长和隐私保护意识的提升, 传统的中心化机器学习方法因涉及敏感数据的集中存储和处理面临挑战. 此外, 不同机构和个体间的“数据孤岛”问题限制了数据的有效利用. 联邦学习(federated learning, FL)作为一种新型分布式机器学习方法, 允许多个参与方在不直接共享数据的前提下, 共同训练模型, 既保护了数据隐私, 又突破了“数据孤岛”的限制. 如今, 联邦学习已经逐渐成为分布式机器学习领域中一种重要的范式和研究热点[1–4]. 在此背景下, 一系列联邦学习的相关应用在医疗[5,6]、金融[7]等有高度隐私保护需求的领域中应运而生. 除了联邦学习的实际运用, 也有许多研究关注于联邦学习算法本身, 旨在提高联邦学习算法的性能.
FedProx算法[8]、SCAFFOLD算法[9]、MOON算法[10]等算法在FedAvg算法[11]的基础上应运而生, 旨在帮助所有参与者共同训练一个能在各参与者(即不同设备或节点)的数据上均表现良好的全局模型. 然而, 联邦学习在具体实践中面临的一个显著挑战是处理非独立同分布(Non-IID)数据问题. 现实世界中, 分布于各个客户端的数据往往因用户行为或偏好的差异而表现出显著的异构性. 这种数据的不一致性给全局模型的训练和泛化能力带来了考验.
一些研究者认识到, 对于彼此互不干扰的参与者而言, 与合作训练得到一个能在所有参与者数据集上均表现良好的全局模型相比, 其本地模型能否在自身的数据上表现良好或者能否适应个性化的需求更值得关注, 并由此产生了个性化联邦学习(personalized federated learning, PFL). 个性化联邦学习的重点是为每个参与者建立个性化的模型, 这些模型能更好地适应各个参与节点的特定数据分布, 展现出更优秀的性能. 其中, FedALA算法[12]是近年来最具代表性的一种个性化联邦学习算法. FedALA算法提出了一种具有高通用性的自适应局部聚合(adaptive local aggregation, ALA)机制, 进一步提升了模型在处理个性化联邦学习场景中的表现. 在FedALA算法中, 其同步通信机制要求所有参与训练的客户端在特定时间上传它们的本地模型, 并暂停本地训练, 直到接收到新的全局模型后才能恢复训练. 这种机制在客户端训练速度存在显著差异时, 可能导致资源浪费: 训练速度较快的客户端需要等待较慢的客户端完成上传, 从而导致等待期间的计算资源未能得到充分利用.
联邦学习以及个性化联邦学习本质上是一种特殊的分布式深度学习. 在深度学习中, 优化器(optimizer)是深度学习工程实现中的核心组件, 对模型的训练效率和最终结果有着不可忽视的影响. 为此, 优化器本身也成为一个广泛研究的重要对象. 然而, 联邦学习领域中的许多现有工作的具体实现往往直接沿用单机深度学习下的设定, 即采用广为流行的SGD[13]、Adam[14]作为优化器. 但单机深度学习下的优化器设定在联邦学习以及个性化联邦学习中是否依旧适用, 仍是一个开放问题.
本文以此为研究切入点, 主要贡献如下.
(1)算法优化: 通过令客户端在等待期间继续进行本地训练对FedALA算法进行改进, 得到pFedALA算法, 旨在缓解FedALA算法中由于客户端之间需要同步而带来的资源浪费, 提升算法效率.
(2)性能评估: 基于两个公开的图像数据集(MNIST和CIFAR-10), 对FedAvg、FedALA与pFedALA算法中使用不同主流优化器的所造成的性能差异进行深入探讨. 重点考察了在非独立同分布数据和数量不平衡环境下, 包括基于狄利克雷分布的实际异构设置(practical heterogeneous setting)和极端异构设置(pathological heterogeneous setting), 不同优化器对算法性能的具体影响.
1 相关工作在联邦学习领域, McMahan 等人提出的FedAvg算法[11]被广泛认可为联邦学习的基石. 该算法提出了联邦学习的基础训练流程, 通过对不同客户端上传的本地模型进行平均来构建一个全局模型, 并将全局模型再次分发给不同客户端以继续训练, 有效地支持了在多客户端在不共享本地数据的情况下共同训练模型. 其实验结果表明, 即便在多数客户端处于离线状态的恶劣通信环境下, FedAvg也能保证模型的良好表现, 特别是在处理大规模分散数据集方面显示出显著优势.
FedAvg算法, 作为联邦学习领域的开创性工作, 首次突显了数据统计异构性这一联邦学习中的核心挑战. 这种异构性源于联邦学习参与者根据各自独特的条件和偏好独立收集数据, 导致数据集不符合传统机器学习对数据独立同分布的假设, 并且各参与者的数据体量也可能存在显著差异. 目前, 已经存在一些联邦学习算法尝试解决该挑战.
作为FedAvg的一个扩展, FedProx算法[8]通过在损失函数中引入一个近似项“2-范数距离”来限制本地训练过程中本地模型与全局模型的差异, 以解决由于数据非独立同分布和数量不平衡引起的客户端间的统计异构性问题. 这一改进使得模型在面对多样化且分散的数据时能更稳定地学习, 从而改善了模型在各类数据分布, 特别是极端异构性数据上的表现. SCAFFOLD算法[9]引入控制变量, 通过方差减少来校正客户端的本地更新, 旨在解决联邦学习中的客户端漂移问题, 有效降低了因数据异构性导致的全局模型性能下降. MOON算法[10]则通过考虑本地模型与全局模型之间的相似性来减轻因数据分布不均匀而引起的数据异构性问题, 增强了模型在不同客户端之间的一致性, 提高了整体模型性能.
以上改进算法均在一定程度上提升了联邦学习在数据统计异构设置下的性能. 然而, 在数据统计异构性显著时, 它们的性能仍难以达到预期, 即难以得到一个可以同时在所有客户端上都表现良好的全局模型. 随着研究的深入, 研究人员发现个性化的客户端本地模型(不再直接等于服务器发送而来的全局模型)可能是更符合现实情形的联邦学习方式, 由此诞生了个性化联邦学习.
在个性化联邦学习领域, FedKD算法[15]基于自适应知识蒸馏和动态梯度压缩技术, 可以最大程度减少94.89%的通信开销, 并达到与集中式模型学习相当的效果. Ditto算法[16]为个性化联邦学习提供了一个简单、通用的框架, 考虑了公平性和鲁棒性的平衡问题. APPLE算法[17]自适应地学习每个客户端从其他客户端的模型中获益情况, 并引入一种方法来灵活控制训练APPLE的焦点在全局和局部目标之间. Per-FedAvg算法[18]对FedAvg进行了改进, 引入元学习方法以更好地适应各个客户端的个性化需求. 在每轮个性化联邦学习中, 该算法先使用元学习方法得到一个较好的模型作为全局元模型, 然后客户端对全局元模型进行微调后得到本地模型. 该算法允许每个客户端在本地对其模型进行个性化优化, 充分结合了全局模型的泛化优势和个性化模型的特定优势, 特别适用于个性化推荐系统或医疗数据分析. pFedMe算法[19]通过引入Moreau Envelope方法, 提出了面向个性化联邦学习的双层优化问题, 解耦了个性化模型的优化过程与全局模型的学习过程, 允许每个客户端独立地训练和更新自己的模型, 同时与全局模型保持一致性. 这种平衡方法使其在处理高度异构的客户端数据时特别有效. FedALA算法[12]通过在FedAvg的基础上加入其创新的自适应局部聚合(ALA)机制, 解决了传统联邦学习算法在处理个体差异时的不足. 在ALA机制中, 每个客户端使用其独有的数据集来生成并动态维护一个私有权重. 该私有权重在每轮学习过程开始时精细化影响全局模型对本地模型中各个元素的贡献程度. 客户端间的本地模型会根据各自的私有权重产生差异, 使得本地模型更适应本地的数据集, 并利用这些差异化的本地模型继续进行训练. ALA机制既显著地提高了模型在各个客户端的个性化表现, 又保持了良好的全局学习效率. 特别地, 由于ALA机制被设计为具有相对独立性的模块, 它可以比较方便地应用到其他联邦学习与个性化联邦学习算法中, 因此受到本文的特别关注.
在深度学习和联邦学习领域中, 优化器的选择对模型训练的效率和效果有显著影响. 随机梯度下降优化器(SGD)[13]和异步随机梯度下降优化器(ASGD)[20]是众多优化器中较为基础的优化算法, 通过在每次迭代中使用一个小批量的数据来更新模型权重. RMSprop优化器[21]通过除以最近梯度的平方的移动平均值来调整学习率, 特别适用于处理非平稳目标的问题. Adam[10]结合了动量和RMSprop的优点, 通过计算一阶和二阶矩估计来自适应地调整每个参数的学习率, 是目前最为广泛使用的优化器. 作为Adam的一种变体, RAdam (rectified Adam)[22]通过引入动态调整的学习率解决了Adam在训练初期可能的不稳定问题. AdaGrad优化器[23]则特别适用于处理稀疏数据, 其主要创新在于对每个参数的学习率进行自适应调整. AdaDelta优化器[24]是AdaGrad的扩展, 旨在减少其学习率随时间单调递减的速度.
2 背景知识● 联邦学习的问题假设: 假设有N个客户端, 其拥有的私有训练数据分别为D1, …, DN. 这些数据集是异构的(Non-IID与数量不平衡). 具体来说, D1, …, DN是从N个不同的分布中抽样, 且有不同的大小. 在中央服务器的帮助下, 联邦学习通过每个客户端在其自身拥有的数据集上进行本地学习, 目标为
通常,
● 联邦学习的具体实践: 由于各个客户端i的本地模型训练无法脱离自身的数据集Di, 因此联邦学习常常通过对各个客户端i的本地模型进行加权平均来间接实现其优化目标. 于是, 联邦学习的过程可以被描述为“模型分发-模型训练-模型聚合”的这一循环往复过程, 也被称为联邦学习迭代. “模型训练”的实质可以理解为客户端i利用自身的数据集Di同步地进行一轮次或多轮次本地训练. 为方便同步, 客户端通常会规定相同且数量适中的本地训练轮次.
3 FedALA的改进算法—pFedALA在联邦学习领域, 创建一个能够广泛适用于各种异构环境的全局模型是一个持续的挑战. 尽管全局模型是服务器通过聚合多个客户端在不同环境下训练的模型构建而成, 但其在特定客户端上的泛化能力往往有限. 为了解决这一问题, 已经有许多卓有成效的工作相继涌现. 其中, FedALA算法以其简单性与通用性而备受关注. FedALA算法蕴含着一种名为ALA的自适应本地聚合机制. 该机制直接插入到“模型分发-模型训练-模型聚合”中, 形成了循环往复的“模型分发-ALA-模型训练-模型聚合”联邦学习迭代. FedALA算法可视为FedAvg算法与ALA机制的直接结合. 其实验表明, ALA机制的加入使得联邦学习在非独立同分布与数量不平衡的数据异构设置下的性能显著提高.
然而, 回归联邦学习的具体实践, 可以很容易发现, “模型分发-模型训练-模型聚合”的联邦学习迭代隐含着对客户端同步性的要求, 即要求各个客户端必须同时进入相同的阶段, 执行相同的步骤. 特别地, 若考虑到各个客户端本身的计算能力与通信环境之间的差异, 为了实现各个客户端的同步, 必然要在每轮联邦学习迭代之间引入足够的等待时间. 此时就很有可能出现, 大部分客户端已经停止本地训练并上传本地模型而等待小部分客户端的情形. 尽管可以设置一个合适的最大等待时间来避免无限等待, 但这依然造成了不可忽视的计算资源浪费, 尤其是对于那些计算能力强且自身数据量大的客户端.
本文提出一种FedALA算法的改进算法, 命名为pFedALA. pFedALA算法吸收了FedALA中最为核心的部分, 在ALA机制的基础上得到了pALA机制, 并形成循环往复的“模型分发-pALA-模型训练-模型聚合”联邦学习迭代.
pFedALA算法的主体与FedALA算法相似, 其核心思想在于摒弃了传统的联邦学习(如FedAvg)在旧的全局模型
| ˆΘti=Θt−1i⊗Wi,1+Θt−1⊗Wi,2 | (1) |
其中, 对于任何合法的
| ˆΘti=Θt−1i+(Θt−1−Θt−1i)⊗Wi | (2) |
通过将权重进行逐元素剪辑并限制在 [0, 1] 范围内, 即
在客户端i等待期间, 不妨记客户端i在本轮联邦学习迭代中上传的本地模型
具体地, pALA机制将式(2)中的本地模型
| Θt−1i=a0×Θt−1i−0+a1×Θt−1i−1+⋯+aj×Θt−1i−j | (3) |
其中,
同样地, 在多聚合中心的设置下,
| Θt−1=b1×Θt−1g−1+b2×Θt−1g−2+⋯+bk×Θt−1g−k | (4) |
其中,
同FedAvg的处理方式一致, 在联邦学习迭代的首轮迭代初始, 本地模型均被初始化为同一个全局模型, 并执行本地模型训练. 从联邦学习迭代的第2轮次迭代初始, 由于客户端接收到了来自上一轮次迭代聚合形成的全局模型, 该全局模型必然与各客户端的本地模型有所差异. 此时, 开始执行pALA机制, 将
| Wi←Wi−η∇WiL(ˆΘi,Ds,ti,Θt−1) | (5) |
其中,
本文实验基于两个公开的图像数据集MNIST[25]与CIFAR-10[26]展开.
MNIST (modified national institute of standards and technology) 是一个由美国国家标准与技术研究院(NIST)创建, 已广泛用于训练各种图像处理系统的大型手写数据集. 该数据集中包含60000个训练样本和10000个测试样本, 每个样本均为一张28×28像素的灰度图像, 表示手写数字0–9. 虽然MNIST数据集相对较简单, 但它仍然涵盖了图像识别中的一些基本挑战, 比如手写数字的多样性和图像的噪音处理, 因而通常被用作计算机视觉和机器学习算法的基准测试.
CIFAR-10 (Canadian institute for advanced research-10) 是一个由加拿大高级研究院人工智能项目(CIFAR)创建, 用于识别普通物体的更复杂的数据集, 常用于计算机视觉研究. 该数据集中包含了60000张32×32彩色图像, 分为10个类别(飞机、汽车、鸟类、猫、鹿、狗、青蛙、马、船和卡车), 每个类别6000个图像. CIFAR-10常用于评估图像识别、机器学习和深度学习算法. 由于它包含了多种类别的彩色图像, 因此比MNIST数据集更复杂. CIFAR-10数据集中不同类别的物体可能有相似的颜色和形状, 而同一类别的物体在不同图像中可能呈现出不同的姿态和背景, 使得它成为深度学习模型尤其是卷积神经网络(CNN)的理想测试数据集.
4.2 评估指标由于联邦学习常应用于图像多分类任务, 本文重点关注Accuracy (ACC)准确率与ROC曲线下的面积(area under curve, AUC)这两个评估指标. 它们是图像多分类任务中常见的评价指标, 其中, 准确率(ACC)表示预测正确的样本数占总样本数的比例, 其值越大越好; AUC表示ROC曲线下部分的面积. 绘制ROC曲线需要进行一系列的步骤, 涉及计算不同分类阈值下的真阳性率(TPR)和伪阳性率(FPR), 然后将这些点连接起来形成曲线. 以下是绘制ROC曲线的一般步骤.
(1) 收集分类器输出: 使用分类器对测试数据进行预测, 并获得每个样本的预测概率值或分类得分. 这些分数通常表示为样本属于某个类别的可能性.
(2) 计算TPR和FPR: 随着阈值的变化, 计算每个阈值下的真阳性率(TPR)和伪阳性率(FPR): TPR = TP/(TP + FN), FPR = FP/(FP + TN), 其中, TP为真阳性数量, FN为假阴性数量, FP为伪阳性数量, TN为真阴性数量.
(3) 绘制ROC曲线: 以每个阈值对应的FPR和TPR值作为坐标点, 在坐标系中进行绘制并连接, 形成ROC曲线.
(4) 计算AUC: 计算ROC曲线下的面积, 即真阳性率与伪阳性率之间的曲线下面积. AUC值范围在0–1之间, AUC越接近1, 表示分类器性能越好.
为了获得所有本地模型的平均测试准确率(mean test accuracy)与所有本地模型的AUC评估指标, 本文在每轮联邦学习迭代结束时对客户端的本地模型进行评估. 实验过程中, 令客户端中25%的本地数据构成测试数据集, 其余75%的数据用于本地训练, 将所有实验运行多次, 得到平均值.
4.3 实验设置MNIST与CIFAR-10数据集常用于测试单机下的深度学习工作. 由于联邦学习中涉及多个客户端, 简单地将MNIST与CIFAR-10数据集随机均匀地分配给各个客户端, 将使得每个客户端拥有的数据符合独立同分布(IID), 违背了数据应符合非独立同分布与数量不平衡的异构设置. 因此, MNIST与CIFAR-10数据集不能直接应用于测试联邦学习工作, 需要将MNIST与CIFAR-10数据集修改为适用于联邦学习的情景.
本文采用两种被广泛认可的模拟方案来建立非独立同分布与数量不平衡的异构设置. 第1种是Li等人[10]使用的基于狄利克雷(Dirichlet)分布的实用异构设置, 具体表示为Dir(β). 利用狄利克雷分布Dir(β)为客户端分配数据样本, 可以使得每个客户端拥有的各类别样本的比例构成具有显著差异, 形成了非独立同分布与数量不平衡. β值越小, 数据分布的异构性越强, 本文设置β = 0.1. 第2种是McMahan等人[11]使用的极端的异构设置. 本文从MNIST/CIFAR-10的10个类中, 仅为每个客户端分配2个类, 且保证每个客户端拥有的数据样本互不相交. 显然, 在第2种设置下, 每个客户端仅有两个分类, 而在第1种设置下每个客户端仍可以有多种分类. 第2种异构设置比第1种设置更具有挑战性.
本文共设置10个客户端, 并假设它们一直保持在线状态且通信畅通. 在模型结构上, 本文统一采用了McMahan等人[11]使用的4层CNN, 并设置优化器的学习率为0.005 (在MNIST上为0.1). 同时, 每个客户端设置了批(batch)大小设置为10, 本地模型训练轮次(epoch)的数量为5. 在pFedALA算法中, 本文设定其中1个客户端训练较为缓慢. 训练缓慢的客户端不会进行额外的本地训练, 而其他客户端则在等待“模型分发”的过程中进行额外1–3轮本地训练. 实验过程中, FedAvg算法、FedALA算法与pFedALA算法在所有任务上均进行100次联邦学习迭代.
本文使用PyTorch-2.1实现FedAvg、FedALA以及pFedALA算法. 实验所用计算机的配置为: Intel Core i5 12400 CPU, 32 GB内存和NVIDIA 4090 GPU, 系统为Ubuntu 23.04.
4.4 实验结果与分析从异构设置的角度, 实验结果可以分别呈现为基于狄利克雷分布的实用异构设置上的实验结果(图1, 图2)与极端的异构设置上的实验结果(图3, 图4).
从算法种类的角度, 实验结果可以被总结为FedAvg算法的实验结果与FedALA算法的实验结果, 分别呈现为表1–表3. 其中, “X/Y”代表了算法在实验过程中取得平均测试准确度的最大值与平均测试AUC值(mean test AUC)的最大值, 加粗数值为对应列中的最大值, 表示在当前优化器下对应的性质指标最好.
|
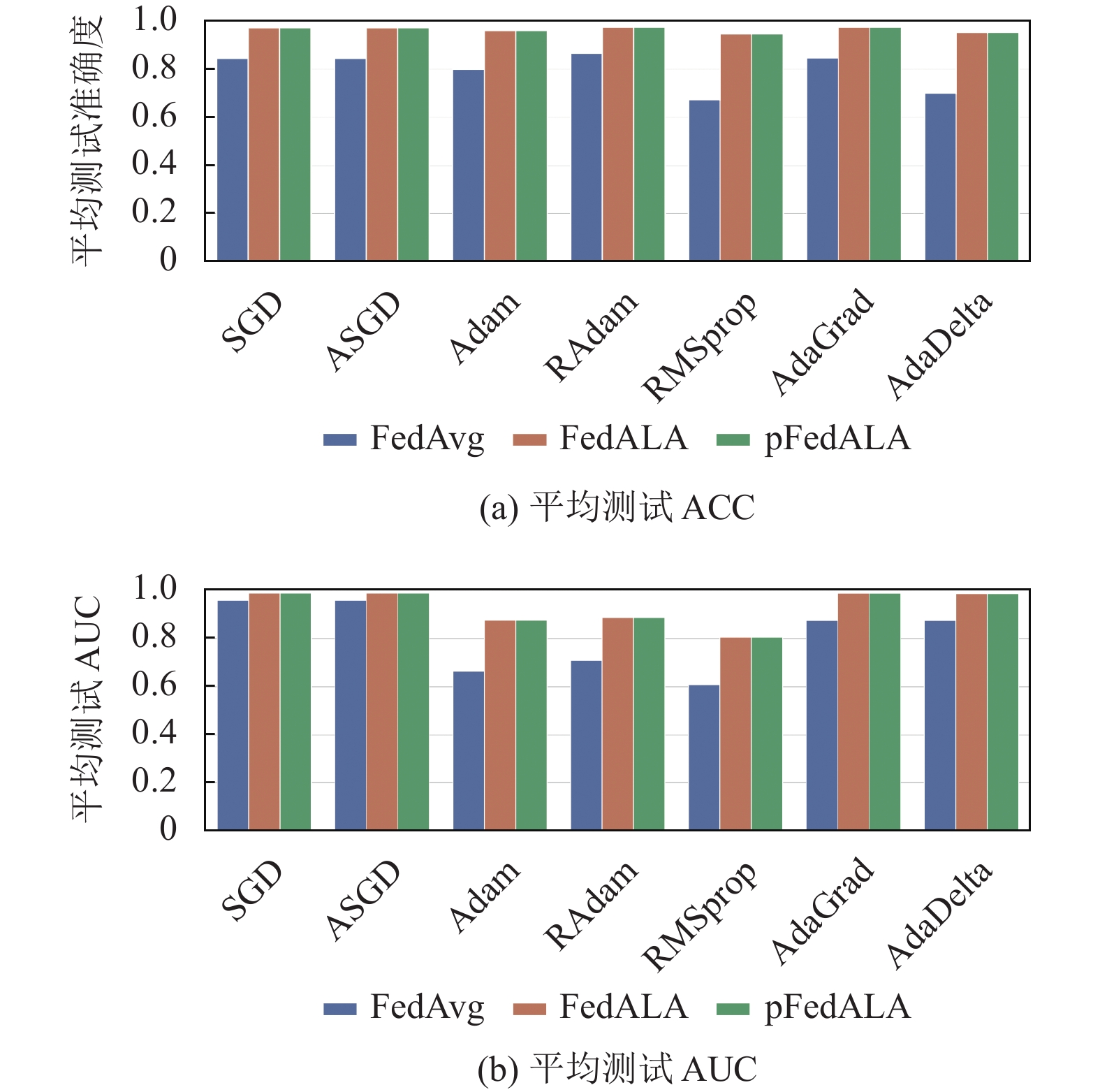
图 1 MNIST基于狄利克雷分布的实用异构设置下的平均测试ACC及AUC |
|
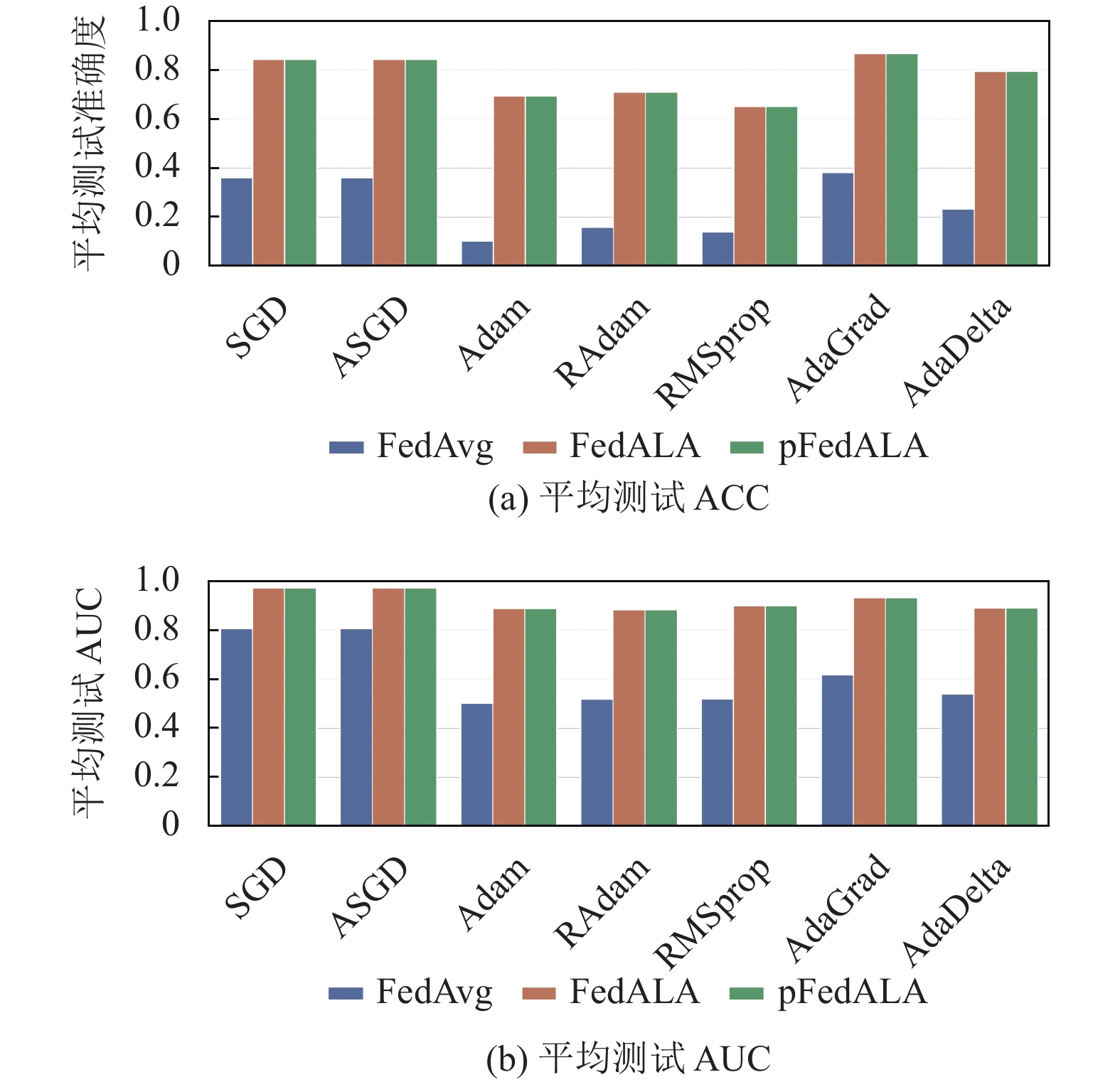
图 2 CIFAR-10基于狄利克雷分布的实用异构设置下的平均测试ACC及AUC |
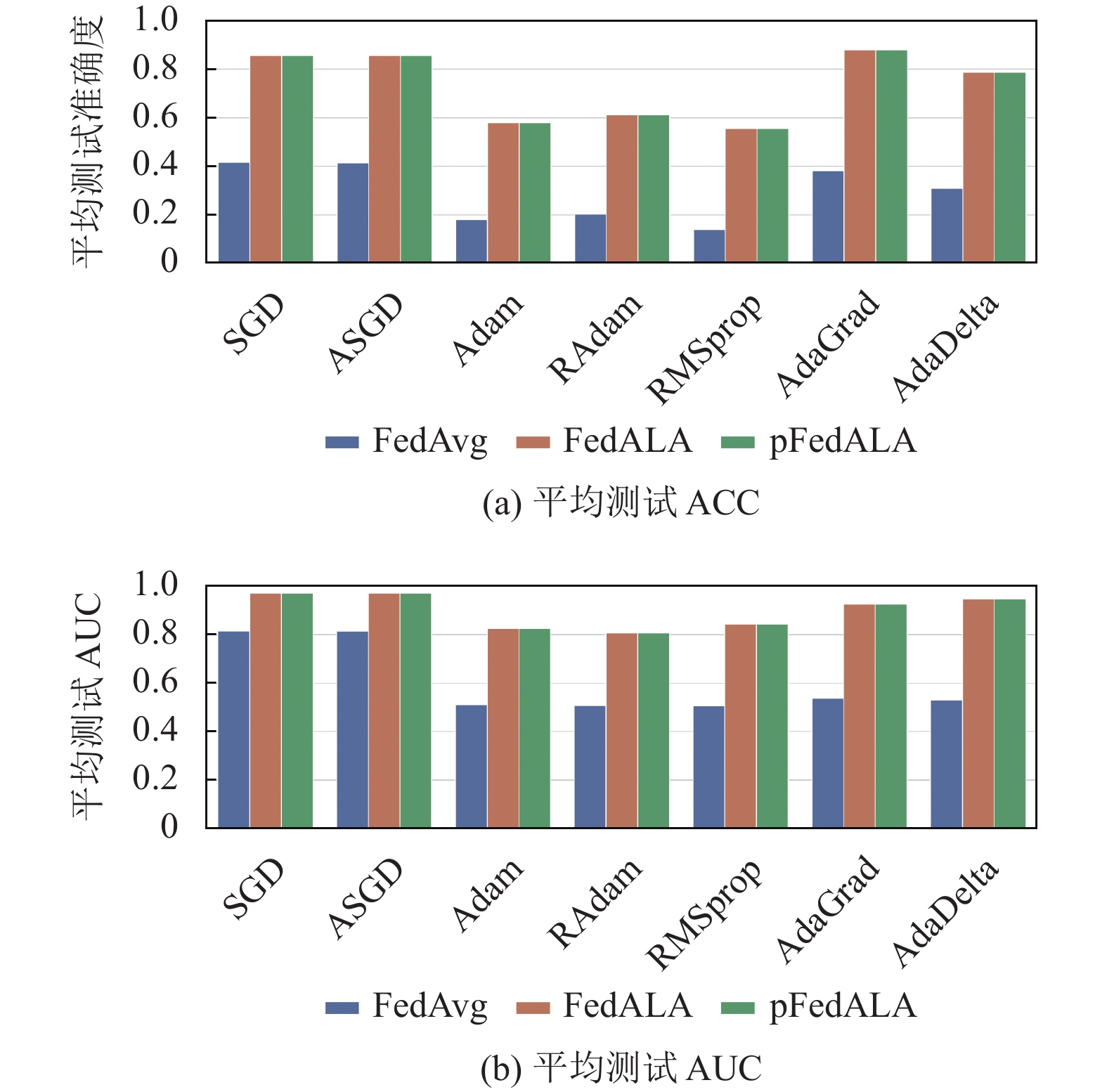
综合图1–图4以及表1–表3进行分析: ① 从算法种类的角度上看, FedALA与pFedALA的算法性能显著地优于FedAvg的性能, 这验证了FedALA以及pFedALA算法比FedAvg算法更能适应非独立同分布)和数量不平衡的异构设置; ② 从异构设置种类的角度上看, 两种异构设置都给联邦学习带来了足够的挑战性. 例如, 在CIFAR-10数据集上, 两种异构设置均使得 FedAvg算法难以正常工作.

|
图 3 MNIST极端的异构设置下的平均测试ACC及AUC |
|
图 4 CIFAR-10极端的异构设置下的平均测试ACC及AUC |
对比FedALA与pFedALA算法, 依据图1–图4中可知, pFedALA的算法性能略优于FedALA算法. 这得益于pFedALA算法可以让那些在等待较慢的客户端结束本地训练的客户端, 充分利用等待时间进行额外的本地训练.
本文主要从优化器的角度研究不同优化器对FedAvg算法、FedALA算法以及pFedALA的影响. 依据图1–图4以及表1–表3可以很清楚地发现, 不同的优化器对算法的性能有着不可忽视的影响: ① SGD、ASGD以及AdaGrad优化器普遍获得了最优的性能表现; ② 在单机深度学习中最为常见的Adam优化器的表现却最为糟糕; ③ 在联邦学习的环境中, SGD优化器和 ASGD优化器比Adam优化器表现得更好. 产生上述的实验结果的可能原因主要包含以下3个方面.
| 表 1 FedAvg算法的综合实验结果 |
| 表 2 FedALA算法的综合实验结果 |
| 表 3 pFedALA算法的综合实验结果 |
(1)鲁棒性和简易性
联邦学习环境中的数据往往是非独立同分布(Non-IID)的, 意味着不同的客户端可能有着不同的数据分布. 这种数据多样性使得优化过程更加复杂, 因为模型需要在各种不同的数据分布上表现良好. SGD 和 ASGD 优化器由于其简易性和较少的超参数调整需求, 更可能对各种数据分布表现出良好的适应性. Adam 优化器通过计算梯度的指数移动平均值和平方梯度的指数移动平均值来调整学习率. 这种自适应学习率的方法在标准的深度学习应用中通常表现出色, 因为它可以更有效地适应单一数据分布的特性. 然而, 在联邦学习场景中, 数据源之间的差异可能导致Adam优化器过度调整学习率, 从而影响模型在不同客户端数据上的泛化能力. 这在一定程度上说明: 在非独立同分布的数据上, 相对复杂的优化算法可能反而不如简单稳定的方法有效.
(2)超参数依赖性
Adam具有较多的超参数, 对超参数设置更为敏感, 其性能在很大程度上依赖于对其超参数(如学习率、β1、β2)的精确调整. Adam 优化器除了学习率之外, 还有两个关键的超参数: β1和β2. 这些参数分别控制了梯度的一阶矩(即均值)和二阶矩(即未中心化的方差)的指数移动平均. 在标准的深度学习应用中, 这些参数通常被设置为通用值(如β1=0.9, β2=0.999), 但在更复杂或异构性更高的场景中, 这些默认值可能并不是最优的. 在联邦学习中, 由于参与学习的各个客户端有着不同的数据分布, 试图找到一个在所有客户端上均表现良好的超参数设置更为困难. 相比之下, SGD优化器和ASGD优化器的超参数主要是学习率, 它们的工作原理相对简单, 并且对超参数的敏感度较低.
(3)数据异构性
联邦学习涉及的数据分布通常具有高度异构性, 这意味着不同客户端的数据可能具有不同的特征和分布. SGD优化器和ASGD优化器是基于梯度的优化方法, 通过在每一步使用一小批样本来更新模型参数. 这种方法相对简单, 不会过分适应任何特定的数据源. Adam优化器由于带有自适应学习率, 可能在某些客户端的特定数据特性上表现得太好, 从而在整体上降低模型的泛化能力.
在联邦学习的环境中, 本文还关注到虽然Adam(RAdam)、AdaGrad、RMSprop均为自适应学习率优化器, 但它们在联邦学习环境中的性能差异可以归因于它们各自的特定机制和行为. 以下几点关键区别可用于解释本文的联邦学习设置中AdaGrad优化器表现优于Adam优化器的原因.
(1)对稀疏数据的适应性
联邦学习环境中的数据通常包含许多稀疏特征. AdaGrad优化器在这种情况下表现更好, 因为它通过为每个参数累积历史梯度的平方和来调整学习率, 这使得它能够为不常更新的特征(如稀疏特征)提供较大的学习步长. 这种机制使得AdaGrad优化器在处理稀疏数据时特别有效, 因为它能够快速调整那些不经常出现的特征的权重. Adam优化器结合了动量(梯度的一阶矩估计)和自适应学习率(梯度的二阶矩估计). 这种复合机制在处理非稀疏、频繁更新的数据时可能更有效, 但在处理稀疏数据时可能不如AdaGrad优化器有效. RMSprop 优化器通过对过去梯度的平方进行指数移动平均来调整每个参数的学习率. 这种方法在处理带有频繁更新特征的数据时效果较好, 但可能在稀疏数据上的性能不如AdaGrad优化器.
(2)超参数的敏感性
Adam优化器与RMSprop优化器的性能在很大程度上依赖于对其超参数(特别是学习率和β值)的精确调整. 在联邦学习这样的复杂环境中, 寻找统一的超参数设置通常是十分困难的. AdaGrad优化器相对简单, 超参数调整需求较少, 这使得它在联邦学习的应用中更容易配置和使用.
由于RAdam优化器只是在Adam优化器的一个改进, 其总体性能与Adam优化器类似. AdaDelta优化器基于AdaGrad和RMSprop的思想发展而来, 旨在解决AdaGrad中学习率随时间递减过快的问题. 它引入了RMSprop中使用的平方梯度的滑动平均概念, 但也可能因其中蕴含的RMSprop的思想不适用于联邦学习, 导致其性能不如AdaGrad优化器.
通过对比表1与表2, 我们还可以发现FedALA算法与pFedALA算法可以令各个优化器的性能表现趋于一致, 这一点在MNIST数据集上表现明显. 产生该现象的主要原因如下.
(1) FedALA与pFedALA算法的自适应局部聚合特性
FedALA与pFedALA算法的核心特性是它能够根据每个客户端的本地数据特性进行自适应调整. 这种调整直接作用于客户端接收到的全局模型, 令全局模型转化为更适合本地数据特性的本地模型, 客户端在转化后的本地模型上进行训练. 这种机制减少了不同优化器之间性能差异的影响, 因为算法本身提供了一种有效的调节和适应机制, 使得各优化器能够更好地适应各自的数据分布.
(2) MNIST数据集的特性
MNIST数据集相对简单, 包含的图像为手写数字, 其特性较为均一. 在这种相对简单的数据集上, 不同优化器之间的性能差异本来就不大, 而FedALA算法可能进一步减少了这些差异. CIFAR-10数据集相对复杂, 所以不同优化器之间的性能差异仍可以体现在FedALA算法的实际运行中.
5 结论本文研究聚焦于联邦学习(FL)以及个性化联邦学习(PFL)中常用算法和优化器在处理非独立同分布和数据不平衡的情境中的表现. 首先, 针对FedALA算法中因客户端之间需要同步而造成的资源浪费现象, 设计得到pFedALA算法. pFedALA算法充分利用客户端的等待时间继续进行本地训练. 接着, 基于MNIST和CIFAR-10数据集, 本文重点考察了在两种不同的Non-IID数据设置—基于狄利克雷分布的异构设置和极端的异构设置下, 常见优化器如SGD、Adam等对FedAvg、FedALA以及pFedALA算法性能的影响.
实验结果表明: 一方面, 个性化联邦学习算法FedALA与pFedALA, 在应对特定参与者的数据分布方面表现出更加优越的性能. 这在很大程度上说明, 在联邦学习环境中引入个性化策略是提高模型性能的有效途径, 尤其是在面对极端的数据异构性时. 本文提出的pFedALA算法因充分利用为了同步而产生的等待时间进行了额外的本地训练, 从而进一步优化了FedALA算法. 另一方面, 传统单机深度学习环境中广泛采用的优化器在联邦学习和个性化联邦学习场景下的表现存在显著差异, 具体表现为: 在处理非独立同分布数据时, 诸如SGD、ASGD、AdaGrad等在内的优化器在联邦学习环境中表现出较强的适应性和鲁棒性, 而诸如Adam和RMSprop等在单机环境中表现优异的优化器在联邦学习环境中的表现较差. 这说明, 优化器的选择在联邦学习相关研究中的作用不可忽视, 在未来工作中, 为联邦学习专门开发的优化器是一个值得研究的方向.
总体而言, 本文的实验证明了pFedALA算法的优越性, 突显了在联邦学习和个性化联邦学习中优化器选择的重要性. 本文工作为实际应用中的算法选择和优化提供了实证基础, 同时也指出了在联邦学习领域进一步研究优化器的必要性. 在后续的研究工作中, 我们将更多地关注优化器在特定联邦学习场景下的性能表现, 并探索更适合这一领域的新型优化策略.
| [1] |
杨强. AI与数据隐私保护: 联邦学习的破解之道. 信息安全研究, 2019, 5(11): 961-965. |
| [2] |
余晟兴, 陈钟. 基于同态加密的高效安全联邦学习聚合框架. 通信学报, 2023, 44(1): 14-28. |
| [3] |
王珊, 荆桃, 肖淦文, 等. 联邦学习下高效的隐私保护安全聚合方案. 计算机系统应用, 2023, 32(11): 175-181. DOI:10.15888/j.cnki.csa.009302 |
| [4] |
田金箫. 提升联邦学习通信效率的梯度压缩算法. 计算机系统应用, 2022, 31(10): 199-205. DOI:10.15888/j.cnki.csa.008748 |
| [5] |
Zheng ZH, Zhou YZ, Sun YL, et al. Applications of federated learning in smart cities: Recent advances, taxonomy, and open challenges. Connection Science, 2022, 34(1): 1-28. DOI:10.1080/09540091.2021.1936455 |
| [6] |
Xu J, Glicksberg BS, Su C, et al. Federated learning for healthcare informatics. Journal of Healthcare Informatics Research, 2021, 5(1): 1-19. DOI:10.1007/s41666-020-00082-4 |
| [7] |
Liu T, Wang Z, He H, et al. Efficient and secure federated learning for financial applications. Applied Sciences, 2023, 13(10): 5877. DOI:10.3390/app13105877 |
| [8] |
Li T, Sahu AK, Zaheer M, et al. Federated optimization in heterogeneous networks. Proceedings of the 2020 Conference on Machine Learning and Systems. Austin: mlsys.org, 2020. 429–450.
|
| [9] |
Karimireddy SP, Kale S, Mohri M, et al. SCAFFOLD: Stochastic controlled averaging for federated learning. Proceedings of the 37th International Conference on Machine Learning. PMLR, 2020. 5132–5143.
|
| [10] |
Li QB, He BS, Song D. Model-contrastive federated learning. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 10708–10717.
|
| [11] |
McMahan B, Moore E, Ramage D, et al. Communication-efficient learning of deep networks from decentralized data. Proceedings of the 20th International Conference on Artificial Intelligence and Statistics. Fort Lauderdale: PMLR, 2017. 1273–1282.
|
| [12] |
Zhang JQ, Hua Y, Wang H, et al. FedALA: Adaptive local aggregation for personalized federated learning. Proceedings of the 37th AAAI Conference on Artificial Intelligence. Washington: AAAI, 2023. 11237–11244.
|
| [13] |
Bottou L. Online algorithms and stochastic approximations. In: Saad D, ed. Online Learning and Neural Networks. Cambridge: Cambridge University Press, 1998. 6.
|
| [14] |
Kingma DP, Ba J. Adam: A method for stochastic optimization. arXiv:1412.6980, 2014.
|
| [15] |
Wu CH, Wu FZ, Lyu LJ, et al. Communication-efficient federated learning via knowledge distillation. Nature Communications, 2022, 13(1): 2032. DOI:10.1038/s41467-022-29763-x |
| [16] |
Li T, Hu SY, Beirami A, et al. Ditto: Fair and robust federated learning through personalization. Proceedings of the 38th International Conference on Machine Learning. PMLR, 2021. 6357–6368.
|
| [17] |
Luo J, Wu SD. Adapt to adaptation: Learning personalization for cross-silo federated learning. Proceedings of the 31st International Joint Conference on Artificial Intelligence. Vienna: IJCAI.org, 2022. 2166–2173.
|
| [18] |
Fallah A, Mokhtari A, Ozdaglar A. Personalized federated learning with theoretical guarantees: A model-agnostic meta-learning approach. Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2020. 300.
|
| [19] |
Dinh CT, Tran NH, Nguyen TD. Personalized federated learning with Moreau envelopes. Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2020. 1796.
|
| [20] |
Zhang W, Gupta S, Lian XR, et al. Staleness-aware async-SGD for distributed deep learning. Proceedings of the 25th International Joint Conference on Artificial Intelligence. New York: AAAI, 2016. 2350–2356.
|
| [21] |
Graves A. Generating sequences with recurrent neural networks. arXiv:1308.0850, 2013.
|
| [22] |
Liu LY, Jiang HM, He PC, et al. On the variance of the adaptive learning rate and beyond. Proceedings of the 8th International Conference on Learning Representations. Addis Ababa: OpenReview.net, 2020.
|
| [23] |
Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization. The Journal of Machine Learning Research, 2011, 12: 2121-2159. |
| [24] |
Zeiler MD. AdaDelta: An adaptive learning rate method. arXiv:1212.5701, 2012.
|
| [25] |
LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
| [26] |
Krizhevsky A. Learning multiple layers of features from tiny images. Technical Report, Toronto: University of Toronto, 2009.
|
 2024, Vol. 33
2024, Vol. 33



