热轧钢作为一种重要工业材料, 在机械制造、航空工业等领域被广泛应用. 在热轧过程中, 由于生产工艺和生产设备限制造成的钢材表面缺陷, 如裂纹、辊印、氧化铁皮等, 对于钢材的耐磨性、抗腐蚀性和疲劳强度等都会产生负面影响^[1]. 目前仍有不少企业采用人工缺陷检测方式, 这种检测方式成本高、效率低^[2]. 随着深度学习算法的发展, 基于卷积神经网络的缺陷检测方法逐渐替代了人工加内存和传统的机器视觉检测方法. 为增强网络表征能力, 提高特征重用, Kou等人^[3]引入密集卷积块提取特征信息, 提出一种基于YOLOv3的钢带缺陷检测模型. 余松森等人^[4]针对现有模型对瓷砖表面微小缺陷识别能力不足的问题, 提出一种轻量型瓷砖表面缺陷检测模型, 极大改善原有模型对小目标缺陷的错检、漏检问题. 上述研究证明了基于深度学习的模型在缺陷检测任务上的优越性. 然而深度学习模型的良好性能往往依赖大量带标签的训练数据. 而在工业领域, 产品制造出现缺陷的比率很低, 数据的稀缺性导致模型泛化性弱, 容易过拟合.

为缓解样本稀缺问题, Kang等人^[5]第1个开发出目标检测的小样本学习模型(FSRW), 在YOLOv2模型框架中引入元特征学习器以实现小样本学习下的端到端的训练模型. Wang等人^[6]认为只在现有模型基础上附加元学习器, 模型记忆效率会随支持集类别数量增加而降低, 因此基于双阶段检测模型提出广义的小样本目标检测(G-FSOD)微调方式, 在提高新类检测精度的同时能保持基类数据的检测精度不下降. 然而, 这些通用型算法无法很好地应对工业场景中不同形状和尺寸的缺陷. 针对这一挑战, 于重重等人^[7]引入动态卷积, 提出一种可变形的特征金字塔网络, 以更好地提取形态各异的缺陷特征. 陈朝等人^[8]基于一个两阶段检测网络, 通过一个缺陷突显模块来更好地利用无缺陷样本增强缺陷区域特征, 获得良好的检测性能. Wang等人^[9]基于Faster R-CNN提出一个小样本模型训练框架, 提升了模型检测的鲁棒性. 上述几种方法针对工业环境下的缺陷检测研究表明小样本学习技术同样适用于工业场景中, 但它们都属于两阶段检测模型, 虽然在检测精度上表现良好, 在检测速率上却难以满足实际工业自动化生产的需求. 同时, 由于带钢表面缺陷存在与背景对比度低、目标尺寸跨度大、小目标较多等问题, 使得缺陷检测更为困难. 为克服上述挑战, 本文采用小样本学习技术, 并基于YOLOv5s单阶段检测模型构建一个小样本钢材表面缺陷检测网络FODNet. 本文主要工作如下: (1)设计一种融合注意力机制的多尺度路径聚合网络作为模型的颈部, 以增强模型对缺陷目标的多尺度预测能力和特征提取能力. (2)提出一种自适应解耦检测结构(coord-decoupled head, Coord-DH), 以更有效地缓解小样本条件下模型的分类任务和定位任务之间的矛盾. (3)提出一种融合Wasserstein距离的边界框回归损失函数(Wasserstein distance-IoU, WD-IoU), 以进一步提升模型对小目标缺陷的检测精度.

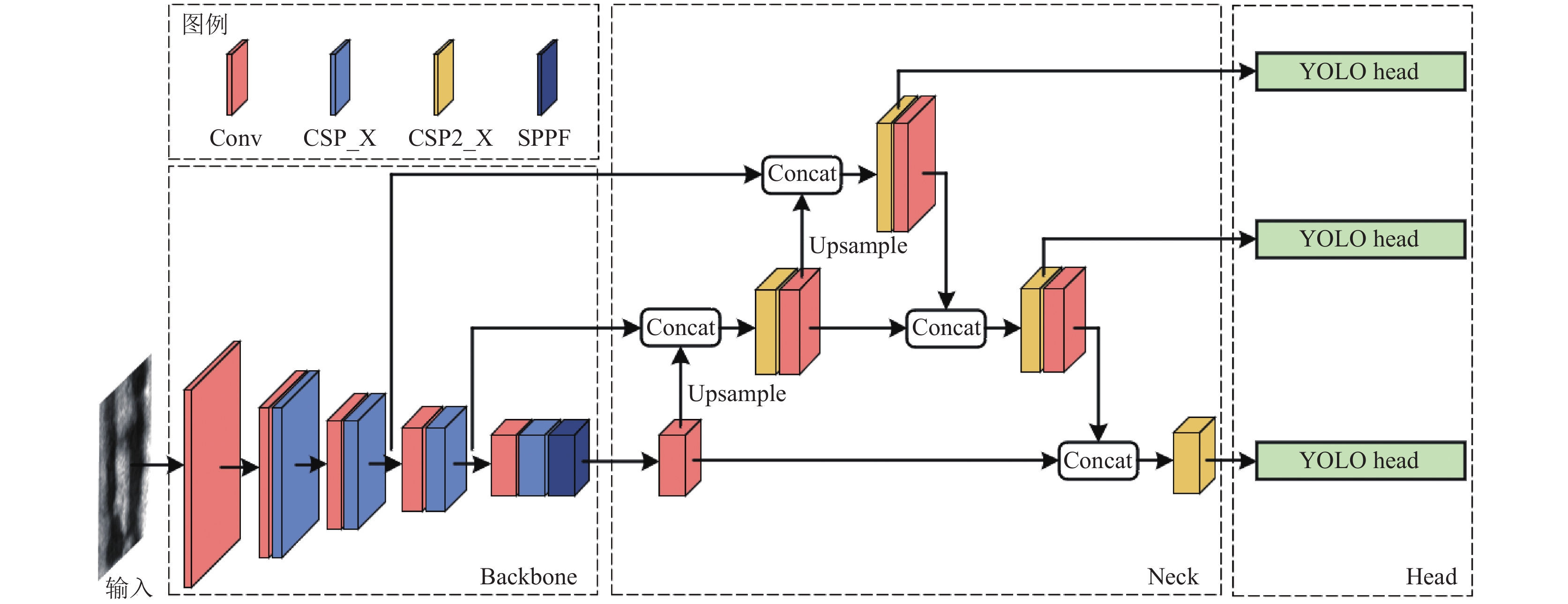
1 YOLOv5模型结构

如图1所示, YOLOv5模型可分为主干网络Backbone、特征融合网络Neck和检测网络Head这3部分. 其中, Backbone采用CSPDarknet53提取特征, 利用CSP结构可以有效减少网络参数和计算量, 提高特征提取效率; 空间金字塔池化结构SPPF则可以将不同尺度的特征图固定在一个尺度进行特征融合. Neck采用路径聚合网络PANet (path aggregation network, PANet)^[10]将不同层次的特征图通过自顶向下和自底向上的方式融合, 以获得更丰富的特征信息. 最后, 通过Head输出3种不同尺度的特征图, 并在特征图上预测各个目标的边界框位置、大小和类别.

2 小样本带钢表面缺陷检测模型

本文提出的FODNet模型结构如图2所示. 与YOLOv5不同, FODNet的Neck部分采用一种融合注意力机制的多尺度路径聚合网络, Head部分采用一种自适应解耦检测结构Coord-DH. 首先, 主干网络对输入图像进行特征提取, 得到20×20、40×40、80×80这3种不同尺度大小的特征图, 再一并传入特征融合部分. 特征融合结构将主干网络提取到的深层特征通过CARAFE模块进行上采样, 减少细节特征丢失; 接着与浅层特征拼接, 实现多尺度特征融合; 再将得到的特征图通过C3SA模块进行全局特征提取, 获得更加丰富的特征信息. 最后, 检测器预测大、中、小型目标, 并通过损失函数计算得到检测结果.

2.1 融合注意力机制的多尺度路径聚合网络

由于带钢表面缺陷与背景对比度低, 且缺陷尺寸大小不一, 因此对缺陷进行有效提取是关键. 为满足需求, 本文在PANet多尺度特征表达结构基础上, 融入Shuffle Attention双路注意力机制和内容感知特征重组的上采样方式 (content-aware reassembly of features, CARAFE)以增强网络的特征提取能力, 从而让模型能够更好地区分缺陷和背景, 进一步提升对不同尺度目标的识别能力.

2.1.1 融合Shuffle Attention双路注意力机制

注意力机制作用于特征图的不同通道和空间位置来抑制不太显著的特征, 帮助网络在样本数据稀缺的情况下更高效地找到应该关注的重点. 为减少算力消耗, 本文引入轻量且高效的Shuffle Attention机制^[11]. 该双路注意力机制可充分利用空间和通道注意力的关系, 使模型损失值更快收敛.

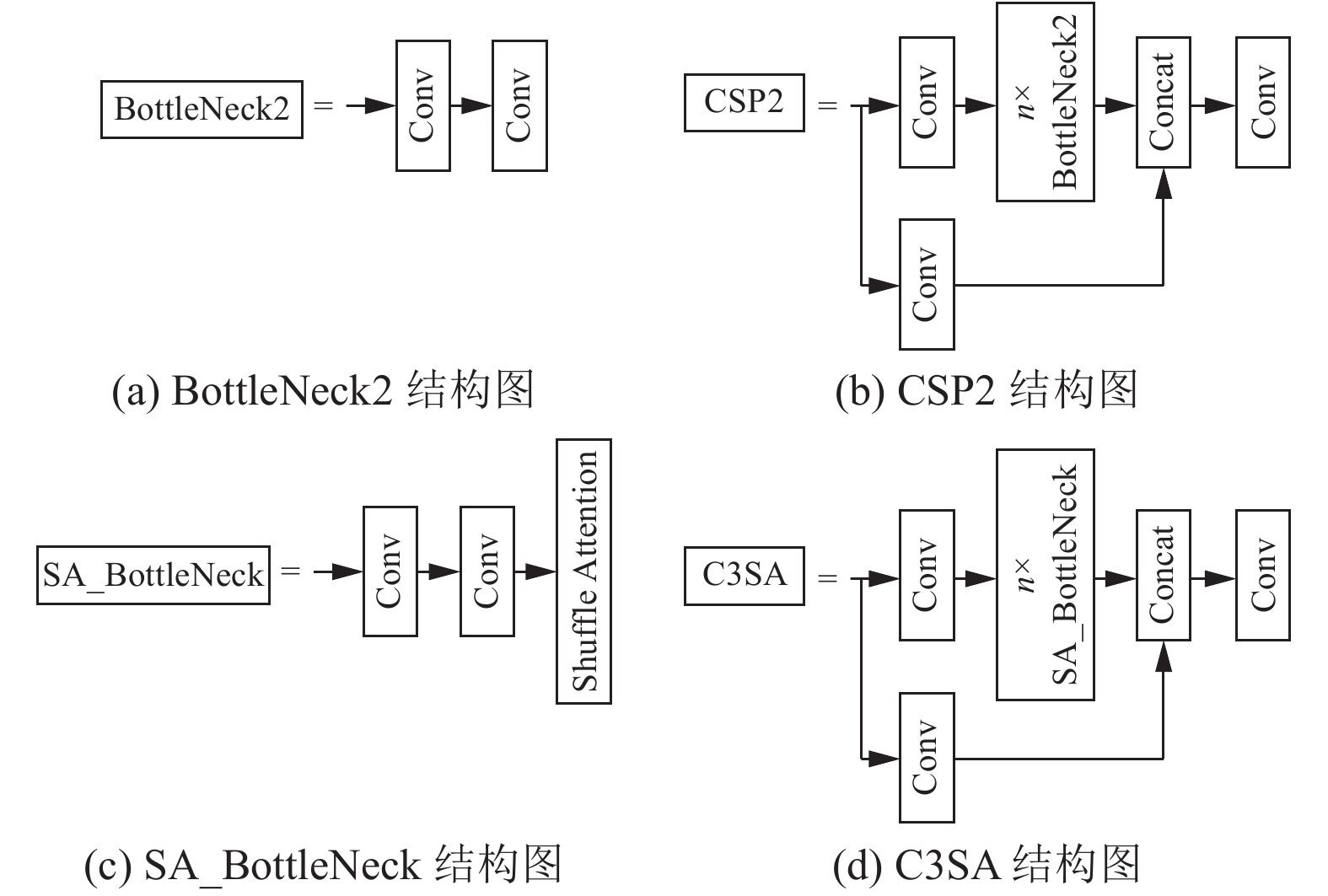
图3中, 本文先将Shuffle Attention与BottleNeck2模块结合为SA_BottleNeck模块, 再整合到CSP2模块中形成C3SA模块, 应用于每个检测器的输入之前. 经过特征融合操作的特征图在传入检测器前, 都会经过C3SA模块进行全局特征提取. 作为C3SA主要的梯度流分支, 融入注意力机制的SA_BottleNeck模块在减少计算量的同时可以获得比原先更加丰富的梯度流信息, 既保证特征图中各尺度特征信息的丰富性, 也抑制冗余信息对检测器的干扰.

如图4所示, Shuffle Attention先将特征图F沿其通道维度划分为g个组, 即F=[F₁, …, F_g], F_k$\in $R^c/g×h×w. 随后F_k沿通道维度被分成F_k1和F_k2, 分别传入通道注意力分支和空间注意力分支. 如式(1), 在通道注意力分支中, F_k1经过全局平均池化操作得到通道统计量s. 接着按照式(2), 将s经过权重卷积和Sigmoid函数操作得到通道注意力权重矩阵, 再与F_k1相乘得到$F{'_{k1}} $. 其中W₁和b₁是通道注意力中的权重矩阵和权重向量.

$ s = {F_{gp}}({F_{k{\text{1}}}}) = \frac{1}{{h \times w}}\sum\nolimits_{i = 1}^h {\sum\nolimits_{j = 1}^w {{F_{k{\text{1}}}}} } (i, j) $

(1)

$ F{'_{k1}} = \sigma ({F_c}(s)) \cdot {F_{k1}} = \sigma ({W_1}s + {b_1}) \cdot {F_{k1}} $

(2)

在空间注意力分支中, 通过对F_k2使用GroupNorm(GN)^[12]获取空间维度信息, 再经过式(3)对不同空间位置进行加权得到特征$F{'_{k2}} $.

$ F{'_{k2}} = \sigma ({W_2} \cdot GN({F_{k2}}) + {b_2}) \cdot {F_{k2}} $

(3)

两个分支结果按通道拼接后, 特征聚合成F′, 再通过通道随机混合实现跨组信息交流.

2.1.2 CARAFE模块

为解决YOLOv5中最邻近插值上采样方式易出现棋盘现象, 丢失部分图像信息的问题^[13], 本文引入CARAFE模块^[14]. 该模块能在更大的感知域中聚合上下文信息, 并在不同位置使用自适应和优化的重组内核, 得到更细腻的高分辨率特征图, 以减少细节特征丢失对多尺度特征融合过程的影响.

CARAFE包含内核预测模块和特征重组模块, 两个模块的处理过程分别如式(4)和式(5)所示. 内核预测模块利用一个k_encoder×k_encoder大小的卷积核在输入特征图X的每个位置l都预测一个上采样核W_l′, 即N(X_l, k_encoder)操作. 然后特征重组模块将输出特征图X′中的每个位置l′都映射回特征图X, 假设上采样核的尺寸为k_up×k_up, 则从X中取出以位置l为中心的k_up×k_up的区域, 即N(X_l, k_up)操作, 再与该点预测出的上采样核W_l′做点积, 即Φ(N(X_l, k_up), W_l′)操作, 最后得到输出X′.

$ {W_{l'}} = \Psi (N({X_l}, {k_{{\mathrm{encoder}}}})) $

(4)

$ X{'_{l'}} = \Phi (N({X_l}, {k_{{\mathrm{up}}}}), {{{W}}_{l'}}) $

(5)

其中, Ψ为内核预测模块, Φ为特征重组模块. l为原目标位置, l′为上采样后的目标位置. N(X_l, k)表示以位置l为中心的X的k×k子区域.

2.2 自适应解耦检测结构Coord-DH

特征融合后的特征图包含更丰富的细节特征和语义特征, 检测头基于这些特征信息进行目标分类和定位. 分类任务依据语义特征学习平移不变性, 定位任务依据细节特征学习平移可变性, 即分类任务希望目标的分类结果不受其所在位置的影响, 而定位任务希望检测网络对目标的位置信息有良好的感知能力, 两个任务相互冲突, 而注释样本稀缺加剧了这一点^[15]. 因此, 本文提出自适应解耦检测结构Coord-DH对目标进行预测. 不同于耦合检测结构将多种信息融合在一个特征图上, 本文的检测结构将分类和定位任务解耦为两个单独的分支, 并自适应地学习两个分支不同的任务需求, 缓解两个任务的矛盾, 提高检测精度.

如图5所示, 输入特征图首先经过1×1卷积进行降维, 而后分为两路分支. 分类分支经过坐标卷积保持平移不变性, 再经过1×1卷积进行分类操作; 回归分支经过坐标卷积学习平移可变性, 再分解成两个平行分支分别进行定位和置信度检测.

在坐标卷积的作用下, 自适应解耦结构可根据任务的不同, 学习不同程度的平移不变性和平移可变性. 如图6所示, 传统卷积因具备平移不变性, 适用于分类任务; 但在处理定位任务时, 传统卷积因无法感知位置信息而表现不佳. 坐标卷积在特征图F后新增原始输入的x和y坐标通道, 使得卷积过程可以感知特征图的空间信息. 因此, 当坐标卷积的坐标通道未学习到任何信息时, 其等同于传统卷积, 具备平移不变性; 当坐标卷积学习到一定信息, 就具备一定的平移可变性, 从而实现解耦检测结构中不同分支自适应地学习不同任务的目的.

2.3 边界框回归损失函数WD-IoU

表1是本文实验使用的NEU-DET数据集^[16]的目标面积大小统计表. 由表1可知, 缺陷面积占比≤5%的目标缺陷数约占缺陷总数的24.2%, 缺陷面积占比≤10%的约占缺陷总数的44.8%, 可见钢材数据中表面小缺陷、中小缺陷的比重不可忽视.

在YOLOv5中, 损失函数CIoU采用交并比(IoU)计算位置边界框损失. 而Wang等人^[17]指出, IoU对小目标边界框的偏移非常敏感, 对小目标不友好. 因此本文针对不同尺寸大小的目标, 提出一种更公平地计算目标边界框偏移的损失函数WD-IoU, 以提高回归精度. WD-IoU由3部分构成.

(1)将实际标签边框和预测框建模为二维高斯分布, 并利用归一化的高斯Wasserstein距离公式计算两个分布间的距离, 以度量它们的相似性^[17]. 由于小目标的前景多集中在边界框中心, 背景多分布于边界框边缘, 因此采用二维高斯分布表示目标边界框, 使得分布权重从中心向边缘逐渐减小, 更符合小目标特性. 公式为:

$ \begin{gathered} W_2^2({N_{{\mathrm{gt}}}}, {N_{{\mathrm{pred}}}}) = \\ \left. {\left\| {\left({{\left[c{x_{{\mathrm{gt}}}}, c{y_{{\mathrm{gt}}}}, \frac{{{w_{{\mathrm{gt}}}}}}{2}, \frac{{{h_{{\mathrm{gt}}}}}}{2}\right]}^{\mathrm{T}}}, {{\left[c{x_{{\mathrm{pred}}}}, c{y_{{\mathrm{pred}}}}, \frac{{{w_{{\mathrm{pred}}}}}}{2} \cdot \frac{{{h_{{\mathrm{pred}}}}}}{2}\right]}^{\mathrm{T}}}\right)} \right.} \right\|_2^2 \\ \end{gathered} $

(6)

并利用指数将Wasserstein距离归一化到(0, 1), 得到式(7):

$ {\textit{NWD}}({N_{{\mathrm{gt}}}}, {N_{{\mathrm{pred}}}}) = \exp \left( - \frac{{\sqrt {W_2^2({N_{{\mathrm{gt}}}}, {N_{{\mathrm{pred}}}})} }}{C}\right) $

(7)

其中, (cx_gt, cy_gt)是实际标签边框的中心点坐标, w_gt和h_gt分别表示其宽和高; (cx_pred, cy_pred)是预测边界框的中心点坐标, w_pred和h_pred分别表示其宽和高. C为常数, 由数据集中目标的平均绝对尺寸决定.

(2)实际标签边框与预测框之间的长宽比差异. 良好的边界框回归损失应考虑预测框与实际标签框的重叠面积、中心点距离和长宽比^[18]. 上述第(1)部分中的NWD相当于同时处理重叠面积和中心点距离问题, 因此再引入EIoU^[19]中的边界框长宽比公式:

$ asp = \frac{{{\rho ^2}({w_{{\mathrm{pred}}}}, {w_{{\mathrm{gt}}}})}}{{C_w^2}} + \frac{{{\rho ^2}({h_{{\mathrm{pred}}}}, {h_{{\mathrm{gt}}}})}}{{C_h^2}} $

(8)

其中, w_gt和h_gt是实际标签边框的宽和高, C_w和C_h是预测框和实际标签边框最小外接矩形的宽和高, ρ为欧氏距离.

(3)实际标签边框与预测框的重叠面积及中心点距离. 考虑到大目标不一定服从二维高斯分布规律, 使用IoU来衡量边界框之间的贴合度更适合评估大目标边界框的偏移程度. 由表1可知, 数据集中大目标的比例较高, 因此两个边界框的重叠面积和中心点距离要素仍需考虑, 公式为:

$ Io{U_{{\mathrm{dis}}}} = IoU - \frac{{{\rho ^2}({A_{{\mathrm{pred}}}}, {A_{{\mathrm{gt}}}})}}{{{c^2}}} $

(9)

$ IoU = \frac{{\left| {{A_{{\mathrm{pred}}}} \cap {A_{{\mathrm{gt}}}}} \right|}}{{\left| {{A_{{\mathrm{pred}}}} \cup {A_{{\mathrm{gt}}}}} \right|}} $

(10)

其中, IoU为预测框与实际标签边框的交并比, A_pred是预测框面积, A_gt是实际标签边框面积, ρ为欧氏距离, c为两个边界框的最小外接矩形对角线长度.

最后, WD-IoU计算公式及WD-IoU损失计算公式如下:

$ WD{\text{-}}IoU = {\lambda _1} \cdot {\textit{NWD}}({N_{{\mathrm{gt}}}}, {N_{{\mathrm{pred}}}}) + {\lambda _2} \cdot Io{U_{{\text{dis}}}} - asp $

(11)

$ Los{s_{WD{\text{-}}IoU}} = 1 - WD{\text{-}}IoU $

(12)

其中, λ₁和λ₂是与数据集相关的比例系数, 取λ₁, λ₂$\in $[0, 1], 且限制WD-IoU的值在[0, 1]范围内. λ₁与λ₂的具体设置将在第3.3节中进一步说明.

3 实验设计与结果分析

为验证本文方法的有效性, 使用东北大学提供的公开数据集NEU-DET对模型的检测性能进行评估. 实验在操作系统Ubuntu 20.04上进行, 硬件配置为AMD Ryzen 5 5600 6-Core Processor, NVIDIA GeForce RTX 3060; 环境配置为Python 3.7 + PyTorch 1.10.1 + Cuda 11.2. 模型网络参数配置如下: 输入图片尺寸为640×640, 采用SGD优化器, 动量因子为0.937, 初始学习率为0.01, 权重衰减因子为0.0005, batch-size为16.

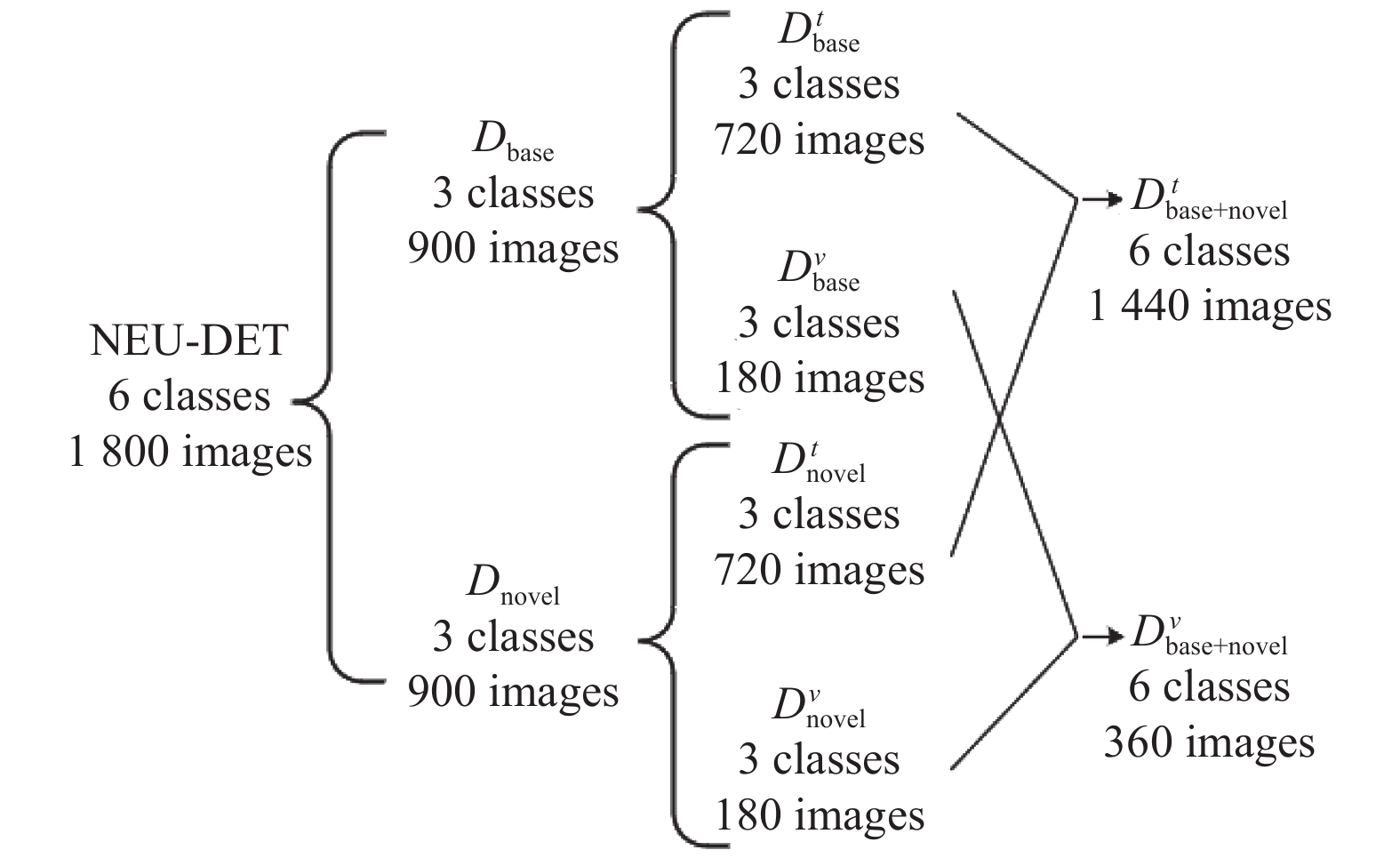
3.1 实验数据集

NEU-DET数据集包含6类典型缺陷, 如图7所示, 每类缺陷包含300张200×200分辨率的图片. 现有的小样本钢材表面缺陷检测研究^[9]将NEU-DET数据集划分为基类C_base (包含夹杂、压入氧化铁皮和划痕)和新类C_novel (包含裂纹、斑块和麻点). 基类数据集D_base包括训练集${{D}}_{{\text{base}}}^{{t}}$720张和验证集${{D}}_{{\text{base}}}^{{v}}$180张, 用于模型预训练和验证; 新类数据集D_novel包括训练集${{D}}_{{\text{novel}}}^{{t}}$720张和验证集${{D}}_{{\text{novel}}}^{{v}}$180张, 微调阶段从${{D}}_{{\text{novel}}}^{{t}}$中随机抽取每种类别k张图像进行训练, 并在$ D_{{\text{novel}}}^{v}$上进行验证.

与上述方法不同, 本文在获取预训练模型后, 使用${{D}}_{{\text{base+novel}}}^{{t}}$进行微调, 即从${{D}}_{{\text{base}}}^{{t}}$和${{D}}_{{\text{novel}}}^{{t}}$中随机采样每种类别k个样本, 并在${{D}}_{{\text{base}} + {\text{novel}}}^{{v}}$上进行验证, 其中k值可取5, 10, 30. 图8是本文的小样本带钢表面缺陷数据集构建方式.

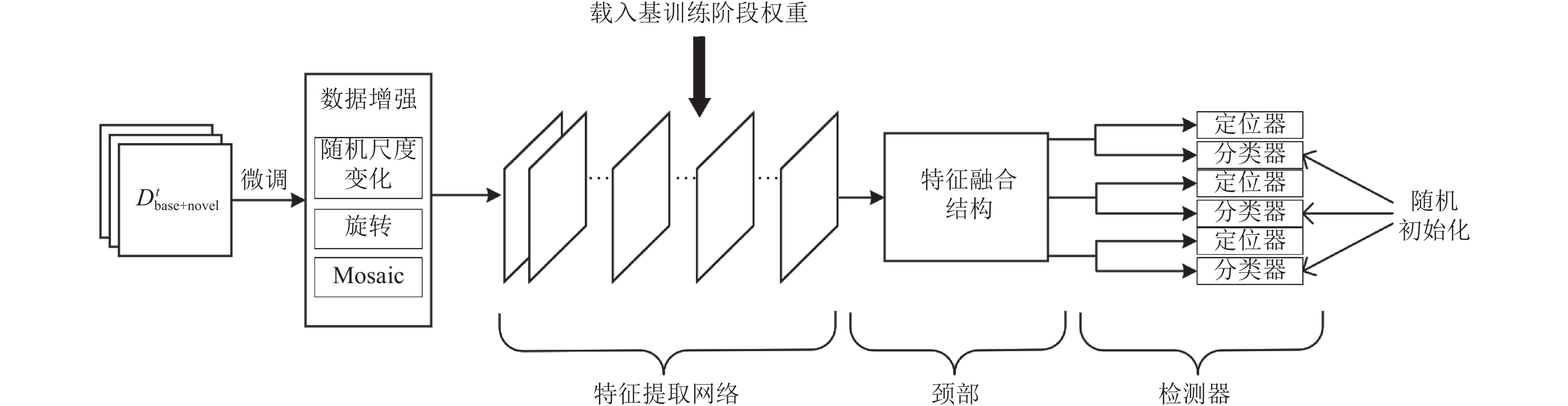
模型训练流程为: (1)基训练阶段采用${{D}}_{{\text{base}}}^{{t}}$进行训练, ${{D}}_{{\text{base}}}^{{v}}$进行验证, 获取预训练模型; (2)随机初始化检测器中的分类器的类别个数为微调阶段的类别个数; (3)冻结预训练模型的主干网络, 并在${{D}}_{{\text{base+novel}}}^{{t}}$上进行微调, 在${{D}}_{{\text{base}} + {\text{novel}}}^{{v}}$上进行验证. 为增强模型的泛化能力, 在基训练阶段和微调阶段每次训练迭代过程中, 输入图片有80%的概率进行随机尺度变化, 以增强模型的尺度不变性; 有50%的概率进行旋转, 以增强模型的旋转不变性; 有100%的概率进行Mosaic数据增强, 以丰富训练数据. 图9是模型微调阶段训练流程图.

3.2 对比实验

为评估本文模型的检测性能, 使用YOLOv5s模型框架作为基线, 记作YOLO+ft; 此外, 还将本文模型分别与自然场景下的小样本研究典型TFA^[6]和工业场景下的小样本研究典型Faster R-CNN (IFDD)^[9]进行比较, 在NEU-DET小样本数据集上进行实验. 其中, *表示模型在微调阶段每种类别随机采样k张图片而非k个样本, 且仅在新类样本上进行训练, 而非使用同等数量的基类和新类样本一起训练^[9], 其他训练设定与本文相同. 实验结果见表2.

从表2可以看出, 无论是采用*训练方式还是非*训练方式, 本文模型在各种条件下(5-shot, 10-shot, 30-shot)都表现出最佳检测性能. 具体而言, 在*训练方式下, 相比基线YOLO+ft*, FODNet*的mAP在3种shot情况下分别增长了6.7%、3.1%和4.7%; 与Faster R-CNN (IFDD)*相比, FODNet*的mAP分别提升了9.66%、5.96%和5.21%; 与TFA*相比, FODNet*的mAP分别提升了25.2%、24.9%和28.4%. 类似地, 在非*训练方式下, 相比YOLO+ft, FODNet的mAP分别提升了6.9%、5.5%和4.5%; 相比TFA, FODNet的mAP分别提升了24.1%、25.0%和25.6%. 实验结果充分证明了FODNet在工业环境下的卓越检测性能. 不过, TFA和TFA*的mAP远低于其他模型, 这说明通用型小样本目标检测模型在处理尺度多变、形态各异的缺陷检测任务时并不适用, 不能直接应用于工业场景中.

此外, FODNet从5-shot到30-shot的mAP增长速度(从60.8%到71.0%)明显快于FODNet* (从62.3%到69.5%), 这种情况也表现在YOLO+ft和TFA上. 这表明本文采用的模型训练方式更适用于小样本模型, 更有助于提升模型的检测性能.

图10展示了在本文数据集划分条件下, YOLO+ft、TFA和FODNet对NEU-DET新类的测试结果. 图中FODNet表现最佳, 而其他算法的检测效果相对不理想. YOLO+ft将裂纹(Cr)样本的上半部分的缺陷识别为多个缺陷, 而改进后的FODNet成功识别为一个缺陷, 显示了FODNet全局信息提取能力的优势. 同时, YOLO+ft将与麻点(Ps)缺陷相似的伪缺陷误识别为真实缺陷, 而FODNet未受伪缺陷干扰, 准确识别出真实缺陷位置. 此外, TFA在斑块(Pa)样本检测中遗漏部分缺陷, 在裂纹(Cr)和麻点(Ps)样本检测中未能发现任何缺陷, 这在工业应用中是不允许发生的. 因此, FODNet拥有更稳定的检测性能, 更适用于工业场景下的带钢表面缺陷检测任务.

3.3 边界框回归损失函数实验分析

λ₁和λ₂是与训练样本的尺寸分布比例相关的系数. 当样本中小目标占比较多时, 就增大λ₁与λ₂的比值以提高高斯Wasserstein距离公式的使用概率; 反之则减小λ₁与λ₂的比值以提高边界框交并比的使用概率. 考虑到微调阶段需要多次随机采样样本进行训练, 即需要设定多组λ₁和λ₂, 因此设置λ₁+λ₂=1来简化取值情况的讨论. 设n为缺陷面积与图像总面积的比值, 缺陷总目标数为N, 面积占比小于n的目标数量为N_s, 取λ₁/λ₂=N_s/(N–N_s), 记损失值为WD-IoU_n. 表3在新类设置5-shot条件下对比了CIoU、NWD以及本文提出的WD-IoU这3种边界框回归损失函数对模型检测性能的影响. 其中, 根据表1对NEU-DET数据集的样本数量统计, 进一步对WD-IoU_n (n=0.05, 0.1, 0.2)分为3种情况讨论.

由表3可知, 相较于原算法的CIoU损失函数, 采用NWD损失函数可在AP₅₀上提升1.2%, 且对小型和中型目标有更好的检测性能, 在AP_S和AP_M上分别提升3.6%和0.8%; 而CIoU损失函数对大目标有更好的检测效果, 其AP_L值比NWD损失函数高出1.1%.

此外, 根据表3数据, 采用WD-IoU_0.1损失函数得到的检测效果最优, 即选取λ₁与λ₂的比值为面积占比≤10%的目标数量与剩余目标数量之比, AP₅₀达到56.2%, 相比原算法提升了2.3%; 同时, 小型和大型目标的检测精度也达到最佳水平, AP_S和AP_L分别为15.9%和36.4%; 并且WD-IoU_0.1损失函数得到的AP_S和AP_L之间的差距也最小, 为20.5%. 实验结果表明, WD-IoU损失函数能够精准回归目标边界框, 提升模型对不同尺寸大小的目标的检测性能.

3.4 消融实验

为评估本文改进的部分对模型性能的影响, 针对新类样本的不同shot条件进行消融实验. non-SA & CARAFE表示模型采用YOLOv5的PANet结构进行特征融合, 而不使用本文提出的特征融合结构, 其他设置与FODNet一致; non-DH表示采用YOLOv5的检测头进行检测, 而不使用Coord-DH检测结构, 其他设置与FODNet一致; non-WD表示模型采用YOLOv5默认的边界框回归损失函数进行损失计算, 而不使用WD-IoU损失函数, 其他设置与FODNet一致. 消融实验结果如表4所示.

从表4结果可以看出, 如果在特征融合结构中不使用C3SA和CARAFE模块, 模型在5-shot、10-shot和30-shot条件下的检测精度将分别下降3.2%、2.1%和2.3%, 这表明上述两个模块对于增强网络的特征提取能力有重要作用, 能够有效地学习关键特征. 如果在检测结构中不使用Coord-DH, 模型在3种shot条件下的检测精度将分别下降2.4%、3.3%和4.5%, 这表明Coord-DH检测结构可以有效缓解分类任务与定位任务之间的矛盾, 有助于提升模型的检测性能. 此外, 若模型不采用WD-IoU损失函数进行预测框回归优化, 模型的检测精度在3种shot条件下会分别下降0.4%、0.6%和0.7%, 可见WD-IoU的使用对模型识别小目标也有一定帮助.

4 结论与展望

为应对工业场景中缺乏足够缺陷样本的挑战, 本文提出一种适用于小样本条件下的带钢表面缺陷检测模型FODNet. 具体地, 通过设计融合注意力机制的多尺度路径聚合网络, 使模型专注于缺陷特征, 增强模型对缺陷目标的多尺度预测能力; 通过提出自适应解耦检测结构Coord-DH, 将模型检测部分解耦为可自适应学习对应任务的分类器和定位器, 缓解了分类和定位任务的矛盾; 通过提出融合Wasserstein距离的边界框回归损失函数WD-IoU, 提升了模型对小目标缺陷的检测精度. 在NEU-DET新类数据集上的对比实验和消融实验结果验证了FODNet的先进性和模型各个模块的有效性. 下一步将会采集工作现场的缺陷图像, 建立一个自己的缺陷数据集进行训练, 并将本文研究的小样本模型部署到工厂中进行运作.