1 引言

自20世纪人工智能迎来了飞速发展, 类脑智能研究也得到了人们广泛的关注. 脉冲神经网络(spiking neural network, SNN)^[1]作为类脑智能研究中的重点, 通过模仿高能效生物网络^[2]的神经动力学机制, 将信息以脉冲信号的形式在神经元之间通过突触进行传播计算, 体现出较好地处理时间序列数据的能力. 研究表明, 作为第3代神经网络, SNN在芯片和交叉学科等方面中取得了较好的表现, 根据脉冲神经元只有在发射脉冲时才会活跃的特性, 将SNN应用到TrueNorth^[3]和Loihi^[4]等神经形态硬件时, 可以实现节能和快速推理计算. 但这种特性也导致训练深层SNN^[5]比较困难, 因为脉冲的不可微性阻碍了反向传播.

目前, 深层SNN训练主要有两种学习算法. 一种是以转换SNN (ANN-converted SNN)^[6–8]为代表的间接监督性学习算法, 该算法可以训练较深层的脉冲神经网络并取得一系列具有竞争性的结果, 但它需要消耗大量的时间步长来保证编码分辨率^[9], 同时转换SNN不能利用时域(temporal domain, TD)信息, 这给神经形态数据集的训练带来困难. 另一种是以时空反向传播为代表的直接监督学习算法^[10–13], 这也是本文采用的算法. 直接监督学习在充分利用时空信息对网络进行训练方面具有很大的潜力, 并且可以减少对时间步长的需求. 虽然直接监督学习算法在一定程度上缓解了转换SNN算法存在的问题, 但仍存在一些不足. 基于直接监督学习的标准化直接训练(standard direct training, SDT)方法采用替代梯度(surrogate gradient, SG)^[14]来缓解SNN的不可微性^[15]. 然而, SG的梯度下降趋势与SNN中的损失范围不匹配, 易使训练结果陷入局部极小值, 导致网络泛化能力较差. 另一个不足之处是脉冲神经网络通过基于梯度的时间反向传播(backpropa-gation through time, BPTT)框架进行训练, 在这样的框架下, 梯度经过逐层的空间域和时间域进行反向传播, 会消耗大量的内存和训练时间, 降低模型的训练性能. 对于一些大规模数据集, 训练成本将显著增加.

针对上述问题, 本文提出了一种基于脉冲神经网络的时空交互图像分类方法. 利用时间有效训练(temporal efficient training, TET)算法^[16], 优化每个时刻的突触前输入, 避免了由于局部极小值产生的误差. 融合空间随时间学习(spatial learning through time, SLTT)算法^[17], 删除计算图中不重要的路径进行反向传播, 并在每个时间步长瞬时计算梯度, 无需存储其他步长信息, 进而降低训练成本. 最后添加空间注意力机制(spatial attention mechanism, SAM)^[18], 增强网络对空间维度上重要特征的捕捉能力, 扩大空间感受野, 从而实现高效率、低能耗的图像分类方法. 相关实验结果及性能对比证明了本文方法的有效性.

2 相关工作 2.1 基础架构

残差网络(ResNet)作为应用最广泛的基本块之一, 在深度网络中取得了巨大的成就, 但由于脉冲的不可微性和二进制脉冲信号的空间表达能力弱等问题, 使得ResNet存在梯度消失的情况. 因此, 本文使用休眠抑制残差网络(dormant-suppressed residual network, DS-ResNet)作为网络的基础架构, 如图1所示.

相对于传统残差网络(residual network, ResNet), DS-ResNet以依赖阈值的批归一化方法(threshold-dependent batch normalization, tdBN)和多层次发射(multi-level firing, MLF)^[19]模块代替批归一化(batch normalization, BN)^[20]和ReLU激活函数, 其中tdBN用于协调分布差并将输入分布归一化, 可以解决梯度消失或爆炸的问题, 同时调节网络整体的脉冲发射率, 并将MLF激活设置在快捷连接方式之前, 减少休眠单元的产生, 从而在非常深的SNN中实现更有效的梯度传播和更有效的离散脉冲信息映射.

2.2 层次发射单元

MLF单元包含多个具有不同水平阈值的泄漏整合发放(leaky integrate-and-fire, LIF)^[21]神经元, 其通过分配每个层级的近似导数的覆盖范围来扩展近似导数的非零区域, 从而减少休眠单元, 并且, MLF单元在激活输入时能够产生具有不同阈值的脉冲, 可以提高其表达能力, 使梯度传播在深度SNN中更有效. MLF单元结构如图2所示.

LIF神经元的正向传播^[22]过程为:

$ x_i^{t + 1, n} = \sum\limits_{j = 1}^{l(n - 1)} {w_{ij}^no_j^{t + 1, n - 1} + b_i^n} $

(1)

$ u_i^{t + 1, n} = {k_\tau } $

(2)

$ o_i^{t + 1, n} = f(u_i^{t + 1, n} - {V_{th}}) = \left\{ {\begin{array}{*{20}{c}} {1, }&{u_i^{t + 1, n} \geqslant {V_{th}}} \\ {0, }&{u_i^{t + 1, n} \lt {V_{th}}} \end{array}} \right. $

(3)

其中, $n$和$l(n - 1)$分别表示第$n$层和第$(n - 1)$层的神经元个数. $w_{ij}^n$是第$(n - 1)$层中第$j$个神经元到第$n$层中第$i$个神经元的突触权值, $T$是时间指标. $u_i^{t, n}$和$o_i^{t, n}$分别为第$n$层第$i$个神经元在$t$时刻的膜电位和输出. $b_i^n$是偏置. ${k_\tau }$是衰变因子. $f( \cdot )$是激活函数. $v$是触发阈值. 当膜电位超过放电阈值时, 神经元将发射一个尖峰, 膜电位被重置为0.

MLF单元正向传播过程可以描述为:

$ {u_i}^{t + 1, n} = {k_\tau }{u_i}^{t, n} \odot (1 - {o_i}^{t, n}) + {x_i}^{t + 1, n} $

(4)

$ {o_i}^{t + 1, n} = f({u_i}^{t + 1, n} - {V_{th}}) $

(5)

$ {\hat o_i}^{t + 1, n} = s({o_i}^{t + 1, n}) $

(6)

其中, $ {u_i}^{t, n} = (u_{i, 1}^{t, n}, u_{i, 2}^{t, n}, \cdots, u_{i, k}^{t, n}, \cdots, u_{i, K}^{t, n}) $和$ o_i^{t, n} = (o_{i, 1}^{t, n}, o_{i, 2}^{t, n}, \cdots, o_{i, k}^{t, n}, \cdots, o_{i, K}^{t, n}) $分别表示在时间$t$的第$n$层中的第$i$个MLF单元的膜电位矢量和输出矢量, $ \odot $表示Hadamard乘积. $ k $和$K $分别表示第$k $级别和级别的数目. ${V_{th}} = ({V_{th1}}, {V_{th2}}, \cdots, {V_{thk}}, \cdots, {V_{thK}})$为阈值向量. 为了便于计算突触前输入${x_i}^{t, n}$, 将脉冲编码器定义为: $s(o_i^{t, n}) = o_{i, 1}^{t, n} + o_{i, 2}^{t, n} + \cdots + o_{i, k}^{t, n}$, $\hat o_i^{t, n} = s(o_i^{t, n})$是第$n$层中的第$i$个MLF单元在时间$t$的最终输出. 然后, ${x_i}^{t, n}$可以通过式(1)来计算, 其中$o_i^{t, n}$被替换为$\hat o_i^{t, n}$.

对比式(2)–式(6)可以看出, MLF单元并没有给网络引入额外的可训练参数, 并且, 利用多尖峰的结合, MLF单元可以区分一些大值的尖锐特征和小值的非尖锐特征.

2.3 标准化直接训练

SDT用$O(t)$表示输出层的突触前输入$I(t)$, 并计算交叉熵损失. 式(7)为标准化直接训练$L_{{\mathrm{SDT}}}$的损失函数式, 其中$T$为模拟总时间, ${L_{{\mathrm{CE}}}}$为交叉熵损失, $y$为目标标号.

$ {L_{{\mathrm{SDT}}}} = {L_{{\mathrm{CE}}}}\left(\frac{1}{T}\sum\limits_{t = 1}^T O(t), y\right) $

(7)

根据链式法则, 使用$ {\textit{Softmax}}S(\cdot) $推理函数得到权值梯度:

$ \frac{{\partial {L_{{\mathrm{SDT}}}}}}{{\partial {{W}}}} = \frac{1}{T}\sum\limits_{t = 1}^T {[S({O_{{\mathrm{mean}}}}) - \hat y]\frac{{\partial O(t)}}{{\partial W}}} $

(8)

其中, $ {O_{{\mathrm{mean}}}} $表示输出${O_{(t)}}$随时间的平均值, $\hat y$表示$y$的单次编码.

在SDT的情况下, 梯度由两部分组成, 误差项$(S ({O_{{\mathrm{mean}}}}) - \hat y)$和输出的偏导数$\partial O(t)/\partial W$. 当训练过程达到局部最小值附近时, 对于所有$t = 1, \cdots, T$项$(S({O_{{\mathrm{mean}}}}) - $$\hat y) $近似为0, 忽略了$\partial O(t)/\partial W$. 对于传统的人工神经网络, 累积动量可能有助于摆脱局部极小值, 但这通常意味着泛化性较差. 然而, 当SNN使用替代梯度训练时, 考虑到梯度和损失的不匹配, 累积动量可能非常小. 激活函数是阶跃函数, 而SG受函数约束. 这种不匹配消散了局部最小值周围的动量, 并阻止了SDT搜索可能意味着更好的泛化性的更平坦的最小值.

2.4 时间反向传播

BPTT是训练循环网络的常用技术之一^[22]. BPTT通过创建循环单元的多个副本来及时“展开”神经网络, 可以将其视为具有绑定权重的(深层)前馈网络. 完成此操作后, 使用前向传播算法来评估整个输入序列上的网络适应性, 而反向传播算法可用于评估损失标准的偏导数相对于所有网络参数. 这种方法虽然计算效率高, 但在内存使用方面也相当密集.

BPTT方法可通过式(9)计算具有${{T}}$个时间步长的SNN中的权重梯度:

$ \nabla {w^l}L = \sum\limits_{t = 1}^T {\left({\frac{{\partial L}}{{\partial {u^l}[t]}}}\right)^T{s^{l - 1}}{{[t]}^T}, l = L, L - 1, \cdots, 1} $

(9)

其中, $w$是权重, $l$是层数索引, $L$是损失函数, ${u^l}[t]$是$t$个时间步长$l$层的膜电位, ${s^l}$是第$l$层的输出脉冲序列.

$ {e^l}[t] \triangleq \frac{{\partial {u^l}[t + 1]}}{{\partial {u^l}[t]}} + \frac{{\partial {u^l}[t + 1]}}{{\partial {s^l}[t]}}\frac{{\partial {s^l}[t]}}{{\partial {u^l}[t]}} $

(10)

定义${e^l}[t]$为$ {u^l}[t + 1] $对$ {u^l}[t] $的灵敏度, 然后利用式(10)可以进一步递归地计算出式(9)中的$ \partial {{L}}/\partial {u^l}[t] $. 特别地, 对于输出层:

$ \begin{split} \frac{{\partial L}}{{\partial {u^L}[t]}} =& \frac{{\partial L}}{{\partial {s^L}[t]}}\frac{{\partial {s^L}[t]}}{{\partial {u^L}[t]}} \\ & +\sum\limits_{t' = t + 1}^T {\frac{{\partial L}}{{\partial {s^L}[t']}}} \frac{{\partial {s^L}[t']}}{{\partial {u^L}[t'']}}\prod\limits_{t'' = 1}^{t' - t} {{ \in ^L}[t' - t'']} \end{split} $

(11)

对于中间层$l = L - 1, \cdots, 1$有:

$ \begin{aligned} \frac{\partial L}{\partial u^L[t]}= & \frac{\partial L}{\partial u^{l+1}[t]} \frac{\partial u^{l+1}[t]}{\partial s^l[t]} \frac{\partial s^l[t]}{\partial u^L[t]} \\ & +\sum_{t^{\prime}=t+1}^T \frac{\partial L}{\partial u^{l+1}\left[t^{\prime}\right]} \frac{\partial u^{l+1}\left[t^{\prime}\right]}{\partial s^l\left[t^{\prime}\right]} \frac{\partial s^l\left[t^{\prime}\right]}{\partial u^l\left[t^{\prime}\right]} \prod_{t^{\prime \prime}=1}^{t^{\prime}-t} \in^l\left[t^{\prime}-t^{\prime \prime}\right] \end{aligned} $

(12)

其中, BPTT方法中计算的膜电位导数可以分解为空间分量和时间分量, 而空间分量在计算的导数中占主导地位.

3 基于脉冲神经网络的时空交互图像分类方法 3.1 分类方法的网络结构

基于脉冲神经网络的时空交互图像分类方法的网络结构主要是由主干网络、两个SAM模块和TET这3个主要部分组成. 主干网络DS-ResNet包括3×3 Conv-tdBN层、MLF层和全连接层(fully connected layer, FC). 具体结构设计如图3所示.

3.2 时间有效训练

为了弥补替代梯度的直接训练方法导致SNN泛化性差的现象, 引入时间有效训练(temporal efficient training, TET)算法来弥补梯度下降过程中的动能损失, 使训练过程收敛到更平坦的最小值, 具有更好的泛化性. 同时, TET提高了SNN的时间可扩展性, 并诱导了一个时间可继承的加速训练.

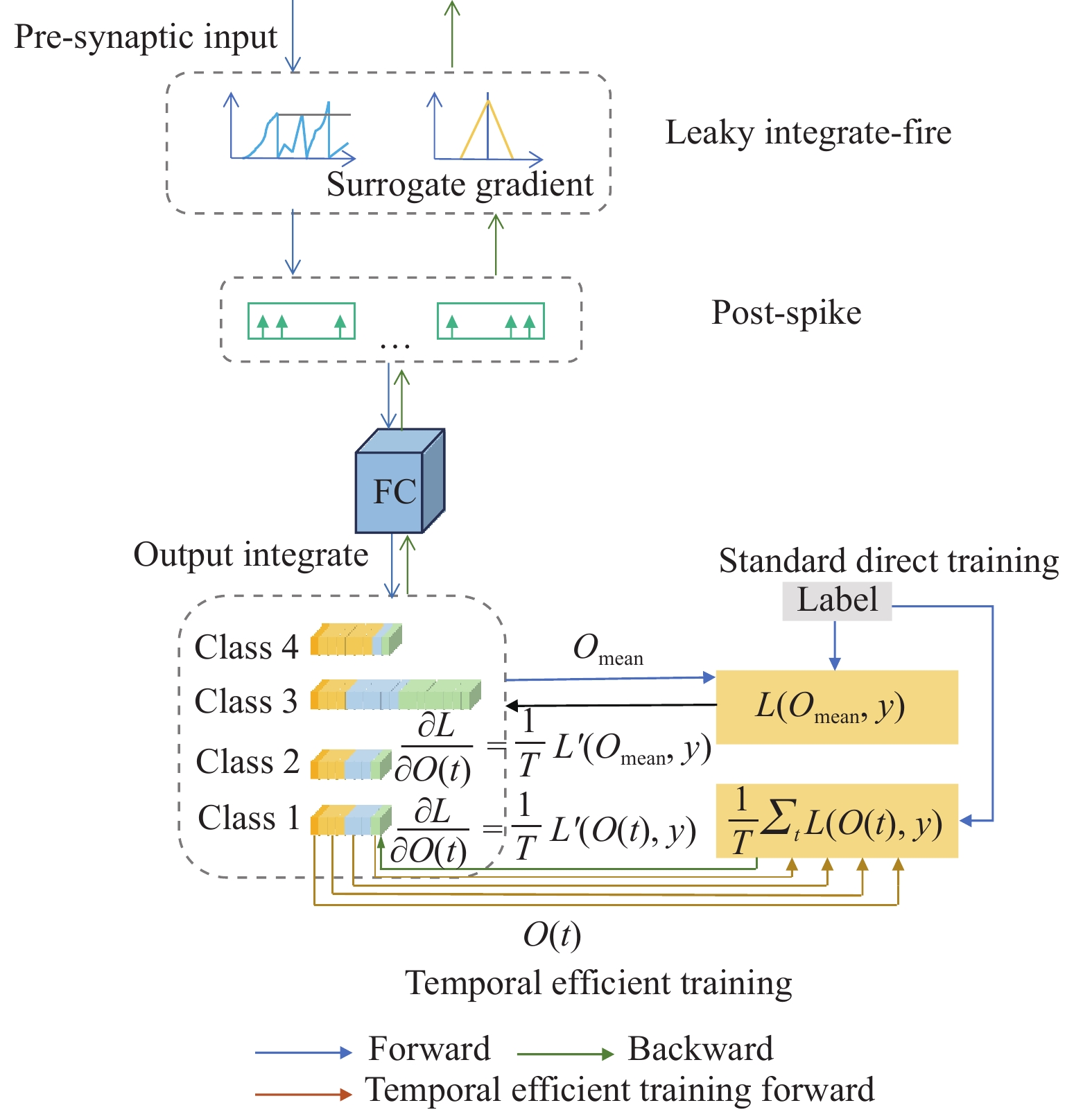
为了得到更广义的SNN, 修改优化目标调整每个矩的输出分布. TET的工作流如图4所示. 它约束每个时刻的输出(突触前输入)接近目标分布. 其损失函数${L_{{\mathrm{TET}}}}$可描述为:

$ {L_{{\mathrm{TET}}}} = \frac{1}{T}\sum\limits_{t = 1}^T {{L_{{\mathrm{CE}}}}[O(t), y]} $

(13)

重新计算损失函数${L_{{\mathrm{TET}}}}$下的权值梯度, 得到:

$ \frac{{\partial {L_{{\mathrm{TET}}}}}}{{\partial W}} = \frac{1}{T}\sum\limits_{t = 1}^T {[S(O(t)) - \hat y]\frac{{\partial O(t)}}{{\partial {{W}}}}} $

(14)

在TET的情况下, 通过重新加权$\partial O(t)/\partial W$的贡献, 可以缓解SDT中梯度和损失不匹配的问题. 由于训练集的早期输出精度不可能达到100%, 第1项$S(O(t) - \hat y)$不可能在SNN的每个时刻都为0. 因此, TET需要第2项$\partial O(t)/\partial W$趋近于0才能使${L_{{\mathrm{TET}}}}$收敛. 该机制增加了局部极小值附近的梯度范数, 并驱动TET寻找权值干扰不会引起$O(t)$巨大变化的平坦局部极小值.

3.3 空间随时间学习算法

为了减少训练时间和内存成本, 在原有的用替代梯度进行时间反向传播基础上, 引入空间随时间学习SLTT算法, 替换BPTT, 构成了一种基于SG的SLTT框架结构.

SLTT删除了BPTT原本计算图中不重要的路径, 仅利用空间分量来进行更有效的反向传播, 减少标量乘法运算的次数, 进而减少训练时间. SLTT还通过在每个时间步长即时计算梯度来实现在线训练, 无需存储其他时间步长的信息, 内存占用与总时间步长无关, 避免了BPTT的显著训练内存成本. 相应权重梯度的公式定义为:

$ \nabla {w^l}L = \sum\limits_{t = 1}^T {{e^l}w[t]} ,\; {e^l}w[t] = e_u^l{[t]^T}{s^{l - 1}}{[t]^T} $

(15)

其中, 行向量$e_u^l[t]$公式为:

$ e_u^l[t] = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{\partial L}}{{\partial {s^L}[t]}}\dfrac{{\partial {s^L}[t]}}{{\partial {u^L}[t]}}, }&{l = L} \\ {e_u^{l + 1}[t]\dfrac{{\partial {u^{l + 1}}[t]}}{{\partial {s^l}[t]}}\dfrac{{\partial {s^l}[t]}}{{\partial {u^l}[t]}}, }&{l \lt L} \end{array}} \right. $

(16)

与式(9)、式(11)相比, 式(15)中所需的标量乘法次数由$\Omega (T2)$减少至$\Omega (T)$, 时间复杂度明显降低, 根据式(15), 在没有来自其他时间步长的信息的情况下, 模型可以独立地计算每个时间步长的误差信号${e^l}{w^{[t]}}$和$e_u^l[t]$. 因此, 如果可以在时间步长$t$瞬时计算出$\partial L/\partial {s^L}[t]$, 则也可以在时间步$t$瞬时计算${e^l}{w^{[t]}}$和$e_u^l[t]$. 那么就没有必要存储整个时间范围的中间状态. 为了实现$\partial L/\partial {s^L}[t]$的瞬时计算, 可以采用损失函数:

$ L = \frac{1}{T}\sum\limits_{t = 1}^T {\ell (o(t), y)} $

(17)

其中, $y$是标签, $\ell $可以是交叉熵函数, 网络的最终输出是$o[t]=W^o s^L[t]$, $W^o$是分类器的参数.

综上所述, 时间步长$t$处的所有中间项, 如$ e_u^l[t] $、$s^l[t] $、$\partial u^{l+1}[t] / \partial s^l[t] $、$ \partial s^l[t] / \partial u^l[t] $从未在其他时间步长中使用, 因此SLTT所需的内存开销与时间步长$ t $的总数无关. 而BPTT具有与存储所有时间步长的所有中间状态相关联的存储器成本. 所以, SLTT相较于BPTT的内存开销较小, 运行速率明显提升.

3.4 空间注意力机制

为了减少信息弥散和增强网络的空间跨维度交互能力, 加强网络在空间维度上对重要特征的捕捉能力, 本文引入了空间注意力模块, 可以利用特征的空间关系生成空间注意力图来获取数据中更重要的信息, 中间特征图通过空间注意力机制(spatial attention mechanism, SAM)^[23]在深度网络的每个卷积块上自适应地细化, 其结构如图5所示.

为了获取空间信息, 使用平均池化和最大池化两次操作对特征图的通道信息进行聚合, 生成两个2D 特征图: $ {F}_{\text {avg }}^s \in R^{1 \times H \times W} $和${F}_{\max }^s \in R^{1 \times H \times W} $分别表示跨通道的平均池化特征和最大池化特征. 然后将它们通过标准卷积层进行连接和卷积, 生成二维空间的注意力图. 具体的计算过程为式(18):

$ \begin{split} {M_s}(F) &= \sigma ({f^{7 \times 7}}([AvgPool({{F}});MaxPool(F)])) \\ & = \sigma ({f^{7 \times 7}}([F_{{\mathrm{avg}}}^s;F_{\max }^s])) \end{split} $

(18)

其中, $ \sigma $表示$ \text { Sigmoid } $函数, $ f^{7 \times 7} $表示滤波器大小为7×7的卷积运算.

4 实验结果与分析 4.1 实验环境

实验环境为Linux操作系统, CPU为AMD EPYC 7642, 显卡为 NVIDIA GeForce RTX 3090, 显存为24 GB, 采用PyTorch 1.13.1和CUDA 11.7环境运行代码. 在CIFAR10、DVS Gesture、CIFAR10-DVS这3个数据集设置训练初始学习率为0.1, batchsize分别为64、16、32, 采用SGD优化器进行优化, 3级阈值$V_{th} $为0.6、1.6、2.6, 权重衰减分别为0.000 1、0.000 1、0.001^[19].

4.2 实验数据集 4.2.1 CIFAR10数据集

CIFAR10数据集^[24]是一个广泛用于识别通用物体的彩色图像数据集. 它包含5万张训练图像和1万张测试图像, 分为10个类别, 大小为32×32. 对于CIFAR10的数据预处理, 遵循标准的数据增强策略. 首先对原始图像进行随机裁剪和翻转, 然后通过减去像素强度的全局平均值并除以沿每个RGB通道的全局标准方差进行归一化.

4.2.2 DVS Gesture数据集

DVS Gesture数据集^[25]是通过捕获29个受试者在3种照明条件下的不同手势而获得的神经形态视觉数据集. 它共有1324个实例, 23个类别的1176个实例作为训练集, 6个类别的288个实例作为测试集, 大小为128×128. DVS Gesture数据集的数据预处理为将原始事件流下采样到32×32, 每30 ms采样一次. 在每个时间步长中, 并且设置训练和测试时间步为40.

4.2.3 CIFAR10-DVS数据集

CIFAR10-DVS数据集^[26]是使用DVS摄像机从CIFAR10数据集转换而来的神经形态视觉数据集. 它由10个类别的10 000个实例组成, 大小为128×128, 随机选择9 000个实例用于训练, 其余的用于测试. CIFAR10-DVS数据集的数据预处理为将原始事件流下采样到42×42, 每10 ms采样一次, 并且设置训练和测试时间步为10.

4.3 评价指标

使用精确度Acc (Accuracy), 参数量Params, 整体时长Time, 内存Memory, 每轮训练时长(Time/Epoch), 作为综合评价指标, 来测评分类效果. TP (true positive)为正确分类图像的数目, FP (false positive)为错误分类图像的数目. Acc的计算公式为:

$ Acc = \frac{{TP}}{{TP + FP}} $

(19)

4.4 消融实验

为了证明本文所提出方法的有效性, 以DS-ResNet为基础网络结构, 在CIFAR10、DVS Gesture、CIFAR10-DVS上进行了评估, 以证明其在训练成本和准确性方面的优越性能. 为公平比较实验结果, 所有参数保持一致, 消融实验结果见表1.

第1组为改进前的CIFAR10数据集模型实验结果, 作为后几组实验的参考基准, 每一轮训练内存占用为9.64 GB, 训练测试时长Time/Epoch为339 s, 精度Acc为94.25%.

第2组由于将TET模块引入模型中, 缓解了梯度和损失不匹配的问题, 使得训练内存占用减少到2.58 GB, Time/Epoch减少到291 s, Acc值也提高了0.21个百分点.

第3组用SLTT算法替换传统网络中的BPTT, 删除计算图中不重要的路径, 虽然Acc值增长不明显, 但训练内存占用和Time/Epoch得到显著降低.

第4组将SAM融入到DS-ResNet模型中, 使模型能够自适应的学习不同区域的注意力权重, 更加关注重要的图像区域, 训练内存占用和Time/Epoch得到一定程度降低, Acc也提升了0.17个百分点.

第5组是本文整体改进方法实验, 与改进前的模型相比, 内存占用降低了46.68%, Time/Epoch仅为改进前的35.7%, 同时, Acc升高了0.46个百分点, 证实了各方法对于模型的有效性.

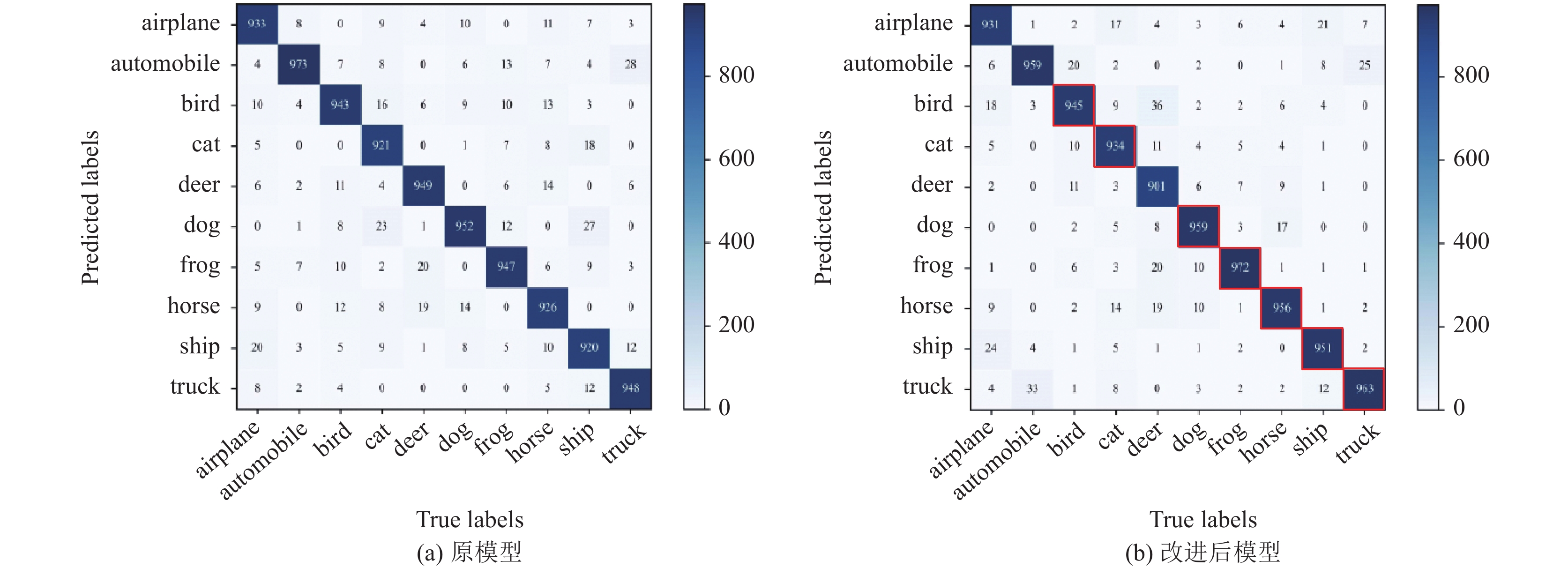
本文对比了CIFAR10数据集每轮训练时的损失, 从图6可以看出改进前后的模型在40轮前一直呈现波动状态, 改进前的模型在46轮损失下降至0.2217, 改进后的模型损失下降至0.2602, 损失差距变得明显, 之后一直保持平稳. 实验结果表明, 本文使用的方法可使网络训练损失达到更低的稳定数值; 另外从图7所示的混淆矩阵可以看出改进后的模型在CIFAR10数据集10个类别中的7个类别上的准确率相较于原模型均有提升, 进一步证明了网络精度的提高.

4.5 对比实验

表2为本文整体改进方法与改进前分别在CIFAR10、DVS Gesture、CIFAR10-DVS数据集上的实验结果对比, 改进后的方法能够在保证精度Acc的情况下, 内存和整体时长均取得明显降低, 大大减少了内存占用和时间需求. 由此可见, 方法在模型的内存消耗与时间需求上有明显优势.

为进一步验证改进后的方法性能, 分别在CIFAR10、DVS Gesture、CIFAR10-DVS数据集上与主流方法进行对比, 每个方法实验环境、训练集、测试集均相同. 从表3结果可以看出, 本文提出的改进方法在各个数据集上均达到了最佳精度, 同时, 参数量与目前最小参数量相比并无明显增加, 方法性能在精度和参数量方面均占优势.

5 结论与展望

针对SNN替代梯度方法中梯度下降趋势与SNN之间损失分布不匹配的问题, 本文融入了TET算法, 优化每个时刻的突触前输入, 弥补梯度下降过程中的动能损失; 引入SLTT算法利用空间分量来进行更有效的反向传播, 减少网络的内存消耗, 缩短训练时长; 添加SAM提升网络在空间维度上重要特征的捕捉能力. 实验结果表明, 本文使用的方法在保证精度提升的条件下, 显著降低了模型的内存消耗和训练时长. 对于CIFAR10、DVS Gesture 、CIFAR10-DVS这3个数据集的内存消耗分别降低了46.68%、48.52%、10.46%, 训练速度分别提升了2.80倍、1.31倍、2.76倍, 为使用SNN实现高效率、低能耗的分类训练提供了可能. 在后续研究中, 将重点关注影响反向传播的因素, 进一步完善时空交互图像分类模型, 提升SNN图像分类的判断能力, 为将来在复杂环境下部署低功耗设备打下坚实基础.